Gazdasági elemzés /Gyakorlati jegyzet/

(1)

Gazdasági elemzés

/Gyakorlati jegyzet/

(2)

2

Gazdasági elemzés

/Gyakorlati jegyzet/

Szerzők:

Takács István

Károly Róbert Főiskola, Üzleti Tudományok Intézete (1-3. fejezet) Baranyai Zsolt

Szent István Egyetem, Gazdaság- és Társadalomtudományi Kar (4-6. fejezet) Fenyves Veronika

Debreceni Egyetem Gazdálkodástudományi és Vidékfejlesztési Kar (7-9. fejezet) Tarnóczi Tibor

Debreceni Egyetem Gazdálkodástudományi és Vidékfejlesztési Kar (10-13. fejezet) Szerkesztő:

Fenyves Veronika Tarnóczi Tibor

Lektor:

Takácsné Dr. György Katalin Károly Róbert Főiskola

Debreceni Egyetem, AGTC • Debrecen, 2013

Gazdálkodástudományi és Vidékfejlesztési Kar

Pannon Egyetem Georgikon Kar

(3)

3

Kézirat lezárva: 2013. április 30.

ISBN 978- 615-5183-70-6

DEBRECENI EGYETEM AGRÁR- ÉS GAZDÁLKODÁSTUDOMÁNYOK CENTRUMA

A kiadvány a TÁMOP-4.1.2.A/1-11/1-2011-0029 projekt keretében készült.

(4)

4 Tartalomjegyzék

1. A gazdasági elemzés általános és speciális módszerei ... 5

1.1. Az átlagszámítások alkalmazása a gazdasági elemzésben ... 5

1.2. A trendszámítás egyes típusainak alkalmazása a gazdasági elemzésben ... 8

1.3. A regressziószámítás gyakorlati alkalmazása ... 14

1.4. Az eltérések számszerűsítésének módszerei ... 17

2. Termelési szerkezet, termékösszetétel elemzése ... 31

3. Az értékesítés elemzése ... 38

4. A termelés változásának elemzéséhez kapcsolódó feladatok ... 51

5. Költséggazdálkodás elemzése ... 59

6. Minőségelemzés ... 60

7. Vállalati erőforrások elemzése: Munkaerő és bérgazdálkodás ... 68

8. Vállalati erőforrások elemzése: Tárgyi eszközgazdálkodás elemzése ... 76

9. Vállalati erőforrások elemzése: Forgóeszözgazdálkodás elemzése... 86

10. Pénzügyi elemzés: Mérlegelemzés ... 94

11. Pénzügyi elemzés: Eredményelemzés ... 107

12. Pénzügyi elemzés: Jövedelmezőség elemzése ... 118

13. Pénzügyi befektetések elemzése ... 126

(5)

5

1. A gazdasági elemzés általános és speciális módszerei

1.1. Az átlagszámítások alkalmazása a gazdasági elemzésben

1. FELADAT

Ismert egy tehenészeti telep termelésére és állományára vonatkozó adatsor 2008 és 2012 között. Az információkat az 1.1. táblázat tartalmazza.

1.1. táblázat. A tehenészeti telep tejtermelésének és szarvasmarha-állományának alakulása 2008 és 2012 között

Év Adott évi tejtermelés [tonna]

Szarvasmarha-állomány (december 31-én)

[darab]

2008 8.400 1.050

2009 7.700 970

2010 8.800 1.100

2011 9.000 1.120

2012 8.500 1.050

Forrás: saját szerkesztés

Feladat: A vizsgált időszakra vonatkozóan az éves átlagos tejtermelés és szarvasmarha-állomány meghatározása.

FELADAT MEGOLDÁSA:

Az átlagos évi tejtermelés kiszámítása – mivel az adatsor statisztikai értelemben ún. tartam idősor -, egyszerű átlagszámítással történik:

8.480 5

42.400 5

8.500 9.000

8.800 7.700

8.400 n

x X

5 1 i

i



 



 



 ^ [tonna/év]

A szarvasmarha-állományra vonatkozó adatok ugyanakkor állapot-idősorok, mert az adatok minden év december 31-én meglévő állomány adatait mutatják, így az éves átlagos állomány a kronologikus átlag számításával határozható meg helyesen. Az elmondottaknak megfelelően

1.06 0 4

4.240 1

5

2 1.050 1.120

1.100 2 970

1.050

1 n

2 x x 2

x X

1 n n

2 i

i 1

k  





 

 







 [darab/év]

Minden elemzés szükséges része az eredmények szöveges értékelése!

(6)

6 Szöveges értékelés

A számítások szerint a vizsgált terminust jelentő 2008-2012 évek átlagában az éves tejtermelés 8.480 tonna, amellyel egy időben az éves átlagos szarvasmarha állomány 1.060 darab volt.

2. FELADAT

Egy mezőgazdasági vállalkozás dolgozóinak december hónapban jutalmat fizetett. A kifizetett jutalom kategóriánkénti megoszlását az 1.2. táblázat tartalmazza.

1.2. táblázat. Adattáblázat a december havi prémium megoszlásáról értékkategóriák szerint

Kiindulási adatok Segédszámítások a középértékek meghatározásához Koncentráció vizsgálata Kifizetett

jutalom (osztály)

Dolgozók

száma Osztály- közép

Összes kifizetett

jutalom Kumulált gyakoriság

Megoszlás Dolgozók Összes

jutalom

(E Ft) (fő) (E Ft) (E Ft) (fő) (%) (%)

- fi xi fixi 

 i

1 i

fi



 n

1 i

i i

f f



 n

1 i

i i

x f

*

0 – 50 5 25 125 5 5 8,8 1,5

50 – 100 12 75 900 5+12 17 21,0 10,6

100 – 150 16 125 2.000 17+16 33 28,1 23,6

150 – 200 9 175 1.575 33+9 42 15,8 18,6

200 – 250 9 225 2.025 42+9 51 5,8 23,9

250 – 300 2 275 550 51+2 53 3,5 6,5

300 – 350 4 325 1.300 53+4 57 7,0 15,3

Összesen 57 - 8.475 - - 100,0 100,0

Forrás: saját szerkesztés Sándorné et al., 1998. 7-9. p. alapján

Feladat: Állapítsuk meg az egy munkavállalóra jutó kifizetett jutalom:

a) átlagát;

b) móduszát;

c) mediánját;

d) koncentrációját.

FELADAT MEGOLDÁSA:

a) Az átlagos jutalom összegének számítása (súlyozott számtani átlaggal):

(7)

7

148,7 57

8.475 f

x f

X n

1 i

i n

1 i

i i







*

[E Ft]

b) A jutalmak módusza (leggyakrabban előforduló, legáltalánosabb érték)

A módusz osztálya az, ahol az m-re igaz, hogy f_m  max  f_i  max  f_i  f₁₀₀ _₁₅₀ 16

    ¹⁶ ¹²  ¹⁶ ⁹ ^118,2

12 50 16

f 100 f

f f

f Δx f

x M

1 m m 1 m m

1 m m m

m

o 







 

 





 







 *

* [eFt]

c) A jutalmak mediánja

A jutalmak mediánja abban a jutalomosztályban lesz, ahol az m-re igaz, hogy:

150 100 m m

1 i

i n

1 i 1 i m

1 i

i 28,5 17 28,5 33 f f

2 f 57

2 f

f _



 











 





 

5

*

* 137,

16 2 17 1 int 57

50 f 100

2 f 1 f int

Δx x M

m

1 m

1

i i

n 1 i

i

m m

e 

 



 



 





 











  









[eFt]

d) A jutalmak koncentrációjának vizsgálata (lásd 1.2. táblázat utolsó két oszlopa valamint az 1.1.

ábra)

A koncentráció vizsgálata a megoszlások vizsgálatával történik, ami vizsgálható a dolgozókra (munkavállalókra), illetve az összes jutalomra vonatkoztatva. A megoszlások vizsgálata táblázatos, illetve grafikus formában egyaránt történhet. A grafikus értékelést az 1.1. ábra mutatja be.

0 5 1 0 1 5 2 0 2 5 3 0

0 – 5 0 5 0 – 1 0 0 1 0 0 – 1 5 0 1 5 0 – 2 0 0 2 0 0 – 2 5 0 2 5 0 – 3 0 0 3 0 0 – 3 5 0

D o lg o z ó k Ö s s z e s ju ta lo m

(8)

8 1.1. ábra. A dolgozók és az összes kiosztott jutalom megoszlása jutalomosztályok szerint

Szöveges értékelés

A dolgozók december havi jutalmának értékelésekor megállapítható:

1) Az átlagos jutalom nagysága 148.700 Ft volt.

2) A legtöbb munkavállaló 118.200 Ft jutalmat kapott, azaz az 1 főre jutó jutalmak e körül az érték körül tömörülnek.

3) A munkavállalók fele 137.500 Ft-nál alacsonyabb, fele pedig magasabb jutalmat kapott.

4) A munkavállalók 8,8%-a az összes jutalomnak csak 1,5%-át stb. A grafikus értékelés segít a koncentráció további vizsgálatánál.

Felhívjuk a figyelmet arra, hogy az előzőekben ismertetett számítások, illetve további, az ún. leíró statisztika fogalomkörébe tartozó indikátorok az Excel táblázatkezelő alkalmazással is könnyen kiszámíthatók. A számítások elvégezhetők beépített függvények használatával (pl.: =ÁTLAG( );

=SZÓRÁS( ), =MIN( ); =MAX( ); MÓDUSZ( ); =MEDIÁN( ) stb.), valamint az Analysis ToolPak Leíró statisztikai moduljával.

Az Analysis ToolPak csomagot először telepíteni szükséges, ennek lépései:

 Korábbi verzióknál (11.0 verzióig – 2003-ig): Eszközök → Bővítménykezelő → Analysis ToolPak („pipát tenni”) → OK!;

 Újabb verzióknál (12.0 verziótól - 2007-től) Office gomb (bal felső sarokban) → Az Excel beállításai → Bővítmények → Kezelés: Excel bővítmények → Ugrás → Analysis ToolPak („pipát tenni”) → OK!).

A telepítést követően az alkalmazás elérése:

 az elemző alkalmazások a korábbi Excel verziók esetében az Eszközök/Adatelemzés menüpontból indíthatók;

 az újabb Excel verzióknál az Adatok/Adatelemzés menüben érhetők el, ahol a kínálkozó listából a Leíró statisztika kiválasztásával tudjuk az elemzéseinket elvégezni.

1.2. A trendszámítás egyes típusainak alkalmazása a gazdasági elemzésben

3. FELADAT

Egy mezőgazdasági vállalkozás 2006-ban tevékenysége diverzifikálásaként sertéshízlalásba kezdett.

Az értékesítés alakulásáról a következő információ áll rendelkezésre (1.3. táblázat):

FELADAT MEGOLDÁSA:

Az adatsor ábrázolásával képet kapunk a változás jellegéről (1.2. ábra). A változás jellege exponenciális, illetve logisztikus görbével is közelíthető. Az utóbbi mellett a termékéletpálya általános tapasztalatokon nyugvó jellemző alakulása szól, ugyanakkor a növekedés üteme

(9)

9 változásának 2012-ben bekövetkező csillapulása még nem biztos, hogy hosszútávon érvényesülő tendencia, (már csak azért sem, mert becslésen alapul). Ezért az ismert tartományban exponenciális közelítés alkalmazása is megfelelő lehet. Ez utóbbi megközelítésmóddal kapott trend hosszú távú kivetítése azonban azt a veszélyt rejti magában, hogy olyan bővülést prognosztizál, amely – például a piaci korlátok miatt – realizálhatatlan, ezért az erre a trendre alapozott vezetői döntések (például fejlesztések elindítása) a vállalkozás gazdálkodásának megrendüléséhez vezethetnek.

Természetesen a legegyszerűbb közelítésmód (a lineáris közelítés) is adhat információt a növekedés átlagos ütemének alakulásáról.

1.3. táblázat. Az értékesítés adatai

* tervezett

Feladat: Az adatsor vizsgálata az analitikus trendszámítás módszerével.

A számítások elvégzésére készítsünk munkatáblázatot!

(i) Lineáris közelítés

1.4. táblázat. Munkatáblázat a lineáris trendfüggvény számításához

Év

Transz- formált

évek

Értéke- sítés

(t)

Részszámítások

x_i x_i’ y_i x_i’² x_i’* yi d_xi d_yi d_xi*d_yi d_xi² d_yi²

2006 -3 5 9 -15 -3 -37,43 112,29 9 1400,90

2007 -2 9 4 -18 -2 -33,43 66,86 4 1117,47

2008 -1 15 1 -15 -1 -27,43 27,43 1 752,33

2009 0 30 0 0 0 -12,43 0,00 0 154,47

2010 1 55 1 55 1 12,57 12,57 1 158,04

2011 2 83 4 166 2 40,57 81,14 4 1646,04

2012 3 100 9 300 3 57,57 172,71 9 3314,47

Összesen 0 297 28 473 0 0,00 473,00 28 8543,71

Év Értékesített mennyiség (tonna)

2006 5

2007 9

2008 15

2009 30

2010 55

2011 83

2012 100^*

1.2. ábra. Az értékesített hízósertés mennyiségének változása (2006-2012)

(10)

10

Átlag 0 42,43

Forrás: saját számítás

Megjegyzés1:

A lineáris trendfüggvény:

b ' x a

y   

A függvény paraméterei:

89 , 16 28 473 '

* '

1 2

1  







 n

i i n

i

i i

x y x

a , illetve

42,43 7

297 n

y b

n

1

i i





 ^

ahol: n = az idősor elemeinek a száma (az évek száma).

A korrelációs együttható:

n d σ

n , d σ

σ , σ n

i d d r

n

1 i

2 yi y

n

1 i

2 xi x

y x n

1 i

x yi 





 



 ^ ^ ^

*

összefüggések felhasználásával

9352 , 0 71 , 8543

* 28

473

*

2

1 2 1

2

1

*

2  





 







 n i

yi n

i xi n

i xi yi

d d

d d r

A korrelációs együttható alapján megállapítható, hogy az adatsor egyenes trendvonallal jól közelíthető. A növekedés átlagos üteme: 16,89 tonna/év.

(ii) Exponenciális közelítés (1.5 táblázat) Megjegyzés1:

n y y

d illetve x x d

n

i i i

yi i

xi









 _ln ^1

ln ln

Az exponenciális trendfüggvény:

y y d illetve x

x

d _xi  _i  _yi  _i 

(11)

11

x

ea

b

y  * ^

5261 , 0 28

730 , 14 '

ln

* '

1 2

1  







 n

i i n

i

i i

x y x

a , illetve

26,53 e

e b 3,2782

7 22,947 n

lny

lnb ^lnb ^3,2782

n

1 i

i









 ^

1.5. táblázat. Munkatáblázat a lineárisra visszavezetett trendfüggvény számításához

Év ^Transz-^formált

évek

Értéke- sítés (t)

Részszámítások

xi x_i’ y_i x_i’² lny x_i’ * ln yi d_xi d_lnyi d_xi*d_lnyi d_xi² d_lnyi² 2006 -3 5 9 1,609 -4,828 -3 -1,67 5,01 9 2,78 2007 -2 9 4 2,197 -4,394 -2 -1,08 2,16 4 1,17 2008 -1 15 1 2,708 -2,708 -1 -0,57 0,57 1 0,33 2009 0 30 0 3,401 0,000 0 0,12 0,00 0 0,02 2010 1 55 1 4,007 4,007 1 0,73 0,73 1 0,53 2011 2 83 4 4,419 8,838 2 1,14 2,28 4 1,30 2012 3 100 9 4,605 13,816 3 1,33 3,98 9 1,76

Összesen 0 297 28 22,947 14,730 0 0,00 14,73 28 7,89

Átlag 0 42,43 3,2782

Az adatsor jellegét leíró exponenciális trendfüggvény:

x x

0,5261

1,69 26,53 e

26,53

y  * ^  *

A növekedés átlagos ütemét a hatványkitevős tag alapja adja, azaz:

69,23%

0,6923 1

e 1 e

g  ^a   ^0,5261   

(12)

12

0,9825 7,89

28 14,73 ²





















*

1 2 ln 1

2

1

ln 2

n

i yi n

i xi n

i

yi xi

d d

d d r

A korrelációs együttható alapján megállapítható, hogy az adatsor exponenciális trendvonallal közelítve szorosabb illeszkedést ad, mint a lineáris közelítés. A növekedés átlagos üteme: 69%

évente a vizsgált időszakra vonatkozóan.

(iii) Logisztikus közelítés

A számításokhoz becsülni kell „A” paraméter értékét. A rendelkezésre álló információk alapján hosszú távon a vállalkozás 150 tonna termék értékesítési lehetőségével számol (azaz A=150).

1.6 táblázat. Munkatáblázat a lineárisra visszavezetett trendfüggvény számításához

Év Transz- formált

évek

Értéke- sítés

(t)

Részszámítások

xi xi’ yi xi’² yi’ xi’y’i dxi d_y’i dxid_y’i dxi

2 d_y’i²

2006 -3 5 9 3,367 -10,102 -3 2,03 -6,10 9 4,13

2007 -2 9 4 2,752 -5,503 -2 1,42 -2,83 4 2,01

2008 -1 15 1 2,197 -2,197 -1 0,86 -0,86 1 0,74

2009 0 30 0 1,386 0,000 0 0,05 0,00 0 0,00

2010 1 55 1 0,547 0,547 1 -0,79 -0,79 1 0,62

2011 2 83 4 -0,214 -0,428 2 -1,55 -3,10 4 2,40

2012 3 100 9 -0,693 -2,079 3 -2,03 -6,08 9 4,11

Összesen 0 297 28 9,342 -19,763 0 0,00 -19,76 28 14,02

Átlag 0 42,43 1,3345

Megjegyzés-1:

n lny lny

d illetve x x d

n

1 i

i i

lnyi i

xi









 ^ , valamint

i i

i y

y A

y 

 ln '

A logisztikus trendfüggvény:

) 0 ( ,

* 1





  a

e b y A

x a

(13)

13

7058 , 0 28

763 , 19 '

'

* '

1 2

1   







 n

i i n

i

i i

x y x

a , illetve

80 , 3 3346

, 1 7 342 , 9 '

ln  ¹     ^ln  ¹^,³³⁴⁶ 



 b e e

n y

b ^b

n

i i

Az adatsor jellegét leíró exponenciális trendfüggvény:

e x

y  





7058 ,

* 0

8 , 3 1

150

A növekedés átlagos ütemét a hatványkitevős tag alapja adja, azaz:

49,37%

0,4937 e

e

g  ^a  ^^0,7058  

 

0,9946

 





















02 , 14

* 28

76 , 19

*

* 2

1 2

' 1

2

1

' 2

n

i i y n

i xi n

i

i y xi

d d

d d r

A logisztikus görbe korrelációs együtthatója mutatja a legszorosabb összefüggést. A növekedés átlagos üteme: 49% évente a vizsgált időszakra.

Ha megnézzük az időszak alatt bekövetkezett átlagos növekedést az induló és az időszak végére elért értékesítés alapján, a növekedés értékére a következő értéket kapjuk:

% 41 , 53 5341

, 0 1 5 1 ⁷ 100

1











 ⁿ ⁿ y y g

A logisztikus közelítés növekedési üteméhez áll legközelebb az így kapott érték.

Az előzőekben ismertetett trendszámítás az Excel táblázatkezelővel egyszerűbben és gyorsabban is elvégezhető. Ennek lépései:

 A grafikus ábrázolást követően az adatsorra kattintunk a jobb egérgombbal, majd a felugró menüből kiválasztjuk a „Trendvonal felvétele...” lehetőséget;

 A megjelenő párbeszédablakban kiválasztjuk a Trend/regresszió típusát, valamint a jelölőnégyzetek kipipálásával utasítjuk a programot, hogy az egyenlet és az R² értéke is látszódjon a diagramon (a „régebbi” Excel verzióban ez utóbbi opciót az „Egyebek fülön” tudjuk elérni).

(14)

14 Az Excel alkalmazással elvégzett trendillesztések outputjai az 1.3. ábrán találhatók.

Fontosnak tartjuk megemlíteni, hogy az eredeti számításaink, illetve az Excellel végzet illesztés során kapott „b” paraméterek különböznek. Az eltérés oka, hogy az Excel nem az általunk használt elv szerint végzi el az idősorok transzformációját (hanem 2006=1, 2007=2, 2008=3, stb.). Ez magyarázza a felírt egyenletek különbségeit. Ugyanakkor azt is meg kell jegyeznünk, hogy trendszámítás során nyerhető „b” paramétereknek nincs igazán jelentősége, nehezen adható neki lényeges közgazdasági tartalom.

y = 16.893x - 25.143 R² = 0.9352

0 20 40 60 80 100 120

2006 2007 2008 2009 2010 2011 2012 Évek

Értékesítés (t)

y = 3.2347e^0.5261x R² = 0.9825

0 20 40 60 80 100 120

2006 2007 2008 2009 2010 2011 2012 Évek

Értékesítés (t)

1.3. ábra. A lineáris- és exponenciális trendillesztés Excel-outputjai

A témához kapcsolódóan jelezzük továbbá azt is, hogy a lineáris trendillesztésnél nyert „a”

meredekségi paraméter Excel-függvény segítségével is számítható: =MEREDEKSÉG( ), szintén megkönnyítve az elemző munkáját.

1.3. A regressziószámítás gyakorlati alkalmazása

4. FELADAT

Egy tehenészeti telepen végzett kísérletben azt vizsgálják, hogy milyen kapcsolat van a fejőstehenek abrakfogyasztása és a kifejt tej mennyisége között. A kísérlet során nyert mérési eredményeket a 1.7. táblázat tartalmazza.

1.7. táblázat. A feletetett abraktakarmány és a kifejt tej mennyisége a kísérletben Feletetett abraktakarmány mennyisége [kg] Kifejt tej mennyisége [liter]

1 9.5

2 14.5

3 15.5

4 16

5 20

(15)

15

6 23

7 26

8 27

Feladat: a kísérlet során nyert adatok kiértékelése. Ennek során elsősorban annak eldöntése, hogy van-e statisztikailag igazolható összefüggés az abrakfogyasztás és a tejtermelés között, valamint annak számszerűsítése, hogy a takarmánydózis növelése hogyan hat a tejtermelésre.

FELADAT MEGOLDÁSA:

A probléma megoldásának első lépéseként ábrázoljuk az adatokat (1.4. ábra).

y = 2.4583x + 7.875 R² = 0.9698

0 5 10 15 20 25 30

0 1 2 3 4 5 6 7 8 9

Feletetett abraktakarmány [kg]

Kifejt tej [liter]

1.4 ábra. A feletetett abraktakarmány és kifejt tej mennyisége összefüggésének grafikus elemezése

Az adatpárok vizuális elemzése pozitív lineáris összefüggést mutat a takarmány-fogyasztás és a tejtermelés között, amit megerősít a két változó között számított Pearson-féle korrelációs koefficiens értéke is: r = 0,9848. (Meg kell jegyezni, hogy a koefficiens számítható a statisztikai tanulmányok során tanult képlettel is, ugyanakkor annál gyorsabb és egyszerűbb megoldást kínál a

=KORREL( ) Excel-függvény. A korrelációs koefficiens értéke tehát meglehetősen szoros összefüggést mutat a két változó között.

A vizsgálatok folytatásaként – a trendszámítás során már ismertetésre került eljárással – az adatsorunkra egy lineáris becslőfüggvényt illesztünk, amely számszakilag kifejezi, illetve becsli az abrakfogyasztás és tejtermelés kapcsolatát.

A becslőfüggvény egyenlete: y= 2,46x + 7,875 Az egyenletből leszűrhető fontosabb tapasztalatok:

 átlagosan 1 kg pótlólagos abraktakarmány a tejtermelést átlagosan 2,46 literrel növeli meg;

(16)

16

 amennyiben az állatok nem kapnak abraktakarmányt (vagyis x=0), a tejtermelés várható, becsült értéke 7,88 liter.

A függvényhez tartozó magas R² érték biztató a becslés pontosságát, megbízhatóságát illetően. A fenti regresszió-számítást a szélesebb körű információ szerzése érdekében végezzük el az Excel Analysis ToolPak csomagjának Regresszió moduljával is. Elvégezve a számítást, röviden nézzük át a regresszió outputját (1.8 táblázat), a teljesség igénye nélkül, a legfontosabb tételekre koncentrálva.

Az output tábla első részében találjuk – többek között – a már ismert korrelációs- és determinációs együttható értékeket. Mint ismert, a determinációs együttható (R²) arra ad választ, hogy a magyarázó változó (vagy más elnevezéssel független változó) az eredmény (vagy függő) változó heterogenitásának mekkora részét képes megmagyarázni. Az eredmények szerint az abraktakarmány feletetett mennyiségének varianciájával a tejtermelés varianciáját 97%-ban lehet megmagyarázni. Kicsit egyszerűbben: az R² érték az illeszkedés pontosságát fejezi ki, és annál pontosabb a becslésünk minél közelebb van az értéke 1-hez. Tehát az általunk kapott 0,97-es érték nagyon jónak mondható. Azt, hogy a regressziós modell együtthatói mennyire megbízhatóak, milyen jól magyarázható a az eredmény változó a magyarázó változóval, a varianciaanalízis (ANOVA) táblázatából tudhatjuk meg. Nem részletezve a varianciaanalízis táblázatát, számunkra a legfontosabb az F szignifikancia értéke. Amennyiben abban – az általánosan elfogadott – 0,05 értéknél kisebb szám szerepel, akkor azt mondhatjuk, hogy az általunk használt regressziós modell statisztikai értelemben jó. Jelen példánkban 0,000 érték ebbe a kategóriába tartozik. Modellünk statisztikailag tehát validált!

1.8. táblázat. A regresszió outputjai

ÖSSZESÍTŐ TÁBLA Regressziós statisztika

r értéke 0,985

r-négyzet 0,970

Korrigált r-négyzet 0,965

Standard hiba 1,147

Megfigyelések 8,000

VARIANCIAANALÍZIS

df SS MS F

F szignifikanciája

Regresszió 1,000 253,823 253,823 192,879 0,000

Maradék 6,000 7,896 1,316

Összesen 7,000 261,719

Koefficiensek Standard hiba t érték p-érték Alsó 95% Felső 95%

Tengelymetszet 7,875 0,894 8,810 0,000 5,688 10,062

Abraktakarmány

mennyisége 2,458 0,177 13,888 0,000 2,025 2,891

(17)

17 Az utolsó, a koefficienseket tartalmazó táblázatrész számunkra a legfontosabb. Ennek első oszlopában (Koefficiensek) találjuk a becslőfüggvény felírásához szükséges paramétereket, amelyek megegyeznek az 1.4. ábrán feltüntetettekkel. Ami többletként megjelenik a táblázatban az a paraméterekhez kapcsolódó konfidencia-intervallum. Ennek értelmezése: mint azt már az előzőekben megállapítottuk, az abraktakarmány 1 kg-mal történő növelése átlagosan 2,46 literrel növeli meg a tejtermelést. Miután becslésről van szó, nem lehetünk benne biztosak, hogy ez az érték teljesen pontos! Sokkal korrektebb, ha azt mondjuk, hogy az abraktakarmány mennyiségének 1 kg- mal történő növelése várhatóan 2,025 és 2,891 literrel növeli meg a tejtermelést (alsó és felső értékek adják a koefficiensekhez tartozó 95%-os konfidencia-intervallumot).

Röviden szólunk még a p-értékről, aminek a többváltozós regressziónál van különösen nagy jelentősége, hiszen ez alapján tudjuk eldönteni, hogy az általunk magyarázó tényezőként bevonásra kerülő változók közül melyek parciális hatása szignifikáns (ha a p-érték 0,05-nél kisebb, akkor az adott változónak a függő változóra vonatkozó parciális hatása statisztikailag is igazolható). A téma iránt érdeklődő hallgatóknak ajánljuk a témával részletesen foglalkozó irodalmak közül Gary Koop:

Közgazdasági adatok elemzés c. könyvét (Budapest: Osiris Kiadó, 2008).

Szöveges értékelés

Elemzéseinek igazolták, hogy statisztikailag igazolható összefüggés van az abraktakarmány mennyisége és a tejtermelés alakulása között. A pótlólagosan megetetett abraktakarmány 1 kg-ja – nagy valószínűséggel – 2,025 és 2,891 liter közötti értékkel növeli a tejtermelést (átlagosan 2,46 literrel).

1.4. Az eltérések számszerűsítésének módszerei

Mint az az elméleti jegyzet keretei között tárgyalásra került, mindhárom eltérések számszerűsítésére használható módszer (a láncbehelyettesítés, az abszolút különbözetek és a százalékos különbözetek módszere) ugyanarra az eredményre vezet. A levezetésekből ez paraméteresen is belátható volt. A következőkben egy példán keresztül kövessük végig a módszerek alkalmazását, és vizsgáljuk meg a kapott eredményt.

5. FELADAT

Egy szántóföldi növénytermesztéssel foglalkozó üzem egyik ágazatáról rendelkezésre álló bázis- és tárgyidőszaki információkat az 1.9. táblázat foglalja össze.

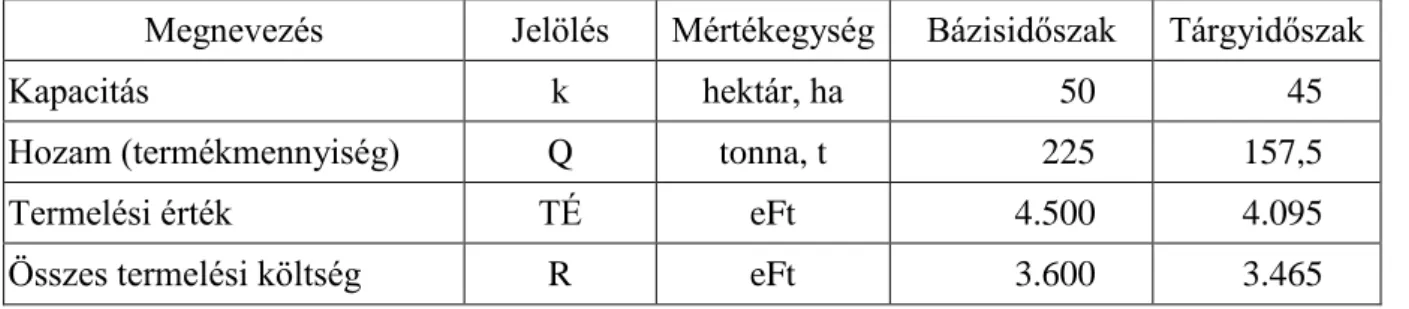
1.9. táblázat. Bázis- és tárgy időszaki információk egy növénytermesztési ágazatról Megnevezés Jelölés Mértékegység Bázisidőszak Tárgyidőszak

Kapacitás k hektár, ha 50 45

Hozam (termékmennyiség) Q tonna, t 225 157,5

Termelési érték TÉ eFt 4.500 4.095

Összes termelési költség R eFt 3.600 3.465

(18)

18

Feladat: Vizsgálja meg, hogyan változott a vizsgált ágazat jövedelme (J) bázis-tárgy időszaki relációban? Az egyes tényezők változásának mekkora számszerűsíthető hatása volt a jövedelem változására?

FELADAT MEGOLDÁSA:

Az elemző feladata: terv–tény elemzés során a jövedelemváltozás okainak számszerűsítése a láncbehelyettesítés, az abszolút- és százalékos különbözetek módszere alkalmazásával.

Számszerűsítendő hatások: Mi változott?

 Kapacitás (k);

 Fajlagos (területegységre vetített) hozam (vagy másként produktivitás) (q);

 Egységár (p);

 Fajlagos (termékegységre vetített) termelési önköltség (r).

A hatások számszerűsítésének menete:

1. lépés: az alapösszefüggés felállítása, a jövedelem keletkezését befolyásoló tényezőkre bontása.

A jövedelem felírható:

 

] [

*

] [

*

Ft r k p q k J vagy

Ft r p q k r q k p q k R TÉ J

 k















ahol:

J = összes jövedelem [Ft];

TÉ = termelési érték [Ft];

R = termelési költség, ráfordítás [Ft];

k = kapacitás-jellemző [ha];

q = produktivitás, termelékenység jellemző [t/ha];

p = termékegység értékesítési ára [Ft/t];

r = termékegységre jutó termelési költség [Ft/t];

rk = területegységre jutó termelési költség [Ft/ha]

2. lépés: Az összefüggésben meghatározott hatótényezők számítása az alapadatokból (1.10.

táblázat)

3. lépés: A jövedelemváltozás okainak számszerűsítése láncbehelyettesítés módszerével (i) Termelési érték változása

Tervezett termelési érték (TÉ0):

500 . 4 20

* 5 , 4

* 50

*

* ₀ ₀

0

0   

t eFt ha

t ha

p q k

TÉ [eFt]

(19)

19 Tényleges termelési érték (TÉ1):

095 . 4 26

* 5 , 3

* 45

*

* ₁ ₁

1

1   

t eFt ha

ha t p

q k

TÉ [eFt]

Termelési érték változása (TÉ):

405 500

. 4 095 .

0 4

1     



TÉ TÉ TÉ [eFt]

Termelési érték változásainak okai

1) Kapacitásváltozás hatása paraméteresen:

0 0 0 0 0

1*q * p k *q * p

k

TÉ_k  

 [eFt]

Behelyettesítve:

450 20

* 5 , 4

* 50 20

* 5 , 4

*

45   





t eFt ha

t ha

t eFt ha

t ha

TÉ _k [eFt]

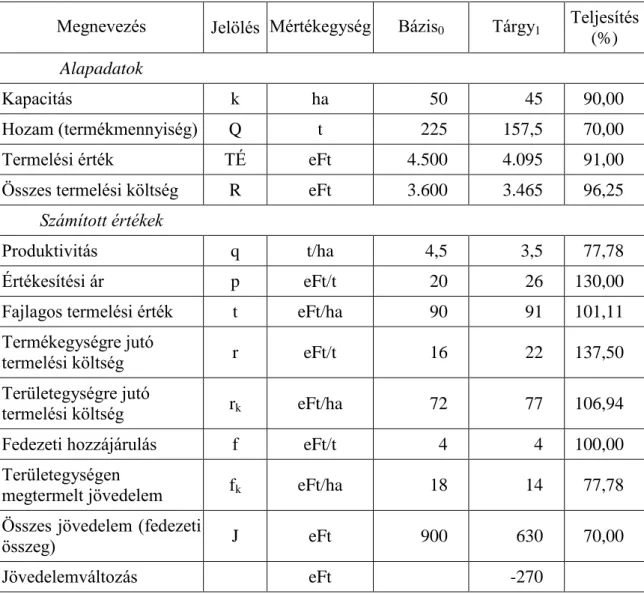
1.10. táblázat. Kiegészítő számítások az eltérések számszerűsítéséhez

Megnevezés Jelölés Mértékegység Bázis0 Tárgy1 Teljesítés (%) Alapadatok

Kapacitás k ha 50 45 90,00

Hozam (termékmennyiség) Q t 225 157,5 70,00

Termelési érték TÉ eFt 4.500 4.095 91,00

Összes termelési költség R eFt 3.600 3.465 96,25

Számított értékek

Produktivitás q t/ha 4,5 3,5 77,78

Értékesítési ár p eFt/t 20 26 130,00

Fajlagos termelési érték t eFt/ha 90 91 101,11

Termékegységre jutó

termelési költség r eFt/t 16 22 137,50

Területegységre jutó

termelési költség rk eFt/ha 72 77 106,94

Fedezeti hozzájárulás f eFt/t 4 4 100,00

Területegységen

megtermelt jövedelem f_k eFt/ha 18 14 77,78

Összes jövedelem (fedezeti

összeg) J eFt 900 630 70,00

Jövedelemváltozás eFt -270

(20)

20

2) Produktivitás változásának hatása paraméteresen:

0 0 1 0 1

1 *q * p k *q * p

k

TÉ _q  

 [eFt]

Behelyettesítve:

900 20

* 5 , 4

* 45 20

* 5 , 3

*

45   





t eFt ha

ha t t

eFt ha

ha t

TÉ _q [eFt]

3) Árváltozás hatása paraméteresen:

0 1 1 1 1

1*q * p k *q * p k

TÉ _p  

 [eFt]

Behelyettesítve:

945 20

* 5 , 3

* 45 26

* 5 , 3

*

45   





t eFt ha

t ha

t eFt ha

t ha

TÉ _p [eFt]

Termelési érték változását befolyásoló tényezők eredő hatása:

Tényező Hatás mértéke

(eFt)

Kapacitás változása -450

Produktivitás változása -900

Árváltozás +945

Hatások eredője (fentiek összege) -405 (ii) Termelési költség változása

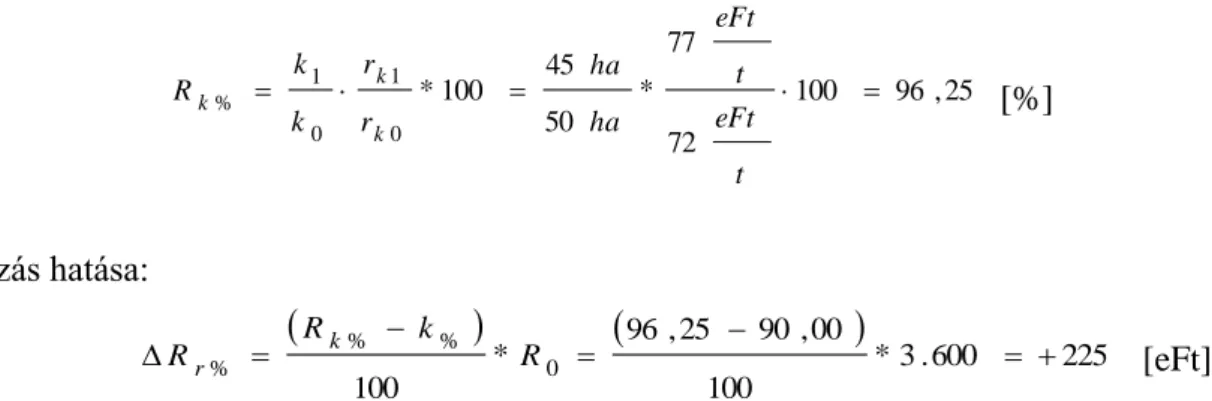
A termelési költséget tervezhetjük termékegységre, illetve gyakrabban kapacitásegységre vetítve. Ennek megfelelően a hatás számszerűsítése eltér.

(A) Termelési költség változását befolyásoló hatások számszerűsítése, ha a termelési költség termékegységre vetítve került tervezésre.

Tervezett termelési költség (R0):

600 . 3 16

* 5 , 4

* 50

*

* ₀ ₀

0

0   

t ha eFt

ha r

q k

R [eFt]

Tényleges termelési költség (R₁):

465 . 3 22

* 5 , 3

* 45

*

* ₁ ₁

1

1   

t eFt ha

ha t r

q k

R [eFt]

(21)

21 Termelési költség változása (R)

135 600

. 3 465 .

0 3

1     



R R R [eFt]

Termelési költség változásának okai

1) Kapacitásváltozás hatása paraméteresen:

0 0 0 0 0

1*q *r k *q *r

k

R_k  

 [eFt]

Behelyettesítve:

360 16

* 5 , 4

* 50 16

* 5 , 4

*

45   





t eFt ha

ha t t

eFt ha

ha t

R_k [eFt]

2) Produktivitás változásának hatása paraméteresen:

0 0 1 0 1

1* q * r k * q *r

k

R_q  

 [eFt]

Behelyettesítve:

720 16

* 5 , 4

* 45 16

* 5 , 3

*

45   





t eFt ha

ha t t

eFt ha

ha t

R_q [eFt]

3) Fajlagos (termékegységre vetített) termelési költség (önköltség) változás hatása paraméteresen:

0 1 1 1 1

1 *q * r k *q * r k

R_r  

 [eFt]

Behelyettesítve:

945 16

* 5 , 3

* 45 22

* 5 , 3

*

45   





t eFt ha

ha t t

eFt ha

ha t

R_r [eFt]

Termelési költség változását befolyásoló tényezők eredő hatása:

Tényező Hatás mértéke

(E Ft)

Kapacitás változása -360

Produktivitás változása -720

Önköltség változás +945

Hatások eredője -135