Bifurkációk komplex rendszerek differenciálegyenleteiben
Simon L. Péter
Eötvös Loránd Tudományegyetem Matematikai Intézet
Alkalmazott Analízis és Számításmatematikai Tanszék
Akadémiai doktori értekezés
2012
Tartalomjegyzék
1. Bevezetés 1
1.1. Reakció-diffúzió egyenletek . . . 2
1.1.1. Reakció-diffúzió egyenletek kutatásának fontosabb területei . 2 1.1.2. Reakció-diffúzió egyenletekkel kapcsolatos saját eredmények . 4 1.2. Hálózati folyamatok . . . 6
1.2.1. Hálózati folyamatokkal kapcsolatos saját eredmények . . . 8
2. Stacionárius megoldások 11 2.1. Irodalmi áttekintés . . . 12
2.2. A "time-map" módszer . . . 14
2.2.1. A "time-map" monotonitása . . . 15
2.2.2. A "time-map" értelmezési tartománya . . . 19
2.2.3. A "time-map" határértékei az értelmezési tartomány határ- pontjaiban . . . 20
2.3. A megoldások száma konvex f esetén . . . 21
2.4. Kvázilineáris egyenlet megoldásainak száma . . . 24
2.5. A megoldások száma szinguláris f esetén . . . 26
2.5.1. A megoldások száma f(u) =u−α+up esetén . . . 27
2.5.2. A megoldások száma f(u) =up−u−α ésn= 1 esetén . . . . 29
2.5.3. A megoldások száma f(u) =u−α−up esetén . . . 32
2.6. Stabilitás konvex és konkáv f esetén . . . 32
3. Utazó hullám megoldások 35 3.1. Utazó hullámok létezése . . . 35
3.2. Utazó hullámok stabilitása . . . 37
3.3. A linearizálással kapott operátor spektruma . . . 38
3.3.1. A spektrum jellemzése az invariáns alterekkel . . . 39
3.3.2. Az Evans-függvény . . . 42
3.4. Stabilitásvizsgálat egy egyenlet,m= 1 esetén . . . 43
4. Hálózati folyamatok 49 4.1. A matematikai modell . . . 49
4.1.1. A csúcsok állapotát leíró dinamikák . . . 49
4.1.2. Hálózatok típusai . . . 52
4.2. Járványterjedés hálózaton . . . 55
4.2.1. Homogén fokszámeloszlású gráf . . . 57 iii
4.2.2. Heterogén fokszámeloszlású gráf . . . 58
4.2.3. Effektív fokszám modell . . . 60
4.2.4. Momentum lezárással felírt modellek . . . 62
4.2.5. Háztartás típusú modellek . . . 64
4.3. A numerikus szimuláció . . . 65
5. SIS dinamika általános gráfon 67 5.1. Alapegyenletek . . . 67
5.2. Az alapegyenletek egyszerűsítése összevonással . . . 71
5.2.1. Összevonás három csúcsú teljes gráf esetén . . . 72
5.2.2. Lineáris differenciálegyenletek összevonása . . . 73
5.2.3. Az SIS dinamikához tartozó alapegyenlet összevonása a gráf automorfizmusainak segítségével . . . 74
5.3. Összevonás különböző típusú gráfokon . . . 77
5.3.1. Összevonás teljes gráf esetén . . . 77
5.3.2. Összevonás csillag gráf esetén . . . 78
5.3.3. Összevonás háztartás típusú gráf esetén . . . 79
5.3.4. Összevonás körgráf esetén . . . 80
5.4. Várható értékekre vonatkozó egyenletek . . . 81
5.4.1. Differenciálegyenlet a csúcsok számának várható értékére . . . 82
5.4.2. Differenciálegyenlet az élek számának várható értékére . . . . 84
6. Közelítő differenciálegyenletek 89 6.1. Az alapegyenlet közelítő differenciálegyenletei . . . 91
6.2. Közelítés elsőrendű parciális differenciálegyenlettel . . . 93
6.3. Sztochasztikus módszer . . . 95
6.4. Végtelen rendszer a momentumokra . . . 99
6.4.1. Kato-féle perturbációs módszer . . . 102
6.4.2. Elemi bizonyítás a (6.3) együtthatók esetén . . . 104
6.5. Operátor félcsoportok módszere . . . 110
Hivatkozások 117
1. fejezet
Bevezetés
A differenciálegyenletek kvalitatív elméletének kezdeteit rendszerint Poincaré mun- kásságáig vezetik vissza, amikor a természettudományokban (akkor elsősorban a fizi- kában) felmerülő összetett rendszereket leíró differenciálegyenletekről kiderült, hogy többségükben nem lineárisak, és ezek megoldása képlettel ritkán adható meg. A komplex rendszer fogalma a természettudományokban, a fizikában, kémiában és bio- lógiában többé kevésbé jól körülhatárolt, rendszerint olyan, sok összetevőből álló rendszert értenek alatta, melynek elemei valamilyen struktúra alapján kapcsolód- nak össze. Ha ebben a struktúrában valamilyen szabályosság van, mint például egy kristály szerkezete, akkor a matematikai modell parciális differenciálegyenletként ad- ható meg. Azonban számos esetben a kapcsolatok sokkal bonyolultabb rendszert alkotnak, mint például az internet szerkezete, vagy egy sejt metabolikus hálózata, ilyen esetekben a matematikai modell egy komplex hálózat, illetve a hálózaton meg- adott differenciálegyenlet-rendszer. A természettudományokban megjelenő komplex rendszerek több esetben nemcsak motiválták a matematikai vizsgálatokat, hanem új matematikai területek megszületésében és fejlődésében jelentős szerepet játszottak.
A XX. század közepétől napjainkig az alábbi három jelentős diszciplína megjelené- sének lehetünk tanúi:
• Káoszelmélet
• Térbeli jelenségek (mintázatok és utazó hullámok) leírása
• Hálózati folyamatok.
Történeti megjelenésük a fenti sorrendben a XX. század hatvanas és nyolcvanas éve- ire, illetve a XXI. század első évtizedére tehető. Érdekes módon mindháromnak van sokkal korábbi matematikai előfutára, Poincaré munkássága a XX. század elején, Kol- mogorov, Petrovszkij, Piszkunov, valamint Turing dolgozatai a XX. század közepén, illetve Erdős és Rényi cikke 1959-ben. Azonban a területek fejlődésének megindulásá- hoz megfelelő számítástechnikai háttérre is szükség volt. Így a káoszelmélet indulását nagyban segítették Lorenz numerikus vizsgálatai a meteorológiában megjelenő egy- szerű háromváltozós közönséges differenciálegyenlet-rendszerrel kapcsolatban. A tér- beli jelenségeket leíró parciális differenciálegyenletek effektív numerikus megoldására a 80-as években érett meg a helyzet, míg a milliós nagyságrendű csúccsal rendelke- ző gráfok számítógépes kezelése a XX. század végén vált elérhetővé. A fenti három
1
területen megindult kutatások a matematika saját belső fejlődésére is nagy hatással voltak. A dinamikai rendszerek kvalitatív elmélete a múlt század hatvanas éveitől jelentős fejlődésnek indult az alkalmazások felől érkező hatásnak köszönhetően. A hetvenes és nyolcvanas évektől fordult az érdeklődés a végtelen dimenziós fázisterű dinamikai rendszerek (lényegében parciális és késleltetett differenciálegyenletek) fe- lé, ahol nagy erővel megindult a véges dimenzióban ismert tételek általánosítása a különböző végtelen dimenziós esetekre. A hálózati folyamatok vizsgálata egyelőre a numerikus kísérletek szintjén mozog, a matematika területén kapcsolódik a gráfelmé- lethez, a Markov-folyamatokhoz és a dinamikai rendszerekhez is, a szerző véleménye szerint még nem alakult ki a jelenségek leírására alkalmas matematikai struktúra.
Saját kutatásaink az elmúlt nagyjából tíz évben a két utóbbi területre, neve- zetesen a reakció-diffúzió egyenletek területére és a hálózaton zajló járványterjedés modellezésének területére estek. Ezeken belül is elsősorban a modellként kapott differenciálegyenletek bifurkációit, azaz a paraméterek változása során bekövetkező kvalitatív változásokat vizsgáltuk. Ilyen témájú kutatási eredményeinket vázlatosan ismertetjük a továbbiakban a bevezetésben, majd a fontosabb részeket fejtjük ki az értekezésben.
1.1. Reakció-diffúzió egyenletek
A reakció-diffúzió egyenletek matematikailag szemilineáris parabolikus parciális dif- ferenciálegyenletek, melyek általános alakja
∂tu=D∆u+f(u), (1.1)
ahol u : R+×Rn → Rm az ismeretlen függvény, f : Rm → Rm folytonosan diffe- renciálható függvény és D pozitív elemű diagonális mátrix (az idő szerinti parciális deriválást, illetve a tér szerinti Laplace-operátort koordinátánként alkalmazzuk azu függvényre). Az egyenlethez különböző peremfeltételek tartozhatnak, utazó hullá- mok vizsgálata esetén például az egyenletet a teljes Rn téren tekintik, ekkor a pe- remfeltételekukorlátosságára vagy végtelenbeli határértékére vonatkoznak. Korlátos tartomány esetén mindhárom típusú szokásos peremfeltétel előfordul a vizsgálatok- ban. A peremfeltétel mellett természetesen az u(·,0)kezdeti függvény megadása is szükséges. Az egyenlet neve a kémiai alkalmazásból származik, ez esetben uk(t, x) a k-adik (k = 1,2, . . . , m) anyag koncentrációját jelenti a t időpontban és az x he- lyen, továbbá a jobboldal első tagja fejezi ki a diffúziót, a második pedig a kémiai reakciókat. Az egyenlet azonban számos más fizikai, biológiai, közgazdasági jelenség modellje is lehet a járványterjedéstől az ingerület vezetésen át a mintázat képző- désig. Reakció-diffúzió egyenletek különböző alkalmazásairól számtalan publikáció között több könyv is található. Ezekről, valamint az elméleti eredményekről adunk összefoglalást a következő szakaszban. Ezt követően mutatjuk be saját eredménye- inket, amelyek reakció-diffúzió egyenletekkel kapcsolatosak.
1.1.1. Reakció-diffúzió egyenletek kutatásának fontosabb területei A reakció-diffúzió egyenletek kutatásának elindításában úttörő szerepet játszó dol- gozatokként a következőket szokás megemlíteni. Fisher 1937-ben írt dolgozata [60] a
1.1. REAKCIÓ-DIFFÚZIÓ EGYENLETEK 3 gének terjedésével foglalkozik, Kolmogorov, Petrovszkij és Piscunov ugyanebből az évből származó munkája [89] az utazó hullámok kutatását indította el, Turing 1952- es cikke [143] pedig a mintázatképződés vizsgálatának előfutára. Számtalan dolgozat megjelenését követően Fife 1979-ben írott könyve [59] összefoglalást adott a kémiai és biológiai alkalmazásokról, valamint a kvalitatív vizsgálat addigi eredményeiről egy egyenletre (m= 1) vonatkozóan (stacionárius megoldások és utazó hullámok létezése és stabilitása). Smoller 1983-as monográfiája [136] az alkalmazások mellett rendsze- rek (m >1) esetében részletesen tárgyalja utazó hullámok létezésének bizonyítását topologikus módszerekkel (Conley-féle index). Grindrod 1991-ben megjelent könyve [69] a mintázatok és utazó hullámok tárgyalásához szükséges matematikai eszközö- ket mutatja be. Kuramoto, valamint Phillipson és Schuster művei [92, 121] a kémiai, Murray és Britton munkái [30, 109] a biológiai, Rubinstein monográfiája [128] az elektro-kémiai, Giovagnili, valamint Zeldovich és munkatársai által írott könyvek [65, 152] pedig az égéselméleti és lángterjedési alkalmazásokról adnak áttekintést.
A több egyenletből álló rendszerek vizsgálata a kilencvenes években terjedt el. Az elsősorban populációdinamikához tartozó biológiai alkalmazásokat Leung [103] mo- nográfiája, a fiziológiai modelleket pedig Keener és Sneyd könyvei [84, 85] tárgyalják.
Farkas Miklós könyvében [57] nemcsak reakció-diffúzió egyenletek, hanem közönséges differenciálegyenlet-rendszerek biológiai alkalmazására is számos példát láthatunk.
A reakció-diffúzió egyenletek kutatása az alkalmazásokon kívül a dinamikai rend- szerek elméletéből nőtt ki, ugyanis az U(t) = u(·, t) függvényt bevezetve az (1.1) egyenlet az
U˙(t) =AU(t) +F(U(t)) (1.2) absztrakt Cauchy-feladatként írható fel. Kézenfekvő tehát megvizsgálni, hogy az
˙
x(t) =f(x(t))közönséges differenciálegyenlet-rendszerre vonatkozó eredmények meny- nyiben általánosíthatók az (1.2) végtelen dimenziós feladatra. Ismert, hogy a közön- séges differenciálegyenlet-rendszer megoldásai dinamikai rendszert határoznak meg.
A (1.2) egyenlet esetében ennek bizonyítása azért sokkal nehezebb feladat, mert a jobboldalon szereplő A operátor nem korlátos. Az ötvenes évektől kezdődően kifejlesztett operátor félcsoport elmélet segítségével kidolgozták az (1.2) Cauchy- feladatra vonatkozó egzisztencia elméletet, melyről például Henry, Rothe, Pazy il- letve Cazenave és Haraux könyvében, valamint Amann dolgozatában olvashatunk [4, 37, 70, 120, 126]. A dinamikai rendszer létezésének bizonyításával megkezdődhe- tett a kvalitatív tulajdonságok tanulmányozása. Ez magában foglalja a stacionárius, periodikus, kaotikus, illetve utazó hullám megoldások létezésének, pontos számának, valamint stabilitásának vizsgálatát. A speciális típusú megoldásokon kívül fontos kér- dés a megoldások aszimptotikus (hosszú idő utáni) viselkedése, valamint az attrakto- rok létezésének kérdése, és vonzási tartományaik meghatározása, melyet általánosan tárgyal Robinson könyve [125], valamint Fiedler és Scheel összefoglaló dolgozata [58].
A közönséges differenciálegyenleteknél tapasztalt jelenségek természetesen a végtelen dimenziós megfelelőjük esetében is megjelennek, számos új jelenség kíséretében. A kvalitatív vizsgálatban fontos szerepet játszanak a variációs módszerek [6, 48, 139], az alsó és felső megoldások konstruálásán alapuló monoton módszerek [48, 118], va- lamint a topológiai módszerek, melyek fő eszközei a Leray-Schauder fokszám és a Conley-féle index [32, 48, 136]. A stacionárius megoldások számával kapcsolatos
eredményekről részletes összefoglalást fogunk adni a 2.1. alfejezetben, addig is az ezzel foglalkozó könyvek és összefoglaló munkák közül kiemeljük Lions dolgozatát [102] és Shi könyvét [134]. Az utazó hullámokat a 3. fejezetben fogjuk részletesen tárgyalni, most csak a [145] monográfiára utalunk. A kvalitatív elméletnek ez a két területe az, amellyel magunk is foglalkoztunk. A következő szakaszban áttekintést adunk az általunk vizsgált kérdésekről.
1.1.2. Reakció-diffúzió egyenletekkel kapcsolatos saját eredmények A különböző alkalmazásokban megjelenő reakció-diffúzió egyenletekkel kapcsolatos eredményeinket ismertetjük először részletesebben. Az elméleti jellegű eredményeket, melyek a stacionárius és utazó hullám megoldásokkal kapcsolatosak csak vázlatosan mutatjuk be, mert ezekről a későbbi fejezetekben részletesen szó lesz.
Alkalmazások
Kémiai hullámok geometriai leírása
Az első, témával kapcsolatos kutatásaink kémiai hullámok geometriai leírására irá- nyultak. Ennek eredményeit tartalmazzák a [156, 157, 158] dolgozatok, melyekben elméleti leírást adunk gyűrű alakú közegben terjedő kémiai hullámokról.
Elektrolit dióda
Később az elektrolit dióda matematikai modellezésével foglalkoztunk. Ez egy nyi- tott kémiai rendszer: a reaktor egy polimer gél, amely egy savas és egy lúgos kö- zeget köt össze, melyek között adott potenciálkülönbség van. A kísérletekben a dióda áram-feszültség karakterisztikáját mérik. A félvezető diódához hasonlóan nyi- tóirányú feszültségnél a karakterisztika nagyobb meredekségű, mint záróirányú ese- tén. Az elektrolit dióda matematikai modellje egy reakció-diffúzió típusú parciá- lis differenciálegyenlet-rendszer, amely a Nernst-Planck egyenletekből származtat- ható. Ezen rendszer analitikus megoldása nem állítható elő, ezért a stacionárius megoldásokat egyrészt a Nernst-Planck egyenletek analitikus megoldásaival, illet- ve ezek megfelelő csatlakoztatásával közelítettük, másrészt numerikusan határoztuk meg [159, 160, 161].
Lángterjedés
A Leedsi Egyetemen működő kutatócsoporttal való együttműködésben lángterjedést leíró reakció-diffúzió egyenletek utazó hullám megoldásait vizsgáltuk több dolgozat- ban. A [162] cikkben az égést egy elsőrendű, exoterm reakció adja meg, a hővesz- teséget egy lineáris függvény írja le. Az ebben szereplő paraméter függvényében numerikusan meghatároztuk a hullám megoldásokat és azok sebességét. A para- méter egy kritikus értéke alatt két megoldása van a peremérték- feladatnak, felette pedig nincs megoldás. Ezen modellben megjelenő különböző bifurkációk részletes numerikus vizsgálatát tartalmazza a [169] publikáció. A [163, 165] dolgozatokban az elsőrendű, exoterm reakció mellett egy endoterm reakció is szerepel, amely a fizikai
1.1. REAKCIÓ-DIFFÚZIÓ EGYENLETEK 5 hőveszteséget pótolja. Az endoterm reakció sebességét jellemző paraméter függvé- nyében meghatároztuk a hullám megoldásokat. Kiderült, hogy itt is nyereg-csomó bifurkáció van egy kritikus paraméter értéknél; ezalatt három megoldás van, felette pedig egy megoldás. A [168] cikkben egy két reakciólépésből álló endoterm reakció is szerepel, amely a hőveszteséget írja le. A témában közölt előző dolgozatainkhoz képest ez egy kémiailag sokkal reálisabb modell. A változók száma az eddigi kettő, illetve három helyet most öt, és a paraméterek száma is növekedett. Így többfé- le bifurkációs diagrammot kellett elkészíteni. Kiderült, hogy bizonyos paraméter tartományokban négy utazó hullám megoldás is van. Két helyen is találtunk nyereg- csomó bifurkációt. Ezután a lángterjedést leíró utazó hullám megoldások stabilitását vizsgáltuk. A [164] dolgozatban a [162] cikkbeli modellben kapott utazó hullám sta- bilitását vizsgáltuk, míg a [166] publikáció a [165] cikkbeli három változós modell utazó hullám megoldásainak stabilitásával foglalkozik. A lángterjedési modellek- ben kapott utazó hullámok stabilitásának vizsgálatával kapcsolatos eredményeket, és az Evans-függvény ilyen rendszerekre történő alkalmazását foglaltuk össze a [167]
cikkben. Két-dimenziós tartományban terjedő utazó hullámok stabilitásának vizsgá- latával is foglalkoztunk. Ebben az esetben a síkhullám terjedési irányára merőleges perturbációi is megmaradhatnak. Ez olyan típusú instabilitás, ami a szokásos egy- dimenzióban terjedő utazó hullámoknál nem léphet fel. Tehát a szokásos értelemben stabilis hullám egy két-dimenziós tartományban tekintve instabilis lehet. Meg lehet határozni az ilyen típusú instabilitás feltételét. A [170] dolgozatban a [162] cikkbeli modell esetében numerikusan meghatároztuk, hogy milyen paraméter értékeknél lép fel ez a bifurkáció.
Kémiai reakciók
A [173, 174] dolgozatokban egy autokatalitikus reakciót tartalmazó reakció-diffúzió egyenletrendszer radiálisan szimmetrikus stacionárius megoldásait vizsgáltuk. Meg- határoztuk, hogy mely reakciórend esetén van ilyen stacionárius megoldás, melyet numerikusan is kiszámítottunk.
A [171, 172] cikkekben a Belouszov-Zsabotyinszkij reakció Oregonátor modelljé- ben az utazó hullám megoldásokat tanulmányoztuk. Az első dolgozatban numeri- kusan meghatároztuk a nyereg-csomó bifurkációt, és elméleti becslést adtunk ennek helyére. A második dolgozatban kimutattuk, hogy az elektromos térerősséget, mint paramétert változtatva nyereg-csomó bifurkáció során két utazó hullám megoldás je- lenik meg. Az utazó hullámok numerikus meghatározásán kívül elméleti becslést adtunk a paraméterek azon értékére, amelyek mellett az utazó hullám megoldások léteznek.
Elméleti vizsgálatok
Az elméleti jellegű eredményeink a stacionárius és utazó hullám megoldásokkal kap- csolatosak.
A stacionárius állapotok számának és stabilitásának vizsgálata során először olyan szemilineáris elliptikus egyenletek bifurkációit vizsgáltuk, melyekben konvex, vagy konkáv nemlineáris tag szerepel. Az egy-dimenziós esetben sikerült a pozitív megoldások számában bekövetkező összes lehetséges bifurkációt leírni [178], melyről
a 2.3. szakaszban lesz szó. Ezeket az eredményeket kvázilineáris egyenletre is álta- lánosítottuk [182], melyet a 2.3. szakaszban tárgyalunk. Több dimenziós esetben a megoldások stabilitását tudtuk jellemezni [179], melyet kvázilineáris egyenletekre is általánosítottunk [180], ezeket az eredményeket a 2.6. szakaszban olvashatjuk.
A [175] dolgozatban játékelméleti modellekből származó, nem-folytonos jobbolda- lú reakció-diffúzió egyenletek megoldásának létezését bizonyítottuk, és a stacionárius megoldások vizsgálatával foglalkoztunk.
A [176] dolgozatban egy Kolmogorov-Petrovszkij-Piscunov típusú nemlinearitást tartalmazó szemilineáris elliptikus egyenletet vizsgáltunk. A probléma egy valószí- nűségszámításbeli kérdés kapcsán vetődött fel. A dolgozatban megmutattuk, hogy az egyenletnek nincs olyan megoldása, amely az egész n-dimenziós téren értelmezve van és értékei 0 és 1 közé esnek.
Több dolgozatban foglalkoztunk olyan szemilineáris differenciálegyenlethez tar- tozó peremérték probléma pozitív megoldásai számának vizsgálatával, melyben a nemlinearitás f(u) = up±u−α alakú, azaz egy negatív és egy pozitív kitevős hat- ványfüggvény összege, a megoldás pedig egy gömb peremén nulla. Itt a fő probléma a nemlinearitás szingularitása a peremen. A nem-szinguláris egyenletre vonatkozó eredmények természetesen erre az esetre nem alkalmazhatók, de sikerült az ott alkal- mazott módszereket a szinguláris esetre is kiterjeszteni. Az f(u) =up+u−α esetet a [183] dolgozatban vizsgáltuk, azf(u) =up−u−αesethez tartozó eredményeink pedig a [184, 185] cikkekben jelentek meg. Ezen eredményeket részletesen a 2.5. alfejezet tárgyalja.
Az utazó hullámokkal kapcsolatos elméleti eredmények az Evans-függvény mód- szerhez kötődnek. A módszer alkalmazásának elméleti hátterét a [177] cikkben írtuk le, melyről a 3. fejezetben olvashatunk.
1.2. Hálózati folyamatok
A hálózati folyamatok matematikai leírását célszerű egy egyszerű, de mégis komoly matematikai kihívást jelentő motiváló példán, nevezetesen az SIS típusú járvány- terjedésen bemutatni. Tekintsünk egyN csúcsú, irányítatlan, hurokélmentes gráfot.
A gráf csúcsai kétféle állapotban, fertőző (I), illetve egészséges (S), lehetnek. A gráf egy csúcsának állapota kétféleképpen változhat: egy I típusú csúcs adott való- színűséggel meggyógyul, azazS típusú lesz, illetve egyS típusú csúcsot azI típusú szomszédai valamilyen valószínűséggel megfertőznek, és maga isItípusú lesz. Mind a fertőzést és a gyógyulást független Poisson-folyamattal írjuk le, azaz egy rövid∆tidő alatt egyS típusú csúcs, melynek kdarabI típusú szomszédja van1−exp(−kτ∆t) valószínűséggel megfertőződik, azaz I típusú lesz, míg egy I csúcs 1−exp(−γ∆t) valószínűséggel meggyógyul, azaz S típusú lesz, ahol τ és γ adott pozitív számok, melyeket fertőzési, illetve gyógyulási rátának fogunk hívni. Az alapvető kérdés az, hogy hogyan változik időben a fertőző csúcsok számának várható értéke. Emellett természetesen fontos kérdés ennek szórása, vagy a még pontosabb leírás kedvéért a fertőző csúcsok eloszlásának időbeli változása.
A járványterjedésen kívül számos más jelenség vezet hasonló matematikai prob- lémához, például a híresztelések terjedése társadalmi hálózaton, vagy az aktivitás
1.2. HÁLÓZATI FOLYAMATOK 7 terjedése biológiai neurális hálózatokon. A hálózati folyamatok vizsgálata viszonylag új kutatási terület, ennek ellenére matematikai leírásáról már megjelentek összefog- laló munkák, Newman, Barabási és Watts könyve [113], Barrat, Barthélemy és Ves- pignani monográfiája [15], valamint kifejezetten a járvány és híresztelés terjedésről Draief és Massoulié könyve [49].
A fenti motiváló példák alapján körülhatárolható az a matematikai struktúra, amelyben vizsgálatainkat végezni fogjuk. Legyen adott egyN csúcsú gráf, melynek csúcsai véges sok (m) állapot valamelyikében lehetnek, és legyen adott egy dinami- ka, amely megadja, hogy a csúcsok állapota hogyan változik a szomszédos csúcsok állapotától függően. A modell egy mN elemű állapottéren megadott folytonos idejű Markov-lánc, melynek állapotegyenlete egy mN egyenletből álló lineáris közönséges differenciálegyenlet-rendszer. Ezt a rendszert a következő szakaszban felírjuk álta- lánosan, majd bemutatjuk, hogy különböző típusú gráfokon, milyen dinamikákat vizsgáltak eddig az irodalomban.
A kutatások célja annak felderítése, hogy a gráf szerkezetének ismeretében mit tudunk mondani a folyamat fenti jellemzőiről. Mivel az állapottér ilyen nagy mé- retű, azért eddig viszonylag kevés olyan eredmény született, ami a gráf szerkezetét kapcsolatba tudta hozni például a fertőző csúcsok számának várható értékével. A kérdés fontossága, és a számítási kapacitás jelentős megnövekedése hatására azonban a kilencvenes évek végére számos olyan dolgozat született (elsősorban biológusok és fizikusok munkái), amelyben különböző gráfokon Monte-Carlo szimuláció segítségével összehasonlították a járványterjedés folyamatát. A Monte-Carlo szimuláció pontos algoritmusát alább fogjuk ismertetni, azt azonban a részletes ismertetés nélkül is ál- líthatjuk, hogy a szimulációk alapján numerikus tapasztalatot szerezhetünk, de elmé- leti összefüggést nem tudunk megállapítani a gráf szerkezete és a folyamat jellemzői között. Az értekezésben azt fogjuk vizsgálni, hogy a folyamatot leíró Markov-lánc alapegyenletének nevezett differenciálegyenletben hogyan jelenik meg a gráf struktú- rája, és a differenciálegyenletek elmélete eszközeinek segítségével mit lehet mondani a gráf szerkezete és a folyamat jellemzői közötti kapcsolatról.
Egy hálózati folyamat leírására természetesen nem kizárólag a fenti matematikai struktúra alkalmas. A 4.2 szakaszban ismertetjük, hogy a járványterjedési dinamikák esetében a fenti modellen kívül milyen más modelleket vezettek be. Hangsúlyozzuk, hogy ebben az értekezésben nem célunk a járványterjedés modellezése. Ez a biológus és fizikus irodalomban nagyon széles körben vizsgált kérdés, melynél a jóság kritéri- uma a mérési adatokkal való egyezés. Ezzel szemben a matematikai vizsgálat célja:
egy adott matematikai modell minél alaposabb megértése, illetve esetleg különböző modellek összehasonlítása matematikai szempontból.
Kutatásai területünk tehát a fenti, a gráffal és a véges állapotterű dinamikával megadott, mN egyenletből álló lineáris rendszer vizsgálata. A cél először a modell formális definiálása, majd a differenciálegyenletek elméletének eszközeivel a modell redukálása olyan egyszerűbb rendszerekre, amelyek kvalitatív vizsgálata minél többet elárul a modell viselkedéséről. A továbbiakban röviden áttekintjük saját kutatási eredményeinket.
1.2.1. Hálózati folyamatokkal kapcsolatos saját eredmények
A hálózati folyamatokkal kapcsolatos saját kutatásaink a dinamikai rendszerek és reakció-diffúzió egyenletek vizsgálata során szerzett tapasztalatainkra épülnek. Ku- tatásaink kezdetén különböző típusú hálózatokat és folyamatokat leíró kompartment modelleket vizsgáltunk a differenciálegyenletek kvalitatív elméletének eszközeivel.
EzutánSIStípusú járványterjedés esetén a2N egyenletből álló alapegyenlet-rendszer redukálásának lehetőségeit tanulmányoztuk. A legutóbbi kutatásaink adaptív háló- zatok megértését célozzák meg. Olyan folyamatokat tanulmányozunk, amelyeknél gráf maga is megváltozik a csúcsok állapotától függően. A folyamat során élek szűn- nek meg, illetve jönnek létre a végpontjaik állapotától függően. Az alábbiakban az e három területen végzett munkánkat foglaljuk össze. Az értekezésben részletesen az alapegyenlet-rendszer redukálásával kapcsolatos eredményeinket mutatjuk be.
Információ és járványterjedés
Amennyiben a gráf pontos szerkezete nem ismert (ez áll fenn általában valós model- lek esetén), akkor a gráf struktúráját valamennyiben magában foglaló, mégis jelentős egyszerűsítéseket tartalmazó modelleket célszerű bevezetni. Ezen modellek esetében az egyszerű járványterjedésnél összetettebb folyamatok is vizsgálhatók. A témával foglalkozó első dolgozatunkban egy olyan közönséges differenciálegyenlet-rendszert vizsgáltunk, amely az úgynevezett preferált kapcsolódással jellemezhető hálózaton történő járványterjedést ír le. Egy ilyen hálózatot olyan véletlen gráffal modellez- nek, amelyben a csúcsok kétféle fokszámúak, nevezetesen vannak sok, illetve kevés szomszéddal rendelkező csúcsok. Ezenkívül a modell megadott paraméterei jellem- zik, hogy a magas illetve alacsony fokszámú csúcsok milyen arányban kötődnek az ugyanolyan, illetve ellenkező típusúakhoz, azaz egy adott típusú (fokszámú) csúcs milyen típusúakhoz való kapcsolódást preferál. A [186] dolgozatban megvizsgáltuk, hogy különböző kapcsolódási preferenciák esetén a differenciálegyenlet-rendszer meg- oldásainak tulajdonságaiból mire lehet következtetni a járvány lefolyását illetően.
Két további dolgozatban [187, 189] olyan differenciálegyenleteket vizsgáltunk, amelyek a járvány terjedésével párhuzamosan a járvánnyal kapcsolatos információ terjedését is modellezik a hálózaton. Ezekben a gráfon a csúcsok kapcsolódását vé- letlenszerűnek tekintjük, a differenciálegyenlet kompartment típusú modellből szár- mazik, mind a fertőző, és az egészséges csúcsok két kompartmentbe sorolhatók, asze- rint, hogy a járvány terjedéséről rendelkeznek-e információval, illetve tájékozatlanok.
Különböző feltételezésekből kiindulva számos differenciálegyenlet-rendszer felírható.
Az egyszerűbb modelleket analitikusan megvizsgálva sikerült az információ és beteg- ségterjedés kapcsolatáról biológiailag is releváns elméleti eredményeket igazolni, és ezekkel a szimulációból kapott eredményeket alátámasztani.
Az alapegyenlet redukciója
Az alapegyenlettel kapcsolatos eredményeink az SIS típusú járványterjedés esetére vonatkoznak. A [188] dolgozatban tetszőleges gráf esetén felírtuk az alapegyenletet, amely az irodalomban addig nem jelent meg. Megmutattuk, hogy a gráf automor- fizmuscsoportjának ismeretében az egyenletrendszer mérete jelentősen csökkenthető
1.2. HÁLÓZATI FOLYAMATOK 9 (akár N lineáris függvénye is lehet, ha a gráfnak elegendően sok automorfizmusa van). Ugyanebben a dolgozatban bebizonyítottuk, hogy tetszőleges gráf esetén az I típusú csúcsok számának várható értéke kielégíti az úgynevezett mean-field differen- ciálegyenletet. A [190] dolgozatban a párok számának várható értékére vonatkozó differenciálegyenleteket is levezettük tetszőleges gráf esetén. Ezeket az eredményeket az értekezés 5.4. szakaszában mutatjuk be. Amennyiben az alapegyenlet redukálható N+ 1egyenletre (például teljes gráf esetén), akkor a redukált rendszerből a várható értékre vonatkozó egyenlet lezárására is levezethetők képletek. Ezzel nem-lineáris, viszont kevés egyenletet tartalmazó rendszert kaphatunk, amely N → ∞ esetén az eredeti egzakt rendszer határátmeneteként adódik. A határátmenet egzakt bizonyí- tását, különböző esetekre a [192, 193, 194] cikkek tartalmazzák. Ezen eredményeket az értekezés 6.1. szakaszában tárgyaljuk.
Adaptív hálózatok
Az adaptív hálózatokkal kapcsolatos munkánk keretében olyan folyamatokat tanul- mányoztunk, amelyeknél az élek létrehozása és megszüntetése a csúcsok állapotától függ. Ez a járványterjedés esetében például azzal motiválható, hogy a fertőzöttekkel a többi csúcs igyekszik megszűntetni a kapcsolatát, és ezzel egyidejűleg új kapcsola- tokat hoz létre. A neurális hálózatok modellezése során is fontos annak vizsgálata, hogy a folyamat során maga a gráf hogyan változik, ennek például az embrionális fejlődés során van hatása az agy kialakulására. Az előző vizsgálatainkhoz hasonlóan a csúcsok kétféle állapotban lehetnek, fertőzött (I) és egészséges (S). Így háromféle él fordulhat elő a gráfban SS, SI ésII típusú. Ezek létrehozására és megszünteté- sére három-három rátát adtunk meg, és felírtunk egy öt-változós differenciálegyenlet rendszert azS ésI típusú csúcsok, valamint a háromféle él számának megváltozásá- ra. A rendszerben két paraméter a csúcsok típusának megváltozásával kapcsolatos, hat paraméter pedig az élek létrehozását és elvágását jellemzi. Ebben a rendszerben számos bifurkáció fordulhat elő. A [191] dolgozatban a differenciálegyenlet megoldá- sait hasonlítottuk össze a Monte-Carlo szimulációból kapott eredményekkel, és azt vizsgáltuk, hogy az élek változását meghatározó dinamikától függően milyen egyezést mutat a kétféle megközelítés. A rendszerben megjelenő bifurkációk elméleti vizsgá- latát a [195] dolgozatban közöltük. Kiderítettük, hogy legfeljebb három egyensúlyi pont lehet, melyek közül az egyik a triviális, ún. fertőzés nélküli egyensúly, melyben az I csúcsok száma nulla. Háromféle bifurkációt találtunk a rendszerben. Az első a fertőzés nélküli egyensúlyban megjelenő transzkritikus bifurkáció, melynek során a triviális egyensúly elveszíti stabilitását, és egy ún. endemikus egyensúly jelenik meg.
A második bifurkáció nyereg-csomó típusú, ennek során két endemikus egyensúly jöhet létre. Végül az egyik endemikus egyensúlyban Hopf-bifurkáció következhet be, amely szuperkritikus típusúnak bizonyul, mivel stabil határciklushoz vezet.
2. fejezet
Reakció-diffúzió egyenletek stacionárius megoldásai
Ebben a fejezetben az egy reakció-diffúzió egyenletre (m= 1) vonatkozó, stacionárius megoldások számával kapcsolatos eredményeinket ismertetjük. LegyenΩ⊂Rnsima határú tartomány, a legtöbb esetben ez gömb lesz, és tekintsük a
∆u+f(u) = 0
szemilineáris elliptikus egyenletet azonosan nulla Dirichlet peremfeltétel, azazu|∂Ω= 0 mellett. Vizsgálatunk tárgya a pozitív megoldások száma. A kérdésfelvetés ilyen formában nagyon általános, az irodalomban több ezer publikáció található ezzel kap- csolatosan, melyek különböző tartományok és különböző nemlinearitások esetén tár- gyalják a kérdést. (A Mathematical Reviews keresője az "elliptic positive solution"
szavakra mintegy 6500 találatot ad.) Általános tartomány esetén a megoldások szá- mának vizsgálatára topológiai, variációs és monoton módszereket, valamint bifur- kációs technikákat alkalmaznak. A nemlinearitások tekintetében jelentős és gyors fejlődésnek lehetünk tanúi az irodalmat tanulmányozva. Először monotonf függvé- nyek esetén vizsgálták a kérdést, majd a konkáv és konvex függvények után olyanok következtek, melyek egy szakaszon konvexek egy másikon pedig konkávak. Az ered- mények nagyrészt a megoldás létezéséről, illetve egyértelműségéről szólnak. Több megoldás létezésének bizonyítása jóval nehezebb feladat, a megoldások pontos szá- mának eldöntése pedig csak speciális esetekben sikerül. Az általunk kitűzött cél az általános kérdésfelvetésnél annyiban egyszerűbb, hogy gömb tartományon vizsgál- juk a feladatot, viszont szeretnénk a megoldások pontos számát megadni, legalábbis bizonyos nemlinearitások esetén. A továbbiakban tehát a
∆u+f(u) = 0 BR-ben (2.1)
u = 0 ∂BR-en (2.2)
peremérték-problémát vizsgáljuk, aholBR az origó közepű R sugarú gömb.
Gömb tartomány esetén a pozitív megoldásokról ismert, hogy radiálisan szim- metrikusak [62], ezért a feladat az alábbi, közönséges differenciálegyenletre vonatkozó
11
peremérték-feladatra redukálódik.
ru′′(r) + (n−1)u′(r) +rf(u(r)) = 0 (2.3) u′(0) = 0, u(R) = 0. (2.4) Célunk tehát ezen feladat pozitív megoldásainak pontos számát meghatározni. A fejezet felépítése a következő. Először a mi vizsgálatainkhoz kapcsolódó ismert ered- ményeket tárgyaljuk, majd vizsgálatunk eszközével a "time-map" leképezéssel kap- csolatos alapvető definíciókat és tételeket ismertetjük. Ezt követően mutatjuk be a konvex f függvényekre, kvázilineáris egyenlet eseténp-konvex függvényekre, vala- mint szinguláris nemlinearitásokra vonatkozó eredményeinket. Végül a stacionárius megoldások stabilitásáról szóló eredményeinket ismertetjük.
2.1. Irodalmi áttekintés
Az irodalomban a (2.1)-(2.2) peremérték-feladat helyett legtöbbször a
∆u+λf(u) = 0 B1-ben (2.5)
u = 0 ∂B1-en (2.6)
problémát vizsgálják, melyben azRhelyett aλa paraméter. Egyszerű változótransz- formáció mutatja, hogy a két feladat az R2 =λhelyettesítéssel ekvivalens. Ugyanis, hau megoldása a (2.1)-(2.2) problémának, akkorU(y) =u(√
λy)megoldása a (2.5)- (2.6) feladatnak. Ebben a szakaszban a (2.5)-(2.6) peremérték-feladattal kapcsolatos eredményeket foglaljuk össze. Megjegyezzük, hogy számos dolgozat foglalkozik a fel- adattal más tartományokon, például gyűrű alakú tartományon, vagy teljes téren [95].
Ezeket az eredményeket itt nem ismertetjük.
A vizsgálatok természetesen az f(u) = u lineáris esetből indultak ki, amelynél pontosan akkor létezik pozitív megoldás, ha λ = λ1, a −∆ operátor sajátértéke.
(Ekkor végtelen sok pozitív megoldás van).
Az első nem-lineáris eredmény az f(u) = up függvényre vonatkozott, Pohozaev 1965-ben bebizonyította [122], hogy pontosan akkor létezik pozitív megoldás, ha p < n+2n−2. A bizonyítás két új gondolaton alapult. Pohozaev egyrészt levezetett egy (később róla elnevezett) azonosságot, melynek radiális megoldásokra vonatkozó alakját, (2.26)-t, később használni fogjuk. Ennek segítségével egyszerűen látható, hogy p ≥ n+2n−2 esetén nincs megoldás. Másrészt variációs módszer alkalmazásával igazolta, hogyp < n+2n−2 esetén van pozitív megoldás (amely egy megfelelően választott funkcionál feltételes szélsőértéke), sőt ez egyértelmű is.
Pohozaev ezen eredménye nagy hatással volt a későbbi vizsgálatokra. Joseph és Lundgren 1973-ban azf(u) = (1 +u)pesetet vizsgálták [78]. Kiderült, hogyp= n+2n−2 esetén itt is jelentősen megváltozik a megoldások száma. Míg a kritikus érték alatt pontosan kettő megoldás van, haλegy adott érték alatt van, és nincs megoldás ezen érték feletti λesetén, addig p > n+2n−2 esetén olyanλ értékek is vannak, amelyeknél végtelen sok pozitív megoldás van. A megoldások pontos számát fázissík analízissel tudták meghatározni, az egyenletet autonóm két-változós rendszerré transzformálva.
A későbbi intenzív kutatásokat Brezis és Nirenberg 1983-as cikke [28] indította el. Ebben foglalkoztak először az f(u) = up +uq esettel, elsősorban akkor, amikor
2.1. IRODALMI ÁTTEKINTÉS 13 p = n+2n−2 és 1 ≤q < n+2n−2. A q = 1 esetben igazolták, hogy a megoldás létezésének feltételen ≥4 esetén λ < λ1, n = 3esetén pedig λ ∈(λ1/4, λ1). A q > 1 esetben megmutatták, hogy bármely pozitívλválasztása mellett létezik megoldás, han≥4, vagyn= 3 és 3< q <5 (ekkor a kritikus kitevő n+2n−2 = 5). Az n= 3 és 1< q ≤3 esetben megmutatták, hogy csak bizonyosλértékek felett van megoldás.
Brezis és Nirenberg ezen cikke nyomán sokan vizsgálták a megoldások pontos számát. Míg Brezis és Nirenberg általános tartományon tanulmányozták a kérdést, addig a megoldások pontos számával kapcsolatos eredmények elsősorban a gömb tartomány és radiális megoldások esetére vonatkoztak. Atkinson és Peletier 1986- ban megmutatták [8], hogy az előbb említett p = 5, n = 3 és 1 < q ≤ 3 esetben gömbön létezik legalább két pozitív megoldás, haλbizonyos érték felett van. Ezután az eredmény után intenzív kutatás indult meg azzal a céllal, hogy kiderítsék, melyn és1≤q < p < n+2n−2 értékek mellett lesz azf(u) =up+uqesetben a pozitív megoldás egyértelmű.
A q = 1 esetben az egyértelműséget különböző módszerekkel egymástól függet- lenül többen is bebizonyították: Zhang [153], illetve Kwong és Li [97] 1992-ben, Srikanth [138] 1993-ban, valamint Adimurthi és Yadava [1] (kvázilineáris egyenlet- re is) 1994-ben. Ezekben a dolgozatokban az egyértelműséget p = n+2n−2 esetén is igazolták.
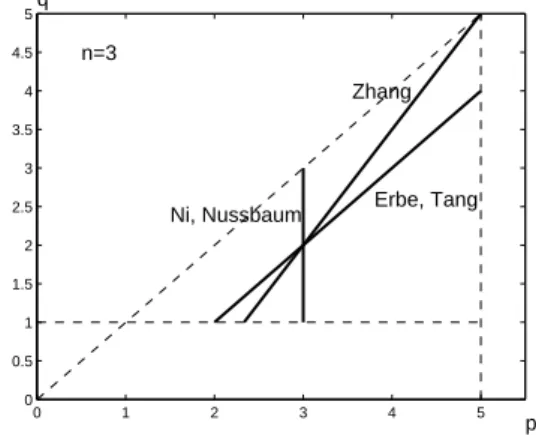
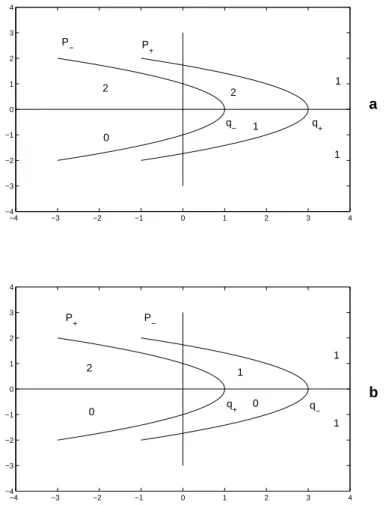
Ha q > 1, akkor láttuk, hogy p = n+2n−2 esetén lehet két megoldás is, azonban a p < n+2n−2 esetben csak egyértelműségi eredmények vannak. Az első, korai ered- mény Ni és Nussbaum nevéhez fűződik [114]. Már 1985-ban bebizonyították, hogy 1 ≤ q < p < n−n2 esetén a megoldás egyértelmű. Zhang 1995-ben [154] azt mutat- ta meg, hogy n(p−1) ≤ 2(q + 1) esetén egyértelmű a megoldás. Végül Erbe és Tang 1997-ben [54] bebizonyították, hogy p−1 ≤q < p < n+2n−2 esetén a megoldás egyértelmű. Ez utóbbi eredményből az is következik, hogy ha n≥6, akkor a teljes vizsgált tartományban, azaz1≤q < p < n+2n−2 esetén egyértelmű a megoldás, ugyan- is n ≥6 esetén n+2n−2 ≤2, így p−1 ≤ q automatikusan teljesül. A három dolgozat [54, 114, 154] eredményét érdemes a (p, q) paraméter síkon összehasonlítani, amint a 2.1. ábrán látható az n = 3 esetben. Az 1 ≤ q < p < n+2n−2 háromszögben a megadott szakaszoktól balra eső részben igazolták a fenti dolgozatok szerzői az egy- értelműséget. Mint láttuk, n≥6 esetén az egész háromszögben egyértelműség van, azonban 2 < n < 6 esetén a háromszög bizonyos részein a megoldások száma nem ismert. Numerikus vizsgálataink azt mutatják, hogy az egyértelműség nem is igaz a háromszög jobboldali éle mellett.
A 0 < q < 1 esetet is többen vizsgálták a megoldások száma szempontjából.
Ouyang és Shi 1999-ben igazolták [116], hogy n ≥ 4 és 1 < p < n−n2 esetén egy bizonyosλérték alatt két megoldás van, felette pedig nincs megoldás. Yadava [149]
megmutatta, hogy ez az állításn= 3esetén és valamivel bővebb(p, q)tartományban is igaz. Ez a tartomány azonban még nem fedte le a0< q <1< p≤ n+2n−2 téglalapot.
Végül Tang 2003-ban igazolta, hogy az állítás fennáll a teljes téglalapban [141].
A 0 < q < p < 1 háromszögben található p és q értékekre az f(u) = up +uq függvény szublineáris, ezért minden λ esetén pontosan egy pozitív megoldása van a (2.5)-(2.6) peremérték-feladatnak, általános tartomány esetén is [29].
A szuperkritikus (p > n+2n−2) tartomány nagy részében nem ismert a megoldások
0 1 2 3 4 5 0
0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Ni, Nussbaum
Zhang
Erbe, Tang n=3
p q
2.1. ábra. A (2.5)-(2.6) peremérték-feladat megoldásának egyértelműségef(u) =up+ uq ésn= 3esetén. A [54, 114, 154] dolgozatokban adott feltételek összehasonlítása.
Az egyértelműség az 1≤q < p < n+2n−2 háromszögben a megadott szakaszoktól balra eső részben teljesül. Azn= 3esetben a kritikus érték n+2n−2 = 5, és a [114] dolgozatban szereplő határ nn−2 = 3.
pontos száma. Mindössze annyit mondhatunk, hogy ha p > q > n+2n−2, akkor a Pohozaev-azonosságból egyszerűen következik, hogy nincs megoldás.
A fenti összefoglalást azf(u) =up+uqfüggvény esetére végeztük el, azonban az említett dolgozatok nagy része általánosabb f függvényekre vonatkozik. Pohozaev [122] dolgozata után többen vizsgálták a konvexf függvény esetét. Mint láttuk, már az f(u) = (1 +u)p esetében is rendkívül bonyolult lehet a bifurkációs diagram, ezért konvex esetben csak az n = 1 esetben lehet teljes leírást adni. Laetsch dolgozatai [98, 99] és Schaaf [130] könyve nyomán megadtuk a bifurkációs diagrammok teljes osztályozását konvex f és n = 1 esetén [178]. A konvex esethez képest konkáv f függvényekre teljesebb leírás adható több dimenziós tartományok esetén is. Erről számos eredményt olvashatunk Castro és munkatársai dolgozataiban [34, 35, 36]. A konvex-konkáv típusú nemlinearitások (amikor f egy szakaszon konvex, egy mási- kon pedig konkáv) vizsgálata Ambrosetti, Brezis és Cerami cikkével kezdődött [5].
Ebben az esetben elsősorban az f(u) = up −uq, f(u) = up +uq (q < 1), illetve f(u) =u(u−b)(c−u) függvények adják a vizsgálatok motivációját. Ezekkel számos szerző foglalkozott [54, 90, 91, 115, 116, 147, 155]. Kiemelendő Ouyang és Shi [116]
dolgozata, melyben bizonyos kiegészítő feltételeket teljesítő konvex-konkáv típusú nemlinearitások esetén megadják a bifurkációs diagrammok teljes osztályozását.
2.2. A "time-map" módszer
Ebben a szakaszban bemutatjuk vizsgálataink legfontosabb eszközét az ú.n. célba- lövéses, vagy "time-map" módszert. A módszer lényege, hogy a (2.3) differenciál- egyenletet először a (2.4) peremfeltétel helyett az
u(0) =c, u′(0) = 0 (2.7)
2.2. A "TIME-MAP" MÓDSZER 15 kezdeti feltétellel tekintjük. Az egyenlet az r = 0 pontban adott kezdeti feltétel mellett szinguláris, így a hagyományos egzisztencia és unicitás tétel nem alkalmaz- ható. Azonban annak bizonyításához hasonlóan igazolható, hogy a fenti kezdeti feltétel mellett létezik egyetlen C2 megoldás u(·, c) bármely c > 0 esetén [137]. Ez- után a peremérték-probléma megoldását az ú.n. célbalövéses módszerrel keressük (shooting), azaz a cértékét változtatjuk mindaddig, amíg olyan megoldást kapunk, amelynek első gyöke aR pontban van. Ehhez definiáljuk az alábbi leképezést (time- map).
T(c) = min{r >0 :u(r, c) = 0} ; D(T) ={c >0 :∃r >0u(r, c) = 0}. (2.8) A (2.3)-(2.4) peremérték-probléma pozitív megoldásainak száma tehát egyenlő a T(c) =R egyenlet c-re kapott megoldásainak számával. Ennek meghatározásához a T leképezés alábbi tulajdonságaira van szükség:
• T értelmezési tartománya;
• T határértéke az értelmezési tartomány határpontjaiban;
• T monotonitása az értelmezési tartomány részintervallumaiban.
A következő szakaszokban a time-map fenti három tulajdonságának általános vizsgálatával foglalkozunk.
2.2.1. A "time-map" monotonitása
A monotonitás meghatározásához célszerű a T függvényt meghatározó u(T(c), c)≡0 u(r, c)>0, 0< r < T(c)
implicit egyenletet használni. Az egyenletet differenciálva, aT függvény deriváltjára az alábbi adódik
∂ru(T(c), c)T′(c) +∂cu(T(c), c)≡0. (2.9) AT szélsőértékeinek vizsgálatakor szükség van a második derivált előjelére azokban a pontokban, ahol az első derivált eltűnik. A fenti egyenletet deriválva azt kapjuk, hogyT′(c) = 0esetén
∂ru(T(c), c)T′′(c) +∂c2u(T(c), c) = 0. (2.10) A (2.9) és (2.10) egyenletekben szereplő c szerinti parciális deriváltakat a variációs egyenletből határozhatjuk meg. A továbbiakban azf függvényről mindig feltételez- zük a kellő simaságot a megfelelő deriváltak létezéséhez. Deriváljuk tehát a (2.3) differenciálegyenletetcszerint. Bevezetve a
h(r, c) =∂cu(r, c), z(r, c) =∂c2u(r, c) függvényeket, az alábbi kezdetiérték-feladatokat kapjuk
rh′′(r, c) + (n−1)h′(r, c) +rf′(u(r, c))h(r, c) = 0 (2.11) h(0, c) = 1, h′(0, c) = 0, (2.12)
rz′′(r, c) + (n−1)z′(r, c) +rf′(u(r, c))z(r, c) +rf′′(u(r, c))h2(r, c) = 0(2.13) z(0, c) = 0, z′(0, c) = 0,(2.14) Ezen függvények segítségével a (2.9) és (2.10) egyenletek az alábbi alakba írhatók
u′(T(c), c)T′(c) +h(T(c), c) = 0, (2.15) u′(T(c), c)T′′(c) +z(T(c), c) = 0, (2.16) ahol az utóbbi csak T′(c) = 0 esetén áll fenn. Vegyük észre, hogy ezekben az egyen- letekben u′(T(c), c) < 0, hiszen T(c) az u függvény első zérushelye. Így T′(c) és T′′(c) előjelét a h ész függvény előjele határozza meg. Ezen függvények gyökeinek elhelyezkedését a Sturm-féle szeparációs tétel segítségével fogjuk vizsgálni. Ezen té- telek alkalmazásakor szükség lesz a v(·, c) =u′(·, c) függvényre. Az erre vonatkozó differenciálegyenletet és kezdeti feltételt az u függvényre vonatkozó (2.3) differenci- álegyenletből (pontosabban annakr-rel elosztott alakjából), valamint a (2.7) kezdeti feltételbőlr szerinti deriválással kapjuk
rv′′(r, c) + (n−1)v′(r, c) + (rf′(u(r, c))−n−1
r )v(r, c) = 0 (2.17) v(0, c) = 0, v′(0, c) = −f(c)
n . (2.18) A deriváltra vonatkozó kezdeti feltételt a (2.3) differenciálegyenletbőlu′′(0)kifejezé- sével és a L’Hospital-szabály alkalmazásával kapjuk. Az alábbiakban, ha nem okoz félreértést, akkor az u, h, z, v függvények második változóját nem írjuk ki, tehát például u(r, c) helyett u(r)-et írunk. A továbbiakban alapvető fontosságú lesz az alábbi Lemma [178].
2.1. Lemma. Ha n= 1, akkor ah függvénynek legfeljebb egy gyöke lehet a[0, T(c)]
intervallumban.
Bizonyítás. Az n= 1 esetben a hésv függvényre vonatkozó (2.11) és (2.17) diffe- renciálegyenlet megegyezik. Ezért a Sturm-féle szeparációs tétel szerint a két függ- vény gyökei elválasztják egymást. Ha a h függvénynek lenne két gyöke a [0, T(c)]
intervallumban, akkor a v függvénynek is lenne gyöke, azaz u′ valahol 0 lenne a (0, T(c)) intervallumban. Ez azonban lehetetlen, ugyanis egyrészt a radiális szim- metriára vonatkozó [62] cikkbeli tételbőlu′(r)<0is következik mindenr∈(0, T(c)]
esetén, másrészt ez elemien is igazolható, ahogy hamarosan látni fogjuk.
A Lemmát a [178] dolgozatban bizonyítottuk ilyen egyszerű formában, ugyanis ennek segítségével konvex nemlinearitás esetén teljes leírás adható a megoldások pon- tos számáról. A későbbi vizsgálatokban alapvető szerepet játszik az alábbi feltétel, melynek az irodalomban "disconjugacy" feltétel a neve:
A hfüggvénynek legfeljebb egy gyöke lehet a [0, T(c)]intervallumban. (2.19) A Lemma szerint, ez bármely f függvény esetén teljesül, ha n= 1. Azonban n >1 esetén csak bizonyos függvényekre igaz. Amint ez közvetve már ismert volt, a (2.19)
2.2. A "TIME-MAP" MÓDSZER 17 feltétel nem igaz például azf(u) = (1+u)p függvény, ésp > n+2n−2 esetén [78], valamint az f(u) =u5+u2 függvény és n= 3 esetén [8]. A feltétel teljesülésének bizonyítása a legtöbb esetben meglehetősen nehéz. Azonban mivel kulcsszerepet játszik a megol- dások pontos számának meghatározásában, azért számos speciális esetben igazolták n >1 esetén is. Az f(u) =up+λuq függvény esetében különböző p és q értékekre a 2.1. szakaszban felsorolt dolgozatok mindegyikében, ahol egyértelműséget igazol- nak, bebizonyítják a (2.19) feltételt. Az f(u) =up−λu függvény esetében Kwong [96] és McLeod [108] igazolták a feltétel teljesülését.
Nézzük meg most, hogy a T deriváltjaira vonatkozó fenti képletek a Sturm-féle szeparációs tétel segítségével hogyan használhatók aT monotonitásának eldöntésére.
A Sturm-féle szeparációs tétel közvetlen alkalmazása helyett, az annak bizonyításá- ban használt alábbi azonosságot fogjuk használni. Legyenek u1, u2 : [r1, r2] → R kétszer folytonosan differenciálható függvények. Ekkor
Z r2
r1
(rn−1u′1(r))′u2(r)−(rn−1u′2(r))′u1(r)dr = (2.20) rn2−1(u′1(r2)u2(r2)−u1(r2)u′2(r2)) +rn1−1(u1(r1)u′2(r1)−u′1(r1)u2(r1)).
2.1. Állítás. Tegyük fel, hogy teljesül a (2.19) feltétel és f szuperlineáris, azaz uf′(u)−f(u) > 0 minden u > 0 esetén, (vagy másszóval f(u)u szigorúan monoton növő). Ekkor fennáll T′<0.
Bizonyítás. Az ués hfüggvényekre (2.3) és (2.11) alapján fennállnak az
(rn−1u′)′+rn−1f(u) = 0, (rn−1h′)′+rn−1f′(u)h= 0 (2.21) differenciálegyenletek. Szorozzuk meg az első egyenleteth-val, a másodikat pedigu- val, vonjuk ki egymásból a kettőt, majd integráljunk a[0, T(c)]intervallumon. Ekkor a (2.20) azonosságot alkalmazvar1= 0,r2 =T(c),u1 =u,u2 =h esetén
Z T(c)
0
rn−1h(r) u(r)f′(u(r))−f(u(r))
dr= (T(c))n−1u′(T(c))h(T(c)).
Ebből következik, hogy ahfüggvénynek van gyöke a[0, T(c)]intervallumban, ugyan- is, ha nem lenne ott gyöke, akkor a baloldal pozitív, a jobboldal pedig negatív lenne.
Most kap szerepet a (2.19) feltétel, ugyanis ekkor a 2.1. Lemma miatt ah függvény- nek nem lehet több gyöke, teháth(T(c))<0. Ebből viszont (2.15) szerint következik T′(c)<0.
2.2. Állítás. Legyenn≥1, és tegyük fel, hogyf szublineáris, azazuf′(u)−f(u)<0 mindenu >0 esetén, (vagy másszóval f(u)u szigorúan monoton fogyó). Ekkor fennáll T′>0.
Bizonyítás. Megmutatjuk, hogy ah függvénynek nincs gyöke a [0, T(c)] interval- lumban. Ugyanis tegyük fel, hogyh(r∗) = 0 ésr∗ a h első gyöke, (ezérth′(r∗)<0).
Szorozzuk meg a (2.21) első egyenletét h-val, a másodikat pedig u-val, vonjuk ki
egymásból a kettőt, majd integráljunk a [0, r∗] intervallumon. Ekkor a (2.20) azo- nosságot alkalmazva r1 = 0,r2 =r∗,u1=h,u2 =u esetén
Z r∗
0
rn−1h(r) f(u(r))−u(r)f′(u(r))
dr = (r∗)n−1u(r∗)h′(r∗).
Ekkor a baloldal pozitív, a jobboldal pedig negatív, amely azt igazolja, hogy a h függvénynek nincs gyöke a[0, T(c)]intervallumban. Így teháth(T(c))>0, melyből (2.15) szerint következik T′(c)>0.
Megjegyezzük, hogy a szuperlinearitás és a szublinearitás a függvény konvexitá- sával függ össze, hiszen az l(u) = uf′(u)−f(u) függvényre l′(u) = uf′′(u). Ezért f′′ > 0 és f(0) ≤ 0 esetén, l(0) ≥ 0 és l′(u) > 0, így uf′(u)−f(u) = l(u) > 0, amennyiben u > 0. Hasonlóan f′′ <0 és f(0)≥0 esetén, l(0)≤0 ésl′(u)<0, így uf′(u)−f(u) = l(u) <0, amennyiben u > 0. Tehát az alábbi egyszerű Állítás áll fenn.
2.3. Állítás. Haf′′>0ésf(0)≤0, akkorf szuperlineáris. Haf′′<0ésf(0)≥0, akkor f szublineáris.
AT függvény monotonitásának vizsgálata után térjünk rá most szélsőértékeinek vizsgálatára.
2.4. Állítás. Tegyük fel, hogy a (2.19) feltétel teljesül és f′′ > 0. Ekkor T′(c) = 0 esetén fennáll T′′(c)<0, azazT szélsőértéke csak maximum lehet.
Bizonyítás. A T′(c) = 0 feltételből (2.15) szerint következik h(T(c)) = 0. Így a (2.19) feltétel miatt h(r) > 0 a [0, T(c)) intervallumban. Végezzük el a h és z függvény Sturm-féle összehasonlítását. Ezekre a függvényekre (2.11) és (2.13) alapján fennállnak a
(rn−1h′)′+rn−1f′(u)h= 0, (rn−1z′)′+rn−1(f′(u)z+f′′(u)h2) = 0 (2.22) differenciálegyenletek. Szorozzuk meg az első egyenletetz-vel, a másodikat pedigh- val, vonjuk ki egymásból a kettőt, majd integráljunk a[0, T(c)]intervallumon. Ekkor a (2.20) azonosságot alkalmazva r1 = 0,r2 =T(c),u1 =h,u2 =z esetén
Z T(c)
0
rn−1h3(r)f′′(u(r))dr = (T(c))n−1h′(T(c))z(T(c)).
Mivel a baloldal pozitív ésh′(T(c))<0(hiszenT(c)ahelső gyöke), azértz(T(c))<
0, melyből (2.16) szerint következik T′′(c)<0.
Teljesen hasonlóan igazolható az alábbi.
2.5. Állítás. Tegyük fel, hogy a (2.19) feltétel teljesül és f′′ < 0. Ekkor T′(c) = 0 esetén fennáll T′′(c)>0, azazT szélsőértéke csak minimum lehet.
Ezen állítások lehetővé teszik, hogy n= 1 esetén teljes leírást adjunk konvex és konkáv f esetén a megoldások számáról. Ehhez azonban még szükség van aT értel- mezési tartományának és határértékeinek meghatározására. Ezekkel foglalkozunk a következő szakaszokban.
2.2. A "TIME-MAP" MÓDSZER 19 2.2.2. A "time-map" értelmezési tartománya
Az értelmezési tartomány meghatározásához célszerű bevezetni az n = 1 esethez tartozó Hamilton- függvényt
H(r) := u′(r)2
2 +F(u(r)), (2.23)
ahol F(u) := Ru
0 f. Az n > 1 esetben ez Ljapunov-függvényként szolgál, ugyanis H′(r) =−n−r1u′2(r)≤0. Könnyen látható, hogy amennyiben az ufüggvénynek van gyöke, akkoru′(r) <0 minden r ∈(0, R]esetén, ahol R jelöli az első gyököt. Ilyen esetben tehát fenn kell állnia azu′′(0)<0 egyenlőtlenségnek, amelyből f(u(0))>0 következik. Ezzel a következőt igazoltuk.
2.6. Állítás. Ha c∈D(T), akkor f(c)>0.
Könnyen kaphatunk ennél jobb feltételt is a Ljapunov függvény segítségével. Ugyanis c∈D(T) esetén bármely d∈(0, c) számhoz van olyan r >0, melyre u(r) =d. Így
F(d) =F(u(r)) =H(r)−u′(r)2
2 < H(r)≤H(0) =F(c), amely az alábbit bizonyítja.
2.7. Állítás. Ha c∈D(T), akkor F(c)> F(d) minden d∈(0, c) számra.
Az értelmezési tartományra tehát fennáll
D(T)⊂ {c >0 : F(c)> F(d) ∀ d∈(0, c) ésf(c)6= 0}=:Pf. (2.24) Az n= 1 esetben pontosan megadható az értelmezési tartomány.
2.8. Állítás. Ha n= 1, akkor D(T) =Pf.
A differenciálegyenlet (2.21) képletbeli alakját integrálva
−rn−1u′(r) = Z r
0
ρn−1f(u(ρ))dρ. (2.25) Ha f pozitív, akkor létezik olyan r1 > 0 és K > 0, hogy minden r > r1 esetén u′(r) ≤ −rn−1K . Ezért ha n ≤ 2, akkor u nem lehet minden r > 0 esetén pozitív, valahol eléri a nullát. Így az alábbit igazoltuk
2.9. Állítás. Legyen n≤2. Ekkor, ha f(u)>0 minden u∈(0,+∞) esetén, akkor D(T) = (0,+∞), azaz ekkor is teljesül D(T) =Pf.
Magasabb dimenzió eseténf pozitivitásából nem következik, hogy D(T) =Pf. Erre a legegyszerűbb példa az f(u) = up függvény p ≥ (n+ 2)/(n−2) esetén. Ekkor ugyanis D(T) = ∅ és Pf = (0,+∞). Az előbbi bizonyítása az alábbi Pohozaev- azonosságon alapul [122].
rnu′2(r) + 2rnF(u(r)) + (n−2)rn−1u(r)u′(r) = (2.26) Zr
0
sn−1[2nF(u(s))−(n−2)u(s)f(u(s))]ds.
Ugyanisp≥(n+2)/(n−2)esetén a jobboldal nem pozitív, míg, ha azufüggvénynek lenne gyöke, akkor ott a baloldal pozitív lenne.
Apkitevőre vonatkozó feltétel éppen a kritikus Szoboljev-kitevőt adja. Pohozsa- ev variációs módszerrel bebizonyította, hogyp <(n+2)/(n−2)esetén van megoldása a peremérték-problémának, akkor D(T) = Pf. Ha azonban az f függvényre fenn- áll f(0) > 0, akkor a (2.25) képlet segítségével, ha pedig az f függvényre lineáris alsó becslés adható, akkor a megfelelő lineáris egyenlettel való Sturm összehason- lítás segítségével megmutatható, hogy a megoldások elérik a nullát, azaz fennáll a következő.
2.10. Állítás. Legyen n ≥ 1, α ∈ (0,+∞]. Ha f > 0 a (0, α) intervallumban és lim inf
u→0 f(u)
u >0, akkor (0, α) ⊂D(T). Következésképpen, haf(α) = 0, akkor (0, α) maximális részintervalluma D(T)-nek.
2.2.3. A "time-map" határértékei az értelmezési tartomány határ- pontjaiban
Az alábbi állításokat a T határértékeiről a [178] dolgozatban bizonyítottuk. A bizo- nyításokat itt nem közöljük. A következő Állítást ismét Sturm típusú összehasonlí- tással lehet igazolni.
2.11. Állítás. Legyenn≥1, és 0∈∂D(T).
(a) Ha f(0)>0, akkor lim
0 T = 0.
(b) Ha f(0) = 0 és f′(0)>0, akkor lim
0 T ∈(0,+∞).
(c) Ha f(0) = 0 és f′(0) = 0, akkor lim
0 T = +∞.
2.12. Állítás. Legyenn≥1, és legyen c >0 a ∂D(T)\D(T) halmaz eleme. Ekkor limc T = +∞.
Az alábbi állítás bizonyításában fontos szerepet játszik azn= 1feltétel, ugyanis ebben az esetben aT függvény integrál előállítását kell használni.
2.13. Állítás. Legyenn= 1, és +∞ ∈∂D(T).
(a) Ha lim
u→+∞ f(u)
u = +∞, akkor lim
+∞T = 0.
(b) Ha lim
u→+∞ f(u)
u =L∈(0,+∞), akkor lim
+∞T = π
2√ L. (c) Ha lim
u→+∞ f(u)
u = 0, akkor lim
+∞T = +∞.
2.14. Állítás. A 2.13. Állítás (c) része fennálln≥1 esetén is.