Arbitrázs és martingálmérték

GAZDÁLKODÁS- ÉS SZERVEZÉSTUDOMÁNYOK DOKTORI ISKOLA

Badics Tamás

ARBITRÁZS ÉS MARTINGÁLMÉRTÉK

PhD értekezés

Témavezet½o: Dr. Medvegyev Péter

Értekezés a PhD fokozat elnyerése érdekében

a Pannon Egyetem Gazdálkodás- és Szervezéstudományok Doktori Iskolájához tartozóan

Írta:

Badics Tamás

A jelölt a doktori szigorlaton 100%-ot ért el,

Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: ... ... igen/nem

...

(aláírás) Bíráló neve: ... ... igen/nem

...

(aláírás) Bíráló neve: ... ... igen/nem

...

(aláírás)

A jelölt az értekezés nyilvános vitáján ... %-ot ért el.

Veszprém ...

(a Bíráló Bizottság elnöke)

A doktori oklevél min½osítése ... ...

(az EDT elnöke)

1. Bevezetés 6

1.1. Az alaptétel . . . 6

1.2. Az értekezés felépítése és újszer½u eredményei . . . 16

2. A Delbaen–Schachermayer-tétel el½ozményei 20 2.1. Az általános egyensúlyelmélett½ol az arbitrázsárazásig . . . 21

2.1.1. Az Arrow–Debreu-egyensúly . . . 21

2.1.2. A Radner-egyensúly . . . 25

2.1.3. Arbitrázsmentesség . . . 29

2.2. Életképesség és a Kreps–Yan-tétel . . . 31

2.3. A sztochasztikus folyamatok általános elmélete . . . 39

3. A pénzpiac modellje több periódus esetén 47 3.1. Pénzpiac végesen generált valószín½uségi mez½o esetén . . . 48

3.1.1. Ön…nanszírozó kereskedési stratégiák . . . 48

3.1.2. Ármérce-invariancia . . . 50

3.1.3. Az arbitrázs fogalma . . . 52

3.2. A Dallang–Morton–Willinger-tétel . . . 54

3.3. Folytonos idej½u pénzpiacok . . . 55

3.3.1. Ön…nanszírozó portfóliók . . . 55

3.3.2. Ármérce invariancia . . . 57

4. Alaptétel szemimartingál modellben 61 4.1. Néhány el½ozetes eredmény . . . 68

4.1.1. A kompaktsági lemma . . . 68 4.1.2. Az L⁰ korlátos és zárt részhalmazainak van maximális eleme 73

4.1.3. Gyenge* topológia és a sztochasztikus konvergencia . . . 77

4.2. Mémin tételére való visszavezetés . . . 80

4.2.1. A sztochasztikus integrálok értékének kiterjesztése a végte- lenbe . . . 81

4.2.2. A lehetséges „kaszálások” terének korlátossága . . . 83

4.2.3. AC₀ Fatou-zártsága és a C gyenge* zártsága . . . 85

4.2.4. A maximális elem és a Fatou-zártság . . . 85

4.2.5. A közelít½o sorozatok egyenletes konvergenciája . . . 86

4.3. A szemimartingál topológiában konvergens sorozat létezése . . . 91

4.3.1. Új mértékre való áttérés . . . 91

4.3.2. Néhány egyszer½u becslés . . . 93

4.3.3. Néhány szörny½u becslés . . . 96

4.3.4. A szemimartingál topológiában konvergens sorozat meghatározása . . . 113

4.4. Az alaptétel többdimenziós szemimartingál modellek esetén . . . 121

5. Martingálmérték és optimális portfóliók 128 5.1. A portfolió választás duális megközelítése véges dimenzió esetén . . 129

5.1.1. A haszonmaximalizációs probléma . . . 129

5.1.2. A minimaxmérték . . . 131

5.1.3. Lagrange-dualitás . . . 132

5.2. A portfolióválasztás duális megközelítése végtelen dimenzió esetén . 137 5.2.1. AC kúp és a martingálmértékek halmaza közti duális kap- csolat . . . 137

5.2.2. A haszonmaximalizálási probléma és a duálisa . . . 140

5.2.3. A minimaxmérték . . . 142

6. A Frittelli-féle alaptétel 145 6.1. Arbitrázs és preferenciák . . . 145

6.1.1. A sztochasztikus dominancia . . . 145

6.1.2. A „no market free lunch” fogalma . . . 147

6.2. Az alaptétel . . . 149

7. Arbitrázsfogalmak karakterizációja 153 7.1. Az arbitrázsmentesség és NFLVR . . . 154

7.2. Az Orlicz-terek elmélete . . . 155

7.3. A "nincs ingyenebéd" feltétel . . . 156 7.4. Az életképesség egy újabb megközelítése . . . 158 8. Az állapotár de‡átor és az egy ár törvénye 159 8.1. Az egy ár törvénye kétperiódusos modellben . . . 159 8.2. Állapotár de‡átor és kockázati prémium . . . 160 8.3. Az egy ár törvényének karakterizációja . . . 163

9. Összegzés 165

10.További kutatási lehet½oségek 168

A szerz½onek az értekezés témájához kapcsolódó publikációi 170

Irodalom 171

1.1. A martingálmérték geometriai interpretációja . . . 13 5.1. Konkáv függvény duális leírása . . . 130

This dissertation deals with the foundation of the theory of asset pricing in a fric- tionless market under the most general assumptions. At this level of abstraction, the pricing techniques, treated in the known monographs on mathematical …nance (e.g. [80], [33], [60] and [9]) do not work, so the semimartingale theory consists mainly of existence statements.

One of the most important problem of asset pricing is the mathematical char- acterization of the economically consistent models of …nancial markets. From the economic point of view the assumption of no-arbitrage –i.e. the assumption that one cannot do business in which one can only gain with strictly positive probability but without exposure to risk –seems a fairly mild condition and it is astonishing what far-reaching consequences it has. Under the Fundamental Theorem of Asset Pricing we mean such types of statements which assert an equivalence between the above-mentioned consistency condition and some mathematical properties of the stochastic process describing asset prices. The fundamental theorem of asset pricing, loosely speaking, asserts that the absence of arbitrage is equivalent to the existence of an equivalent probability measure, under which the discounted price process is a "martingale", which means that there is a new …ctive probability – the martingale measure – under which one can’t systematically gain on average.

It will be showed, the martingale measure play important role both in the theory of complete and incomplete markets.

The aim of the dissertation is to survey the literature and the mathematical and economic antecedents of the fundamental theorem of asset pricing for semi- martingale models, to present a didactic uni…ed treatment of the semimartingale approach of asset pricing and to simplify some of the original proofs. A new fea- ture of the dissertation is that it does not focus on questions of pricing but on the relations of the arbitrage theory and the classical theory of economics.

Questa tesi si occupa della fondazione della teoria della valutazione mezzi …nanziari in un mercato privo di attrito sotto l’ipotesi più generale. A questo livello di astrazione, le tecniche di valutazione, trattati nelle monogra…e noti sulla …nanza matematica ([80], [33], [60] e [9]) non funzionano, quindi la teoria semimartingala consiste principalmente di dichiarazioni esistenzali.

Uno dei problemi più importanti della valutazione è la caratterizzazione matem- atica dei modelli economicamente coerenti dei mercati …nanziari. Dal punto di vista economico l’assunzione di non-arbitraggio - cioè l’ipotesi che non si puµn fare business in cui si può solo guadagnare con probabilità strettamente positiva, ma senza esposizione al rischio - sembra una condizione abbastanza mite, ed è sor- prendente quanto sono lontane le conseguenze di vasta portata che ha. Sotto il teorema fondamentale di valutazione si intende che questi tipi di dichiarazioni che a¤ermano un’equivalenza tra la condizione di coerenza di cui sopra e alcune pro- prietà matematiche del processo stocastico che descrivono i prezzi dei mezzi. Il teorema fondamentale di valutazione, in un senso non troppo preciso, a¤erma che l’assenza di arbitraggio è equivalente alla esistenza di una misura di probabilità equivalente, sotto il quale il processo di prezzo scontato è una "martingala", che signi…ca che c’è una probabilità nuova …ttizia - la martingala misura - in cui non si può sistematicamente guadagnare in media. Sarà mostrato che la misura mar- tingala ha un ruolo molto importante sia nella teoria dei mercati completi che in quelle incompleti.

Lo scopo della tesi è quello di una rassegna della letteratura e degli antecedenti matematici ed economici del teorema fondamentale di valutazione per i modelli semimartingale, e presentare un trattamento didattico uni…cato dei semimartingale approccio della valutazione e di sempli…care alcune delle prove originali. Una nuova caratteristica del lavoro di tesi è che non si concentra su una questione

della valutazione, ma sulle relazioni tra la teoria arbitraggio e la teoria classica dell’economia.

Jelen értekezés a súrlódásmentes pénzpiacon történ½o árazás elméletének alapjaival foglalkozik, a lehet½o legáltalánosabb, szemimartingál árfolyamatokon alapuló meg- közelítésben. Az absztrakciónak ezen a szintjén az ismert pénzügyi matematikáról szóló monográ…ák (ld. pl.: [80], [33], [60] és [9]) által tárgyalt speciális árazási eljárások legtöbbje már nem m½uködik, így a szemimartingálokra vonatkozó elmélet els½osorban egzisztencia bizonyításokból áll.

Az eszközárazás elméletének egyik legalapvet½obb kérdése, hogy egy pénzpiaci modellt mikor tekintünk közgazdasági szempontból konzisztensnek és milyen ma- tematikai tulajdonságokkal karakterizálható egy ilyen modell. Közgazdasági szem- pontból az arbitrázsmentesség feltevése, vagyis az a feltevés, hogy a pénzpia- con nem köthetünk olyan üzletet amin pozitív valószín½uséggel nyerünk, anélkül hogy bármit is kockáztatnánk, nem t½unik túlságosan megszorítónak, és egészen megdöbbent½o, hogy milyen szerteágazó következtetéseket lehet levonni ebb½ol az ártalmatlannak t½un½o feltevésb½ol. A pénzügyi eszközök árazásának alaptételén általában olyan típusú állításokat értünk, amelyek a konzisztencia fenti közgaz- dasági követelményének és a pénzpiacot – pontosabban az eszközök árait – leíró sztochasztikus folyamat valamely matematikai tulajdonságának ekvivalenciájáról szólnak. A legtöbb modellben bizonyítható annak az általános elvnek valamilyen formája, miszerint az arbitrázsmentesség feltevése ekvivalens azzal az állítással, miszerint a létezik egy olyan valószín½uség, amiszerint az értékpapírok diszkontált árfolyamata egy bizonyos értelemben martingál. Mint látni fogjuk, az ún. mar- tingálmérték mind a teljes, mind a nemteljes piacok elméletében fontos szerepet játszik.

Jelen értekezés célja részben az alaptétel szemimartingálokra vonatkozó iro- dalmának, valamint közgazdaságtani és matematikai el½ozményeinek áttekintése, részben pedig a szemimartingálokra vonatkozó elmélet didaktikus egységes keretben való tárgyalása, helyenként pedig az eredeti cikkekben található bizonyítások egy-

szer½usítése. Az értekezés egy újszer½u vonása, hogy nem az árazás kérdésére öszpon- tosít, hanem az arbitrázselmélet és a klasszikus közgazdaságtan kapcsolódási pont- jait kívánja hangsúlyozni.

Bevezetés

1.1. Az alaptétel

A közgazdasági elmélet központi eleme a hatékony piacok elmélete, vagy ahogyan az elméletet vitatók nevezni szokták a piaci fundamentalizmus. Ez a széles kör- ben használt gondolatrendszer képezi a pénzügyi eszközök árazásának, illetve a rá épül½o piaci kockázatkezelés gyakorlatának hátterét. A gondolatrendszer három alapvet½o feltételre épül. Az egyik a teljesség feltételezése, a másik az arbitrázs hiányának megkövetelése, a harmadik pedig a tranzakciós költségek elhanyagol- hatósága. Mind a három inkább egy elv mint egy konkrétan megfogható matem- atikai állítás. A teljesség feltétele némiképpen elnagyoltan azt mondja ki, hogy a piacokon lev½o nagyszámú eszköz között jelent½os redundancia van. Éppen ezért ele- gend½o a termékek egy sz½uk csoportjának, az alaptermékeknek meg…gyelni az árát, a többi termék ára már ezekb½ol matematikai úton leszármaztatható. A leszár- maztathatóság oka az arbitrázsmentesség és a tranzakciós költségek hiánya. A matematikai, úgymond képletszer½u kapcsolat esetén az elhanyagolható tranzak- ciós költségek miatt a teljesség által garantált matematikai összefüggés alapján az alaptermékekb½ol létrehozható, kikeverhet½o egy kompozit termék, amely úgymond replikálja az eredeti terméket és így a két termék ára meg kell hogy egyezzen.

Két azonos méret½u és korú tojás ára azonos kell, hogy legyen, függetlenül attól, hogy melyik tyúk tojta. Ellenkez½o esetben úgymond arbitrálni lehetne, vagyis az olcsóbb terméket meg lehetne venni, és a vele azonos tulajdonságú de drágább terméket el lehetne adni és így biztos pro…tra lehetne szert tenni. Közgazdasági szempontból természetesen mind a három feltétel vitatható, különösen a korlát-

lan és kontrolálatlan használatuk problémás. Ugyanakkor ezek az elvek mélyen és alapvet½oen meghatározzák a pénzügyi világ gondolatrendszerét, ahogyan a piaci szerepl½ok a piacot látják, vagy látni vélik. A pénzügyi szektor legf½obb tevékenysége éppen a redundancia feltárásában van¹. A redundanciára épül½o fedezéssel a kocká- zat csökkenthet½o, illetve a termékekben lev½o kockázatok elvileg átcsomagolhatóak és az egyes piaci szerepl½ok számára diverzi…káltan kínálhatók.

Még a naiv intuició alapján is érezhet½o, hogy a három feltétel közül a teljesség feltétele a leginkább vitatható. Természetesen a kulcskérdés az, hogy milyen esz- közök állnak rendelkezésünkre a kompozit termék kialakításakor. Matematikailag milyen transzformációk használhatók amikor a redundanciát ki akarjuk aknázni?

Modellezési oldalról ez úgy fogalmazható meg, hogy milyen operációk engedhet½ok meg a kompozit termékek el½oállításakor? Természetesen minél b½ovebb és minél

„vadabb” matematikai eszközöket engedünk meg, annál szélesebb lesz az el½oál- lítható termékek köre. Így tehát adott modellen belül beszélhetünk csak a teljes- ségr½ol. Nyilvánvaló módon a matematikai modellekben szerepl½o el½oállíthatóság és a tényleges el½oállíthatóság nem fedi egymást. Már az egyszer½u lineáris kombináció is olyan kompozit termékeket enged meg, amelyek a valóságban nem realizálhatóak.

Például hogyan állítjuk el½o két termék irracionális súlyokkal vett lineáris kombiná- cióját? És akkor még nem is említettük a sztochasztikus integrálok különböz½o osztályait és egyéb, a területen alapvet½o m½uveleteket, amikor az el½oállíthatóságot egy id½oben folytonosan változó súlyrendszerrel valósítjuk meg².

Nyilván a közgazdasági elmélet azon aspektusai kerülnek be a matematikai modellekbe, amelyek a matematika eszköztárával jól kezelhet½ok. Érdekes módon az alapvet½o teljesség feltétele matematikailag nehezebben tárgyalható, így a vezet½o matematikusok inkább az arbitrázsmentesség feltételére koncentráltak. Ennek oka, hogy az arbitrázsmentesség gondolata jól beilleszthet½o a modern matematika egyik központi elméletébe, a dualitáselméletbe. Jelen értekezésben kizárólag az arbit- rázsmentesség feltételére fogunk koncentrálni, és a teljesség feltételével nem kívá- nunk élni.

Az arbitrázsmentesség végs½o soron azt állítja, hogy a lehetséges kompozit ter- mékek között csak egy olyan van, amely nem negatív, nevezetesen az azonosan

1A fel nem tárt redundancia mögött általában a piac nem kell½o hatékonysága áll, amit ki lehet használni és így közvetett módon a hatékonyságot növelni lehet. Legalábbis ez az ideológia.

2Úgymond dinamikusan fedezünk, vagyis folyamatosan minden id½opontban más és más, nyil- ván irracionális súlyokkal replikáljuk az adott pénzügyi eszközt. Vagyis már maga a redundancia fogalma is az alkalmazott matematikai fogalomrendszer keretében értelmezhet½o.

nulla³. Vagyis az arbitrázsmentesség azt állítja, hogy két halmaz csak egy közös pontban metszi egymást⁴. A közgazdasági matematikában triviálisan ismert észre- vétel, hogy ez a helyzet jól jellemezhet½o a szeparáló hipersíkokról szóló tétellel⁵. A tétel használatához két dolgot kell tenni: biztosítani kell, hogy a halmazok konvexek és hogy zártak legyenek. A konvexitás feltétele általában viszonylag egyszer½uen garantálható, elég feltenni, hogy a lehetséges stratégiák konvex módon kombinálhatók legyenek. A dolog emlékeztet a játékelmélet kevert stratégiáinak bevezetésére. A stratégiai halmazok konvexitása egy olyan bevett és rutinsze- r½uen használt feltétel a közgazdasági elméletben, amelynek használata jószerével már fel sem t½unik. Míg a stratégiai halmazok konvexitása például az általános egyensúlyelméletben széles körben használt, de azért vitatott feltétel, a pénzügyi elméletben minden további nélkül elfogadott⁶. A pénzügyi elméletben a konvexitás eléréséhez egyedül azt kell feltenni, hogy a pénzügyi termékekb½ol szabadon port- foliót lehet csinálni, vagyis szabadon vehetjük a termékek lineáris kombinációit.

Az egyedüli újszer½unek mondható probléma, hogy vehetjük-e a termékek negatív együtthatóval vett kombinációit vagy sem⁷.

Miként látni fogjuk a probléma az elválasztandó halmazok zártságával van, amely zártság biztosítása az alább ismertetett tételek bizonyításának legf½obb ne- hézsége. Ennek oka, hogy természetes módon a pénzügyi elmélet valószín½uségi változókkal foglalkozik, és valószín½uségi változók esetén már magának a konver- genciának a fogalma sem egyértelm½u. Másképpen fogalmazva a pénzügyi elmélet megalapozását adó arbitrázstételek matematikai szempontból lényegében mege- gyeznek a közgazdasági elmélet területén használt szokásos dualitási eszköztárral.

3Vagyis nem lehet olyan portfoliót összeállítani, amely egy valószín½uséggel nem negatív miközben pozitív valószín½uséggel pozitív.

4Egészen pontosan arról van szó, hogy a lehetséges portfoliók halmaza és a nem negatív valószín½uségi változók halmaza csak egy pontban –a nulla pontban –metszik egymást.

5Ezt az elvet számtalan tételben használjuk. Jószerével ez az els½o olyan gondolat, amivel egy matematikus közgazdász tanulmányai során megismerkedik. A lineáris programozás dualitási tétele, a jóléti közgazdaságtan második tétele, a Kuhn–Tucker tételek, a játékelmélet nyereg- ponttételei stb. Dualitáselmélet alatt azokat a matematikai eredményeket értjük, amelyek a konvex halmazok hipersíkkal való elválaszthatóságára épülnek.

6Valójában a konvexitás a pénzügyi eszközök területén jóval természetesebb mint az általános egyensúlyelméletben. Az oszthatatlanság megkövetelése mindig is az általános egyensúlyelmélet kritikájának egyik eleme volt. Az oszthatatlanság kérdése a pénzügyekben nem játszik szerepet.

7Érdekes módon a matematikai elméletben az egyik legfontosabb közgazdaságilag inspirált áttörés a feltételes optimalizációban a nem negatív változók bevezetése és az ebb½ol ered½o komp- likációk kezelése volt. Ez nagyban hozzájárult a konvex analízis kidolgozásához. Mivel a pénzü- gyekben az egyes változók lehetnek negatívak is, a stratégia halmazok általában alterek, ami a tárgyalást egyszer½usíti.

A matematikai eszköztár elvi szintjén az eltérés egyedül abból származik, hogy mivel a modellek dinamikusak és sztochasztikusak is, ezért a matematikai objek- tumok, amelyek körében a konvex analízis szokásos gondolatait alkalmazni kell, matematikailag nagyon bonyolultak.

A szeparáló sík közgazdasági interpretációja mindig is a közgazdasági elmélet központi kérdése volt⁸. Az általános és rutinszer½uen használt válasz az, hogy a szeparáló sík az egyensúlyi árakat, vagy valamilyen szempontból az optimális árakat írja le. Az arbitrázselméletben a szeparáló hipersík mint martingálmérték jelenik meg. A martingálmérték a Lagrange-szorzók dinamikus, sztochasztikus környezetbeli párja. Jelen értekezés, az eszközárazás egyik központi problémájára, a martingálmérték létezésére vonatkozó irodalom áttekintésével, az arbitrázselmélet egyik matematikailag legmélyebb területének és a klasszikus közgazdaságtannak a kapcsolódási pontjait igyekszik feltárni.

Az arbitrázselmélet egyik központi fogalma a martingál, ami a sztochasztikus folyamatok egy igen speciális osztályát jelöli. A martingál tulajdonság lényege legegyszer½ubben a számegyenesen vett véletlen bolyongás fogalmából kiindulva érthet½o meg. Képzeljük el, hogy az origóból kiindulva, minden periódusban egyenl½o valószín½uséggel vagy jobbra vagy balra lépünk egyet. Ekkor minden t-re, a t- edik id½opontbeli helyzetünk egy valószín½uségi változó. Ha történetesen a t-edik id½opillanatban a számegyenesapontjában vagyunk, akkor a következ½o pillanatban a helyzetünk várható értéke éppena lesz, és ez természetesen független attól, hogy hogyan jutottunk az a helyzetbe. A martingál tulajdonság a véletlen bolyon- gás ezen tulajdonságának egy általánosítása. Kissé leegyszer½usítve a dolgot, a valószín½uségi változók egyX(1),X(2),... sorozata martingál, ha mindent-re igaz, hogy X(t) = a esetén az X(t+ 1) várható értéke is éppen a. Kissé formálisabb jelölést használva E[X(t+ 1)j F^t] = X(t), ahol F^t -algebra jelöli a befektet½ok információs struktúráját at-edik id½opontban.⁹

A pénzügyi eszközök árazásának alaptétele¹⁰ kissé pongyolán megfogalmazva azt állítja, hogy egy értékpapírpiacon akkor nincs „arbitrázs”, ha létezik egy az eredetivel ekvivalens valószín½uségi mérték¹¹, amelyre vonatkozóan az értékpapírok

8Gondoljunk csak a lineáris programozás duális megoldásának interpretációjára, vagy a La- grange szorzók közgazdasági tartalmára.

9Ld.: 10. de…níció.

10A ”fundamental theorem of asset pricing„ elnevezést a fentihez hasonló értelemben el½oször P. H. Dybvig és R. A. Ross [31] használta.

11Két mérték ekvivalenciája azt jelenti, hogy mindkét mérték szerint ugyanazok a nullmérték½u halmazok.

diszkontált árait leíró folyamat egy bizonyos értelemben „martingál”(ld. 24., 26.

és 31. tétel), vagyis létezik olyan új valószín½uségi mérték, amely alatt pénzügyi esz- közök segítségével nem lehet szisztematikusan átlagban nyerni. Hogy egészen pon- tosak legyünk, az állítás ebben a formában inkább csak egy alapelv, ami akkor válik ténylegesen igazolható állítássá, ha pontosan de…niáljuk az „arbitrázsmentesség”

és „martingál" fogalmakat. Mint látni fogjuk, ezek pontos tartalma modellosztá- lyonként eltér½o lehet. Ezen a ponton érdemes egy nyilvánvaló, de azért igen fontos megjegyzést tenni. A tétel nem azt állítja, hogy a pénzügyi eszközök az arbit- rázs hiánya esetén martingált alkotnak, vagyis hogy hosszú id½o átlagában nem lehet rajtuk pénzügyi eszközökkel nyerni¹². A martingál tulajdonság kikénysze- rítéséhez két dolgot kell tenni. Egyrészt a folyamatokat diszkontálni kell, más- részt az egyes kimenetelekhez tartozó valószín½uségeket ki kell cserélni egy mester- séges valószín½uségre. Vagyis az egyes kimenetelek esetén elérhet½o nyereségeket és veszteségeket nem azok bekövetkezésének tényleges valószín½usége szerint kell súlyozni, hanem egy mesterségesen vett súlyrendszer szerint. A két mérték ekvi- valenciája azt jelenti, hogy a pozitív valószín½uség½u halmazok súlya nem lesz nulla és fordítva. A szeparáló sík az új és a régi valószín½uségek arányát adja meg. Mit jelent az, ha egy halmaz valószín½usége a kétszeresére n½ott és mit jelent az, ha a felére csökkent? Az elmélet a maga tiszta voltában erre nem ad választ, pusztán annyit mond, hogy az alkalmas súlyok megadhatóak¹³. Másképpen a nincsen ar- bitrázs feltétel, vagyis hogy két alkalmas konvex halmaznak nincsen közös pontja, a modell megfelel½oen speci…kált feltételei miatt pontosan azt jelenti, hogy van elválasztó sík, amely normálisának segítségével az egyes valószín½uségeket ténylege- sen átskálázva az eredeti folyamat az átskálázott valószín½uségek esetén hosszú id½o átlagában pusztán pénzügyi eszközökkel nem lesz manipulálható.

A matematikai alapprobléma szemléltetéséhez tekintsünk egy olyan kétperió- dusos pénzpiaci modellt, ahol az állapottér az =f!₁; !₂gkételem½u halmaz. AP valószín½uségi mértéket ap= (p₁; p₂) vektor reprezentálja, aholp₁ =P(f!₁g)>0,

12Nyilván lehet. A martingál tulajdonságot sok esetben félreértik. Hosszú id½o átlagában a valós valószín½uségekhez tartozó valós világban lehet pozitív nyereséget biztosítani. Ezt a matem- atikai fantáziavilágban létez½o martingálmérték alatt nem lehet megcsinálni. De senki sem állítja, hogy a két valószín½uség azonos. A martingálmérték a nyer½o esetek valószín½uségét csökkenti, a veszteségekét növeli, így az esélyeket átlagban kiegyenlíti. Az arbitrázs hiánya csak bizonyos igen enyhe konzisztencia feltételt ír el½o, de a konzisztencia feltételek közé nem tartozik az, hogy hosszú id½o átlagában nem lehet nyerni.

13Ezek a súlyok kulcsszerepet játszanak a származtatott termékek árazásában, de erre most nem térünk ki. Az ekvivalencia azt jelenti, hogy a súlyok, arányok kiszámolásakor nem lép fel semmilyen nullával való osztásból származó probléma.

p2 =P(f!2g)>0, P(;) = 0 és P(f!1; !2g) = 1. Ekkor az feletti valószín½uségi változók halmaza éppen az R², és a fentiek alapján az x 2 R² valószín½uségi vál- tozó várható értéke a px skaláris szorzat. Tegyük fel, hogy a pénzpiacon egy nulla kamatozású kockázatmentes kötvénnyel és egy kockázatos értékpapírral lehet kereskedni, és a kockázatos értékpapír hozama a fenti halmazon értelmezettR valószín½uségi változóval írható le. Ekkor rendre H₁ és H₂-vel jelölve az els½o pe- riódusban kötvénybe illetve kockázatos értékpapírba fektetett pénzmennyiséget, a H = (H₁; H₂)kereskedési stratégia ki…zetése nyilván aH₁+H₂(1+R)valószín½uségi változó.

A fenti modellben feltételes követelésnek nevezzük azR²beli elemekkel reprezen- tálhatóf = (f₁; f₂)ki…zetéseket, melyekp₁valószín½uséggelf₁ ésp₂ valószín½uséggel f₂ ki…zetést biztosítanak a követelés birtokosának. Jelöljük A-val a zérusvektortól különböz½o nemnegatív koordinátájú R²-beli elemek halmazát, valamint K-val a nulla induló vagyonnal megvalósítható összes lehetséges kereskedési stratégiák ki-

…zetéseinek halmazát, vagyis azonH₁+H₂(1+R)ki…zetéseket melyekreH₁+H₂ = 0. Ekkor azt mondjuk hogy nincs arbitrázs, ha K \A=;, vagyis ha nulla in- duló vagyon segítségével nem juthatunk olyan második periódusbeli véletlen ki-

…zetéshez, mely minden kimenetel esetén nemnegatív, és legalább egy kimenetel esetén pozitív érték½u. Például az (1;1) vagy az (1;0); illetve az (0;1) ki…zetés vektorok – vagyis feltételes követelések – arbitrázst tartalmaznak, ugyanis po- zitív valószín½uséggel nyereséget biztosítanak, miközben a veszteség valószín½usége nulla. Vegyük észre, hogy ez nem függ a valószín½uségi mérték megválasztásától, mindaddig, amíg egyik kimenetel valószín½usége sem nulla, vagyis amíg a szóban forgó valószín½uség az eredetivel ekvivalens. Következésképpen a piac arbitrázs- mentességének tulajdonsága invariáns az ekvivalens valószín½uségi mérték megvá- lasztására vonatkozóan. Ez a meg…gyelés motiválja a következ½o jelölés bevezetését.

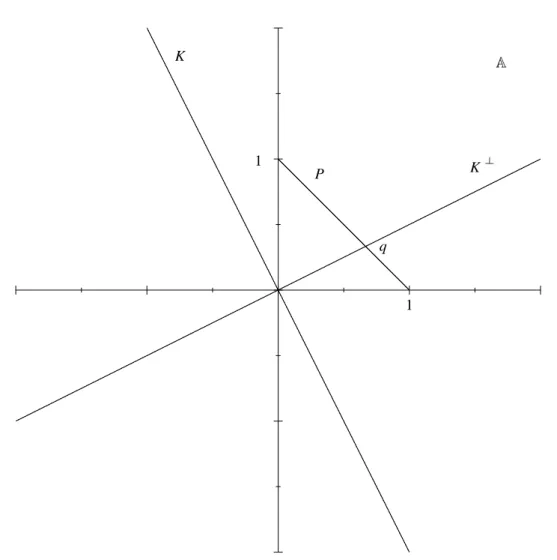
Jelöljük P-vel az x₁ > 0; x₂ > 0 és x₁ +x₂ = 1 feltételeknek elegettev½o R²-beli (x₁; x₂) elemek halmazát. Ez utóbbi halmaz geometriailag egy olyan nyílt sza- kasszal reprezentálható, melynek végpontjai (0;1) és (1;0) (ld.: 1.1. ábra). A P halmaz elemeihez, csakúgy mint a(p₁; p₂) vektor esetében láttuk egyértelm½uen hozzá tudunk rendelni egy valószín½uségi mértéket¹⁴. Minden ilyen mérték ekvi- valens lesz a P valószín½uségi mértékkel, hiszen mindkét mérték szerint csak az üres halmaz nulla valószín½uség½u, s½ot könnyen belátható, hogy minden P-vel ekvi-

14Minden (x₁; x₂)2 P vektort azonosítsunk azzal a valószín½uségi mértékkel, mely szerint az

!₁kimenetel valószín½usége x₁ és az!₂ valószín½uségex₂.

valens valószín½uségi mérték P-beli elemmel reprezentálható.¹⁵

Érdemes hangsúlyozni, hogy ha nincs arbitrázs, akkor a ( 1; 1) szintén nem lehet eleme a K-nak ugyanis a pénzügyekben ha valamely változó megengedett, akkor általában a negatívja is megengedett, mivel az egyik vektor a termék vételét, a másik az eladását reprezentálja, és a vétel, illetve az eladás eredménye egymás ellentettje. Ugyancsak pénzügyi feltételek miatt feltehetjük, hogy a termékek negatív súlyok felhasználásával is kombinálhatóak, így aK egy lineáris altere R²- nek. Következésképpen aKegy origón áthaladó egyenessel reprezentálható, amely egyenes a nincsen arbitrázs feltétel miatt nem metszi a pozitív síknegyedet (ld.: 1.1.

ábra). A geometriai interpretáció alapján nyilvánvaló, hogy a nincs arbitrázs felté- tel ekvivalens azzal, hogy aK-ra mer½oleges vektorok K^? halmazára K^?\P 6=;. Ez azt jelenti, hogy van olyan q 2 P valószín½uségi mérték, amely mer½oleges min- denx2K-ra. Mivel két vektor pontosan akkor mer½oleges egymásra ha a skaláris szorzatuk zérus, ezért ez azt jelenti, hogy van olyan q 2 P valószín½uségi mérték, hogy minden K-beli x-re qx = 0, vagyis amely mellett a K minden elemének várható értéke nulla. Mivel ez speciálisan a (H₁; H₂) = ( 1;1)kereskedési straté- gia 1 + (1 +R)ki…zetésvektorára is teljesül, ez azt jelenti, hogyR várható értéke zérus, vagyis a kockázatos értékpapír ára q szerint martingál. Összefoglalva az eddigieket, a fenti geometriai okoskodásból világosan látszik, hogy az itt tárgyalt kétdimenziós pénzpiacon pontosan akkor nincs arbitrázs, ha létezik egy az erede- tivel ekvivalens martingálmérték.

A továbbiakban fontos szerepet fog játszani aC =K R²+ halmaz¹⁶, és annak C⁰ polárisa¹⁷. Mivel a C halmaz konvex kúp, vagyis az összeadás mellett zárt a nemnegatív konstanssal való szorzásra, ezért

C⁰ =fy2Rⁿ j(8x2C) :yx 0g:

15A félreértések elkerülése végett megjegyezzük, hogy bár mind aK mind aP halmaz elemeit ugyanaban a koordináta rendszerben ábrázoltuk, ezen halmazok pontjai egymással még csak köszön½o viszonyban sem állnak. Általános egyensúlyelméleti analógiával élve azt mondhatjuk, hogy míg a K halmaz a jószágtér egy részhalmza, a P halmaz minden eleme egy árrendszert határoz meg, és valójában a jószágtér duálisában fekszik. Mivel véges dimenzióban mind a primál térnek mind a duálisának pontjai ugyanazonRⁿ-beli pontokkal reprezentálhatóak, ezért aKés aP közös koordinátarendszerben ábrázolható.

16Kreps nevéhez f½uz½odik az a felismerés, hogy általánosabb modellek esetén szükség van az ún.

díjmentes lomtalanítási feltevésre (ld.: [64]). Ezen feltevés mellett a zérus indulóvagyon révén elérhet½o ki…zetések halmaza nemK lesz, hanemK R²+.

17A konvex analízis szóhasználatával egy B 2 Rⁿ halmaz polárisának nevezzük, és B⁰-lal jelöljük azfy2Rⁿj(8x2B) :yx 1ghalmazt.

P K

q

A

K

a

1 1

1.1. ábra. A martingálmérték geometriai interpretációja

Fenti geometriai interpretációból világosan látszik, hogy egyrészt az ekvivalens martingálmértékek pontosan aC ésA halmazokat elválasztó szeparáló hipersíkok egységnyil¹ normájú normálvektorai, másrészt aC⁰ egységnyi normájú elemeinek halmaza éppen az ekvivalens martingálmértékek halmazával egyezik meg.

Minthogy az arbitrázselméletben nem beszélhetünk egyensúlyról, ígyhát egyen- súlyi árról sem, ezért meg kell mondanunk, hogy ebben az esetben milyen értelem- ben beszélhetünk egy feltételes követelés áráról. A fenti modellben azt mond- juk, hogy egy f = (f₁; f₂) feltételes követelés arbitrázsmentes ára s, ha a mo- dellt de…niáló értékpapírpiacot kiegészítve az(f_i s)=s, i= 1;2hozamú feletéte- les követeléssel mint értékpapírral, az így kapott kib½ovített piac arbitrázsmentes marad. Modellünkben egy f követelést replikálhatónak nevezünk, ha valamely H = (H₁; H₂) kereskedési stratégia ki…zetése, vagyis H₁ +H₂(1 +R) éppen f.

Megmutatjuk, hogy érvényes az ún. kockázatsemleges értékelés elve, miszerint tetsz½oleges replikálható f követelés arbitrázsmentes ára éppen az f követelésnek a q martingálmérték szerinti várható értéke. Mivel f el½oállítható a ( H₂; H₂) és a (H₁+H₂;0) stratégiák összegeként is, és ( H₂; H₂) ki…zetése K-beli, ezért a fentiek alapján, és a várhatóérték képzésének linearitásából következik, hogy azf q szerinti várható értéke éppen H₁+H₂, ami éppen a H kereskedési stratégiához szükséges kezd½o vagyon. Ha az f követelés s ára nagyobb volna mint H₁ +H₂, akkor azf követelést eladva, e-mellett aH kereskedési stratégiát követve, továbbá s (H₁+H₂)összeget a kockázatmentes kötvénybe fektetve, a kib½ovített piac egy olyan kereskedési stratégiáját kapjuk, amely s (H₁+H₂) biztos ki…zetést biz- tosít, ugyanakkor zérus kezd½ovagyon segítségével megvalósítható, vagyis arbitrázs.

Ezzel beláttuk hogy az s nem lehet nagyobb mint az f q szerinti várható értéke.

Hasonló arbitrázs megfontolásokkal belátható, hogy s nem lehet kisebb sem mint azf q szerinti várható értéke. Ahogy arra már korábban utaltunk, általános eset- ben nem az értékpapírok árfolyamata, hanem azok diszkontált árfolyamata lesz a martingálmérték szerint martingál. Ebben az esetben a kockázatsemleges értékelés elve azt mondja, hogy tetsz½oleges replikálható követelés arbitrázsmentes ára ép- pen a követelés diszkontált értékének valamely martingálmérték szerinti várható értéke. Természetesen el½ofordulhat, hogy bizonyos ki…zetések az adott modell- ben nem replikálhatóak, vagyis a modell nem teljes. Ebben az esetben a feltételes követelések árazása nem oldható meg a befektet½ok preferenciáinak explicit szerepel- tetése nélkül. Látni fogjuk, hogy az ekvivalens martingálmérték ebben az esetben is fontos szerepet játszik bizonyos portfolióválasztási döntések vizsgálatában.

A bemutatott gondolatmenet minden különösebb bonyodalom nélkül kiterjeszt- het½o a többdimenziós modellekre, mindaddig, amíg a probléma véges dimenziós marad, hiszen ezekben az esetekben aK halmaz triviálisan zárt, mivel tetsz½oleges topologikus vektortér véges dimenziós altere zárt. A releváns dinamikus sztoc- hasztikus modellekben azonban –pl. amikor az id½ohorizont végtelen, vagy az id½o- paraméter folytonos, vagy csak egyszer½uen nem végesen generált a valószín½uségi mez½o – a feltételes követelések tere tipikusan végtelen dimenziós, és – ahogy funkcionálanalízisb½ol tudjuk –ilyenkor a matematikai problémák zöme topológiai természet½u, így többek között a K zártsága sem fog automatikusan teljesülni, s½ot ennek biztosítása teszi ki a bizonyítások túlnyomó részét.

A bemutatott kétdimenziós példa jól mutatja az arbitrázsárazás lényegét, ám több szempontból félrevezet½o. A modell egy speciális vonása a véges számú perió-

dus feltételezése. Látni fogjuk, hogy végtelen számú kereskedési periódus esetén, korlátlan er½oforrásra támaszkodva, egy valószín½uséggel biztos pozitív ki…zetéshez juthatunk, ezért ezeket a stratégiákat ki kell zárnunk a lehetséges stratégiák közül.

Ennek eredményeképpen aKhalmaz általános esetben már nem altér, hanem csak kúp lesz. A fenti modell egy másik kellemes tulajdonsága, hogy a primer tér –ál- talános egyensúlyelméleti terminológiát használva a jószágtér, vagyis esetünkben a feltételes követelések tere –és a duális tér –vagyis az árrendszert, speciálisan a mar- tingálmértéket tartalmazó tér –ugyanabban a koordinátarendszerben ábrázolható.

Általánosabb, és egy kicsit precízebb megfogalmazásban, tetsz½oleges n-dimenziós szeparált topológikus vektortér topológikusan izomorf¹⁸ az Rⁿ térrel, így ebben az esetben nincs értelme sem egy absztrakt topológia fogalom bevezetésének, sem a primer- és duális terek megkülönböztetésének. Végtelen dimenziós topológikus vektortérben azonban a topológia megválasztása már nem egyértelm½u, ezért jóval nehezebb biztosítani hogy mind a primer tér, mind annak topológikus duálisa¹⁹ illeszkedjen a közgazdasági problémához. Ez legtöbbször sem a végtelen dimenziós általános egyensúlyelméletben, sem az arbitrázselméletben nem teljesül. Ilyenkor a célnak megfelel½o árrendszer létezését többek között a szerepl½ok preferenciáira vonatkozó megkötésekkel lehet biztosítani.

A martingálmérték létezésér½ol szóló els½o állítást M. Harrison és S. R. Pliska [44]

bizonyítják arra az esetre, amikor a valószín½uségi mez½o végesen generált. Azóta a tételnek számos általánosítása született. Ezek közül az egyik legismertebb a Dalang–Morton–Willinger-tétel (ld.:[19]), ami már teljesen általános valószín½uségi mez½ob½ol indul ki, de felteszi, hogy az id½oparaméter diszkrét és az id½ohorizont véges.

Szintén úttör½o jelent½oség½u Krepsnek az az eredménye (ld. [64]), miszerint az ún.

„nincs ingyenebéd”feltétel egyenérték½u az ekvivalens martingálmérték létezésével.

Bár Kreps ezen eredménye már szemimartingál modellekre is alkalmazható, az ebben szerepl½o „nincs ingyenebéd” fogalom sajnos közgazdaságtanilag nehezen interpretálható. Szemimartingál modellekre a probléma kielégít½onek tekinthet½o megoldását végülis F. Delbaen és W. Schachermayer adják meg ([21] és [23]). Ez utóbbi eredmény a pénzügyi matematika egyik csúcsteljesítménye²⁰. Bizonyítása igen hosszadalmas, és a funkcionálanalízis valamint a sztochasztikus folyamatok

18Vagyis algebrailag izomorf és homeomorf.

19Vagyis a primer téren értelmezett folytonos, lineáris funkcionálok tere.

20A Bichteler–Dellacherie-tételb½ol tudjuk, hogy a szemimartingál a legáltalánosabb szto- chasztikus folyamat, amely szerint egy viszonylag jó tulajdonságú sztochasztikus integrál de…niál- ható, ezért a Delbaen–Schachermayer-tétel a maga nemében egy igen általános állítás.

– P. A. Meyer és a strassbourgi-iskola matematikusai által a 60-as évek végét½ol kezdve kidolgozott – általános elméletének mély eredményeit használja. Bár a Delbaen–Schachermayer-tétel bizonyítását Kabanov [57] némileg egyszer½usítette, meggy½oz½odésünk szerint annak bizonyítása továbbra is csak kevesek által hoz- záférhet½o. Kevésbé ismert, hogy az alaptételnek létezik egy közgazdaságtanilag a Delbaen–Schachermayer-tétellel azonos tartalmú és mélység½u, Frittelli nevéhez f½uz½od½o változata (ld.:[38] és [39]), amely az arbitrázsmentesség preferenciák segít- ségével történ½o karakterizációján alapul, és melynek bizonyítása jóval egyszer½ubb matematikai eszközöket igényel.

Jelen értekezés célja részben az alaptétel szemimartingálokra vonatkozó iro- dalmának, valamint közgazdaságtani és matematikai el½ozményeinek áttekintése, részben pedig a szemimartingálokra vonatkozó elmélet didaktikus egységes keretben való tárgyalása, helyenként pedig az eredeti cikkekben található bizonyítások egy- szer½usítése. Az értekezés egy újszer½u vonása, hogy nem az árazás kérdésére öszpon- tosít, hanem az arbitrázselmélet és a klasszikus közgazdaságtan kapcsolódási pont- jait kivánja hangsúlyozni.

1.2. Az értekezés felépítése és újszer½u eredményei

Az értekezés második fejezete bemutatja azokat a fontosabb közgazdaságtani és matematikai el½ozményeket, amelyek a Delbaen–Schachermayer-tétel bizonyításához elvezettek. Ebben a fejezetben megmutatjuk, hogy a martingálmérték fogalma szorosan kapcsolódik a bizonytalanság melletti általános egyensúlyelmélet Arrow–

Debreu-féle modelljéhez, valamint a Radner-egyensúly fogalma segítségével megad- juk a martingálmérték egy lehetséges közgazdasági interpretációját. Látni fogjuk, hogy a martingálmérték valójában egy a replikálható portfoliók alterér½ol az összes feltételes követelések terére kiterjesztett árazó funkcionált reprezentál, ennek meg- felel½oen ebben a fejezetben az alaptétel –a 60-as és 70-es évek pénzügyi irodalmával összhangban – mint az árazó funkcionál kiterjeszthet½oségének problémája jelenik meg.

Ebben a fejezetben megadjuk az arbitrázs pontos de…nícióját kétperiódusos modellre, majd rámutatunk hogy általános²¹valószín½uségi mez½o, vagyis –általános egyensúlyelméleti analógiával élve – végtelen dimenziós jószágtér esetén az arbit- rázsmentesség már nem elégséges feltétele a kiterjesztett árazó funkcionál létezé-

21Vagyis nem végesen generált.

sének, ezért szükséges az arbitrázsmentességnél er½osebb fogalmak, az életképesség ésnincs ingyenebéd fogalmak bevezetése. Látni fogjuk, hogy az alaptétel végtelen dimenzióra való kiterjesztése nem zökken½omentes, a fellép½o topológiai problémák miatt a funkcionálanalízis klasszikus szeparációs tételei nem alkalmazhatóak.

A fejezet utolsó alpontjában, egy tömör történeti áttekintést követ½oen, megad- juk többek között a …ltráció, az el½orejelezhet½o folyamat, a martingál, a lokális martingál és szemimartingál pontos de…nícióját, és ismertetjük a sztochasztikus folyamatok általános elméletének néhány kevésbé ismert, kés½obb felhasználásra kerül½o eredményét, továbbá a lognormális modellen keresztül megmutatjuk, hogy a Girsanov-transzformáció segítségével az ekvivalens martingálmérték igen egysz- er½uen meghatározható.

A harmadik fejezetben az arbitrázsmentesség fogalmát kiterjesztjük több perió- dusos modellekre és kimondjuk az alaptétel diszkrét, véges id½ohorizontra vonatkozó alakját. Ez a fejezet tárgyalja az ön…nanszírozó portfólió fogalmát és az ehhez szorosan kapcsolódó ármérce invariancia tételt, amit [53] alapján általános szemi- martingál modellekre is bizonyítunk.

Ezt követ½oen a negyedik fejezetben [21] alapján teljes bizonyítását közöljük a Delbaen és Schachermayer nevéhez f½uz½od½o alaptételnek. A disszertáció ezen fe- jezete a legkidolgozottabb és ebben találhatóak a disszertáció újszer½unek mondható technikai jelleg½u eredményei.²² Bár valóban újnak mondható bizonyítást nem sike- rült adnunk a tételre, ennek ellenére az eredeti bizonyítást számos ponton egysze- r½usítettük és összességében érthet½obbé tettük. Többek között sikerült lényegesen leegyszer½usíteni a 4.1.1. alpontban található 36. lemma bizonyítását, valamint az alaptétel bizonyításában kulcsszerepet játszó 4.1.3. alpontbeli 40. tételre az iro- dalomban található Mackey–Arens-tételen alapuló bizonyítás helyett egy valamivel elemibb bizonyítást közlünk.²³ Ezenkívül a 4.1.2. alpontbeli 37. lemma [21]- beli transz…nit indukciós bizonyítása helyett el½oször bemutatunk egy transz…nit rekurzión alapuló bizonyítást, majd egy teljesen elemi bizonyítást. Végül érdemes kiemelni, hogy az 4.1.1. alpontban sikerült pontosan tisztázni a bizonyításban többször is felhasznált 35. lemma szerepét, és sikerült olyan alakban megadni, amely némileg jobban illeszkedik az itteni alkalmazásokhoz.

Az ötödik fejezetben megmutatjuk, hogy az alaptételhez szorosan kapcsolódik

22Megjelent: Badics T. – Medvegyev P.: Pénzügyi eszközök árazásának alaptétele lokálisan korlátos szemimartingál árfolyamok esetén, Szigma, 2009/3.4.

23Az eredmény publikálását követ½oen Rásonyi Miklós szóbeli közléséb½ol megtudtuk, hogy Ka- banovnak létezik egy az ittenihez hasonló, feltehet½oleg publikálatlan bizonyítása.

a portfólió optimalizálás dualitáselmélete, ugyanis az eredeti haszonmaximalizá- ciós probléma ekvivalens egy a martingálmértékek halmazán való minimalizálás- sal, ami a gyakorlati alkalmazásokban dualitási technikák felhasználásával oldható meg. Ebben a fejezetben el½oször röviden ismertetjük a pénzügyi eszközök árazásá- nak duális megközelítését, a Bellini–Frittelli-féle dualitási tételt és annak egy ér- dekes, szemimartingál modellekre történ½o alkalmazását (ld. [7]), majd a hatodik fejezetben bemutatjuk az alaptétel Frittelli-féle alakját melynek szintén teljes bi- zonyítását közöljük, végül, miután áttekintettük az Orlicz-terekre vonatkozó szük- séges el½oismereteket, [38], [39] és [62] alapján megmutatjuk hogy a legfontosabb arbitrázs fogalmak a befektet½ok preferenciái segítségével is karakterizálhatóak.

Ennek a fejezetnek egyik fontos üzenete az a felismerés, hogy Frittelli és Klein fent említett eredményei közgazdasági szempontból új megvilágításba helyezik a Delbaen–Schachermayer-féle elméletet.

A hetedik fejezetben részletesen tárgyaljuk az egy ár törvényének fogalmát, annak az állapotár de‡átor segítségével történ½o matematikai karakterizációját, valamint az egy ár törvényének és az arbitrázsmentesség fogalmának viszonyát.

Mivel tárgyalásunkban a f½o hangsúly egyértelm½uen a szemimartingálokra vo- natkozó elmélet áttekintése, ezért a bemutatott – többnyire jóval egyszer½ubben interpretálható – véges dimenziós esetek els½osorban az egyes témák és fogalmak intuitív felvezetését szolgálják, ennek megfelel½oen ezen speciális esetek tárgyalása többnyire kevésbé precíz, helyenként pedig vázlatos, annál is inkább, mert ezen eredmények nagy részének igényes tárgyalása megtalálható az idézett monográ-

…ákban és tankönyvekben. Ez alól kivételt képez a portfolió dualitáselméletér½ol szóló 5.1. alfejezet, ami a konvex analízis dualitási módszereinek, így például a Lagrange-dualitás, az er½os- és gyenge dualitási tételek alkalmazására hívja fel a …gyelmet, ezért kissé eltér az eredeti – és valamivel elemibb – [24]-beli tár- gyalástól. A szemimartingálokra vonatkozó fejezetekben azonban minden eset- ben törekedtünk a lehet½o legprecízebb kifejtésre, valamint részletes bizonyítá- sok és hivatkozások közlésére. Az ezen fejezetekben felhasznált matematikai ap- parátus magában foglalja a topológiát, a mértékelméletet, a funkcionálanalízis dualitáselméletét, a Hilbert-terek elméletét, a halmazelméletet, a sztochasztikus folyamatok általános elméletének viszonylag új fejezeteit, valamint a konvex analízis és az Orlicz-terek elméletének néhány eredményét.

Végezetül hangsúlyozzuk, hogy az értekezés szándékosan nem foglalkozik sem az eszközárazás konkrét problémáival, így a Black–Scholes- és Cox–Ross–Rubinstein-

modellel, vagy ezek különféle változataival (ld.: [10] és [16]), sem az ún. súrlódásos modellekkel, vagyis azokkal a modellekkel, melyekben a kereskedésnek tranzakciós költségei vannak.²⁴ Bár a terület az értekezés témájával igen szoros kapcsolatban van, terjedelmi okokból szintén nem foglalkozunk sem a pénzügyi eszközök árazásá- nak második alaptételével²⁵, sem általánosságban a pénzpiacok teljességének prob- lémájával.

24Az alaptétel súrlódásos modellekre való kiterjesztéseir½ol [58], [90] és [42] cikkekben olvashatunk.

25A pénzügyi eszközök árazásának alaptétele azt mondja ki, hogy egy pénzpiac pontosan akkor teljes, ha az ekvivalens martingálmérték egyértelm½u.

A Delbaen–Schachermayer-tétel el½ozményei

Ebben a fejezetben áttekintjük a Delbaen–Schachermayer-tétel közgazdaságtani és matematikai el½ozményeit. El½oször megmutatjuk, hogy a kétperiódusos Arrow–

Debreu egyensúlyi modellben a martingálmérték létezése az egyensúly triviális következménye. Ebben a modellben a martingálmérték nem más mint az Arrow–

Debreu-féle állapotárak egy alternatív reprezentációja.

A 2.1.2. alpontban az Arrow–Debreu-egyensúly egy olyan általánosításával foglalkozunk, amelyben a fogyasztók már nem feltételes jószágokkal, csak érték- papírok egy sz½ukebb családjával kereskednek, így jutunk az ún. Radner-egyensúly fogalmához. Megmutatjuk, hogy a martingálmérték létezése ebben az esetben a Radner-egyensúly els½orend½u feltételének következménye. A martingálmérték ebben a modellben azt mutatja meg, hogy adott ! kimenetel esetére egy pótlóla- gos egységnyi ! kimenetelhez tartozó Arrow–Debreu értékpapír hányszoros ha- szonnövekményt eredményez az egy pótlólagos egységnyi els½o periódusbeli biztos vagyonnövekedés haszonnövekményéhez képest.

A 2.1.3. alpontban az általános egyensúlyelméleti megközelítésr½ol áttérünk egy olyan parciális egyensúlyi modellre, melyben a pénzügyi eszközök árai adot- tak. Ekkor az árazási probléma megoldásához természetesen semmiféle egyensú- lyi feltételre nincs szükség, hiszen a martingálmérték – ami egy a replikálható követelések terén értelmezett árazó funkcionált reprezentál –a pénzügyi eszközök áraiból már meghatározható. Ezzel elérkeztünk az értekezés alapproblémájához.

Ha az árazó funkcionál meghatározásához sem az egyensúly feltételére sem a fo- gyasztók preferenciáira nincs szükség, akkor mi az a konzisztencia feltétel, ami

lehet½oleg az egyensúlynál enyhébb megkötést jelent, és egyúttal biztosítja az árazó funkcionál létezését. Ebben az összefüggésben kerülnek bevezetésre azéletképesség, azarbitrázsmentesség és anincs ingyenebéd fogalmak. Rámutatunk hogy általános valószín½uségi mez½o esetén az arbitrázsmentesség már nem elégséges feltétele az árazó funkcionál létezésének, ezért szükséges az arbitrázsmentességnél er½osebb fo- galmak, azéletképesség és nincs ingyenebéd fogalmak bevezetése.

A 2.2. alfejezetben részletesen tárgyaljuk a szeparáló hipersík és a martin- gálmérték kapcsolatát és a végtelen dimenzióban történ½o szeparációval kapcso- latos matematikai problémákat. A bevezetésben láttuk, hogy abban az eset- ben, amikor a lehetséges ki…zetések tere véges dimenziós, az alaptétel egy egy- szer½u szeparációs tétellel könnyen bizonyítható. A bizonyítás végtelen dimenzióra történ½o átvitelekor azonban – csakúgy mint az általános egyensúlyelmélet ered- ményeinek általánosításakor – több nehézséggel kell megküzdenünk. A mi szem- pontunkból a legnagyobb nehézséget az okozza, hogy bár az L¹ tér duálisa az L¹ tér¹, az L¹ tér duálisa nem az L¹ tér. A probléma megoldását a Kreps–Yan-féle szeparációs tétel jelenti.

Végül a 2.3. alfejezetben röviden ismertetjük azokat a matematikai el½ozménye- ket, amelyek a sztochasztikus folyamatok Markov-folyamatoktól független általános elméletének megszületésében szerepet játszottak, és áttekintjük az elmélet néhány, a kés½obbiekben nélkülözhetetlen újabb eredményét.

Mivel ebben a fejezetben csak az irodalmi el½ozményeket tekintjük át, ezért az itt ismertetett állításokat kevésbé formálisan tárgyaljuk és minden esetben bizonyítás nélkül közöljük.

2.1. Az általános egyensúlyelmélett½ol az arbit- rázsárazásig

2.1.1. Az Arrow–Debreu-egyensúly

A martingálmérték közgazdasági tartalmának megértése végett induljunk ki a bi- zonytalanság melletti választás Arrow–Debreu-féle általános egyensúlyi modell- jéb½ol. Mint ismeretes, az eredetileg determinisztikus általános egyensúlyelméletet a feltételes jószág fogalmának bevezetésével el½oször Arrow [2] alkalmazta olyan

1Valójában általánosan teljesül, hogy tetsz½olegesp <1-re azL^ptér duálisaL^q, ahol ¹_p+¹_q = 1.

szituáció leírására, ahol a szerepl½ok indulókészletei bizonytalanok, vagyis függenek a megvalósuló világállapottól. Az ötletet kés½obb Debreu [17] általánosította. (Ld.

még: [18], modernebb feldolgozásban pl. [71] vagy [68].)

Vegyünk egy M számú szerepl½ob½ol álló cseregazdaságot. Tegyük fel, hogy a gazdaság szerepl½oi K számú jószágot fogyasztanak, és ezekb½ol a jószágokból az egyes egyének rendelkezésére álló mennyiségek a bekövetkez½o világállapot füg- gvényei, és az állapottér, vagyis a lehetséges világállapotok halmaza az = f1; 2; :::; Sg véges halmaz. Tegyük fel, hogy a gazdaság szerepl½oi kereskedhet- nek ún. feltételes jószágokkal, és alkalmazzuk a determinisztikus általános egyen- súlyelméletet a feltételes jószágok piacára. Az k-adik jószághoz és az ! 2 kimenetelhez tartozó egységnyi feltételes jószág egy olyan jog, amely az! kimene- tel esetén egységnyi, minden más kimenetel esetén zérus mennyiség½u – feltétel nélküli –k-adik jószágot biztosít a jog birtokosának. Úgy is mondhatnánk, hogy a feltételes jószágok valójában a …zikai jószágokra szóló feltételes követelések.

Feltesszük hogy a gazdaság szerepl½oi, az els½o periódusban, még miel½ott tisztában lennének azzal, hogy ténylegesen melyik világállapot következett be, kereskedhet- nek a feltételes jószágok piacán². Ilyen módon tehát az eredetileg K dimenziós R^K jószágteret egy KS dimenziós R^{K S} jószágtérré b½ovítettük ki, melynek ele- meit c_k!-val jelöljük, és valamely c = (c₁; :::c_S) 2 R^{K S} feltételes jószágvektor birtokosa egy olyan joggal rendelkezik, amely révén az !2 f1; 2; :::; Sgkimenetel esetén ac_! = (c_1!; :::; c_K!)2R^K jószágkombinációhoz jut. A negatív koordináták természetesen a jószág második periódusban való szállításának kötelezettségeiként értelmezend½oek. Tegyük fel, hogy a szerepl½ok mindegyike rendelkezik egy az ezen a jószágtéren értelmezett preferenciarendezéssel, és jelöljük -^m-vel az m-edik fo- gyasztó preferenciarendezését. Tegyük fel továbbá, hogy a második periódusban az egyes szerepl½ok által a tényleges …zikai – vagyis nem feltételes – jószágokból birtokolt mennyiség függ a kimenetelt½ol, és jelöljük e^m 2 R^{K S}-el az m-edik sze- repl½o által birtokolt – feltételes – indulókészletet. Ekkor a – determinisztikus – Walrasi egyensúly fogalmát a most bevezetett feltételes jószágokra alkalmazva az ún. Arrow–Debreu-egyensúly fogalmához jutunk.

1. De…níció. Egy a

c₁¹; :::c_S¹; :::; c₁^M; :::; c_S^M 2 R^{K SM}

2Hangsúlyozzuk, ebben a periódusban nem jószágok, csupán a fenti értelemben vett „jogok”

cseréje történik.

vektor által meghatározott allokáció és egy p = (p₁₁; :::; p_KS) 2 R^{K S} árrendszer együttesét Arrow–Debreu egyensúlynak nevezünk, ha minden m-re teljesül, hogy a c ^m = (c₁^m; :::c_S^m)vektor (más néven feltételes fogyasztási terv) azm-edik fogyasztó optimális választása a

n

c^m 2 R^{K S} jp c^m p e^mo

költségvetési halmazra és a -^m preferencia relációra vonatkozóan, és XM

m=1

c ^m = XM m=1

e^m.

Az els½o jóléti tétel következményeként, a lokális telhetetlenségi feltétel tel- jesülése esetén, az egyensúlyban a kockázat elosztása Pareto-hatékony lesz³. Ha a jószágok közül egyet pénznek tekintünk, akkor az ennek egységére vonatkozó, a ténylegesen realizált világállapottól függ½o feltételes követeléseket Arrow–Debreu értékpapíroknak szokás nevezni. Az ! kimenetelhez tartozó Arrow–Debreu érték- papír tehát egy olyan feltételes követelés, amely az ! kimenetel esetén egységnyi, minden más kimenetel esetén zérus ki…zetést biztosít a követelés birtokosának.

Az Arrow–Debreu értékpapírok egyensúlyi árai tulajdonképpen a kimenetelekhez rendelnek számértékeket, amely számértékek egy korlátos mértéket de…niálnak.

Ennek a mértéknek a normálásával a kimenetelek árai egy valószín½uségi mértéket határoznak meg. Ha a valószín½uségi mez½o végesen generált, akkor minden feltéte- les követelés el½oállítható az Arrow–Debreu értékpapírok lineáris kombinációjaként.

Ebb½ol következ½oen többek között létezik kockázatmentes értékpapír. Ezek után már könnyen levezethet½o, hogy tetsz½oleges értékpapír els½o periódusbeli egyensúlyi ára éppen a kockázatmentes értékpapír hozama szerint diszkontált második perió- dusbeli lehetséges árainak imént megkonstruált mérték szerinti várható értéke lesz.

Vagyis a mi terminológiánk szerint a diszkontált árfolyam az ily módon de…niált

„…ktív” valószín½uség szerint martingál⁴. Ezt a mértéket Arrow [3] kockázatsem-

3Ezen a ponton a kockázat fogalmát nem szokás pontosan de…niálni, a szóhasználat itt arra utal, hogy a fogyasztók (kockázatkerül½o befekte½ok esetén) nemcsak intertemporálisan, de az állapotok között is igyekeznek a fogyasztásukat „simítani”, vagyis a kockázatukat csökkenteni, illetve egymás között megosztani. Egészen pontosan a feltételes jószágok elosztása lesz Pareto- hatékony.

4Két id½operiódus esetén, ha az els½o id½opontban nincsenek valódi valószín½uségi változók, akkor a martingál tulajdonság pontosan azt jelenti, hogy a második periódusban realizálódó valószín½uségi változó várható értéke éppen az els½o periódusban felvett érték.

leges valószín½uségnek nevezi.

Az Arrow–Debreu értékpapírokkal való kereskedés modellje valójában nem túl- ságosan életszer½u, de a modellnek van egy –empirikus kezelhet½oség szempontjából – nem elhanyagolható következménye. Ha az általános egyensúlyi megközelítés helyett egy parciális egyensúlyi megközelítést alkalmazva feltételezzük, hogy a kereskedett értékpapíroknak nem csak a második periódusbeli ki…zetései, de az els½o periódusbeli árai is adottak, akkor az említett összefüggésb½ol a martingálmérték már meghatározható. Ha eltekintünk az Arrow–Debreu értékpapírokkal való keres- kedést½ol, de feltesszük, hogy a létez½o értékpapírokkal való kereskedés révén minden lehetséges jöv½obeli pénzügyi ki…zetés el½oállítható⁵, vagyis elég sokféle értékpapír van a piacon ahhoz, hogy kifeszítsék a logikailag lehetséges ki…zetések halmazát, akkor a jöv½obeli ki…zetések a preferenciáktól –speciálisan a kockázattal szembeni attit½udt½ol – függetlenül⁶ beárazhatóak. Ebben az értelemben az Arrow–Debreu árak egyfajta árazási szabályt, pontosabban egy árazó funkcionált reprezentálnak, amely az összes elképzelhet½o feltételes követelések terén is értelmezve van.

Eddig feltételeztük, hogy a szerepl½ok csak az els½o periódusban kereskednek a feltételes jószágokkal, tehát a csere még azel½ott megtörténik, miel½ott a szerepl½ok tudomást szereznének a ténylegesen megvalósuló világállapotról. Els½o lépésként vizsgáljuk meg mi történne, ha megengednénk, hogy a szerepl½ok a tényleges világál- lapot megismerését követ½oen kereskedjenek a feltétel nélküli, vagyis a …zikai jószá- gokkal⁷. Megmutatjuk, hogy a fogyasztók ez utóbbi piacon már nem fognak kereskedni.

Tegyük fel, hogy az els½o periódusban kereskedtek a feltételes jószágok piacán, és megvalósult a c₁¹; :::c_S¹; :::c₁^M; :::; c_S^M 2 R^{K SM} Arrow–Debreu-egyensúly.

Tegyük fel, hogy az ! állapot következett be. Ekkor a kötelezettségek teljesítése után az m-edik fogyasztó a c_!^m = (c_1!^m; :::c_K!^m) 2 R^K kosárhoz jut. Tegyük fel, hogy létezik a …zikai jószágoknak egy olyan(c¹_!; :::; c^M_! )2 R^{K M} allokációja, hogy mindenm esetén

(c₁^m; :::; c_!^m; :::; c_S^m)-m (c₁^m; :::; c^m_!; :::; c_S^m);

5Vagyis feltételezzük, hogy a piac teljes.

6Egészen pontosan arról van szó, hogy nincs szükség a hasznossági függvények explicit szere- peltetésére, de valójában az arbitrázsmentesség feltétele implicit módon feltételezi a preferenciák monotonitását.

7Ebben az összefüggésben szokás a feltételes jószágok piacát „forward”piacnak a …zikai jószá- gok piacát „spot” piacnak is nevezni.

és legalább egy m-re a preferencia reláció szigorú értelemben teljesül, valamint fennáll a PM

m=1c^m_! PM

m=1e^m_! reláció. Ez azonban lehetetlen hiszen ez ellent- mondana a c₁¹; :::c_S¹; :::c₁^M; :::; c_S^M Arrow–Debreu egyensúlyi allokáció Pareto- optimalitásának.

2.1.2. A Radner-egyensúly

Arrow [2]-ben megjegyzi, hogy a fenti Arrow–Debreu egyensúlyi elosztás megkap- ható olyan módon, hogy feltesszük, hogy a szerepl½ok az els½o periódusban csak Arrow–Debreu értékpapírokkal kereskedhetnek, a második periódusban pedig ke- reskedhetnek a jószágok piacán. A magyarázat egyszer½u. Ha a szerepl½ok keresked- hetnek a második periódusban a …zikai jószágokkal, akkor az els½o periódusbeli kereskedés egyetlen célja az, hogy a szerepl½ok megosszák a vásárlóerejüket az egyes világállapotok között. Ezzel az eljárással az eredetileg SK számú jószá- got tartalmazó határid½os piac már csak egy S számú jószágból álló piaccá zsu- gorodott. Ahhoz azonban hogy a szerepl½ok ne csak a pénzben mért vásárlóere- jüket tudják simítani hanem a tényleges fogyasztásukat is, el½ore kell látniuk a második periódusbeli spot árakat⁸, és csak akkor beszélhetünk egyensúlyról, ha a szerepl½ok várakozásai konzisztensek a modellel, vagyis egyensúlyban, minden egyes kimenetelre vonatkozóan a spot árakra vonatkozó várakozások megegyeznek a tényleges egyensúlyi spot árakkal.

A fenti gondolatot kés½obb R. Radner [83] formalizálta és általánosította több periódus esetére. Az ún. Radner-egyensúly abban az esetben is értelmezhet½o, ha Arrow–Debreu értékpapírok helyett csak néhány kockázatos értékpapírral keresked- hetnek a gazdaság szerepl½oi, ezáltal a Radner-egyensúly fogalma fontos kiinduló- pontjává vált mind a pénzpiacok egyensúlyi elméletének mind a nemteljes piacok elméletének. Az alábbiakban [71] és [20] alapján ismertetjük a Radner-egyensúly fogalmát két periódus esetére.

Használjuk továbbra is a fenti modell jelöléseit, és tegyük fel, hogy a gazdaság szerepl½oi ezúttal N+ 1 számú pénzügyi eszközzel is kereskedhetnek, melyek közül az els½o –a továbbiakban0indexel jelölt –egy rögzített kamatozású kockázatmentes kötvény, és aj-edik eszközb½ol az els½o id½operiódusban vásárolt mennyiséget j jelöli.

A kimenetelek száma S, a fogyasztó az els½o periódusban zérus indulóvagyonnal, és a második periódusban ! kimenetel esetén e_! 2 R^K készlettel rendelkezik és

8Mely árakat természetesen nem tekintünk a modell által adottnak.