Bevezetés a transzportelméletbe

Bevezetés a transzportelméletbe

Makai Mihály

2014. február 3.

1. fejezet

Előszó

A fizikai gondolkodás középpontjában álló egyik probléma a mikroszkopikus és a makroszko- pikus jelenségek közötti kapcsolat. Közismert, hogy a mechanikai jelenségek (pl. ütközések) megfordíthatók, reverzibilisek. Ugyanakkor a nagyszámú ütközés következtében előálló mak- roszkopikus folyamat (pl. a rántotta sütés) nem megfordítható, irreverzibilis folyamat. A statisztikus fizika egyik ága megmutatta, hogy a mikrovilágot képviselő részecskék reverzibilis ütközéseiből hogyan származtathatók a makrovilágban megfigyelhető irreverzibilis változá- sok. A mikrovilág és a makrovilág közötti kapcsolattal a statisztikus fizika foglalkozik.

Tekintettel arra, hogy a hővel, általában az energiacsere kérdésével számos gyakorlati kér- dés áll kapcsolatban (gondoljon az olvasó a vízmelegítőre, az energiafajták átalakításának–

hibás szóhasználattal az energiatermelés–problémáira), a kérdéskör a mérnökök érdeklődé- sének is középpontjában áll. Nincs ez másként a nukleáris energiával kapcsolatos kérdések esetében sem. Jelen munka tárgya a részecskék ütközései révén létrejövő transzportfolyama- tok vizsgálata. A munka célja modern tudást adni a jövő mérnökeinek, fizikusainak kezébe az előttük álló, elsősorban a modern energiatermeléshez kapcsolódó (atomerőművek és fú- ziós berendezések) feladatok megoldásához. A könyv célja nem konkrét recepteket, hanem összefüggéseket, eljárásokat, technikákat megismertetni az olvasóval.

A nukleáris létesítményekben végbemenő folyamatok leírásához elengedhetetlen az alábbi jelenségek megértése:

• turbulens áramlások;

• a neutrongáz viselkedése;

• a plazmajelenségek.

Az első két jelenség többnyire az atomreaktorokban (fissziós reaktorok), a harmadik a fúziós reaktorokban alapvető jelentőségű. A részecskék (fotonok, neutronok, stb.) ütközéseinek törvényszerűségeiből megismerhetjük a szóró közeg (pl. szilárd test, oldat, rendezetlen anyag) alapvető jellemzőit, hibáit. A szórásvizsgálatokat számos ipari eljárásban (pl. szegecsek, turbinalapátok) rutinszerűen alkalmazzák.

A fenti jelenségek közös vonása, hogy nagyszámú részecske ütközése során kialakult mak- roszkopikus állapotokban megfigyelhető jelenségekről van szó. Ez a jelenségkör a transzport- elmélet nevet viseli. A transzportelmélet jelenségeinek köre a fentieknél természetesen sokkal általánosabb. Jelen munka célja elméleti alapot biztosítani azokhoz a reaktorokkal kapcso- latos munkákhoz (Monte-Carlo programok írása és használata, neutrontranszport jelenségek

numerikus vizsgálata, az áramlási jelenségek numerikus és elméleti vizsgálata, a plazmán végzett mérések értelmezése), amelyekkel naponta találkozunk a reaktorokkal, biztonsági elemzésekkel, tervezéssel kapcsolatos munkák során. Itt jegyzem meg, hogy a transzport fo- lyamatok ismerete fontos szerepet játszik a neutronok és fotonok anyagvizsgálatban történő felhasználásában is. A modern neutron-spektroszkópia, a sugárvédelem alapjai is rendelkez- nek transzportelméleti vonatkozásokkal.

Külön érdemes szót ejteni azokról a folyamatokról, amelyek során nincs lehetőség arra, hogy kialakuljon a lokális termikus egyensúly. A sugárzás következtében kialakuló plaz- mában, amely egy csillag fotoszférájában alakul ki, nem lehet számítani lokális termikus egyensúly kialakulására. Az ADS¹. fém céltárgyába becsapódó nagyenergiájú részecskenya- láb leírása szintén nem tételezheti fel termikus egyensúly kialakulását. Ilyen esetekben csak a reménytelennek tűnő feladat marad: meg kell oldani a transzportegyenletet. A megfigyelhető mennyiségek és a lokális fizikai tulajdonságok közötti kapcsolat merőben más, mint egyensú- lyi állapotban. Hasonló jelenségeket lehet felhozni a meteorológia, a csillagászat vagy számos mérnöki munka (pl. robbanómotorok tervezése) kapcsán. E feladatok közös jellemzője, hogy az érintett fizikai jelenségek több skálán is megjelennek, általában az atomi (vagy szubatomi) skáláktól a makroszkopikus skálákig. Az USA Energiaügyi Minisztériuma (Department of Energy (DOE)) a XXI. század első éveiben kezdte szervezett keretek közé terelni ezeket a kutatásokat.

Az említett terület–a transzportelmélet – magában foglalja a plazmatranszportot, ahol töltött részecskék mozgását vizsgáljuk, az élő sejtek közötti anyagtranszportot, ami élettani felentőségű kérdés, az épületek és a környezet közötti anyagtranszportot, hogy csak néhányat említsünk a nagyszámú alkalmazások közül. A fenti kérdésekkel több kiadvány is foglalkozik [9], [Kar], [Ivá], [Szent], nem beszélve az interneten elérhető nagyszámú anyagról.

Jelen munka célja a transzportelmélet alapjainak tárgyalása olyan szintig, amely lehe- tővé teszi a neutronfizikai és plazmafizikai alkalmazások megalapozását. A tárgyalt témák az alapoktól az alkalmazásokig terjednek. A tárgyalás a statisztikus rendszerekkel indul, a statisztikus részecskék eloszlásának vizsgálatától a makroszkopikus állapotfüggvény megha- tározásával folytatódik, majd alkalmazások tárgyalásával zárul. Az előadások anyagában az elvi alapokat modellezési technikák (Monte-Carlo-módszer, molekuláris dinamika, Sn ésPn

módszer) ismertetése egészíti ki. Külön fejezet foglalkozik a közelítő módszerekkel (véges differenciák, nagy örvény módszer) és egy modern technikával, amely a közelítő módszerek vizsgálatában kapott szerepet az elmúlt évtizedben. Terjedelmi korlátok miatt most ezeket a fejezeteket kihagytuk, csakúgy, mint a véletlen folyamatok alkalmazását is. Az alkalmazások közül a plazmatranszport és a neutronszórás alapjait tárgyaljuk.

Igyekeztem az utóbbi évek eredményeit is felhasználni. Így szót ejtek a kíméletes mérés, a Bose-Einstein-kondenzátum terén az utóbbi években elért eredményekről. A közelítő mód- szerek algebrai eszközökkel (nevezetesen az eredeti egyenlet szimmetriáinak meghatározása és a közelítő egyenletek szimmetriáinak vizsgálata) több, mint tíz éves ugyan, azonban gyors elterjedése a modern számítógépes algoritmusoknak köszönhető.

Feltesszük, hogy az olvasó a jelenségek magfizikai és statisztikus fizikai alapjait ismeri, noha a felhasznált termodinamikai, statisztikusfizikai alapok lényeges részeit megismételjük.

A felhasznált matematikai apparátus az analízis, statisztika és absztrakt algebra terén kíván előismereteket. Ezeket az előismeretek a Budapesti Műszaki Egyetem (BME) mérnök-fizikus szakán meghirdetett tárgyak biztosítják. Az érdeklődő olvasó a megadott hivatkozásokból felelevenítheti ismereteit.

1Gyorsítóval meghajtott szubkritikus rendszer (accelerator driven subcritical system)

A szövegben csak egyszerű bizonyításokat közlünk, az idézett tételek bizonyításának for- rását megadjuk, az olvasó ott találja a bizonyítást.

A tárgyalást gyakran megszakítja egy Feladat. Ebben az Olvasó egyszerű példákat talál az éppen tárgyalt kérdéssel kapcsolatban. A Feladat célja többé-kevésbé egyszerű alkalma- zások bemutatása.

Jelen munka a BME-en mérnökfizikus hallgatóknak tartott "A neutrontranszport alapjai"

és a "Bevezetés a plazmatranszportba" című előadások anyagára épül.

Köszönetnyilvánítás

Az egyik szerző (MM) ezúton fejezi ki köszönetét azoknak, akiktől az itt közölt anyag jelentős részét tanulta: Fényes Imrének, Geszti Péternek és Pál Lénárdnak. A szerző abban a szerencsében részesült, hogy utóbbi két tanára a jegyzet elkészítésében is tanácsokkal látta el.

Tartalomjegyzék

1. Előszó 1

Előszó 3

Tartalomjegyzék 3

2. A statisztikus rendszer 10

2.1. A statisztikus rendszer leírása . . . 11

2.1.1. Klasszikus rendszer leírása . . . 14

2.1.2. Kvantumos rendszer leírása . . . 15

2.2. Klasszikus autonóm rendszerek . . . 19

2.2.1. Stabilitás . . . 24

2.2.2. Káosz . . . 25

2.3. A mérés . . . 30

2.3.1. Irreverzibilitás . . . 38

2.4. Termodinamikai kölcsönhatások . . . 42

2.5. Liouville-tétel . . . 43

2.6. Megfigyelhető mennyiségek . . . 45

2.7. Lineáris válasz . . . 46

2.8. A transzportelmélet alkalmazása . . . 48

3. A Boltzmann-egyenlet 51 3.1. A Boltzmann-egyenlet . . . 52

3.2. Aszimptotikus megoldás . . . 56

3.2.1. Az aszimptotikus eloszlásfüggvény meghatározása . . . 57

3.2.2. Termodinamikai alapmennyiségek . . . 60

3.3. Eltérések az ideális gáztól . . . 63

3.3.1. A van der Waals-állapotegyenlet . . . 64

3.3.2. Viriálegyütthatók . . . 65

3.4. Eloszlásfüggvény külső erőtérben . . . 67

3.4.1. Debye-Hückel-elmélet . . . 68

4. Transzportjelenségek, mérlegek 72 4.1. Relaxációs paraméterek . . . 73

4.2. Megmaradó mennyiségek . . . 74

4.3. H-függvény . . . 77

4.4. Fenomenológikus mérlegegyenletek . . . 79

4.4.1. Alapegyenletek . . . 83

4.4.2. Mérlegegyenletek elektromágneses térben . . . 92

4.5. Stacionárius állapot . . . 107

4.6. Mikroszkopikus elmélet . . . 108

4.7. Fázisok egyensúlya . . . 110

4.7.1. Egyensúlyi állapot . . . 110

4.8. Közvetett transzport . . . 112

4.9. Skálák . . . 117

4.10. Hasonlóság . . . 119

4.11. Bifurkáció és káosz . . . 120

5. A Boltzmann-egyenlet nemegyensúlyi állapotban 122 5.1. Nulladrendű közelítés . . . 123

5.2. Elsőrendű közelítés . . . 126

5.3. Hidrodinamikai egyenletek . . . 129

5.3.1. A hidrodinamikai egyenletek korrekt származtatása . . . 134

5.4. Hilbert módszere . . . 138

5.5. A Chapman-Enskog–sorfejtés . . . 140

5.6. Linearizálás . . . 143

5.6.1. A Fokker-Planck-egyenlet . . . 143

5.6.2. A linearizált Boltzmann-egyenlet . . . 144

5.6.3. A diffúziós közelítés . . . 146

5.7. Egyéb ütközési integrálok . . . 148

6. Kollektív jelenségek 151 6.1. Koordinátázás . . . 152

6.2. Bogoljubov-sorfejtése . . . 154

6.3. Sorfejtések . . . 160

6.3.1. Általánosított hidrodinamikai egyenletek . . . 161

6.4. Aszimptotikus elmélet . . . 164

6.4.1. Véges rács . . . 164

6.4.2. Aszimptotikus analízisaszimptotikus analízis . . . 167

6.5. Turbulencia . . . 172

6.5.1. A hidrodinamikai egyenletek és a Boltzmann-egyenlet . . . 174

6.5.2. Ekvivalens rendszerek . . . 174

6.5.3. Haladó perturbáció . . . 176

7. Az egyensúlyi eloszlás 179 7.1. Gibbs-sokaságok . . . 180

7.2. Variációs elv . . . 184

7.3. Termodinamika . . . 186

7.4. Statisztikus dinamika . . . 190

7.4.1. A statisztikus dinamika modellje . . . 191

7.4.2. Dinamika a statisztikus dinamikában . . . 192

7.4.3. A hidrodinamikai határátmenet . . . 196

7.5. A hidrodinamikai egyenletek korrekciója . . . 198

7.6. Nemegyensúlyi termodinamika . . . 200

7.6.1. Statisztikus megalapozás . . . 200

8. Statisztikus rendszerek modellezése 206 8.0.2. A közvetett transzportegyenlet egy analitikus megoldása . . . 207

9. Plazmatranszport 212

9.1. Bevezetés . . . 213

9.2. A plazmafizika alapjai . . . 216

9.2.1. Mágneses erővonalak stabilitása . . . 221

9.2.2. Koordinátarendszer . . . 223

9.3. A mágneses erővonalak változása . . . 224

9.4. Klasszikus plazma . . . 226

9.5. Önkonzisztens tér . . . 228

9.5.1. Az erővonalak befagyása . . . 230

9.5.2. Plazmakinetika . . . 230

9.5.3. Landau-csillapodás . . . 232

9.5.4. Drift kinetika . . . 235

9.5.5. Girokinetika . . . 240

9.5.6. Időfüggő drift Hamilton-függvény . . . 241

9.6. Transzport tranziensek . . . 242

9.6.1. AzL-H átmenet . . . 242

9.6.2. ELM-Edge Localized Modes . . . 243

9.7. A plazma mérlegegyenletei . . . 246

9.8. Instabiltások . . . 248

9.8.1. Áram által generált instabilitások . . . 248

9.8.2. Ellenállás által generált instabilitás . . . 253

9.8.3. Mágneses térerőfelületek által generált instabilitás . . . 255

9.8.4. Nyomás által generált instabilitás . . . 256

9.8.5. Mikroinstabilitások . . . 257

9.9. Stabilitásvizsgálat . . . 258

9.9.1. Módszerek . . . 259

9.10. Skálatörvény, hasonlóság . . . 265

9.11. Tokamak transzport mechanizmusok . . . 268

10.A neutronszórás alapjai 274 10.1. Szórás szabad magon . . . 275

10.2. Koherens- és inkoherens szórás . . . 276

10.3. Fermi-féle pszeudópotenciál . . . 277

10.4. Neutronoptika . . . 278

10.5. Teljes visszaverődés . . . 278

10.6. Bragg-reflexió . . . 280

10.7. Kisszögű szórás . . . 281

10.8. Sugárgyengülés . . . 282

10.9. Lassú neutronok szórása . . . 283

10.9.1. Rugalmas szórás kristályon . . . 284

10.9.2. Neutronszórás és korrelációs függvények . . . 285

10.10.Fluktuáció-disszipáció tétel . . . 286

Irodalom 291 11.1. Függelék: Fourier-transzformáció 291 11.1. Fourier-sor . . . 292

11.2. Fourier-transzformáció . . . 292

12.2. Függelék: Operátorok spektruma 294

13.3. Függelék: Peremérték feladatok 298

13.1. Lineáris elliptikus egyenletek . . . 300

14.4. Függelék: Vektorok, mátrixok, tenzorok 302 14.1. Vektorok, mátrixok, tenzorok . . . 303

14.2. Deriváltak . . . 304

14.3. Koordináta transzformációk . . . 305

14.3.1. Egyensúlyi toroidális mágneses tér leírása . . . 308

14.4. Adiabatikus invariánsok . . . 310

Névmutató . . . 316

Tárgymutató . . . 317

Ábrák jegyzéke

2.1. A Bose-Einstein kondenzátum megvalósítása . . . 12

2.2. Vonzó ill. taszító csomópont . . . 22

2.3. Nyeregpont . . . 22

2.4. Elliptikus fixpont . . . 22

2.5. Lorenz attraktor . . . 23

2.6. Különös attraktor . . . 24

2.7. Határciklus . . . 26

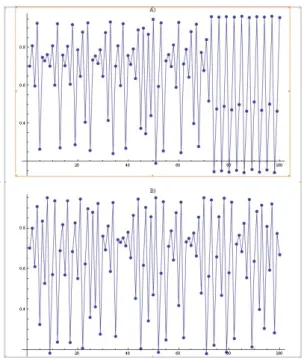
2.8. A logisztikai leképezés iterációja x = 0.7-ből kiindulva A)rc −r = −0.02 B)rc−r= 0.02 . . . 29

2.9. A Maxwell-démon működéséhez [Wiki] . . . 34

2.10. Szilárd Leó gépe [Mich] . . . 34

2.11. Két független interferométer . . . 35

2.12. Kíméletes mérés . . . 40

2.13. Neutron spin-visszhang mérés A jelölést ld. a 2.3.6. példánál . . . 40

3.1. A szórásnál használt jelölések . . . 54

4.1. Foton behatolási mélysége különböző anyagokban . . . 74

4.2. Fázisegyensúly aT ésV változókban . . . 111

4.3. Három fázis egyensúlya aP, T változókban . . . 112

4.4. Három fázis egyensúlya aT−V változókban . . . 113

6.1. A szórásnál használt jelölések . . . 159

9.1. Plazma a világűrben: szupernova robbanás . . . 214

9.2. Villamcsapás . . . 214

9.3. Geometria leírása TOKAMAK-ban . . . 219

9.4. Pálya elektromágneses térben . . . 236

9.5. Pálya elektromágneses térben . . . 236

9.6. A mágneses drifthez . . . 240

9.7. Csapdázott és szabad részecskék . . . 240

9.8. L-H átmenet . . . 246

9.9. Káosz kialakulásaL−H átmenet során . . . 247

9.10. Időtartamok és méretek a plazmában . . . 249

9.11. Kolbász-instabilitás . . . 250

9.12. Termikus energia összetartás idejének összehasonlítása 12 kísérleti berendezés H-módusában . . . 268

10.1. A neutron törésmutatóhoz . . . 279

Táblázatok jegyzéke

2.1. Összeadás Turing-géppel . . . 33

5.1. A kölcsönhatási potenciál ésν(v)kapcsolata . . . 145

7.1. Statisztikus okaságok . . . 183

7.2. Néhány munkafajta . . . 187

7.3. Kölcsönhatások és energiák . . . 188

9.1. Transport veszteségekhez vezető instabilitások tokamakban . . . 269

2. fejezet

A statisztikus rendszer

A statisztikus rendszer

2.1. A statisztikus rendszer leírása

A transzportelmélet a statisztikus fizika egyik ága. Mint minden fizikai elmélet, a transz- portelmélet vizsgálódásai is egy modell keretében történnek. Ezt a modellt statisztikus rendszernek nevezzük, a rövidség kedvéért a statisztikus jelzőt gyakran elhagyjuk.

Tekintsünk egy rendszert, amely N >> 1 részből áll. A részek közötti kölcsönhatások legyenek fizikai természetűek. A rendszer részei lehetnek

• elemi részecskék (pl. kvarkok, neutronok, protonok, elektronok, fotonok).

• atomok vagy molekulák (pl. hidrogén, hélium, metán, C60 molekula, cukor, fehérje, lipid, DNS).

• domének (pl. a legtöbb kristályt nem egyetlen kristályrács alkotja, hanem véges méretű kristályrácsok sokasága. Egy-egy rácsot egy határfelület választ el a szomszédos rácstól.

Azt a tartományt nevezzük doménnek, amelyen belül a szerkezet homogén.)

A részek közötti kölcsönhatás lehet közelhatás (pl. ütközés) vagy távolhatás. Ez utóbbit egy erőtér közvetíti, az erőteret gyakran egy potenciállal szoktuk leírni. Amennyiben a vizsgált rendszer nem áll kölcsönhatásban más rendszerekkel, zárt rendszerről beszélünk.

A rendszert alkotó részek lehetnek klasszikusak, ekkor a klasszikus mechanika szabálya- it kell alkalmazni mozgásukra (beszélhetünk pályáról, a rész helye és impulzusa, energiája egy adott időpontban lehet egyszerre meghatározott érték). Ha a részek leírására a kvan- tummechanika törvényeit kell alkalmazni, akkor érvényes a Pauli-féle kizárási elv, a kon- jugált mennyiségek nem vehetnek fel egyszerre pontos értéket, érvényes a Heisenberg-féle bizonytalansági elv, nem beszélhetünk pályáról stb. Erről az olvasó a kvantummechanika alapmunkáiban [Marx], [Land3]részletesen tájékozódhat.

A klasszikus részekből álló rendszert röviden klasszikus rendszernek nevezzük. Egy klasszikus rendszerben a részek mozgásegyenleteit fel lehet írni, amennyiben a részekre ható erők ismertek. Minden részt saját mozgásegyenlete ír le, noha a részek között lehet csatolás a kölcsönös erőhatások miatt. A rendszer szabadsági fokainak száma arányos a részek szá- mával. Amennyiben a részeket tömegpontnak tekinthetjük, az egyes részek szabadsági foka a független térkoordináták számával egyenlő, így három dimenzióban a rendszer szabadsági foka a részek száma szorozva hárommal. A pontrendszerek fizikája szerint egy ilyen rendszer mozgásegyenleteit a kezdeti állapot ismeretében meg lehet oldani¹. A klasszikus rendszer mozgásegyenleteinek megoldása (aszimptotikusan nagy időkre) erősen függ a kezdeti felté- teltől. Előfordulhat, hogy a kezdőfeltételek kis megváltozása a rendszer későbbi állapotát jelentősen megváltoztatja. Ezt a jelenséget egy egyszerű közelítésben megvizsgáljuk a követ- kező részben.

A megfigyelések szerint egy klasszikus rendszer állapotát sokkal kevesebb változóval le lehet írni, mint a rendszert alkotó részek száma. Például egy nagyszámú részecskét tartal- mazó gáz állapotát nyomása, térfogata, hőmérséklete, és a gáz tömege alapján meg lehet adni. Ezért várható, hogy a mozgásegyenletek vizsgálata túlzottan részletes leírását ad- ja a klasszikus rendszernek. Egyszerűbb leíráshoz vezethet a kapott eredmények alkalmas átlagolása.

EgyN részecskéből álló rendszer leírását kimerítően megadja a részecskék helye és im- pulzusa, amennyiben feltesszük, hogy a részecskék közötti kölcsönhatás csak e mennyiségek

1Zárt megoldás már a háromtestprobléma esetében sem adható meg.

függvénye. A leíráshoz használt 6N dimenziós teretΓ-térnek nevezik. A rendszer állapotát egy 6N koordinátával jellemezhető pont adja meg. A részek mozgását a részecskékre ható erők ismeretében megoldható mozgásegyenletek írják le. Egy alternatív leírási mód a rend- szert azzal jellemzi, hány olyan részecske tartózkodik a rpont adottd³rinfinitezimális kör- nyezetében, amelyek sebessége adott vkörülid³vinfinitezimális térfogatba esik. Ez a leírás egy hatdimenziós térben, a µ-térben megadandó sűrűségfüggvény meghatározását igényli.

Lehetséges a vizsgált rendszer jellemzése a makroszkopikus rendszerek leírására használatos fogalmakkal (térfogat, sűrűség, nyomás, hőmérséklet) is. Ezt a leírást hidrodinamikai leírás- nak nevezik, a makroszkopikus változókat le lehet származtatni aΓ-térbeli, vagy aµ-térbeli eloszlások segítségével. A dimenziók összehasonlítása is azt mutatja, hogy egy makroszko- pikus állapot nagyszámú, egymástól különböző mikroszkopikus állapottal is megvalósítható.

Kézenfekvő nem az egyedi mikroszkopikus állapotokat vizsgálni, hanem közvetlenül azon mikroszkopikus állapotok sokaságait, amelyek adott makroszkopikus állapothoz tartoznak.

Ezt a Gibbstől származó ötletet is meg lehet valósítani (ld. 7.1. alfejezet).

Amennyiben azSrendszert fel lehet osztani olyan részekre, hogy egy-egy részen belül a makroszkopikus állapotot egyetlen függvény írja le, azt mondjuk, hogy S több fázisból áll.

Egy fázison belülSadott része (fázisa) állapotát egy függvény írja le. A fázisok nem mindig különíthetők el geometriai értelemben. Például egy forró csőben áramló folyadék a folyadék és gőz fázisok széles skáláján megvalósítható, a folyadékban található gőz buborékoktól a gőzben található vízcseppekig folytonos az átmenet.

A kvantumos rendszer elnevezést olyan fizikai rendszerekre alkalmazzuk, amelyek részei- nek viselkedését a kvantummechanika írja le. Egy ilyen rendszerben a részeket a Schrödinger- egyenlet írja le, a részek leírása hullámfüggvény segítségével történik. A kvantumos rendszer energiája elkent, ami alatt azt értjük, hogy a nagyszámú rész miatt az energiasajátérté- kek nagyon közel helyezkednek el, mindig van valamilyen kölcsönhatás a környezettel, ezért lényegében nincs stacionárius állapot. Kis gerjesztés lecsengéséhez is nagy időre van szükség.

Közismert, hogy jellemzően kvantummechanikai jelenségek (pl. a szuperpozíciók léte) nem figyelhető meg makroszkopikus méretekben. Ebből a szempontból érdekes lehet, hol húzódik a makroszkopikus rendszer alsó határa. Ezt jól lehet vizsgálni pl. kétréses interferen- cia segítségével. Kísérletek szerint hélium illetve hidrogénatomok esetén még megfigyelhető a molekula hullámtermészete. Kastler szerint [Kastl] fontos kérdés lenne annak vizsgálata, hogy a növekvő méretek esetén (pl. fullerén molekula, metán) esetén mikor veszti érvényét a részecske jelleg és adja át helyét a makroszkopikus viselkedésnek. Az átmenet feltehetően folytonos és a nagyobb tömegek miatt egyre nagyobb felbontású, azaz drágább, kísérletekre lenne szükség.

2.1. ábra. A Bose-Einstein kondenzátum megvalósítása

Az 1990-es évek óta több makroszkopikus állapotban is megfigyeltek szuperponált állapo-

tot, így pl. megfigyelték makroszkopikus számú foton szuperponált állapotát üregrezonátor- ban, detektálták aC60 fullerén molekula anyaghullámainak interferenciáját, és a kvantum- számítógép egységeinek vizsgálatához végzett kísérletek során megvalósítottak szuperponált állapotban lévő atomokat úgy, hogy az állapotot ellenőrzés alatt is tartották. A XXI. szá- zad első éveinek eredménye a "Schrödinger-macskája" állapot létrehozása rádiófrekvenciás szupravezető kvantum interferencia (SQUID= superconducting quantum interference devi- ce) állapot létrehozása. Egy nemrégi eredmény [LASci] pedig a Bose-Einstein-kondenzáció (BEK) megvalósítása egySmakrorendszerben. Ez utóbbival részletesebben is foglalkozunk.

Több elképzelés is született makroszkopikus BEK állapot létrehozására. Ha vonzó köl- csönhatású bozonokat összezárunk egy potenciálvölgyben és adiabatikusan lehűtjük azokat a bozonok alapállapoti energiájáig, kialakulhat makroszkopikus szuperponált állapot. Ha a bozonok számára a potenciálvölgyben rendelkezésre áll két hiperfinom nívó (legyen a két nívó A ésB), egy újabb lehetőség nyílik. Kezdetben legyen a BEK minden részecskéje az A állapotban. Gerjesszük az A → B átmenet rezonanciafrekvenciájával megegyező rádió- frekvenciájú (RF) impulzussal az atomokat. A RF impulzus legyen rövid a BEK dinamika időállandójához képest. A gerjesztés eredményeként minden atom az AésB állapotok szu- perpozíciójában lesz, a BEK egészének makroállapota pedig ilyen egyrészecske állapotok szuperpozícióinak direktszorzata lesz. Azaz, a sokrészecske-rendszer állapota is egyrészecske állapotfüggvények szorzataként írható fel, vagyis a makroszkopikus állapot is szuperpozíció.

A kezdeti állapot fejlődését leíró Hamilton-operátorban szerepel az atomok közötti vonzó kölcsönhatás, ezért egy idő után beáll a makroszkopikus szuperpozíció állapota, amelyben minden atom egyszerre található azA ésB állapotban. A megfelelő állapotfüggvény:

|Ψ>= 1

√2(|NA,0B>+|0A, NB >), (2.1) ahol a direktszorzatban az A állapotban lévő részecskék száma N_A és a B állapotban lévő részecskék számaNb van kiírva, a braketek a megfelelő hullámfüggvényeket jelölik.

KezdetbenS nyílt rendszer, hiszen kölcsönhatásban (pl. hőcsere) áll a környezettel. Ez a kölcsönhatás a szuperponált állapotot igen rövid idő alatt lerombolja, ez a dekoherencia.

Ha a dekoherencia ideje nagyon rövid lenne, akkor ezen állapotok léte a BEK szempontjából lényegtelenek lennének, hiszen azokat meg sem lehetne figyelni. Elvileg egyetlen ütközés a BEK valamelyik atomja és egy nem kondenzált atom között elegendő a szuperponált állapot megszűnéséhez. A szuperponált állapot dekoherenciájának becsült ideje

tBEK∼ 1

NEN², (2.2)

ahol N az atomok (vagy bozonok) száma a BEK-ban,NE pedig a nemkondenzált bozonok száma. Mivel XXI. század első éveinek technikája az alábbi korlátokat szabja meg: 1 ≤ Ne ≤10⁴ és10 ≤N ≤10⁷, a dekohenrecia ideje 16 nagyságrendet is változhat, pl. 1000 sec-tól10⁻¹³ sec-ig.

Tekintsük a 2.1. ábrát, amely a BEK kialakításának elvét mutatja be. A kondenzált állapotot egy széles mágneses csapdában készítjük elő, ebben nagyszámú atomot tartunk fogva. Az atomok a csapdában diszkrét energianívókon helyezkednek el. A csapdában opti- kai eszközökkel kialakítható egy alacsonyabb energiákat megengedő gödör (ld. a 2.1. ábra jobbról második részét). A csapdát úgy alakítjuk ki, hogy a gödörben csak egyetlen kötött nívó alakuljon ki. Adiabatikus hűtéssel az atomokat ebbe az állapotba kondenzáljuk. Ezután a mágneses csapdát kinyitjuk (ld. a 2.1. ábra jobbról harmadik részét), a nem kondenzált atomok többsége elpárolog, ez csökkenti a szuperponált állapotra veszélyes ütközések való- színűségét. Ám azok az atomok még veszélyeztetik a szuperponált állapotot, amely atomok

ugyan kötött állapotban vannak, de közel találhatóak a szabad (azaz nem kötött) állapothoz, legyen ezen állapotokhoz tartozó energia∆E. Ezek az atomok nem párolognak el, ha a BEK egyik atomja ilyen részecskével ütközik, a szuperponált állapot lebomlik. Az ilyen állapotban lévő részecskék számát egy szimmetrizálásnak nevezett eljárással csökkenteni lehet, ezzel az eljárással egyúttal a szuperponált állapot élettartamát is meghosszabbítjuk.

Alkalmazzunk egyν frekvenciájú RF impulzust, amely alkalmas egy koherensA→Bát- menet gerjesztésére. A kondenzátum most is makroszkopikus szuperponált állapotban van, de állapota különbözik (2.1)-től, mert a RF impulzus megváltoztatja a betöltési számokat.

Ugyanakkor a nem-kondenzált egyrészecske bozonállapotok energiaspektruma is módosul.

Kialakul két energialétra, amelyek egymáshoz képest el vannak tolva 2ν-vel (ld. a 2.1. ábra negyedik részét). Mindkettőben kötött állapotok alakulnak ki, de az egyik állapotainak ener- giái lefelé tolódnak el, ezen energiaállapotok felelnek meg az A↔ B cserére szimmetrikus állapotoknak; a másik állapot energiái felfelé tolódnak el, ezek nyilván az A ↔ B cserére aszimmetrikus állapotoknak felelnek meg. A ∆E <2ν sávba eső állapotokból csak a szim- metrikusak maradnak meg, az aszimmetrikusak elpárolognak. Szerencsére azA↔Bcserére szimmetrikus állapotok nem fenyegetik a szuperponált állapotot, mert a Hamilton-operátor is szimmetrikus, ezért a kölcsönhatás csak egy közös fázisszorzót eredményez. A kötött álla- potok betöltési számait a lézer intenzitásával szabályozni lehet, ezért a szuperponált állapot élettartamát jelentősen meg lehet hosszabbítani.

A kvantumos rendszer hullámfüggvénye nem építhető fel, mert a szükséges információnak csak egy töredékével rendelkezünk. Be lehet viszont vezetni a sűrűségmátrixot (ld. alább).

A statisztikus fizika tárgya egy S statisztikus rendszer leírása. Feltesszük, hogy S fel- bontható részrendszerekre, amelyek között kölcsönhatás állhat fenn. A kölcsönható rész- rendszerek cserélhetnek anyagot, energiát, impulzust vagy impulzusmomentumot. A köl- csönhatások a gravitációs kölcsönhatást (energiacsere egy formáját) kivéve szigetelhetőek, azaz, megakadályozhatóak. Csak véges méretű rendszerekkel foglalkozunk, az ábrákon S határa egy zárt vonal (térben pedig egy zárt felület), amely elválasztja a vizsgált statisztikus rendszert a környezettől. A statisztikus rendszer állhat kölcsönhatásban a környezetével (pl.

a környezet biztosíthat állandó hőmérsékletetSszámára). Akár klasszikus, akár kvantumos leírást használunk, feltesszük, hogyS állapotának leírása lehetséges az alkotó részek leírása segítségével, vagyis, a rendszer egészének állapotát meghatározza az alkotórészek állapota.

2.1.1. Klasszikus rendszer leírása

Legyen azSstatisztikus rendszer szabadsági fokainak számas, ekkor leírhatósdarab álta- lános koordinátávalq1, . . . , qs, éssdarab impulzussalp1, . . . , ps. Mivel a rendszer állapota a részek állapotainak direkt szorzata, a rendszer energiája gyakorlatilag folytonosnak tekint- hető. S egy tetszés szerint kiválasztott részrendszere kölcsönhatásban áll a rendszer többi részével. E kölcsönhatás közben energiacsere megy végbe, a kölcsönhatás energiája sokkal nagyobb, mint a rendszer nívói közötti energiakülönbség. Ezért feltehetjük, hogy elegendően hosszú idő alatt a rendszer minden lehetséges állapotát elegendően sokszor veszi fel. Legyen

w= lim

T→∞

∆t

T (2.3)

ahol∆tazSrendszer a∆p∆qtérfogatban eltöltött ideje. Vezessük be aρ(p, q)statisztikus mátrixot az alábbi definícióval:

dw=ρ(p, q)dpdq. (2.4)

Egyf(p, q)függvény középértéke definíció szerint hfi=

Z

ρ(p, q)f(p, q)dpdq= lim

T→∞

1 T

Z

f(t)dt. (2.5)

Az ilyen rendszert, amelyben az időátlag megegyezik a sokaságátlaggal, ergodikus rendszer- nek nevezik. Természetesen a (2.4)-(2.5) összefüggések statisztikus jellegűek, akárcsak min- den makroszkopikus mennyiség kifejezése. Ennek oka: a statisztikus leírásban nagyszámú változó szerepel (minden részecske impulzusa és helye), miközben a makroszkopikus testek leírásához kisszámú változó is elegendő. Amennyiben egy makroszkopikus testet írunk le, ez a véletlen jelleg alig látható, mert a makroszkopikus mennyiségek hosszú idejű átlaga alig mu- tat változást. Megmutatható, hogy a szórás és az átlagérték hányadosa arányos 1/√

N-nel.

Amennyiben egy zárt, makroszkopikus rendszer bármely makroszkopikus részrendszerében a részrendszert jellemző összes makroszkopikus fizikai mennyiség nagy relatív pontossággal (ld. fent) megegyezik saját átlagértékével, azt mondjuk, a zárt rendszer statisztikus (termo- dinamikai) egyensúlyban van. Ha egy kezdeti időpillanatban a zárt makroszkopikus rendszer nincs statisztikus egyensúlyban, az később feltétlenül újra statisztikus egyensúlyi állapotba kerül. Azt az időtartamot, amely alatt a statisztikus egyensúlyba történő átmenet lezajlik, relaxációs időnek nevezzük.

2.1.2. Kvantumos rendszer leírása

Legyen az S rendszer a kvantummechanika által leírható. Legyen S₁ egy részrendszer S- ben, amelyben N₁>>1 részecske található. Feltesszük, hogy az alrendszerek között nincs kölcsönhatás. Az alrendszer energianívóinak száma exponenciális függvényeN₁-nek, hiszen a teljes rendszer állapotait független részecske-állapotok direktszorzataként kapjuk meg. Bont- suk fel azSrendszert egyS1és egyS2részrendszerre. Legyenek a részrendszerek elegendően nagyok ahhoz, hogy belső energiájukhoz képest az S1 ésS2 közötti kölcsönhatás energiája elhagyható legyen. Ekkor azt mondjuk S1 ésS2 egymással gyengén kölcsönható részrend- szerek.

Amennyiben S1 ésS2 egymással gyengén kölcsönható részrendszerek, statisztikai érte- lemben is függetlennek tekinthetőek. Ekkor azS1ésS2egyesítésével kapott rendszer elosz- lásfüggvénye ρ12dp12dq12, ahol az infinitezimális elemek: dp12=dp1dp2ésdq12=dq1dq2. A statisztikus függetlenség miatt

ρ12dp12dq12=ρ1dp1dq1ρ2dp2dq2. (2.6) Ebből adódóanρ₁₂=ρ₁ρ₂.

A kvantumos rendszer leírása során a fizikai világ matematikai modelljét használjuk. A modellben azt fogalmazzuk meg, hogyan írjuk le a fizikai állapotot, a megfigyelhető mennyi- ségeket, a mérést, az időbeni fejlődést, azaz dinamikát.

1. A fizikai állapot egy fizikai rendszer teljes leírását adja. A fizikai állapotot a Hilbert-tér egy elemével írjuk le. Azonos fizikai állapotot rendelünk azonban egy komplex, skalár szorzóban eltérő Hilbert-tér elemeihez, vagyis, a Hilbert-tér vektorait ekvivalencia osz- tályokba soroljuk, azonos osztályba tartoznak a komplex szorzóban eltérő vektorok.² 2. Egy megfigyelhető mennyiség a fizikai rendszer olyan jellemzője, amelyet elvileg mérni

lehet. A megfigyelhető fizikai mennyiségeket önadjungált, lineáris operátorokkal írjuk le. Az operátorokat kövér betűkkel (pl. A) jelöljük.

3. A kvantummechanikában egy megfigyelhető mennyiséghez egyAoperátort rendelünk.

A megfigyelés eredménye az A operátor egy a sajátértéke. A mérés után a fizikai állapot A egyik sajátvektorába, mégpedig az a sajátértékhez tartozó sajátvektorába megy át.

2Ezeket az egyszerűbb szóhasználat kedvéért sugárnak szokás nevezni.

4. Egy kvantumállapot időbeli fejlődését egy unitér operátor írja le, az időfüggést a Schrödinger-egyenlet írja le:

dψ

dt =−iHψ. (2.7)

IttHa Hamilton-operátor.

Ismeretes, hogy az állapotfüggvény normálása tetszőleges, ezért ezért ahol a normálás tetszőleges volta hangsúlyos, ott s hullámfüggvény szinonímájaként a sugár szót használ- juk. Amennyiben a vizsgált kvantumos rendszer egymással kölcsönható részrendszrekből áll, akkor az alábbi meglepő állítások igazak³:

1. Az összetett rendszert alkotó részrendszer állapotát nem egyetlen sugár írja le.

2. A mérés nem ortogonális projekció.

3. Az időbeli fejlődést nem unitér operátor írja le.

Az állításokat bemutatjuk egy egyszerű példán.

2.1.1 Példa. (Kétkomponensű rendszer) Tekintsünk egySrendszert, amelynek két ré- sze A és B. Legyen a két részrendszer egy-egy bozon, spinjükegy adott z irányban a 0 vagy 1 értéket vehet fel. Az S rendszeren végzett mérésből szeretnénk következtetni A állapotára.

Tegyük fel, hogy AésB korreláltak és Sállapotát

|ψ >S=a|0>A⊗|0>B +b|1>A⊗|1>B (2.8) adja meg. A (2.8) állapoton elvégzett mérés eredményekéntS a (2.8)-ben szereplő ortogoná- lis állapotok valamelyikébe kerül, |a|² valószínűséggel |0>_A|0>_B-be és a mérés eredménye (emlékezzünk: A spinjét mérjük)0; viszont |b|² valószínűséggel a mérés után a |1>_A|1>_B állapot marad meg, a mérés eredménye ezért1. Ha olyan mérést szeretnénk, amely azS-en elvégezve olyan eredményt ad, amely kizárólagAállapotától függ, ennek alakja csakMA⊗1B

lehet. Itt MA egy öndajungált operátor, amely csak A-n hat, 1B pedig a B-n ható egység- operátor. A mérés várható értéke a (2.8) állapotban:

< ψ|MA⊗1B|ψ >=

(a∗A<0|⊗B <0|+b∗B <1|⊗B<1|)(MA⊗1B) (a|0>A⊗|0>B+b|1>A⊗|1>B)

=|a|²_A<0|MA|0>A+|b|²_A<1|MA|1>A.

(2.9)

Ez a kifejezés átalakítható a következő formára:

<MA>=spur(MAρa), (2.10) ahol

ρA=|a|²|0>AA<0|+|b|²|1>AA<1|. (2.11) ρ_A joggal nevezhető az S összetett rendszerbeliA részrendszer sűrűségoperátorának.

3Az állítások annak következtében meglepőek, hogy a vizsgált rendszer legalább két részből áll, ezért állapotát a részek állapotának direktszorzata írja le, ld. Ref. [LASci].

Vizsgáljuk meg az S1,S2 részrendszerekből álló S rendszert. Ebben a rendszerben azA operátorral jellemzett fizikai mennyiség várható értéke:

< a >=

Z Z

Ψ^∗(p1, q1, p2, q2)AΨ(p1, q1, p2, q2)dp1dq1dp2dq2. (2.12) Vezessük be aρ(p₁, q₁, p⁰₁, q⁰₁)függvényt az alábbi definícióval:

ρ(p₁, q₁, p⁰₁, q⁰₁) = Z

Ψ(p₁, q₁, p₂, q₂)Ψ^∗(p⁰₁, q⁰₁, p₂, q₂)dp₂dq₂. (2.13) A definícióból következik, hogyρ(p1, q1, p⁰₁, q⁰₁)önadjungált:ρ^∗(p1, q1, p⁰₁, q₁⁰) =ρ(p⁰₁, q⁰₁, p1, q1).

ρ-t sűrűségmátrixnak nevezik. Diagonális elemei megadják azS1részrendszer koordinátái- nak valószínűségeloszlását:

ρ(p1, q1, p1, q1) = Z

|Ψ(p1, q1, p2, q2)|²dp2dq2 (2.14)

< a > = Z

[Aρ(p1, q1, p⁰₁, q⁰₁)]_p0

1=p₁,q⁰₁=q₁dp1dq1. (2.15) A fenti integrálban azAoperátor csakp1, q1-re hat. Vegyük észre, hogy a sűrűségmátrix egy általánosítása a fizikai rendszer leírásának, hiszen olyan esetekben is alkalmazható, amikor a fizikai rendszer csak több hullámfüggvény lineáris kombinációjával írható le.⁴

A részrendszerek közötti kölcsönhatás fontos szerepet játszik az entrópia definíciójában.

Noha az entrópiáról csak a 3 fejezetben lesz, szó, az alábbi két példában az entrópiáról is előfordul abban bízva, hogy az olvasó korábbi ismeretei elegendőek a két példa gondolatme- netének követéséhez.

2.1.2 Példa. (Részrendszerek) Osszuk fel a zárt S-t rendszertS₁,S₂, . . . részrendszer- re, tegyük fel, hogy az részrendszerek kölcsönhatása elhanyagolható. Az S rendszer állapota legyen a fázistér dΓ térfogatában, amely kifejezhető a részrendszerek által elfoglaltdΓn térfo- gatokkal:

dΓ =Y

n

dΓ_n. (2.16)

Ekkor a részrendszerek energiájának összege az egész rendszer lehetséges energiáinak egy meg- adott intervallumába esik. Tegyük fel, hogySmikrokanonikus sokaság, energiájaE₀. Legyen dw annak valószínűsége, hogyS adΓ állapotok egyikében található:

dw=áll ·δ(E−E0)Y

n

dΓn. (2.17)

Osszuk felS-t nagyszámú részrendszerre, ezek közül vizsgáljunk egy adott részrendszert, Sn-t. Legyen wn e részrendszer eloszlásfüggvénye. Amennyiben ismerjük a wn függvényt, kiszámíthatjuk Sn energiájának valószínűségeloszlását. Annak valószínűsége, hogy Sn pon- tosan a fázistér dΓn elemében található, csak azN-ik részrendszerEn energiájától függ:

w_n=w_n(E_n). (2.18)

Jelölje Wn(E)dE annak valószínűségét, hogy azn-ik részrendszer energiája (E, E+dE)-be esik. Ezt a valószínűséget úgy kapjuk meg, hogy a wn(En) valószínűséget megszorozzuk a azoknak a kvantumállapotoknak a számával, amelyek energiája (E, E+dE)-be esik. Jelölje

4Az ilyen állapotot szuperponált állapotnak nevezik.

Nn(E)Snazon állapotainak számát, amelyek energiája legfeljebbE. Ekkor az(E, E+dE)-be eső állapotok száma

dN_n(E) dE dE.

Ebből aWn(E)energia szerinti valószínűség eloszlásra ezt kapjuk:

W_n(E) =dN_n(E)

dE w_n(E), (2.19)

W_n(E)-t úgy kell normálni, hogy mindenn-re teljesüljön Z

Wn(E)dE= 1.

Általános megfontolások alapján [Lan5][13-17.o.] aWn(E)függvényeknek éles maximuma van az E =< E > átlagértékénél és csak e pont körül különbözik lényegesen nullától. A Wn(E)görbe jellemzésére bevezetjük a ∆E szélességet az alábbi definícióval:

Wn(E)∆E= 1, (2.20)

minden n-re. Felhasználva (2.19)-t,

w_n(E)dN_n(E)

dE ∆E= 1. (2.21)

S_n azon állapotainak száma, amelyek energiája (E, E+dE)-be esik

∆Γn =dNn(E)

dE ∆E. (2.22)

∆Γn tehát a Sn részrendszer makroszkopikus állapotának mikroszkopikus állapotok szerinti

"elkentségére" jellemző, neve statisztikus súly, logaritmusa pedig

Sn = ln ∆Γn (2.23)

Sn entrópiája.

2.1.3 Példa. (Energianívók sűrűsége) Megmutatjuk, hogy egy S rendszerben az ener- gianívók sűrűsége a részecskék számának exponenciálisan növekvő függvénye. Mivel az S rendszerre vonatkozóan (2.20) szerint

∆Γ = 1

w(E), (2.24)

ezért

Sn = ln Γn=−<lnWn(E)> .

Az S rendszer állapotai és a részrendszerek állapotai között fennáll a (2.16) kapcsolat. Az entrópia (2.23) definíciója miatt

S=X

n

Sn,

vagyis a részrendszerek entrópiája összeadódik. Megfordítva a (2.23) definíciót, Sállapotai- nak száma így adható meg:

4Γ =e^S(E),

a nívók távolsága pedig 4E

4Γ =4Ee^−S(E)=4Ee^−PnSn(E)=4EY

n

e^−Sn(E). (2.25) Vagyis,S nívóit úgy kapjuk meg, hogy a részrendszerek nívóit "összefésüljük". Ezért a mak- roszkopikus rendszer energianívói közötti távolság a részecskeszám növekedésével exponenci- álisan csökken.

AzSstatisztikus leírására, általában, az alábbi lehetőségek adódnak:

• Γ-tér: azS-et alkotóN részecskep1, . . . , pN impulzusával ésq1, . . . , qN koordinátájával írjuk le.

• Bevezetjük a sűrűségfüggvényt: legyen f(r,v, t) az r körüli infinitezimális d³r térfo- gatbantidőpontbanvsebességgel rendelkező részecskék száma.

• µ-tér: azSáltal kitöltött térfogatot felosztjuk elemi térfogatokra. Az elemi térfogatok nem infinitezimálisak, de elegendően nagy számú részecskét (kb. 10⁹) tartalmaznak.

Az S-et alkotó v sebességű részecskék minden t időpontban egy d³rd³v fázisponttal jellemezhetőek. A sebességefelosztást úgy választjuk, hogy a részecskék eloszlása foly- tonosnak legyen tekinthető. Egy N részecskéből álló rendszer a µ-térben N pontot foglal el. Ad³rd³v fázispontokba eső részecskék számaf(r, v, t)d³rd³v.

• Gibbs-sokaságok. Elkészítjük azSrendszer nagyszámú példányát, ezek csak a kezdeti feltételben térnek el. A fizikai mennyiségek átlagait vesszük a sokaság elemei felett.

A fenti leírások segítségével sikeresen tárgyalhatóak az alábbi fizikai rendszerek:

• ideális gázok: így viselkednek szobahőmérsékleten az egymással gyengén kölcsönható atomokból, molekulákból álló gázok.

• neutrongáz: az energiatermelésben használt atomreaktorok működése leírható egy na- gyon híg neutrongáz segítségével. Itt a neutronok ütközése elhagyható, a neutronok viszont a magokkal ütköznek.

• reális gázok: amennyiben a hőmérsékletet csökkentjük, egyre fontosabb lesz a gázt alkotó atomok közötti kölcsönhatás. Ilyen szobahőmérsékleten a széndioxid, alacsony hőmérsékleten a nitrogén.

• Bose-Einstein kondenzátum (ld. 2.1 fejezet).

2.2. Klasszikus autonóm rendszerek

Vizsgáljuk meg, hogyan írható le egy S statisztikus rendszer időbeli fejlődése az állapot- térben. Két kérdést vizsgálunk meg: a stabilitást és a káosz kialakulását. Mindkét kérdést általános formában vizsgáljuk, az evolúciós egyenletek segítségével.

A fizikai folyamatok időbeli fejlődését általános formában így írhatjuk:

∂Ψ(x, t)

∂t =AΨ(x, t) +Q(t). (2.26)

IttQ(t)adott forrás, elkülönítettük az időváltozót, a többi független változótxtartalmazza.

AzAoperátorban található műveletek az xváltozóra hatnak. A (2.26) egyenlet megoldása zárt alakban felírható⁵:

Ψ(x, t) =e^tAΨ(x,0) + Z t

0

e^(t−s)AQ(s)ds. (2.27)

Itt az operátor exponenciális függvényét az alábbi képlettel lehet meghatározni:

e^−tA= lim

n→∞

1 + t

nA −n

. (2.28)

Az itt szereplő negatív hatványokArezolvensének pozitív kitevőjű hatványaival írhatóak le.

A továbbiakban az egyszerűség kedvéért áttérünk egy speciális eset vizsgálatára.

Legyen Q(t) = 0, vagyis nincs külső forrás. Legyen a megoldástér véges dimenziós, a bázis legyenφ1(x), . . . , φn(x), a megoldást pedig kifejtjük a bázis szerint:

Ψ(x, t) =

n

X

i=1

yi(t)φi(x). (2.29)

Ekkor a megoldást teljes mértékben leírják az y_i(t) együtthatók. Amennyiben a (2.26) egyenlet ú.n. autonóm egyenlet[Pontr], akkor

dy_i(t)

dt =f_i(y₁, . . . , y_n), i= 1, . . . , n. (2.30) az időfüggő együtthatók az (2.30) autonóm egyenletekből kaphatóak meg. Azfifüggvények- ről feltesszük, hogy adottak azRⁿtér egyn-dimenziós részintervallumán,fiés első deriváltjai folytonosak a fenti részintervallumon. Az autonóm egyenlet megoldása egyn-dimenziós tér- ben egy görbét ír le az idő függvényében.

2.2.1 Példa. (Az autonóm rendszerek bővítése) Az időtől expliciten függőfifüggvénnyel felírt (2.30) egyenlet is autonóm egyenlet. Vezessük be azn+ 1-ik koordinátát az alábbi mó- don: yn+1=at és adjuk az (2.30) egyenletekhez a

dyn+1

dt =a

egyenletet. Így egy n+ 1 változós autonóm egyenletrendszerre jutottunk.

Az autonóm egyenletek jelentőségét az adja, hogy az (2.30) egyenlet az Rⁿ tér elemeit az Rⁿ tér elemeire képezi le. Az autonóm egyenletek tulajdonságait ezért tanulmányozni lehet Rⁿ teret önmagába leképező transzformációk vizsgálatakor. A matematikában az iterációs eljárások bőséges példát szolgáltatnak az ilyen leképezésekre.

Az autonóm rendszerek megoldása rendelkezik az alábbi érdekes tulajdonságokkal.

1. Megmutatható, hogy amennyibeny_i=ψ_i(t), i= 1, . . . , nmegoldása a (2.30) egyenlet- nek, akkorψ_i(t+c), i= 1, . . . , n szintén megoldás.

2. Amennyiben (2.30) megoldását a fázistérben haladó görbével (egy trajektóriával) írjuk le, meg kell adni a haladás irányát is. Amennyiben azyi=ψi(t), i= 1, . . . , nmegoldá- son kívül van egy másikyi=ψ_i⁰(t), i= 1, . . . , nmegoldás is, akkor a két megoldás által leírt trajektóriáknak vagy nincs közös pontja, vagy a trajektóriák egybeesnek, azaz, ψi(t) =ψ_i⁰(t)mindeni-re.

5A mátrix exponenciális függvénnyel óvatosan kell bánni, ld. [12].

3. Tegyük fel, hogy az yi = ψi(t), i = 1, . . . , n megoldás a t1 és t2 időpontokban meg- egyezik, vagyis, a trajektória két különböző időpontban áthalad a fázistér egy pontján.

Ebben az esetben két lehetőség áll fenn. Az első: ψi(t) = const, a trajektória egy pontban áll, nem változik az idővel. Az ilyen pontot a megoldás stacionárius vagy egyensúlyi pontjának nevezzük. A második: létezik olyan T periódusidő, amelyre ψi(t+T) =ψi(t), i= 1, . . . , n, de a trajektória két|τ1−τ2|< T közbenső pontja nem esik egybe. Ebben az esetben a megoldást periodikusnak nevezzük.

4. A trajektória pontjai egyn-dimenziós vektorteret alkotnak.

5. A fázistér(a1, . . . , an)pontja akkor és csak akkor stacionárius pont, ha fennállfi(a1, . . . , an) = 0, i= 1, . . . , n.

A probléma további egyszerűsítése érhető el, ha a (2.30)-ben szereplő függvények lineá- risak. Ekkor az egyenlet alakja:

˙

y=Ay. (2.31)

Vizsgáljuk meg ezt az esetet n = 2 mellett. A trajektóriák változása általános vonásokat mutat. Tegyük fel, hogy az Amátrix sajátértékei különbözőek és nem nullák, sajátvektorai legyenek h₁,h₂. Ekkor a (2.31) egyenlet megoldását így írhatjuk:

y=c₁h₁e^λ1t+c₂h₂e^λ2t, (2.32) ahol c1, c2 valós számok. A(h1,h2)bázison a megoldás

y=ξ1h1+ξ2h2, (2.33)

vagyis a megoldás ξ1 ésξ2 koordinátája

ξ₁=c₁e^λ1t;ξ₂=c₂e^λ2t (2.34) általában nem ortogonális koordinátákat jelöl, hiszen a h1,h2 sajátvektorok lineárisan füg- getlenek, de nem feltétlenül ortogonálisak. Egy affin leképezéssel⁶, ahol a transzformáció az x n-elemű vektor komponenseinek transzformációját írja le. a fázistér P = (ξ₁, ξ₂) pontja átvihető egy olyan P^∗ pontba, amelynek koordinátáit már ortogonális tengelyeken mérjük.

A lehetségesP pontok egyPtérben, a lehetségesP^∗ pontok egyP^∗térben helyezkednek el.

Vizsgáljuk meg az autonóm rendszer lehetséges pályájánaky pontjának képét aP^∗ térben.

Az y = (0,0) pont egyensúlyi pont, hiszen nem változik az idővel. Néhány további pályatípus:

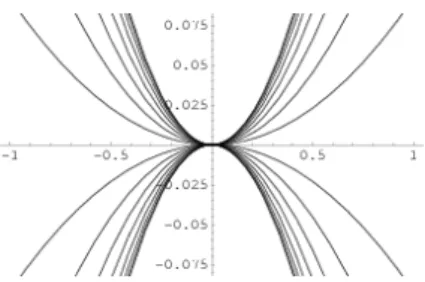
Csomópont. Legyenλ₁λ₂>0 és mindkét sajátérték különbözzön nullától, továbbá legyen

|λ1|<|λ2|.Vizsgáljuk először aλ₁<0,λ₂<0esetet. A tett feltevések mellett a (2.33) pálya bárhonnan indul, az origóba tartt→ ∞esetén, ld. 2.2. ábra. A görbék torlódási pontját (esetünkben ez origót) vonzó fixpontnak nevezik. Haλ₁ >0, akkor a pályák ugyanazok maradnak, ám irányuk megfordul: az origó környezetéből induló pályák a végtelenbe tartanakt→ ∞esetén, ekkor az origót taszító fixpontnak (csomópontnak) nevezik. ⁷

Nyeregpont. Amennyibenλ1<0< λ2, a pálya egyenleteξ1/c1=ξ2/c2e^(λ1−λ2)t=állandó, ld. 2.3. ábra. Az ábra a (2.33) kifejezés ξ1 és ξ2 együtthatóit ábrázolja. Az origót most nyeregpontnak (vagy hiperbolikus pontnak) nevezik.

6Az (x→x⁰) affin transzformáció általános alakja

x⁰_i=

n

X

j=1

aijxj+bj

7Vegyük észre, hogy at→ −tesetén a vonzó fixpont taszító fixponttá válik és viszont.

2.2. ábra. Vonzó ill. taszító csomópont

2.3. ábra. Nyeregpont

Elliptikus fixpont. Ha a gyökök komplexek, azok csak konjugált párok lehetnek. Ekkor ξ1(t) = A1e^−atcos(bt−f1) és ξ2(t) = A2e^−atcos(bt−f2), ahol A1, A2-amplitúdók;

f1, f2-fázisállandók;λ=a±iba komplex sajátérték pár. Ekkor a pályák logaritmikus spirálba transzformálhatók, ld. 2.4. ábra. Az origó ebben az esetben fixpont, elne- vezése ebben az esetben fókusz. Amennyiben a = 0, a sajátértékek tiszta képzetes számok [Szépf][ 216-221 old.], a pályagörbék ellipszisek, amelyek lineáris transzfor- mációval körökké alakíthatóak. Az origón, amelyet ekkor centrumnak vagy elliptikus fixpontnak neveznek, egyetlen görbe sem halad át.

Parabolikus fixpont. Amennyiben az egyik sajátérték (λ₁) nulla, a másik pedig negatív, a megoldásokξ₁(t) =const,ξ₂(t) =e^−|λ2|t, mindenξ₂= 0egyenesen fekvő pont fixpont, ide konvergál minden megoldás hat→ ∞. A szinguláris pontok nem stabilak, hiszen a legkisebb változás elrontja az A mátrix által leírt leképezés szingularitását, azaz a dx/dt= 0feltételt kielégítő pontot. Az ilyen fixpontot parabolikus fixpontnak nevezik, ez a paraméterek változása után nyeregponttá, vagy csomóponttá alakul át.

-3 -2 -1 1 2 3

-3 -2 -1 1 2

2.4. ábra. Elliptikus fixpont

2.5. ábra. Lorenz attraktor

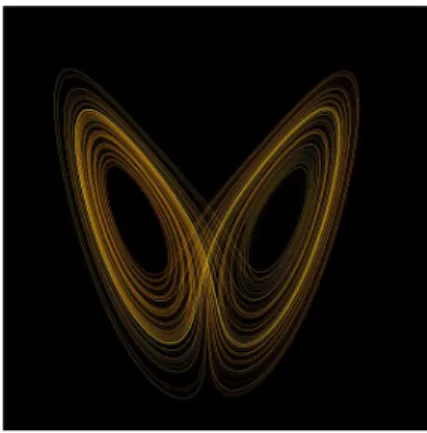
Különös attraktor A disszipatív S rendszer által elfoglalt térfogat az idővel csökkenhet (ld. Liouville-tétel). A kaotikus viselkedést mutató disszipatív rendszerek állapota aszimptotikusan nagy idők esetén egy olyan térfogatba zárható, amelynek jellemző mérete nem nulla. Azt a tartományt, amelybeS pontjai bezárhatóak t→ ∞esetén, különös attraktornak nevezik. A különös attraktorok a fázistér véges részét foglalják el, végesben helyezkednek el és korlátosak. Fontos tulajdonságuk a hiperbolicitás: a pálya két közeli pontja egyre távolabb kerül egymástól.

2.2.2 Példa. (Lorentz-attraktor) Példának tekintsük a Lorentz-attraktort, amely az alábbi differenciálegyenlet-rendszer vizsgálatához kapcsolódik:

˙

x = s(y−x) (2.35)

˙

y = x(r−z)−y (2.36)

˙

z = xy−bz, (2.37)

ahols a Prandtl-szám;r a Rayleigh-szám; b pedig egy paraméter. Az(x(t), y(t), z(t)) függvényeket mutatja a 2.5. ábra,r= 28,s= 10, ésb= 8/3értékek mellett. Az ábrán az tengely felfelé mutat, az xtengely jobbra, azy tengely pedig hátra mutat. Az ábra jól mutatja, hogy miért hasonlítja a különös attraktort több szerző egy tál spagettihez.

A legtöbb dinamikai rendszer esetében az S rendszert ábrázoló görbe egy pontba, egy ciklusba vagy más jól definiálható halmazba végződik. Vannak azonban kivételek.

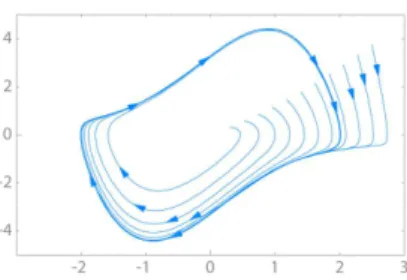
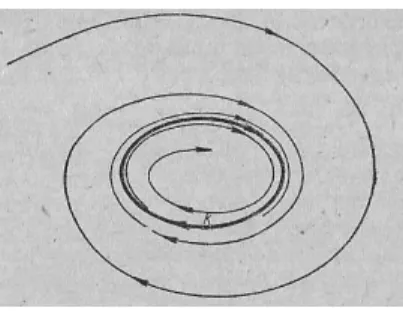
Határciklus. A fázistérben pályák egy része egy (többdimenziós) tóruszhoz közelít, mintegy rácsavarodik a tóruszra. Általában azt a halmazt, amelyhez azS-t ábrázoló pálya tart (feltéve, hogy ilyen halmaz létezik), határciklusnak nevezik, ld. 2.7. ábra.

2.2.3 Példa. (Van der Pol-oszcillátor) A Van der Pol-oszcillátor elektromos rez- gőkörök vizsgálata során került előtérbe. Tekintsük a

¨

x+µ(x²−1) ˙x+x= 0 (2.38)

egyenletet, ahol x = (x, y) a koordinátákat jelöli. Amennyiben µ = 0, a harmonikus oszcillátort kapjuk, haµ >0, akkor disszipáció lép fel ésµértékétől függően a rendszer gyorsan egyensúlyba juthat, vagy elérheti a határciklusát. A 2.6. ábra azarctan(x1/x2) fázist mutatja az idő függvényében. A vastagon jelölt határciklust a fázistérben haladó

2.6. ábra. Különös attraktor

görbe elérheti kívülről is, belülről is. Amennyiben a határciklust nem sikerül gyorsan elérni, az energiadisszipáció miatt a pálya gyorsan egy fixpontba jut: minden energiáját elveszti és megáll.

Megjegyezzük, hogy a Navier-Stokes-egyenletnek (ld. 5.2 fejezet) két dimenzióban létezik vé- ges átmérőjű globális attraktora. Parabolikus parciális differenciálegyenleteknek létezhetnek véges dimenziós attraktorai. Az egyenlet diffúzív része csillapítja a megoldásban jelen lé- vő nagyfrekvenciájú komponenseket, ez bizonyos esetekben globális attraktor kialakulásához vezet.

2.2.1. Stabilitás

Az evolúciós egyenletek vizsgálatában jelentős szerepet kap annak eldöntése, hogyan változik a megoldás, ha a kezdőpontot megváltoztatjuk. A kérdést az autonóm egyenletek esetében vizsgáljuk meg. Tegyük fel, hogy előírjuk a t = 0 esetény(0) =ξkezdőfeltételt. A továb- biakbanφ(t, ξ)-vel jelöljük a (2.31) egyenlet megoldását,φtehát egy vektorfüggvény, amely a t skalár és aξ vektor függvénye. Fennáll tehát aφ(0, ξ) =ξösszefüggés. Az alábbiakban ismertetendő Ljapunov-féle stabilitás azt vizsgálja, mennyire távolodik el a megoldás nagy időkre akkor, ha a kezdőfeltételt kicsit megváltoztatjuk. Ljapunov gondolatmenete alkalmas a nemlineáris (2.30) egyenlet stabilitásának vizsgálatára is.

A (2.30) egyenleta stacionárius pontját Ljapunov szerint stabilnak nevezzük, ha 1. létezik olyan kis ρ > 0, hogy |ξ−a| < ρ esetén a (2.30) egyenlet φ(t, ξ) megoldása

meghatározott mindent >0időpontban;

2. mindenε >0-hoz létezik olyan0< δ < ρ, amelyre |ξ−a|< δesetén |φ(t, ξ)−a|< ε mindent >0-ra.

3. Amennyiben létezik olyan 0 < σ < ρ, amelyre |ξ−a| < σ esetén egy kezdetben egymáshoz közeli megoldásokat a leképezés tetszőlegest időpontban egymáshoz közeli megoldásokba képez le, azaz fennáll

t→∞lim |φ(t, ξ)−a|= 0 a (2.30) egyenletet aszimptotikusan stabilnak nevezzük.

Az alábbi, Ljapunovtól származó tétel segítségével megállapítható egy a stacionárius pont stabilitása. Vezessük be a (2.30) egyenlettel kapcsolatban az alábbin×n-es mátrixot.

Legyen

A=

∂fi(a)

∂x_j

, i= 1, . . . , n;j= 1, . . . , n. (2.39)

1 Tétel(Ljapunov-tétele) Ha az A mátrix minden sajátértékének valós része negatív, akkor a (2.30) egyenletrendszer a stacionárius pontja aszimptotikusan stabil. Pontosabban létezik elegendően kis σszám, amelyre |ξ−a|< σ esetén fennáll

|φ(t, ξ)−a| ≤r|ξ−a|e^−αt, aholr ésαpozitív, ξ-től független számok.

A tétel bizonyítása megtalálható Pontrjagin [Pontr] könyvének 26. paragrafusában. A (2.30) autonóm egyenlet stabilitásának vizsgálata során jól használható a Ljapunov-függvény. A V(y)függvényt Ljapunov-függvénynek nevezzük, ha rendelkezik az alábbi tulajdonságokkal:

• Legyeny(t)olyan megoldása a (2.30) autonóm egyenletnek, amely kielégíti ay(t₀) =y₀ kezdeti feltételt. Legyen azy(t)megoldás nem azonosan nulla. EkkorV(y(t))>0aP fázistér egyDkörnyezetében, amely tartalmazza az y(t₀)pontot is.

• A (2.30) autonóm egyenlet mindeny(t)megoldására teljesül d

dtV(y(t)) =

n

X

k=1

∂V

∂yk

dy_k dt =

n

X

k=1

∂V

∂yk

f_k. (2.40)

Amennyiben y(t) = 0akkor ^dyt_d(t) = 0, vagyis ez a pont a megoldás egyensúlyi állapota. Az y(t) = 0egyensúlyi állapot akkor és csak akkor stabil Ljapunov-féle értelemben, ha

• LétezikV(y) Ljapunov-függvény, és az eleget tesz a dV /dt <0 feltételnek a D tarto- mányban haladóy(t)megoldás minden pontjában

• AV(y)Ljapunov-függvény egyetlenDtartománybeliy(t)trajektória mentén sem azo- nosan nulla.

Ha a φ(t0)pontot tartalmazó D környezet tartalmaz egy D0 korlátos tartományt, benne a φ(t0)pontot, továbbáD0-banV(y) =V0, aholV0>0állandó, akkorφ(t0)aszimptotikusan stabilD0-ban. Ha létezik az egészPtéren értelmezettV(y)Ljapunov-függvény, és||y(t)|| →

∞eseténV(y)→ ∞, akkor aφ(t0)megoldás globálisan aszimptotikusan stabilis.

2.2.2. Káosz

Ebben a részben az (2.26) egyenlet Q = 0, azaz, forrás nélküli megoldásait vizsgáljuk.

Egyelőre kihasználjuk, hogy mind az (2.26), mind az (2.30) egyenlet a P fázistér pontjait képezi le magára a fázistérre. Ezt az egyenlet integrálásával lehet belátni. Fel lehet tenni a kérdést, létezik-e olyanD⊂P tartomány, amelyet azS rendszer nem képes elhagyni, azaz, amelyet a (2.26) egyenlet kiintegrálás után önmagára képez le. Az ilyenDtartományokat az autonóm rendszer esetéhez hasonlóan így szokás felosztani:

• Fix pont: a fázistér olyan pontja, amelyet nem tud a megoldás elhagyni. Azy fixpont tulajdonsága: fi(x) = 0,i= 1, . . . , n.

• Különös attraktor-1. A fázistérben haladó zárt görbe, amelyet a megoldás nem tud elhagyni. Ilyen a periodikus megoldás, de elképzelhető, hogy csak aszimptotikusan tart a megoldás egy zárt görbéhez.

• Határciklus. Előfordulhat, hogy a zárt görbe végtelen hosszú. Ez a helyzet például akkor, ha a végtelen hosszú görbe rá van tekerve egy tóruszra, úgy, hogy a görbe sohasem metszi önmagát.

2.7. ábra. Határciklus

• Különös attraktor-2. Ez a típus a kaotikus viselkedéshez kapcsolódik, a megoldás egy korlátos halmazban marad, de a halmaz dimenziója kisebb a fázistér dimenziójánál és nem egész szám. Ilyen pálya alakulhat ki disszipatív rendszerekben sorozatos bifurká- ciók után.

A fixpont jellemzését korábban megadtuk. A periodikus megoldást is tárgyaltuk már. A határciklust az egyszerűség kedvéért kétdimenziós fázistérben vizsgáljuk. Az alábbi tételek bizonyítottak autonóm rendszerekre, ld. [Pontr], 28. paragrafusát. Később megmutatjuk, az általános (2.26) egyenlet és az (2.30) egyenlet között analógia áll fenn.

2 Tétel(Határciklus) Legyen x = φ(t) egy határciklusa az (2.26) egyenletnek, n = 2 mellett. LegyenKegy zárt trajektória, amelyet a fenti megoldás határoz meg. Egy zárt görbe aPteret–most síkot–két diszjunkt részre osztja: belső és külső részre. Mivel a (2.26) egyenlet megoldásainak nincs metszéspontja, mindenK-tól különböző görbe vagy a külső, vagy a belső tartományban halad. Két egymást kizáró lehetőség áll fenn: a K közelében haladó görbék feltekerednek K-ra vagy t→ ∞ vagy t→ −∞esetén. Ez a megállapítás a külső és a belső görbékre is vonatkozik.

Amennyiben a külső vagy belső görbe t → ∞ esetén tekeredik fel K-ra, a K határciklust stabilnak nevezzük. Amennyiben a külső vagy belső görbe t → −∞ esetén tekeredik fel K-ra, aK határciklust teljesen instabilnak nevezzük (ld. 2.7. ábra).

Legyen ψ(t) az (2.30) egyenlet megoldása. A megoldástér P pontját a ψ(t) megoldás ω-határpontjának nevezzük, ha létezikt0-nál nagyobb, korlátlanul növekvőt1, t2, . . . , tk, . . . , limk→∞tk =∞pontok sorozata úgy, hogy fennáll

k→∞lim ψ(tk) =P.

Az ω-határcikluspontok Ohalmazátω-határsokaságnak nevezzük. Megmutatható, hogy az Osokaság nem üres, zárt, korlátos, és teljes trajektóriákat tartalmaz. Ez utóbbi azt jelenti, hogy amennyiben a ξpont benne vanO-ban, akkor aΦ(t= 0) =ξkezdeti feltételt kielégítő Φ(t, ξ)megoldás is benne van azOsokaságban.

Legyen D az (2.30) egyenlet fázisterének egy korlátos részhalmaza, amelyen az (2.30) jobboldalán álló függvények parciális deriváltjai folytonos függvények. Ekkor kimondható az alábbi tétel, amely a határciklus létezését mondja ki adott feltételek fennállása esetén.

3 Tétel(Határciklus létezése) Legyen φ(t)a (2.30) egyenlet megoldása n= 2 esetén.

Legyen φ(t) megadva minden t ≥ t0 esetén, és ezen t értékekre a megoldás legyen benne az F korlátos, zárt tartományban, amelyet tartalmaz D. Legyen továbbá az O sokaság ω- határhalmaza a φ(t) megoldásnak. Ha az O halmaz nem tartalmaz fixpontot, akkor az egy