ÁLTALÁNOS JÁRMŰGÉPTAN
A projekt címe: „Egységesített Jármű- és mobilgépek képzés- és tananyagfejlesztés”
A megvalósítás érdekében létrehozott konzorcium résztvevői:
KECSKEMÉTI FŐISKOLA
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM AIPA ALFÖLDI IPARFEJLESZTÉSI NONPROFIT KÖZHASZNÚ KFT.
Fővállalkozó: TELVICE KFT.
Szerkesztette:
SZABÓ ANDRÁS
Írta:
ZOBORY ISTVÁN
Lektorálta:
KULCSÁR BÉLA
Rajzoló:
KISS CSABA
A mintafeladatokat kidolgozta:
CSÁSZÁR LÁSZLÓ
ÁLTALÁNOS
JÁRMŰGÉPTAN
Egyetemi tananyag
2011
Császár László, Budapesti Műszaki és Gazdaságtudományi Egyetem Közlekedésmér- nöki Kar
LEKTORÁLTA: Dr. Kulcsár Béla
Creative Commons NonCommercial-NoDerivs 3.0 (CC BY-NC-ND 3.0) A szerző nevének feltüntetése mellett nem kereskedelmi céllal szabadon másolható, terjeszthető, megjelentethető és előadható, de nem módosítható.
ISBN 978-963-279-591-1
KÉSZÜLT: a Typotex Kiadó gondozásában FELELŐS VEZETŐ: Votisky Zsuzsa
TÁMOGATÁS:
Készült a TÁMOP-4.1.2.A/2-10/1-2010-0018 számú, „Egységesített jármű- és mobil- gépek képzés- és tananyagfejlesztés” című projekt keretében.
KULCSSZAVAK:
Fizikai mennyiségek megadása, mértékrendszerek, méréstechnikai alapok,
járművek mechanikai folyamatai, járművek áramlástani folyamatai, járművek hőtani folyamatai, gépek együttműködése és irányítása.
ÖSSZEFOGLALÁS:
A jegyzet bevezető ismereteket ad a további mérnöki tanulmányokhoz.
Célja a középiskolában tanult fizikai és matematikai ismeretekre alapozva megismertetni a hallgatóságot a közlekedést megvalósító járművek egyszerű műszaki folyamataival, bevezetést adni a méréstechnika elemeibe, fejleszteni a járművek működésével kapcsolatos elemi fizikai folyamatok felismerését, és számítási feladatok megoldásával való gyakorlat kezelését. Gyakorlati célja még a tárgynak az eltérő középiskolai fizikai ismeretek egyetemi szintű homogenizálása és a matematikai tárgyalásmód – bár visszafogott – továbbfejlesztése.
Tartalomjegyzék
Előszó ... 8
0 Bevezetés ... 9
1 Fizikai mennyiségek megadása, mértékrendszerek ... 11
1.1 járműgéptanban használt fizikai mennyiségek ... 11
1.2 A fizikai mennyiség dimenziója, mértékegysége és mérőszáma ... 14
1.3 Prefixumok ... 19
1.4 Mértékrendszerek ... 20
2 Méréstechnikai alapok ... 22
2.1 Bevezető megjegyzések ... 22
2.2 A mérőrendszer felépítése ... 23
2.3 A mérési hibák két fő csoportja... 25
2.3.1 A rendszeres hibák ... 25
2.3.2 A véletlen hibák ... 26
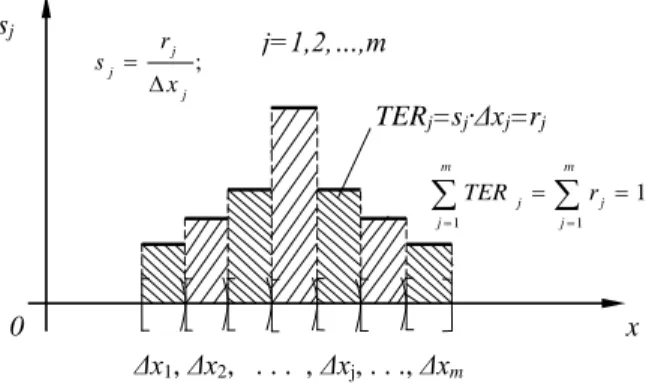
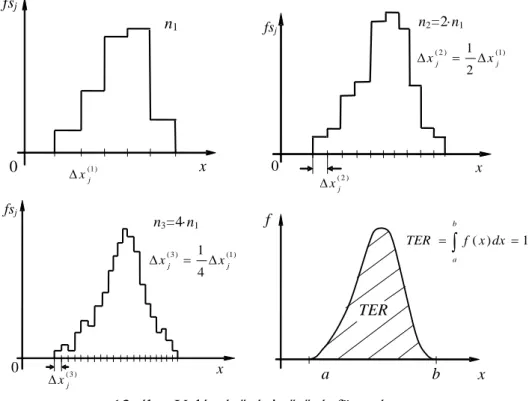
2.4 A mérési adatok csoportosítása – hisztogramok ... 32
2.4.1 A gyakorisághisztogram ... 32
2.4.2 A relatív gyakoriság hisztogram ... 33
2.4.3 A relatív gyakoriság sűrűséghisztogram ... 34
2.4.4 A valószínűségi sűrűségfüggvény bevezetése ... 35
2.5 A véletlen hibával terhelt mérési eredmények gyakorlati kezelése ... 37
2.6 Abszolút és relatív hiba ... 38
2.7 A közvetett mérés, a hibaterjedés jellemzése ... 39
2.7.1 Egyváltozós függvénykapcsolat esete... 39
2.7.2 Többváltozós függvénykapcsolat esete... 42
2.8 A jelleggörbe kimérése ... 45
3 Járművek mechanikai folyamatai ... 49
3.1 Az anyagi pont mozgásjellemzői ... 49
3.1.1 A helyvektor mint az idő függvénye ... 49
3.1.2 Az elmozdulásvektor, mint kétváltozós függvény ... 50
3.1.3 A sebességvektor, mint az idő függvénye ... 51
3.1.4 A gyorsulásvektor mint az idő függvénye ... 52
3.2 Speciális síkbeli mozgások ... 56
3.2.1 A körmozgás ... 56
3.2.2 A szögsebesség, mint az idő függvénye ... 56
3.2.3 A szöggyorsulás, mint az idő függvénye ... 57
3.2.4 Az egyenletes körmozgás ... 58
3.2.5 A határozatlan integrálról ... 59
3.2.6 Állandó gyorsulású haladó mozgás ... 60
3.2.7 Állandó szöggyorsulású forgómozgás ... 65
3.3 Járművek mozgásciklusa – menetábra ... 66
3.4 Egyszerű hajtásrendszerek ... 68
3.4.1 A fogaskerékhajtás... 69
3.4.2 A szíjhajtás ... 74
3.4.3 A dörzskerekes hajtás ... 77
3.5 Járművek működési ciklusának erőhatásviszonyai ... 77
3.6 Járművek ideális működési ciklusának energetikai viszonyai ... 79
3.7 Gépek energiahasznosítása változó veszteségek esetén ... 81
3.8 Gépek periodikus mozgásai ... 86
3.8.1 Harmonikus lengőmozgás ... 87
3.8.2 A kulisszás hajtómű ... 93
3.8.3 A forgattyús hajtómű ... 97
3.8.4 A gépek forgásának egyenlőtlensége – lendítőkerék ... 99
4 Járművek áramlástani folyamatai ... 105
4.1 A nyugvó folyadék egyensúlya ... 105
4.1.1 A folyadék nyomása ... 105
4.1.2 Nyugvó folyadék energiatartalma és munkaképességei ... 108
4.1.3 Nyugvó folyadék és szilárd test egyensúlya, hajók úszása és stabilitása ... 111
4.2 Folyadékáramlások... 113
4.2.1 Alapfogalmak ... 113
4.2.2 Áramvonal, áramcső kontinuitás ... 116
4.2.3 Az ideális folyadékra vonatkozó Bernoulli egyenlet ... 117
4.2.4 Folyadékszállítás dugattyús szivattyúval ... 121
4.2.5 Valóságos folyadékok veszteséges áramlása ... 126
4.2.6 A veszteséges Bernoulli egyenlet, csővezetéki áramlások ... 127
4.3 Az impulzus tétel és alkalmazásai ... 130
4.3.1 Impulzustétel áramcsőre ... 130
4.3.2 Az impulzus tétel alkalmazásai, egyszerű turbinák ... 133
5 Járművek hőtani folyamatai ... 136
5.1 Az ideális gáz állapotegyenlete ... 136
5.2 Hőmennyiség, fajlagos hőkapacitás... 137
5.3 A hőtan első főtétele... 140
5.4 Elemi állapotváltozások ... 143
5.4.1 Az izochor állapotváltozás ... 144
5.4.2 Az izobár állapotváltozás ... 145
5.4.3 Az izotermikus állapotváltozás ... 146
5.4.4 Az adiabatikus állapotváltozás ... 147
5.4.5 A politropikus állapotváltozás ... 147
5.5 Hőerőgép létrehozhatósága ... 148
5.6 Motorikus körfolyamatok ... 149
6 Gépek együttműködése és irányítása ... 155
6.1 A gépek jelleggörbéinek alaptípusai ... 155
6.2 Gépek együttműködése, munkapont, stabilitás ... 158
6.3 Vezérlés és szabályozás ... 160
7 Mintafeladatok ... 163
7.1 1. Gyakorló feladat: mérési eredmények feldolgozása ... 163
7.2 2. Gyakorló feladat: regressziós görbe illesztése mérési adatokra ... 167
7.3 3. Gyakorló feladat: csavarvonal menti mozgás vizsgálata ... 172
7.4 4. Gyakorló feladat: hajtásrendszer vizsgálata ... 176
7.5 5. Gyakorló feladat: lendítőkerék méretezése ... 184
7.6 6. Gyakorló feladat: több merev testből álló rendszer vizsgálata ... 189
7.7 7. Gyakorló feladat: tartály oldalfalán elhelyezett tisztítónyílás fedelének vizsgálata ... 194
7.8 8. Gyakorló feladat: Síklapátozású vízikerék vizsgálata... 198
7.9 9. Gyakorló feladat: Dízelmotorban lezajló termodinamikai folyamatok
vizsgálata ... 211
Ábrajegyzék ... 220
Táblázatjegyzék ... 224
Irodalomjegyzék ... 225
Előszó
Az „Általános járműgéptan” c. tárgy heti két órás előadással és heti egy órás laborfoglalkozással szerepel a BME Közlekedésmérnöki Karán a közlekedésmérnöki BSc szak és a járműmérnöki BSc szak tantervében. A tantárgy bevezető ismereteket ad a további mérnöki tanulmányokhoz.
Célja a középiskolában tanult fizikai és matematikai ismeretekre alapozva megismertetni a hallgatóságot a közlekedést megvalósító járművek egy- szerű műszaki folyamataival, bevezetést adni a méréstechnika elemeibe, fejleszteni a járművek működésével kapcsolatos elemi fizikai folyamatok felismerését, és számítási feladatok megoldásával való gyakorlat kezelé- sét. Gyakorlati célja még a tárgynak az eltérő középiskolai fizikai ismere- tek egyetemi szintű homogenizálása és a matematikai tárgyalásmód – bár visszafogott – továbbfejlesztése. A jelen jegyzet azon előadásaim anyagát tartalmazza, amelyeket a BME Közlekedésmérnöki Karán az elsőéves hallgatóknak tartottam a 2006/2007 tanév őszi félévtől kezdődően.
Budapest, 2010. szeptember 17.
a szerző
Bevezetés
A járművek az összes gépek G sokaságának egy J részsokaságát képezik.
Minden jármű gép, de nem minden gép jármű. A viszonyokat az 1. ábra síkbeli ponthalmazok J G relációjával szemlélteti. A gép fogalmának megadása a következőképp történhet: „ A gép tervezett fizikai folyama- toknak ad keretet valamilyen közvetlen vagy közvetett emberi szükséglet kielégítésére”. Ilyen értelemben kell az előzőek szerint a gépnek bizonyu- ló járművek kérdéskörét is megközelíteni. Azon emberi szükséglet, ame- lyet a járművek kielégítenek a közlekedési szükséglet. Idézzük fel ezért, hogy mi is a közlekedés? A közlekedéstudomány meghatározása szerint a közlekedés „személyek és dolgok rendszeres ismétlődő helyváltoztatá- sa”. Egyrészről fizikai szempontból tehát itt bizonyos tömegek nem egy- beeső pontok közötti térbeli áthelyezéséről van szó. Másrészről a megha- tározásban lényeges dolog a rendszeres ismétlődő jelleg szerepeltetése, ugyanis az egyedi mozgásfolyamat – legyen az járművel történő akár személy vagy árú áthelyezés – a gyakorító jelleg hiánya miatt nem minő- sül közlekedésnek! A fentiekből következően azt mondjuk, hogy a közle- kedés tömegjelenség.
J
a járművek sokasága a gépek sokasága
G
1. ábra Gépek és járművek
Ilyen meggondolások után visszatérve a közlekedés fizikai jelentéséhez világosan kirajzolódik, hogy tömegek rendszeres mozgással megvalósuló térbeli áthelyezése egy adott közlekedési pályán tömegáram értékkel jel- lemezhető, melynek jele m és mértékegysége
m = kg/s vagy a nagyság- rendeket célszerű mérőszám elérése érdekében figyelembe véve t/h lehet.A jármű mint gép jellemzője, hogy minden esetben rendelkezik egy, az utasokat vagy dolgokat befogadó szerkezeti egységgel, nevezzük ezt kép- letesen „tartálynak”, és ennek a tartálynak a közel vízszintes helyzetét, és
a közlekedési pálya menti vezérelt mozgását további, a „tartály” körül el- helyezett alkalmas gépi egységek biztosítják: a hordmű, a hajtómű és a fékmű.
A fentiek alapján közelebbről behatárolható az „Általános járműgéptan”
c. tárgy célja: a járművek üzeme során megvalósuló egyszerű fizikai folyamatok megismerését célul kitűző ismeretanyag elsajátíttatása.
Mint az a fentiekből következik, feltételezve a hallgatóság járműtechnikai érdeklődését a tárgy alapvetően épít a középiskolából megszerzett fizikai és matematikai ismeretekre.
Az „Általános járműgéptan” c. tárgy a következő fejezetekből épül fel:
1. Fizikai mennyiségek megadása, mértékrendszerek 2. Méréstechnikai alapok
3. Járművek mechanikai folyamatai 4. Járművek áramlástani folyamatai 5. Járművek hőtani folyamatai
6. Gépek együttműködése és irányítása
1 Fizikai mennyiségek megadása, mértékrendszerek
1.1 járműgéptanban használt fizikai mennyiségek
Valamely fizikai mennyiség tulajdonságot vagy állapotot határoz meg. A tulajdonságot meghatározó mennyiségek legtöbbje anyagjellemző (pl.
hőtágulási együttható, viszkozitás, stb.). Az állapotot meghatározó meny- nyiségek (az állapotjellemzők) kétfélék lehetnek:
extenzív jellemzők: kiterjedéssel kapcsolatosak, valamely térrész disz- junkt felbontásán additivitás érvényesül. Pl.: energia, tömeg, stb. Az extenzív mennyiségekre megmaradási törvények érvényesülnek (pl.
energia-megmaradás, tömegmegmaradás, stb.). Az additivitási tulaj- donság szemléltetésére a 2. ábra egy téglalap alakú tartomány egy V térfogatot jellemez. A V térfogatú tartományt elemidegen (diszjunkt) részekre bontjuk, de úgy, hogy a Vi résztérfogatok egyesítése kiadja a teljes V térfogatot. Adva tehát a V1,V2,..., Vn térfogat sorozat, amelyre
j i ha V
Vi j ,
és V V
n
i
i
1teljesül. Legyen a V térfogatba foglalt össz-tömeg m(V), az egyes Vi résztérfogatokba foglalt tömeg pedig mi(Vi), i=1,2,…,n, akkor az additivitás azt jelenti, hogy m(V) =
n
i
i
i V
m
1
)
( teljesül, azaz a teljes térfogatba foglalt tömeg a résztérfogatokba foglalt tömege ösz- szege. A V térfogatba foglalt m össz-tömeg helyett a V térfogatba fog- lalt E össz-energiára hasonlóképpen az m(E) =
n
i
i
i E
m
1
)
( összefüg- gést kapjuk.
V
V
1V
2V
3V
4V
5V
6... … … V
n2. ábra A vizsgált térrész felbontása
intenzív jellemzők: hatás erősségére jellemzők, a kiterjedéstől függet- len mennyiségek. (Pl.: hőmérséklet, nyomás, tömegsűrűség, stb.) Valamely adott V térrészben (térfogatban) jelen lévő extenzív és extenzív jellemzők között sajátos viszony áll fenn, amelyet a következő tétel fo- galmaz meg.
Tétel: A jelenlévő extenzív mennyiség áramlásának szükséges fel- tétele a vele kapcsolatban álló valamely intenzív mennyiség térbeli inhomogenitása.
A tétel tehát azt állítja, hogy ha valamely térrészben áramlik egy intenzív jellemző, akkor a vele kapcsolatban lévő valamely intenzív jellemző el- oszlása nem lehet egyenletes (azaz homogén) a vizsgált térrészben.
A tétel érvényesülésére két egyszerű, szemléletes példát mutatunk be. Az első példa – amely egy hidrosztatikai rendszerre vonatkozik – azt szem- lélteti, amikor az intenzív jellemző adott térbeli inhomogenitása nem biz- tosít egyben elégséges feltételt is a vele kapcsolatban lévő extenzív jel- lemző áramlásához.
p
0p
p
0 gz
3. ábra Inhomogén intenzív jellemző I.
A 3. ábrán felrajzolt nyitott tartályban a folyadék nyugalomban van. A fo- lyadék V térfogatú térrészt tölt ki. A hidrosztatikus nyomás – mint inten- zív jellemző – eloszlása inhomogén a V térrészben, hiszen a folyadékfel- szín alatti mélységgel lineárisan növekszik. Folyadékáramlás – tömeg- áram – mégsem alakul ki, mert a tartályban lévő folyadékrészek egyensú- lyának feltételei az inhomogén nyomásviszonyok ellenére biztosítottak Tehát a vizsgált példában az intenzív jellemző inhomogenitása nem veze- tett a extenzív jellemző áramlásához!
T1
T2
T3
4. ábra Inhomogén intenzív jellemző II.
A második példa – amely egy termikus rendszerre vonatkozik – azt mu- tatja be, hogy egyes esetekben a térrészben jelenlévő intenzív jellemző inhomogenitása esetén beáll a vele kapcsolatban álló extenzív jellemző áramlása, tehát esetenként az intenzív jellemző inhomogenitása elégséges feltételt ad a vele kapcsolatban lévő extenzív jellemző áramlásához. A 4.
ábrán felrajzoltunk egy téglalap alakú szilárd testet, melynek kezdeti hő- mérséklet eloszlását a környezeti hőmérséklet értékével azonos homogén (a térrészben egyenletes) eloszlásúnak tekinthetjük. Egy meghatározott időpontban kezdjük el hegesztőpisztoly lángjával melegíteni a test jobb alsó sarkát. A lánggal bevitt hőenergia a testben vezetéssel terjed tova, és eközben megvalósul a test felmelegedési folyamata (belső energia növe- kedés), mely folyamat előbb időfüggő, majd állandósult hőmérséklet el- oszláshoz vezet a test belsejében. Az állandósult – de nem egyenletes (nem homogén) – hőmérséklet eloszlás akkor áll be a test belsejében, amikor a test felszínén a konvekcióval ugyanannyi hő áramlik ki a kör- nyező légtérbe, mint amennyit a láng bevezet a testbe. A példában az áramlásba jövő extenzív jellemző a hőenergia, amely az inhomogén hő- mérsékletmező mint intenzív jellemző eloszlás hatására jön áramlásba.
Hőmérsékletkülönbség ugyanis vezetésképes szilárd testben szükségsze- rűen hőenergia áramlást okoz, amely a hőmérséklet kiegyenlítődés irá- nyába indul meg, mindig a melegebb helytől a hidegebb hely felé. A 4.
ábrán feltüntettük az állandósult hőáramlás esetén jelentkező állandó hő- mérsékletű (izoterm) vonalakat, és ezekre merőlegesen feltüntettük az adott helyen érvényesülő hőáram vektorokat is. Összefoglalva: a most vizsgált termikus rendszerben az intenzív jellemző (a hőmérséklet elosz- lás) inhomogenitása maga után vonta a vele kapcsolatban álló extenzív jellemző (a hőenergia) áramlását. Most tehát az intenzív jellemző inho- mogenitása nem csupán szükségesnek, de egyidejűleg elégségesnek is bi- zonyult a vele kapcsolatban lévő extenzív jellemző áramlásához.
1.2 A fizikai mennyiség dimenziója, mértékegysége és mérőszáma A fizikai mennyiségek jellemzésének egyik fontos módját adja a mennyi- ségek dimenziójának értelmezése.
Definíció: Valamely fizikai mennyiség dimenzióján annak mérő- számtól és mértékegységtől független tartalmát – a minőségének azonosítását – megadó információt értjük. A dimenzió mennyiségi- leg határozatlan. Az x-szel jelölt fizikai mennyiség dimenziójának jele: Dim(x).
A fizikai mennyiségek közül ésszerűen kiválasztott alapmennyiségekre származtatott mennyiségek rendszere építhető. Az alapmennyiségekhez alapdimenziókat, a származtatott mennyiségekhez pedig az alapdimenzi- ók függvényeként kiadódó származtatott dimenziókat lehet rendelni.
Tekintsük a következő tárgyalásunk szempontjából alapvető három ha- gyományos alapmennyiséget, a távolságot, a tömeget és az időt. A jelölé- seket a következők szerint vesszük fel:
1. távolság, jele: s , dimenziója: Dim(s) = L, 2. tömeg, jele: m , dimenziója: Dim(m) = M, 3. idő, jele: t , dimenziója: Dim(t) = T.
Tekintsünk ezek után példákat az alapmennyiségekből képzett származta- tott mennyiségek és azok származtatott dimenzióinak képzésére. Előre bocsátjuk, hogy ha egy fizikai mennyiség betűjele elé a Δ jelet írjuk, az azt jelenti, hogy a szóban forgó mennyiség kis növekményét tekintjük. Pl.
Δs egy kis távolságnövekményt, Δt pedig egy kis időnövekményt jelent.
1. sebesség, értelmezése: v =
t s
, dimenziója:
Dim(v) = LT-1
T L ) Dim(
)
Dim(
t
s ,
2. gyorsulás, értelmezése: a =
t v
, dimenziója:
Dim(a) = -2
-1
T L T
T L ) Dim(
)
Dim(
t
v ,
3. erő, értelmezése: F = m a, dimenziója:
Dim(F) = Dim(m) Dim(a) = M L T -2 4. nyomás, értelmezése: p =
A F
, dimenziója:
Dim(p) = -1 -2
2 -2
T L M L
T L M ) Dim(
)
Dim(
A
F .
Rögzítsük azt az eredményt, hogy a vizsgált példák esetében a származta- tott dimenziók mindenkor az alapdimenziók hatványszorzataként voltak felírhatók. Általános esetben is ugyanez a helyzet, valamely x fizikai mennyiség dimenziója mindig felírható az alapdimenziók hat- ványszorzataként a következő alakban:
Dim(x) = L i M j T k , ahol i, j, k kitevők egész számok.
A tárgyalásunknak ezen a pontján fontos hangsúlyozni, hogy valamely fi- zikai mennyiség dimenziója nem egyenlő a tekintett mennyiség mérték- egységével.
Az x fizikai mennyiség dimenziója ugyanis a megadott definíció szerint mennyiségileg határozatlan minőség azonosító szimbólum (amelyre szimbolikus algebrai műveletek vannak értelmezve). Az x fizikai mennyi- ség mértékegysége ezzel szemben a tekintett fizikai mennyiség megálla- podásszerűen egységnyinek tekintett részét határozza meg. Az x mérték- egységébe foglalt mennyiséget [x] jelöli. Ezzel a mértékegység fogalom- mal lehetővé válik a fizikai mennyiségek numerikus értékekkel történő jellemzése. Egy x mennyiség numerikus jellemzése úgy történik, hogy megadjuk azt az {x} valós számértéket – az x mennyiség mérőszámát –, amellyel meg kell szorozni a mértékegységbe foglalt mennyiséget, hogy a tekintett x-ben jelen lévő mennyiséget kapjuk. Képletben:
x = {x} [x] = mérőszám mértékegység.
A mérőszámnak tehát csak a tekintett adott mértékegység megválasztásra nézve van értelme. Természetszerűen adott fizikai mennyiség esetén a mértékegység elvileg sokféleképp megválasztható. Legyen adva pl. [x]1
és [x]2 az x mennyiség két különbözőnek választott mértékegysége.
Ezek figyelembe vételével az x mennyiség a következő alakban írható fel:
x = {x}1 [x]1 = {x}2 [x]2 .
A most felírt összefüggés adja meg az alapját a x fizikai vizsgált mennyi- ség különböző mértékegységekhez tartozó mérőszámai átszámításának.
Amennyiben a két különböző mértékegységbe foglalt mennyiség arányát ismerjük, és adott az [x]1 -hez tartozó {x}1 mérőszám is ismert, akkor az [x]2 -höz tartozó keresett {x}2 mérőszámot a nyilvánvaló
{x}2 = {x}1
2 1
] [
] [
x
x = {x}1 k
kifejezés szolgáltatja. A bevezetett k szorzó neve: átszámítási szorzó, és a két különböző mértékegységbe foglalt mennyiség arányszámaként van ér- telmezve.
Az elmondottakat egy, az erő mérőszámának meghatározásával kapcsola- tos példával szemléltetjük. A régebben általánosan használt „műszaki mértékrendszerben” az erő mértékegység az 1 kp erő volt. Az 1 kp erő- egység meghatározását az adta, hogy ekkora erő egy 1 kg tömegű testet 9.80665 m/s2 gyorsulással mozgat. Az erő mértékegysége a jelenleg szab- ványos mértékrendszerben az 1 N. Az 1 N erőegység meghatározását – mint ismeretes – az adja, hogy az 1 N nagyságú erő 1 kg tömegű testet 1 m/s2 gyorsulással mozgat. Ha tehát [F]1= kp és [F]2 = N , akkor feltehető a kérdés, hogy 10 kp erő hány N? Az eddigi jelöléseink szerint tehát is- mert az erő kp-ban mért mérőszáma: {F}1 = 10 és keresett az {F}2 szám- értéke. Tekintetbe véve, hogy most a korábban bevezetett átszámítási szorzó értékére a k = [F]1/[F]2 = 9,80665/1 = 9,80665 szám adódik, a ke- resett {F}2 számérték felírható:
{F}2 = {F}1 k = 10 . 9,80665 = 98,0665 . Tehát 10 kp az 98, 0665 N.
A mértékegység és a mérőszám kérdéskörét még egy analógia bemutatá- sával szemléltetjük. Ismeretes, hogy a fizikában vektormennyiségeket és skalármennyiségeket különböztetünk meg. A vektormennyiségek meg- adásához nagyságuk, irányuk és értelmük megadása szükséges. A skalár mennyiségeket mérőszámuk (skálán leolvasható előjeles nagyságuk) egy- értelműen jellemzi. A szokásos 3-dimenziós geometriai tér vektorait irá- nyított egyenesdarabokként foghatjuk fel.
Ebben az esetben a vektor nagysága az irányított egyenesdarab (nem ne- gatív) hossza, abszolút értéke jellemzi. A vektor iránya azon tartó- egyenessel van megadva, amelyre az irányított egyenesdarab illeszkedik.
A vektor értelme azzal van megadva, hogy az irányított egyenesdarab nyílhegye az irány-egyenesen merre mutat. Attól függően, hogy a hossz- egységet miképp választjuk meg, beszélhetünk különböző egységvekto- rokról. A legegyszerűbb esetet tekintve vizsgáljuk az 5. ábra szerinti víz- szintes egyenesre illeszkedő x vektort. Az ábrán feltüntettünk két külön- bözőnek választott ugyancsak vízszintes egységvektort, az e1 és e2 vekto- rokat. A bevezetett két egységvektor változat mindegyike vektorjelleg hordozó, és ezekre támaszkodva alkalmas előjeles x1 és x2 skalár szorzó- számok segítségével kétfélképp is előállítható a tekintett x vektor:
x = x1 e1, x = x2 e2 .
x
x 0
e1
e2
2 2 1 1
e x x
e x x
5. ábra Vektormennyiség
Mivel azonban a két előállítás ugyanazon vektort adja, a két kifejezés jobb oldalai egymás között is egyenlők kell, hogy legyenek, azaz
x1 e1 = x2 e2 .
A kapott egyenlőség alkalmas arra, hogy ismerve az egységvektorok hosszainak arányát az előjeles skalár szorzószámok (az adott egységvek- torra vonatkozó koordináták) összefüggését is megadhassuk. Ha pl. x1-et ismerjük, akkor x2 kifejezhető a következő alakban:
x2 = x1
2 1
e
e = x1 k .
A kapott kifejezés tökéletes analógiát mutat a fizikai mennyiségek külön- böző mértékegységhez tartozó mérőszámai összefüggésének levezetése- kor kapott képlettel. A szereplő k =e1 /e2 hányados itt is átszámítási szorzóként értelmezhető. Ezek szerint az egységvektorok, mint vektorjel- leg hordozó objektumok analógiában állnak a mértékegységekkel, amely utóbbiak szintén a vizsgált fizikai mennyiség jellegét hordozzák. A vekto- rok különböző egységvektorokra vonatkozó skalárkoordinátái pedig tö-
kéletes analógiában vannak a vizsgált fizikai mennyiség különböző mér- tékegység választáshoz tartozó mérőszámaival.
Az eddigiekben a mértékegység és a mérőszám összefüggését általános vonatkozások előtérbe helyezésével tárgyaltuk, és megismertük a fizikai mennyiség különböző mértékegység választások esetén adódó mérőszá- mai közötti átszámítás képletét. A következőkben a mértékegységek kér- déskörét abban az összefüggésben vizsgáljuk, hogy a már tárgyalt alap- mennyiségekhez alapmértékegységeket rendelve, a származtatott mennyi- ségek mértékegységeit visszavezetjük az alapmértékegységektől függő ki- fejezésekre. Nézzük tehát rendre a már korábban is tekintett alapmennyi- ségeket és adjuk meg a hozzájuk tartozó alapmértékegységeket:
1. távolság, jele: s , [s] = m, 2. tömeg, jele: m , [m] = kg, 3. idő, jele: t , [t] = s.
A példánkban korábban is vizsgált származtatott mennyiségek mérték- egységei mármost a következők lesznek:
1. sebesség, v =
t s
, [v] = ms-1 s
m ] [
]
[
t
s ,
2. gyorsulás, a =
t v
, [a] = -2
2 ms
s m s
/s m ] [
]
[
t
v ,
3. erő, F = m a, [F] = kg m/s2 = kg m s -2 = N, 4. nyomás, p =
A F
, [p] = 2 -1 -2
-2
s m kg m
s m kg ] [
]
[
A
F = Pa.
A bemutatott származtatási példák meggyőzően mutatják, hogy a szár- maztatott mennyiségek dimenzióinál tárgyaltakhoz hasonlóan a származ- tatott mennyiségek mértékegységei is kifejezhetők az alapmértékegységek hatványszorzataiként. Figyeljünk fel arra, hogy a hatványszorzatos kifeje- zéseket az erő és a nyomás esetében egyszerűbb, egy betűs jelöléssel el- látva bevezettük a jól ismert N mértékegységet, amelybe foglalt erő az 1 kg tömeget 1 m/s2 gyorsulással mozgatja, és a Pa mértékegységet, amely- be foglalt nyomást az 1 m2-re ható 1N nyomóerő okozza.
1.3 Prefixumok
A fizikai mennyiségekkel való gyakorlati munka esetében célszerű olyan mértékegységeket választani, amelyek egyrészről jól meghatározott és szabványos kapcsolatban vannak a választott kiindulási mértékegységek- kel vagy egyenesen az alapmértékegységekkel, és biztosítják annak lehe- tőségét, hogy alkalmazásuk mellett szemlélettel átfogható (nem csillagá- szati nagyságú, vagy elképzelhetetlenül kicsi) nagyságú mérőszámok lép- jenek be.
A fenti követelményt teljesíti a mértékegységhez kapcsolt prefixumokkal képzett mértékegység-választék bevezetése a mértékegységeket növelő és csökkentő új mértékegységek alkalmazásával. Az új mértékegységeket a mértékegységbe foglalt mennyiségnek tíz bizonyos hatványai szerinti szorzóval változtatott értékei eredményezik. A prefixumok szabványos betűjelölését mindig – mint azt neve is mutatja – a mértékegység elé írjuk.
Egyes prefixumok a mértékegységbe foglalt mennyiséget növelik. Ezek a következők:
Exa 1018 jele: E Peta 1015 jele: P Tera 1012 jele: T Giga 109 jele: G Mega 106 jele: M
kilo 103 jele: k ---
hekto 102 jele: h deka 101 jele: da
A prefixumok másik csoportjának elemei a mértékegységbe foglalt meny- nyiséget csökkentik. Ezek a következők:
atto 10-18 jele: a femto 10-15 jele: f piko 10-12 jele: p nano 10-9 jele: n mikro 10-6 jele: milli 10-3 jele: m ---
centi 10-2 jele: c deci 10-1 jele: d
A prefixumok mindkét megadott táblázatában szaggatott vonal választja el a tíz harmadik illetve mínusz harmadik hatványával változó prefixu-
mokat, a tíz- és százszoros illetve egy tized- és egy századszoros mérték- egység értékeket indikáló prefixumoktól. Az utóbbi prefixumok csak a szokásos összetételekben alkalmazhatók, (pl. cm, hl, dg, stb.). A daN mértékegység alkalmazását a Magyar Mérésügyi Törvény egyenesen megtiltja. A tíz harmadik illetve mínusz harmadik hatványával változó prefixumok viszont korlátozás nélkül használhatók. Felhívjuk azonban a figyelmet a prefixumok alkalmazásával kapcsolatban egy fontos korláto- zásra: kettős prefixum nem használható!
1.4 Mértékrendszerek
A fizikai mennyiségek átfogó kezelését mértékrendszer alkalmazása kere- tében lehet megvalósítani. Előző tárgyalásunkban bemutattuk, hogy az alapmennyiségekből hogyan lehet származtatott mennyiségeket képezni.
Az alapmennyiségekhez tartozó alapmértékegységek megválasztása után a származtatott mennyiségek mértékegységeinek – a származtatott mér- tékegységeknek – az alapmértékegységre történő visszavezetését is meg- mutattuk. A jelzett származtatási eljárással a mértékegységeknek az ösz- szes szóba jöhető fizikai mennyiségre kiterjedő összefüggő rendszerét kapjuk, amelyet mértékrendszernek nevezünk. A fizika és a műszaki tu- domány fejlődése során több mértékrendszer is kidolgozásra és alkalma- zásra került. A különböző metrikus alapú mértékrendszereken kívül az angolszász mértékrendszer elterjedtsége volt jelentős a XX.-században.
Nem célja a jelen tárgynak a különböző mértékrendszerek ismertetése. A következőkben a koherens (összehangolt) mértékrendszer definícióját adjuk meg annak fontossága miatt.
Definíció: Egy mértékrendszert akkor nevezünk koherensnek, ha a származtatott mennyiségek mértékegységei előállíthatók az alap- mértékegységek konstans együtthatók nélküli hatványszorzatai- ként.
A Magyarországon törvénnyel bevezetett SI (System International) mér- tékrendszer koherens. Alapmennyiségei és alapmértékegységei:
hosszúság m
szög rad
tömeg kg
idő s
Néhány fontos származtatott mennyiség:
sebesség m/s m s-1
szögsebesség rad/s rad s-1
gyorsulás m/s2 m s-2
szöggyorsulás rad/s2 rad s-2
erő N kg m s-2
nyomaték Nm kg m2 s-2
nyomás Pa =N/m2 kg m-1 s-2
munka J=N m kg m2 s-2
teljesítmény W=J/s kg m2 s-3
2 Méréstechnikai alapok
2.1 Bevezető megjegyzések
A mérnöki munkának igen fontos része a mérésekkel történő információ- szerzés a műszaki objektumok – esetünkben a járművek – sajátosságainak széles spektrumáról. A mérések célját tekintve két lényegi osztály külö- níthető el:
1. Adatgyűjtés;
2. Ellenőrzés.
Az adatgyűjtés a műszaki objektum működését meghatározó adatok mé- réses felvételét jelenti, mintegy ténymegállapító numerikus adatsokaság generálását valósítja meg. Az ellenőrzés funkciója a tudatosan létrehozott, tervezett műszaki objektumok és az azokban végbemenő tervezett folya- matok megvalósítása (gyártás, kivitelezés) közben és a megvalósult üzem során ténylegesen kialakult jellemzőinek felvételével, a tervezett értékek- kel való megegyezés mértékét hivatott értékelni.
A méréssel vizsgált műszaki fizikai jelenségek köre két lényegi osztályba sorolható:
1. Determinisztikus jelenségek;
2. Sztochasztikus jelenségek
Determinisztikus jelenségek esetén a tekintetbe vett körülmények a jelen- ség kimenetelét elvileg egyértelműen meghatározzák. Sztochasztikus je- lenségek esetében a tekintetbe vett körülmények rendszere nem határozza meg egyértelműen a jelenség kimenetelét, több különböző valószínűség- gel bekövetkező kimenetel lehetséges. A sztochasztikus jelenség kimene- tele véletlen esemény, melynek elemzéséhez valószínűségszámítási fo- galmak és statisztikai eljárások szükségesek. Tárgyalásunk során ki fog derülni, hogy a determinisztikus jelenségek méréses vizsgálatában a min- denkor felmerülő véletlen hibák miatt végül is a sztochasztikus jelenség kategóriájára találunk. Végül is érvényesül a mérnököt tudatos óvatos- ságra intő sajátos elv: „minden csupán valószínű, semmi sem teljesen bi- zonyos”.
2.2 A mérőrendszer felépítése
A mérési tevékenység megvalósításához célszerűen összeállított mérő- rendszer szükséges. A vizsgálandó fizikai mennyiséget a mérőrendszer bemenetére kapcsolva a kimeneten megjelenik a mérési eredmény. A mé- rőrendszer legfontosabb része a mérőátalakító, amely a bevezetett fizikai mennyiség hatására kiadja a mérési jelet. Bár sok esetben az átalakítás egyszerű geometriai vagy mechanikai transzformációt jelent, mégis a ki- menő mérési jel legtöbbször villamos mennyiség (feszültség, áramerős- ség, stb.) formájában jelenik meg. Maga az átalakítás tehát legtöbbször azt jelenti, hogy a bemenetre kapcsolt, nem szükségképp villamos meny- nyiséget a bemeneti jellemzővel lehetőleg arányosan változó villamos jel- lé alakítsuk.
vizsgált mennyiség mérési eredmény
környezeti zavarás
"zaj"
mérőátalakító
6. ábra Mérőrendszer vázlata
A 6. ábrán vázolt módon a mérőátalakító tehát az a mérőrendszer elem, amely a mérendő mennyiséggel közvetlenül kapcsolatba kerül, és amely- nek bemenő jele (gerjesztése) a mérendő mennyiség, kimenő jele a mérési eredmény pedig a mérendő mennyiséggel ismert – kívánatos módon line- áris – függvénykapcsolatban álló (leggyakrabban villamos) mennyiség.
Ha a mérőrendszer ideálisan pontos jelátalakítást végezne és a mérési eredmény információtorzulás nélkül kerülne leolvasásra, még akkor is számolni kell a mérési funkció megvalósulása közben a mérőrendszert érő külső zavaróhatásokkal (szaknyelven: „zajjal” ), és ezért a mérési ered- mény még akkor is bizonyos hibával terhelt lesz, még a fentebb említett két ideális feltétel fennállása esetén is.
A gyakorlati mérőrendszerek azonban nem ideálisan pontosak, és a méré- si eredmények leolvasása során is keletkeznek bizonyos hibák. Így mérési a hibák három fő forrását az alábbiak adják:
a mérőrendszer tökéletlensége,
leolvasási pontatlanság,
környezeti zavarás.
A mérőrendszer tökéletlenségével kapcsolatosan utalunk arra, hogy szá- mos műszer esetében számítani kell a csapágyak vagy más vezetőelemek súrlódás okozta határozatlan beállására, az egyes szerkezeti elemek mé- rettűréseivel behatárolt geometriai hibákra, a beépített villamos alrendsze- rek nemlinearitásaival, stb.
7. ábra Leolvasási hiba
A leolvasási pontatlanság szemléletes magyarázatát adja a 7. ábrán vázolt elrendezés, aholis a függőlegesen mozgó mutató helyzetének a mellette lehelyezkedő skála jelzővonalaitól való távolságot kellene leolvasni. Ha a leolvasó személy nem merőlegesen, hanem ezen merőlegestől β szöggel eltérő ferde irányból néz a skálára, akkor a helyes értéktől δ távolsággal eltérő skálapontot azonosítana. Ha a mutatónak a sálától vett vízszintes távolsága h, és leolvasó szem skálától vett ugyancsak vízszintes távolsága H, továbbá a leolvasó szem a merőleges rátekintés helyétől függőlegesen Y távolságban végzi a leolvasást, akkor a δ leolvasási hiba és az Y elhe- lyezkedési hiba között egyszerű függvénykapcsolat adódik a tg β = Y/(H- h) = δ /h összefüggés alapján:
δ = Y
h H
h
.
Mivel a leolvasó személy helyzetét megadó Y távolság a szándékolt merő- leges rátekintéshez tartozó Y = 0 érték körül leolvasásról leolvasásra vé- letlenszerűen oszlik el, ezért a származtatott δ hiba is véletlen hiba lesz.
A környezeti zavarás vonatkozásában a mérőrendszer mechanikai és vil- lamos elemeinek működésviszonyait befolyásolja a mindig változó kör- nyezeti hőmérséklet és páratartalom, valamint a műszereket alátámasztó rendszer pillanatnyi rezgésállapota. A mondott változások nagyrészt vé- letlenszerű zavaróhatásként azonosíthatók, és hozzájárulnak a mérési eredményt terhelő bizonytalan nagyságú véletlen hibákhoz.
2.3 A mérési hibák két fő csoportja
A fentiekben áttekintettük a mérési hibák létrejöttének három fő forrását.
Most más szempontból vizsgálva a kérdést, mérési hibákat a rendszeres (szisztematikus) hibák és a véletlen hibák osztályának megkülönbözteté- sével két lényegi osztályba soroljuk.
2.3.1 A rendszeres hibák
A rendszeres hibák a mérőrendszer tökéletlenségével kapcsolatosak és a mérés megismétlésekor a mérési eredményt szisztematikusan, minden esetben ugyanúgy torzítják. A rendszeres hibát elvileg korrigálni lehet ka- librálási diagram alkalmazásával, amely diagram úgy készül, hogy ugya- nazon mennyiséget egy szisztematikus hibával terhelt mérőrendszerrel és egy nagyon pontos (igen kis szisztematikus hibájú) mérőrendszerrel egyi- dejűleg mérjük és a két mérőrendszer által mutatott kimenő értékeket egy diagram két tengelyére feltéve kalibrálási görbét határozunk meg. A 8.
ábrán felrajzolt diagram koordináta rendszerének vízszintes tengelyére kalibrálandó (gyengébb minőségű, nagy szisztematikus hibájú) műszer ál- tal kiadott x1 mérési eredményt tesszük fel. A koordinátarendszer függő- leges tengelyére pedig a pontosabb, kalibráló műszerrel nyert x2 mérési e- redményt tesszük fel. Elegendően sok különböző bemenő érték mellet mérve, a két összetartozó koordinátaérték felrajzolt pontsorozata alapján megrajzolható a g kalibrálási görbe, amelyik lényegét tekintve a két mű- szer szolgáltatta mérési eredmények összefüggését megragadó az x2 = g(x1) függvénykapcsolat megjelenítője. A diagram konstrukciója alapján nyilvánvaló, hogy abban az esetben, amikor a két műszer azonos kialakítású – pl. mind a kettő igen pontos – akkor a kiadódó x2 = g(x1) függvény képe a 45–os egyenes lesz. A ténylegesen vizsgált műszerek esetében adódó kalibrálási görbék is a 45–os egyenes környezetében szi- gorúan monoton növekedést és folytonos lefutást mutatnak, ami biztosítja a gyakorlati kalibrálási függvény inverzének létezését. Mármost a pontat- lan műszer skálázását a kalibráló műszeren mért y2i skálaponti értékeinek a kalibrálási függvény g-1 inverz függvényének alkalmazásával y1i = g-1(y2i) alakban tudjuk meghatározni, ahol tehát y2i befutja pontos ka- libráló műszer skálaosztásait.
45°
x2
x1 pontos
kalibráló műszerrel mért eredmény
a skála már a pontos értékeket mutatja
gyengébb, kalibrálandó műszerrel mért eredmény
x2=g(x1) hitelesítő vagy kalibráló görbe
8. ábra Kalibrálási görbe
A vázolt eljárás lényege abban foglalható össze, hogy a pontos műszer sa- játosságait mintegy „átvetíthetjük” a gyengébb műszerre, és így mindig meg lehet mondani, hogy a tökéletlen műszerrel (a szisztematikus hibával dolgozó műszerrel) mért érték nagyon jó közelítéssel milyen tényleges ér- téknek felel meg.
2.3.2 A véletlen hibák
A véletlen hibák oka a bizonytalansággal jelentkező környezeti zavarás- ban és leolvasási pontatlanságban van. A véletlen hibák jelenléte az egye- di mérési eredmények megbízhatatlanságát okozza. A véletlen hibák min- denkori jelenléte miatt érvényes a mérnökök között közismert mondás:
„egy mérés nem mérés !”.
A véletlen hiba nem küszöbölhető ki, azonban azonos körülmények kö- zött megismételt mérések eredményének kiértékelésével a véletlen hibát statisztikailag jellemezni lehet.
Tekintettel arra, hogy a méréssel kapcsolatos rendszeres (szisztematikus) hibákról feltételezhetjük, hogy azokat a kalibrálással elhanyagolhatóan kicsire csökkentettük, a további tárgyalásunkban csak a véletlen hibákkal terhelt mérési eredmények jellemzésére, azaz a véletlen hibák kezelésére szorítkozunk.
A matematikai jellemezhetőség érdekében a véletlen hibával terelt bi- zonytalan alakulást mutató mérési eredményt valószínűségi változónak tekintjük. Az alábbiakban megadjuk a valószínűségi változó definícióját.
Definició: az olyan x-eket, amelyek nagyságát előre megadni nem lehet, de amelyek megadott [a,b] intervallumba esésük va- lószínűségét függetlenül megismételt kimenetelek szolgáltatta adatsorozat alapján statisztikailag becsülni lehet, valószínűségi változóknak nevezzük.
A megismételt mérések szolgáltatta adatsorozatban lévő információ ad alapot a véletlen hibák alakulásával kapcsolatos bizonytalanság elhárítá- sára.
0
pontos érték xp
x1
…
xn
9. ábra Szóródó mérési eredmények
Legyen az azonos körülmények között egymástól függetlenül n-szer meg- ismételt mérés véletlen hibával terhelt eredmény sorozata az x1, x2,…, xn
számsorozat. Azt mondjuk, hogy ez az adatsorozat az x mérési eredmény valószínűségi változóra vonatkozó n-elemű realizációs sorozat. A kiadó- dó realizációs sorozat véletlen hibával terhelt elemei a vizsgált fizikai mennyiség ismeretlen és általunk meghatározni kívánt xP pontos értéke körül jobbra és balra körülbelül egyenlő arányban fognak szóródni.
A 9. ábrán a felvett félegyenesre kis függőleges vonalakkal bejelöltük a szóban forgó szóródó mérési eredmények értékeit. Rátekintve az ábrán látható függőleges vonalakra, érzékelhető a vonalak sűrűsödési helyénél az x valószínűségi változó ingadozási középpontja, amelyhez tartozó vé- letlentől már nem függő konstans értéket az x valószínűségi változó vár- ható értékének nevezzük és M(x)-szel jelöljük. Ezen megállapítás után a méréssel vizsgált mennyiség ismeretlen xP pontos értékét megalapozottan azonosíthatjuk az x mérési eredmény valószínűségi változó M(x) várható értékével, azaz érvényesnek vehetjük az
xP = M(x)
egyenlőséget. A további vizsgálatok egzakt keretekben történő folyatatása most már azt a kérdést veti fel, hogy miképpen lehet az x1, x2,…, xn reali- zációs sorozatból (az x valószínűségi változóra vett n-elemű mintából) matematikailag megalapozott becslést adni az M(x) várható értékre nézve, és ezzel együtt az M(x)-szel egyenlő, számunkra lényeges és meghatá- rozni kívánt xP pontos értékre.
Jelen tárgyalásunkban nem bocsátkozunk a matematikai statisztikai becs- lések elméleti taglalásába, azonban megadjuk az M(x) várható érték köze- lítő meghatározására a mért n-elemű x1, x2,…, xn realizáció sorozat eleme- inek számtani középértékével definiált becslést:
M(x) xn=
n x x
x1 2 ... n
=
n
i
xi
n 1
1 .
Az így bevezetett xn maga is egy valószínűségi változó realizációs érté- keként tekintendő, hiszen a véletlen ingadozásnak alávetett realizációs ér- tékek függvényeként (számtani átlagaként) van értelmezve. Ennek fényé- ben rögzítsük azt a tényt, hogy egy adott n-elemű minta esetén kiszámolt (xn)1 számtani középértékkel egy másik - ugyancsak x-re nézve az előző méréssorozattól függetlenül vett – ugyancsak n-elemű realizációs soro- zatból számolt újabb (xn)2 számtani közép érték általában nem lesz egyenlő! Így tehát a különböző n-elemű mintasorozatokból számított számtani átlagok is véletlen ingadozást mutatnak. A szokásos méréstech- nikai esetekben ezen utóbbi ingadozás középpontja az eredeti x mérési eredmény M(x) várható értékkel azonosnak adódik. Azonban mint később látni fogjuk a mondott számtani átlagok M(x) körüli szóródása a jóval ki- sebb mint az x-re vett eredeti mintasorozat elemek ugyancsak M(x) körüli szóródása.
Az xn M(x) közelítés a mérések n számának növelésekor egyre javul, mivel érvényesül a nagy számok gyenge törvénye, miszerint annak való- színűsége, hogy a minta számtani átlaga a várható értéktől abszolút érték- ben tetszőlegesen kicsi -nál nagyobb mértékben tér el n ∞ esetén zé- rushoz tart.
A mérési eredményeknek a várható érték körüli elhelyezkedésének jel- lemzésére – a szóródás jellemzésére – elvileg öt különböző mennyiség jöhet szóba.
1. A terjedelem (rendzs)
Az n számú x1, x2,…, xn mérési eredmény az x valószínűségi változó n elemű realizációs sorozata. Kiválasztva a mérési sorozat legkisebb és leg- nagyobb elemét értelmezhetjük a minta terjedelmét az
xi xi r max min
számértékkel.
2. Az átlagtól vett előjeles eltérések számtani közepe
Mivel a mintaelemek átlagtól vett eltérései előjeles mennyiségek, köny- nyen kimutatható hogy ez a dn –nel jelölt középérték mindig zérust ad, és ezért ez nem alkalmas a szóródás jellemzésére. A számtani közép definí- ciója szerint ugyanis:
. 1 0
) 1 1 (
1 1
n n n n
i n i n
i i
n nx x x
n x n x x n d
3. Átlagos abszolút eltérés
A mintaelemek átlagtól vett eltéréseinek előjeles voltából fakadó fenti ne- hézséget azáltal lehet pl. kiküszöbölni, hogy az eltérések abszolút értékét vesszük. Az így adódó mindig n nemnegatív szóródási jellemző alakja :
n
n
i
i xn
x n 1
. 1 0
4. Az átlagos négyzetes eltérés – a tapasztalati szórás
A mintaelemek átlagtól vett eltéréseinek előjeles értékeiből négyzetre emeléssel is kaphatunk nemnegatív értékeket. A négyzetre emelést meg- valósító függvény folytonos differenciálhatósága miatt több szempontból előnyösebb tulajdonságokat biztosít, ezért a következő módon járhatunk el. Először képezzük a mintaelemek átlagtól vett eltérései négyzeteinek számtani átlagát. Ez a mennyiség az n számú mérési eredmény tapaszta- lati (idegen szóval empirikus) szórásnégyzete, amely szintén mindig nem- negatív:
2
n
n
i
i xn
x n 1
2 0 . 1
A most meghatározott empirikus szórásnégyzetből négyzetgyököt vonva kapjuk az n számú mérési eredmény tapasztalati szórását, amelyet méltán nevezhetünk a mérési eredmények számtani átlagtól vett átlagos négyze- tes eltérésének:
2 1
1 2
n
i i n
n x x
n
.
Természetszerű, hogy a szereplő négyzetgyök pozitív értékét kell tekinte- nünk.
Tárgyalásunk ezen pontján kell rámutatni arra nyilvánvaló összefüggésre, hogy maga az x valószínűségi változóként tekintett mérési eredményt és ennek az M(x) várható értékét elvileg is vizsgálhatjuk, és képezhetjük az x-M(x) kifejezést. Ebben a különbségben az x egy valószínűségi változó, míg M(x) ennek konstans (véletlentől már nem függő, „kiközepelt”) vár- ható értéke, azonban az x-M(x) különbség nyilvánvalóan örökli első tag- jának, az x-nek a véletlentől való függését, és ezért maga is valószínűségi változóként azonosítható. Az így kapott x-M(x) valószínűségi változót négyzetre emelve a kiadódó mennyiség egy újabb, most már nemnegatív valószínűségi változót ad. Ezen utóbbi nemnegatív valószínűségi változó várható értéke definálja az eredeti x valószínűségi változó mindig nemnegatív elméleti szórásnégyzetét (varianciáját) a következő kifejezés szerint:
0 )]
( [ )
( 2
2 x x x
def
M M
D .
Figyelembe véve az elméleti szórásnégyzet jelentését, azonnal adódik, hogy ez az x valószínűségi változó saját várható értékétől vett eltérése négyzetének várható értéke, és így jelentésében közel áll a n2 tapasztalati szórásnégyzethez, és az utóbbinak mintegy az elméleti értékét definiálja.
Gyakorlatban tehát azt várnánk, hogy az n-elemű mintából számított n2
tapasztalati szórásnégyzet közel lesz az elméleti szórásnégyzethez. Mivel a tapasztalati szórásnégyzet a véletlen mintaelemektől függ, így maga is valószínűségi változó, felmerül az a kérdés, hogy a kiadódó n2 valószí- nűségi változó ingadozási középpontja, azaz a várható értéke megegye- zik-e a D2(x)elméleti szórásnégyzettel? A válasz sajnos nemleges, azaz mint az itt nem tárgyalt módon kimutatható, az:
) (n2
M D2(x)
összefüggés érvényes. Ezt a matematikai statisztikában úgy fogalmazzuk, hogy n2 nem torzítatlan becslése a D2(x) elméleti szórásnégyzetnek, és ez a torzítottság főként kis n megfigyelési számnál, kevés mérési eredmény esetén lényeges. Ezen torzítás azonban könnyen kiküszöbölhető a követ- kezőkben bevezetésre kerülő korrekcióval.