Kristályosítók dinamikus folyamatainak modellezése és szimulációja

KRISTÁLYOSÍTÓK DINAMIKUS

FOLYAMATAINAK MODELLEZÉSE ÉS SZIMULÁCIÓJA

DOKTORI (PhD) ÉRTEKEZÉS

Készítette: ULBERT ZSOLT a Veszprémi Egyetem

Vegyészmérnöki Tudományok Doktori Iskolája keretében

Témavezető: Dr. Lakatos Béla

egyetemi docens, a műszaki tudomány kandidátusa

Folyamatmérnöki Tanszék Veszprémi Egyetem

Veszprém

2002

KRISTÁLYOSÍTÓK DINAMIKUS FOLYAMATAINAK MODELLEZÉSE ÉS SZIMULÁCIÓJA

Értekezés doktori (PhD) fokozat elnyerése érdekében Írta:

Ulbert Zsolt

Készült a Veszprémi Egyetem Vegyészmérnöki Tudományok Doktor Iskolája keretében Témavezető: Dr. Lakatos Béla

Elfogadásra javaslom (igen / nem) ……….

(aláírás) A jelölt a doktori szigorlaton …... % -ot ért el.

Veszprém, ...

a Szigorlati Bizottság elnöke Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: …... …... igen /nem

……….

(aláírás) Bíráló neve: …... …... igen /nem

……….

(aláírás) Bíráló neve: …... …... igen /nem

……….

(aláírás) A jelölt az értekezés nyilvános vitáján…...% - ot ért el.

Veszprém, ……….

a Bíráló Bizottság elnöke A doktori (PhD) oklevél minősítése:…...

………

Az EDT elnöke

Tartalmi kivonat

Kristályosítók dinamikus folyamatainak modellezése és szimulációja A doktori értekezésben a szerző egy szimulációs tanulmányt mutat be, amelyben kristályosítók dinamikai viselkedését tanulmányozza. A dolgozat tárgyát olyan kristályosítók és jelenségek vizsgálata képezi, amelyek reprezentálják a leggyakoribb kristályosító típusokat és a kristályosítási folyamatot kísérő jelenségeket.

A szerző részletes matematikai modelleket dolgozott ki a folyamatos kevert szuszpenziójú és osztályozott termékelvételű izoterm és hűtéses kristályosítók, valamint a folyamatos kevert szuszpenziójú és reprezentatív termékelvételű vákuum kristályosítók dinamikai vizsgálatára. A vákuum kristályosító leírásában mind a kristályszuszpenzió, mind a gőztér állapotának dinamikus változásait figyelembe vette.

A szerző egy új matematikai modellt is bemutat a folyamatos, kevert szuszpenziójú, nem tökéletes mikrokeveredésű kristályosítók vizsgálatára, amelyben feltételezi, hogy a folyadékfázis elemekből áll, és a kristálypopulációt leíró populációs mérlegegyenlet mellett a folyadékelemek változásait és koncentráció eloszlását is populációs mérlegegyenlet írja le.

A szerző a kristályosító modellek populációs mérlegegyenleteinek megoldásában a momentumok módszere mellett a súlyozott reziduum módszerek körébe tartozó adaptív végeselemű ortogonális kollokáció kidolgozását és alkalmazását mutatja be. A végeselemű ortogonális kollokáció alkalmazásához kapcsolódóan olyan, az aktuális számítási intervallumnak és a végeselemek felosztásának adaptív meghatározási módszereit adja meg, amelyek a populációs mérlegegyenlet(ek) hatékony megoldását teszik lehetővé a kristályosítók dinamikus folyamatainak szimulációjában.

Az értekezésben bemutatott dinamikai vizsgálatok magukban foglalják a folyamatos kevert szuszpenziójú és reprezentatív termékelvételű izoterm, hűtéses és vákuum kristályosítók vizsgálatát, valamint az osztályozott elvétel, a méretfüggő kristálynövekedési kinetika és a nem tökéletes mikrokevertségű folyadékfázis hatásának tanulmányozását. A közölt eredmények egyrészt a kinetikai paraméterek hatását mutatják be a kristályosítók működési jellemzőinek, mint a kristályosító hozam, az átlagos kristályméret és a méreteloszlás, dinamikájára, másrészt a bemeneti változók perturbációjának hatását mutatják a kristályosítók tranziens viselkedésére. A folyamatos kevert szuszpenziójú és reprezentatív termékelvételű hűtéses és vákuum kristályosító dinamikai vizsgálata azt mutatja, hogy a különböző bemeneti változók perturbációja jelentősen megváltoztatja a kristályosítóban kialakuló túltelítési szintet és a kristályosító hőmérsékleti viszonyait. Az osztályozott termékelvétel alkalmazása esetén a különböző mérettartományokban alkalmazott gyorsított elvételnek eltérő hatása van a kristályosító stabilitására. A folyamatos kevert szuszpenziójú, nem tökéletes mikrokeveredésű kristályosító dinamikai vizsgálata azt mutatja, hogy a részleges szegregáció tartományában kapott kristályosítási dinamika jelentősen eltér a kevert szuszpenziójú és reprezentatív termékelvételű kristályosító dinamikájától.

Az értekezésben bemutatott eredmények azt mutatják, hogy a kristályosítók számítógépes szimulációja jelentősen hozzájárulhat a kristályosítókban lejátszódó folyamatok mélyebb megismeréséhez, és fontos szerepet tölt be a kristályosítók tervezésével és működtetésével kapcsolatos feladatok megoldásában.

Abstract

Modelling and Simulation of Dynamic Processes of Crystallizers In the dissertation the author presents a modelling and simulation study, in which the dynamic processes of crystallizers are analysed. Detailed population balance models were developed for describing the dynamic behaviour of the mixed suspension isothermal, cooling and vacuum crystallizers. Furthermore, a mathematical model has also been elaborated for describing crystallization processes under non-perfect micromixing conditions.

Applying the method of moments and the finite element orthogonal collocation method solved the mixed sets of the partial and ordinary differential equations of the population balance models. Connecting with the application of the finite element orthogonal collocation method, adaptive procedures were elaborated for determining the actual global computation interval and for distributing the finite elements on that very interval. Simultaneous application of these procedures provides an efficient method for solving the population balance equation and simulating dynamic changes of the size distribution of crystals.

The dynamic analyses presented in the dissertation include the investigation of the continuous mixed suspension isothermal, cooling and vacuum crystallizers and the analysis of the effects of the non-perfect micromixing conditions on the dynamic behaviour of mixed suspension isothermal crystallizers. The study of the influence of the classified product removal and of the size dependent growth rate of crystals has also been carried out.

The results presented in the thesis show that computer simulation of crystallizers may advantageously contributes to the deeper understanding of crystallisation processes in crystallizers, and may play important role in the solution of problems arisen in designing and operating crystallizers.

Zusammenfassung

Modellierung und Simulation der Dynamischen Prozesse von Kristallisatoren

In der Dissertation wird eine Simulationsstudie vorgestellt, bei der das dynamische Verhalten von Kristallisatoren untersucht wird. Es wird ein ausführliches mathematisches Modell für die dynamische Prüfung von isothermischen und gekühlten Kristallisatoren, Vakuumkristallisatoren und von denen von stetig gemischter Suspension angegeben. Ein weiteres mathematisches Modell wird vorgestellt, mit dem der Kristallisierungsprozess, der bei nicht vollkommenen Mikromischbedingungen verläuft, beschrieben werden kann.

Bei der Lösung der Populationswaagegleichungen der Kristallisierungsmodelle werden die Methode der Momente und die Anwendung der orthogonalen Kollokation mit endlichen Elementen vorgestellt. Zur Anwendung der orthogonalen Kollokation mit endlichen Elementen wird solch eine adaptive Aufteilungsmethode angegeben, die für die Ergänzung der Methode der orthogonalen Kollokation mit endlichen Elementen geeignet ist und die wirksame Lösung der Kristallpopulationswaagegleichung für die Bestimmung der Dynamik der Maßverteilung ermöglicht.

Die in der Dissertation vorgestellten dynamischen Prüfungen enthalten die Prüfungen von Kristallisatoren von stetig gemischter Suspension, von isothermischen und gekühlten Kristallisatoren und Vakuumkristallisatoren mit einer representativen Produktentnahme, und enthalten die Untersuchungen der klassifizierten Entnahme, maßabhängigen Kristallanschusskinetik und der Wirkung der Sumpfphase von nicht vollkommener Mikromischung.

Die Ergebnisse der Dissertation darstellen, dass die Computer-Simulation von Kristallisatoren zu einer tieferen Erkenntnis der in den Kristallisatoren verlaufenden Prozesse wesentlich beitragen kann, und kann eine wichtige Rolle bei der Lösung von Aufgaben bei dem Entwurf und der Betätigung von Kristallisatoren spielen.

TARTALOMJEGYZÉK

Bevezetés 8

Jelölésjegyzék 10

1 A kristályosítók dinamikai vizsgálatában elért kutatási eredmények

irodalmi áttekintése 12

1.1. A kristályosítás folyamata 13

1.1.1. A kristályosítás kinetikája 14

1.1.1.1. A kristálygóc képződés kinetikája 15

1.1.1.1.1. Elsődleges homogén gócképződés 15 1.1.1.1.2. Elsődleges heterogén gócképződés 16

1.1.1.1.3. Másodlagos gócképződés 17

1.1.1.2. A kristálynövekedés kinetikája 18

1.2. A kristálypopuláció méreteloszlásának jellemzése 20

1.3. A kristályosítók matematikai modellezése 21

1.3.1. A populációs mérlegegyenlet 22

1.3.2. A kevert szuszpenziójú és reprezentatív termék elvételű (MSMPR)

kristályosítók leírása 24

1.3.2.1. A stacionárius működési állapot leírása 25 1.3.2.2. A folyamatos működési állapot leírása 26 1.3.2.3. A szakaszos működési állapot leírása 28 1.3.3. A kevert szuszpenziójú és osztályozott termékelvételű (MSCPR)

kristályosítók leírása 29

1.3.4. A kristálynövekedési sebesség diszperziója 32 1.3.5. A nem ideális kevertségű kristályosítók leírása 33 1.3.6. A kristályosítási folyamat leírása a kristályok agglomerizációja

és törése esetén 36

1.4. A populációs mérlegegyenlet megoldása 38

1.4.1. A momentumok módszere 39

1.4.2. Véges differencia módszerek 40

1.4.3. A súlyozott reziduum módszere 41

2. A kristályosítók matematikai modelljeinek megadása és numerikus

megoldása 44 2.1. A folyamatos kevert szuszpenziójú izoterm kristályosítók matematikai

modelljei és numerikus megoldásuk 44

2.1.1. Az MSMPR és MSCPR izoterm kristályosítók matematikai modellje 44 2.1.2. Az MSMPR izoterm kristályosító matematikai modelljének

momentum transzformációja 48

2.1.3. Az MSCPR izoterm kristályosító matematikai modelljének

megoldása adaptív végeselemű ortogonális kollokációval 50 2.1.4. A számítási intervallum adaptív végeselem felosztása 57 2.2. A folyamatos kevert szuszpenziójú nemizoterm kristályosítók

matematikai modelljei és numerikus megoldásuk 62 2.2.1. Az MSMPR és MSCPR hűtéses kristályosítók matematikai modellje 62

2.2.2. Az MSMPR hűtéses kristályosító matematikai modelljének

momentum transzformációja 65

2.2.3. Az MSCPR hűtéses kristályosító matematikai modelljének

megoldása adaptív végeselemű ortogonális kollokációval 67 2.2.4. Az MSMPR vákuum kristályosító matematikai modellje 70 2.2.5. Az MSMPR vákuum kristályosító matematikai modelljének

momentum transzformációja 76

2.3. A folyamatos kevert szuszpenziójú nem tökéletes mikrokeveredésű

izoterm kristályosító matematikai modellje és numerikus megoldása 80 2.3.1. A kevert szuszpenziójú nem tökéletes mikrokeveredésű

izoterm kristályosító matematikai modellje 80 2.3.2. A kevert szuszpenziójú nem tökéletes mikrokeveredésű

izoterm kristályosító matematikai modelljének momentum

transzformációja 85

3. Szimulációs vizsgálatok 87 3.1. A folyamatos kevert szuszpenziójú izoterm kristályosítók

dinamikus folyamatai 87

3.1.1. Az MSMPR izoterm kristályosító dinamikai vizsgálata 87 3.1.2. Az MSMPR izoterm kristályosító matematikai modelljének

validálása kísérleti adatok alapján 96

3.1.3. Az MSCPR izoterm kristályosító dinamikai vizsgálata 100 3.2. A folyamatos kevert szuszpenziójú nemizoterm kristályosítók

dinamikus folyamatai 109

3.2.1. Az MSMPR hűtéses kristályosító dinamikai vizsgálata 109 3.2.2. Az MSMPR hűtéses kristályosító dinamikai vizsgálata

méretfüggő kristálynövekedési sebesség feltétel mellett 115 3.2.3. Az MSMPR vákuum kristályosító dinamikai vizsgálata 119 3.3. A folyamatos kevert szuszpenziójú nem tökéletes mikrokeveredésű

kristályosító dinamikus folyamatai 123

Összefoglalás 128

Tézisek 132 Az értekezés témaköréből készült publikációk 135

Az értekezés témaköréhez részben kapcsolódó publikációk 136

Theses 137 Irodalom 140

Köszönetnyilvánítás 146 1. Melléklet. A folyamatos kevert szuszpenziójú izoterm

kristályosítók szimulációs eredményei 147 2. Melléklet. A folyamatos kevert szuszpenziójú nemizoterm

kristályosítók szimulációs eredményei 152

Bevezetés

Az oldatból történő kristályosítás széleskörűen alkalmazott művelet számos ipari területen, mint a vegyipar, gyógyszeripar és élelmiszeripar. A kristályosítóban lejátszódó kinetikai folyamatok, a kialakuló kristálypopuláció, valamint a kristályosítót leíró állapotváltozók, mint például az anyalúg koncentráció és kristályosító hőmérséklet között kialakuló visszacsatolt kölcsönhatások a kristályosítási folyamatok nagyfokú összetettségét eredményezik, amely nehézségeket okozhat a kristályosítók működtetésében és irányításában. Ez különösen érvényes a nemizoterm kristályosítók esetére, ahol a kinetikai folyamatok a hőmérsékletet és anyalúg koncentrációt tekintve nemlineárisak, és a kristályosító hőmérsékletében bekövetkező változások jelentősen befolyásolhatják a kinetikai folyamatokat, és ennek következtében a kristályosító dinamikáját. A kristályosítás folyamatát számos jelenség kísérheti, mint a méretfüggő kristálynövekedés, méretnövekedési diszperzió, kristálytörés és agglomerizáció stb., amelyek jelentősen befolyásolják a kialakuló kristálypopulációt, és ez által a kristályosítók működését. Mindezek azt mutatják, hogy a kristályosítási folyamatok mélyebb megismerése és tanulmányozása fontos szerepet tölthet be a kristályosítók működtetésével kapcsolatos feladatok megoldásában.

Az utóbbi évtizedekben jelentősen megnövekedtek a kristályosítás folyamatát és a kristályosító berendezések működését vizsgáló kutatások, és a dolgozat témájának aktualitását mutatja a területen megjelenő növekvő számú tudományos közlemény. A kutatások főbb területei a kristályosítási folyamatok kinetikája, a kristályosítók matematikai modellezése, valamint a kristályosító berendezések és technológiák tervezése. Ez utóbbi magában foglalja a különböző irányítási struktúrák alkalmazását is.

A kristályosítási folyamat kutatásaiban a kísérleti módszerek mellett fontos szerepet tölt be a számítógépes szimuláció, amelynek fejlődését az információ technológiában megfigyelhető gyors előrehaladás segítette. A kristályosítók számítógépes szimulációjában a digitális számítástechnika alkalmazásának elterjedésével előtérbe került a populációs mérlegegyenletek hatékony megoldási módszereinek alkalmazása. A hagyományos momentum módszer mellett elterjedtek a nagyobb számítási igényű numerikus módszerek alkalmazásai, amelyek többnyire a méreteloszlás stacionárius változásainak meghatározására irányulnak. E tekintetben a kristályokat leíró populációs mérlegek megoldásában a leggyakrabban használt módszerekké a súlyozott reziduum módszerek váltak.

A doktori értekezés elsősorban az oldatból történő kristályosítás modellezéséhez, a számítási módszerek fejlesztéséhez, valamint a dinamikus folyamatok szimulációval való vizsgálatához kíván hozzájárulni. Ezeken a területeken eddig viszonylagosan kevesebb eredmény és tudományos közlemény született. Vizsgálataim céljai közé tartozott az izoterm kristályosító dinamikai vizsgálata mellett a nemizoterm körülmények között lejátszódó kristályosítási dinamika vizsgálata hűtéses és vákuum kristályosító esetében egy részletes, nemizoterm matematikai modell felállításán keresztül, valamint a súlyozott reziduum módszer alkalmazásával a méreteloszlás dinamikus változásainak meghatározása. Megadok egy olyan matematikai modellt, amellyel a folyadékfázis mikrokevertségének hatása tanulmányozható a kristályosítási folyamatok esetében. Az értekezés tárgyát képezi továbbá a méretfüggő kristálynövekedés mellett kialakuló méreteloszlás vizsgálata, valamint az ipari kristályosítás területén gyakran alkalmazott osztályozott termékelvételű kristályosítók tanulmányozása.

A doktori értekezés 1. fejezetében a tématerületen született kutatási eredményeket foglalom össze. Áttekintést adok a kristályosítás kinetikai folyamatainak kutatásában és

a kristályosítók matematikai modellezése területén elért tudományos eredményekről, továbbá a populációs mérlegegyenletek megoldásában használt numerikus módszerekről.

A dolgozat 2. és 3. fejezete tartalmazza a kristályosítási folyamatok modellezésében, számításában és szimulációjában elért eredményeimet. A 2. fejezetben a dolgozat tárgyát képező kristályosító típusok matematikai modelljeit adom meg. Felírom a folyamatos tökéletesen kevert és osztályozott termékelvételű izoterm és hűtéses kristályosító, valamint a folyamatos tökéletesen kevert és reprezentatív termékelvételű vákuum kristályosító modelljét. Bemutatok továbbá egy új matematikai modellt a nem tökéletes mikrokeveredési feltételek mellett lejátszódó kristályosítási folyamatok vizsgálatára. A kidolgozott modellegyenletek megoldására a hagyományos momentum módszer és a súlyozott reziduum módszerek körébe tartozó végeselemű ortogonális kollokáció alkalmazását mutatom be. A végeselemű ortogonális kollokáció alkalmazásához kapcsolódóan az aktuális (teljes) számítási intervallumnak és az végeselemek felosztásának adaptív módszereit mutatom be, amelyek a kristályosítás populációs mérlegegyenleteinek hatékony megoldását teszik lehetővé a méreteloszlás dinamikájának meghatározásában.

A 3. fejezetben a kidolgozott kristályosító modellek megoldásával nyert szimulációs eredményeket mutatom be. Az eredményeket hat különálló részben foglalom össze, amelyek az egyes kristályosító típusok vizsgálati eredményeit tartalmazzák. A megadott modellek megoldásával a kristályosítók dinamikai vizsgálatát végeztem, de egy, a dolgozatban kidolgozott kristályosító modell validálását is bemutatom a folyamatos kevert szuszpenziójú kristályosítóban kapott irodalmi kísérleti adatok felhasználásával.

A vizsgálatokban egyrészt a modell paraméterek hatását tanulmányoztam a kristályosító működési jellemzőinek, mint a kristályosító hozam, átlagos kristályméret és a kristályok méreteloszlásának dinamikájára, másrészt a bemeneti változók perturbációjának hatását vizsgáltam a kristályosítók tranziens viselkedésére. A dinamikai vizsgálatok magukban foglalják az osztályozott termékelvétel, a méretfüggő kristálynövekedési kinetika, valamint a nem tökéletes mikrokevertségű folyadékfázis hatásának tanulmányozását.

A dolgozatot az összefoglalás, a tézisek magyar és angol nyelvű változatai, az irodalomjegyzék és a mellékletek zárják.

Jelölésjegyzék

kR tömegátadási tényező, kg/m²hPa a dimenziómentes méretnövekedési

sebesség paraméter kv térfogati formatényező

A felület, m² L lineáris méretváltozó, m

m tömeg, kg b gócképződési sebesség túltelítési

hatványkitevője M móltömeg

M közelítő polinom fokszám B0 gócképződési sebesség,

(darab góc)/m³s n méreteloszlás sűrűségfüggvény, (darab kristály)/m⁴

B0 dimenziómentes gócképződési

ND adaptív végeselem felosztási sebesség

paraméter

0

B~ átlagos gócképződési sebesség, NI adaptív végeselem felosztási

(darab góc)/m³s paraméter

c koncentráció, kg/m³ NS adaptív végeselem felosztási cs telítési koncentráció, kg/m³ paraméter

Cpc kristály fajhő, KJ/kg°C p koncentráció eloszlás Cpsv oldószer fajhő, KJ/kg°C sűrűségfüggvény,

(darab folyadékelem)/m³c Da dimenziómentes paraméter

DG kristálynövekedési sebesség- P egyensúlyi gőznyomás, Pa diffúziós paraméter, m²/s Pv gőzfázis nyomás, Pa

q térfogatáram, m³/h e1, e2 szabályozási eltérés

f dimenziómentes méreteloszlás r1 adaptív végeselem felosztási fˆ transzformált dimenziómentes paraméter

r2 adaptív végeselem felosztási méreteloszlás

paraméter F dimenziómentes paraméter

R gázállandó, J/molK F kilépő gőz térfogatáram, m³/s

R koncentráció csökkenési g kristálynövekedési sebesség

sebesség, kg/m³h túltelítési hatványkitevője

Rsv párolgási sebesség, kg/h G mérettől függő kristálynövekedési

sebesség, m/s s túltelítés, kg/m³

s0 µ0 momentum léptéktényező G0 mérettől független kristály-

s1 µ1 momentum léptéktényező növekedési sebesség, m/s

s2 µ2 momentum léptéktényező G0 dimenziómentes mérettől

s3 µ3 momentum léptéktényező független kristálynövekedési sc koncentráció és sűrűség

sebesség tag, m/s léptéktényező

0

G~ mérettől független átlagos sL lineáris méret léptéktényező kristálynövekedési sebesség, m/s sn méreteloszlás léptéktényező h szelekciós függvény st idő léptéktényező

I szorzótényező sT hőmérséklet léptéktényező ka felületi formatényező sd gőzfázis sűrűség léptéktényező kb gócképződési sebességi állandó sv kristályosító térfogat

ke gócképződési sebességi léptéktényező

paraméter S túltelítési arány

kg kristálynövekedési sebességi S kristálytérfogat képződési sebesség, m³/m³h

állandó

kp gócképződési sebességi állandó t idő, h

kr reakciósebességi állandó T hőmérséklet, °C

Alsó indexek Tv gőzfázis hőmérséklet, °C

U hőátszármaztatási tényező,

KJ/m²h°C in bemeneti érték

V térfogat, m³ out kimeneti érték

Vt vákuum kristályosító térfogat, m³ sv oldószer z dimenziómentes hőmérséklet set alapjel zv dimenziómentes gőzfázis max maximum

hőmérséklet 0 kezdeti érték

xm az n méreteloszlás m-ik

dimenziómentes momentuma Felső indexek y dimenziómentes koncentráció

ysv dimenziómentes oldószer * referencia pont

koncentráció G gőz állapot

∆Eb aktiválási energia, KJ/kmol L folyadék állapot

∆Eg aktiválási energia, KJ/kmol

∆Hc kristályosítási hő, KJ/kg Rövidítések

∆Hpsv oldószer párolgáshő, KJ/kg

B forrás Görög karakterek D nyelő

Polinom definíciók α méretnövekedési paraméter, m^-1

βb dimenziómentes paraméter

Lagrange alap polinom βg dimenziómentes paraméter

δ(x) Dirac delta

Az xi, i=1,...,k+1 interpolációs pontok alapján meghatározott k-ad fokú li(x), i=1,...,k+1 Lagrange alap polinomok definíciója az alábbi:

δi,j Kronecker delta

ε oldattérfogati hányad φ(L) méretnövekedési függvény µm az n méreteloszlás m-ik

( ) ( )

( )

∏

≠= −

= ¹ −

1 k j

i

jj i j

j

i x x

x x x

l , i=1,...,k+1

momentuma

πk a p koncentráció eloszlás k-dik momentuma

ρ sűrűség, kg/m³ Legendre polinom

ρc kristálysűrűség, kg/m³

ρv gőzfázis sűrűség, kg/m³ Az x=[0,1] intervallumon értelmezett transzformált k-ad fokú Legendre polinomot az alábbi összefüggés adja meg (Chang és Wang, 1984):

τ tartózkodási idő, h υ dimenziómentes térfogat ς dimenziómentes lineáris méretváltozó

( ) ( ) ( )

( )

[ ]

∑

=

−

−

−

= ^{j k} −

j

j k j

k x

j k j

j x k

P

0 2

!

!

! 2 ξ dimenziómentes idő 1

ζ dimenziómentes sűrűség

ζc dimenziómentes kristálysűrűség ζv dimenziómentes gőzfázis sűrűség

1. A kristályosítók dinamikai vizsgálatában elért kutatási eredmények irodalmi áttekintése

A kristályosítási irodalmat áttekintve megállapítható, hogy a kristályosítás kinetikai folyamatai már jól tisztázódtak köszönhetően a 70-80-as évek intenzív kísérleti munkájának. Bár teljes mélységében a folyamatok még nem ismertek, a kinetikai folyamatokat jól leíró empirikus összefüggéseket adtak a szerzők a kristálygóc képződés és a kristálynövekedés sebességére mind a mérettől függő, mind a mérettől független esetben. A kinetikai összefüggések empirikus paraméterei kísérleti adatok által meghatározhatók és jól használhatók a kristályosítók leírásánál és szimulációs vizsgálatainál.

A kristályosítókat leíró matematikai modellek a populációs mérlegegyenleten alapulnak, amelynek általános formáját Randolph és Larson (1988) adták meg. Ezt a modellt sikeresen alkalmazták a kutatók a kristályosítók leírásában, és az irodalomból kitűnik, hogy a vizsgálat tárgyai többnyire az MSMPR és MSCPR kristályosítók voltak, amelyek nyújtottak a kristályosítókra jellemző stabilitási viszonyok vizsgálatára. A kristályosítók komplett szimulációjában a szerzők többsége a populációs mérlegegyenlet mellett a kristályosítóra vonatkozó tömeg- és energiamérleget is megadták, azonban a nemizoterm feltételek melletti dinamikai vizsgálatok lényegesen kisebb számban találhatók az irodalomban.

A 70-es évektől előtérbe került a növekedési sebesség diszperziójának jelensége, amely egy újabb taggal bővítette Randolph és Larson (1988) által megadott általános populációs mérlegegyenletet. Zumstein és Rosseau (1987) a módosított populációs mérlegegyenlet felhasználásával már jelentős kutatási eredményeket értek el e jelenség szimulációs vizsgálatában. A méreteloszlás diszperzióját meg lehet figyelni a térbeli koordináták mentén is, azonban a csőáramlási modellnek megfelelő kristályosítók leírása és átfogó dinamikai vizsgálata még nem valósult meg. Randolph és White (1977) modelljükben bevezették a növekedési sebesség diszperziójának megfelelő tagot, valamint a kristályok konvektív áramlását és a méreteloszlás térbeli diszperzióját leíró tagokat. Azonban a modellt csak egyszerűsített esetekben oldották meg, és nem vizsgálták a kristályok térbeli eloszlását.

A kristályosítók működését befolyásoló egyik legfontosabb tényező a mikrokevertség szintje, amelynek leginkább a makroszinten tökéletesen kevert kristályosítók esetében van jelentősége. A mikrokeveredés leírására alkalmazható modellek lényegében a kémiai reaktorok mérnöki területén fejlődtek ki. Az ott megalkotott modellek maradéktalanul felhasználhatók a kristályosítók működésének tanulmányozásában is. A mikrokeveredés hatásának vizsgálata még kis területet tölt be a kristályosítók működésének szimulációs vizsgálatában, mindössze néhány példa mutatható be az erre irányuló kutatásokból.

Az alkalmazott matematikai módszereket tekintve kezdetben a momentumok módszere jelentette a fő megoldási módszert a populációs mérlegegyenlet esetében.

Később a számítástechnikai eszközök gyors elterjedésével és fejlődésével kezdtek elterjedni az olyan módszerek, amelyeket nagy számítási igényük miatt nem tudtak használni korábban. Ezek közé tartozik a súlyozott reziduum módszer, amelynek alkalmazása egyre nagyobb számban figyelhető meg az irodalomban. A súlyozott reziduum módszerek alkalmazása a momentum módszer több hátrányát küszöböli ki. A leglényegesebb különbség a két módszer között, hogy a súlyozott reziduum módszerrel a teljes információt megkaphatjuk a méreteloszlás dinamikai változásáról. További előnyként említhető, hogy az MSCPR kristályosítók szimulációja esetében elősegíti olyan általános formájú szelekciós függvények alkalmazását is, amely a momentum

módszer esetében nem lehetséges. A következő években további olyan matematikai módszerek elterjedése várható, amelyeket a kristályosítók matematikai modellezésében még kis számban alkalmaznak, de más tudományterületek által már hatékonyan alkalmazott megoldási módszereknek számítanak a parciális differenciálegyenletek megoldásában. Ezek a módszerek az adaptív súlyozott reziduum módszer, a mozgó végeselem módszer, valamint az áramlástani kutatásokban használt modern véges differencia algoritmusok.

1.1. A kristályosítás folyamata

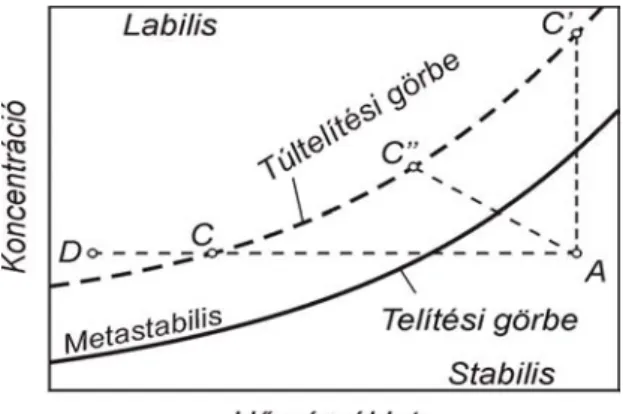
Az oldatból történő kristályosítás a desztilláláshoz és extraháláshoz hasonlóan komponens-dúsítási művelet. A komponensdúsítás az adott komponens fázisok közti különböző megoszlásán alapul. Kristályosítás esetében a szelektív komponens- megoszlás a folyékony és szilárd fázis között jön létre. Ha egy oldatban az oldott komponens a szilárd fázissal egyensúlyban van, az oldat telített. A telített oldat kismértékű hűtéssel vagy oldószer elpárologtatással túltelítetté válik. A túltelített oldatban az oldott komponens koncentrációja nem egyensúlyi, és bármilyen külső hatásra - így keverésre, vagy oltókristályoknak az oldatba jutásával - megjelenhet az oldott komponensre nézve tiszta, kristályos fázis. A túltelítettség foka jelentősen befolyásolja a kristályosítás folyamatát. Ostwald (1897) vizsgálatai alapján a túltelítettség tartománya egy labilis és egy metastabil tartományra osztható (1.1. ábra).

Az ábrán folytonos vonal jelöli az oldott komponensre vonatkozó oldhatósági görbét, míg a felső szaggatott vonal a túltelítési koncentráció értéket mutatja a hőmérséklet függvényében. Az oldat metastabilis túltelítettségi koncentráció tartománya a telítési és a túltelítési görbe közötti terület. A túltelítés labilis tartománya a hőmérséklet- koncentráció diagramon a túltelítési görbe fölött foglal helyet.

1.1. ábra. Az oldat telítési és túltelítési állapotának ábrázolása.

Az egyensúlyi telítési görbe alatti stabil tartományhoz a telítetlen oldat tartozik, ezen a hőmérsékleten sem kristálygóc képződés, sem kristálynövekedés nincs. A labilis túltelítettségi tartományban a kristálygóc képződés spontán megindulhat, majd elkezdődik a kialakult gócok növekedése. A metastabilis túltelítettségi tartományban spontán kristálygóc képződés nem lehetséges, mivel a rendszer nem éri el a kristálygóc képződés termodinamikai potenciálját. Azonban, ha a metastabilis túltelítettségi tartományban az oldatot oltókristályokkal beoltjuk, a telítettségi viszonyoknak megfelelően addig, amíg az oldat el nem éri az egyensúlyi telítettségi koncentrációt, a kristályok növekedhetnek. Amennyiben az oldatban szilárd kristályos fázis nincs jelen, a metastabil állapot egy egyensúlyi állapotnak tekinthető. Az egyensúly energiaszintje magasabb, mint a stabilis egyensúly energiaszintje, ahhoz azonban, hogy a rendszer a

metastabilis állapotból kimozdulva stabilis állapotba kerüljön, többletenergiával aktiválni kell a folyamatot. Ezt a többlet energiát jelképezheti a labilis tartományba való túltelítés. A metastabil-labilis zónahatár elhelyezkedése nagymértékben függ az oldat viszkozitásától, szennyezettségétől, a keverés mértékétől stb. Az alkalmazott kristályosítási technológia a kristályosítandó komponens oldhatósági adataitól függ, és az a módszer határozza meg, amellyel az adott komponensre nézve a szükséges túltelítés mértéke elérhető. A legtöbb anyag oldhatósága a hőmérséklet emelésével növekszik. Ha a komponens oldhatósága az oldat hőmérsékletétől nagymértékben függ, akkor hűtéses, ha nem változik, akkor bepárlásos technológiát alkalmaznak. A hűtéses kristályosítást szimbolizálja az 1.1. ábrán az A-C vonal. A telítetlen oldatnak megfelelő A pontból kiindulva az oldatot a C pontig hűtik, ahol az oldat túltelítetté válik és a kristálygóc képződés már termodinamikailag lehetséges. A gócképződés beindulhat spontán, mechanikai hatás által, vagy megkezdődhet oltókristályok hozzáadásával, továbbá elősegítheti heterogén gócképző szennyeződések jelenléte is. Gyakran, a jó oldhatósággal rendelkező komponensek esetében még további hűtés is szükséges a D pontig. A bepárlásos kristályosítást az A-C’ izoterma szimbolizálja. A túltelítettséget az oldószer elpárologtatása réven érik el, mialatt az oldat hőmérséklete állandó marad. Az egyidejűleg hűtéssel és bepárlással történő kristályosítási műveletet, a vákuum kristályosítást az A-C’’ vonal jelképezi. Ebben az esetben az oldat részleges elpárolgásának adiabatikus hatására hűl le a rendszer a vákuumnak megfelelő forrásponti hőmérsékletre. Az oldat túltelítettsége az elpárolgás következtében fellépő koncentrációnövekedés és az adiabatikus hűlés hatására alakul ki. E technológiákon kívül gyakran használják a kisózást és a precipitációs kristályosítást. A kisózásos technológiák a komponensek eltérő oldhatóságán alapulnak. A homogén oldathoz egy, az adott anyagnál jobb oldhatósággal rendelkező, közös iont tartalmazó komponenst adnak, amelynek hatására az eredetileg oldott komponens oldhatósága lecsökken, és az kicsapódik. A precipitációs kristályosítás esetében kémiai reakció segítségével állítják elő a kristályosítandó komponenst. A keletkező komponens túltelíti az oldatot, majd az oldhatóságától függő mennyiségben kicsapódik.

1.1.1. A kristályosítás kinetikája

Számos kinetikai folyamat felismerhető a kristályosítás folyamatában, azonban a kristályosítás kinetikáját az irodalomban két domináns sebességi folyamattal jellemzik:

a kristálygóc képződéssel és a kristálynövekedéssel. További kinetikai folyamatként a kristályok agglomerizációja és törése említhető, de mint a vonatkozó irodalomból kitűnik, ezeknek a folyamatoknak kisebb jelentőséget tulajdonítanak a szerzők. A kristálygóc képződést és kristálynövekedést leíró kinetikai egyenletek a jelenségek megfigyeléséből vagy elméleti analízisből származnak. Bár számos erőfeszítés történt a sebességi modellek fejlesztésére, a kristályosítási irodalom még nagyrészt kísérleti adatokon és empirikus összefüggéseken alapul. Az empirikus összefüggések hátránya, hogy csak speciális esetekben biztosítanak kielégítő eredményt. Az elméleti analízis alapján megadott sebességi modellek is számos bizonytalanságot tartalmazhatnak, elsődlegesen a modellalkotásban alkalmazott egyszerűsítések miatt. A legszélesebb körben használt sebességi modellekben a tapasztalati megfigyeléseket elméleti összefüggésekkel kapcsolják össze, és ezek az egyenletek a változók széles tartományában jó közelítést adnak.

A kristályosítási folyamat kinetikájáról összefoglaló tanulmányt adtak Randolph és Larson (1988), Mucskai (1971), Garside (1985), Dirksen és Ring (1991), Rawling és társai (1993) valamint Tavare (1995a).

1.1.1.1. A kristálygóc képződés kinetikája

Kristályosítás során az új részecskék gócképződés által keletkeznek. A gócképződés az a jelenség, amelynek során valamely metastabilis, vagy labilis állapotú egyfázisú rendszerben az anyafázistól elkülönülnek a már stabilis új fázis parányi részecskéi.

Általánosságban mondható, hogy a gócképződés az egyik legjelentősebb kinetikai folyamat, azonban a gócképződési folyamat még a kristályosítás kevésbé értelmezett folyamatai közé tartozik, és elméletileg jól megalapozott kinetikai összefüggésekkel való leírása összetett feladatot jelent. A kristálygócok két különböző mechanizmus alapján alakulhatnak ki: elsődleges vagy másodlagos gócképződés által. Az elsődleges gócképződés homogén illetve heterogén gócképződési folyamatra osztható. Homogén gócképződésről akkor beszélünk, amikor a kristálygócok a túltelítés eredményeként keletkeznek az oldatból, és a gócképződés spontán indul meg. Heterogén gócképződés esetében az új részecskék oldhatatlan szennyező anyagok jelenléte által keletkeznek. A szennyező anyagok olyan felületi helyeket biztosítanak, ahol a kristálygócok a kisebb energiaszükséglet következtében könnyebben kialakulhatnak. A másodlagos gócképződést a kristályosítandó komponens már kivált kristályai indukálják. A kristálygócok a szuszpendált kristályokból mechanikai hatásra keletkezhetnek, amelynek során a szétesett, töredezett kristálydarabok, szilánkok képezik az új kristálygócok alapjait. A kristálygóc képződési mechanizmusok jelentősen különböznek egymástól és ennek megfelelően a sebességi egyenletek is különböző formákat vesznek fel.

1.1.1.1.1. Elsődleges homogén gócképződés

Homogén gócképződésről akkor beszélünk, ha a rendszerben katalitikus hatású szennyező komponens nincs. Homogén gócképződés során az oldatban lévő oldott komponens és a kivált szilárd fázis között létrejövő szabadenergia változás egyenlő a gócképződési energiával. Metastabilis rendszerben a stabilis fázist képviselő kristálygóc képződési energiája a felületi és térfogati képződési energia algebrai összege. A felületi képződési energia pozitív előjelű és a részecskeméret négyzetével arányos. A térfogati képződési energia negatív mennyiség és a részecskeméret harmadik hatványával arányos. Így a kristályképződési energia a részecskeméret függvényében egy maximummal rendelkezik, amelynek abszcissza értéke a kritikus gócméret. A kritikus gócméret alatti molekulacsoport neve embrió. A kritikus gócméretet elérő góc akár visszaoldódik az oldatba vagy akár megindul a növekedése, a folyamatot energia felszabadulás kíséri, mivel a kritikus gócmérethez tartozó energiaszint energiamaximum. Ha a kristályosítási energia nagyobb, mint az energiamaximum, akkor a keletkezett embrió már nem esik szét, hanem stabil góccá válik és kialakul az új fázis. Az embriók folyamatosan képződnek és szétesnek a rendszer helyi energiaszintjétől függően. A stabil kristálygóc feltehetően úgy alakul ki, hogy előbb kettő, három, esetleg több molekula laza asszociációt képez, amelyek azonban ott, ahol a helyi túltelítettség kisebb, újra széteshetnek. Ahol viszont a helyi túltelítettség nagyobb, a néhány molekulából álló csoportok molekula láncokat alkotnak. Az így kialakult molekulaláncok ugyancsak újra széteshetnek, mivel még nem stabil képződmények. Több molekula lánc találkozásakor viszont molekula rétegek alakulhatnak ki és végül stabil kristályrács képződhet. A kristálygócok akkor jelennek meg, amikor a részecskék elegendő nagyságú, a rácsszerkezet szerint rendezett olyan magokat képeznek, amelyek már nem szuperoldhatóak. A gócképződésnek reakciókinetikai jellege van. A gócképződés energiája energiamaximumot képviselő

valódi aktiválási energia, amely azonos a folyamatot kísérő szabadentalpia változással.

A kritikus méretű stabil góc akkor keletkezik, ha a rendszer aktiválási energiája a kritikus gócméret kialakulásához szükséges szabadentalpia változással

( )

megegyező értékű. Az Arrhenius egyenlet analógiájára a térfogat és időegység alatt keletkező gócok száma az alábbi egyenlettel fejezhető ki (Volmer és Weber, 1926):

Gmax

∆



 



 ∆−

=

= RT

A G dt

B₀ dN exp ^max (1.1.1)

ahol a sebességi állandó, R a gázállandó és T a hőmérséklet. Behelyettesítve a kritikus gócméretre számított szabadentalpia változás értékét az alábbi összefüggés adódik:

A



 



−

= R T S

A M

B_{0 3 3} ³₂ ²₂ ln 3

exp 16

ρ

πσ (1.1.2)

ahol a szilárd-folyadék határfelületi feszültség, M a komponens móltömege, ρ a kristálygóc sűrűsége és S a túltelítés. Az S túltelítés az oldat aktuális c koncentrációjának és a c egyensúlyi telítési koncentrációnak a hányadosa. Az (1.1.2) összefüggésből látható, hogy az anyafázis túltelítettsége és a gócképződési sebesség szorosan összetartozó mennyiség. Ha az oldat koncentrációja a telítési koncentrációnak felel meg, azaz S=1, a gócképződés energiája végtelen és B

σ

s

0=0. Növekvő túltelítettség esetében azonban S>1 és a gócképződési sebesség értéke növekvő tendenciát mutat a túltelítési arány függvényében.

Nielsen (1964) szerint az (1.1.1) egyenlet adott hőmérsékleten jól közelíthető a túltelítés hatványfüggvényével, azonban ezek a közelítések nagy hatványkitevőket követelnek. A közelítés egy másik formája a metastabilis koncepción alapul és azzal számol, hogy a gócképződés nem jelenik meg nagyon alacsony túltelítési foknál (Miers és Isaac, 1906):

, (1.1.3)

i m

b c c

k

B₀ = ( − ) c_m >c_s

ahol az oldat aktuális koncentrációja. cc m egy olyan túltelítési koncentráció értéket jelöl, amely nagyobb a telítési koncentrációnál, de amely alatt spontán gócképződés nem játszódik le. k a gócképződési sebességi állandót jelöli, amely a hőmérséklet függvénye. A k sebességi állandó hőmérséklet függése megadható az Arrhenius egyenlet alapján, míg az i konstans értékét kísérleti úton határozzák meg. A legtöbb szervetlen kémiai komponens esetében c

b b

m értéke közel esik az egyensúlyi telítési koncentrációhoz és több kísérleti munkában megfelelő eredményeket értek el úgy, hogy cm értékét az egyensúlyi koncentrációval helyettesítették:

(1.1.4)

i b i s

b c c k s

k

B₀ = ( − ) =

1.1.1.1.2. Elsődleges heterogén gócképződés

A gócképződés sebessége nem független a telített oldatban jelenlévő heterogén szennyeződések hatásától és sok esetben a gócképződést a rendszerbe jutó szennyeződések, por stb. okozzák. Igen tiszta folyadékokban is előfordulhatnak heterogén szennyezések, így a legtöbb rendszerben heterogén hatásra indul meg a gócképződés. A heterogén szilárd fázis jelenlétének jelentős hatása van a felületén kiváló kristályos fázis és a folyadék közti felületi erők egyensúlyára, amely döntően

befolyásolja a gócképződés aktiválási energiáját és így annak sebességét. Ha a gócképződés sebességét heterogén komponens aktiválja, akkor a gócképződés alacsonyabb túltelítési állapotban indul meg, mint a homogén rendszerben, és a heterogén gócképződés kritikus aktiválási energiája mindig kisebb, mint a homogén gócképződés kritikus aktiválási energiája. A heterogén gócképződési sebességet leíró egyenletek formája hasonló, mint az (1.1.1) vagy (1.1.3) egyenlettel megadott homogén gócképződési sebesség összefüggés.

1.1.1.1.3. Másodlagos gócképződés

A másodlagos gócképződés során a kristálygócok az oldatból már kivált kristályokból keletkeznek mechanikai hatásra. Az elsődlegesen keletkezett kristálymagok felületének környezetében a felületaktív erők hatására a kristályrácsba még be nem épült, embrió méretű molekulacsoportok helyezkednek el. Kevert folyadékrendszerekben a változó helyi turbulencia okozta nyíróerő és a kristályok ütközése elég az embriók leszakítására, amelyek túltelített környezetbe jutva nagy valószínűséggel kristálygóccá válnak. Több másodlagos gócképződési folyamat vehető figyelembe. Az új kristálygócok képződése történhet a kristályok ütközése által (kristály-kristály, kristály-fal, kristály-keverő), agglomerátumok törésével, intenzíven kevert rendszerekben a kristályok felületi nyíródásával, vagy részecskék lemosódásával az oltókristályok felületéről. A szilárd-folyadék határfelület fontos szerepet tölt be az összes másodlagos gócképződés esetében. A kísérleti megfigyelések azt mutatják, hogy a másodlagos gócképződési folyamat egy fontos forrása a kristálygócok keletkezésének, és jelentős hatása van a kristályosítók átfogó működésére.

Cayey és Estrin (1967) munkájukban bemutatták, hogy kevert szuszpenzióban a másodlagos gócképződés sebessége a szuszpenzióban jelenlévő kristályok számától függ. Clontz és McCabe (1971) kevert szuszpenziójú kristályosítóban végzett kísérletekben megmutatták, hogy a másodlagos gócképződési folyamat elsődlegesen a kristályok egymás közötti ütközésének az eredménye. A kísérletekben azt tapasztalták, hogy a folyadék által okozott felületi nyírófeszültség nem indukál jelentős gócképződést, de a kristályok alacsony energiájú ütközése növeli a másodlagos gócképződési folyamatot. A képződött gócok mennyisége nagymértékben függött a túltelítés nagyságától és az ütközések energiaszintjétől is, azaz a keverés intenzitásától.

Az egyszerű hatvány alakú gócképződési sebességi modellek, mint az (1.1.1) vagy (1.1.3) egyenletek, nem alkalmasak a másodlagos gócképződési sebesség leírására mivel nem tartalmazzák azt az információt, amely a kristály-kristály és kristály-keverő ütközések frekvenciájára és az általuk indukált ütközési energia nagyságára vonatkozik.

A kapcsolatok megfogalmazása ezen hatások között nehéz, de néhány kísérleti munka azt mutatja, hogy kevert szuszpenziókban, azonos energiainput mellett, a másodlagos gócképződési sebesség a szuszpenzió sűrűség és a túltelítés hatványától függ:

(1.1.5)

i j s

b s

k B₀ = ρ

ahol a kristályszuszpenzió sűrűsége és k a sebességi állandó. A hatványkitevő értéke többnyire a mechanikai energiainput nagyságától függ, de a hőmérséklet és az oldott, valamint oldhatatlan szennyeződések mennyisége szintén hatással van az értékére. A másodlagos gócképződési sebesség számítására gyakran használják a következő összefüggést:

ρs _b j

(1.1.6)

i j k

b s

k B₀ = µ

ahol a kristályosítóban kialakuló kristálypopuláció méreteloszlásának k-ik momentumát reprezentálja. A fenti összefüggésben leggyakrabban a harmadik momentumot használják, amely az esetek többségében megfelelőnek bizonyul a másodlagos gócképződés hatásainak figyelembevételére.

µk

1.1.1.2. A kristálynövekedés kinetikája

A kristályok növekedése két egymást követő részfolyamatban játszódik le. Az első lépésben a kristályt körülvevő lamináris filmen keresztül az oldott komponens diffúzióval a kristály felületéhez jut. A diffúziós elmélet feltételezi, hogy a kristályhoz tapadó lamináris filmben ∆ koncentrációesés játszódik le, és a kristályfelület környezetében az oldat c koncentrációja nem túltelített, hanem egyensúlyi telítési érték.

Így a diffúziós folyamat hajtóereje:

c

(1.1.7) cs

c c= −

∆

A második lépésben a kristály felületén lejátszódó kémiai reakció során a komponens a kristályrácsba épül. Ezt a lépést részecske integrációs lépésnek hívják és a sebességét részecske integrációs sebességnek nevezik. A kristályok növekedését két ellenállás korlátozhatja: az egyik a folyadékfázisban lejátszódó komponensátadás ellenállása, a másik a komponens molekulának a rácsba való beépülése alkalmával fellépő ellenállás. Ha a növekedési sebesség a lamináris rétegen keresztül való diffúzió által gátolt, a kristály növekedését diffúziógátolt növekedésnek nevezzük. Sok esetben, különösen a nem kevert rendszerekben lényegében ez a szabályozási mechanizmus.

Ebben az esetben a kristály tömegnövekedési sebességét az alábbi módon lehet kifejezni:

) (c c_s X A

D dt

dm = − (1.1.8)

ahol a diffúziós állandó, D X a filmvastagság és a kristály felülete. A

Amikor a diffúziós ellenállás elhanyagolható, a kristálynövekedési sebesség a kristály felületén végbemenő részecske integráció sebességétől függ, amely reakciókinetikai jellegű. Az integráció sebessége független a rendszer áramlástani viszonyaitól és a komponens diffúziós sebességétől. A kristály tömegnövekedési sebessége ebben az esetben, elsőrendű kinetikát feltételezve, az alábbi komponensátadási egyenlettel írható le:

)

( _s

rA c c

dt k

dm = − (1.1.9)

ahol a k reakciósebességi állandó hőmérséklettől függő mennyiség, amelyre érvényes az Arrhenius egyenlet.

r

A kristályok felületi növekedésének mechanizmusára különböző elméletek léteznek, amelyek közül két lényegesebbet lehet megemlíteni. Az első a felületi gócképződés által gátolt növekedés. Ezen elmélet szerint a kristályhoz adszorptíven tapadó folyadékfilmben több molekula egyesül, és ún. kétdimenziós kristálygócot képeznek a felületen, amelyre a kristályrács következő réteghálója épül. A mechanizmus sebességét a felületi gócképződés sebessége határozza meg, amely egy magas energiakorlát átlépését követeli meg. A kétdimenziós kristálygóc képződése jelentős mértékben függ az oldat túltelítettségétől, azonban a kétdimenziós góc képzéséhez szükséges elméleti túltelítettségi érték sok esetben jelentősen magasabb, mint amelyet gyakorlati mérések során tapasztalnak. A felületi növekedés mechanizmusának egy valószínűbb elmélete a

spirális diszlokáció. A kristályok növekedése során torzulások, diszlokációk keletkezhetnek a rácsban. A rácshiba oka többféle lehet, ilyen például a szennyező komponens jelenléte, hőmérséklet ingadozás vagy a helyi túltelítettség ingadozása stb.

A rácshibák környezetében a kristálylap felülete egyenetlenségeket tartalmaz, amelyek alacsony energiájú helyeket biztosítanak a szilárd molekulák beépülésére és a további kristálynövekedés kiindulási pontjai, gócai lehetnek. Az olyan kristályok felülete, amelyek e mechanizmus szerint növekszenek, nem egyenletes, és a felületen egy csavar mintájú profil megjelenése látható. A kétdimenziós gócképződéshez szükséges aktiválási energia ebben az esetben nem játszik szerepet és a kristály igen alacsony túltelítettségi fokon is növekedhet.

Ha a kristály növekedésére a komponens diffúzió és a részecske integráció is jelentős hatással van, elsőrendű felületi reakciókinetikát feltételezve, a kristály tömegnövekedési sebessége az alábbi formában írható:

) )(

/

( _r c c^s k

D X

DA dt

dm −

= + (1.1.10)

A kristályokra vonatkozó k térfogati és felületi formatényező felhasználásával az (1.1.10) összefüggés a következő alakban írható:

v ka

(

r a

v c c

k D X

L Dk dt

L

k d −

= +

) / ( )

( ^{3 2}

ρ

)

A (1.1.11) egyenletből a kristály jellemző méretének változási sebessége az alábbi:

(

g c c

k dt G

dL= ₀ = −

)

))

(1.1.12) és

(

(

v

a

g k X D k

k Dk

/

3 +

= ρ (1.1.13)

A (1.1.12) egyenlet a legáltalánosabban használt növekedési sebesség összefüggés.

Az egyetlen korlátja, hogy feltételezi, hogy a növekedési sebesség nem függvénye a kristályméretnek.

Különböző kristályosító rendszerekben megfigyelhető, hogy a kristály jellemző méretének növekedési sebessége függ a kristály méretétől. A kristálynövekedési sebesség méretfüggése a hidrodinamikai környezetnek és a kristályfelület jellemzőinek tulajdonítható. Nagyobb méretű kristályszemcse mozgásához nagyobb turbulencia tartozik, és így a szemcséhez tapadó X folyadékfilm vastagsága csökken. Azonban azok a tényezők, amelyek a méretfüggő növekedést okozzák még nem tisztázottak teljesen, és leggyakrabban olyan empirikus összefüggések felhasználásával írják le azokat, amelyekben a növekedési sebességet összekapcsolják a kristálymérettel.

Bransom (1960) egy hatványfüggvényt ajánlott a méretfüggő kristálynövekedési sebesség leírására a következő formában:

(1.1.14)

(

)

g c c L

k

G= −

Az a és b állandók kísérleti adatokból meghatározhatók, de az összefüggés hátránya, hogy zérus növekedési sebességet jósol az L kristályméret esetében. Más szerzők, mint Canning és Randolph (1967) olyan modellt javasolnak, amely ezt a problémát kiküszöböli:

=0

(1.1.15)

( )

(

)

G

G= ₀φ = ₀ 1+α

(1.1.16)

(

g c c

k

G₀ = −

)

Ebben az összefüggésben G az kristálymérethez tartozó növekedési sebességet definiálja, amely a túltelítés és hőmérséklet függvénye és α empirikusan meghatározott konstans. Az (1.1.15) összefüggés további módosításaként Abegg és társai (1968) egy kétparaméteres kifejezést javasolnak a méretfüggő növekedés kifejezésére:

0 L=0

, b (1.1.17)

(

)

G

G= ₀ 1+α ≤1

Midlarz és Jones (1989) olyan általános összefüggést adnak meg, amelyben a φ függvény egy minimális és maximális érték között változhat az L kristályméret függvényében:

( )

( )

(

)

G

G= _{0 max}+ _min − _max ^−α , α>0 (1.1.18)

Az összefüggés értelmében a kristálynövekedési sebesség értéke aminG0 ha L=0 és amaxG0 ha L→∞.

1.2. A kristálypopuláció méreteloszlásának jellemzése

A szemcsediszperziós rendszerekben a független, különálló szilárd részecskék különböző tulajdonságokkal jellemezhetők. A részecskék mindegyikéhez hozzá lehet rendelni az őt leíró tulajdonságokat, mint például alak, méret, hőmérséklet, összetétel stb. A kristályosítási gyakorlatban a kristályokat az összetétel mellett leginkább a megjelenési formájukkal és a méretükkel jellemzik. A különböző kristályosítási eljárásokban a kristályok egy jellemző forma és méretbeli eloszlással keletkeznek.

Amennyiben a keletkező kristályok formája közel egyforma, a kristálypopuláció méreteloszlását jellemezni lehet egyváltozós folytonos eloszlásfüggvényekkel. Az eloszlásfüggvények alkalmazásának a jelentősége a méreteloszlások minőségi leírásában van. A méret szerinti eloszlásban a kristályok több tulajdonsága is figyelembe vehető. Így beszélhetünk a méret szerinti számosság, felületi, térfogati vagy tömegeloszlásról. A kristályok méreteloszlásának jellemzésére számos empirikus eloszlásfüggvény található az irodalomban. Randolph és Larson (1988) részletes összefoglalást közöl a méreteloszlások leírására alkalmas eloszlásfüggvényekről.

A szemcsés anyagok méreteloszlásának jellemzésére gyakran használják a lognormális eloszlást, amely aszimmetrikus formájú és a sűrűségfüggvénye az alábbi:

( )







>

≤

= − ⁻

0 ha 2 ,

1

0 ha ,

0

2 2

2 ln

L L e

L L

f ^{L m}

σ

π σ

(1.2.2)

ahol m és σ a ξ valószínűségi változó természetes alapú logaritmusának várható értéke illetve szórása.

Szintén kétparaméteres eloszlás az általánosított gamma eloszlás, amelynek sűrűségfüggvénye a következő formájú:

( )

( )( )







 + >

Γ



 

−

≤

=

+ , ha 0

1 exp

0 ha ,

0

1 L

a b a

b L aL

L L

f

a

a (1.2.3)

Az a és b paraméterek konstansok. Az általánosított gamma eloszlás a

[ ]

intervallumon értelmezett eloszlás és a formája szintén aszimmetrikus. A b konstans az eloszlás móduszát adja meg, míg az a konstans az eloszlás aszimmetriáját befolyásolja.

További kétparaméteres függvényekként a Rosin-Rammler és a módosított béta eloszlást lehet megemlíteni, amelyeket elterjedten alkalmaznak a méreteloszlások jellemzésére. A Rosin-Rammler eloszlás sűrűségfüggvénye az alábbi:

∞ , 0

( )

(

)

f = ⁻¹exp− (1.2.4)

ahol a p és r az eloszlás két paramétere. A módosított béta eloszlás sűrűségfüggvénye az alábbi módon írható:

( )

(

)

L A

f = 1 1−

(1.2.5) (1.2.6)

( )

∫

= ¹

0

1 L dL L

A ^{αβ β}

Az eloszlás két paramétere az α és β. Mivel a módosított béta eloszlás a [0,1]

intervallumon értelmezett, a méreteloszláshoz való illesztésekor a méreteloszlás adatokat a [0,1] intervallumra kell transzformálni. Mind a Rosin-Rammler, mind módosított béta eloszlás aszimmetrikus tulajdonságú, az eloszlások módusza valamint szórása a két paraméter által fejezhető ki.

Egy négyparaméteres eloszlást definiál a tangeshiperbolikus eloszlás (Blickle és társai, 1998a), amelynek a sűrűségfüggvénye illetve eloszlásfüggvénye a következő formájú:

(1.2.7)

( ) ( ) ( ) [ ( ) ]





≤ +

+

<

+

− +

= + ⁻

−

0 ha

, 0

0 ha ,

1 ²

1 1

bL a

bL a bL

a th bL

a th bL a L mnb

f

n m n

n

(1.2.8)

( ) ( )





≤ +

+

<

= +

0 ha

, 0

0 ha ,

bL a

bL a bL

a L th

F

m n

A tangeshiperbolikus eloszlásfüggvény előnye a fenti eloszlásfüggvényekhez képest, hogy mind a sűrűségfüggvény, mind a kumulatív függvényalak analitikus formában adható meg. Az m és n paraméter függvényében a sűrűségfüggvény profilja számos, más eloszlásra jellemző formát vehet fel, amely a hatékony alkalmazását teszi lehetővé a legkülönfélébb eloszlások jellemzésében. A tangeshiperbolikus eloszlás alkalmazását mutatták be különböző szemcsediszperziós folyamatok leírására Blickle és társai (1998b,1998c), Ulbert és társai (1995a,1995b,1998), Farkas és társai (1995,1996), valamint Sisak és társai (1997).

1.3. A kristályosítók matematikai modellezése

A kristályosítók működésének egyik legfontosabb jellemzője a képződő kristályok méret szerinti eloszlása. A kristályok méreteloszlása jelentős hatással van magára a kristályosítási folyamatra, de meghatározza a kristályosítási végtermék végső felhasználását is. A kristályosítóban kialakuló aktuális méreteloszlás szorosan összefügg a kristályosító működésével, annak termelékenységével és stabilitásával. A kristályok méreteloszlását jelentősen befolyásolják az üzemzavarok, mint például az elvétel vagy betáplálás rövid szünetelése, a betáplálási hőmérséklet ingadozása vagy a kristályszuszpenzió recirkulációs sebességének megváltozása stb. A hőmérséklet ingadozása különösen befolyásolja a méreteloszlást, mivel a gócképződés sebessége

nagymértékben függ a hőmérséklettől. A kristályosítási folyamat belső mechanizmusát, egyedülállóan, a folyamatok visszacsatoltsága jellemzi, amely a méreteloszlást tekintve egy belső önszabályozási mechanizmust eredményez és jelentős hatással van a stabilitásra. A visszacsatolási folyamatot a kristálytömeg képződési sebessége és a rendelkezésre álló kristályfelület által befolyásolt túltelítési szint határozza meg. A túltelítés mértéke határozza meg a gócképződés és kristálynövekedés sebességét, amelyek egy adott időpontban ismét hatással lesznek magára a méreteloszlásra. Számos kísérleti munkában tapasztalták, hogy a kristályosítók olyan kinetikai tartományban is működhetnek, ahol az átlagos kristályméret értékében csillapítatlan oszcilláció figyelhető meg. Az oszcilláló működésre az a jellemző, hogy nem egy külső zavar által generált instabilitásról van szó, hanem a visszacsatolt belső folyamatok hatásának köszönhető.

A kristálypopuláció méreteloszlását jellemezni lehet különböző eloszlásfüggvényekkel. Erre a célra, mint az előző fejezetben ismertetésre került, számos eloszlásfüggvény található a vonatkozó irodalomban. Azonban egy gyártási folyamat során a kialakuló kristálypopuláció méreteloszlása folyamatosan változhat, és a kristálypopulációnak ez a fajta empirikus jellemzése bizonyos korlátokat tartalmaz.

Egyrészt nehéz az eloszlásfüggvények paramétereit annak a műveletnek a paramétereivel összekapcsolni, amellyel az adott kristálypopulációt előállították. A kapcsolatok a paraméterek között függvények, de a paraméter identifikációval meghatározott függvények, amelyek nem minden esetben a teljes műveleti paraméter vektoron értelmezett függvények, a legtöbbször csak egy adott műveleti paraméter vektor esetére alkalmazhatóak. Másrészt, ha a folyamatokat időben akarjuk leírni és a méreteloszlás dinamikai vizsgálata a cél, a paraméterek kapcsolatait leíró függvények időben változnak, és meghatározásuk még összetettebb feladatot jelent. Továbbá, az esetek többségére az a jellemző, hogy egy adott eloszlástípus nem írja le megfelelő pontossággal a kristályok aktuális méreteloszlását a gyártási folyamat teljes időtartama alatt, mivel annak profilja folyamatosan változhat. A kristályosítási művelet során kialakuló méreteloszlás leírásának másik módja a fizikai-kémiai rendszerek megmaradási és mérlegelveire támaszkodik. Ebben az esetben a méreteloszlást a kristályosítás részfolyamataira érvényes transzportelméleti törvényszerűségek és kinetikai modellek felhasználásával írjuk le. Az összefüggések és a rendszer változói alapján differenciális mérlegegyenlet írható fel a kristályok méreteloszlásának változására és az így definiált matematikai modell megoldása szolgáltatja a méreteloszlás dinamikai változását. A kristályosítási folyamatot leíró differenciális mérlegegyenletek lehetőséget nyújtanak a méreteloszlás dinamikai vizsgálatára, és egyben a rendszer részletesebb analízisére is. A kristályok méreteloszlását leíró parciális differenciálegyenletet leggyakrabban populációs mérlegegyenletként hivatkozzák az irodalomban.

A kristályosítók átfogó matematikai leírását mutatják be Randolph és Larson (1988) valamint Tavare (1995a).

1.3.1. A populációs mérlegegyenlet

A populációs mrlegegyenletet Randolph (1964), valamint Hulburt és Katz (1964) vezették be először a részecske populációk eloszlásának leírására, majd Randolph és Larson (1988), valamint Ramkrishna (2000) adtak átfogó leírást az alkalmazásáról és matematikai kezeléséről.

A részecske műveletek során a részecskék tulajdonságainak változása egy többdimenziós fázistérben figyelhető meg. A fázistér koordinátái két csoportra