Model Predictive Control of Crystallisers
PhD Thesis
Nóra Moldoványi
Supervisor: János Abonyi and Béla Lakatos PhD School of Chemical Engineering Sciences
Department of Process Engineering University of Pannonia
Veszprém, Hungary
2008
KRISTÁLYOSÍTÓK MODELL PREDIKTÍV SZABÁLYOZÁSA
Értekezés doktori (PhD) fokozat elnyerése érdekében Írta:
Moldoványi Nóra
Készült a Pannon Egyetem Vegyészmérnöki Tudományok doktori iskolája keretében Témavezető: Dr. Abonyi János és Dr. Lakatos Béla
Elfogadásra javaslom (igen / nem) ……….
(aláírás) A jelölt a doktori szigorlaton …... % -ot ért el,
Az értekezést bírálóként elfogadásra javaslom:
Bíráló neve: …... …... igen /nem ……….
(aláírás) Bíráló neve: …... …... igen /nem
……….
(aláírás)
A jelölt az értekezés nyilvános vitáján …...% - ot ért el
Veszprém, ……….
a Bíráló Bizottság elnöke A doktori (PhD) oklevél minősítése…...
………
Az EDT elnöke
Tartalmi kivonat
Kristályosítók modell prediktív szabályozása
A disszertáció a folyamatos üzemű kristályosítók modellezésével, modell-analízisével és modell prediktív szabályozásával (MPC) foglalkozik, mely kérdéskör mind tudományos, mind ipari szempontból rendkívül fontos és aktuális. Ipari hagyományokból kifolyólag a vizsgálat célja egy olyan megoldásrendszer kidolgozása, mely lehetővé teszi, hogy ezen nemlineáris objektum megfelelően szabályozható legyen robosztus, lineáris modelleket tartalmazó MPC-vel. A szerző ipari tapasztalatát felhasználva megmutatta, hogy az MPC alkalmazható folyamatos kristályosítók szabályozására is.
Az értekezés első felében egy izoterm kristályosító modellje került bemutatásra és elemzésre, melynek során kijelölésre került a stabil munkapont és bebizonyosodott, hogy bizonyos méretű oltókristályok alkalmazása könnyebben szabályozhatóvá teszi a kristályosítót. Az eredmények igazolják, hogy az izoterm kristályosító szabályozástani elemzéséhez Matlab-ban kifejlesztett modell prediktív szabályozó sikeresen alkalmazható a kristályok átlagos szemcseméretének és méreteloszlás szórásnégyzetének szabályozására.
Az ipari környezetben való megvalósíthatóságot az értekezés másik fele egy vákuumkristályosító modellje és szabályozása kapcsán mutatja be. A folyamatos vákuumkristályosító modell prediktív szabályozása a Honeywell ipari szoftverkörnyezetében került megvalósításra. A javasolt megoldás integrálja a jelenleg elérhető legkorszerűbb eszközöket. Az MPC alapjául szolgáló lineáris modell mátrix a Honeywell által frissen kifejlesztett automatikus identifikálási algoritmussal került meghatározásra. A Honeywell MPC-je, a Profit Controller a szerző ötlete alapján OPC-n (eredetileg OLE (Object Linking and Embedding) keresztül került összekötésre a Matlab- ban lévő a szerző által implementált technológia szimulátorral. Futtatási eredmények alapján valószínűsíthető, hogy a Profit Controller megfelelően szabályozza és optimalizálja a folyamatos kristályosítót (modelljét) és a javasolt megközelítésmód ipari környezetben is alkalmazható.
Abstract
Model Predictive Control of Crystallisers
This dissertation is about the modelling, model analysis and model predictive control (MPC) of continuous crystallisers, what is a very important and up-to-date area both from an academic and industrial point of view. Because of industrial traditions the goal of the dissertation is to develop a solution system, by which this nonlinear object can adequately be controlled with a robust MPC working with linear models. The author - applying her industrial experiment – shows that MPC is a feasible controller for continuous crystallisers.
In the first part of the dissertation the model and the analysis of the model of an isothermal crystalliser is presented. The stable operating point is defined and it is demonstrated that the object becomes easier controllable with certain seeding. The model predictive controller, developed in Matlab, was successfully applied for the control of the average crystals size and size-distribution variance.
In the second part, the feasibility in an industrial environment is demonstrated through the model and the control of a vacuum crystalliser. The model predictive control of the vacuum crystalliser is achieved in the industrial used software environment from Honeywell. The proposed solution integrates the most up-to-date tools. The fundamental development of the linear model matrix in the MPC uses Honeywell’s newly developed automated identification method. The MPC of Honeywell, the Profit Controller was connected to the technology simulator implemented by the author to Matlab via OPC (originally OLE (Object Linking and Embedding) for Process Control). The results of the control verify that Profit Controller may adequately control and optimise the continuous crystalliser (model) and the suggested solution can be applied in the industry.
Zusammenfassung
Modell Prediktive Kontroller zu Kristallisatoren
Die Dissertation gibt sich mit der Modellierung der Kristallisatoren in dem kontinuierlichen Betrieb, mit der Analisierung des Modell und mit der Modell- prediktiven Regelung ab. Diese Themen sind besonders wichtig und aktuell auch in der Wissenschaft und auch in der Industrie.
Der Ziel der Untersuchungen war ausarbeiten eine Lösungsystem, was erlaubt die Regelung mit MPC des nicht linearen Objekts. Der MPC sollte robust sein, der MPC hatte lineare Modelle. Auf Basis der industriellen Erfahrungen des Autors wurde dargestellt für uns, der MPC war verwendbar für die Regelung des kontinuierlichen Kristallisators.
In dem ersten Teil der Dissertation waren die Demonstration und die Analysierung eines Modells des Isotherm-Kristallisators und wurde der stabile Arbeitspunkt festgestellt. Es wurde nachweisen, dass die Regelung des Kristallisators durch Anregelkristallen mit bestimmten Massen wird einfacher. Die Ergebnisse haben bewiesen, dass der in Matlab entwickelte MPC war erfolgsreich verwendbar für die Regelung, der Massen des Kristallen und der Massenverteilung.
Die Realisierbarkeit in der Industrieumgebung wurde in dem zweiten Teil durch das Modell und die Regelung eines Vakuumkristallisators dargestellt. Die prediktive Regelung des Modells eines Vakuumkristallisators in kontinuierlichen Betrieb wurde in der Honeywell Industriel-software Umgebung realisiert. Die empfohlene Lösung integrierte die heute erreichbare modernste Mittels. Die lineare Modellmatrix für den Grund des MPCs wurde mit einem neuen automatisierten Identifikations-Algorithmus festgestellt. Der Honeywell MPC (Profit Controller) wurde mit dem technologischen Simulator, der von dem Autorimplementiert ist, durch OPC (OLE for Process Control)verbunden. Die Ergebnisse der Testlaufen bewiesen, dass der Profit Controller hat ausreichend gesteuert und optimalisiert das Kristallisator(modell), und die empfohlene Lösungsystem auch in der Industrieumgebung verwendbar ist.
Contents
1 Introduction... 11
1.1 Motivation... 11
1.2 Roadmap for the dissertation ... 12
2 Control of crystallisers... 13
2.1 Brief review ... 13
2.1.1 Optimal control ... 13
2.1.2 Linear and non-linear modelling... 14
2.1.3 Model predictive control... 15
2.2 Message of SINC-PRO workshop ... 17
3 Modelling of Crystallisers... 19
3.1 Crystallisation ... 19
3.2 Modelling... 19
3.3 Moment equation model of the isotherm crystalliser ... 20
3.3.1 Dimensionless equations, scaling ... 23
3.3.2 Analysis of the model ... 26
3.3.2.1 Stability and bifurcation... 26
3.3.2.2 Controllability and observability... 27
3.3.2.3 Relative –gain array... 28
3.3.3 Conclusions... 29
3.4 Mathematical model of vacuum crystallisers ... 30
3.4.1 The moment equation model ... 31
3.4.2 The dimensionless model... 33
3.4.3 Summary ... 35
4 Model Predictive Control of crystallisers ... 36
4.1 Birth of MPC... 36
4.2 Concept of MPC ... 37
4.3 Advanced variation of MPC ... 42
4.4 MPC of an isotherm crystalliser ... 45
4.4.1 Demonstration of the linearity around the operating point... 45
4.4.2 Results of simulations... 45
4.4.2.1.1 Comparison with PID controllers ... 49
4.4.3 Conclusions... 51
4.5 MPC of a vacuum crystalliser... 52
4.5.1 The control problem... 52
4.5.2 Honeywell’s MPC, the Profit Controller ... 53
4.5.3 Identification ... 57
4.5.3.1 The automated identification method... 57
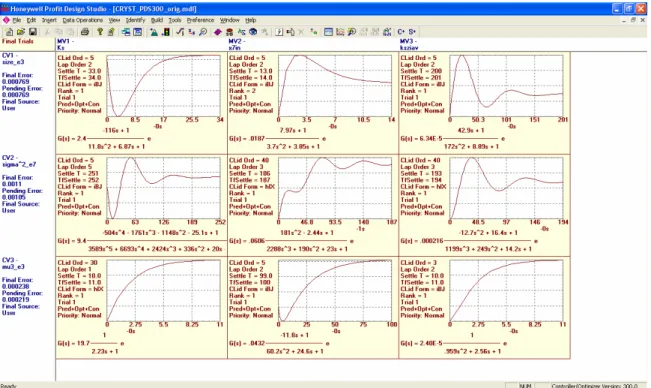
4.5.3.2 Identification of the crystalliser model... 61
4.5.4 Control study... 66
4.5.4.1 Test for controllability... 66
4.5.4.2 MPC control of vacuum crystalliser with OPC connection... 68
4.5.4.2.1 OPC connection ... 69
4.5.4.2.2 Graphical User Interface (GUI) ... 71
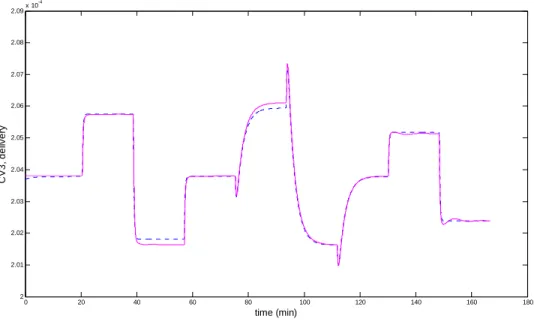
4.5.4.2.3 Results of the control study... 73
4.5.4.2.4 Control with disturbance... 76
4.5.4.2.5 Comparison with PID controllers ... 80
4.5.4.2.6 Operating range... 84
4.5.5 Conclusions... 87
5 Conclusions... 88
5.1 Theses ... 88
5.2 Possible practical applications ... 90
5.3 Future possibilities... 90
5.4 Publications... 91
5.4.1 Publications directly related to this thesis... 91
5.4.2 Partly related publications... 94
6 Tézisek magyar nyelven ... 95
7 References... 98
Preface
This thesis summarizes the contribution of my research work for obtaining a PhD degree in Chemical Engineering Science at the Department of Process Engineering at the University of Pannonia. I have been working for Honeywell for 3.5 years as an APC engineer, developing and commissioning many model predictive controllers. My industrial experience helped me greatly in my academic studies during the PhD work.
This dissertation would never have been written without the help and continuous support of several people. First of all, I want to express my sincere gratitude to Professor Béla Lakatos, for introducing me to crystalliser modelling, providing me with essential literature and consulting for many years.
I would also grateful thank to Professor János Abonyi, the head of Department of Process Engineering for the encouragement and support especially in the last months. Next, let me thank my colleagues at Honeywell, Peter Kiss, Adam Strobl and Howard Boder for their good ideas. I am also grateful to my managers at Honeywell, László Petrányi, Gábor Breznay, Hitesh Gowan and Ged Blenkharn for financial and moral support.
Finally, special thanks for the patience and the encouragement to my parents and to Zsolt.
Notation
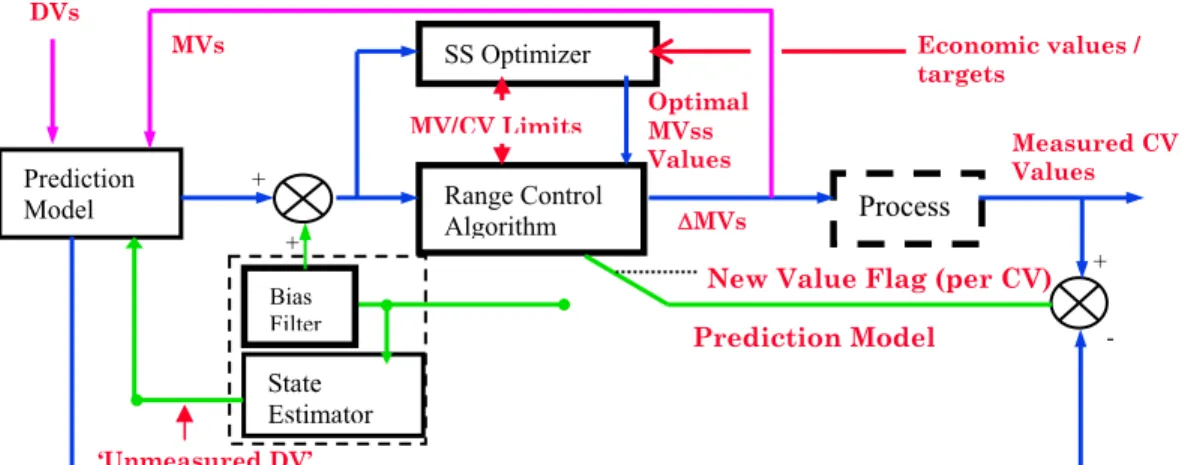
APC Advanced Process Control
CV Controlled Variable
DV Disturbance Variable MPC Model Predictive Controller
MV Manipulated Variable
OPC originally OLE for Process Control OLE Object Linking and Embedding RCA Range Control Algorithm
SS steady state
a constant of the crystal growth rate [m-1] b exponent of secondary nucleation rate Bp primary nucleation rate [no m-3s-1] Bb secondary nucleation rate [No m-3s-1] c concentration of solute [kgm-3]
cs equilibrium saturation concentration [kgm-3] Dap dimensionless parameter for primary nucleation Dab dimensionless parameter for secondary nucleation g exponent of crystal growth rate
F flow rate [kgs-1]
G crystal growth rate [ms-1] H enthalpy [Jkg-1]
j exponent of secondary nucleation rate ke parameter of primary nucleation rate
kg rate coefficient of crystal growth [m3g+1 kg-g s-1] kp rate coefficient of primary nucleation [no m-3s-1]
kb rate coefficient of secondary nucleation [no m3b-3 kg-b s-1] kV volume shape factor
L linear size of crystals [m]
n population density function [no m-4] q volumetric flow rate [m3s-1]
sc scale factor of the concentration [kg-1m3]
sm scale factor of the mth order moment of n (m=0,1,2,...) xm mth order dimensionless moment (m=0,1,2,...)
y dimensionless concentration of solute W evaporation rate
Greek letters
α dimensionless parameter ß dimensionless parameter
γ dimensionless crystal growth rate δ parameter of Volmer’s model ε voidage of suspension
µm mth order moment of n [mm-3] Θ dimensionless nucleation rate ρc density of crystals [kgm-3] ξ dimensionless time
Subscripts
0 initial value
in inlet value
p primary nucleation
b secondary nucleation
S steady state
1 Introduction
Crystallisation is one of the oldest chemical engineering processes. It is a widely used cleaning, separation and grain producing technique in the chemical industry, particularly within the pharmaceutical works.
From the point of view of controlling a crystalliser the main quality criterions are the properties of the produced crystals, first of all the size and the size-distribution.
Crystallisation is a multi-variable system, with multi input and multi output (MIMO) often with strong coupling. Thus a good, modern control technique is possible using a model-based MIMO control system. There are only few examples in the literature for this (Myerson et al, 1987; Jager et al, 1992; Miller and Rawlings, 1994; Rohani et al, 1999/1; Rohani et al, 1999/2)
A predictive type of control would be more appropriate technology than the corrective type, because crystal size can not be decreased under crystallisation conditions. One of the main problems is that for a proper model-based control of the size-distribution, because of the mentioned properties of the population balance equation, high-order control is required, which gives practical difficulties. The crystallisers are dissipative systems (Lakatos and Sapundzhiev, 1997), so that a crystalliser as a dynamical system possesses finite dimensional global attractors (Temam, 1988) that create an adequate base for the synthesis and usage of a good quality, low-order model-based control system. At the same time it means that for the synthesis of the model-based control system of the crystallisers the momentum-model – generated from population balance equations as linear differential equations – can be used with close approximation. Chui and Cristofides (1999) applied this property to design a nonlinear SISO (single input and single output) controller.
1.1 Motivation
There are only a few examples in the literature for the MPC of the crystallisers, mainly from the academic area and nearly nothing published from industry. The goal of this
dissertation is to attempt to fill in this gap, to create a bridge between the academy and industry and to show that MPC is an adequate controller for continuous crystallisers. For these purposes a solution system was developed, which contains the development and analysis of the engineering models used as technology simulators, development of the model predictive controller with a software package used in the industry and the connection of that two via OPC (originally OLE (Object Linking and Embedding) for Process Control). The control studies on that system unambiguously show that MPC is a possible technology solution for the control of the crystallisers.
1.2 Roadmap for the dissertation
In this dissertation a model-based MIMO control system of a crystalliser is presented. For the synthesis of the control system the multi-variable state-space model of the isotherm and vacuum crystallisers were composed, analyzed and after controlled with different model predictive controllers (MPC).
After some review of the literature (Section 2) in Section 3 a mathematical model is presented for isotherm continuous crystallisers using population balance equations for the crystals, of the balance equations for solvent and crystallising substance. The Eigen values of Jacobian matrix of the system are analysed, the parameters of a stable steady states were defined by stability and bifurcation tests.
Section 3.4 summarises the model of the vacuum crystalliser.
In Section 4 after some introduction of the model predictive controller, the model of the isotherm crystalliser is analyzed for controllability and observability. For the control studies a model predictive controller (MPC) was developed, the simulation studies of the crystalliser control were carried out in Matlab.
In Section 4.4 the vacuum crystalliser - as a process to be controlled - is carried out through an advanced process control (APC) project of Honeywell. The model was step tested in Matlab, than the linear model matrix was performed by Honeywell’s new automated identification method. Profit Controller, the Honeywell’s MPC controller, was connected to the crystalliser, to the Matlab model, via OPC (OLE for Process Control) The theses are presented in Section 5 with the list of the publications.
2 Control of crystallisers
2.1 Brief review
Faster computers and advances in sensor technologies and simulation and control algorithms are removing the main bottlenecks that limited progress in crystallisation control in the 1970s- 1980s. Model identification, experimental design, and optimal control algorithms are being increasingly applied to crystallisation processes in industry, including pharmaceuticals processes which have been resistant to systematic first- principles approaches. Further advances are expected to lead to even more utilization of these techniques to reduce time-to-market, which is key in the pharmaceutical industry, and to increase productivity, which is important in the bulk chemicals industry.
Crystallisation processes have all the characteristics that make an interesting control problem--partial differential equations, nonlinear dynamics, significant uncertainties, unmeasured state variables, significant disturbances, sensor noise, etc. (Braatz, 2002) 2.1.1 Optimal control
An open loop control problem can be formulated where the seed mass, the mean size of seed crystals, the width of the seed crystal size distribution, and the temperature profile are decision variables (Chung et al., 1999; Miller and Rawlings, 1994). Many objective functions have been studied, including the mean size of product crystals, the ratio of standard deviation to mean size, and the ratio of nucleated crystal mass to seed crystal mass at the end of operation (Eaton and Rawlings, 1990).
The optimal solution for each objective function is calculated using successive quadratic programming. A parametric analysis shows the significant importance of optimization of the seed distribution for a wide range of nucleation and growth kinetics (Chung et al., 1999). Under the presence of disturbances, modelling error, or tracking error, the states of the crystalliser do not follow the optimal path. One way to address this problem is to incorporate robustness into the computation of the optimal path (Ma and Braatz, 2000).
However, the performance of this approach will be limited by the chosen measured variables and the use of open loop control.
Several optimal feedback control algorithms including model predictive control have been proposed for batch processes (Eaton and Rawlings; 1990; Rawlings et al., 1993).
Even more recently, feedback control algorithms are being developed to reduce the sensitivity of the product quality to model uncertainties and disturbances, while being applicable to nonlinear distributed parameter systems (Chiu and Christofides, 2000). One approach, which couples geometric control with bilinear matrix inequalities, allows the direct optimization of robust performance (Togkalidou and Braatz, 2000; VanAntwerp et al., 1997; VanAntwerp et al., 1999). In contrast to most approaches to robust nonlinear control, this approach introduces no conservatism during the controller synthesis procedure. Also, no prior limitations are required regarding the speed of the unmodeled dynamics; instead, engineering intuition is incorporated into weights which bound the unmodeled dynamics, similarly to the linear time invariant case (Morari and Zafiriou, 1989; Skogestad and Postlethwaite, 1996). Application to a crystallisation process demonstrated robustness to a wide range of nonlinear and time-varying perturbation (Togkalidou and Braatz, 2000).
Usually the feedback controller is designed to follow a temperature trajectory that comes from, for example, solving an open loop optimal control problem. It has been conjectured, however, that a lower sensitivity to parameter uncertainties and disturbances may result from using the solution concentration as a function of temperature as the setpoint trajectory instead (Gutwald and Mersmann, 1990). Such a formulation, which includes time only as an implicit variable in the setpoint trajectory, can be used in formulating either open loop or closed loop optimal control design procedures. More research is needed to completely resolve whether such implicit-in-time optimal control formulations are superior to the standard formulation.
2.1.2 Linear and non-linear modelling
Control of crystal quality and in particular crystal size distribution (CSD) and crystal purity is of special interest in crystallisation processes. Control of these properties is challenging due to the complexity and non-linearity of the process and because of the lack of reliable on-line instrumentation to measure the above-mentioned crystal qualities.
The physical model of a crystallisation process consists of a set of coupled non-linear integro-differential equations (mass and energy balances) and a partial differential equation (population balance). This model has to be solved numerically with acceptable speed and accuracy for effective model-based control. Various methods have been suggested for this purpose (Rawlings et al., 1993).
An alternative to the physical modelling is process identification techniques in which the input-output sequences are used to develop linear auto-regressive exogenous (ARX) models for the crystallisation process. Previous research (Jager et al., 1992) recommends that in order to improve the crystallisers control, as many inputs and outputs as possible must be exploited. There have been, however, relatively few studies and experimental implementation of multivariable controllers on continuous crystallisers. Those few studies which have attempted multivariable control of crystallisation processes, have used linear models in spite of the fact that both the steady-state and dynamic behaviour of the process exhibit strong non-linearities.
2.1.3 Model predictive control
For control of a system which is represented by a nonlinear model, two general approaches may be taken. The first approach is to linearise the model and use linear control design techniques. Small signal approximation around the operating condition, exact linearisation using differential geometric theory and variable transformation are among various techniques (Daoutidis and Kravaris, 1991; Kravaris and Soroush, 1990), employed for linearization of non-linear models. The second approach involves non- linear control design techniques. Non-linear model-based control design, and more specifically non-linear model predictive control (NMPC), and the differential geometric approach, are common techniques for control of a system which is represented by a nonlinear model. The main advantage of the NMPC approach is its intuitive interpretation and its ability to deal with variables constraints whereas the geometric approach has a solid theoretical foundation. The relation between the two non-linear control techniques has been discussed by Soroush and Kravaris (1993). Model predictive control has received wide acceptance in industry (Qin and Badgwell, 2003). The predecessors of the non-linear MPC algorithm, namely the dynamic matrix control
(DMC) (Culter and Ramaker, 1980) and model algorithmic control (MAC) (Mehra and Rouhani, 1980) use the non-parametric impulse and step responses of the system as the process model. A quadratic objective function is minimized which for an unconstrained minimization, results in a closed-form solution. Proposed non-linear MPC techniques range from a simple extension of DMC, based on successive linearization of the non- linear model (Garcia, 1984; Gattu and Zafiriou, 1992), to more elaborate and computationally intensive techniques involving discretisation of the model followed by solution via non-linear programming (Bequette, 1991; Biegler and Rawlings, 1991).
Application of neural networks in control has been a fast growing research activity in the past few decades and may have a promising future. Neural networks have been used as a feedforward model, as inverse model in supervisory control, and as an optimizer. A good survey study on the application of neural networks in control is given in Hunt et al.
(1992).
In non-linear model predictive control, a solution of the non-linear dynamic model is required in each optimization iteration. In quadratic dynamic matrix control (QDMC) (Garcia and Morshedi, 1986) the process models linearised once for the entire trajectory, whilst in nonlinear quadratic matrix control (NLQDMC), the process model is linearised iteratively in each control interval (Lee and Recker, 1994). Exact linearisation using Lie derivatives has been employed in Soroush and Kravaris (1993) in which the exact inverse of the process model is obtained. However, for non-minimum phase processes such as a crystallisation process, exact linearisation results in an unstable inverse. An alternative to the sequential solution is to use a simultaneous solution of the process model and the optimisation algorithm. In this approach, model equations are transformed to algebraic equations, which reduce an infinite-dimensional optimization problem (optimal control) to a finite-dimensional problem (non-linear programming) (Morshedi, 1986). The ability of neural network-based model predictive control has been discussed by many workers including Dayal et al. (1994); Hunt and Sarbaro (1991); Nahas et al.
(1992); Psichogios and Ungar (1991); Takahashi (1993). Little work has been reported on the multivariable control of crystallisation processes (Jager et al., 1992). This is primarily due to the lack of reliable techniques for the on-line measurement of crystal qualities of interest, namely; crystal size distribution (CSD), crystal morphology, and
crystal purity. On the other hand, dynamic modelling of the crystallisation processes is still rudimentary, especially in predicting the nucleation rate, growth rate, agglomeration rate, and other number-affecting phenomena (Miller and Rawlings, 1994). Attempts have been made by Eek (1995) to linearise the non-linear model of a crystalliser followed by model reduction and linear model predictive control. In de Wolf et al. (1989) and Jager et al. (1992) an ARX model structure was used to identify a multi-input-single-output (MISO) model for a continuous crystalliser which was then used to derive the state-space formulation of the process. In Myerson et al. (1987) a multivariable optimal control of a mixed-suspension mixed-product removal crystalliser was studied. The controller was based on the linearised moments equations and mass and energy balance equations. An extended Kalman filter was used for state estimation.
In the paper of Rohani (1999/2) non-linear modelling and control of a continuous crystallisation process uses the combined concepts of neural networks (for modelling) and non-linear model predictive control (for control). In this outstanding study (Rohani, 1999/2) the linear ARX model (for comparison) and the non-linear feedforward neural network with parallel-parallel connection were used as process models. The control is achieved using the model predictive control strategy. This is an extension of the work by Eek (1995) in which he considered only the linear quadratic model predictive control of a crystallisation process. The use of neural network in non-linear model predictive control approach alleviates the main disadvantage of using the non-linear physical model which demands high computational load in each optimization step.
To summarize, the study of the crystallisation processes has so far mostly relied on linearised models and therefore application of linear control theory. (Such as this dissertation.) This is in spite of the fact that both steady-state and dynamic behaviours of the process exhibit strong non-linearities.
2.2 Message of SINC-PRO workshop
As an engineer of Honeywell I had the chance to take part in the SINC-PRO workshop in Delft in 2005. The objective of the SINC-PRO workshop was to demonstrate the achievements of the SINC-PRO project, which is aimed at a dramatic increase in both the
efficiency and effectiveness of crystallisation processes. Effectiveness refers to desired product quality, whereas efficiency implies a reduction in costs as well as a reduction of the time-to-market for new products through the realisation of “first time right”
production. It was shown in the workshop this objective was achieved by the development of advanced techniques for modelling optimisation and control of industrial crystallisers operating in both continuous and batch mode.
SINC-PRO has developed a control system that enables crystallisation processes to meet market demands while satisfying production, safety, health and environmental constraints. This innovative, integrated control system consists of:
1. A tool for the rigorous and hybrid modelling of crystallisation processes that can be used for parameter estimation using experimental data, for optimization of design and operation, and for supply of models that form the starting point for model-based control applications.
2. An observer / feedback system based on hybrid models using Extended Kalman filter techniques.
3. A control toolbox consisting of a Model Predictive Control system applicable to a wide range of crystallisation processes independently of their configuration and conditions.
The developed modelling and control tools have been applied and validated to a considerable number of case studies both in industry and in research institutes. The results are not published, because of industrial sponsorship, except the PhD thesis of Bermingham. (2003)
The conclusion for me of this workshop is that the field of MPC of crystallisers is an active developing area; there is demand from industry.
3 Modelling of Crystallisers
3.1 Crystallisation
Crystallisation, one of the oldest and most important unit operations, is widely used in the chemical industry for purification, separation, and/or production step, yielding good quality crystals. It is a practical method to obtain a concentrated chemical substance in a form that is pure, appealing and convenient to handle.
Industrial crystallisation research associated with basic commodity products provided the initial impetus for continuous crystalliser studies in the early sixties. The two simple and ideal continuous crystalliser models are the plug flow and the complete mixing flow models, which represent two extremes.
Randolph and Larson (1971) introduced the term mixed suspension mixed product removal (MSMPR) crystalliser to represent the ideally mixed-flow configuration. This type of crystalliser unit will ensure perfect mixing without any spatial variations of attributes within the whole contents, and is therefore analogous to the continuous stirred tank reactor (CSTR) used in chemical engineering. Thus, the crystalliser behaves as thought it were perfectly mixed, i.e. in any arbitrary small element of volume or clump, regardless of its location in the mixed section of the crystalliser, a full and uniform crystal size distribution to exist. (Tavare, 1995).
3.2 Modelling
“A model (M) for a system (S) and an experiment (E) is anything to which E can be applied in order to answer questions about S.” (Minsky, 1965) A model may be valid for one experiment and invalid for another; the model validation always relates to an experiment or class of experiments to be performed on a system, rather than to the system alone.
“Modelling means the process of organizing knowledge about a given system.” (Zeigler, 1984)
By performing experiments, we gather knowledge about the system. However, in the beginning, this knowledge is completely unstructured. By understanding what are causes and what are effects, by placing observations in a temporal as well as spatial order, we organize the knowledge that we gathered during the experiments. No wonder that every single discipline of science and engineering is interested in modelling, and uses modelling as a problem-solving tool. (Cellier, 1991)
The mathematical model of the crystalliser system, being a mixed set of ordinary differential equations and the population balance equation, include monosized and heterosized nucleation size dependent growth of crystals, possible seeding, classified product removal and fines removal with dissolution of fines. (Ulbert, 2002, Ulbert and Lakatos, 2007, Ulbert and Lakatos, 2005, Lakatos et al, 2006)
In the next sections the engineering models of isotherm and vacuum crystallisers will be presented, that were used in the control experiments in Section 4.
3.3 Moment equation model of the isotherm crystalliser
The mathematical model of a continuous MSMPR crystalliser consists of the population balance equation for crystals, of the balance equations for solvent and crystallizing substance, and of the equations describing the variation of the equilibrium saturation concentration. In the present analysis, the crystalliser is assumed to be isothermal, thus the equilibrium saturation concentration c* is constant during the course of the process.
(Lakatos, 1994, Lakatos, 1996 and Lakatos et al., 2007) It is assumed that the following conditions are satisfied:
(1) the volumetric feed and withdrawal rates of the crystalliser are constant and equal, thus the working volume is constant because in common operation it is set to be constant, (but the model can be used in varying volume case as well with some minor changes);
(2) the crystals can be characterized by a linear dimension L;
(3) all new crystals are formed at a nominal size Ln≅0 so that we assume Ln=0;
(4) crystal breakage and agglomeration are negligible;
(5) no growth rate fluctuations occur;
(6) the overall linear growth rate of crystals G is statistically size-dependent and has the form of the power law expression of supersaturation, the empirical form is the following:
; (3.1)
( aL
c c k
G= g( − *)g 1+ )
(In this case a=0, independent of the size)
(7) the primary nucleation rate Bp is described by the Volmer model derived from the Gibbs-Thomson relationship (Mullin, 1993)
⎟⎟
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜⎜
⎜
⎝
⎛
⎟⎠
⎜ ⎞
⎝
− ⎛
=
ln * exp
2
c c k k
Bp pε e (3.2)
the secondary nucleation rate Bb is described by the power law empirical relation
(3.3)
b j b
b k c c
B = ( − *) µ3
where µ3 is the third of the ordinary moments of the population density function n, which are defined as
(3.4)
...
3 , 2 , 1 , 0 , ) , (
0
=
=
∫
∞Lmn Lt dLmµm
With these assumptions the population balance equation governing the crystal size dynamics becomes:
[ ] [ ]
0 , 0
) , ( ) , ) (
, (
*) , , ( ) , (
>
>
−
⎟=
⎠
⎜ ⎞
⎝
⎛ +
L t
t L n t L n L q
t L n c L c G t
t L
V n in
∂
∂
∂
∂
(3.5)
subject to the following initial and boundary conditions:
(3.6)
0 ), ( ) 0 ,
(L =n0 L L≥ n
0 ,
*), , ( ) , (
*) , , (
lim0 = = ≥
→ G cL c n L t B cc p b t
L ν ν (3.7)
(3.8)
0 , 0 ) , (
lim = ≥
∞
→ n Lt t
L
Here, n(L,t)dL expresses the number of crystals having sizes in the range L to L+dL at time t in a unit volume of suspension.
The mass balance of the crystallizing substance has the form
[
c]
qcin q[
c cdt c
V dε +(1−ε)ρ = − ε +(1−ε)ρ
]
(3.9)with the initial condition
(3.10)
) 0
0
( c
c =
where the voidage of suspension ε is related to n and L by
(3.11)
∫
∞−
=
−
=
0
3 1 3 ( , )
1 kVµ kV Ln Lt dL ε
Finally, the mass balance of the solvent is written in the form ( )
sv sv qcsvin q c dt
c
V dε = − ε (3.12)
with the initial condition
. (3.13)
) 0
0
( sv
sv c
c =
Therefore, the state at time t≥0 of the continuous isothermal MSMPR crystalliser is given by the triple [c(t),csv(t),n(t)], and its dynamics is described by the distributed parameter model formed by the mixed set of partial and ordinary differential eqs (3.5), (3.9) and (3.12), subject to the initial and boundary conditions (3.6-8) (3.10) and (3.13).
The evolution in time of this system occurs in the state space R2×N that is the Descartes product of the vector space R2 of concentrations and of the function space N of the population density functions. Consideration of dynamical problems of crystallisers in this product space, however, seems to be quite complex and not constructive. In the present study, we concentrate on a reduced case, considering the problem in a finite dimensional state space model based on the moments of the population density function instead of the distributed parameter system (3.5)-(3.8).
Since the overall crystal growth rate (3.1) is a linear function of size L, the population balance Eq. (3.5) can be converted into an infinite set of recursive ordinary differential equations for the moments of population density function:
( )
VB p or bdt q
V dµ = µ in−µ + ν =
ν,
0
0 0 (3.14)
Primer (Bp) or secondary (Bb) nucleation is used, depend on which is the determinant.
( min m) g( *)g( m1 m)
m q Vmk c c a
dt
Vdµ = µ −µ + − µ − + µ m=1,2,3 (3.15)
which can be closed by Eq.(3.9), describing the mass balance of the crystallizing substance, at the equation for the third order moment. Then Eq.(3.9) takes the form
) (
*) )(
( 13
)
( ρ µ2 µ3
ε
ε c c k k V c c c a
q dt
V dc = in− + V g c− − g + (3.16)
So
) (
*) ( 13
)
( µ2 µ3
ε
ε c c k k Vc c c a
q dt
V dcsv = svin− sv + V g sv − g + (3.17)
where csv stands for the concentration of solvent.
The first four moment equations from the system (3.14-15) with Eqs (3.16-17) provide a closed moment equations model of the crystalliser.
3.3.1 Dimensionless equations, scaling
We introduce the following set of dimensionless variables
svin c svin sv c sv in
c in c
m m m
tt x s m y s c c y s c c y sc y s c
s = = = − = − = =
= , µ , 0,1,2,3, ( *), ( *), ,
ξ
into Eqs (3.14)-(3.17), where st, sc and sm, m=0,1,2,3, are scale factors defined as
* } max{
: 1
c s c
in
c = − , s0:=6kVkg3st−3(max{cin}−c*)3g
( in ) g
t g
Vk s c c
k
s1:=6 2 −2 max{ }− *2 s2:=3kVkgst−1(max{cin}−c*)g , s3:=kV
and max{cin} denotes the maximal value of inlet concentration, as well as the set of dimensionless parameters
q s V t st = t :=
τ , α:=(ρ−c*)(max{cin}−c*)−1 β:=kgast−1(max{cin}−c*)g
( in ) g
t g V p
ap k k k s c c
D :=6 3 −4 max{ }− *3 j g t ( in )g b
b V
ab k k k s c c
D :=6 1− 3 −4 max{ }− *3 +
* } max{
* *
: c c
c c s
in
c = −
γ =
Then the dimensionless governing equations take the form:
b x p
x d
dx in
,
0 ,
0
0 = − +Θ ν =
τ
ξ ν (3.18)
3 , 2 , 1 ),
( 1
min− + + =
= x x y x − m x m
d dx
m g m
m
m β
τ
ξ (3.19)
( 3) 1 32 3
) 3 ( ) (
1 x
x x y y x
y y d
dy in g
− +
− −
−
= − α β
τ
ξ (3.20)
( 3) 1 2 3 3 ) 3 (
1 x
x x y y x
y y d
dysv svin sv sv g
− + +
−
= − β
τ
ξ (3.21)
subject to the initial conditions
0 0
0, 0,1,2,3, (0) , (0) )
0
( m sv sv
m x m y y y y
x = = = = (3.22)
where
( )
⎟⎟
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜⎜
⎜
⎝
⎛
⎟⎟⎠
⎜⎜ ⎞
⎝
− ⎛ +
−
=
γ Θ γ
y x k
Dap e
p
2 3
ln exp
1 (3.23)
and
j ab b b =D y x3
Θ . (3.24)
It follows from physical reasoning that the physically admissible solutions to Eqs (3.18- 21) should satisfy the constraints
1 1
0 , 0
, 0
, 0
,
0 3 3 3max min
1 0 2 3 2
2 0 1 1 0
0 ≤ ≤ ≤ ≤ ≤ ≤ < = − <
≤
≤
≤ y yin x x m x Ax m x A x m x x ε
where x0m denotes the maximal value of the zero order moment, while
⎟⎟⎠
⎜⎜ ⎞
⎝
⎛ −
=
ρ
ε *
1
min c
V Vsv
(3.25)
where Vsv is the volume of solvent in the crystalliser.
The parameters, which in the case of primary and secondary nucleation form the vectors of real numbers pp=(τ,α,g,β,Dap,ke,γ) and pb=(τ,α,g,β,Dab,b,j), respectively, are also bounded:
0 , 0 , 0 , 0 , 0 ,
0 ,
, 0 , 0 ,
0 ≥ ≥ ≥ min ≥ ≥ ≥ ≥ ≥ ≥
≥ α β β γ
τ g Dap Dab ke b j (3.26)
As a consequence, the state of crystalliser (3.18)-(3.21) is represented by the vector of variables (x0,x1,x2,x3,y, ysv), and its time evolution occurs in the feasible region of solutions of the six-dimensional state space R6.
The behaviour of crystalliser in the neighbourhood of a stationary state may be deduced by examining the Eigen values of the Jacobian matrix of Eqs (3.18-21) at this state (using equations for steady state conditions) which becomes: (for details see the supplemented CD)