Ökonometriai modellek alkalmazása a sportgazdaságban

Ö KONOMETRIAI MODELLEK ALKALMAZÁSA A SPORTGAZDASÁGBAN

F

D

I

– R

G

2018.

© Fűrész Diána Ivett, Rappai Gábor – 2018

A tankönyv az EFOP-3.4.3-16-2016-00005 Korszerű egyetem a modern városban: Értékközpontúság, nyi- tottság és befogadó szemlélet egy 21. századi felsőoktatási modellben pályázat támogatásával készült.

Lektorálta: dr. habil Ács Pongrác, egyetemi docens ISBN: 978-963-429-294-4

Kiadja: Pécsi Tudományegyetem Pécs, 2018.

Tartalom

1 Bevezetés ... 7

2 Az ökonometria statisztikai alapjai ... 13

2.1 Statisztikai alapműveletek ... 14

2.1.1 Középértékek ... 15

2.1.2 Szóródási mérőszámok ... 17

2.1.3 Két speciális változó átlaga és szórása ... 19

2.2 Kapcsolatszorossági vizsgálatok ... 20

2.2.1 Asszociációs kapcsolat szorosságának mérése ... 22

2.2.2 Vegyes kapcsolat elemzése ... 23

2.2.3 Korrelációs mérőszámok... 25

2.3 Trendelemzés ... 27

2.3.1 Mozgóátlagolás ... 28

2.3.2 Analitikus trendszámítás ... 30

2.4 Valószínűségelméleti alapok ... 35

2.4.1 Eloszlás- és sűrűségfüggvény ... 35

2.4.2 Várható érték, variancia ... 36

2.4.3 Nevezetes statisztikai eloszlások ... 37

2.5 Becsléselméleti alapfogalmak ... 39

2.5.1 Becslési módszerek ... 39

2.5.2 A becslőfüggvény tulajdonságai ... 41

2.6 Hipotézisellenőrzés... 43

2.6.1 A hipotézisellenőrzés menete ... 44

2.6.2 Szignifikancia szint és szignifikancia érték ... 45

3 Regressziószámítás ... 47

3.1 Kétváltozós lineáris regressziós modell ... 47

3.1.1 Paraméterbecslés a kétváltozós modellben ... 48

3.1.2 A modell illeszkedésének vizsgálata ... 53

3.2 A kétváltozós modell kiterjesztése ... 56

3.2.1 Többváltozós lineáris modell ... 56

3.2.2 Nemlineáris regresszió ... 60

3.2.3 Dummy változók a regressziós modellben ... 66

3.2.4 Dinamikus specifikáció ... 71

3.3 Próbakészítési elvek az ökonometriában ... 72

3.4 Az LNM alkalmazási feltételei ... 75

3.4.1 Heteroszkedaszticitás ... 76

3.4.2 Normalitás-próbák ... 78

3.4.3 Reziduális autokorreláció... 79

3.4.4 Multikollinearitás ... 83

3.5 Az ökonometria speciális tesztjei... 85

3.5.1 Kihagyott, illetve felesleges változó esete ... 85

3.5.2 Helytelen függvényforma kimutatása ... 86

3.5.3 Strukturális törés kimutatása, paraméterek stabilitásának vizsgálata ... 88

3.6 Többegyenletes modellek ... 89

3.6.1 Szimultaneitási torzítás ... 91

3.6.2 Identifikálhatóság ... 92

3.6.3 Exogenitás és Hausman-teszt ... 93

3.6.4 Paraméterbecslés szimultán egyenletrendszerben ... 94

4 Sztochasztikus idősor-modellezés ... 97

4.1 Stacionaritás, fehér zaj, véletlen bolyongás ... 97

4.2 Box-Jenkins modellek ... 107

4.2.1 MA-folyamatok ... 107

4.2.2 AR-folyamatok ... 108

4.2.3 ARMA-folyamatok ... 110

4.2.4 ARIMA-modellek ... 111

4.3 Exponenciális simítás ... 114

4.4 Előrejelzések készítése ... 115

4.5 Többváltozós idősori modellek ... 121

4.5.1 Okság az ökonometriában ... 121

4.5.2 Vektor autoregresszív modellek ... 124

4.5.3 Kointegrált idősorok, hibakorrekciós modell ... 130

5 Sportgazdasági esettanulmányok... 139

5.1 Keresleti függvények a sportolók piacán ... 139

5.1.1 A sportolói munkaerőpiac sajátosságai ... 140

5.1.2 Játékos-keresleti modellek specifikációja ... 143

5.1.3 A keresleti modellek paraméterbecslésének tapasztalatai ... 147

5.2 Korrelációanalízis és hálózatelemzés az átigazolási piacon ... 147

5.2.1 Korrelációs kapcsolatok a változók között ... 148

5.2.2 Átigazolási hálózatok vizsgálata ... 150

5.2.3 Összegzés ... 155

5.3 Bérek hatása a sportegyesületek eredményességére ... 156

5.3.1 Problémafelvetés, illetve a korábbi vizsgálatok eredménye ... 156

5.3.2 Módszertani alapvetés ... 157

5.3.3 Az adatállományok legfontosabb jellemzői ... 159

5.3.4 A labdarúgó Bajnokok Ligája 2005/06-os szezonjának elemzése ... 160

5.3.5 További érdekességek a kosárlabda, illetve labdarúgó top-ligák eredményeiben... 164

5.3.6 Konklúziók ... 166

5.4 Mitől lesz kiegyensúlyozott egy bajnokság? ... 167

5.4.1 A verseny kiegyensúlyozottságának elmélete, korábbi kutatási eredmények ... 167

5.4.2 A koncentráció speciális mérőszámai ... 168

5.4.3 Empirikus eredmények ... 171

5.4.4 Konklúziók ... 177

5.5 Hatással van-e az alapszakasz kiegyensúlyozottsága az NBA végeredményére? ... 177

5.5.1 Adatállomány és módszertan ... 178

5.5.2 Modellezési eredmények ... 182

5.5.3 Összegzés ... 184

5.6 Eseményelemzés a Rio-i Olimpia példáján keresztül ... 185

5.6.1 Eseményelemzés módszere ... 186

5.6.2 A vizsgált események, illetve a vizsgált idősorok ... 188

5.6.3 Modellbecslési eredmények ... 189

Felhasznált irodalom ... 193

Index... 201

7

1 Bevezetés

A társadalmi-gazdasági jelenségek alapos megismeréséhez mindenképpen szükség van a rájuk vo- natkozó adatok összegyűjtésére, rendszerezésére, az adatokban rejlő információk tömörítésére, az események közötti összefüggések feltárására. Az adatgyűjtéssel és -elemzéssel foglalkozó tudomány a statisztika, melyet sokan – okkal – a társadalomtudományok matematikájának is neveznek. A metafora jól mutatja a statisztikai módszertan mibenlétét: egyrészt erősen matematikai megalapo- zottságú, másrészt viszont – mivel a társadalomban a természettel ellentétben sokkal kevesebb de- terminisztikus összefüggést találunk – a vizsgált jelenségek alakulásában nagy szerepet kap a vélet- len: vagyis a statisztika szemlélete alapvetően sztochasztikus.

Az általános statisztikai módszertant alkalmazva számos új (rész)diszciplína honosodott meg a tu- dományban, melyek azonban nem az alkalmazott eljárásokban, hanem a vizsgálat tárgyában külön- böznek egymástól. Ezen „osztódás” eredményeképpen beszélhetünk biometriáról, pszichometriá- ról, szociometriáról stb. A „metriák”, vagyis a statisztikai adatokat és matematikai modelleket alkal- mazó tudományok sorában jelent meg mintegy száz évvel ezelőtt az ökonometria.

Az ökonometria – közkeletű definíciója szerint – a matematika, a statisztika és a közgazdaságtudomány határterülete (közös része), amely a gazdasági jelenségek mérésére (mérhetőségére), illetve modellezésére alapoz. Az ökonometria születését 1930-ra, az Ökonometriai Társaság (Econometric Society) alapításának idő- pontjára tehetjük. A tudományterület megerősödésének legfontosabb eszköze az 1933-ban először publikált Econometrica folyóirat, amely mára a világ egyik legmagasabban respektált közgazdaság- tudományi folyóiratává vált. Az ökonometria – valószínűleg éppen erőteljes módszertani megala- pozottságának köszönhetően – jelentős tudományos sikereket tudhat magáénak: az 1969 óta kiosz- tott közgazdasági Nobel-emlékdíjak közül a legszűkebb értelmezésben is legalább féltucat¹, kifeje- zetten erről a területről származó eredményeket honorált.

A gazdasági jelenségek megértésének roppant fontos lépése, hogy feltárjuk, van-e, és ha igen, mi- lyen irányú és szorosságú az ok-okozati összefüggés két vagy több esemény között. Mivel a gazda- ság szereplőinek viselkedése nem állandó, a vizsgált jelenségek környezete is folyamatosan változik.

A jelenségek között akár kölcsönhatások is lehetnek, így az említett kauzalitás (okság) feltárása csak gondosan specifikált modellekkel lehetséges. Minden modellre – így az ökonometriai modellre is igaz, – hogy nem más, mint a valóság egyszerűsített változata. Ezért a modellezés során a (számunkra) lényeges elemeket kiemeljük, a lényegtelenektől pedig eltekintünk. Érdemes mindig szem előtt tar- tani, hogy egy modell mindig kompromisszum eredményeképpen jött létre: egyrészről törekszünk a valósághűségre, másrészt szeretnénk, ha a modellünk átláthatóan egyszerű lenne. Mivel ezen két kívánalom egymásnak szinte mindig ellentmond, ezért optimálisnak azt a modellt tekintjük, amely már elég jól magyarázza a jelenségek alakulását, de még átláthatóan egyszerű.

1 Mivel a közgazdasági Nobel-díjak legtöbbjében találhatunk empirikus kutatást, így annak eldöntése, hogy melyek az ökonometriai eredményekért odaítélt díjak, nem egyértelmű. A hivatalos méltatások alapján biztosan ökonometriai modellezésben elért eredményért kapta a díjat Frisch és Tinbergen (1969, dinamikus ökonometriai modellek); Klein (1980, ökonometriai modellek a gazdaságpolitika megalapozásában); Haavelmo (1989, az ökonometria valószínűségelméleti megalapozása); Heckman és McFadden (2000, mikroökonometria); Engle és Granger (2003, idősor-modellek az ökono- metriában); valamint Sargent és Sims (2011, vektorautoregresszív modellek és okság az ökonometriában).

9 Amikor sikerült elérnünk azt a modellt, amely valamennyi, általunk fontosnak tartott hipotézisellen- őrzés szűrőjén átjutott, következik a modell eredményeinek felhasználása. Az ökonometriai model- lek felhasználása – leegyszerűsítve – három területen történik:

 elemzés,

 előrejelzés,

 szimuláció.

A kutatók is sokszor megfeledkeznek róla, ám a paraméterek becslését, a hipotézisek vizsgálatát követően előállt modell – bármilyen korrekt legyen is statisztikai (ökonometriai) szempontból, – mit sem ér, ha a valósággal (természetes logikával) összevetve nem állja meg a helyét. Biztosan nem fogadhatunk el olyan modellezési eredményeket, amelyek az eredményváltozó értékét „kivezetik”

annak értelmezési tartományából, vagy olyan eredményekre jutnak, melyek formál logikai úton cá- folhatók. Ez a logikai verifikáció (vagy – negatívan hozzáállva – falszifikáció) a modellezés végső, de nem elhagyható fázisa.

Az ökonometriai modellezés az elmúlt közel száz évben rengeteget változott, fejlődött. Míg mint- egy 50 évvel ezelőtt a becslési módszerek fejlesztése állt a középpontban, az 1980-as években a hangsúly áttolódott a tesztelésre. Napjainkban – miközben az előbbi két terület továbbra is roppant fontos – a legtöbb kutató unikális adatállományok összegyűjtésével, sokszor bizarrnak tűnő mo- dellspecifikációval próbál új eredményeket elérni. A módszertan változása mellett az ökonometriai vizsgálatok tárgya is sokat változott az elmúlt évszázadban. Míg a kezdetekben szinte kizárólag csak a nemzetgazdaság makro-összefüggéseit (GDP és az ezt alakító tényezők) modellezték, az elmúlt 25-30 évben olyan új területek is megjelentek, melyek már önálló nevet kívánnak maguknak: így alakult ki a tőkepiaci jószágok áralakulását modellező pénzügyi ökonometria, vagy a gazdaságföldrajz (földrajzi gazdaságtan) vizsgálódásait modellalapokra helyező térökonometria.²

Annak felismerése, hogy a sport jelentős gazdasági szerepet is betölt, körülbelül az 1970-es évekre tehető. Valószínűleg az 1972-es Müncheni Olimpia volt az első olyan megaesemény, amikor a sportrendezvények időütemezését a szponzorok (pl. tv-társaságok) is befolyásolták; a versenyzők mellett az általuk hordott felszerelések is vetélkedtek, vagyis elindult a sportgazdaság.

Mára a gazdasági szempontok olyan mértékben átszövik a sportot (gondolva itt nem csak az él- sportra, de a szabadidő-, legújabb nevén egészség-sportra is!), hogy a korábbi amatőr-profi osztá- lyozás mellett kialakult egy új kategória, a kommercializálódott sport fogalma is. A globalizáció és a technológia rohamos fejlődésének következtében a média szerepe és befolyása a sportban egyre jelentősebbé vált: köszönhetően annak, hogy a sportszolgáltatások szinte az egész világon elérhe- tővé váltak, a sport iránti kereslet hatalmas növekedést ért el. Mi sem bizonyítja ezt jobban, mint az a tény, hogy a világ egyik legsikeresebb sportvállalkozása, a Manchester United mára több, mint 24 országban, összesen 200 hivatalos szurkolói irodát, valamint 333 millió szurkolót mondhat ma- gáénak világszerte.

2 A pénzügyi ökonometria kérdésfeltevéseinek és speciális módszereinek magyar nyelvű összefoglalása elolvasható Rappai (2013) könyvében, a térökonometria iránt érdeklődőknek ajánljuk Varga (2002) kitűnő cikkét.

10 A sporttudomány gazdasági kérdésekkel foglalkozó része még nem tart ott, hogy az ökonometriá- ban önálló alosztályt alkosson, ugyanakkor örvendetesen szaporodnak azok a tanulmányok, melyek nagy adatállományokon, korrekt sztochasztikus módszertant alkalmazva keresik a választ a kutatási kérdéseikre. Különösen igaz ez az észak-amerikai nagy ligákat (NBA, NHL, NFL) elemző tanul- mányokra, már csak azért is, mert itt hatalmas adatbőség (big data) áll a kutatók rendelkezésére, még az egyébként mindig szenzitív gazdasági területen is. A sportgazdasági kutatók legfontosabb kérdései az alábbiak:

 hogyan növelhető a sportrendezvények iránti kereslet, vagyis milyen tényezők tekinthetők a nézőszám-változás okának?

 milyen összefüggések mutathatók ki a sportolók bérezése és a csapatok eredményessége között; mennyit érdemes játékosra költeni; hogyan érdemes viselkedni a játékos-piacon?

 milyen mértékben és mikor térülnek meg a sportba fektetett infrastrukturális beruházások?

 mitől válik egy sportklub gazdasági értelemben is nyereségessé; kiket tekinthetünk a gazdál- kodást tekintve benchmark-nak?

 a pénzmultiplikátort is figyelembe véve milyen megtérüléssel bír egy szponzor (állam, vagy piaci szereplő) sportba juttatott támogatása?

Könyvünkben nem tudunk (és nem is akarunk) válaszolni valamennyi itt feltett kérdésre, ráadásul a kérdések sora még sokáig folytatható lenne. Alapvető célunk az, hogy a (magyarországi) sport- gazdaság-kutatóknak, illetve – és ezt talán még fontosabbnak tartjuk – sport-menedzsereknek jól használható módszertani segédletet adjunk, ha a fenti vagy azokhoz hasonló kérdéseket kívánnak megválaszolni.

A Bevezetést követő három fejezetben rövid, lényegre törő, a szokásos bizonyításokat sem tartal- mazó módszertani alapvetés következik, a hosszas és a gyakorlati alkalmazás szempontjából sok- szor felesleges levezetéseket gyakori irodalmi hivatkozásokkal pótoltuk. Előbb az általános statisz- tika leggyakrabban használt eljárásait, majd a keresztmetszeti adatokon alkalmazott regresszió-ana- lízist, végül a sztochasztikus idősor-modellezés alapjait tekintjük át. Ezek a fejezetek csak annyiban utalnak a sportgazdaságra, hogy a bennük szereplő, elsősorban a megértést segítő illusztratív példák adatállományai a sporthoz kötődnek. Az 5. fejezet hat esettanulmányt tartalmaz, ezek mindegyike elhangzott már sporttudományi konferenciákon, vagy általános gazdaságtudományi tudományos rendezvények sporttal és statisztikával/ökonometriával foglalkozó szekciójában. Az itt bemutatott spotgazdasági modellekkel célunk annak illusztrálása volt, hogy az ökonometriai módszertana ha- tékonyan alkalmazható a sporttudományban is. Az előadások szerkesztett változataiban többször előkerülnek olyan fogalmak, eljárások, melyeket a könyv módszertani fejezeteiben már részleteseb- ben tárgyaltunk, ezeket az esettanulmányokban újra ismertetjük, minden alkalommal olyan tárgya- lásmóddal, ahogy a konkrét modellezési probléma igényli.

A könyvben szereplő grafikus illusztrációk, a mintapéldák és az esettanulmányok modellbecslései a GNU Regression, Econometric and Time-series Library programcsomag gretl2017d verziójával készültek.

A gretl egy szabadon használható (freeware) ökonometriai szoftver, amely mind az oktatásban, mind a kutatásban jól hasznosítható, ám semmiképpen sem szeretnénk, ha az Olvasó úgy gondolná, hogy

11 a bemutatott eljárások csak ezzel a programcsomaggal reprodukálhatók. A statisztikai-ökonomet- riai módszertan informatikai támogatása jelentős mértékű, ajánljuk, hogy miden felhasználó válasz- sza ki a számára legkényelmesebb, leginkább átlátható programcsomagot, kódbankot.

Köszönjük tanszéki, intézeti Kollégáinknak – akik egyes esettanulmányokban szerzőtársként is köz- reműködtek – hogy az elmúlt időszakban többször is véleményezték a készülőfélben lévő írást, valamint számos élénk vitában segítettek fókuszálni a mondanivalónkat. Természetesen minden, a végső változatban maradt hiba a szerzőket terheli.

Meggyőződésünk, hogy a sportbéli eredményesség elengedhetetlen feltétele a professzionálisan működtetett gazdasági háttér, de emellett abban is biztosak vagyunk, hogy sportvállalkozásba (nem csak sportegyesület mögött álló gazdasági társaságot, de a sportfogyasztási, illetve sport-szolgálta- tási piacon megjelenő céget is értve ezalatt) invesztálni nyereséges tevékenység lehet. Úgy gondol- juk, hogy az erőteljes konkurencia-harcban jó „fegyver” lehet a modellezési ismeret, ugyanis így a megérzéseink mellett támaszkodhatunk az empirikus adatokon nyugvó, verifikált tényekre is!

Könyvünkkel a sportgazdaság szereplőinek döntéseihez kívántunk jól használható segédeszközt nyújtani

a szerzők.

12

13

2 Az ökonometria statisztikai alapjai

A gazdasági-társadalmi – így a sportgazdasági jelenségeket – folyamatokat különféle tulajdonságok, ismérvek jellemzik. Ezeket a tulajdonságokat, a megfelelő mérési skálát³ felhasználva, feleltetjük meg minőségi vagy mennyiségi kategóriáknak. Az alacsonyabb rendű skálák alapvetően kvalitatív jelle- gűek, elsősorban a megkülönböztetést, rangsorolást szolgálják. Fokozatai lehetnek kifejezések, mi- nőségi jegyek vagy numerikus számértékek. A magasabb rendű skálákon az azonosítást, hozzáren- delést kizárólag számszerű, kvantitatív értékekkel végezzük el. A mérési eljárás során a sokaság egye- deit minősítjük az ismérvváltozatok szerint. A gyakorlatban sokszor használjuk – meghatározóan a mennyiségi ismérvek esetében – az ismérv kategóriája helyett a változó kifejezést is. Figyelembe véve, hogy a kvantitatív változók (mennyiségi ismérvek) mérésére használt skálák lehetnek folyto- nosak, illetve diszkrétek (ezek esetében az ismérvváltozatok száma a mérés pontosságának javítá- sával sem növelhető) a változókat három fő csoportba sorolhatjuk:

 folytonos kvantitatív változók, ilyen a gazdasági adatok többsége;

 diszkrét kvantitatív változók, melyek elkülönített értékeket vesznek fel, az értékek leg- többször pozitív egész számok;

 kategorizált, vagy kategóriás változók, amelyek alapvetően a minőségi ismérvek változa- tainak megkülönböztetésére szolgálnak.

A gazdasági-társadalmi jelenségek megismerése során kiindulópontunk az egyedek felmérése. A vizsgálat szempontjából fontos megfigyelésekről (sportolók, vállalkozások stb.) általában rendelke- zünk a nevüket, címüket tartalmazó listával, statisztikai szakszóval, a lajstrommal. A lajstrom alapján eljutunk a vizsgálat tárgyát képező egyedekhez, beazonosítjuk azokat, majd felmérjük jellemző tu- lajdonságaikat, meghatározzuk az ismérvek (változók) konkrét értékeit.

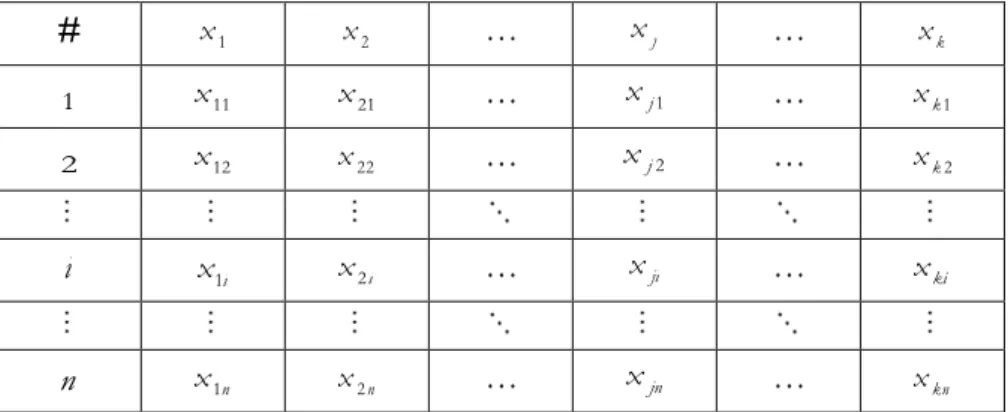
Az egyedeket tartalmazó adatállomány általános alakja a következő:

# x1 x2 xj _xk

1 x11 x₂₁ x_j1 x_k1

2 x12 x₂₂ x_j2 x_k2

i x_1i x2i xji _xki

n x1n x_{2 n} x_jn x_kn

2-1. táblázat: Az egyedi adatállomány általános alakja

Láthatjuk, hogy a fenti adatállomány n egyedet (megfigyelést) és k változót tartalmaz, vagyis ösz- szességében n k adatból áll. A statisztikában alkalmazott egyedi adatállományok nagyon hasonlí- tanak a lineáris algebrából ismert mátrixokra, ezért a fenti formátumú adatállományt gyakran hívják adatmátrixnak is.

3 A statisztikai terminológia megkülönböztet nominális (névleges), ordinális (rang), intervallum és arány skálákat (lásd pl. Pintér-Rappai, 2007).

14 Az 2-1. táblázatban bemutatott egyedi adatállomány lehet

 keresztmetszeti (azonos időpontból, különböző egyedekre vonatkozó), vagy idősoros (azonos egyed több különböző időpontban felmért adatát tartalmazó); továbbá

 teljes körű (alapsokaságot tartalmazó), illetve részleges (minta) felvétel során keletkező.

Noha az adatmátrix általános alakjában (formájában) nincs különbség az előbbi altípusok között, ám az elemzési eszköztár megválasztása során hangsúlyozottan ügyelnünk kell az adatállomány leg- fontosabb jellemzőire. A következőkben az adatállományok tömörítésének, elemzésének leggyak- rabban használt eszközrendszerét, vagyis az általános statisztika módszertanát mutatjuk be.

2.1 Statisztikai alapműveletek

A statisztika módszertanának legalapvetőbb eszköztára (sorbarendezés, középértékek meghatáro- zása, szóródás elemzése, stb.) általánosan ismert, így ebben az alfejezetben csak a későbbi egységes jelölés és terminológia-használat kedvéért tekintjük át a legfontosabb műveleteket.

Az egész alfejezeten végighúzódó példánk legyen a következő!

Az NBA 2017/18-as szezonjában a legjobban kereső 120 játékos éves bére az alábbi (a bérek ezer $-ban):

16 819 18 600 21 475 28 704 14 875 19 047 17 514 18 600 20 755 21 775 15 210 15 000 16 450 20 544 15 210 20 200 23 500 17 514 18 600 16 767 24 599 18 901 28 531 16 563 21 991 23 776 33 286 16 000 22 642 31 269 21 589 16 972 16 544 16 200 16 450 20 200 14 780 18 820 15 100 18 600 22 642 17 514 22 169 22 642 17 170 16 450 34 683 27 734 24 773 17 037 16 740 27 740 25 687 16 972 17 808 17 514 16 537 17 808 21 405 20 660 16 972 15 840 14 560 17 584 29 513 20 200 20 200 16 759 23 000 16 740 21 405 17 191 22 344 15 420 28 299 20 452 20 200 26 153 18 734 17 892 20 200 17 562 20 200 16 740 20 200 25 000 23 776 22 230 19 323 21 536 18 600 16 000 21 881 23 112 23 963 20 340 21 405 16 120 22 086 23 776 17 125 17 127 28 531 16 200 21 665 15 000 23 112 16 120 23 776 18 600 21 405 16 450 17 266 25 289 18 003 15 000 26 244 29 728 20 200 18 132 Láthatjuk, hogy a megfigyeléseink rendezetlenek, első ránézésre kevés információt hordoznak.

Jelöljük az előbbi felsorolás (lajstrom) elemeit (az egyedi adatokat) a továbbiakban az x x₁, ₂, szimbólumokkal! (Figyeljünk oda, hogy a fenti adathalmaz nem egy korábban bemutatott adatállo- mány, hanem annak csak egy oszlopa, vagyis itt csak egy változónk van, ezért nem használtunk még egy alsó indexet!)

15 A legegyszerűbb statisztikai műveletek az adatok leszámlálásához, illetve sorba rendezéséhez kö- tődnek, elvégzésükhöz semmilyen statisztikai előtanulmány nem kellene. Egy adathalmazt jól jelle- mez annak számossága, illetve legkisebb és legnagyobb eleme.

A kiválasztott kosárlabdázók esetében:

 az adathalmaz számossága:n120;

 a legmagasabb fizetés: x_max 34 683 ezer $;

 a legalacsonyabb fizetés: x_min 14 560 ezer $.

Az adatállomány jellemzése során a minimum és a maximum mellett gyakran használatosak a sorba (rangsorba) állított megfigyelések más kitüntetett pontjai is, melyeket kvantiliseknek nevezünk. A kvantilisek olyan osztópontok, amelyek a rangsorba rendezett számszerű ismérvértékek 2,3,4, ,r -ed részét jellemzik. Definíciónk szerint a j-edik kvantilis az a változóérték, amelynél az összes elő- forduló érték j r -ed ( j 1, 2, ,r1) része kisebb, illetve 1 j r -ed része nagyobb.

A statisztikai elemzésekben kitüntetett szerepet játszó néhány kvantilis:

 medián (felező)

 tercilis (harmadoló),

 kvartilis (negyedelő)

 kvintilis (ötödölő),

 decilis (tizedelő),

 percentilis (századoló).

Mindezen értékek közül leggyakrabban a mediánt használjuk, amely a sokaság felező pontjaként értelmezett, vagyis a medián az a szám, amelynél a megfigyeléseink fele kisebb, fele nagyobb. (Abban az esetben, ha páros számú megfigyelésünk van, mediánként a két „középső” érték átlagát szoktuk használni.)

A legfontosabb statisztikai alapműveletekkel célunk, hogy a megfigyelt adathalmazt tömören jelle- mezzük, ehhez a középértékeket és a szóródási mérőszámokat használjuk fel.

2.1.1 Középértékek

Alapozó statisztika könyvekből ismeretes, hogy a középértékeknek két fajtája van. Megkülönböztet- jük a

 számított és a

 helyzeti középértékeket.

16 Általánosságban a számított középértékek – ismertebb nevükön átlagok – a mennyiségi változó azon értékei, amellyel a sokaság valamennyi egyedének számértékét helyettesítve, a sokaság előfor- duló értékeiből számított kiválasztott, az elemzés szempontjából fontos jellemző változatlan marad.

Attól függően, hogy melyik sokasági jellemző konstans voltára törekszünk, különféle átlagokról beszélhetünk. Így megkülönböztetünk számtani, mértani (geometriai), harmonikus, illetve négyze- tes (kvadratikus) átlagot.

A leggyakrabban használt mutató⁴, a számtani átlag, az a szám, amellyel egy n elemű sokaság összes egyedének értékét helyettesítve, azok értékösszege változatlan marad, vagyis

1 n

i i

x nx





Innen már egyszerűen megkapjuk a számtani átlag legegyszerűbb kiszámításához tartozó képletet:

1 n

i i

x

x n





A számtani átlagról tudjuk, hogy

 közepes, vagyis nem lehet kisebb az adatok minimumánál és nem lehet nagyobb a maxi- mumnál;

 lineárisan transzformálható, azaz a változók lineáris kombinációjának átlaga megegyezik az átlagok lineáris kombinációjával;

 négyzetes minimum tulajdonsággal rendelkezik.

A helyzeti középértékek a már említett medián, vagyis a középső érték és a módusz, ami a leggyako- ribb (leggyakrabban előforduló) értéket jelöli.

A mintapéldában az említett három középérték:

 a számtani átlag: x 20 251 ezer $;

 a medián: Me19 185 ezer $;

 a módusz : Mo20 200 ezer $.

Érdemes belegondolni, hogy az átlag meghatározásához szükségünk van az ún. értékösszegre is, ami nem más, mint az összes megfigyelt érték összege: a 120 kosárlabdázó esetén 2 430 138 ezer $, vagyis meghaladja a 2 400 milliárd $-t.

Megjegyzendő, hogy az ilyen kis elemszámú, rendkívül heterogén sokaságok esetén a módusz viszonylag kis előfordulási gyakoriságoknál keletkezik (esetünkben 9 játékosnak volt egyaránt 20 200 ezer $ a fizetése), ami ezen mutató felhasználását korlátozhatja.

4 A számtani átlag olyannyira elterjedt, hogy általában jelző nélkül használjuk, vagyis ha a későbbiekben csak átlagot írunk, a számtani átlagra gondolunk.

17 A középértékek rövid bemutatását lezárandó jegyezzük meg, hogy egy adott adatállományt célszerű mindhárom bemutatott mutatóval jellemezni, hiszen így elejét vehetjük az abból eredő félreérté- seknek, miszerint az átlag és a medián közepes, de nem feltétlenül tipikus, a módusz viszont tipikus, de nem feltétlenül közepes.

2.1.2 Szóródási mérőszámok

Adataink bemutatása nem állhat meg az egy (esetleg három) számértékkel történő tömör jellemzés- nél. Egyrészt, mivel az átlagok, illetve helyzeti középértékek egyike sem felel meg tökéletesen min- den kívánalomnak, másrészt mivel az egyedi adatokban rejlő információk éppen a tipikustól, az átlagostól, a várhatótól való eltérésben rejlenek. Érdemes ezért árnyalni a tömör információt azzal, ha a centrális tendenciát kifejező középérték mellett arra is kitérünk elemzésünkben, hogy mennyire homogén sokaságot képvisel az adott középérték.

Szóródásnak nevezzük a sokaság egyedeinek különbözőségét. Minél kevésbé szóródik egy adathal- maz, annál homogénebb, és ellenkezőleg, a heterogén sokaság szóródása nagy. A szóródás jelensé- gét számos mérőszámmal mérjük, itt csak a leggyakoribb mutatószámokra térünk ki.

A terjedelem (range), mint a szóródás legegyszerűbb mérőszáma, a legnagyobb és legkisebb ismérvér- ték különbsége. Ez az intervallum meghatározza azt az értékközt, amelyen belül az ismérvértékek szóródhatnak. Magától értetődő, hogy amennyiben valamennyi számérték azonos, a maximális és minimális érték is megegyezik, tehát az adott ismérv nem szóródik.

A terjedelem képlete:

max min

R x x (2.2)

A terjedelem könnyen számítható, jól értelmezhető mérőszám, azonban hátránya, hogy csak a szél- sőértékekre (minimumra, illetve maximumra) épít. Ezért egy-egy kiugró szélsőérték erősen befo- lyásolja nagyságát, ugyanakkor a szóródásról nem ad elegendő információt.

A szóródás leggyakrabban alkalmazott mérőszáma a szórás. Szórásnak nevezzük az átlagolandó ér- tékek számtani átlagtól való eltérésének négyzetes átlagát, vagy – más megfogalmazásban – a má- sodrendű centrális momentum négyzetgyökét. A szórás meghatározása a

 

1

1 ⁿ

i i

x x n 





 (2.3)

képlettel történik. Mivel tudjuk, hogy a számtani átlag rendelkezik a négyzetes minimum tulajdon- sággal, így a szórás mérőszámában zavaró szisztematikus torzító hatásra nem kell számítani.

A szórás négyzetét varianciának hívjuk. A variancia, noha önálló jelentéstartalommal nem bír, sok statisztikai eljárás központi mutatószáma.

A variancia képlete:

18

 

2 1

-

n i i

x x n





 (2.4)

A variancia mérőszámának fontos alkotóeleme az ún. eltérés-négyzetösszeg (Sum of Squares, SS) kife- jezés, amelynek átalakítása könnyen adódik

 

1 1

n n

i i

i i

SS x x x nx

 







Ebből tehát a variancia a négyzetes átlag négyzetének és a számtani átlag négyzetének a különbsége, amit a variancia átlagfelbontásának is nevezzük.

A szórás – a középértékekhez és a terjedelemhez hasonlóan – az eredeti változók mértékegységében fejezhető ki. Sok esetben azonban szükség lehet arra, hogy a mértékegységtől elvonatkoztassunk (mutatószámainkat skálafüggetlenné tegyük), és ezáltal könnyen összehasonlíthassunk különféle mértékegységekben mért jelenségeket, illetve azok szóródását. A mértékegységtől független, relatív jellegű szóródási mutatót, az ún. relatív szórást nyerjük, ha a szórást a számtani átlag százalékában mérjük (feltéve, hogy az átlag nem nulla!).

A relatív szórás:

V x

(2.5) Amelyről bebizonyítható⁵, hogy 0V  n1. Tehát ne lepődjünk meg azon, ha a relatív szórás mutatója esetleg 1-nél nagyobb érték lesz; ez rendkívül heterogén sokaságra utal!

A statisztikai elemzések során gyakran használatos az ún. korrigált szórás mutatója, amelynek leggya- koribb alkalmazási területe a következtetéses statisztika. A korrigált szórás kiszámításának képlete:

 

1

1

n i i

x x

s n





 



Könnyen beláthatóan a korrigált szórás némiképpen meghaladja (felülről közelíti) a szórást, ám különbségük nagy elemszám esetén elenyésző.

A mintapéldában szereplő adatállományban az említett szóródási mutatók az alábbiak szerint alakulnak:

 terjedelem: R20 123 ezer $;

 eltérés-négyzetösszeg: SS2 154 785 491;

 variancia: Var 17 956 546;

5 A bizonyítás lásd pl. Hajdu és mtsai. (1994)

19

 szórás:  4 238 ezer $;

 korrigált szórás: s4 255 ezer $;

 relatív szórás: V 20,9 %.

Az eredmények szerint a 120 kosárlabdázó fizetése átlagosan több mint 4 millió $-ral, azaz közel 21%-kal tér el az átlagfizetésüktől (szórás, illetve relatív szórás mutatója alapján). Érde- mes észrevennünk, hogy a mutatók egy része az eredeti, természetes mértékegységben (ese- tünkben ezer $-ban) keletkezik, a relatív szórás skála függetlenül %-os formában jelenik meg, ugyanakkor a variancia, illetve az eltérés-négyzetösszeg technikai szám, mértékegységüket nem értelmezzük!

2.1.3 Két speciális változó átlaga és szórása

A hagyományos mennyiségi ismérvek elemzése mellett érdemes röviden áttekintenünk két gyakran használt transzformációt, illetve a transzformáció eredményeként keletkezett változó átlagát és szó- rását. A két vizsgált adatművelet

 a skálafüggetlenség érdekében alkalmazott standardizálás, illetve

 az ismérvváltozatok számának drasztikus csökkentését eredményező bináris kódolás.

Azokban az esetekben, amikor különböző változók együttes elemzése a cél, sokszor szembesülünk azzal a problémával, hogy az ismérvek eltérő mértékegysége, illetve terjedelme megnehezíti össze- hasonlításukat. Ilyenkor alkalmazzuk a standardizálás műveletét, amikor az eredeti változóértékeket az alábbi transzformációval⁶ módosítjuk:

i i

x x

z 

  (2.7)

A transzformált változó átlaga és szórása könnyen számítható:

1 1 1

2 2

1 2 1

2

0

1

n n n

i

i i

i i i

n n

i i

i i

z

x x

z x nx

z n n n

x x

z SS

n z n n

  

 

   

  

 

   



  

  

 

     



  

 

vagyis a standardizált (mértékegység nélküli) változó átlaga 0, szórása 1.

Szintén gyakran kerül arra sor, hogy a vizsgált változó ismérvváltozatai közül számunkra csak egy a fontos (kitüntetett kimenet), ezért a változót kétállapotúvá, azaz binárissá kódoljuk.⁷ Ezt a válto-

6 A standardizált változóérték elterjedt angol elnevezése z-score, ezért is a jelölés.

7 Nyilván bizonyos minőségi ismérvek esetén eleve is csak két kimenetel képzelhető el (pl. szemüveges, vagy nem), ilyenkor nincs szükség kódolásra, de a továbbiak ugyanúgy érvényesek.

20 zót többféle néven említi a szakirodalom: Bernoulli változó, binomiális változó, fiktív változó, mes- terséges változó, dummy változó, vakváltozó stb. Az ilyen dummy változó mindössze két értéket ve- het fel: az 1-es érték valamilyen tulajdonság meglétét; a 0-s érték a tulajdonság hiányát jelöli. A bináris, dummy változónak sajátos a számtani átlaga és a szórása, amit az alábbiakban fejtünk ki.

Legyen D bináris változó két lehetséges ismérvértéke D₀ 0 és D₁ 1, az ezekhez rendelt gya- koriságok pedig f és ₀ f1! Tudjuk, hogy f₀ f₁ n.

A dummy változó számtani átlagaebből következően:

0 0 1 1 1

f f f

D p

n n

  

   (2.8)

amely megegyezik az 1-gyel jelzett ismérvváltozat relatív gyakoriságával. Az ismérv alternatív volta biztosítja, hogy a 0-val jelzett kimenetel relatív gyakorisága 1 p .

A bináris dummy varianciája az alábbi módon képezhető:

 

   

 

 

0 1

2 0 1 2

1 1 1

D

f p f p

p p p p p p

n

  

      



A variancia négyzetgyöke, vagyis a dummy változó szórása





D  p p

 (2.9)

amelyről roppant egyszerűen belátható, hogy akkor maximális, ha p0, 5. Mindez roppant logi- kus, hiszen korábban már kifejtettük, hogy a szórás a sokaság heterogenitását mutatja, és most azt kaptuk, hogy egy bináris változóval jellemzett populáció akkor a leginkább heterogén, ha benne mindkét ismérvváltozat fele-fele arányban fordul elő.

2.2 Kapcsolatszorossági vizsgálatok

A gazdasági jelenségek elemzése gyakran igényli annak megállapítását, vajon két vagy több lényeges statisztikai ismérv kapcsolatban áll-e egymással. Az ismérvek lehetnek egymástól függetlenek; köztük a kapcsolat lehet sztochasztikus, illetve függvényszerű (determinisztikus). A változók között tendenciasze- rűen, valószínűségi jelleggel érvényesülő összefüggést sztochasztikus kapcsolatnak nevezzük: any- nyit jelent, hogy egy egyednek az egyik ismérv egy adott ismérvváltozatához való tartozásából kö- vetkeztethetünk arra, hogy ez az egyed egy másik ismérv melyik változatához tartozik. Az esetek egy bizonyos százalékában azonban következtetésünk hibás lesz. Minél szorosabb az összefüggés a változók között, azaz minél közelebb áll a kapcsolat a függvényszerűhöz, annál kisebb a valószí- nűsége a tévedésnek. A fentiek alapján kézenfekvő, hogy a statisztikai módszertan megkísérli vala- milyen eszközzel az ismérvek közötti kapcsolatok szorosságát (illetve egyáltalán a kapcsolat meglé- tét) számszerűsíteni, ezáltal a következtetés hibáját mérsékelni, de legalábbis meghatározni.

21 A sztochasztikus kapcsolatok csoportosítása leggyakrabban a bennük szereplő ismérvek típusa alapján történik. Ennek megfelelően beszélhetünk asszociációs, vegyes és korrelációs kapcsolatról. Asz- szociációs kapcsolatnak a minőségi ismérvek; korrelációs kapcsolatnak a mennyiségi ismérvek kö- zötti kapcsolatot nevezzük; vegyesnek pedig azon kapcsolatokat, melyben mind minőségi, mind mennyiségi ismérvek szerepelnek.

Egy másik kézenfekvő csoportosítása a sztochasztikus kapcsolatoknak a bennük szereplő változók száma alapján történő osztályozás. Ennek megfelelően például a két ismérv közötti kapcsolatot kétváltozós, a három ismérv közötti összefüggést háromváltozós kapcsolatnak nevezzük (termé- szetesen a sor folytatható). A sztochasztikus kapcsolatok elemzése során felhasznált statisztikai módszereket két csoportba oszthatjuk:

 alapsokaság elemzését kapcsolatszorossági mérőszámokkal végezzük,

 minta elemzése során az ismérvek közötti kapcsolat szignifikáns voltát tesztelő hipotézisel- lenőrzési eljárásokat alkalmazunk.

Ebben az alfejezetben a leggyakrabban használt kapcsolatszorossági mérőszámokról lesz szó. Egy kapcsolatszorossági mérőszámtól elvárjuk, hogy

 abszolút értéke a 0 – 1 zárt intervallumban legyen,

 szélsőértékeit csak függetlenség, illetve determinisztikus kapcsolat esetén vegye fel,

 legyen monoton, azaz a szorosabb kapcsolathoz nagyobb abszolút értékű mutatószám tar- tozzon.

Az abszolút értéküket tekintve 0 és 1 közötti intervallumban értelmezett kapcsolatszorossági mé- rőszámok jól interpretálhatók: a 0 a függetlenséget, az 1 a függvényszerű kapcsolatot jelenti, a köz- tes értékek sztochasztikus kapcsolat meglétét mutatják. Egy sztochasztikus kapcsolatot gyengének tartunk, ha a mutató abszolút értéke 0,3 alatt van, az erős összefüggést az mutatja, ha a mérőszám abszolút értéke 0,7 felett található.

A társadalmi-gazdasági elemzések során gyakran szembesülünk olyan kérdéssel, melyben nem csu- pán kettő ismérv kapcsolatát kell elemeznünk. A kettőnél több változót tartalmazó összefüggések esetében a sztochasztikus kapcsolatokat számszerűsítő mutatószámoknak három típusát különböz- tethetjük meg, annak alapján, hogy milyen mértékben használják ki az összes vizsgálatba vont vál- tozóban rejlő információt. Így beszélhetünk^:

 totális együtthatókról, amelyekkel csak két változó összefüggését elemezzük úgy, hogy telje- sen figyelmen kívül hagyjuk a vizsgálatba vont további változó(k) hatását,

 parciális mutatókról, melyekkel két változó összefüggését úgy vizsgáljuk, hogy „kiszűrjük” a vizsgálatban szereplő összes többi változó hatását,

 többszörös együtthatóról, mellyel a vizsgálatban szereplő összes változónak a kapcsolatát számszerűsítjük.

Az előbbiekből következik, hogy amennyiben vizsgálatunkban mindössze két változó szerepel, úgy ezek között mindig totális kapcsolatszorossági együtthatót használunk.

22 2.2.1 Asszociációs kapcsolat szorosságának mérése

Az asszociációs kapcsolat mérése kombinációs gyakorisági (ún. kontingencia) táblázat alapján tör- ténik. A kontingencia táblázat általános sémája:

A ismérv vál- tozatai

B ismérv változatai

Összesen

B1 B₂ B_b B_o

A1 f₁₁ f₂₁ f1b f_1o f1.

A2 f₂₁ f22 f2b f_2o f_2.

Aa f_a1 fa2 f_ab f_ao fa.

As f_s1 fs2 f_sb f_so f_s.

Összesen f.1 f.2 f.b f.o n

2-2. táblázat: Kontingencia táblázat

Ismeretes, hogy amennyiben az A és B ismérvek függetlenek egymástól, akkor annak valószínűsége, hogy egy egyed az A és a _a B ismérvváltozattal jellemezhető, kifejezhető a peremvalószínűségek _b szorzataként, vagyis

. .

a b

ab

f f

p  n  n

Ebből meghatározhatók a függetlenség esetére vonatkozó feltételezett gyakoriságok:

. .

a b

ab

f f

f n

 

 (2.10)

Amennyiben az ismérvek nem függetlenek egymástól, akkor a tényleges gyakoriságok eltérnek a (2- 10) képletekben meghatározottaktól. Ezen eltérések annál nagyobbak, minél távolabb van a kap- csolat a függetlenségtől. A fentiekből kiindulva megszerkeszthetjük a négyzetes kontingencia mutatóját:

 

2

1 1

s o ab ab

a b ab

f f

f



  

   

 (2.11)

A mutató értéke a ^{0  2}





   

2

min , 1

C s o n

 

 (2.12)

23 ami már a 0 és 1 közötti zárt intervallumban található, és alkalmas az asszociáció szorosságának mérésére.

Tekintsük a következő egyszerű példát! Egy egyetemi évfolyam 250 hallgatójából 150 lány, akik közül 100-an rendszeresen sportolnak. A fiúk közül 80-an sportolnak rendszeresen. Az adatok az alábbi nagyon egyszerű táblázatba rendezhetők:

Hallgató neme Sportolási szokások

Rendszeresen Nem rendszeresen Összesen

Lány 100 50 150

Fiú 80 20 100

Összesen 180 70 250

Kiszámítható a négyzetes kontingencia:

2 2

2

180 150 70 100

100 20

250 250

180 150 70 100 5, 3

250 250

 

     

   

   

    

 

Amiből meghatározható a Cramer-mutató

2 1^5,9 250 ^0,145

C  

  ami gyenge kapcsolatra utal.

A minőségi ismérvek közötti kapcsolatnak számos további mérőszáma ismert, ezek jelentős része a négyzetes kontingencia mutatójára épül.

2.2.2 Vegyes kapcsolat elemzése

A gyakorlati elemzések során gyakran merül fel annak az igénye, hogy különböző típusú – minőségi és mennyiségi – ismérvek egymás közötti kapcsolatát elemezzük. Ez annyit jelent, hogy megkísé- reljük a kvalitatív ismérv alapján képzett csoportok kvantitatív ismérv szerinti különbözőségét számszerűsíteni, a változók közötti kapcsolat szorosságát megállapítani.

A vegyes kapcsolat elemzése az ún. varianciaanalízis-modellre épül. Legyen a minőségi ismérv szerinti a-adik csoport i-edik eleme az alábbi módon felírva

ai a ai

x     x (2.13)

vagyis x a sokaság egészére vonatkozó átlag, az a-adik csoporthoz tartozó csoporthatás és az _ai adott elemhez tartozó egyedhatás összege. Ha az utóbbi két komponenst így definiáljuk

a a

ai ai a

x x

x x

  

  

24 vagyis a csoporthatás a csoportátlag eltérése a főátlagtól és az egyedhatás az adott megfigyelés elté- rése a saját csoportátlagától, akkor a (2.13) összefüggés triviálisan teljesül. Elvégezve az ún. eltérés- négyzetösszeg dekomponálást, felírhatjuk, hogy

 

   

 

 

1 1 1 1 1 1 1

a a a

n n n

s s s s

ai a ai a a ai a

a i a i a a i

x x x x x x x x x x

      

          

   

ami a szokásos jelölésekkel

K B

SS SS SS (2.14)

vagyis a teljes eltérés-négyzetösszeg a csoportok közötti, illetve a csoportokon belüli eltérés-négy- zetösszegek összege.

A vegyes kapcsolat szorosságát a szóráshányados méri:

K 1 B

SS SS

H  SS   SS (2.15)

A kapcsolatszorossági mérőszám négyzetét (H²) magyarázó erőként értelmezzük.

Példaként elemezzük a következő fiktív adatállományt! Egy országban néhány látványcsapat- sport bajnokságra vonatkozó nézőszámok az alábbi jellemzőkkel rendelkeznek:

Jellemző Sportág

Labdarúgás Kézilabda Kosárlabda Csapatok száma a bajnokságban

Átlagos nézőszám A nézőszám szórása

20 10 000

2 000

12 4 000 1 500

10 2 500 1 000

Mivel a kapcsolatban minőségi (sportág) és mennyiségi (nézőszám) ismérv is szerepel, így ve- gyes kapcsolatról van szó. A kapcsolat szorosságának vizsgálatát a szóráshányados mutatója alapján végezzük el. Ennek számítása:

20 10 000 12 4 000 10 2 500

6 500 20 12 10

x       

 

 

 

 

20 10 000 6 500 12 4 000 6 500 10 2 500 6 500 480 000 000

SSK       

2 2 2

20 2 000 12 1500 10 1000 117 000 000

SSB      

2

480 000 000

0,897 480 000 000 117 000 000

0,801 H

H

 





25 A fentiek alapján tehát megállapítható, hogy a sportág és a nézőszám között szoros sztochasz- tikus kapcsolat található, a sportág szerinti hovatartozás a nézőszám szerinti szóródás 80%-át magyarázza meg.

A vegyes kapcsolat elemzésének lényegesen összetettebb módozatai is ismertek (többutas varian- ciaanalízis, diszkriminancia-analízis), azonban ezek bemutatásától most terjedelmi okok miatt elte- kintünk.

2.2.3 Korrelációs mérőszámok

A mennyiségi ismérvek közötti összefüggést korrelációs kapcsolatnak nevezzük. Az ilyen kapcsolat vizsgálata során alkalmazott eljárások lényegesen különböznek a korábban bemutatott asszociációs és vegyes kapcsolat elemzésére használt módszerektől, mivel a mennyiségi ismérvek általában in- tervallum-, illetve arányskálán mérhetők, így esetükben nemcsak az ismérvváltozatok különböző- ségét, hanem a különböző változóértékek távolságát, hányadosát is értelmezhetjük.

A korrelációs kapcsolat alapvetően a következő két, lényeges kérdésben tér el a korábban tárgyalt sztochasztikus kapcsolatoktól:

 a kapcsolatnak értelmezzük az irányát: pozitívnak nevezzük, ha az egyik változó növekedése a másik növekedését vonja maga után, illetve a csökkenés csökkenést eredményez, valamint negatívnak, ha a két ismérv változása ellentétes irányú,

 a szorosság mellett a kapcsolat jellege is lényeges: megkülönböztetünk lineáris, monoton, illetve változó irányú kapcsolatokat.

A leggyakrabban alkalmazott korrelációs mérőszámok a

 lineáris kapcsolat esetén használatos lineáris korrelációs együttható,

 monoton kapcsolat esetén alkalmazott Spearman-féle rangkorrelációs együttható.

A lineáris korrelációs kapcsolat mérése a kovariancia mutatójára épül. Ismeretes, hogy a kovariancia elsőrendű vegyes, centrális momentum, melynek⁸ képlete:







1 12

n

i i

i

x x x x

C n



 





A kovariancia mutatója jól hasznosítható a mennyiségi ismérvek közötti kapcsolat irányának meg- állapítása során, hiszen a mutató értéke pozitív, ha az egyes változók saját átlaguktól való eltérésé- nek iránya megegyezik; és negatív fordított esetben. Mivel a kovariancia abszolút értéke nem lehet nagyobb a két változó szórásának a szorzatánál, ezért viszonylag egyszerűen nyerjük a lineáris korre- lációs együtthatót:

8 A továbbiakban a kétváltozós lineáris kapcsolatok vizsgálata során az általános adatállomány első és második válto- zójával példálózunk, ezzel nem sértve semmilyen általánosítást.

26

1 2

12 12

x x

r  C

  (2.17)

amely teljesíti a kapcsolatszorossági mérőszámokkal szemben támasztott követelményeket.

Abban az esetben, ha a mennyiségi ismérvek közötti kapcsolat nem egyenesvonalú, de feltételez- hető, hogy monoton, a (2.17) képlet alapján számított korrelációs együttható torzít. Ezért ilyenkor az eredeti változóértékek helyett azok rangszámaival (rangsorban elfoglalt helyével) számolunk, az intervallum-skálát ordinális skálává egyszerűsítve. A rangszámokból számított lineáris korrelációs együttható a Spearman-féle rangkorrelációs együttható, melynek képlete

 

 

1 2

1

12 2

6

1

n

x x

i i

i

R R

n n





  



ahol R_i^x1,R_i^x2 az i-edik megfigyelés x₁, illetve x₂ változó szerinti rangszáma (rangsorban elfoglalt helyezése).

Kettőnél több mennyiségi ismérv kapcsolatának elemzése a korrelációs mátrixon alapul. A mátrix a kétváltozós (totális) korrelációs együtthatókat tartalmazza:

11 12 1

21 22 2

1 2

k k

k k kk

r r r

r r r

r r r

 

 

 

  

 

 

R

Kihasználva, hogy a változók önmagukkal mért korrelációja értelemszerűen 1 és a korrelációs együttható szimmetrikus, a mátrixot általában a következő egyszerűbb alakban írjuk fel:

21

1 2

1 1

k k 1

r r r

 

 

 

  

 

 

R

A korrelációs mátrix segítségével kiszámíthatók a többváltozós kapcsolat esetében fontos parciális, illetve többszörös mutatószámok is. Legyen Q mátrix a korrelációs mátrix inverze, azaz

1

qij ^

  

Q R , ekkor az első és a második változó közötti parciális korrelációs együttható felírható

12 12.3 ,

11 22 k

r q

q q

  (2.19)

formában. A parciális korrelációs együtthatók megmagyarázzák, hogy milyen szoros a kapcsolat két tetszőlegesen választott változó között, ha kiszűrjük az összes többi változó hatását.

27 Szintén a korrelációs mátrix inverzének felhasználásával számíthatjuk ki a többszörös korrelációs együtt- hatót, melyet R -rel jelölünk. Például az első változóra vonatkoztatva

11

1 1

R  q (2.20)

megmutatja, hogy az adatállomány összes többi változója milyen szoros kapcsolatban áll a kiválasz- tott változóval. A mutatónak inkább a négyzete, az ún. többszörös determinációs együttható hasz- nálatos, ez ugyanis megmutatja, hogy az adatállomány változói együttesen milyen mértékben képe- sek megmagyarázni a kiválasztott változó szóródását.

Mivel a könyv nagy részében korrelációs kapcsolatot vizsgálunk, az előbbi mérőszámokra itt nem mutatunk példát.

2.3 Trendelemzés

Abban az esetben, ha a korábban bemutatott adatállományunk idősoros szemléletű, megfigyelése- inket időpontok alkotják. Alkalmazzuk ilyenkor a vizsgálandó jelenséget leíró idősorok általános jelölésére az y szimbólumot, ahol az index mutatja, hogy éppen a t-edik időpillanathoz tartozó _t adatot vizsgáljuk (t 1, 2, ,T ). Külön figyelmet érdemelnek azon idősorok, melyeknél megfigye- léseink évnél kisebb egységre (negyedévre, hónapra, dekádra, napra, napon belül órára, stb.) vonat- koznak. Az ilyen idősorok esetében alkalmazhatjuk – az előbbiek analógiájára – a y_{t j,} jelölést, ahol az első index jelöli a vizsgált évet, a második index pedig az éven belüli kisebb naptári egységet. A gazdasági életben használt empirikus idősorok legtöbbjeinél a megfigyelt érékek azonos távolságra vannak egymástól (tehát éves, negyedéves, vagy havi bontású idősorokat vizsgálunk). Az ilyen idő- sorokat ekvidisztánsnak nevezzük, és a továbbiakban – ha csak az ellenkezőjét nem említjük – ilye- nekkel foglalkozunk.

Az idősor-elemzés kiindulópontja a jelenségben tartósan meglevő alaptendencia (trend) kimutatása.

Legáltalánosabban megfogalmazva a t-edik időpillanathoz tartozó megfigyelés a trend szerint a vár- ható érték és egy véletlen tag eredőjeként állítható elő:

t ˆt t

y  y  (2.21)

ahol ˆy az alapirányzat szerint a t-edik megfigyeléshez tartozó érték, _t _t pedig a véletlen ingadozás ugyanezen megfigyeléshez tartozó konkrét értéke. Véletlennek tekintjük a teljesen váratlanul bekö- vetkező események (pl. földrengés, háború, válság) hatását, de ugyanígy itt, a véletlen tagban jelen- nek meg a modellből kihagyott jelenségek hatásai is.

Abban az esetben, ha a jelenség alakulásában nem lenne semmilyen tendencia, az előbbi összefüg- gés a y_t  y _t formára redukálódna, vagyis az alapirányzat szerinti érték minden esetben azonos, az idősor átlagával megegyező érték lenne. Ugyanakkor az elemzésre érdemes idősoraink sokszor