Műszaki és természettudományos alapismeretek tananyagainak fejlesztése a mérnökképzésben
Pályázati azonosító: TÁMOP-4.1.2.A/1-11/1-2011-0054
Hajba Tamás, Harmati István, Környei László, Szalay Krisztina SZE-MTK, Matematika és Számítástudomány Tanszék
Valószínűség-számítás és matematikai statisztika
2013. május 31.
c
COPYRIHGHT: Hajba Tamás, Harmati István, Környei László, Szalay Krisztina
Széchenyi István Egyetem, M˝uszaki Tudományi Kar, Matematika és Számítástudomány Tanszék Lektor: Dr. Kovács Gergely;
Dr. Kárász Péter, Óbudai Egyetem Neumann János Informatikai Kar, egyetemi docens Creative Commons NonCommercial-NoDerivs 3.0 (CC BY-NC-ND 3.0)c
A szerz˝o nevének feltüntetése mellett nem kereskedelmi céllal szabadon másolható, terjeszthet˝o, megjelentethet˝o és el˝oadható, de nem módosítható.
ISBN 978-963-7175-95-4
Kiadó: Széchenyi István Egyetem, M˝uszaki Tudományi Kar Támogatás:
Készült a TÁMOP-4.1.2.A/1-11/1-2011-0054 számú, "M˝uszaki és természettudományos alapismeretek tananyagainak fejlesztése a mérnökképzésben" cím˝u projekt keretében.
Kulcsszavak: valószín˝uségszámítás, valószín˝uség-számítás, a valószín˝uség-számítás axiómái, feltételes valószín˝uség, diszkrét eloszlás, folytonos eloszlás, valószín˝uségi vektorváltozó, nagy számok törvényei, központi határeloszlás tétel, matematikai statisztika, hipotézisvizsgálat, statisztikai próba
Tartalmi összefoglaló: A jegyzet a m˝uszaki alapképzésben (BSC) oktatott Valószín˝uség-számítás és matematikai statisztika tantárgy anyagát öleli fel. A tananyag feldolgozásához szükséges a középszint˝u érettségi anyagán túl az Analízis, illetve a Lineáris algebra és többváltozós függvények tárgy ismerete. A jegyzet tagolása, a nagy számú részletesen kidolgozott feladat és önellen˝orz˝o kérdés el˝osegíti a tananyag önálló feldolgozását is.
Tisztelt Olvasó!
Tananyagunkat interaktív részeket és bels˝o hivatkozásokat is tartalmazó PDF formátumban készítettük el.
Kiderült azonban, hogy technikai okokból ez a teljes verzió a Tankönyvtár.hu weblapra nem tud felkerülni, épp az interaktív elemek miatt. Ezért a jegyzetb˝ol két változat készült:
• On-line változat: A tankonyvtar.hu-ról elérhet˝o, honlapról olvasásra szánt verzió.
• Teljes változat: A Széchenyi István Egyetem e-learning szerverér˝ol letölthet˝o, interaktív elemeket is tartalmazó, teljes változat. (https://elearning.sze.hu/moodle/course/view.php?id=12)
Ön most az on-line változatot olvassa.
A kétféle verzió tartalmában teljesen azonos, csak az on-lineból hiányoznak a teljes képerny˝os eset navigáló ikonjai, bizonyos bels˝o linkek és az interaktív önellen˝orz˝o részek sem m˝uködnek.
Ezért azt ajánljuk, hogy a tananyaggal való ismerkedésre használja az on-line változatot, mert ezt minden, internet-kapcsolattal rendelkez˝o gépr˝ol eléri, de ha elmélyülten szeretné a kapcsolódó tárgyat tanulni, akkor töltse le saját gépére a teljes változatot és azt saját gépén tárolva az AcrobatReader (Adobe Reader) program segítségével teljes képerny˝os módban olvassa.
Gy˝or, 2014. június 2.
Dr. Horváth András szakmai vezet˝o
Ez a tananyag egyelektronikus jegyzet.
2013-ban, a megjelenés évében annyira elterjedtek az elektronikus tartalomfogyasztásra alkalmas eszközök, hogy bátran feltételezhetjük: az egyetemisták túlnyomó többsége rendelkezik saját számítógéppel, tablet-géppel vagy elektronikus könyvolvasóval. A tananyag elektronikus formája sok el˝onnyel rendelkezik a nyomtatotthoz képest:
• Aktív tartalmak: az elektronikus változatban bels˝o kereszthivatkozások, küls˝o linkek, mozgóképek, stb.
helyezhet˝ok el. A tartalomjegyzék fejezetszámai, az egyenlet- és ábrasorszámok automatikusan bels˝o linket jelentenek, így biztosítják a kényelmes és gyors bels˝o hivatkozást, de a Szerz˝o tetsz˝oleges helyre tud akár a dokumentum belsejébe, akár egy küls˝o webhelyre mutató linket elhelyezni, ami a szokásos klikkentéssel aktivizálható.
• Rugalmasság: a nyomtatott könyv statikus, míg az elektronikus jegyzet esetében könny˝u hibajavításokat, frissítéseket alkalmazni.
• Er˝oforrás-takarékosság, környezetvédelem: az elektronikus formában való terjesztés sokkal kisebb terhelést jelent a környezetre, mint a nyomtatott. Különösen igaz ez, ha a tananyagban sok a színes ábra.
A használt fájlformátum: PDF.
A Portable Document Format az Adobe által kifejlesztett formátum, mely igen széles körben elterjedt. Sok helyr˝ol szerezhetünk be programot, mely a PDF fájok olvasására alkalmas. Ezek egy része azonban nem tartalmazza a teljes szabvány minden elemét, ezért speciális tartalmak nem, vagy nem pontosan jelenhetnek meg, ha nem az Adobe olvasóját, az AdobeReader-t használjuk. (Letölthet˝oinnen.)
A legtöbb megjelenít˝oprogram jól fogja kezelni az alapszöveget, ábrákat és linkeket, de gondok lehetnek a speciálisabb funkciókkal, pl. a beágyazott dokumentumok kezelésével, az aktív tesztek, kérd˝oívek használatával.
A jegyzetképerny˝on való megjelenítésrelett optimalizálva.
A jelenlegi általánosan elérhet˝o könyvolvasó hardverek mérete és felbontása kisebb, mint a nyomtatott könyveké és a számítógépek monitorai általában fektetett helyzet˝uek. Ehhez igazítottuk a formátumot arra optimalizálva, hogy fektetett kijelz˝on teljes képerny˝os üzemmódban lehessen olvasni. Ehhez állítottuk be a karaktertípust és -méretet valamint azt is, hogy csak kis margót hagyunk, minél több pixelt biztosítva ezzel a tartalomnak. Azért, hogy teljes képerny˝os üzemmódban is lehessen navigálni, a margón kis navigáló-ikonokat helyeztünk el, melyek a megszokott módon kezelhet˝ok:
• Lapozás el˝ore és hátra: a függ˝oleges oldalak közepén elhelyezett, nyújtott nyilakkal.
• Címoldalra ugrás: kis házikó szimbólum a bal fels˝o sarokban.
• Vissza és el˝oreugrás a dokumentumban: két kicsi szimbólum a bal fels˝o részen. Ezek nem azonosak a lapozással, hanem a web-böngész˝ok vissza- és el˝orelépéséhez hasonlóan a hiperlinkeken való navigálást szolgálják.
A jegyzetsegítséget nyújt a tanulás ütemezésében.
A megtanulandó tanagyag a szokásos fejezet-alfejezet felosztáson túl leckékre való bontást is tartalmaz. A leckék különböz˝o számú alfejezetb˝ol állhatnak, de közös bennük, hogy a Szerz˝o megítélés szerint egy lecke
„egyült˝o helyben” megtanulható, azaz várhatóan 1–1,5 óra alatt feldolgozható.
A leckék elején rövid leírás található a tárgyalt témakörökr˝ol, a szükséges el˝oismeretekr˝ol, a végén pedig önellen˝orz˝o kérdések, melyek sok esetben a PDF fájlban (AdobeReader-rel) aktív tartalomként jelennek meg feleletkiválasztós teszt, számszer˝u vagy képletszer˝u kérdés formájában. Érdemes tehát leckénként haladni a tanulásban, mert ez segít az ütemezés tervezésében illetve a leckevégi ellen˝orzések segítenek annak eldöntésében, tovább szabad-e haladni vagy inkább ezt vagy az el˝oz˝o leckéket kell újra el˝ovenni.
Ha a tananyag indokolja, nagyobb egységeket „modulokba” szervezünk és a modulok végén a leckevégi önellen˝orzéshez képest komolyabb feladatblokkot találhatunk.
1. Bevezet˝o
I. MODUL | A valószín ˝uség-számítás alapjai
1. lecke
2. A valószín˝uség-számítás axiómái
2.1. Események, m˝uveletek eseményekkel 2.2. A valószín˝uség-számítás axiómái
2.3. Az axiómák egyszer˝ubb következményei
2. lecke
3. A klasszikus és a geometriai valószín˝uségi mez˝o 3.1. A klasszikus valószín˝uségi mez˝o
3.1.1.Kombinatorika
3.1.2.Visszatevéses és visszatevés nélküli mintavétel
3. lecke
3.2. A geometriai valószín˝uségi mez˝o
4. lecke
4. Feltételes valószín˝uség, függetlenség 4.1. Feltételes valószín˝uség
4.2. A teljes valószín˝uség tétele és a Bayes-tétel 4.3. Események függetlensége
5. lecke
5. Modulzáró feladatok
II. MODUL | A valószín ˝uségi változó és jellemz ˝oi
6. lecke
6. A valószín˝uségi változó 6.1. A valószín˝uségi változó
6.1.1.Diszkrét valószín˝uségi változó 6.1.2.Folytonos valószín˝uségi változó 6.2. Az eloszlásfüggvény
7. lecke
6.3. A s˝ur˝uségfüggvény
8. lecke
7. A várható érték és a szórás
7.1. Diszkrét valószín˝uségi változó várható értéke 7.2. Folytonos valószín˝uségi változó várható értéke
9. lecke
7.3. A szórás
10. lecke
8. Modulzáró feladatok
11. lecke
9. Nevezetes diszkrét eloszlások 9.1. Az indikátor változó eloszlása 9.2. Binomiális eloszlás
9.3. Hipergeometriai eloszlás
12. lecke
9.4. Geometriai eloszlás
9.5. Negatív binomiális eloszlás 9.6. Poisson-eloszlás
13. lecke
10.Nevezetes folytonos eloszlások 10.1.Egyenletes eloszlás
10.2.Exponenciális eloszlás 10.3.Normális eloszlás
10.3.1.Standard normális eloszlás
14. lecke
11.Kapcsolatok a nevezetes diszkrét eloszlások között (határeloszlás tételek) 11.1.A hipergeometriai eloszlás közelítése binomiális eloszlással
11.2.A binomiális eloszlás közelítése Poisson-eloszlással
15. lecke
12.Modulzáró feladatok
IV. MODUL | Valószín ˝uségi változók viszonyának jellemzése
16. lecke
13.Valószín˝uségi változó függvényének eloszlása
13.1.Diszkrét valószín˝uségi változó függvényének eloszlása
17. lecke
13.2.Folytonos valószín˝uségi változó függvényének eloszlása
18. lecke
13.3.Valószín˝uségi változó függvényének várható értéke és szórása
19. lecke
14.Több valószín˝uségi változó együttes eloszlása
14.1.Két diszkrét valószín˝uségi változó együttes eloszlása 14.2.Diszkrét valószín˝uségi változók függetlensége
20. lecke
14.3.Két valószín˝uségi változó együttes eloszlásfüggvénye
21. lecke
14.4.Két folytonos valószín˝uségi változó együttes s˝ur˝uségfüggvénye 14.5.Folytonos valószín˝uségi változók függetlensége
22. lecke
14.6.Több valószín˝uségi változó együttes eloszlása
23. lecke
15.Valószín˝uségi változók összege és átlaga
15.1.Valószín˝uségi változók összegének és átlagának várható értéke
24. lecke
15.2.Független valószín˝uségi változók szorzatának várható értéke
25. lecke
15.3.Független valószín˝uségi változók összegének és átlagának szórása
27. lecke
16.Modulzáró feladatok
V. MODUL | Egyenl ˝otlenségek
28. lecke
17.A Markov- és a Csebisev-egyenl˝otlenség 17.1.A Markov-egyenl˝otlenség
29. lecke
17.2.A Csebisev-egyenl˝otlenség
30. lecke
18.A nagy számok törvényei
18.1.A nagy számok törvénye az átlagra
31. lecke
18.2.A nagy számok törvénye a relatív gyakoriságra
32. lecke
19.Modulzáró feladatok
VI. MODUL | Határeloszlás tételek
20.Határeloszlás tételek
33. lecke
20.1.A de Moivre–Laplace-tétel
34. lecke
20.2.A központi határeloszlás tétel
35. lecke
21.Modulzáró feladatok
VII. MODUL | Matematikai statisztika
36. lecke
22.A matematikai statisztikában használatos eloszlások 22.1.Aχ2 eloszlás
22.2.A Student-eloszlás 22.3.F-eloszlás
37. lecke
23.A matematikai statisztika alapfogalmai 23.1.Statisztikai minta, statisztikai függvények 23.2.Hisztogramok
23.3.Konfidencia (megbízhatósági) intervallumok
38. lecke
24.Hipotézisvizsgálat
24.1.Statisztikai hipotézisek 24.2.A statisztikai próba menete
24.2.1.A statisztikai próba elméleti lépései 24.2.2.A statisztikai próba gyakorlati lépései 24.3.Hibalehet˝oségek
25.1.Várható értékre vonatkozó egymintás próbák 25.1.1. Egymintás u-próba
25.1.2. Egymintást-próba
40. lecke
25.1.3.Kétmintás u-próba 25.1.4.Kétmintás t-próba
25.2.Szórások egyenl˝oségére vonatkozó próba 25.2.1.F-próba
41. lecke
26.Nem-paraméteres próbák 26.1.Aχ2-próba
26.1.1.Illeszkedésvizsgálat 26.1.2.Homogenitásvizsgálat 26.1.3.Függetlenségvizsgálat
42. lecke
27.Modulzáró feladatok
43. lecke
Feladatok megoldása
1. Bevezet˝o
A valós életben lépten-nyomon találkozunk olyan eseményekkel, melyek kimenetelét el˝ore nem tudjuk teljes magabiztossággal megmondani, de a mindennapi életünket jelent˝os mértékben befolyásolják. Bizonytalan, el˝ore pontosan nem meghatározható ideig tart egy vásárlás, nem tudjuk el˝ore, hogy hányan fognak el˝ottünk sorban állni a postán, a munkahelyre való eljutáshoz szükséges id˝o sem jósolható meg teljes biztonsággal, még ha a megszokott útvonalon haladunk is.
A m˝uszaki alkalmazások területén is b˝oségesen el˝ofordulnak a fentiekhez hasonló véletlen jelenségek. Ilyen lehet például egy termék élettartama, valamely mérés pontatlansága, egy forgalmi csomóponton adott id˝o alatt áthaladó járm˝uvek száma, helyi tömegközlekedésben résztvev˝o autóbusz utasainak száma egy adott pillanatban, az autóbusz tényleges menetideje, egy telefonvonal leterheltsége egy adott id˝oszakban, a hibás pixelek száma egy monitoron stb.
A valószín˝uség-számítás témája véletlen tömegjelenségekre vonatkozó törvényszer˝uségek megállapítása.
Véletlen jelenségne azt nevezzük, aminek a kimenetelét a tekintetbe vett, vagy az ésszer˝uség határain belül tekintetbe vehet˝o, rendelkezésre álló feltételek még nem határozzák meg egyértelm˝uen. Tömegjelenségen olyan jelenséget értünk, amely nagy számban megy végbe egyszerre, vagy (legalábbis elméletben) tetsz˝olegesen sokszor megismételhet˝o. Az ezekb˝ol levonható törvényszer˝uségek statisztikai jelleg˝uek, azaz nagy számú végrehajtás során átlagosan érvényes törvények.
A jegyzet hét nagyobb részre, modulra tagolódik, melyek egy-egy nagyobb anyagrészt ölelnek fel. A modulok fejezetekre, azok pedig leckékre tagolódnak. Az egyes leckékben megjelen˝o tananyag nagyságát úgy alakítottuk ki, hogy annak megértése, feldolgozása másfél-két óra alatt lehetséges legyen. A matematikai témájú egyetemi tankönyvekben megszokottDefiníció,Tétel,Bizonyításhármas mellett a következ˝o tartalmi elemek is megjelenek:
• Önálló feladat: A lecke mélyebb megértését el˝osegít˝o ellen˝orz˝o feladatok, melyek megoldása nem szerepel a jegyzetben.
• Érdekesség: A lecke elméleti anyagához kapcsolódó, a valós életb˝ol származó példák.
• Aktivitás: Önállóan (sokszor a gép mell˝ol felkelve) elvégzend˝o, általában nem a szokásos matematikai feladatmegoldást igényl˝o, gyakran kísérletek, megfigyelések elvégzését követel˝o feladatok.
Minden lecke végén található egy-egy rövid feladatsor (Ellen˝orz˝o kérdések). A feleletválasztós kérdéseknél a helyesnek gondolt válasznak megfelel˝o négyzetbe kell kattintani, a válaszadás után látszik, hogy a válasz jó volt-e. A számítási feladatok végeredményét a feladat után szerepl˝o téglapba kell beírni, a magyar szokásoktól eltér˝oen nem tizedesvessz˝ovel, hanem ponttal (ezután a biztonság kedvéért nyomjuk meg az Enter-t is). A helyes válasz az Ans gombra kattintva tekinthet˝o meg.
A nagyobb anyagrészeket felölel˝o modulokatModulzáró feladatsorzárja. A helyes válaszok itt már nem jelennek meg, csak a teszt kitöltése végén jelenik meg a helyes válaszok száma.
I. MODUL
A valószín ˝uség-számítás alapjai
1. LECKE
Eseményalgebra
1. lecke 1. oldal
2. A valószín˝uség-számítás axiómái 2.1. Események, m˝uveletek eseményekkel
Kísérlet alatt egy véletlen tömegjelenség megfigyelését értjük. Tekintsünk egy ilyen kísérletet. Ennek egy lehetséges kimenetele az elemi esemény. Az egy kísérlethez tartozó elemi események összessége azeseménytér, amelyetΩ-val jelölünk. Az eseménytér részhalmazaiteseményeknek nevezzük. Az esemény definíciója szerint az elemi események egyetlen elemet tartalmazó események. Ha egyAeseményre vonatkozóan kísérletet végzünk, és a kísérlet során adódó aelemi esemény eleme azA-nak (a ∈ A), akkor azt mondjuk, hogy az Aesemény bekövetkezik.
Példa: Dobjunk fel egy dobókockát. Ennek a kísérletnek hat lehetséges kimenetele van, így az eseménytér Ω ={1,2,3,4,5,6}.
LegyenA az az esemény, hogy 7-nél kisebbet dobunk,B az, hogy nyolcast dobunk, C az, hogy 3-nál kisebbet dobunk,Daz, hogy kettest dobunk, mígEaz, hogy legalább négyest dobunk. Ekkor
A={1,2,3,4,5,6}, B=∅, C={1,2}, D={2}, E ={4,5,6}.
Látszik, hogy az A esemény a kísérlet minden kimenetele esetén bekövetkezik. Az ilyen eseményt biztos eseménynek nevezzük. Mivel a biztos esemény az összes elemi eseményt tartalmazza, ezért a biztos eseményt isΩ-val jelöljük. AB esemény viszont sosem következik be; az ilyen eseményt lehetetlen eseménynek nevezzük és (mivel egyetlen elemi eseményt sem tartalmaz)∅-zal jelöljük.
Figyeljük meg továbbá, hogy aDesemény bekövetkezése esetén aCesemény is bekövetkezik, míg aDés azE események nem tudnak egyszerre bekövetkezni (kizárják egymást).
Ha az A és B esemény egyszerre sohasem következik be, akkor az A és B eseményeket egymást kizáró eseményeknek nevezzük. Halmazokkal kifejezve ez azt jelenti, hogyA∩B=∅.
Az el˝oz˝o oldali példában aC(3-nál kisebbet dobunk) és E (legalább 4-est dobunk) egymást kizáró események.
A B
Ω 2.1. ábra. Egymást kizáró események.
Ha azAesemény bekövetkezésekor minden esetben egy másik, B esemény is bekövetkezik, akkor azt mondjuk, hogy azAesemény bekövetkezése maga után vonja aB esemény bekövetkezését. Halmazokkal kifejezve ez azt jelenti, hogyArészhalmazaB-nek, azazA⊂B.
Az el˝oz˝o oldali példában aCesemény (kettest dobunk) bekövetkezése maga után vonja a D esemény (3-nál kisebbet dobunk) bekövetkezését.
A B
Ω
2.2. ábra. AzAesemény maga után vonjaB-t.
Aktivitás:Írjon fel a füzetébe a kockadobással kapcsolatosan három, egymást páronként kizáró eseményt!
Az események között (a halmazm˝uveletekhez hasonlóan) az alábbi m˝uveleteket értelmezzük:
1. lecke 3. oldal
Az A és B események A +B összege az az esemény, amely akkor következik be, ha az A és B események közül legalább az egyik bekövetkezik.
Példa: Legyen az A esemény, hogy párosat dobunk a dobókockával, a B pedig, hogy legalább ötöst dobunk.
Ekkor
A+B ={2,4,5,6}.
A B
Ω 2.3. ábra. AzAésBesemények összege.
Az A és B események A ·B szorzata az az esemény, amely akkor következik be, haAésB is bekövetkezik.
Legyen az A esemény, hogy párosat dobunk a dobókockával, a B pedig, hogy legalább ötöst dobunk.
Ekkor
A·B ={6}.
A B
Ω 2.4. ábra.AzAésB események szorzata.
Önellen ˝orzés :
1.Legyen azAesemény, hogy 3-mal osztható számot dobunk, aB pedig, hogy 4-nél kisebbet. Mivel egyenl˝o A+B?
{1,2,3} {1,2,3,6} {3} {6}
Az A és B események A − B különbsége az az esemény, amely akkor következik be, ha azA esemény bekövetkezik, de aB esemény nem.
Példa. Legyen a kockadobásnál az A esemény, hogy négyest vagy hatost dobunk, B pedig, hogy ötnél kisebbet dobunk. Ekkor
A−B ={6}, B−A={1,2,3}.
A B
Ω
2.5. ábra. AzAésBesemények különbsége.
2-1. önálló feladat: LegyenAaz az esemény, hogy az ötöslottó húzáson mind az öt kihúzott szám páros, míg B az az esemény, hogy legfeljebb egy páros szám van a kihúzottak között. Írja fel, hogy mit jelentenek az A−B, B−A, A, B események!
2.1. feladat. Egy irodaházban három lift m˝uködik. Jelölje A1,A2, illetve A3 azt az eseményt, hogy egy nap folyamán az els˝o, második, illetve harmadik lift hibamentesen m˝uködik. Fogalmazzuk meg, hogy mit jelentenek a következ˝o események:
a)A1·A2·A3, b)A1+A2+A3, c)A1·A2·A3, d)A1·A2·A3, e)A1·(A2+A3), f)A1+A2+A3 .
1. lecke 5. oldal
Az A esemény A ellentettje (komplementere) az az esemény, amely akkor következik be, ha azA esemény nem következik be. Az A esemény komplementere nem más, mint az Ω eseménytér és az A esemény különbsége: A= Ω−A.
Példa. Legyen a kockadobásnál az A esemény, hogy prímszámot dobunk. Ekkor
A={1,4,6}.
A
Ω
2.6. ábra. AzAesemény komplementere.
Megoldás:
a) Három esemény szorzatáról van szó, ezért a szorzat esemény azt jelenti, hogy mindhárom lift hiba nélkül m˝uködik.
b) Mivel itt összegr˝ol van szó, ezért a megadott esemény azt jelenti, hogy vagy az els˝o, vagy a második, vagy a harmadik gép meghibásodik a nap folyamán, amit röviden úgy is mondhatunk, hogy legalább az egyik lift meghibásodik.
c) Az esemény azt jelenti, hogy mindegyik lift elromlik a nap folyamán.
d) Itt éppen az a, rész komplementer eseményér˝ol van szó, azaz annak az ellentettjér˝ol, hogy mindegyik lift jól m˝uködik. Ennek a komplementere az, hogy nem mindegyik lift m˝uködik jól, amit egyszer˝ubben úgy is mondhatunk, hogy legalább az egyik meghibásodik. Vegyük észre, hogy ez megegyezik a b-beli eseménnyel! (Vigyázat: gyakori hiba, hogy valaki a mindegyik lift jól m˝uködikellentettjének a mindegyik lift meghibásodik-ot tartja; ne essünk ebbe a hibába!)
e) A megadott esemény azt jelenti, hogy az els˝o gép jól m˝uködik, a másik kett˝ob˝ol viszont legalább az egyik meghibásodik.
f) AzA1+A2+A3esemény azt jelenti, hogy legalább az egyik lift jól m˝uködik; így ennek a komplementere az, hogy egyik lift sem m˝uködik jól. Vegyük észre, hogy a megadott esemény megegyezik a c-beli eseménnyel!
⇐2.1. feladat
2.2. feladat. Egy dolgozó minden reggel autóval megy a munkahelyére. Útja során három vasúti keresztez˝odésen kell áthajtania. Jelölje Ai azt az eseményt (i = 1,2,3), hogy az i. átjárón várakozás nélkül haladhat át (azaz nem jön a vonat). Fejezzük ki azAi események segítségével a következ˝o eseményeket:
a) mindhárom átjárónál pirosan villog a szemafor; b) a második átjárónál várakoznia kell, a másik kett˝onél nem;c)legalább egy átjárónál várakoznia kell;d)pontosan egy átjárónál kell várakoznia.
Megoldás:
a) A három esemény egyike sem következik be, azaz a mindhárom eseménynek a komplementere következik be, vagyis azA1,A2,A3szorzatáról van szó. Tehát amindhárom átjárónál várni kellesemény a következ˝o lesz
A1·A2·A3.
b) AzA2 esemény nem következik be, mígA1 ésA3 igen, így azA1,A2,A3 események szorzatát kell venni, vagyis amásodik átjárónál várni kell, a másik kett˝onél pedig nemesemény az alábbi lesz:
A1·A2·A3.
c) Vegyük észre, hogy a legalább egy átjárónál várakozni kell esemény nem más, mint a mindegyik átjárón várakozás nélkül haladhatunk átesemény komplementere, ezért a következ˝o alakban írható:
A1·A2·A3.
d) A pontosan egy átjárónál kell várnunk esemény háromféleképpen következhet be: vagy az els˝o átjárónál kell várnunk, és a másik kett˝onél nem, vagy a másodiknál kell várnunk és a másik kett˝onél nem, vagy
1. lecke 7. oldal
a harmadiknál kell várnunk, és a másik kett˝onél nem (ezek közül a második eseményt a b részben már felírtuk). Tehát ennek a három eseménynek kell vennünk az összegét, így a pontosan egy átjárónál kell várnunkesemény a következ˝o alakban írható:
A1·A2· A3+A1·A2·A3+A1·A2·A3.
⇐2.2. feladat
Mivel az eseményeket halmazként értelmeztük, ezért az események közötti összeadás, szorzás ugyanolyan tulajdonságokkal rendelkezik, mint a halmazok körében az unió és a metszet, azaz
kommutatív: A+B=B+A A·B =B·A
asszociatív: (A+B) +C=A+ (B+C) (A·B)·C=A·(B·C)
disztributív: A·(B+C) =A·B+A·C A+B·C= (A+B)·(A+C)
Egy tetsz˝oleges A esemény, a komplementere (A), a biztos esemény (Ω) és a lehetetlen esemény (∅) között érvényesek a következ˝o egyszer˝u m˝uveleti tulajdonságok:
A+A=A A·A=A
A+ Ω = Ω A·Ω =A
A+∅=A A· ∅=∅
A+A= Ω A·A=∅
Két esemény (AésB) különbsége átalakítható szorzattá:
A−B =A·B. Itt is érvényesek a halmazok körében ismert De Morgan azonosságok:
A+B=A·B A·B=A+B.
2.3. feladat. Bizonyítsuk be, hogy tetsz˝olegesA, B ésC eseményekre teljesül az(A−B)·C = (A·C)−B összefüggés!
Megoldás: 1. módszer:
(A−B)·C = (A·B)·C= (A·C)·B = (A·C)−B.
Az 1. és 3. egyenl˝oségnél azA−B =A·Bazonosságot, míg a második egyenl˝oségnél a szorzat kommutativitását és asszociativitását használtuk fel.
2.módszer: Az állítást Venn-diagramok segítségével szemléletesen is „bizonyíthatjuk".
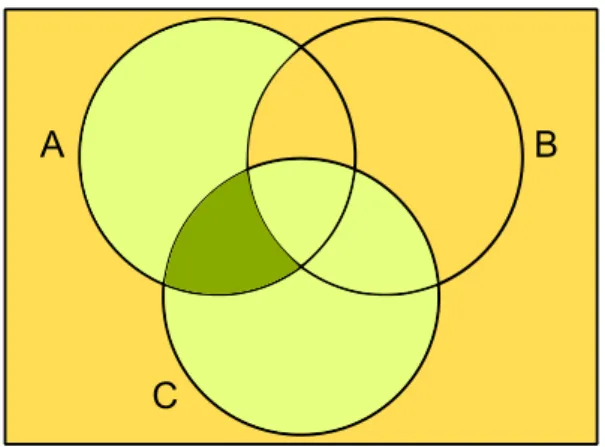
Ábrázoljuk el˝oször a bal oldalt. AzA−B eseménynek az ábrán azAésBhalmazok különbsége felel meg; ezt láthatjuk a 2.7. ábra bal oldalán. AzA−B és aC esemény szorzatának az ábrán az A−B és a C halmazok metszete felel meg. Az így kapott, (A−B)·C eseménynek megfelel˝o halmazt a2.7. ábra jobb oldali részén láthatjuk.
Most ábrázoljuk a bizonyítandó állítás jobb oldalát. AzA·C eseménynek az AésC halmazok metszete felel meg; ezt láthatjuk a2.8. ábra bal oldalán. Az(A·C)−Beseménynek pedig azA·CésBhalmazok különbsége felel meg; ezt láthatjuk a 2.8. ábra jobb oldalán. A két ábra jobb oldalát összehasonlítva valóban azt kapjuk, hogy
(A−B)·C= (A·C)−B.
⇐2.3. feladat
1. lecke 9. oldal
A B
C
A B
C
2.7. ábra. Bal oldal: azA−B esemény; jobb oldal: az(A−B)·Cesemény (2.3. feladat).
A B
C
A B
C
2.8. ábra. Bal oldal: azA·C esemény; jobb oldal: az(A·C)−B esemény (2.3feladat).
2.2. A valószín˝uség-számítás axiómái
Ha egy véletlen tömegjelenséget (A) nagyon sokszor, azonos körülmények között megfigyelünk, akkor a tapasztalat szerint a bekövetkezések és az összes kísérletek számának aránya egy meghatározott számérték körül ingadozik, és az ingadozások a kísérletek számának növelésével általában egyre kisebbek lesznek (lásd az 2.9 ábrát). Azt a számot, amely körül ez az arány ingadozik, az esemény valószín˝uségének nevezzük és P(A)-val jelöljük.
2.1. definíció: Ha egy kísérletetn-szer azonos körülmények között megismételve azAeseménykAesetben következik be, akkor ezt a kA számot azA esemény gyakoriságának nevezzük. A gyakoriság és a kísérletek számának hányadosát, kA
n-et pedig azAesemény relatív gyakoriságának hívjuk.
0 20 40 60 80 100
0 0.5
1
(a)n= 100
0 200 400 600 800 1000
0 0.5
1
(b) n= 1000
2.9. ábra. A fej relatív gyakoriságának id˝obeni alakulása egy 100 és egy másik, 1000 dobásból álló fej vagy írás kísérletsorozatban.
1. lecke 11. oldal
Mivel a fentiek szerint az A esemény kA
n relatív gyakorisága az esemény P(A) valószín˝uségéhez tart, ezért a relatív gyakoriság tulajdonságaiból következtethetünk a valószín˝uség tulajdonságaira is.
Ha egy kísérlettel kapcsolatos A esemény gyakorisága kA , akkor nyilvánvaló, hogy az A esemény relatív gyakorisága0és1közötti érték, azaz
0≤ kA
n ≤1.
Mivel azAesemény relatív gyakorisága azAesemény valószín˝usége körül ingadozik, a 0≤P(A)≤1
feltételnek is igaznak kell lennie.
A biztos esemény mindig bekövetkezik, ezért relatív gyakorisága mindig1, azaz kΩ
n = 1. Ezért a
P(Ω) = 1 egyenl˝oségnek is teljesülnie kell.
Ha A és B egymást kizáró események, akkor az A +B esemény (kA +kB)-szer következik be. A relatív gyakoriságokra áttérve innen azt kapjuk, hogy
kA+B
n = kA+kB
n = kA
n + kB
n .
Mivel az A+B esemény relatív gyakorisága az A+B esemény valószín˝usége körül ingadozik, az A, illetve a B esemény relatív gyakoriságai pedig azA, illetve a B esemény valószín˝usége körül, ezért egymást kizáró események esetén a
P(A+B) =P(A) +P(B) egyenl˝oségnek is fenn kell állnia.
A relatív gyakoriság tulajdonságai alapján célszer˝u a következ˝oket tekinteni a valószín˝uség-számítás axiómáinak:
1. Az adottΩeseménytér minden egyesAeseményéhez tartozik egy0és1közé es˝oP(A)szám, azaz 0≤P(A)≤1,
amelyet azAesemény valószín˝uségének (valószín˝uségi mértékének) nevezünk.
2. A biztos esemény valószín˝usége1, azazP(Ω) = 1.
3. Az egymást páronként kizáró események összegének valószín˝usége az egyes események valószín˝uségeinek összegével egyenl˝o, azaz ha azA1,A2, . . . ,Ak, . . .események eseténAi·Aj =∅(hai6=j), akkor
P(A1+A2+. . .) =P(A1) +P(A2) +. . . . Tömörebben:
P X
k
Ak
!
=X
k
P(Ak).
1. lecke 13. oldal
2.3. Az axiómák egyszer˝ubb következményei
2.1. tétel: AzAesemény komplementerének valószín˝usége1−P(A).
Bizonyítás: Tudjuk azt, hogy Ω = A+A, továbbá azt is, hogy A és A egymást kizárják (A·A = ∅), tehát alkalmazhatjuk a 3. axiómát:
1 =P(Ω) =P(A+A) =P(A) +P(A).
Az els˝o egyenl˝oségnél azt használtuk, hogy a biztos esemény valószín˝usége 1 (2. axióma). Kifejezve a komplementer esemény valószín˝uségét azt kapjuk, hogyP(A) = 1−P(A).
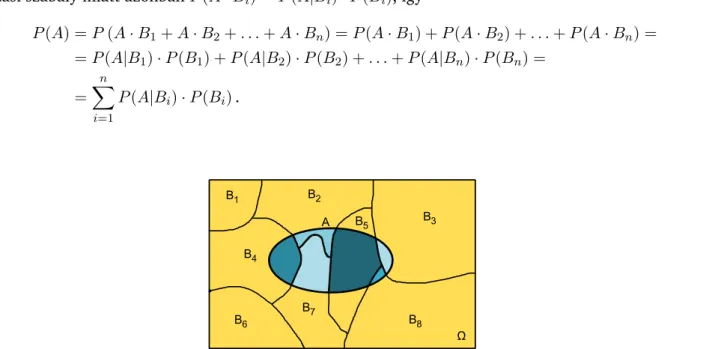
2.2. definíció: Az A1,A2, . . . ,An események teljes eseményrendszert alkotnak, ha egymást páronként kizárják és összegük a biztos esemény, azaz haAi·Aj =∅(hai6=j), ésA1+A2+. . .+An= Ω.
A teljes eseményrendszer tulajdonképpen az eseménytér felbontása olyan diszjunkt részhalmazokra, melyek együttesen lefedik a teljes eseményteret. Az ábrán a B1, B2. . . ,B8 események teljes eseményrendszet alkotnak.
B1
B4
B2
B3
B7 B5
B8 B6
Ω
Példa: Felírjuk egy-egy cédulára 1-t˝ol 8-ig az egész számokat, és a cédulákat beletesszük egy dobozba. Ezután kihúzunk a dobozból egy cédulát. A következ˝o események teljes eseményrendszert alkotnak:
1. A1: a kihúzott szám az egyes; A2: a kihúzott szám nem az egyes. EkkorA1 ésA2 teljes eseményrendszert alkot, mert egyrészt kizárják egymást, hiszen egyszerre nem következhetnek be, másrészt a kett˝o közül az egyik biztosan bekövetkezik, így összegük a biztos esemény.
2. A1: a kihúzott szám négynél kisebb; A2: a kihúzott szám a négyes A3: a kihúzott szám négynél nagyobb.
Az A1, A2 és A3 események most is teljes eseményrendszert alkotnak, hiszen egyszerre nem következhet be bel˝olük kett˝o (bármelyik kett˝o kizárja egymást), másrészt viszont valamelyik biztosan be fog közülük következni (összegük a biztos esemény).
Aktivitás:A fenti példában adjon meg legalább 2 további teljes eseményrendszert!
2.2. tétel: Ha az A1,A2, . . . ,An események teljes eseményrendszert alkotnak, akkor valószín˝uségeik összege1, azazP(A1) +P(A2) +. . .+P(An) = 1.
Bizonyítás: Mivel a teljes eseményrendszer tagjai egymást páronként kizárják, ezért a 3. axióma miatt az összegük valószín˝usége megegyezik a valószín˝uségeik összegével. Másrészt a teljes eseményrendszer tagjainak összege a biztos esemény, melynek a valószín˝usége a 2. axióma miatt 1. Ebb˝ol már követezik az állítás.
Formálisan:
P(Ω) =P(A1+A2+. . .+An) =P(A1) +P(A2) +. . .+P(An) 1 =P(A1) +P(A2) +. . .+P(An)
2.3. tétel: AzAésB eseményekA−B különbségének valószín˝usége
P(A−B) =P(A)−P(A·B).
1. lecke 15. oldal
Bizonyítás: Mivel az A−B ésA·B események összege A, továbbá az A−B és A·B események kizárják egymást, ezért alkalmazhatjuk a 3. axiómát.
P(A) =P((A−B) + (A·B)) =P(A−B) +P(A·B),
amib˝ol átrendezéssel azt kapjuk, hogyP(A−B) =P(A)−P(A·B).
Aktivitás: Venn-diagram segítségével gy˝oz˝odjön meg róla, hogy az A−B és A·B események egyrészt kizárják egymást, másrészt összegükA-val egyenl˝o!
A fenti tétel speciális esete a következ˝o:
2.4. tétel: HaA⊂B, akkorP(B−A) =P(B)−P(A).
2.5. tétel: AzAésB események összegének valószín˝usége
P(A+B) =P(A) +P(B)−P(A·B).
Bizonyítás: AzAésB−Aegymást kizáró események (A·(B−A) =∅), másrészt összegük azA+Besemény.
A 3. axióma alkalmazásával azt kapjuk, hogy
P(A+B) =P(A+ (B−A)) =P(A) +P(B−A).
AP(B−A)tagra alkalmazva a2.3. tételt kapjuk, hogy
P(A+B) =P(A+ (B−A)) =P(A) +P(B−A) =P(A) +P(B)−P(A·B).
Aktivitás: Venn-diagram segítségével gy˝oz˝odjön meg róla, hogy azAésB−Aesemények egyrészt kizárják egymást, másrészt összegükA+B-vel egyenl˝o!
2.4. feladat. Legyen azAesemény valószín˝usége0,4, aBesemény valószín˝usége0,8, az együttes bekövetkezés valószín˝usége pedig0,3. Határozzuk meg az alábbi valószín˝uségeket:
a)P(A+B) b)P(A−B) c)P(B−A) d)P(A)
e)P(B) f)P(A·B) g)P(B−A) h)P(A+B).
Megoldás:
a)
P(A+B) =P(A) +P(B)−P(A·B) = 0,4 + 0,8−0.3 = 0,9. b)
P(A−B) =P(A)−P(A·B) = 0,4−0,3 = 0,1. c)
P(B−A) =P(B)−P(A·B) = 0,8−0,3 = 0,5. d)
P(A) = 1−P(A) = 1−0,4 = 0,6. e)
P(B) = 1−P(B) = 1−0,8 = 0,2.
f) Vegyük észre, hogy a De-Morgan azonosság szerintA·B =A+B. Ezt felhasználva P(A·B) =P(A+B) = 1−P(A+B) = 1−0,9 = 0,1.
1. lecke 17. oldal
g) Használjuk fel a két esemény különbségére vonatkozó összefüggést!
P(B−A) =P(B·A) =P(B·A) = 0,3. h) A De-Morgan azonosság szerintA+B =A·B. Ezt felhasználva
P(A+B) =P(A·B) = 1−P(A·B) = 1−0,3 = 0,7.
⇐2.4. feladat
Megjegyzés: Az ilyen típusú feladatoknál hasznos lehet, ha Venn-diagrammal ábrázoljuk magunknak az eseményeket. Például azfrészben rajzoljuk fel el˝oször azAesemény komplementerét (ami azA-nak megfelel˝o halmaz komplementere), utána rajzoljuk fel a B esemény komplementerét, majd vegyük a két esemény összegét, ami a két felrajzolt rész uniójának felel meg. Észrevehetjük, hogy pontosan az A·B rész maradt ki, vagyis azt kaptuk, hogy A+B = A·B. Így a feladatot akkor is meg tudjuk oldani, ha nem jut eszünkbe valamelyik azonosság!
2.5. feladat. AzAesemény bekövetkezése maga után vonja aBesemény bekövetkezését. Fejezzük ki az : a)P(A+B) b)P(A·B) c)P(B−A) d)P(A−B)
e)P(A·B) f)P(A·B) g)P(B−A) h)P(A−B).
valószín˝uségeket aP(A)ésP(B)valószín˝uségek segítségével.
Megoldás: Az, hogy azAesemény bekövetkezése maga után vonja aB esemény bekövetkezését, pontosan azt jelenti, hogyA⊂B.
a) MivelA⊂B, ezértA+B =B, ígyP(A+B) =P(B).
b) MivelA⊂B, ezértA·B =A, ígyP(A·B) =P(A).
c) P(B−A) =P(B)−P(A·B) =P(B)−P(A).
d) AzA−B esemény azt jelenti, hogyA bekövetkezik, B viszont nem. Mivel jelen esetbenA ⊂B, ezért ez sosem fordulhat el˝o, ígyA−B =∅, ígyP(A−B) =P(∅) = 0.
e) MivelA⊂B, ezért haAbekövetkezik, akkorB is bekövetkezik, ígyP(A·B) =P(∅) = 0.
f) MivelA⊂B, ezértB⊂A, ígyP(A·B) =P(B) = 1−P(B). g) P(B−A) =P(B·A) =P(B·A) =P(A).
h) P(A−B) =P(A·B) =P(A·B) =P(A).
⇐2.5. feladat
2.6. feladat. Egy üzemben az elkészült termékek a min˝oség szempontjából els˝o-, másod-, illetve harmadosztályúak lehetnek. Jelentse Aazt az eseményt, hogy a raktárból véletlenszer˝uen kiválasztott termék els˝oosztályú, B azt, hogy másodosztályú, C pedig azt, hogy harmadosztályú. Tudjuk,hogy P(A) = 0,3, míg P(B) = 0,5. Számoljuk ki a következ˝o valószín˝uségek értékét!
a)P(C) b)P(A+B) c)P(A+B) Megoldás:
a) Mivel min˝oség szempontjából minden termék pontosan az egyik osztályba esik bele, így a három esemény teljes eseményrendszert alkot, ezért P(A) +P(B) +P(C) = 1. Ebb˝ol aC esemény valószín˝uségére 1− 0,3−0,5 = 0,2adódik.
b) Az A ésB egymást kizáró események, ezért P(A·B) = P(∅) = 0. Ebb˝ol azt kapjuk, hogy P(A+B) = P(A) +P(B)−P(A·B) = 0,3 + 0,5−0 = 0,8.
c) AzA+B esemény azt jelenti, hogy egy termék vagy nem els˝oosztályú, vagy nem másodosztályú. Vegyük észre, hogy ez minden termékre igaz, vagyis azA és aB események összege a biztos esemény. Ebb˝ol azt kapjuk, hogyP(A+B) =P(Ω) = 1.
1. lecke 19. oldal
Másik módon is megkaphattuk volna az eredményt. A De Morgan azonosság szerintA+B =A·B, amib˝ol P(A +B) = P(A·B) = 1−P(A ·B) adódik. Mivel egy termék nem lehet egyszerre els˝oosztályú és másodosztályú is, ezértA·B=∅. ÍgyP(A+B) = 1−P(∅) = 1−0 = 1.
⇐2.6. feladat
Önellen ˝orzés
1.LegyenA, BésC három esemény. Mit jelent azA·(B+C)esemény?
Mindhárom esemény bekövetkezik.
Pontosan két esemény következik be.
AzAesemény bekövetkezik, és aB ésC közül is bekövetkezik legalább az egyik.
Legalább az egyik esemény bekövetkezik.
2.Az alábbi események közül melyik fejezi ki azt, hogy az A és B események közül pontosan az egyik következik be?
A+B A+B A·B A·B+A·B
3.Az alábbi események közül melyik fejezi ki azt, hogy azA, B, Cesemények közül egyik sem következik be?
A+B+C A+B+C A·B·C A+B·C
4.HaP(A) = 0,7, P(B) = 0,5ésP(A·B) = 0,4, akkor mennyiP(A+B)?
5.Tudjuk, hogy aB esemény maga után vonja azAeseményt, ésP(A) = 0,8, P(B) = 0,5. MennyiP(A·B) valószín˝uség értéke?
6.Az A, B és C események teljes eseményrendszert alkotnak. Tudjuk, hogy P(A) = 0,1 és P(B) = 0,5.
Mennyi aP(A+B)valószín˝uség értéke?
Megold.
Megold.
Megold.
2. LECKE
A klasszikus valószín ˝uségi mez ˝o
3. A klasszikus és a geometriai valószín˝uségi mez˝o 3.1. A klasszikus valószín˝uségi mez˝o
3.1. definíció: Ha egy kísérlettel kapcsolatban az elemi események száma véges (n), és minden elemi esemény valószín˝usége egyenl˝o n1
, akkor akféleképpen bekövetkez˝oAesemény valószín˝usége P(A) = kedvez˝o esetek száma
összes eset száma = k n.
Ebben az esetben azt mondjuk, hogy az események és ezek valószín˝uségei klasszikus valószín˝uségi mez˝ot alkotnak.
Mint majd látni fogjuk, a kedvez˝o, illetve az összes eset száma a legtöbb esetben kombinatorikus úton határozható meg a legegyszer˝ubben, ezért el˝oször példák segítségével áttekintjük a kombinatorika alapeseteit.
3.1.1. Kombinatorika
3.1. feladat. Az 1,2,3,4,5 számjegyek felhasználásával hány olyan ötjegy˝u szám készíthet˝o, melyben minden számjegy csak egyszer szerepel?
Megoldás: Az els˝o helyre még bármelyik számjegyet írhatjuk. Bámit is írunk az els˝o helyre, utána a második helyre már csak 4, a harmadik helyre már csak 3, a negyedik helyre 2, az ötödikre pedig egyetlen lehet˝oségünk marad. Így összesen5·4·3·2·1 = 5! = 120szám készíthet˝o. ⇐3.1. feladat
Teljesen hasonló gondolatmenettel belátható, hogynkülönböz˝o elem összes lehetséges sorrendjének (aznelem permutációinak) a száma:
n·(n−1)· · · ·2·1 =n!.
2. lecke 2. oldal
3.2. feladat. Hány különböz˝o, nem feltétlenül értelmes tízbet˝us szó (úgynevezett anagramma) készíthet˝o a MATEMATIKA szó bet˝uib˝ol?
Megoldás: A feladat tehát az, hogy három A, két M, két T, és egy-egy E,I, illetve K bet˝u felhasználásával hány tízbet˝us szó készíthet˝o. Els˝o nekifutásra különböztessük meg egymástól az azonos bet˝uket (például legyen egy piros, egy kék, és egy sárga A bet˝u, stb). Ekkor a 10 bet˝ub˝ol10!szó készíthet˝o. Így azonban minden egyes szót többször is megszámoltunk: az A bet˝uk miatt minden szót 3!-szor számoltunk meg, aT bet˝uk miatt mindent 2!-szor, míg azM bet˝uk miatt mindent2!-szor. Ezért az összes különböz˝o 10 bet˝us anagramma száma:
10!
3!·2!·2! = 151200.
⇐3.2. feladat
Ugyanígy látható be, hogy ha adott nelem, melyek között vannak megegyez˝oek is, nevezetesen az 1. típusú elemb˝ol n1 , a második típusúbóln2, . . . ak.típusúból nk darab van (n1+n2+. . . nk = n), akkor aznelem összes lehetséges sorrendjének (az ismétléses permutációinak) a száma:
n!
n1!·n2!·. . .·nk!.
3.3. feladat. Hány háromjegy˝u szám készíthet˝o az 1,2,3,4,5, számjegyekb˝ol, ha minden számjegy legfeljebb egyszer szerepelhet?
Megoldás: Az els˝o helyre még öt számjegy közül választhatunk. Ha az els˝o számjegyet leírjuk, akkor a második helyre már csak négy lehet˝oségünk marad, végül az utolsó helyre már csak három számjegy közül választhatunk.
Így összesen5·4·3szám készíthet˝o a megadott módon. ⇐3.3. feladat
Hasonlóan belátható, hogy aznelemb˝ol készíthet˝o olyankhosszú sorozatok száma (k≤n), melyben egy elem legfeljebb egyszer szerepelhet:
n·(n−1)·. . .·(n−k+ 1).
3.4. feladat. Feldobunk nyolcszor egy dobókockát, és a kapott számokat egymás után írjuk. Hány különböz˝o nyolcjegy˝u számot kaphatunk így?
Megoldás: Mivel mind a nyolc számjegy hatféle lehet, ezért68= 1679616féle nyolcjegy˝u számot kaphatunk.
⇐3.4. feladat
Hasonlóan belátható, hogy aznelemb˝ol készíthet˝o olyankhosszú sorozatok száma, melyben egy elem többször is szerepelhet:
nk.
3.5. feladat. Az ötöslottón 90 számból sorsolnak ki ötöt. Hány különböz˝o végeredménye lehet a sorsolásnak?
Megoldás: Az els˝o húzásnál még 90 szám közül választhatunk, a másodiknál már csak 89 közül, a harmadiknál 88 közül, a negyediknél 87, míg az utolsónál 86 közül; ez összesen90·89·88·87·86 lehet˝oség. Igen ám, de így a húzás sorrendjét is figyelembe vettük, ezért minden egyes lehet˝oséget 5!-szor megszámoltunk (hiszen 5 számot ennyiféleképpen lehet sorbarendezni). Ezért a különböz˝o végeredmények száma:
90·89·88·87·86
5! = 43 949 268.
⇐3.5. feladat
Vezessük be a következ˝o jelölést: legyen 0 ≤ k ≤ n, és legyen nk
(olvasd: „n alatt a k") azzal a számmal egyenl˝o, ahányféleképpennkülönböz˝o elemb˝ol ki lehet választanikdarabot (az el˝oz˝o feladat megoldása tehát
90 5
). Az el˝oz˝o gondolatmenettel belátható, hogynkülönböz˝o tárgybólkdarabot n
k
= n·(n−1)·. . .·(n−k+ 1) k!
féleképpen lehet kiválasztani.
2. lecke 4. oldal
3.6. feladat. : Három fajta fagyiból (eper, vanília, csoki) hányféleképpen állíthatunk össze egy négygombócos sétálókelyhet (egy fajtából természetesen többet is vehetünk)?
Megoldás: Minden sétálókehelyhez rendeljünk hozzá egy egyesekb˝ol és nullákból álló sorozatot a következ˝o módon: el˝oször írjunk egy 1-est (ez felel meg az epernek), majd írjunk utána annyi nullát, ahány gombócot veszünk az eperb˝ol; ezután ismét írjunk le egy 1-est (ez felel meg a vaníliának), majd írjunk utána annyi 0-t, ahány gombócot veszünk a vaníliából; aztán megint írjunk egy 1-est (csoki), és utána annyi 0-t, amennyi gombócot a csokiból veszünk. Például egy 2 eperb˝ol és 2 csokiból álló kehelynek az 1001100 sorozat felel meg. Egy ilyen sorozatban három darab 1-es lesz (hiszen 3 fajta fagyi van), négy darab 0 lesz benne (hiszen 4 gombócot veszünk), és 1-essel fog kezd˝odni. Viszont minden ilyen tulajdonságú sorozatnak (amely 1-essel kezd˝odik, három darab 1-es és négy darab 0 van benne) egyértelm˝uen meg tudunk feleltetni egy sétálókelyhet.
Ez azt jelenti, hogy a különböz˝o sétálókelyhek száma megegyezik az el˝obb felsorolt tulajdonságú sorozatok számával. Tehát azt kell megmondani, hogy hány olyan hét tagból álló, nullákat és egyeseket tartalmazó sorozat van, mely 1-essel kezd˝odik, és négy darab 0 van benne. Ezeknek a száma viszont 64
(hiszen a négy darab 0-t hat hely valamelyikére kell elhelyeznünk), így a különböz˝o sétálókelyhek száma 64
= 15. ⇐3.6. feladat
Ugyanezen gondolatmenet segítségével belátható, hogy ha n különböz˝o elem közül k darabot akarunk kiválasztani úgy, hogy egy elemet többször is választhatunk, akkor a lehetséges kiválasztások száma
n+k−1 k
.
A kombinatorikai alapesetek átnézése után lássunk most néhány klasszikus valószín˝uségi mez˝ovel kapcsolatos feladatot.
3.7. feladat. Bankkártyánk PIN-kódjának egy valódi négyjegy˝u számot kell megadnunk. Véletlenszer˝uen választjuk ki a számot. Mi a valószín˝usége, hogy
a) a kódunk mind a négy számjegye különböz˝o;
b) a kódunkban van 1-es számjegy;
c) a kódunkban pontosan egy darab 6-os számjegy van?
Megoldás:
a) A valódi négyjegy˝u számok száma9·103(hiszen az els˝o helyre 9, a másik három helyre 10 számjegy közül választhatunk), így az összes eset száma 9000. A jó esetek száma9·9·8·7, hiszen az els˝o helyre kilenc számjegy közül választhatunk, ezután a második helynél szintén kilenc (nem írhatjuk ugyanazt, amit az els˝o helyre) lehet˝oségünk van, a harmadik helynél már csak 8, míg a negyediknél 7. Így a keresett valószín˝uség
9·9·8·7
9·103 = 0,504.
b) Ebben az esetben egyszer˝ubb a komplementer eseménynek kiszámolni a valószín˝uségét. Akódban van 1-es esemény komplementere akódban nincs 1-esesemény. Mivel8·9·9·9 olyan valódi négyjegy˝u szám van, melyben nincs egyes, így
P(a kódban van 1-es) = 1−P(a kódban nincs 1-es) = 1−8·9·9·9
9·103 = 0,352.
c) Az, hogy a kódban pontosan egy darab hatos van, négyféleképpen valósulhat meg: vagy az els˝o, vagy a második, vagy a harmadik, vagy a negyedik helyen van 6-os, a többi helyen pedig nem 6-os van. Így a jó esetek száma1·9·9·9 + 8·1·9·9 + 8·9·1·9 + 8·9·9·1 = 2025. Ebb˝ol a kérdéses valószín˝uség: 20259000 = 0,225.
2. lecke 6. oldal
⇐3.7. feladat
3.8. feladat. Egy rejtvénypályázatra 30 férfi és 20 n˝o küldött be jó megoldást. A helyes megfejt˝ok között 3 díjat sorsolnak ki: egy TV-t, egy telefont és egy porszívót. Mindenki legfeljebb egy dolgot nyerhet. Mi a valószín˝usége, hogy
a)csak n˝oi nyertes lesz; b)Kovács út nyer valamit?
Megoldás:
a) A sorsolás mindegyik lehetséges kimeneteléhez rendeljünk hozzá egy három tagból álló sorozatot: az els˝o tag legyen a TV-t nyer˝o személy, a második a telefont nyer˝o személy, míg a harmadik a porszívót nyer˝o személy. Az összes eset száma megegyezik az 50 pályázóból képezhet˝o, 3 tagból álló sorozatok számával, ezek száma pedig50·49·48. A jó esetek száma, tehát amikor csak n˝oi nyertes lesz20·19·18, így a kérdéses valószín˝uség 20·19·1850·49·48 ≈0,058.
b) Kétféle módon is eljárhatunk. 1. módszer: Az, hogy Kovács úr nyer valamit, háromféleképpen valósulhat meg: vagy a TV-t, vagy a telefont, vagy a porszívót nyeri meg. Számoljuk meg külön-külön a három lehet˝oséghez tartozó eseteket, majd ezek összegeként kapjuk a jó esetek számát. Ha Kovács nyeri a TV-t, akkor a telefont 49-en, míg a porszívót 48-an nyerhetik meg, így azon esetek száma, amikor Kovács nyeri a TV-t1·49·48. Hasonlóan számolhatjuk meg azon esetek számát, amikor Kovács úr telefont, illetve porszívót nyer. Ebb˝ol a kérdezett valószín˝uség:
P(Kovács úr nyer valamit) = 1·49·48 + 49·1·48 + 49·48·1
50·49·48 = 0,06.
2. módszer: Használjuk fel aP(A) = 1−P(A)összefüggést. Azon esetek száma, amikor Kovács Úr nem nyer semmit49·48·47, hiszen a TV-t 49, ezután a telefont 48, míg a porszívót 47 embernek adhatjuk oda.
P(Kovács úr nyer valamit) = 1−P(Kovács úr nem nyer semmit) = 1−49·48·47
50·49·48 = 1−0,94 = 0,06.
⇐3.8. feladat
Aktivitás:Számolja ki az el˝oz˝o feladatbeli valószín˝uségeket abban az esetben is, ha egy ember több díjat is nyerhet!
3.1.2. Visszatevéses és visszatevés nélküli mintavétel
A különböz˝o mintavételi eljárások számos területen játszanak fontos szerepet. Tegyük fel például, hogy min˝oségellen˝orzés során egy cég meg akarja vizsgálni, hogy az aznap gyártott termékek hány százaléka hibás. A legtöbb esetben nincs lehet˝oség az összes termék megvizsgálására, mert az túl sok pénzbe és id˝obe kerülne. Ezért egy szokásos eljárás az, hogy véletlenszer˝uen kiválasztanak néhány terméket (mintát vesznek), és a bennük található hibás termékek számából „következtetnek” az összesben található hibások számára. A közvéleménykutatások hasonlóképpen m˝uködnek: egy párt támogatottságának megállapításához nem kérdezik meg az ország összes lakosát, hanem csak néhány kiválasztott embert (egy reprezentatív mintát), és az ˝o válaszaikból vonnak le az ország teljes lakosságára vonatkozó következtetést.
Aktivitás: Nézzen utána az interneten, hogy Magyarországon a közvéleménykutatásokkor körülbelül hány embert szoktak megkérdezni!
Visszatevéses mintavétel
Visszatevéses mintavétel esetén a minta elemeit egyesével választjuk ki, majd a vizsgálat után visszatesszük
˝
oket, és ezután vesszük a következ˝ot, stb.
3.9. feladat. 100 termék között 20 selejtes van. Visszatevéses mintavétellel kiválasztunk 6 terméket. Mi a valószín˝usége, hogy
a) az els˝o 4 termék selejtes, a többi jó;
2. lecke 8. oldal
b) az els˝o 2 termék jó, a többi selejtes;
c) pontosan 4 selejtes van a kiválasztott termékek közt?
Megoldás:
a) Mivel minden egyes húzásnál 100 termék közül választhatunk, így az összes eset száma1006.A jó eseteknél az els˝o 4 húzásnál 20, az utolsó 2 húzásnál 80 termék közül választhatunk, így a jó esetek száma204·802. Így a kérdezett valószín˝uség:
P(els˝o 4 selejt, utolsó 2 jó) = jó esetek száma
összes eset száma = 204·802 1006 =
20 100
4
· 80 100
2
= 0,001024.
b) A jó esetek száma802·204, így a kérdéses valószín˝uség:
P(els˝o 2 jó, utolsó 4 selejt) = jó esetek száma
összes eset száma = 802·204 1006 =
80 100
2
· 20 100
4
= 0,001024.
c) A kihúzottak között pontosan 4 selejtes esemény felbontható egymást kizáró események összegére: (az els˝o négy termék selejtes, a többi jó)+(az 1.,2.,3.,5. termék selejtes, a többi jó)+. . .. Az el˝oz˝o két rész alapján világos, hogy a felbontásban szerepl˝o mindegyik esemény valószín˝usége
80 100
2
·
20 100
4
. Már csak az a kérdés, hogy hány esemény van a felbontásban? Éppen annyi, ahányféleképpen kiválaszthatjuk annak a 4 húzásnak a sorszámát, amikor selejteset akarunk húzni; ezek száma 64
. Felhasználva, hogy egymást kizáró események összegének a valószín˝usége a valószín˝uségek összege, azt kapjuk, hogy
P(pontosan 4 selejtes van) = 6
4 80
100 2
·20 100
4
= 0,01536.
⇐3.9. feladat
A3.9. feladat eredményét könnyen általánosíthatjuk: Legyen adottN termék, melyek között a selejtesek száma s. Visszatevéses mintavétellel veszünk egynelem˝u mintát. Az egyszer˝uség kedvéért a selejtesek arányát jelöljük p-vel (azazp= Ns). Ekkor a megoldás során használt módon belátható, hogy
P(a mintábankselejtes van) = n
k
·pk·(1−p)n−k.
Jó tanács: A képlet „bemagolása” helyett próbáljuk inkább azt megérteni és megjegyezni, hogy hogyan „jön ki”. Ha ez sikerül, akkor mindig fel tudjuk majd idézni a formulát.
Visszatevés nélküli mintavétel
A visszatevés nélküli mintavételnél az elemeket kiválaszthatjuk egyszerre (nem számít a sorrend), vagy egyesével is, ügyelve arra, hogy a már kiválasztott elemeket ne tegyük vissza (ebben az esetben számít a sorrend). Oldjuk most meg a3.9. feladatot visszatevés nélküli mintavétellel.
Adott tehát 100 termék ,melyek közül 20 selejtes. Visszatevés nélküli mintavétellel kiválasztunk 6 terméket. Azt akarjuk meghatározni, hogy mennyi annak a valószín˝usége, hogy 4 selejtes van a kiválasztott termékek közt.
Tegyük fel el˝oször, hogy a termékeket egyszerre választjuk ki (a sorrend nem számít). Ekkor az összes eset száma 1006
, hiszen ennyiféleképpen lehet 100 termékb˝ol 6-ot kiválasztani. Most nézzük a jó esetek számát: a kiválasztott termékek közt akkor lesz 4 selejtes, ha a selejtesekb˝ol 4-et, a jó termékekb˝ol pedig 2-t választunk ki, így a jó esetek száma 204
· 802
. Ebb˝ol azt kapjuk, hogy
P(4selejtes termék) = 20
4
· 80
2 100
6
≈0,0107.
Gondoljuk meg, hogy mi változik, ha az elemeket egyesével választjuk ki (vagyis a sorrend is számít). Tegyük fel például, hogy a mintavételnél az 1,2,3,4,5,6 termékeket választottuk ki. Ha a kiválasztás sorrendje nem
2. lecke 10. oldal
számít, akkor ez egy esetnek felel meg, míg ha sorrend is számít, akkor6!-féleképpen választhattuk ki ezt a hat terméket. Általában is elmondható, hogy minden egyes, a kiválasztás sorrendjét nem számító esetnek 6!eset felel meg, ha a sorrendet is figyelembe vesszük. Ez azt jelenti, hogy a sorrendet figyelembe vévé a jó esetek száma6!-szorosa lesz a sorrendet nem számoló esetek jó esetek számának, míg a sorrendet figyelembe véve az összes eset száma6!-szorosa lesz a sorrendet nem számoló összes eset számának. Vagyis mind a jó esetek, mind az összes eset száma a 6!-szorosára n˝o, így a hányadosuk nem változik, vagyis a kérdéses valószín˝uség marad ugyanaz.
Fogalmazzuk most meg az eredményeinket általánosan is: Ha N számú termékb˝ol s számú selejtes, akkor visszatevés nélküli mintavétellel kiválasztva a termékek közül n darabot, annak a valószín˝usége, hogy a kiválasztott termékek köztkselejtes van
P(kselejtes) = s
k
·
N −s n−k N
n
,
és a valószín˝uség nem függ attól, hogy a termékeket egyszerre, vagy pedig egyesével választjuk ki.
Természetesen a képlet bemagolása helyett inkább a képlet „logikájának” a megértése javallott!
3.10. feladat. Egy színházi el˝oadás szünetében a jelenlev˝o 420 néz˝o között kisorsolnak 10 darab színházbérletet a következ˝o évadra. Mennyi a valószín˝usége, hogy egy négytagú családnak legalább az egyik tagja nyer bérletet? (1 ember csak 1 bérletet nyerhet).
Megoldás: Az, hogy legalább az egyikük nyer, azt jelenti, hogy 1,2,3 vagy 4 családtag nyer. Egyszer˝ubb lesz a dolgunk, ha a komplementer esemény, azaz annak a valószín˝uségét számoljuk ki, hogy egyikük sem nyer bérletet. Mivel 420 ember közül sorsolnak ki 10-et, így az összes eset száma 42010
. Az, hogy egyikük sem nyer semmit, azt jelenti, hogy mind a 10 nyertest a többi 416 ember közül sorsolják ki. Ezen esetek száma 41610
.
Így azt kapjuk, hogy
P(valamelyikük nyer) = 1−P(egyikük sem nyer) = 1− 416
10 420
10
≈1−0,9078 = 0,0923.
⇐3.10. feladat
3.11. feladat. Oldjuk most meg az el˝oz˝o feladatot abban az esetben, ha egy ember több bérletet is nyerhet!
Megoldás: Miként el˝obb, itt is a komplementer esemény valószín˝uségéb˝ol fogjuk meghatározni annak valószín˝uségét, hogy a család legalább egy tagja nyer valamit. Mivel most 420 ember közül úgy sorsolnak ki 10-et, hogy egy ember akár többször is nyerhet, ezért az összes eset száma42010. Azon esetek száma, amikor egyikük sem nyer semmit (vagyis amikor a nyertesek a többi 416 ember közül kerülnek ki)41610. Így azt kapjuk, hogy
P(valamelyikük nyer) = 1−P(egyikük sem nyer) = 1−41610 42010 = 1−
416 420
10
≈1−0,9087 = 0,0913.
⇐3.11. feladat
A 3.10. és a3.11. feladatokban kapott eredmények láthatólag igen közel vannak egymáshoz. Tudjuk azt, hogy ha visszatevéses modellel számolunk (3.11.), akkor a sorsolás folyamán végig állandó annak a valószín˝usége, hogy nem a családhoz tartozó néz˝o nyer. Mivel a kisorsolt bérletek száma (10) viszonylag kevés az összes néz˝o számához (420) és a nem a családhoz tartozó néz˝ok számához (416) képest, ezért ha visszatevés nélküli modellel számolunk (mint a 3.10. feladatban), a sorsolás folyamán akkor is csak kis mértékben változik meg ez a valószín˝uség, így a kapott végeredmény is igen közel lesz a visszatevéses modellel számított értékhez. Ezt részletesebben fogjuk majd tárgyalni a14. leckében.
2. lecke 12. oldal
3.12. feladat. Egy kaparós sorsjegyen azt olvassuk, hogy minden negyedik sorsjegy nyer. Veszünk 3 sorsjegyet.
Mennyi a valószín˝usége, hogy pontoson két nyertes lesz köztük?
Megoldás: Mivel egy kiválasztott sorsjegyet nem adhatunk vissza, ezért itt visszatevés nélküli mintavételr˝ol van szó. Azonban visszatevés nélküli mintavételnél a kérdezett valószín˝uség kiszámításához ismernünk kellene az összes sorsjegy számát is! Mit lehet ilyenkor tenni? El˝oször is feltételezhetjük, hogy az összes sorsjegy száma elég nagy, bizonyára milliós nagyságrend˝u. Mivel a kihúzott sorsjegyek száma mind a nyertes, mind a nyeretlen sorsjegyek számához képest kicsi, ezért akármilyen sorsjegyet húzunk els˝ore, a nyertes szelvények aránya gyakorlatilag nem változik; ugyanez mondható el a többi húzás esetén is. Vagyis dolgozhatunk úgy, mintha a nyertes szelvények aránya minden egyes húzás során1/4lenne. Ez pedig azt jelenti, hogy visszatevés nélküli mintavétel helyett visszatevésessel számolunk, természetesen így a kérdéses valószín˝uség egy közelít˝o értékét kapjuk.
A feladat szövege szerint minden negyedik sorsjegy nyer, ami azt jelenti, hogy a nyertes szelvények aránya 14, azazp= 14. Így a kérdéses valószín˝uség közelít˝o értéke
P(2 nyertes sorsjegy)≈ 3
2
·1 4
2
·3 4
1
= 0,140625.
Arra, hogy mikor alkalmazható ez módszer, a14. leckében még visszatérünk. ⇐3.12. feladat
Önellen ˝orzés
1.A0,1,2,3,4,5számjegyekb˝ol hány valódi hatjegy˝u, 5-re végz˝od˝o szám készíthet˝o, ha minden számjegyet csak egyszer használhatunk fel?
2.Kitöltünk egy ötöslottó szelvényt. Mennyi a valószín˝usége, hogy legalább két találatunk lesz?
0,0233 0,225 0,0314 0,0195
3.Nyolcan moziba mennek. Egy nyolc székes sorba ülnek le, a jegyeket véletlenszer˝uen osztják el egymás közt. Mennyi a valószín˝usége, hogy András és Viki egymás mellett fog ülni?
4.A 32 lapos magyar kártya csomagból visszatevéses mintavétellel kiválasztunk 3 lapot. Mennyi a valószín˝usége, hogy pontosan egy piros lesz a kiválasztott lapok között? Az eredményt három tizedesjegy pontossággal adja meg!
5.Feldobunk egy dobókockát háromszor egymás után. Mi a valószín˝usége, hogy a dobott számok közt lesz páros is?
Megold.
Megold.
Megold.
Megold.
3. LECKE
A geometriai valószín ˝uségi mez ˝o
3.2. A geometriai valószín˝uségi mez˝o
A klasszikus valószín˝uségi mez˝o csak olyan esetekben használható, amikor véges sok elemi eseményünk van, és ezek valószín˝usége megegyezik. El˝ofordulhat azonban, hogy egy kísérletben a szóba jöhet˝o elemi események száma nem véges, de még csak nem is megszámlálhatóan végtelen. Ilyenkor a klasszikus értelmezés természetesen nem alkalmazható. Ennek ellenére bizonyos esetekben számolhatunk a jó esetek száma
összes eset száma formulával analóg módon.
3.2. definíció: Ha egy kísérlettel kapcsolatos események egy geometriai alakzat részhalmazainak feleltethet˝ok meg úgy, hogy az egyes események valószín˝usége az eseményekhez rendelt részhalmaz geometriai mértékével (hosszúság, terület, térfogat) arányos, akkor az események és valószín˝uségeik geometriai valószín˝uségi mez˝ot alkotnak. LegyenA egy ilyen kísérlettel kapcsolatos esemény. A kísérlettel kapcsolatban szóba jöv˝o teljes alakzat mértéke legyenM, azAeseménynek megfelel˝o részalakzaté pedigm . AzAesemény valószín˝usége ekkor a következ˝o módon számolható:
P(A) = m M.
A definíció szerint tehát akkor beszélünk geometriai valószín˝uségi mez˝or˝ol, ha a teljes eseménytérnek egy geometriai alakzat feleltethet˝o meg, továbbá minden eseménynek ennek az alakzatnak egy részhalmaza feleltethet˝o meg oly módon, hogy az esemény valószín˝usége csak az alakzat mértékét˝ol (hossz/terület/térfogat) függ, míg az alakzat elhelyezkedését˝ol és alakjától független.