VÉGESELEM-MÓDSZER
A projekt keretében elkészült tananyagok:
Anyagtechnológiák Materials technology Anyagtudomány
Áramlástechnikai gépek CAD tankönyv
CAD Book
CAD/CAM/CAE elektronikus példatár CAM tankönyv
Méréstechnika
Mérnöki optimalizáció Engineering Optimization Végeselem-analízis
Finite Element Methode
Szerkesztette:
KOVÁCS ÁDÁM
Írta:
MOHAROS ISTVÁN OLDAL ISTVÁN
SZEKRÉNYES ANDRÁS
VÉGESELEM-MÓDSZER
Egyetemi tananyag
Gépészmérnöki Kar Óbudai Egyetem
Bánki Donát Gépész- és Biztonságtechnikai Mérnöki Kar
Szent István Egyetem Gépészmérnöki Kar
2011
Gazdaságtudományi Egyetem Gépészmérnöki Kar,
Moharos István, Óbudai Egyetem Bánki Donát Gépész- és Biztonságtechnikai Mérnöki Kar, dr. Oldal István, Szent István Egyetem Gépészmérnöki Kar
LEKTORÁLTA: Horváthné dr. Varga Ágnes, dr. Keppler István, dr. Pomázi Lajos, dr. Uj József
Creative Commons NonCommercial-NoDerivs 3.0 (CC BY-NC-ND 3.0) A szerző nevének feltüntetése mellett nem kereskedelmi céllal szabadon másolható, terjeszthető, megjelentethető és előadható, de nem módosítható.
ISBN 978-963-279-539-3
KÉSZÜLT: a Typotex Kiadó gondozásában FELELŐS VEZETŐ: Votisky Zsuzsa
TÁMOGATÁS:
Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0029 számú, „KMR Gépészmérnöki Karok informatikai hátterű anyagai és tartalmi kidolgozásai” című projekt keretében.
KULCSSZAVAK:
Végeselem-módszer, ANSYS, COSMOS/M, rúdfeladat, hajlított rúd, síkfeszültség, síkalakváltozás, rúdszerkezet, forgásszimmetrikus, lemez, héj
ÖSSZEFOGLALÁS:
A tananyag ismerteti a végeselem-módszer kialakulásának történetét, matematikai alapjait és szerepét a gépészmérnöki tervezői munkában. Tárgyalja a módszer megértéséhez szükséges kontinuummechanikai alapfogalmakat és egyenleteket. Bemutatja a tervező munkákban leggyakrabban használt elemtípusokat (rúd, gerenda, sík, tengelyszimmetrikus, vékony lemez és héjelemek). A teljes potenciális energia minimum elvéből kiindulva tartalmazza a térben diszkretizált lineárisan rugalmas testekre vonatkozó mátrix egyensúlyi egyenlet levezetését és a különféle
modellekre vonatkozó együttható mátrixok felépítését. Rúdfeladatoknál bemutatja a mozgásegyenlet felépítését és a sajátfrekvenciák számítási módját.
Az elméleti fejezetek megértését nagyban elősegíti a számos kidolgozott mintapélda és az ipari
TARTALOMJEGYZÉK
1. A VÉGESELEM-MÓDSZER KIALAKULÁSÁNAK TÖRTÉNETE, A MÓDSZER FEJLŐDÉSE, ELTERJEDÉSE, SZEREPE A GÉPÉSZMÉRNÖKI TERVEZŐI
MUNKÁKBAN ... 11
1.1.Ókori alkalmazás ... 11
1.2.Variációszámítás kialakulása, alapfogalmai ... 12
1.2.1. Brachisztochron (legrövidebb idő)-probléma ... 12
1.2.2. Funkcionálok, variáció ... 14
1.2.3. Direkt módszer ... 16
1.3.Ritz-módszer ... 18
1.4.Modern végelem-módszer kialakulása ... 20
1.4.1. Erőmódszer ... 20
1.4.2. Mozgásmódszer ... 20
1.5.Végeselem-módszer a műszaki gyakorlatban ... 20
1.6.Melléklet ... 22
1.6.1. Variációszámítás műveleti szabályai ... 22
1.6.2. Euler-Lagrange differenciálegyenlet ... 23
Bibliográfia ... 24
2. KONTINUUMMECHANIKAI ALAPFOGALMAK. A RUGALMASSÁGTAN DIFFERENCIÁLEGYENLET-RENDSZERE ÉS PEREMÉRTÉK PROBLÉMÁJA. .... 25
2.1.Kontinuummechanikai alapfogalmak ... 25
2.2.Rugalmasságtan differenciálegyenlet-rendszere és peremérték problémája ... 33
2.2.1. Egyensúlyi egyenletek ... 33
2.2.2. Geometriai egyenletek ... 36
2.2.3. Anyagegyenletek ... 40
2.2.4. Peremfeltételek ... 41
2.2.5. Peremérték probléma ... 41
Bibliográfia ... 42
3. A RUGALMASSÁGTAN ENERGIAELVEI, VARIÁCIÓS ELVEI, VÉGESELEM- MÓDSZER, MEREVSÉGI EGYENLET MEGHATÁROZÁSA ÉS MEGOLDÁSA SÍKBELI, HÚZOTT RÚDELEMRE ... 43
3.1.Közelítő mezők ... 43
3.1.1. Kinematikailag lehetséges elmozdulásmező ... 43
3.1.2. Statikailag lehetséges feszültségmező ... 43
3.2.Virtuális munka elve ... 44
3.3.Potenciális+ energia minimum elve ... 45
3.4.Lagrange-féle variációs elv ... 47
3.5.Mozgásmódszeren alapuló végeselem-módszer ... 48
3.5.1. Vektormezők bevezetése ... 48
3.5.2. Rugalmasságtani probléma és megoldási módszere ... 51
3.5.3. Végeselem, közelítő elmozdulásmező ... 52
3.6.Merevségi egyenlet meghatározása és megoldása síkbeli, húzott rúdelemre ... 55
3.6.1. Merevségi egyenlet 2D húzott rúdelemre ... 55
3.6.2. Példa ... 60
Bibliográfia ... 63
4. SÍKBELI HÚZOTT RUDAK VIZSGÁLATA VÉGESELEM MÓDSZEREN ALAPULÓ
PROGRAMRENDSZER SEGÍTSÉGÉVEL ... 64
4.1.Síkbeli rúdszerkezetek ... 64
4.2.A rúdszerkezetek modellezéséhez alkalmazott végeselemek ... 65
4.2.1. TRUSS elemek tulajdonságai ... 65
4.2.2. A BEAM elemek tulajdonságai ... 66
4.3.Feladat megoldás ... 67
4.4.Megjegyzések ... 76
5. SÍKBELI HAJLÍTOTT RUDAK VARIÁCIÓS FELADATA, MEREVSÉGI EGYENLETEI, MEGOLDÁSA VÉGESELEM-MÓDSZERREL ... 77
5.1.Síkbeli hajlított rúdelem variációs feladata ... 77
5.2.Feladatmegoldás végeselem-módszerrel ... 79
5.2.1. Az elem merevségi mátrixa ... 79
5.2.2. A szerkezet teljes merevségi mátrixa ... 85
5.2.3. A teljes egyenletrendszer és megoldása ... 86
5.3.Megjegyzések ... 87
6. SÍKBELI HAJLÍTOTT RUDAK VIZSGÁLATA VÉGESELEM MÓDSZEREN ALAPULÓ PROGRAMRENDSZEREK SEGÍTSÉGÉVEL ... 88
6.1.rúdszerkezetek ... 88
6.2.A modellezés során alkalmazott végeselemek ... 88
6.2.1. A BEAM elemek tulajdonságai ... 89
6.2.2. A nyírásból származó alakváltozás figyelembevétele ... 89
6.3.Feladat megoldás ... 91
6.4.Megjegyzések ... 104
7. A POTENCIÁLIS ENERGIA MINIMUM ELVÉNEK ALKALMAZÁSA TÉRBELI HAJLÍTOTT RÚDELEMRE, RITZ-MÓDSZER ÉS VÉGESELEM MÓDSZER ALKALMAZÁSA ... 106
7.1.Térbeli rúdelem variációs feladata ... 106
7.2.Feladatmegoldás végeselem módszerrel ... 111
7.3.Megjegyzések ... 114
8. TÉRBELI HAJLÍTOTT RUDAK VIZSGÁLATA VÉGESELEM MÓDSZEREN ALAPULÓ PROGRAMRENDSZEREK SEGÍTSÉGÉVEL ... 115
8.1.Térbeli rúdszerkezetek ... 115
8.2.A modellezés során alkalmazott végeselemek ... 115
8.2.1. A BEAM3D elemek tulajdonságai ... 116
8.2.2. A BEAM3D elem speciális tulajdonságai ... 118
8.3.Feladat megoldás ... 121
8.4.Megjegyzések ... 136
9. RÚDSZERKEZETEK DINAMIKÁJA, A TÖMEGMÁTRIX BEVEZETÉSE, SAJÁTFREKVENCIA MEGHATÁROZÁSA ... 137
9.1.A végeselem-módszer kiterjesztése ... 137
9.2.Rugalmas testek sajátrezgés feladatának végeselemes megfogalmazása ... 137
9.3.Síkbeli rúdszerkezet sajátlengéseinek számítása végeselem módszerrel ... 139
9.3.1. Az elem tömegmátrixának meghatározása ... 140
9.3.2. Az elem merevségi mátrixának meghatározása ... 142
9.3.3. Az rendszer teljes tömeg- és merevségi mátrixa ... 143
9.4.Megjegyzések ... 145
10. TÉRBELI RUDAK DINAMIKAI VIZSGÁLATA, SAJÁTFREKVENCIA MEGHATÁROZÁSA VÉGESELEM-MÓDSZEREN ALAPULÓ
PROGRAMRENDSZEREK SEGÍTSÉGÉVEL ... 147
10.1. Bevezetés ... 147
10.2. Az alkalmazott végeselemek tulajdonságai ... 147
10.3. A feladat ismertetése ... 148
10.4. A feladat végeselemes megoldása ... 149
10.5. Megjegyzések ... 158
11. BEVEZETÉS SÍKFELADATOK TÉMAKÖRBE. SÍKFESZÜLTSÉGI, SÍKALAKVÁLTOZÁSI ÉS FORGÁSSZIMMETRIKUS (TENGELYSZIMMETRIKUS) MODELLEK ALKALMAZÁSA ... 159
11.1. Síkfeladatok alaptípusai ... 159
11.2. Egyensúlyi egyenlet, elmozdulás és alakváltozás ... 160
11.3. Konstitutív egyenletek ... 162
11.3.1. Síkfeszültségi állapot ... 163
11.3.2. Síkalakváltozási állapot ... 164
11.4. Síkfeladatok alapegyenletei ... 165
11.4.1. Kompatibilitási egyenlet ... 165
11.4.2. Az Airy-féle feszültségfüggvény ... 166
11.4.3. A Navier-féle egyenlet ... 167
11.4.4. Peremérték-feladatok ... 168
11.5. Példák síkfeszültségi állapotra ... 169
11.5.1. Négyzet alakú lemez peremterhelésének meghatározása ... 169
11.5.2. Tangenciálisan terhelt lemez vizsgálata ... 171
11.6. Síkfeladatok alapegyenletei polárkoordináták segítségével ... 173
11.7. Tengelyszimmetrikus síkfeladatok ... 176
11.7.1. Tömör körhenger és vastagfalú cső ... 177
11.7.2. Forgó tárcsák ... 179
Bibliográfia ... 183
12. SÍKFESZÜLTSÉGI ÁLLAPOT MODELLEZÉSE VEM PROGRAMRENDSZEREK SEGÍTSÉGÉVEL. MODELLEZÉS, KIÉRTÉKELÉS PROBLÉMAKÖRÉNEK ELEMZÉSE ... 185
12.1. Síkfeladatok végeselemes megoldása ... 185
12.2. Lineáris három csomópontos háromszögelem ... 187
12.2.1. Az elmozdulásmező interpolációja ... 187
12.2.2. A merevségi mátrix számítása ... 190
12.2.3. A terhelések megadása ... 191
12.3. Kidolgozott példa lineáris háromszögelemre – síkfeszültségi állapot ... 193
12.4. Kvadratikus hat csomópontos háromszögelem ... 202
12.5. Izoparametrikus négy csomópontos négyszögelem ... 202
12.5.1. A geometria interpolációja ... 202
12.5.2. Az elmozdulásmező interpolációja ... 206
12.5.3. Az alakváltozási jellemzők számítása, Jacobi mátrix és Jacobi determináns206 12.5.4. A Jacobi determináns jelentősége, példa ... 209
12.5.5. A feszültségmező számítása ... 211
12.5.6. A merevségi mátrix számítása ... 211
12.5.7. A tehervektor számítása ... 212
12.6. Numerikus integrálás, a Gauss-féle szabály ... 214
12.6.1. Egydimenziós Gauss-szabály ... 215
12.6.2. Kétdimenziós Gauss-szabály ... 216
12.7. Kidolgozott példa az izoparametrikus négyszögelem alkalmazására ... 219
12.8. Kvadratikus izoparametrikus négyszögelem ... 225
Bibliográfia ... 227
13. FORGÁSSZIMMETRIKUS ÁLLAPOT MODELLEZÉSE VEM PROGRAMRENDSZEREK SEGÍTSÉGÉVEL. MODELLEZÉS, KIÉRTÉKELÉS PROBLÉMAKÖRÉNEK ELEMZÉSE ... 228
13.1. Tengelyszimmetrikus feladatok végeselemes megoldása ... 228
13.2. Forgásszimmetrikus lineáris háromszögelem ... 231
13.3. Kidolgozott példa tengelyszimmetrikus háromszögelemre ... 233
13.4. Forgásszimmetrikus izoparametrikus négyszögelem ... 237
13.5. Kidolgozott példa tengelyszimmetrikus, izoparametrikus négyszögelemre ... 240
Bibliográfia ... 248
14. VÉKONYFALÚ HÉJAK, LEMEZEK MODELLEZÉSE. A VÉGESELEM HÉJMODELLEK ELMÉLETÉNEK BEMUTATÁSA ... 249
14.1. Lemez és héjmodellek ... 249
14.2. A Kirchhoff-féle lemezelmélet alapegyenletei ... 249
14.2.1. Az elmozdulásmező ... 249
14.2.2. Az alakváltozási jellemzők ... 250
14.2.3. A feszültségmező és a középfelület igénybevételei ... 250
14.2.4. Az egyensúly és mozgásegyenletek ... 252
14.3. Vékony lemezek végeselemes megoldásának egyenletei ... 255
14.4. A technikai héjelmélet alapegyenletei ... 257
14.4.1. Geometriai összefüggések ... 257
14.4.2. Élerők és élnyomatékok, egyensúlyi egyenletek ... 260
14.4.3. Elmozdulásmező, alakváltozási jellemzők ... 261
14.4.4. Közelítések a technikai héjelmélet keretein belül ... 263
14.5. Héjak végeselemes modellezésének főbb lépései ... 264
Bibliográfia ... 266
15. SÍKBELI ÉS SÍKRA MERŐLEGES TERHELÉSŰ, SÍKBELI VÉKONYFALÚ HÉJAK MODELLEZÉSE VÉGESELEM-MÓDSZEREN ALAPULÓ PROGRAMRENDSZEREK SEGÍTSÉGÉVEL ... 267
15.1. Hajlított lemezelemek ... 267
15.2. Háromszög alakú sík lemezelem vagy Tocher-féle háromszögelem ... 267
15.3. Kidolgozott példa a Tocher-féle háromszög alakú lemezelem alkalmazására ... 272
15.4. Inkompatibilis téglalap alakú lemezelem ... 275
15.5. Kidolgozott példa az inkompatibilis téglalap alakú lemezelemre ... 280
15.6. Kompatibilis téglalap alakú lemezelem ... 283
15.7. Síkbeli és síkra merőleges terhelésű lemezek ... 286
Bibliográfia ... 286
16. TÉRBELI VÉKONYFALÚ HÉJAK MODELLEZÉSE VÉGESELEM-MÓDSZEREN ALAPULÓ PROGRAMRENDSZEREK SEGÍTSÉGÉVEL ... 287
16.1. Egyszerű síkhéj-elemek ... 287
16.2. A lineáris síkmembrán és a Tocher-féle hajlított háromszögelem szuperpozíciója ... 287
16.3. Kidolgozott példa a lineáris síkmembrán és a Tocher-féle (hajlított) háromszögelem összekapcsolására ... 293
Bibliográfia ... 299
17. EGYSZER ÉS KÉTSZER GÖRBÜLT HÉJAK MODELLEZÉSE VÉGESELEM-
MÓDSZEREN ALAPULÓ PROGRAMRENDSZEREK SEGÍTSÉGÉVEL ... 300
17.1. Görbült héjelemek ... 300
17.2. Vékony körhenger-héjelem ... 300
17.3. Forgásszimmetrikus héjfeladatok – kúpos héjelem ... 307
17.4. Vastagfalú héjelemek ... 313
17.5. Átmeneti elem héjelem és térbeli elem összekapcsolásához ... 319
Bibliográfia ... 320
18. TÉRBELI FELADATOK VIZSGÁLATA VÉGESELEM-MÓDSZEREN ALAPULÓ PROGRAMRENDSZEREK SEGÍTSÉGÉVEL. 3D-S ELEMEK BEMUTATÁSA. .... 321
18.1. Hexaéder elemek ... 321
18.1.1. 8 csomópontú hexaéder elem ... 322
18.1.2. 20 csomópontú hexaéder elem ... 324
18.1.3. 32 csomópontú hexaéder elem ... 325
18.1.4. Pentaéder elemek ... 327
18.2. Tetraéder elemek ... 327
18.2.1. 4 csomópontú tetraéder elem ... 330
18.2.2. 10 csomópontú tetraéder elem ... 331
18.2.3. 20 csomópontú tetraéder elem ... 334
18.3. Hierarchikus alakfüggvények ... 335
18.4. Merevségi mátrix és csomóponti terhelések előállítása ... 335
18.4.1. Gauss-féle numerikus integrálás ... 335
18.4.2. 3D-s elemek merevségi mátrixának előállítása ... 336
18.4.3. Csomóponti terhelések előállítása térfogati terhelésből ... 337
18.4.4. Csomóponti terhelések előállítása felületi terhelésből ... 337
Bibliográfia ... 339
19. TÉRBELI FELADATOK VIZSGÁLATA VÉGESELEM-MÓDSZEREN ALAPULÓ PROGRAMRENDSZEREK SEGÍTSÉGÉVEL. 3D-S ELEMEK ALKALMAZÁSA. . 340
19.1. Geometriai modell létrehozása ... 340
19.1.1. Eredeti geometria kiegészítése ... 340
19.1.2. Élek, sarkok modellezése ... 341
19.1.3. Terheletlen részek modellezése ... 341
19.1.4. Szimmetrikus alkatrészek modellezése ... 342
19.2. Végeselem-modell létrehozása ... 342
19.2.1. Hálózás beállításai ... 343
19.2.2. Elemméret hatása ... 343
19.2.3. Elemtípus hatása ... 345
19.3. Peremfeltételek ... 347
19.3.1. Terhelések ... 348
19.3.2. Kényszerek ... 350
20. MODELLEZÉSI, PONTOSSÁGI, ALKALMAZHATÓSÁGI KÉRDÉSEK. A KÜLÖNBÖZŐ VÉGESELEM MODELLEK ÖSSZEHASONLÍTÁSA, EREDMÉNYEK VIZSGÁLATA. ... 353
20.1. Tartók modellezése ... 353
20.1.1. Kör keresztmetszetű tartó vizsgálata ... 353
20.1.2. Vékony falú zárt szelvényű rúd modellezése ... 355
20.1.3. Vékony falú nyitott szelvényű rúd modellezése ... 357
20.1.4. Vastag falú cső modellezése ... 363
Bibliográfia ... 367
21. SZÁMÍTÁSI EREDMÉNYEK KIÉRTÉKELÉSE ÉS ALKALMAZÁSA A GÉPÉSZMÉRNÖKI TERVEZÉSI ÉS MINŐSÍTÉSI FELADATOK MEGOLDÁSÁBAN. VÉGESELEM SZÁMÍTÁSOK ÉS SZABVÁNYOS MÉRETEZÉSI ELJÁRÁSOK KAPCSOLATA. ... 368
21.1. Végelem-módszer pontossága ... 368
21.1.1. Hibabecslés h típusú közelítéskor ... 370
21.1.2. Hibaszámítás h típusú közelítéskor ... 377
21.1.3. p típusú közelítés ... 380
21.1.4. Konvergencia szinguláris helyeken ... 381
21.1.5. Modellezési hibák ... 381
21.2. Számított eredmények kiértékelése ... 381
21.2.1. Folyáshatárnál magasabb feszültségek ... 381
21.2.2. Szinguláris helyek ... 382
21.2.3. Szabványos eljárások és a VEM ... 382
Bibliográfia ... 383
1. A VÉGESELEM-MÓDSZER KIALAKULÁSÁNAK TÖRTÉNETE, A MÓDSZER FEJLŐDÉSE, ELTERJEDÉSE, SZEREPE A GÉPÉSZ- MÉRNÖKI TERVEZŐI MUNKÁKBAN
1.1. Ókori alkalmazás
Véges elemek: alkalmazásukkal bonyolult (és adott körülmények között nem megoldható) feladatokat egyszerűsítünk le. Az egyszerűsítés alapja, hogy a test geometriáját véges számú kisebb, egyszerűbb alakú elemre bontjuk, így megoldhatóvá válik a probléma. Ekkor a keve- sebb, de bonyolultabb számítás helyett több, de egyszerűbb számítást kell elvégeznünk.
A diszkretizáció alkalmazása geometriai problémák megoldására – kör kerülete, területe (1.1 ábra)
– henger, gömb térfogata, – egyéb bonyolult geometriák.
a) b)
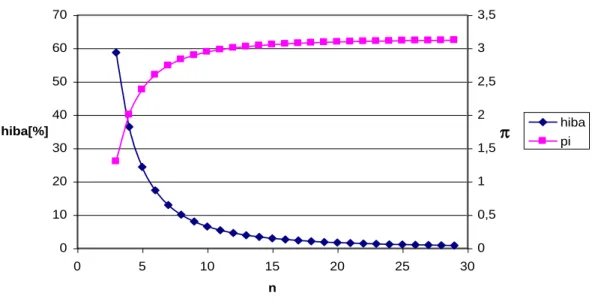
1.1. ábra: Kör területének közelítése
A kör területének számításakor a körlapot n darab egyenlő szárú háromszögre bontjuk 1.1.a) ábra szerint. Ekkor a közelítő értékének és hibájának alakulása a felosztás függvényében látható az 1.2. ábrán, ahol
n n n
2 sin 360 2
cos 360
, és 2 100%
sin 360 2
cos 360
n n n
hiba .
1.2. ábra: π számított értéke és hibája a felosztás növelésekor
Tszu Csang Csik kínai mérnök (i. sz. 480-ban) feltételezhetően téglalapok segítségével megál- lapította, hogy értéke 3,1415926 és 3,1415927 között van.
1.2. Variációszámítás kialakulása, alapfogalmai 1.2.1. Brachisztochron (legrövidebb idő)-probléma
1696-ban Bernoulli fogalmazta meg a problémát, amely megoldásának keresése elindította a variációszámítás kifejlődését.
A probléma: adott két különböző magasságban és nem egy függőlegesen egyenesen elhe- lyezkedő pont. Vegyük azokat a két pont által kijelölt függőleges síkban lévő görbéket, ame- lyeken a magasabb pontból kezdősebesség és súrlódás nélkül indítva eljuthat egy anyagi pont az alacsonyabban fekvő pontba. Kérdés, hogy létezik-e ezek között a görbék között olyan, amelyet a pont minimális idő alatt fut be és ha igen, hogyan lehet meghatározni?
1.3. ábra: Brachisztochron-probléma A keresett y függvény grafikonja átmegy P1 és P2 pontokon, tehát:
0 ) 0 (
y és y(x ) y . (1.1)
P1
P2
x
y
x2
y2
0 10 20 30 40 50 60 70
0 5 10 15 20 25 30
n hiba[%]
0 0,5 1 1,5 2 2,5 3 3,5
hiba
pi
Energiamegmaradás tétele adott esetre:
mgy mv2 2
1 . (1.2)
A sebesség:
dt
v ds. (1.3)
Az elemi úthossz:
ds 2 dx 2 dy 2 (1.4)(1.2) tömeggel egyszerűsítve és helyettesítve (1.3) és (1.4)-t:
dt gy dy dt
dx
2 2
2
1 (1.5)
rendezve:
dx gy dx dt dy dt
dx 2
2 2
(1.6)
dt gy dx dx
dy 2
1
2 2
. (1.7)
Szétválasztva a változókat, az út megtételéhez szükséges T idő:
2
0
2
2 '
x 1
y dx g
T y . (1.8)
Keressük azt a függvényt, amely eleget tesz (1.1)-nek és amelyre (1.8)-nak minimuma van. A megoldás egy ciklois:
2 2 1 1
1arcsin 2 )
( c x x c
c c x
t
y , (1.9)
ahol c1,c2 állandók az (1.1) feltételekből meghatározhatók.
Ez a probléma, ahol egy skalár mennyiség minimalizálásához függvényt kellett keresni, irányította a figyelmet a variációszámítás felé és indította el annak fejlődését.
1.2.2. Funkcionálok, variáció
A brachisztochron problémához hasonló a természet- és társadalomtudományokban sokszor előfordul. Találkozunk olyan mutatókkal, mennyiségekkel, amelyek értékét függvények hatá- rozzák meg. Legegyszerűbb eset egy határozott integrál értéke, amely a kiválasztott függ- vénytől függ. De ilyen egy ívhossz, felület, térfogat vagy egy tartó potenciális energiája is. Az ilyen mennyiségeket a funkcionálnak nevezzük.
Valamely halmaznak a valós számok halmazába való leképezését (valós) funkcionálnak vagy operátornak nevezzük.
Az általános matematikai definíciónak egy speciális esete, amikor a függvények halmazát a valós számok halmazába való leképezését nevezzük funkcionálnak.
Legyen: f R3 R adott függvény, és yRR megengedett függvény, amely ér- telmezési tartományán folytonosan deriválható yC1[x1,x2] és átmegy a tartomány szélein rögzített P1 (x1,y1), P2 (x2,y2) pontokon:
1 1) (x y
y , y(x2) y2. (1.10)
Ekkor minden y függvényhez rendeljük hozzá az
2
1
) ( ' ), ( , ]
[
x
x
dx x y x y x f y
I (1.11)
valós számot. Így értelmezzük az I funkcionált.
A feladat legtöbbször a funkcionálok szélsőértékének meghatározása. A szélsőérték lehet abszolút vagy lokális.
Ha I
y funkcionál teljes értelmezési tartományán fennáll y~y függvényre, hogy
y I yI ~ , akkor I
~ abszolút minimum. yHa I
y funkcionál értelmezési tartományának egy részén fennáll, hogy I
y I y~ , akkor
yI ~ lokális minimum.
A variációs probléma klasszikus értelmezése analógiát mutat a differenciálszámítással.
Lagrange a differenciál mintájára bevezette a variációt – a jele – és megadta a vele való műveleti szabályokat. Vizsgáljuk a klasszikus értelmezést:
~ függvény variációja y y, amelyről tudjuk, hogy y(x1)0 és y(x2)0. y a tartomány x1 és x2 végpontjaiban ismert függvényértékeknél eltűnik, közte tetszőleges. Ekkor
y y
y egy függvénysereget (megengedett függvény) ad, amely tartalmazza a megoldást.
A funkcionál variációját úgy értelmezzük, hogy
2
1
x
x
dx f
I
. (1.12)
A feladat ~ megoldását akkor kapjuk, ha a funkcionálnak minimuma van. Variációs meg-y fogalmazásban
0
I . (1.13)
Ez a szélsőérték szükséges feltétele.
Az abszolút és lokális minimum analógiájára egy funkcionál (pl. potenciális energia) mini- mumon alapuló módszer esetében definiálhatjuk egy probléma egzakt és közelítő megoldását.
Egzakt megoldás, ha az összes lehetséges függvény közül választjuk ki azt, amelyikre a funkcionál minimális.
Ennek előállítása csak nagyon egyszerű esetekben lehetséges. A legtöbb esetben az egzakt megoldást nem tudjuk megtalálni, mivel analitikusan nem tudjuk megoldani az egyenleteket, a végtelen számú függvény közül mindet megvizsgálni szintén nem lehetséges. A problémát akkor is meg kell oldani, ha nem tudjuk a pontos megoldást előállítani, ekkor közelítő megol- dást keresünk.
Közelítő megoldás, ha nem az összes lehetséges függvény közül választjuk ki azt, ame- lyikre a funkcionál minimális.
x y
y
x1 x2
P2
P1
y
1.4. ábra: Variáció Lagrange-féle klasszikus értelmezése
A közelítő megoldások megkeresésére jöttek létre a direkt módszerek. Az Euler-féle törött vonalak Euler variációs módszerének elemei voltak. A módszer a matematika modern eszkö- zeinek birtokában újra előtérbe került, és a variációszámítás direkt módszerének alapja.
1.2.3. Direkt módszer
A funkcionál szélső értékét adó extremális függvények meghatározása volt a variációszámítás első problémáinak egyike.
Euler módszerének lényege: vezessük vissza a problémát véges sok változótól függő függvények szélsőértékeinek vizsgálatára. Azaz megengedett függvényeknek véges sok (n számú) adattal leírható függvényeket veszünk és a funkcionálként definiált integrált (1.11) egy közelítő összeggel helyettesítjük. Ha n tart végtelenhez, a közelítő összeg tart az integrál értékéhez.
Euler megoldása: szakaszonként lineáris, folytonos függvények, „Euler-féle törött vona- lak” használata. Osszuk fel
x1,x2
intervallumot n1 egyenlő szakaszra és adjunk meg tet- szőleges 1,...,n valós számokat. Ekkor a szakaszok hossza:1
1 2
n
x t x .
Az
x1,y1
, x1t,1
, x12t,2
,..., x1nt,n
, x2,y2
pontokat összekötő törtvonalak egy folytonos függvényt alkotnak, amelynek két végpontja a rögzített P1 (x1,y1) és) , ( 2 2
2 x y
P .
1.5. ábra: Euler-féle tört vonalak Ekkor az (1.13) funkcionált módosíthatjuk:
t t
i x f I
n
i
i 1 , , 1 , (1.14)
x y
x1 x2
P2
P1
x +it1
i
t
n1: y2
.Ha a funkcionál In közelítő értéke valamely Euler-féle tört vonalon szélsőértéket vesz fel, akkor az
x1,y1
, x1t,1
, x12t,2
,..., x1nt,n
, x2,y2
pontokban0
j
In
, j1,...,n. (1.15)
Vezessük be a parciális deriváltra a függvény alsó indexeként a változót, ami szerint deri- válunk:
y fy f
: ,
: '
' y
fy f
, …
és az alapfüggvényre az
t t j x f
f j : 1 , j,j j 1
jelölést.
Így:
' ' 1
y j y j
y j j
n f t f f
I
. (1.16)
(1.15) és (1.16)-ból rendezve:
' 0
' 1
t f f
fy j y j y j . (1.17)
Ha n, t0 és a tört vonalak sorozata tart egy kétszer folytonosan deriválható y függvényhez, akkor (1.17)-ből előáll
0 ) ' , , ( )
' , ,
( f ' x y y
dx y d y x
fy y , (1.18)
vagy más formában '0
y f dx
d y
f . (1.19)
differenciálegyenlet, amely az f alapfüggvényhez tartozó Euler-Lagrange differenciálegyen- let. Megoldása y, amely az (1.11) funkcionál minimumát adja. Így az (1.13) és (1.18) kifeje- zés egy adott funkcionál szélsőérték keresési probléma különböző megfogalmazását jelenti.
Ezt az egyenletet a matematikában egyparaméteres függvénysereg szélsőértékének vizsgála- tából kapjuk (1.6. melléklet), azonban Euler tört vonalai a direkt módszerek alapját képezik, ezért vizsgáltuk a klasszikus értelmezést.
A törtvonalak alapján vegyük a megengedett függvények valamely k sorozatát és az ab- szolút szélsőértékre vonatkozó probléma k-adik lépésben a
ki i
ai 0
(1.20)
összeget, amely minden lépésben egy függvényt ad. Az így kapott függvénysorozat határ- függvényének (ha konvergens) az extremális voltát vizsgáljuk. Ezt a módszert felhasználhat- juk:
– variációs feladatok közelítő megoldására,
– ha a határfüggvény szélsőértéket vesz fel, akkor kielégíti (1.18)-at, így egy differenciálegyenlet megoldását vezethetjük vissza variációs problémára.
Ezt hívjuk a variációszámítás direkt módszerének.
1.3. Ritz-módszer
A Ritz-módszerben a variációszámítás direkt módszerét alkalmazzuk közelítő megoldás kere- sésére, a végeselem-módszertől eltérően itt még a teljes tartományt egy függvénnyel írjuk le.
Definíció: Legyen n sorozat egy lineáris normált téren és an sorozat valós számokon.
n sorozat teljes, ha minden elemhez létezik
n
an
a11 ...
sorozat, amely tetszőlegesen megközelíti.
Definíció: Legyen I funkcionál, és n sorozat ennek értelmezési tartományán. Azt mond- juk, hogy I minimalizálható n lineáris kombinációinak halmazán, ha teljesül:
– létezik olyan lineáris normált tér, amelynek része I értelmezési tartománya és amelyre
n teljes,
– n minden lineáris kombinációja I értelmezési tartományában van, – minden n esetében létezik In minimális eleme, ahol
n
i i i
I a
Dn
1
: . (1.21)
Ritz tétele szerint, ha I funkcionál n sorozat lineáris kombinációinak halmazán minima- lizálható, I -nek létezik minimális eleme és folytonos, akkor az In funkcionál minimális függvényeiből álló yn sorozat I funkcionál minimalizáló sorozata.
Ritz módszere a rugalmasságtanban
Válasszuk funkcionálnak a rugalmas test potenciális energiáját. n számú, véges paraméter segítségével előállítunk egy kinematikailag lehetséges (definíciók a 3.1.1. és 3.3. fejezetek- ben) elmozdulásmezőt közelítő függvényt. A potenciális energia minimum elve kimondja, hogy a potenciális energia a valós elmozdulások esetében minimális.
A kinematikailag lehetséges elmozdulásmezőt egy függvénysorral közelítjük:
) ,..., , (
... 1 2
1 1 an n u a a an
a u
. (1.22)
Az ebből felírt potenciális energia is ugyanezt az n számú paramétert tartalmazza:
) ,..., ,
(a1 a2 an
. (1.23)
A potenciális energia egy funkcionál, így szélsőértékét
0
(1.24)
esetben veszi fel. Azaz:
0
2 ...
2 1 1
n n
a a a a
a a
. (1.25)
Mivel ez paraméterektől függő integrál, a szélsőértéket a paraméterek szerinti deriváltak zérus értékénél vesz fel:
0
1
a ,
0
2
a ,
…,
0
an , n darab lineáris algebrai egyenlethez jutunk amely a felvett n függvények együtt- hatóit adja. Természetesen, mivel a függvénysort felvesszük, így közelítő megoldást kapunk.
A módszer fontos eleme, hogy az (1.22) elmozdulásmező kinematikailag lehetséges legyen, azaz kielégítse a kinetikai peremfeltételeket. Ilyen függvényeket bonyolultabb esetekben ne- héz találni, ezért egyszerűbb feladatok megoldására alkalmas a módszer. A végeselem- módszer abban jelent előrelépést, hogy a test geometriáját egyszerű elemekre bontja, így kö- zelítő függvények könnyen előállíthatóak.
1.4. Modern végelem-módszer kialakulása 1.4.1. Erőmódszer
1940-es években megjelennek a sugárhajtású repülőgépek. A nagy sebesség miatt bonyolul- tabb geometriájú szerkezetek jelennek meg, csapott és delta szárnyak. Ezek számítására a korábbi módszerek nem felelnek meg. A repülésnél nem lehet a számítási bizonytalanságokat nagy biztonsági tényezőkkel kompenzálni, mert a felhasznált anyagok is drágábbak, valamint az üzemeletetési költségek is megnövekednek. Felmerült az igény egy bonyolult geometriákat is megfelelő pontossággal kezelő számítási módszerre.
Levy alkalmazta először az erőmódszert, amely a klasszikus rugalmasságtan alapjain az erők egyensúlyából indul ki, és ebből számít elmozdulásokat. 1947-ben csapott szárnyú repü- lőgépekre publikálta megoldását. Delta szárny esetében problémák merültek fel az erőmód- szer alkalmazásával, más megközelítésre volt szükség a megoldásához.
1.4.2. Mozgásmódszer
Az erőmódszerrel párhuzamosan kutatások folytak az elmozdulásokon alapuló módszer kifej- lesztésére és alkalmazására. A Boeing cég egy Turner által vezetett kutatócsoportja 1956-ban publikált egy új módszerrel megoldott problémát. Ennek lényege egy feltételezett elmozdulá- sokkal felírt merevségmátrixon alapuló módszer gyakorlati alkalmazása volt, ami a modern végeselem-módszer lényegét már tartalmazta.
A következő évtizedekben megszülettek a két és háromdimenziós alkalmazások, nagy lehajlási és egyéb geometriai és anyagi nemlineáris megoldások.
A konvergencia vizsgálata és a mátrixegyenletek és rugalmasságtani elvek analógiájának felismerése után a 60-as években a rugalmasságtan variációs elveinek alapjára helyezték a végeselem-módszert. Ekkor terjedt el széles körben a virtuális elmozdulások elvén alapuló módszer, és szinte egyeduralkodóvá vált. Az alkalmazott matematikai problémák és kidolgo- zásuk, a számítástechnika fejlődése folyamatosan tart.
A végeselem-módszert ma már szerkezeti, hő-, áramlástani, elektromos, mágneses lineáris és nemlineáris feladatokra és ezek kombinációira, kapcsolt feladatokra is alkalmazzák. A számítógépek teljesítménye és a piacon megtalálható szoftverek kezelhetősége eljutott arra a szintre, hogy a mérnökök kezébe egy könnyen tanulható és felhasználóbarát eszközt adnak.
Azonban az elméleti ismeretek hiányában a peremfeltételek, modellek nem megfelelő kivá- lasztásával a kapott megoldás sok esetben nem a valóságos feladat megoldása.
1.5. Végeselem-módszer a műszaki gyakorlatban
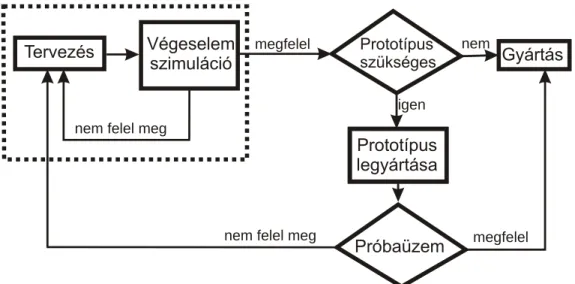
A végeselem-módszer elterjedése a gyakorlatban megváltoztatta a klasszikus gyártási folya- matot (1.6. ábra), beépült a gyártási láncba.
Prototípus legyártása
nem felel meg
Gyártás
Tervezés Próbaüzem megfelel
1.6. ábra: Klasszikus gyártási modell egyszerűsített folyamatábrája
A gyártási költség jelentős része a kísérleti darabok legyártása és próbaüzemének végrehajtá- sa. Mivel ezekhez szükség van anyagra, annak megmunkálására, a próbaüzemhez szükséges peremfeltételek biztosítására, kísérleti eszközökre. Természetesen szükség van mind a proto- típus-gyártás, mind a próbaüzem elvégzéséhez szakszemélyzetre. Ezen költségek csak nagy darabszám és/vagy magas termékár esetén térülnek meg. Ezt a költséget csökkenti jelentős mértékben a végeselemes szimuláció (1.7. ábra).
Prototípus legyártása
Gyártás Tervezés
Próbaüzem
megfelel
nem felel meg
Végeselem
szimuláció Prototípus szükséges
megfelel nem felel meg
igen
nem
1.7. ábra: Végeselemes szimulációval segített gyártási modell
A szükséges prototípusok számát csökkenti a végeselemes szimuláció, amennyiben jól model- lezhető problémáról van szó, akkor akár el is hagyható a prototípus legyártása. Ekkor már a sorozatgyártásra lehet azonnal berendezkedni, és elegendő a nullszérián próbaüzemet végezni.
A szimuláció nemcsak a szilárdsági vizsgálatok területén nyújt segítséget, hanem a tech- nológiai tervezéskor is. Léteznek olyan célszoftverek is, amelyekkel egy fröccsöntési, ková- csolási, mélyhúzási, stb. folyamatot tudunk szimulálni, így ezek a magas szerszámköltségű gyártási módszerek is olcsóbbá válnak.
Elmondhatjuk, hogy a tervezéskor alkalmazott végeselem-modellezés több területre is kiterjed:
– termék szilárdsági, hőtani, áramlástani, elektromos, mágneses vizsgálata, használati körülmények közt, amely a termék minőségét javítja, költségét (pl. súly) csökkenti, – termék gyártás közbeni szimulációja (gyártástechnológia szimulációja), az optimális
költségű, de megfelelő termék gyártástervezéséhez,
– szerszámok szimulációja, amely azok élettartamát, optimális üzemi feltételeit adja.
A végeselem-módszer természetesen nemcsak a gépgyártásban terjedt el, hanem egyéb tu- dományterületeken is. A gépgyártás analógiájára elmondhatjuk, hogy a szükséges prototípu- sok, kísérleti modellek száma csökkenthető, így a tervezés összességében olcsóbb, gyorsabb, pontosabb.
1.6. Melléklet
1.6.1. Variációszámítás műveleti szabályai u függvény, F F(x,u,u') funkcionál.
A függvény variációja annak kismértékű megváltoztatása, jele: u. A funkcionál első variációja:
' u' u u F u
F F
, (1.26)
teljes differenciája:
' '
' du
u du F u dx F x F F
. (1.27)
F1, F2 funkcionál esetén fennáll:
2 1 2
1 )
(F F F F
, (1.28)
2 1 2 1 2
1 )
(F F F F F F
, (1.29)
2 2
2 1 2 1 2
1
F
F F F F F
F
, (1.30)
F nF
Fn n
( ) 1 . (1.31)
u függvényre fennáll:
dx u du
dx
d , (1.32)
u(x)dx
u(x)dx . (1.33)
1.6.2. Euler-Lagrange differenciálegyenlet
Legyen: f R3 R adott függvény (alapfüggvény), és yRR megengedett függ- vény, amely értelmezési tartományán folytonosan deriválható yC1[x1,x2] és átmegy a tartomány szélein rögzített P1 (x1,y1), P2 (x2,y2) pontokon: y(x1) y1, y(x2) y2.
Ekkor minden y függvényhez rendeljük hozzá az
2
1
) ( ' ), ( , ]
[
x
x
dx x y x y x f y
I (1.34)
valós számot.
Keressük azt az y függvényt, amelyre I[y] funkcionál stacionárius. (Egyéb feltételek mellett szélső értéket vesz fel).
Legyen: RR tetszőleges függvény, rögzített pontokkal 0
) ( )
(x1 x2
, (1.35)
és R valós szám. Ekkor definiálható egy R2 R egyparaméteres függvénysereg:
) ( ) ( ) ,
(x y x x
. (1.36)
x y
(x, )
y= (x)
x1 x2
P2
P1
y(x)
1.8. ábra: A variációs feladat megoldása és variált görbéi (1.34)-ba (1.36)-ot helyettesítve:
2
1 2
1
) ( ' ) ( ' ), ( ) ( , )
( ' ), ( ,
x
x x
x
dx x x
y x x
y x f dx x x x f
I . (1.37)
Adott (x) függvény esetén I funkcionál csak függvénye. I() akkor lesz stacionári- us (teljesíti a szélsőérték szükséges feltételét), ha
0
d
dI , (1.38)
és
0
. (1.39)
A paraméteres integrálok differenciálási szabályai szerint:
' 0 ' '
'
2
1 2
1 2
1
x
x x
x x
x
y dx dx f
y dx f
y f y
f d
dI
. (1.40)
' ' y f
integráljára alkalmazzuk a parciális integrálás szabályát:
2 1 2
1 2
1 ' ' ' '
x
x x
x x
x
y dx f dx
d y
dx f y
f
. (1.41)
(1.41) jobb oldalának első tagja zérus (1.35) szerint, ennek megfelelően (1.40)-be helyet- tesítve:
' 0
2
1
x
x
y dx f dx
d y
f . (1.42)
Mivel tetszőleges, így az integrál csak akkor lehet zérus, ha 0 '
y f dx
d y
f .
Ezt Euler-Lagrange differenciálegyenletnek nevezzük.
Bibliográfia
[1] Páczelt István, Végeselem-módszer a mérnöki gyakorlatban, I. kötet. Miskolci Egye- temi Kiadó, Miskolc, 1999.
[2] Égert János, Keppler István, A végeselemmódszer mechanikai alapjai, Universitas- Győr Kft., Győr, 2007.
[3] Kósa András, Variációszámítás, Tankönyvkiadó, Budapest, 1973.
2. KONTINUUMMECHANIKAI ALAPFOGALMAK.
A RUGALMASSÁGTAN DIFFERENCIÁLEGYENLET-RENDSZERE ÉS PEREMÉRTÉK PROBLÉMÁJA.
2.1. Kontinuummechanikai alapfogalmak
Modell: a vizsgált jelenséghez hasonlóan viselkedő, annak egyszerűsített mása.
Szilárdságtani problémák megoldásához szükségünk van:
– geometriai, – anyag-,
– kapcsolati (terhelés, kényszer) modellekre.
A geometriai modellek dimenzió szerint lehetnek:
– 0 dimenziós: pontszerű test, ha elhanyagoljuk az összes geometriai méretét,
– 1 dimenziós: ha egyik mérete a másik két kiterjedéséhez képest elhanyagolható. A klasszikus rudak, tartók, rácsos szerkezetek, és a végeselem-módszerben használt vonalelemek.
– 2 dimenziós: egy mérete elhanyagolható a másik két méretéhez képest. Lemezek, héjak.
– 3 dimenziós: testmodell, egyik méretét sem hanyagoljuk el. Azonban ez legtöbbször nem jelenti a teljes geometriát, mert a mechanikai szempontból elhanyagolható, de a számítási igény növelő részeit fölösleges a modellben megjeleníteni.
Kontinuum (test) modell: folytonos (folytonosan deriválható) függvényekkel leírható, tetszőleges számú (végtelen) részre felosztható modell. A kontinuum testek pontjait adott koordinátarendszerben
k z j y i x
r (2.1)
vektorral írjuk le.
dx y
z
dy dz
x
kontinuum test elemi térfogat
r j i
k
2.1. ábra: Kontinuum test és elemi hasáb
Elemi test: egy kontinuum test elemi (tetszőlegesen kis méretű) része, modelltől függően elemi tömeg vagy elemi térfogat.
Merev test: olyan test, amely bármely két pontjának távolsága állandó. Függetlenül a terhelés nagyságától.
Rugalmas test: alakváltozásra képes test. Terhelés hatására pontjainak távolsága változik.
Lineárisan rugalmas anyagmodell: a terhelés és alakváltozás közt lineáris függvény- kapcsolat van.
Nemlineárisan rugalmas anyagmodell: a terhelés és alakváltozás közt nemlineáris függ- vénykapcsolat van.
Képlékeny anyagmodell: az anyag a terhelés megszűnése után nem nyeri vissza eredeti alakját. Számos képlékeny anyagmodell létezik a lineáris és nemlineáris ill. rugalmas és kép- lékeny tulajdonságok dominanciájától függően.
lineárisan rugalmas nemlineárisan rugalmas képlékeny
2.2. ábra: Anyagmodellek
Izotróp anyag: az anyag viselkedése iránytól független, bármelyik irányban azonos tulaj- donságokat mutat.
Elmozdulásvektor: a test egy pontjának elmozdulásvektora a test adott pontjának terhe- lés előtti P és utáni P' helyzetének (helyvektorának) különbsége.
k w j v i u
uP P P P (2.2)
Elmozdulásmező: a test összes pontjának elmozdulásvektora a (2.1) helyvektor függ- vényében.
k r w j r v i r u r
u( ) ( ) ( ) ( ) (2.3)
Kis elmozdulás: a test pontjainak elmozdulása elhanyagolhatóan kicsi a test geometriai méreteihez képest.
Kinematikai peremfeltételek: a test ismert (vagy előírt) elmozdulásai.
Dinamikai peremfeltételek: a test ismert (vagy előírt) terhelései.
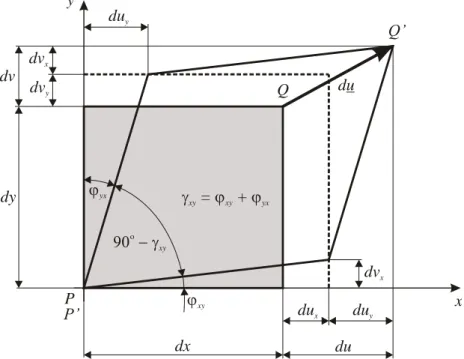
Alakváltozás: a test egyes pontjainak egymáshoz képest történő fajlagos (egységnyi hosszra vonatkozó) elmozdulása.
– fajlagos nyúlás: a vektor hosszának megváltozása,
– szögtorzulás: az egymásra merőleges tengelyek szögváltozása (2.4.b. ábra), a szög- torzulás szimmetrikus.
– A merevtest-szerű mozgást (2.4.a. ábra) nem vesszük figyelembe.
y
z x
rP
P
P’
uP
terhelés előtt
terhelés után rP’
2.3. ábra: Elmozdulásvektor
Alakváltozási vektor: adott irányú egységvektor eltolódását leíró vektor. i,j,k egységvektorokkal (triéder) értelmezve:
k j
i
ax x xy xz 2 1 2
1
, (2.4)
k j
i
ay yx y yz 2 1 2
1
, (2.5)
k j i
az zx zy z 2
1 2
1 , (2.6)
ahol
zx xz zy yz yx
xy
, , .
A vektorok koordinátáinak tulajdonságai:
– fajlagos nyúlások: x,y,z mértékegység nélküli jellemzők,
0
, a hossz növekszik,
0
, a hossz csökken.
– szögtorzulások: xy,yz,xz mértékegységük radián
0
, a szög csökken,
0
, a szög növekszik.
P
x y
x
P’ P’
y
1
y
yx
xy = xy +yx
a) b)
2.4. ábra: Merevtest-szerű mozgás és alakváltozás x-y síkban
Alakváltozási állapot: adott pontban az összes irányhoz tartozó alakváltozási vektorok összessége. Leírása lehetséges: egységkocka triéderének alakváltozási vektoraival, alak- változási tenzorral, Mohr-körön.
Tenzor: lineáris, homogén vektor-vektor függvény. Leírása diadikus formában vagy adott koordinátarendszerben definiált mátrixszal.
Alakváltozási tenzor: rugalmas test adott pontjának alakváltozási állapotát írja le úgy, hogy tetszőleges irányhoz hozzárendeli az adott irány alakváltozási vektorát. Adott koordinátarendszerben leírt vektorhármassal definiálható diadikus vagy mátrixos formában.
– Diadikus formában:
k a j a i
ax y z
. (2.7)
– Mátrixos formában:
z yz xz
zy y
xy
zx yx
x
2 1 2
1 2
1 2
1 2
1 2
1
, (2.8)
amely oszlopaiban x, y, z irányhoz tartozó alakváltozási vektorok koordinátái szerepelnek.
n egységvektorral definiált irányhoz tartozó an alakváltozási vektor:
n
an . (2.9)
y
z
x
x
i j
k
y
z
xy
2 1
xz
2 1
yx
2 1
yz
2 1
zx
2 1
zy
2 1
2.5. ábra: Alakváltozási állapot alakváltozási vektorkoordinátákkal
Alakváltozási tenzormező: a test összes pontjának alakváltozási tenzora a helyvektor függvényében.
r r
r
r r
r
r r
r r
z yz
xz
zy y
xy
zx yx
x
2 1 2
1
2 1 2
1
2 1 2
1
(2.10)
Feszültség: a test belső felületén megoszló erőrendszer sűrűségvektora (intezitása).
Mértékegysége: Pa
m
N 1
1 2 .
Feszültségvektor: a feszültséget feszültségvektorral adjuk meg. Adott pontban, n irányhoz, dA felületelemhez rendelt
n feszültségvektor:
dA F d
n
. (2.11)
– Adott felületen a feszültségvektor felületre merőleges koordinátáját normál feszültségnek nevezzük, jele: .
0
, húzás esetén,
0
, nyomás esetén.
– A feszültségvektor felülettel párhuzamos koordinátáit csúsztató feszültségeknek nevezzük, jele: .
k j
i, , vektorokkal definiált felületeken a feszültségvektorok:
k j
i xy xz
x x
, (2.12)
k j
i y yz
y yx
, (2.13)
k j i zy z
z zx
, (2.14)
ahol xy yx,yz zy,xz zx.
Feszültségállapot: adott pontban az összes irányhoz tartozó feszültségvektorok összes- sége. Leírása lehetséges: elemi hasábon feszültségvektorok koordinátáival, feszültségi ten- zorral, Mohr-körön.