Szétválasztási hálózatok szintézise: különböző tulajdonságokon alapuló szétválasztó módszerek egyidejű alkalmazása

(1)

Szétválasztási hálózatok szintézise:

Különböző tulajdonságokon alapuló szétválasztó módszerek egyidejű

alkalmazása

Doktori (PhD) értekezés

Heckl István

témavezető: Dr. Friedler Ferenc

Pannon Egyetem

Műszaki Informatikai Kar

Informatikai Tudományok Doktori Iskola

2007

(2)

Szétválasztási hálózatok szintézise: Különböző tulajdonságokon alapuló szétválasztó módszerek egyidejű alkalmazása

Értekezés doktori (PhD) fokozat elnyerése érdekében Írta: Heckl István

Készült a Pannon Egyetem Informatikai Tudományok Doktori Iskolája keretében Témavezető: Dr. Friedler Ferenc

Elfogadásra javaslom (igen / nem)

(aláírás) A jelölt a doktori szigorlaton ...%-ot ért el

Veszprém ...

a Szigorlati Bizottság elnöke Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: ... (igen / nem)

(aláírás) Bíráló neve: ... (igen / nem)

(aláírás)

A jelölt az értekezés nyilvános vitáján ...%-ot ért el

Veszprém ...

a Bíráló Bizottság elnöke

A doktori (PhD) oklevél minősítése: ...

...

Az EDT elnöke

(3)

Tartalomjegyzék

Tartalomjegyzék ... iii

Táblázatok jegyzéke ...v

Ábrák jegyzéke ...vi

Kivonat ...ix

Abstract...x

Abstrakt ...xi

Köszönetnyilvánítás... xii

1. Bevezetés...1

1.1. Szétválasztó hálózatok szintézise (SNS) ...1

1.2. Hőcserélő hálózatok szintézise (HENS)...2

1.3. Célkitűzések...2

1.4. Alapfogalmak...3

1.4.1. SNS...3

1.4.2. HENS...6

2. Szakirodalom áttekintése...9

2.1. SNS...9

2.1.1. Heurisztikus módszerek ...10

2.1.2. Evolúciós módszerek ...11

2.1.3. Algoritmikus módszerek ...12

2.2. HENS...14

2.2.1. HENS hálózatok ...14

2.2.2. Energiaintegrált SNS hálózatok ...16

3. SNS feladat több szétválasztó család felhasználásával ...20

3.1. Szétválasztó családok...20

3.2. Az SNS-Multi feladat definiálása...23

3.3. A szétválasztók tulajdonságai ...25

3.4. Szigorú szuperstruktúra...30

3.5. Az SNS-Multi feladattípus szigorú szuperstruktúrája ...33

3.5.1. Az SNS-Multi optimális struktúráinak tulajdonságai...33

3.5.2. Az RSS-Multi algoritmus...38

3.6. Az SNS-Multi matematikai modellje ...44

3.7. Feladatok...52

4. Energiaintegrált SNS feladat ...69

4.1. Bevezetés ...69

4.2. Feladat definiálása ...71

4.3. Az SNS rész szuperstruktúrája...71

4.4. Hőforrások és hőnyelők azonosítása ...72

4.5. Hőmérséklet intervallum diagram ...76

4.6. Lehetséges hőcserék...80

4.7. Matematikai modell ...81

4.8. Feladatok...86

5. Az SNS-Multi feladat redukált szuperstruktúrája ...102

(4)

5.2. Egyszerűsítések...102

5.2.1. Egyszerűsítés azonos megosztási arány alapján ...102

5.2.2. Egyszerűsítés azonos bemeneti összetétel alapján ...104

5.3. A redukált szuperstruktúra generálása...109

5.4. A redukált szuperstruktúra matematikai modellje ...111

5.5. Matematikai komplexitás ...112

5.6. Feladat...116

6. SNS feladatok vizsgálata PNS eszközökkel ...122

6.2. Tiszta termékes feladat...123

6.2.1. Három komponenst tartalmazó feladat...124

6.2.2. Négy komponenst tartalmazó feladat ...128

6.2.3. A tiszta termékes feladat korlátjai...130

6.3. Több szétválasztó család ...130

6.4. Kevert termékek...132

7. Összefoglalás...137

8. Melléklet: Hőcsere módozatok összehasonlítása ...140

Új tudományos eredmények...143

Tézisek ...143

Theses ...144

A doktori képzés ideje alatt végzett publikációs tevékenységem ...145

Irodalomjegyzék ...148

Jelölésjegyzék ...154

(5)

Táblázatok jegyzéke

3.1. táblázat: Extra szétválasztók száma a komponens szám függvényében ...29

3.2. táblázat: SNS hálózatok anyagmérlegeinek típusai különböző matematikai modellek esetén ...48

3.3. táblázat: A betáplálás és a termékek komponensáramai a 3.7.1. feladatnál...52

3.4. táblázat: A felhasználható szétválasztók a 3.7.1. feladatnál ...53

3.5. táblázat: Célfüggvény értékek összehasonlítása a 3.7.1. feladatnál...59

3.10. táblázat: A betáplálás komponensáramai és a termékekre vonatkozó feltételek a 3.7.4. feladatnál...64

3.14. táblázat: A 9C3F4P és 10C4F4P feladat méretének összehasonlítása...68

4.1. táblázat: A 4.8.1. feladat adatai ...87

4.2. táblázat: A szétválasztók adatai a 4.8.1. feladatnál ...87

4.3. táblázat: A komponens és kompozit áramok arányai a 4.8.1. feladatnál ...91

4.4. táblázat: A hőcserélők egyesített költségegyütthatói a 4.8.1. feladatnál...91

4.5. táblázat: A soros és az energiaintegrált módszer összehasonlítása a 4.8.1. feladatnál ...95

4.7. táblázat: A szétválasztók adatai a 4.8.2. feladatnál...96

4.9. táblázat: A szétválasztók adatai a 4.8.3. feladatnál...98

4.10. táblázat: A soros és az energiaintegrált módszer összehasonlítása a 4.8.3. feladatnál ...101

5.1. táblázat: SN(n) és CN(n) értéke néhány n esetén...115

5.2. táblázat: A betáplálás és a termékek komponensáramai az 5.6. feladatnál...116

5.3. táblázat: A felhasználható szétválasztók az 5.6. feladatnál ...116

6.2. táblázat: A felhasználható csomópontok a 6.2.1. feladatnál...126

(6)

Ábrák jegyzéke

1.1. ábra: Összetett, nem-éles szétválasztó grafikus ábrázolása. ...4

1.2. ábra: Egyszerű, éles szétválasztó grafikus ábrázolása. ...5

1.3. ábra: Keverő grafikus ábrázolása. ...5

1.4. ábra: Megosztó grafikus ábrázolása. ...6

1.5. ábra: Hőcserélő grafikus ábrázolása...8

3.1. ábra: Egyszerű, éles szétválasztókat tartalmazó szétválasztó család tagjai...20

3.2. ábra: Két szétválasztó család lehetséges tagjai...22

3.3. ábra: Műveletei egységek hatása a folytonosságra...27

3.4. ábra: Nem folytonos komponensáram vektor...28

3.5. ábra: Extra szétválasztók 4 komponens esetén...29

3.6. ábra: Példa szétválasztók megadására. ...30

3.7. ábra: Algoritmikus módszerek lépései. ...30

3.8. ábra: Matematikai programozási modellek típusai...32

3.9. ábra: Egyszerű út a betáplálástól az S szétválasztóig. ...35

3.10. ábra: Nem-egyszerű út a betáplálástól az S^b szétválasztóig...35

3.11. ábra: tr1 transzformáció szemléltetése. ...36

3.12. ábra: N* partícionálása a tr1 transzformációkat követően...37

3.13. ábra: tr2 transzformáció szemléltetése. ...38

3.14. ábra: Operátorok szemléltetése. ...41

3.15. ábra: Különböző családba tartozó, de azonos hatású szétválasztók...44

3.16. ábra: Az SNS feladat műveleti egységei. ...46

3.17. ábra: Azonos típusú szétválasztók összevonása: összevonás előtt. ...51

3.18. ábra: Azonos típusú szétválasztók összevonása: összevonás után...51

3.19. ábra: Keverők és megosztók összevonása...52

3.20. ábra: A 3.7.1. feladat szigorú szuperstruktúrájának generálása: Iniciálás...54

3.21. ábra: A 3.7.1. feladat szigorú szuperstruktúrájának generálása: 1. iteráció. ...54

3.24. ábra: A 3.7.1. feladat szigorú szuperstruktúrájának generálása: 13. iteráció, teljes szuperstruktúra...56

3.25. ábra: A 3.7.1. feladat optimális struktúrája: mindhárom szétválasztó család felhasználható. ...58

3.26. ábra: A 3.7.1. feladat optimális struktúrája: az 'a' szétválasztó család használható fel...58

3.27. ábra: A 3.7.1. feladat optimális struktúrája: a 'b' szétválasztó család használható fel. ...59

3.28. ábra: A 3.7.1. feladat optimális struktúrája: a 'c' szétválasztó család használható fel. ...59

(7)

3.29. ábra: A 3.7.2. feladat optimális struktúrája. ...61

3.30. ábra: A 3.7.2. feladat egyszerűsített optimális struktúrája...61

3.32. ábra: A 3.7.4. feladat optimális struktúrája, a termékek feltételekkel adottak. ...65

3.33. ábra: A 3.7.4. feladat optimális struktúrája, a feltételeket kielégítő termékek adottak. ...65

4.1. ábra: Vegyipari rendszer tervezésének fő lépései...69

4.2. ábra: Lehetséges hőcsere módozatok szétválasztó előtti keverő léte vagy hiánya esetén: a) izoterm keverés; b) nincs keverés; c) direkt hőközlés. ...72

4.3. ábra: Lehetséges hőcsere módozatok. ...73

4.4. ábra: Példa a fajhő automatikus számítására. ...75

4.5. ábra: Elemi áramok és látens hők hőmérséklet intervallum diagramon ábrázolva. ...77

4.6. ábra: Hőáram és hőmérséklet intervallum megosztása...77

4.7. ábra: Hőátadás 2 illetve 1 hőcserélővel...79

4.8. ábra: Kompozit áramok...80

4.9. ábra: Lehetséges hőcserék HSS2-ből...81

4.10. ábra: A 4.8.1. feladat szuperstruktúrája és az azonosított hőforrások és hőnyelők..88

4.11. ábra: A 4.8.1. feladat elemi áramai és látens hői hőmérséklet intervallum diagramon. ...89

4.12. ábra: A 4.8.1. feladat kompozit áramai és látens hői hőmérséklet intervallum diagramon. ...89

4.14. ábra: A 4.8.1. feladat soros megoldásához tartozó szétválasztó hálózat...95

4.15. ábra: A 4.8.1. feladat soros megoldásához tartozó hőcserélő hálózat...95

4.16. ábra: A 4.8.2. feladat energiaintegrált megoldásához tartozó szétválasztó hálózat. 97 4.17. ábra: A 4.8.2. feladat energiaintegrált megoldásához tartozó hőcserélő hálózat. ....97

4.18. ábra: A 4.8.3. feladat energiaintegrált megoldásához tartozó szétválasztó hálózat. 99 4.19. ábra: A 4.8.3. feladat energiaintegrált megoldásához tartozó hőcserélő hálózat. ..100

4.20. ábra: A 4.8.3. feladat soros megoldásához tartozó szétválasztó hálózat...100

4.21. ábra: A 4.8.3. feladat soros megoldásához tartozó hőcserélő hálózat...101

5.1. ábra: Azonos típusú szétválasztók összevonása: összevonás előtt. ...103

5.2. ábra: Azonos típusú szétválasztók összevonása: összevonás után...103

5.3. ábra: Szétválasztók összevonása azonos összetételű bemenet esetén...106

5.4. ábra: Azonos részek az RSS-Multi szuperstruktúrájában...107

5.5. ábra: Összevont szétválasztók a szuperstruktúrában. ...108

5.6. ábra: Megosztók és keverők hálózatának egyszerűsítése. ...108

5.7. ábra: Szemléltető ábra az 5.19. egyenlethez...112

5.8. ábra: SN(n) és CN(n) növekedésének összehasonlítása...116

5.9. ábra: Redukált szuperstruktúra generálása: iniciálás és az 1. iteráció...117

(8)

5.10. ábra: Redukált szuperstruktúra generálása: 2. iteráció. ...118

5.11. ábra: Redukált szuperstruktúra generálása: 3. iteráció. ...119

5.12. ábra: Redukált szuperstruktúra generálása: 18. iteráció, teljes szuperstruktúra...120

5.13. ábra: Az 5.6. feladat optimális struktúrája...121

6.1. ábra: Műveleti egység grafikus reprezentációja. ...123

6.2. ábra: PNS hálózat grafikus reprezentációja...123

6.3. ábra: A 3C1FPP feladat szuperstruktúrája. ...125

6.4. ábra: Szétválasztó és vele ekvivalens műveleti egység. ...126

6.5. ábra: A 6.2.1. feladat maximális struktúrája...127

6.6. ábra: SSG által előállított lehetséges struktúrák a 6.2.1. feladatnál. ...127

6.7. ábra: 6.2.1. feladat optimális SNS struktúrája. ...127

6.9. ábra: A 6.2.2. feladat optimális PNS struktúrája. ...129

6.10. ábra: A 6.2.2. feladat optimális SNS struktúrája. ...129

6.14. ábra: Keverők és kevert termékek bevezetése a maximális struktúrába. ...133

6.15. ábra: Keverő megvalósítása több műveleti egységgel a maximális struktúrában. .133 6.16. ábra: Termék megvalósítása több anyaggal, a 6.4.1. feladat maximális struktúrája. ...135

7.1. ábra: Vizsgált témák. ...137

8.1. ábra: Lehetséges hőcsere módozatok. ...140

8.2. ábra: Hőátadás 2 illetve 1 hőcserélővel...141

(9)

Kivonat

Szétválasztási hálózatok szintézise: Különböző tulajdonságokon alapuló szétválasztó módszerek egyidejű alkalmazása

A szétválasztási hálózatok szintézisénél (SNS) általánosan alkalmazott feltevés az, hogy a felhasználható szétválasztók egy szétválasztó családba tartoznak, vagyis egy adott fiziko-kémiai tulajdonságot használnak fel az összes szétválasztás elvégzésénél. A disszertációban kiterjesztettük az SNS feladatot több szétválasztó család egyidejű alkalmazására egyszerű és éles szétválasztók esetére. Az optimális megoldást garantáló szuperstruktúra, az úgynevezett szigorú szuperstruktúra, meghatározására alkalmas algoritmust dolgoztunk ki. Megadtuk a szigorú szuperstruktúrához tartozó matematikai modellt, amelynek megoldásából meghatározható a garantáltan optimális struktúra.

Kidolgoztuk a szétválasztó hálózat és a kapcsolódó hőcserélő hálózat integrált módon való szintézisére alkalmas módszert, majd összehasonlítottuk a soros és az integrált megközelítést bemutatva az utóbbi előnyeit. Módszert adtunk az egy és több szétválasztó családon alapuló SNS feladatok folyamat hálózat szintézis (PNS) feladatokká való transzformálására, lehetővé téve a PNS-hez kidolgozott algoritmusok alkalmazását.

(10)

Abstract

Separation Network Synthesis: Simultaneously Considering Separation Methods Based on Different Properties

In the available separation network synthesis methods the separators are assumed to belong to the same separator family, i.e., all the separations are effected by a single physical or chemical property. In the present thesis, the SNS problem is extended to simultaneously considering multiple families of simple and sharp separators. An algorithm is developed for generating such a superstructure, which guarantees the optimal solution, termed as the rigorous superstructure. The mathematical programming model based on the rigorous superstructure is also given. The network generated from this model is proved to be optimal. A novel method is elaborated for the integrated synthesis of the separation and the heat-exchanger network. The comparison of the sequential and the integrated approaches shows the advantages of the latter. A method is given for the transformation of an SNS problem comprising a single or multiple separation families to a process network synthesis (PNS) problem. This renders it possible to use algorithms available for PNS.

(11)

Abstrakt

Die Syntese von Trennungsnetzen: Die gleichzeitige Anwendung von auf verschiedenen Eigenschaften basierenden

Trennungsmethoden

Bei der Syntese der Trennungsnetze (STN) ist eine allgemein angewandte Annahme, dass die anwendbaren Trenner zu einer Trennergruppe gehören, das bedeutet, dass sie bei der Verwirklichung von allen Trennungen eine bestimmte physisch-chemische Eigenschaft verwenden. In der Dissertation haben wir die STN-Aufgabe auf die gleichzeitige Anwendung verschiedener Trennungsfamilien im Falle von einfachen und scharfen Trennern. Wir haben einen geeigneten Algorythmus zur Bestimmung der die optimale Lösung garantierenden Superstruktur, der sogenannten strengen Superstruktur ausgearbeitet. Wir haben das zur strengen Superstruktur gehörende mathematische Modell angegeben, aus dessen Lösung die garantiert optimale Struktur festzustellen ist.

Wir haben die Methode, die zur integrierten Synthese von dem Trennungsnetz und dem anschließenden Wärmeaustauscher-Netz geeignet ist, ausgearbeitet, dann haben wir die reihige und die integrierte Annäherung verglichen, gezeigt dabei auch die Vorteile der integrierten Annäherung. Wir haben eine Methode für die Transformierung der auf einer oder mehrerer Trennungsfamilien basierenden STN-Aufgaben zur Prozess-Netz-Synthese (PNS) – Aufgaben angegeben, und dabei auch die Anwendung der zur PNS ausgearbeiteten Algorythmen ermöglicht.

(12)

Köszönetnyilvánítás

Ezúton szeretnék köszönetet mondani témavezetőmnek, Dr. Friedler Ferenc professzor úrnak, folyamatos útmutatásáért és támogatásáért, mellyel a bemutatásra kerülő eredményeim és PhD dolgozatom megszületését segítette. Köszönetet mondok L. T. Fan professzor úrnak, aki eredményeim és dolgozatom megszületéséhez a kémiai előismereteket és a szakirodalmat biztosította. Köszönöm minden kollégámnak a kreatív, együttműködő és jó hangulatú légkört, amiben dolgozhattam. Mindezek felett szeretném megköszönni szüleimnek azt a céltudatos, elszánt és kitartó ösztönzést és támogatást, amellyel tanulmányaim során elkísértek.

(13)

1. Bevezetés

1.1. Szétválasztó hálózatok szintézise (SNS)

A dolgozat témája szétválasztási hálózatok szintézise, amely a folyamatszintézis egy fontos területe. Ez utóbbi általában foglalkozik azzal, hogy hogyan kell megvalósítani valamilyen ipari, vegyi vagy bármilyen más folyamatot, ha adottak a kívánt termékek és a rendelkezésre álló különböző nyersanyagok és elemi folyamatok. Folyamatszintézis feladat lehet például egy szennyvíztisztító, egy kőolaj finomító vagy egy műanyag gyár megtervezése. A feladat szintézis jellege azt jelenti, hogy sok elemi lépést kell összekapcsolni és belőlük egy hálózatot építeni úgy, hogy az megvalósítsa a kívánt feladatot. A hangsúly a hálózat szerkezetén és nem annak építőkockáin van.

A szétválasztási hálózatok szintézise vagy angol elnevezés alapján separation network synthesis, röviden SNS feladat eredeti célja, hogy az adott többkomponensű folyamok összetevőit szétválassza. Ezt nevezzük tiszta termékes (pure products - PP) feladatnak. Mivel ekkor a szétválasztók sorrendje teljesen meghatároz egy struktúrát, a feladatot szétválasztási sorrend meghatározásának (separation sequencing) is hívják.

Később a feladat értelmezése úgy bővült, hogy az előállítandó termékek már több komponenst is tartalmazhatnak (mixed products - MP). Mi úgy fogalmazzuk meg az SNS feladatot, hogy célunk valahány, több komponensből álló, homogén folyam összetételének és folyam nagyságának a megváltoztatása úgy, hogy azok teljesítsék a kívánalmakat.

A szétválasztó hálózatok jelen vannak az élet minden területén a vegyipartól kezdve, az élelmiszeriparon és a mezőgazdaság feldolgozó iparain át egészen a gyógyszeriparig. Legfontosabb alkalmazásuk még ma is az olajiparban van, a feladat felvetése is innen ered, de a téma jelentősége rohamosan nő, különösen a bió-technológia területén.

Egy szétválasztási feladat számtalan módon megoldható. Ezek közül a valamilyen szempontból legkedvezőbb, általában legolcsóbb, megoldást szeretnénk megtalálni. A szétválasztási hálózat költsége egy termelő rendszer költségének jelentős része, akár 50%-a, ezért az optimális szétválasztó hálózat azonosítása önmagában és a teljes termelő rendszer szintjén is fontos.

Az SNS feladat megoldása egy szétválasztási hálózat, amelynek fő alkotóelemei a szétválasztók, de tartalmazhat még megosztókat, keverőket, tárolókat és csővezetékeket.

Ezeknek a költsége általában elhanyagolható a szétválasztók költségéhez képest, így a hálózat költségét leggyakrabban a benne lévő szétválasztók költségének összegeként definiálják. Egy szétválasztási hálózat folyamat ábráján néha a megosztókat és a keverőket is ábrázolják, mert itt a folyamok elágaznak, illetve egyesülnek.

(14)

Az SNS feladat megoldási módszerei különböznek abban, hogy milyen részletességgel modelleznek egy szétválasztót. Minél pontosabb a modell, annál jobban írja le a tényleges szétválasztót, azáltal, hogy egyre több és több működési paramétert vesz figyelembe, optimalizálási változóként kezelve azokat. Másik oldalról viszont egy pontosabb, ezért bonyolultabb modellt csak sokkal kisebb méretben lehet megoldani belátható időn belül. Tapasztalataink azt mutatják, hogy a hálózat struktúrájának nagyobb hatása van a költségre, mint az egyes szétválasztók működési paramétereinek, valamint számos strukturális kérdés tisztázatlan, ezért a dolgozatban az optimális struktúra meghatározására törekszünk egyszerű és éles szétválasztókat feltételezve.

1.2. Hőcserélő hálózatok szintézise (HENS)

A hőcserélő hálózat szintézis feladat, angol elnevezés alapján heat exchanger network synthesis, röviden HENS, lényege, egy olyan rendszer tervezése, amely kielégíti a fellépő fűtési és hűtési igényeket. Kezdetben ezeket az igényeket kizárólag a rendszerbe kívülről behozott eszközökkel, például forró gőzt előállító bojlerrel, hűtőtoronnyal elégítették ki.

Később, a növekvő energiaárak hatására előtérbe került az a törekvés, hogy amennyire lehetséges, a kívülről hozott eszközök használatát mérsékelni kell úgy, hogy a rendszerben amúgy is jelenlevő hűtési igényt, mint hőforrást használják, és ezzel csökkentsék a bojler terhelését. Hasonlóképpen, a rendszer egy fűtési igénye egy másik részről történő hőelvonást is jelent, amit kihasználva a hűtőtorony méretét csökkenthetjük. Az optimális HEN meghatározásakor ma már figyelembe veszik a felhasznált hőcserélők költségét is és egy az összköltségre optimális hálózat megtervezése a cél.

A HENS egy bonyolult, kombinatorikus jellegű feladat, ami abból adódik, hogy egy rendszerben számtalan módon lehet a hőcseréket végrehajtani. Az optimális hőcserélő hálózat megtalálása nagyon fontos feladat. Majdnem minden vegyipari rendszernek része a HEN, amely a teljes költség jelentős hányadát képviseli. Az SNS és a HENS feladat szoros kapcsolatban áll egymással, mert hagyományosan egy termelő rendszer tartalmaz mind szétválasztási hálózatot, mind hőcserélő hálózatot. Ami ennél is fontosabb, hogy a fűtési és hűtési igények jelentős része a szétválasztó hálózat működéséhez szükséges.

1.3. Célkitűzések

A dolgozat célja, különböző típusú SNS feladatok strukturális vizsgálata és olyan algoritmusok és modellek tervezése, amelyek hatékonyan alkalmazhatóak a vizsgált feladattípusok megoldására.

A dolgozat második fejezete bemutatja az SNS témakör irodalmát, külön hangsúlyt helyezve az egyszerű és éles szétválasztás algoritmikus módszereire. A

(15)

harmadik fejezet olyan SNS feladatokat vizsgál, ahol több szétválasztó család áll rendelkezésre. Egy szétválasztó család alatt azokat a szétválasztókat értjük, amelyek ugyanazon elv alapján működnek. Például a desztillációt alkalmazó szétválasztók egy családot alkotnak. A dolgozat negyedik fejezete energiaintegrált szétválasztási hálózatok generálásával foglalkozik. A bemutatott módszer lehetőséget ad a szétválasztókban jelentkező látens hők és a szétválasztók között futó hideg és meleg folyamok közötti hőcserére. Az optimalizálás alatt figyelembe vesszük a szétválasztók, a hőforrások, hőnyelők és a hőátadás költségét. Az ötödik fejezet strukturális szempontból újravizsgálja a lineáris költségű éles szétválasztókat tartalmazó SNS feladat szuperstruktúráját.

Bemutatjuk, hogyan lehet egyszerűsíteni a szuperstruktúrát úgy, hogy közben nem zárunk ki lehetségesen optimális megoldásokat. A csökkenés nagyságát számszerűen mutatjuk be. Végül a hatodik fejezetben megmutatjuk, hogyan lehet alkalmazni a folyamat hálózat szintézisben megismert eszközöket SNS feladatokra.

1.4. Alapfogalmak

1.4.1. SNS

Hogy a dolgozat pontos, világos és egyértelmű legyen a fontosabb fogalmakat, illetve azok szinonimáit itt definiáljuk. A folyam a tudományos életben folytonosan haladó anyagot (általában folyadékot) jelent, amelynek nagyságát (hozamát) tömeg/idő illetve térfogat/idő típusú mértékegységben adják meg. Például egy reaktor és egy tároló között lévő csővezetékben mozgó anyagot folyamnak tekinthetünk. A folyam nagyságának van olyan értelmezése is, hogy az az egységnyi területen, egységnyi idő alatt áthaladó dolog (anyag, energia, elektron, hő, űrtartalom, stb.) mennyisége. Ebből az értelmezésből úgy kapjuk meg az előzőt, hogy a csővezeték teljes felületére integrálunk.

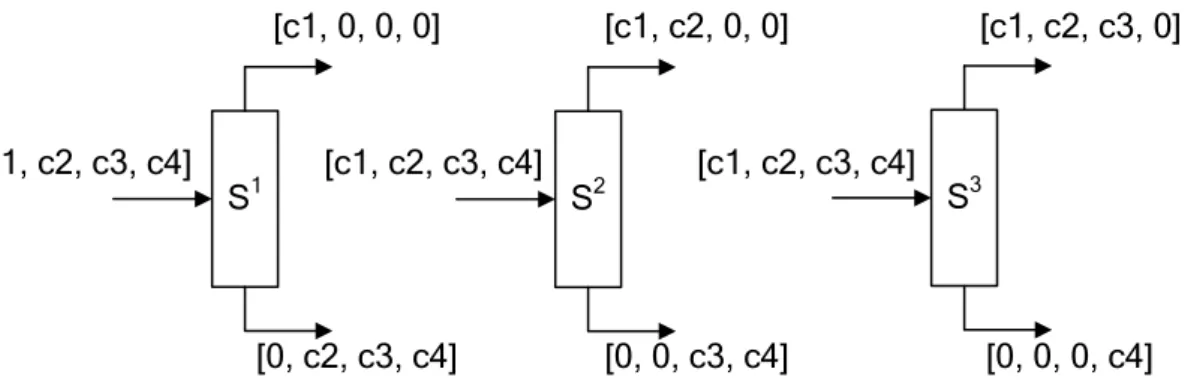
Egy folyamot felfoghatunk a benne lévő komponensekhez tartozó komponensáramok összegeként úgy, mintha az egyes komponensek egymás mellett lévő, de különálló csövekben futnának. Ha ismerjük a teljes folyam nagyságát és az összetételét, akkor a komponensáramok nagysága egyszerűen kiszámolható. A folyamokat elhelyezkedésük szerint csoportokra bonthatjuk. Az SNS feladat által feldolgozandó folyamokat betáplálásnak, az előállítandó folyamokat termékeknek és minden más folyamot köztes folyamnak hívunk. Egy szétválasztóba belépő folyamot bemenetnek, a kilépő folyamokat pedig felső és alsó kimenetnek nevezzük. Ha lepárló típus szétválasztóról van szó, akkor a felső kimenetet párlatnak, az alsó kimenetet fenékterméknek hívjuk. A gyakorlatban léteznek összetett szétválasztók, amelyek kettőnél több kimenettel rendelkeznek, de a jelen dolgozatban csak egyszerű szétválasztókat tekintünk, amelyeknek egy bemenete és két kimenete van.

Egy folyamban lévő komponenseket a szétválasztás alapjául szolgáló tulajdonság, például relatív illékonyság, alapján sorba szokás állítani. Az így kapott komponens

(16)

sorrend lehetőséget ad arra, hogy a komponensekre ne névvel, hanem sorszámmal hivatkozzunk. Egy folyamot általában komponensáram vektorral reprezentálunk úgy, hogy egy sorvektorban megadjuk a komponensáramok nagyságát a komponens sorrend szerint. Például a [12, 2, 6] folyam nagysága 20, az első komponens aránya 60%, a másodiké 10%, a harmadiké pedig 30%. Azt mondjuk, hogy egy szétválasztó az i-dik komponens után vág, ha a bemenetét úgy alakítja át, hogy az i-nél nem nagyobb sorszámú komponensek a felső kimenetbe, az i-nél nagyobb sorszámú komponensek az alsó kimenetben koncentrálódnak. Éles szétválasztásról beszélünk akkor, ha a koncentrálódás tökéletes, vagyis a kérdéses komponensek teljes egészében a felső illetve alsó kimenetbe kerülnek. Ellenkező esetben nem-éles szétválasztásról beszélünk. Egy tetszőleges, k kimenetelű szétválasztó matematikailag egy rendezett k+1-esel írható le strukturális szempontból, lásd Kovács (2000). Az első k tag mindegyike egy-egy diagonális mátrix, amelyek az adott kimenetekhez tartoznak, a k+1-dik tag pedig a szétválasztó költségfüggvénye. Amennyiben a főátló elemei vagy nullák, vagy egyesek, akkor a szétválasztás éles. Egy általános szétválasztó működését, lásd az 1.1. ábra, az 1.1.

és 1.2. egyenletek írják le, ahol f_a a bemenet, f_b_i a kimenetek komponensáramainak a vektorai, L_i az egyes kimenetekhez tartozó mátrixok, I pedig az egység mátrix. Az 1.2.

ábra egy olyan egyszerű és éles szétválasztót ábrázol, amely az i-dik komponens után vág, a szétválasztó működését az 1.3.-1.6. egyenletek írják le.

S

1 [ 1,1, 1,2,..., 1, ]

b b b b n

f = f f f

2 [ 2,1, 2,2,..., 2, ]

b b b b n

f = f f f

,1 ,2 ,

[ , ,..., ]

k k k k

b b b b n

f = f f f

,1 ,2 ,

[ , ,..., ]

a a a a n

f = f f f

1.1. ábra: Összetett, nem-éles szétválasztó grafikus ábrázolása.

i i

a b

f L = f i = 1, 2, …, k 1.1.

1 k

i i

L I

=

å

= ^1.2.

(17)

Sⁱ

,1 ,2 ,

[ , ,..., ]

a a a a n

f = f f f

1 [ 1,1, 1,2,..., 1, ] [ ,1, ,2,..., , ,0, 0,..., 0]

b b b b n a a a i

f = f f f = f f f

2 [ 2,1, 2,2,..., 2, ] [0,0,..., 0, , 1, , 2,..., , ]

b b b b n a i a i a n

f = f f f = f ₊ f ₊ f

1.2. ábra: Egyszerű, éles szétválasztó grafikus ábrázolása.

, 1,

a k b k

f = f k = 1, 2, …, i 1.3.

1,

0= f_{b k} k = i+1, ... n 1.4.

2,

0= f_{b k} k = 1, 2, …, i 1.5.

, 2,

a k b k

f = f k = i+1, ... n 1.6.

Egy keverő egy kimenettel és kettő vagy több bemenettel rendelkezik, lásd 1.3.

ábra. A bemeneteire érkező folyamokat egyesíti úgy, hogy minden komponensáramra érvényes az anyagmegmaradás. Egy keverő költségét nullának tekintjük, hiszen ez sokszor nem más, mint két cső egyesülése. A keverő működését az 1.7. egyenlet írja le, ahol f_{a j}_i_, az i-dik bemenet j-dik komponensárama és f_{b j}_, pedig a kimenet j-dik komponensárama.

, ,

1 ⁱ

k

a j b j i

f f

=

å

= j = 1, 2, …, n 1.7.

... M

1 [ 1,1, 1,2,..., 1, ]

a a a a n

f = f f f

2 [ 2,1, 2,2,..., 2, ]

a a a a n

f = f f f

,1 ,2 ,

[ , ,..., ]

k k k k

a a a a n

f = f f f

,1 ,2 ,

[ , ,..., ]

b b b b n

f = f f f

1.3. ábra: Keverő grafikus ábrázolása.

Egy megosztó egy bemenettel és kettő vagy több kimenettel rendelkezik, lásd 1.4.

ábra. A megosztó úgy bontja szét a bemenetét több kimenetre, hogy a bemenetek és a kimenetek összetétele megegyezik. A D megosztó minden kimenete jellemezhető egy megosztási arány l_b_i nevű változóval, amely kifejezi, hogy az egyes kimenetekbe a bemenet hány százaléka kerül. A megosztó költségét szintén nullának tekinthetjük, mert

(18)

az elhanyagolható a szétválasztók költsége mellett. Egy keverő az 1.8. és 1.9.

egyenletekkel írható le, ahol _,

b ji

f az i-dik kimenet j-dik komponensárama és f_a,j a bemenet j-dik komponensárama. A szétválasztó, a keverő és a megosztó közös elnevezése műveleti egység. A műveleti egységek minden változója nem-negatív.

i i

b fa fb

l = i = 1, 2, …, k 1.8.

1

1 ^k _b_i

i

l

=

å

^1.9.

D ...

1 [ 1,1, 1,2,..., 1, ]

b b b b n

f = f f f

2 [ 2,1, 2,2,..., 2, ]

b b b b n

f = f f f

,1 ,2 ,

[ , ,..., ]

k k k k

b b b b n

f = f f f

,1 ,2 ,

[ , ,..., ]

a a a a n

f = f f f

1.4. ábra: Megosztó grafikus ábrázolása.

1.4.2. HENS

A hőcserélő hálózat egy olyan, általában folytonos, rendszer, amelyben egyes folyamok hőmérsékletét növelni, másokét pedig csökkenteni kell. Az első csoport tagjait hidegáramoknak hívjuk, mert bemeneti hőmérsékletük alacsonyabb, mint a kimeneti.

Hasonló megfontolásból a második csoport tagjait melegáramoknak nevezzük. A két csoportot együttesen hőáramoknak hívjuk. Ahhoz, hogy adott m tömegű anyag hőmérsékletét DT-el megváltoztassuk DQ energiára van szűkség, amelynek értékét az 1.10. képlet segítségével számolhatjuk ki, ahol c az anyag fajhője. Mivel folytonos rendszert vizsgálunk, ezért m helyett f-t, vagyis folyam nagyságot használunk, DQ alatt pedig az időegység alatt szükséges energiamennyiséget értjük.

Q c m T

D = × ×D 1.10.

Egy hőcserélő hálózat működését a termodinamika tételei irányítják. Az első tétel az energia megmaradást fogalmazza meg, vagyis azt, hogy zárt rendszerben az energia összértéke nem változik, csak egyik formából alakul át egy másikba. A második tétel hőáramlás irányát szabja meg, mindig a melegebb helyről a hidegebb hely felé. Érdemes megvizsgálni egy desztilláló oszlopot ezeknek a tételeknek a fényében. Az oszlop általában, nem fogyasztja az energiát, hiszen a lepárlón keresztül körülbelül annyi energiát veszünk ki az oszlopból, mint amennyit a kiforralón keresztül betáplálunk.

Ilyenkor valójában az exergia, a felhasználható energia, csökken. Az exergia egy rendszer tényleges munkavégző képessége, amely csak a rendszer környezetével együtt értelmezhető. Az exergia csökkenése mindig az entrópia növekedésével jár együtt, mértékegysége az energiához hasonlóan Joule. A desztilláló oszlop csökkenti az exergiát,

(19)

hiszen kiforralójába nagyobb hőmérsékleten szállítjuk a hőt, mint azt a lepárlójából visszakapjuk, vagyis egy sok mindenre felhasználható hőből egy kevesebb dologra használható, ilyen tekintetben rosszabb, hőt kapunk. A hőcserélő hálózatok lényege az, hogy az egyszer már használt hőt újból és újból felhasználjuk egészen addig, amíg ezt a második tétel engedi.

Egy hőcserélő hálózat tartalmazhat látens hő forrásokat és nyelőket, amelyek alatt olyan hűtési illetve fűtési igényeket értek, amelyek nem járnak hőmérsékletváltozással.

Például egy desztilláló oszlop kiforralója látens hő nyelőnek tekinthető, mert az energia bevitel halmazállapot változást eredményez. Szétválasztás szempontjából nézve egy többkomponensű elegy hőmérséklete változik elpárologtatás közben, de a hőcserélő hálózatot tekintve a desztilláló oszlop kiforralójának hőmérséklete állandónak tekinthető állandósult állapotban. Ilyen értelemben például egy exoterm reakciót látens hő forrásnak tekinthető, ha a keletkező hőt folyamatosan elszállítják és így a reakció izoterm. Látens hő források és nyelők jellemzően reaktorokban és szétválasztókban jelentkeznek. A párolgáshő megadja, hogy tömegegységekként mennyi hő szükséges egy elegy elpárologtatásához. Hasonlóan, a reakcióhő megadja, hogy adott mennyiségű anyagban végbemenő reakció mennyi hőt szabadít fel vagy igényel. Az értekezésben a párolgáshőt és a reakcióhőt közös néven a látens hő együtthatójának nevezem, és L-el jelölöm.

Segítségével adott mennyiségű anyag energiaigénye kiszámolható, lásd 1.11. m a forrásban vagy reakcióban résztvevő anyag tömege. Folytonos rendszerek esetén tömeg helyett folyam nagyságot használunk, ekkor az időegység alatt szükséges energia mennyiséget kapjuk meg.

Q L m

D = × 1.11.

Melegenergia szolgáltatóknak, angolul hot utility, nevezzük azokat az eszközöket, amelyek a rendszeren kívülről hoznak be hőt azon igények kielégítésére, amelyek máshogy már nem teljesíthetőek gazdaságosan. Melegenergia szolgáltató lehet például egy bojler, amely nagy nyomású gőzt állít elő vagy egy megcsapolt turbina, amelyből közép illetve kisnyomású gőz nyerhető. A hidegenergia szolgáltatók, angolul cold utility, a rendszerben fel nem használható hőt vonják ki. Általában vizet vagy levegőt használnak hűtő közegnek, például hűtőtorony. Az energiaszolgáltatók lehetnek meleg- illetve hidegáram típusúak, például forró olaj és hűtővíz, de lehetnek látens hő típusúak is, például nagy nyomású gőz. A melegenergia szolgáltatók költsége általában többszöröse a hidegenergia szolgáltatókénak. Kivétel ez alól, amikor a környezeti hőmérsékletnél alacsonyabb hőfokú hidegenergia szolgáltatóra van szükség.

A melegáramokat, látens hő forrásokat és melegenergia szolgáltatókat együttesen hőforrásoknak nevezzük. Hasonlóan a hidegáramokat, látens hő nyelőket és hidegenergia szolgáltatókat hőnyelőknek hívjuk. A hőnyelők és a hőforrások közötti hőátadás hőcserélőkön keresztül valósul meg. A hőcserélőket többféleképpen szokás ábrázolni,

(20)

lásd 1.5. ábra. A hőcserélőket csoportosíthatjuk a bennük lévő áramok egymáshoz viszonyított iránya alapján. Eszerint léteznek egyenáramú, ellenáramú, keresztáramú illetve vegyes áramú hőcserélők. A gyakorlatban a vegyes áramú hőcserélők a legáltalánosabbak. A fizikai kialakítás szerint csőköteges (shell and tube) és lemezes (plate) hőcserélőket különböztetünk meg. Az utóbbi nagyobb hőátadó felülete révén hatékonyabb, ugyanakkor drágább is. A termodinamika második tétele alapján hőcsere akkor lehetséges, ha a hőforrás melegebb, mint a hőnyelő. Gyakorlatban megkövetelünk egy minimális hőmérséklet különbséget, DT_min, a hőforrás és a hőnyelő között. Úgy vesszük, hogy ennél kisebb hőmérséklet különbségek esetén hőcsere nem lehetséges.

C3

15 °C 25 °C

H2 52 °C

38 °C

2640 kJ

C8

13 °C 22 °C

7950 kJ

38 °C 52 °C

14 °C 1230 kJ

41 °C

C1 H7

ST

a) b) c)

1.5. ábra: Hőcserélő grafikus ábrázolása.

A hőcserélő hálózatokat rács diagram segítségével szokás megjeleníteni, amelynek felső része a meleg- alsó része pedig a hidegáramokat tartalmazza. Egy hideg- és melegáramot összekötő szakasz egy hőcserélőt reprezentál, lásd az 1.5. ábra c) részét .

(21)

2. Szakirodalom áttekintése

2.1. SNS

Az SNS feladatok szakirodalma a téma fontossága miatt hatalmas. A feladatok különbözhetnek megfogalmazásban és megoldási módszerben. A cikkeket különböző szempontok alapján csoportosíthatjuk. Értelemszerűen egy cikk több csoportba is tartozhat, de az is előfordulhat, egy adott csoportosítási szempont egy adott cikkre nem értelmezhető.

Betáplálás szám szerint lehetnek egy vagy több betáplálásos feladatok. Az egy betáplálásos módszerek jelenleg még elterjedtebbek, mert a gyakorlati példák nagy részénél csak egy betáplálás van, de a több betáplálásos módszerek is fokozatosan teret nyernek, hiszen a betáplálásokat függetlenül kezelve általában nem lehet megkapni az optimális megoldást. A termékek minőségét tekintve vannak tiszta termékes és kevert termékes feladatok. Az előbbi az utóbbinak egy speciális esete. A komponens szám, a betáplálás szám, a termékek száma és minősége alapján egy konkrét feladatot gyakran jelölnek a következő képen: xCyFzP, ahol x a komponens szám, y a betáplálás szám és z a termékek száma vagy P tiszta termékek esetén. Például 3C1F2P feladat esetén egy három komponenst tartalmazó betáplálásból kell előállítani két kevert terméket.

Az alkalmazott matematikai modell lehet lineáris (LP), konvex, nem-lineáris (NLP), egész változókat tartalmazó lineáris (MILP) és egész változókat tartalmazó nem-lineáris (MINLP). Habár az operációkutatás fejlődése és a számítástechnikai teljesítmény növekedése miatt a megoldók egyre jobbak, mindegyik modelltípusra meg lehet mondani, hogy mi az a változó szám, amelyre még reális időn belül tud megoldást mondani. Például egy LP megoldó jelenleg néhány százezer változó nagyságú feladatnak tudja meghatározni az optimális megoldását személyi számítógépen.

A modellek megoldása történhet sztochasztikus és determinisztikus módszerekkel. Például a szimulált hűtés vagy a genetikus programozás sztochasztikus, a korlátozás és szétválasztás valamint a külső közelítés módszere determinisztikus. A sztochasztikus módszerek elméletileg sem tudják garantálni az optimális megoldást, mégis eléggé elterjedtek, mert nagyméretű feladatokra is jól alkalmazhatóak. A determinisztikus módszerek elméletben garantálják az optimumot, de a gyakorlatban a számítógépek számábrázolási pontatlansága akadályozhatja őket. Az intervallum aritmetikán alapuló megoldók figyelembe veszik ezt a pontatlanságot, de ezek a megoldók még nem elterjedtek és a számítási igényük is nagyobb.

A szétválasztók modellje alapján megkülönböztetünk egyszerű és összetett, valamint éles és nem-éles szétválasztókat. Egyszerű szétválasztó esetén pontosan egy bemenetet és két kimenetet tételezünk fel, míg összetett szétválasztóknál a bemenetek és

(22)

a kimenetek száma több lehet. Éles szétválasztás esetén adott komponens a szétválasztónak csak az egyik kimenetén jelenik meg, nem-éles szétválasztónál pedig kettő vagy több komponens mindkét kimeneten jelen van. Az éles szétválasztó gyakorlatban csak nehezen valósítható meg, mégis sokan használják ezt a fajta modellt, mert legtöbbször a szétválasztási hálózat struktúrája a legfontosabb költségtényező. A megoldási módszerek integráltság szerint is csoportosíthatóak. Nagyobb részük csak a szétválasztási hálózat szintézisével foglalkozik, de sok módszer az energiaintegrációt is figyelembe veszi, néhány pedig a teljes folyamatszintézis megvalósítását tűzte ki, aminek egyik fontos része a szétválasztó hálózat.

A megoldási módszerek egyik legelterjedtebb osztályozása a keresési technika alapján történik. Eszerint megkülönböztethetünk heurisztikus, evolúciós és algoritmikus módszereket. A heurisztikus módszerek lényege, hogy gyorsan és viszonylag egyszerűen kapjunk egy kedvező megoldást úgy, hogy végrehajtunk adott számú heurisztikus szabályt, amelyeket a mérnöki tudás és tapasztalat alapján alkottunk meg. Ma is születnek heurisztikus módszerek, mert azok lehetőséget adnak olyan nagy méretű feladatok vizsgálatára, amelyek máshogyan nem lehetségesek. Az evolúciós módszerek két részből állnak. Először egy lehetséges megoldás megtalálása a cél, amelyet azután iteratív módon javítunk különböző szabályok figyelembe vételével egészen addig, amíg további javulás már nem érhető el. Az evolúciós módszerek a heurisztikus módszerekből alakultak ki úgy, hogy amikor már sok heurisztikus szabályt írtak fel egy feladatra, akkor prioritásokat kellett köztük megállapítani, és eljárásokat kidolgozni a szabályok alkalmazásának mikéntjére. Az algoritmikus módszerek számítógépen vannak megvalósítva, szisztematikus megoldás menetet biztosítanak az optimum garantálhatóságát szem előtt tartva. A szisztematikusságot általában úgy biztosítják, hogy megadnak egy úgynevezett szuperstruktúrát, amely az összes megoldás struktúrát tartalmazza. A szuperstruktúrából egy matematikai programozási modellt generálnak, amelyet valamilyen módszerrel megoldanak. Az utóbbi három osztály nemcsak SNS feladatokra, hanem általában a folyamatszintézis feladatokra is értelmezhetőek.

2.1.1. Heurisztikus módszerek

Siirola és Rudd (1971) kifejlesztették az AIDES programot szétválasztási hálózatok szintézisére. A program a termékek és a források párosításán alapszik. A párosítások kiértékelése egy pontozó függvény segítségével történik, amelyet heurisztikus szabályok segítségével alkottak. A kiértékelések után egy LP választotta ki úgy a párokat, hogy a pontszámokat maximálják. Ezután ismételten heurisztikus szabályokat használtak, hogy a kiválasztott párokból megkapják a szétválasztási sorrendet. Gomez és Seader (1976) egy új módszert mutatott be különböző struktúrák becslésére. A becslés lehetővé tette a keresési tér csökkentését, ezáltal könnyítve meg egy optimális közeli megoldás megtalálását. Mahalec és Motard (1977) bemutatták a Baltazar programot több SNS

(23)

hálózatot generálására, amelyekből különböző szempontok alapján lehet választani, illetve a modellt tovább finomítani. Westerberg (1985) alapos áttekintést adott a desztilláción alapuló szétválasztási hálózatok szintéziséről. Definiálta az alapproblémát és annak különféle kiterjesztéseit. Bemutatta a TQ diagram használatának előnyét a több-hatású desztilláló oszlopok esetén és hangsúlyozta a nem-éles szétválasztás fontosságát. Fonyó és munkatársai (1985) az SNS feladat energia integrációval történő megoldását tűzték ki célul. Ehhez a hőcserélő hálózatokból ismert pinch technológiát alkalmazták, amely jellegét tekintve heurisztikus.

Cheng és Liu (1988) nem-éles szétválasztókat tartalmazó SNS feladatot oldott meg. Definiálta, hogy mit tekint éles, majdnem-éles, fél-éles és nem-éles szétválasztónak (a desztillátumban a könnyű kulcs komponensből rendre több, mint 98, 95, és 80 százalék van). Példával igazolta, hogy létezik olyan feladat, ahol nem-éles szétválasztókat használva jobb megoldás érhető el, mint éles szétválasztókat használva. A probléma reprezentálásához és vizsgálatához grafikus eszközöket hozott létre, a komponens hozzárendelési diagramot és a szétválasztási specifikus táblázatot, valamint megalkotott hat heurisztikus szabályt, amelyek között a prioritásokat is meghatározta. Bamopoulos és munkatársai (1988) nem-éles szétválasztók felhasználásával terveztek szétválasztási hálózatokat. Munkájukat grafikus (anyag hozzárendelési diagram) és algebrai eszközök (visszanyerési mátrix, szétválasztási faktor mátrix) segítségével végezték. Heurisztikus szabályokat fogalmaztak meg, amelyeket az előbb említett mátrixokra alkalmazták. Hu és szerzőtársai (1993) heurisztikus szabályok és a köztük fennálló prioritások megadásával alkottak módszert egyszerű és éles szétválasztókat tartalmazó SNS feladat megoldására.

A módszer lehetőséget ad a betáplálás egy részének közvetlen termékbe történő vezetésére illetve korlátozott mértékben szétválasztók párhuzamos működésére. Shah és Kokossis (1997) felismerték, hogy a tisztán heurisztikus szabályokon alapuló módszerek nem lehetnek eredményesek. Olyan új eljárást dolgoztak ki, amely heurisztikus szabályok, egyszerűsített modellek és matematikai programozási modellek együttes használatával állít elő néhány optimum közeli szétválasztási hálózatot. Emtir és munkatársai (1999) olyan heurisztikus módszert alkalmaztak, amely figyelembe veszi a háromkomponenses bemenettel rendelkező szétválasztók energia igényét.

Összehasonlították az integrált és a csatolt szétválasztók energia igényét különböző költségű hőforrásokra.

2.1.2. Evolúciós módszerek

Westerberg és munkatársai (1974) részletesen leírták az evolúciós módszer menetét és az elvárt tulajdonságait. Ilyen tulajdonság például a teljesség, amely szerint az evolúciós szabályokat alkalmazva minden lehetséges struktúrába el kell tudni jutni vagy a megfordíthatóság, amely kimondja, hogy két szomszédos struktúra között mindkét irányban kell lenni egyikből a másikba átvivő szabálynak. Példaképpen a szétválasztási

(24)

hálózatok szintéziséhez megadtak egy evolúciós módszert. Stephanopoulos és Westerberg (1976) az evolúciós folyamatszintézisről készítettek tanulmányt.

Összegyűjtötték és összehasonlították az evolúciós lépések szabályait, különböző stratégiákat mutattak be e szabályok alkalmazására, és módszereket dolgoztak ki a folyamat hálózatok összehasonlítására. Seader és Westerberg (1977) hét különböző heurisztikán alapuló szabályt gyűjtött össze, amelyek felhasználásával egy leszámláláson alapuló evolúciós stratégiát dolgoztak ki. A szabályaik közül a legfontosabbak: először a legkönnyebb szétválasztást végezzük el; először azt a komponenst válasszuk le, amelyből sok van; illékonyság szerint csökkenő sorrendbe válasszuk le a komponenseket. Az algoritmus következő változata figyelembe vette következő szabályokat is: a szennyeződés minimalizálásának érdekében lehetőleg párlatként állítsuk elő a termékeket; a korrózív komponenseket minél előbb válasszuk ki, lásd Rudd és szerzőtársai (1973).

Nath és Motard (1981) a hálózatszintézis feladat megoldására egy új evolúciós módszert javasoltak. Kifejlesztettek egy rang függvényt, amelynek segítségével számszerűsíteni lehetett adott szétválasztó kicserélésének a jóságát. Nem csak a legjobb cserét hajtották végre, hanem minden olyant is, amelynek a rangja a legjobbétól csak maximum adott százalékban tért el. Ezt a munkát folytatta Lu és Motard (1985). Egy olyan hierarchikus módszert mutattak be, amelyben a felső szint által választott szétválasztási problémát az alsó szint oldja meg éles szétválasztókat használva. A két szint automatikusan kommunikál egymással, de lehetőséget ad felhasználó által történő beavatkozásra is. Mindkét szint működése heurisztikus szabályokon és belőlük alkotott evolúciós algoritmuson alapul. Muraki és Hayakawa (1984) két részből álló evolúciós módszert mutatott be, egy betáplálás két többkomponensű termékké történő szétválasztására. Az első részben az optimális elrendezésű hálózatot határozták meg, a második részben az így kapott hálózat folyamait optimalizálták. A két lépést addig ismételték, amíg további javulást már nem lehetett elérni. Később módszerűket javították, Muraki és szerzőtársai (1986), ezután pedig nem-éles szétválasztók kezelésére is alkalmassá tették, lásd Muraki és Hayakawa (1988). Fraga és McKinnon (1994) párhuzamosan működő számítógépekkel oldott meg szintézis feladatot úgy, hogy post- order módon járta be a szuperstruktúrát.

2.1.3. Algoritmikus módszerek

Thompson és King (1972) az elsők között foglalkoztak szétválasztási hálózatok szintézisével. Részben algoritmikus, részben heurisztikus módszert adtak, amelyet már akkor számítógéppel valósítottak meg. Egyik fontos eredményük a tiszta terméket előállító hálózatok számának megadása. A képlet zárt alakja megmutatja, hogy már ennél a feladattípusnál is exponenciálisan nő a lehetséges megoldások száma. Whal és Lien (1990) megadja a három kimenettel rendelkező, összetett szétválasztókból álló, tiszta

(25)

termékeket előállító hálózatok számát rekurzív és zárt formulával. A képlet zárt alakja bonyolult, de Floquet és szerzőtársai (1993) egy ekvivalens egyszerűbb formulát adott meg. Ezen kívül megadták n komponens esetén a k kimenettel rendelkező szétválasztók számát is. Floudas (1987) az egybetáplálásos, kevert termékeket előállító, éles szétválasztókat tartalmazó szétválasztási hálózatok szintézisét vizsgálta. A szétválasztók költségét nem-lineáris függvénnyel írta le és megadott egy szuperstruktúrát, amely feltételezése szerint tartalmazza az összes lehetségesen optimális struktúrát. A szuperstruktúra n komponens esetén n-1 szétválasztót tartalmaz és minden szétválasztó előtt van egy keverő is. A betáplálás egy kezdeti megosztás után kapcsolódik az összes szétválasztóhoz. A szétválasztók kimenetei egyrészt kapcsolódnak a termékekhez, másrészt pedig a keverőkhöz is, amennyiben a keverő utáni szétválasztó tud vágni az adott folyamon. A matematikai modell változói az anyagáramok összetételei és nagyságai. A kapott modellt GAMS-ben oldották meg. Később Aggarwal és Floudas (1990) kiterjesztették a korábbi módszert nem-éles szétválasztók használatára is, azzal a feltételezéssel, hogy csak a kulcs komponensek találhatóak meg a szétválasztó mindkét kimenetén. Az egyes szétválasztók költségét szimulációs eljárással és regressziós analízissel számolták ki és minden szétválasztóból pontosan egyet vettek fel a szuperstruktúrába. Az alkalmazott MINLP matematikai modellben az egyes szétválasztók élessége optimalizálási változóként szerepel. A matematikai modell megoldása egy olyan dekompozíciós módszerrel történik, amelynek lényege, hogy a mester és a szolga feladat is lehetőleg konvex legyen. A megoldót megvalósították GAMS alatt.

Wehe és Westerberg (1987) három-, négy- és ötkomponenses feladatokkal foglalkoztak. A háromkomponenses feladatra sikerült felírniuk egy lineáris modellt, a négy- és ötkomponenses feladatra pedig megadtak egy algoritmust, amelyben LP-vel számoltak alsó, NLP-vel felső korlátokat és MILP segítségével határozták meg a megosztó anyagáramainak a tulajdonságait. Szintén Wehe és Westerberg (1989) foglalkozott a szétválasztók minimális számával olyan hálózatokban, amelyek nem-éles szétválasztókat tartalmaznak. Három különböző módszerrel próbálták a minimumot meghatározni. Az első, a betáplálás és a termékek komponensáramaiból képzett mátrix szabadsági fokán alapszik, a második, egy újonnan bevezetett paraméteren, a szétválasztás fokon alapszik, a harmadik pedig a kívánt terméktisztaságoktól függ. Habár a kapott minimumok nem mindig élesek, mégis alkalmasak arra, hogy jelentősen szűkítsék a keresési teret.

Quesada és Grossmann (1995) bemutatták a gyakran használt összetétel és komponensáram alapú modelleket. Az összetétel alapú modellben a szétválasztókat leíró egyenletek nem-lineárisak, a komponensáram alapú modellben, pedig ugyanez igaz a megosztók egyenleteire. A modelleket vizsgálva megmutatták, hogy komponensáram alapú modell felírható a megosztókra vonatkozó megosztási hányad típusú változók nélkül is. Bemutattak olyan speciális eseteket is, amikor a modell lineárissá válik,

(26)

például, ha a megosztók csak két kimenettel rendelkeznek, illetve, amikor csak az azonos összetételű folyamok keverése megengedett. A két modellt úgy vonták össze, hogy az eredeti modellekből kiválasztották a lineáris egyenleteket és új egyenleteket vezettek be a két modell változói között fennálló viszony leírására. Az így alkotott egyesített modell alsó korlátot kiszámítására alkalmas. A modellt szétválasztás és korlátozás algoritmusban használták fel, amelyet a Floudas (1987) által bemutatott szuperstruktúrára alkalmaztak lineáris költségű szétválasztókat feltételezve.

Kovács és szerzőtársai (1993) a struktúra szempontjából vizsgáltak különböző típusú SNS problémákat. Megállapították, hogy egyes általánosan elfogadott feltételezések nem minden esetben igazak. Megadtak egy olyan feladatot, amely esetében az optimális megoldás recirkulációt tartalmaz, holott az eddig ismert módszerek eleve kizárták a kör lehetőségét az optimális megoldásban. Később példát adtak olyan SNS feladatokra is, amelyek optimális megoldásában redundáns szétválasztó szerepelt, illetve a kikerülő folyam nem volt maximális, lásd Kovács és szerzőtársai (1995). Ezek a példák arra ösztönözték őket, hogy a kérdést matematikai szigorúsággal kezeljék. Bevezették a szigorú szuperstruktúra fogalmát, amely nem csak feltételezhetően, hanem bizonyítottan tartalmaz minden lehetségesen optimális struktúrát. Megadták a szigorú szuperstruktúrát a 2F3CPP feladatra konkáv költségfüggvény esetén és több betáplálásos, kevert termékes feladatra lineáris költségfüggvény esetén, lásd Kovács és szerzőtársai (2000). Az utóbbi feladathoz megadtak egy lineáris matematikai modellt, ami azért fontos, mert korábban lineáris költség esetén is csak nem-lineáris modellek voltak ismertek. Munkájuk értékét növeli, hogy folyóiratban publikált, korábban optimálisnak vélt megoldásnál jobb struktúrát találtak, sőt bizonyították, hogy valóban a globális optimumot adták meg.

Demicoli és Stichlmair (2003) a szakaszos működésű, összetett szétválasztókat vizsgálták. Egy olyan új működési módot javasoltak, amelyben a háromkomponenses betáplálás középső komponense hatékonyan kinyerhető. Első lépésben a szétválasztó zárt üzemmódban dolgozik teljes refluxxal. A második lépésben, nyílt üzemmódban, az összetett oszlop úgy viselkedik, mint egy egymáson elhelyezkedő normál és fordított működésű desztilláló oszlop.

2.2. HENS

2.2.1. HENS hálózatok

Linnhoff és szerzőtársai (1979) áttekintették az addig ismert hőcserélő hálózatok szintézisére szolgáló eljárásokat, abból a szempontból, hogy azok a gyakorlatban mennyire alkalmazhatóak. Megállapították, hogy habár számos eljárást tettek közzé a szakirodalomban, azok ipari felhasználása nem terjedt el. Felhívták arra is a figyelmet, hogy hálózat tervezésekor nem csak az egyes műveleti egységek, de a hálózat tulajdonságait is szem előtt kell tartani.

(27)

A hőcserélő hálózatok tervezésének új lendületet adott a pinch technológia kifejlesztése, lásd például Linnhoff és Flower (1978), Linnhoff és Hindmarsh (1983). A pinch vagy szűkületi hőmérséklet olyan hőmérséklet értéket jelent, amelyen keresztül nem történik hőcsere egy minimális energia felhasználású hőcserélő hálózatban. A pinch hőmérsékletet például a kaszkád diagram segítségével lehet meghatározni, amely tartalmazza, hogy az egyes hőmérséklet intervallumokban mekkorák az eredő hőigények.

Egy intervallum csak az alatta levő intervallumnak adhat át energiát, hiszen az alacsonyabb hőmérsékletű. Ha egy intervallum energiaigénye akkora, hogy azt a felette lévő intervallumokból nem lehet kielégíteni, akkor melegenergia szolgáltatót kell alkalmazni. Az ilyen intervallum alsó határa a pinch hőmérséklet. A hőmérséklet intervallumokat a hideg- és melegáramok kezdeti és vég hőmérsékletei határozzák meg.

A kaszkád diagram megadja a rendszer hideg- illetve melegenergia igényét is.

Nagyon szemléletesen jellemzik a rendszert a hideg és a meleg kompozit görbék, amelyek az összes hideg- illetve melegáramot egyesítik hőmérséklet - entalpia diagramon. A két görbe legközelebbi pontja a pinch hőmérsékletet mutatja, a görbék végeinek a különbsége az entalpia tengelyen pedig a hideg- illetve melegenergia igényt adja meg. Hasonlóan hasznos a nagy kompozit görbe, amely mind a hideg-, mind a melegáramokat magába foglalja. A pinch technológia segít a minimális szétválasztó szám meghatározásában is. Érdekes tulajdonság, hogy a minimális hőcserélő szám csak akkor érhető el, ha a pinchen keresztül is történik hőcsere vagyis a minimálisnál nagyobb az energia befektetés. Nyilvánvaló, hogy egyensúlyra kell törekedni a hőcserélők befektetési költsége és a rendszer energia költsége között.

Linnhoff és Ahmad (1990) egy a pinch technológián alapuló tervezési módszert mutatott be. A módszer költség célokat definiál és ezeket a célokat még a tervezés előtt optimalizálja úgy, hogy közben lehetővé teszi a felhasználói közbeavatkozást. A kapott megoldás általában 5%-nál nem rosszabb a globális optimumnál. A pinch technológia ma is folyamatosan fejlődik, ma már hőcserélő hálózatok tervezése mellett egyéb területeken is használják. Előnye, hogy segíti a probléma megértését és nagyobb méretű feladatokra is alkalmazható.

Mára az algoritmikus módszerek is előtérbe kerültek. Közéjük tartoznak az úgynevezett szállítási modellek, amelyeknek számos változata létezik. A kaszkád diagramon alapszanak, vagyis hőmérséklet intervallumokat határoznak meg, amelyeken belül szabadon történhet hőcsere, de egy intervallum maradék hője, csak az alatta lévő intervallumba továbbítható, lásd Cerda és szerzőtársai (1983), Papoulias és Grossmann (1983). Barbaro és Bagajewicz (2005) szintén a szállítási modell egy tovább fejlesztett változatát dolgozták ki. Módszerük különbözik mind a hagyományos dekompozíción és pinch technikán, mind pedig a szuperstruktúrán alapuló módszerektől. Egy lépésben határozzák meg az optimális megoldást egy MILP modell segítségével. A módszer erőssége, hogy figyelembe veszi az áramok megosztását és a nem izotermikus keverést.