Tömbfázisú elektrolitok és kalciumcsatornák nagykanonikus Monte Carlo szimulációja
Doktori (Ph.D.) értekezés
Készítette:
Malasics Attila okleveles vegyész
Témavezető:
Dr. Boda Dezső
Pannon Egyetem Kémiai Intézet
Fizikai Kémia Intézeti Tanszék 2010
Értekezés doktori (PhD) fokozat elnyerése érdekében
*a Pannon Egyetem Kémia Doktori Iskolájához tartozóan*.
Írta:
MALASICS ATTILA
**Készült a Pannon Egyetem Kémia Doktori iskolája/ programja/alprogramja kere- tében
Témavezető: Dr. Boda Dezső
Elfogadásra javaslom (igen / nem)
(aláírás)**
A jelölt a doktori szigorlaton …... % -ot ért el,
Az értekezést bírálóként elfogadásra javaslom:
Bíráló neve: …... …... igen /nem ……….
(aláírás) Bíráló neve: …... …...) igen /nem
……….
(aláírás) ***Bíráló neve: …... …...) igen /nem
……….
(aláírás) A jelölt az értekezés nyilvános vitáján …...% - ot ért el.
Veszprém, ……….
a Bíráló Bizottság elnöke A doktori (PhD) oklevél minősítése…...
………
Az EDT elnöke
Tömbfázisú elektrolitok és kalciumcsatornák nagykanonikus Monte Carlo szimulációja
A dolgozat alapvető célkitűzése elektrolitok inhomogén rendszereinek – ezen belül az L-típusú kalciumcsatorna egy egyszerű modelljének - tanulmányozása nagykanonikus Monte Carlo (GCMC) szimulációs technikával. Az elektrolitot egy implicit oldószermodell keretein belül vizsgáltuk, ahol az ionokat töltött merevgöm- bök, míg az oldószert egy dielektromos háttér formájában vettük figyelembe. Az L- típusú kalciumcsatorna pontos szerkezetét nem ismerjük, ezért annak egy redukált modelljét használjuk, ami azon a minimális szerkezeti információn alapszik, hogy a csatorna szelektív szűrője 4 db negatív töltésű glutaminsavat tartalmaz. Az oldallán- cok végén elhelyezkedő karboxil csoportokat a szűrőhöz kötött, de abban szabadon mozgó szerkezeti ionokkal modellezzük. Szimulációink során az inhomogén fázis egyensúlyban volt egy adott összetételű tömbfázisú elektrolittal. Ahhoz, hogy ezt a rendszert nagykanonikus sokaságon szimulálni tudjuk, ismernünk kell az előírt ösz- szetételnek megfelelő kémiai potenciálokat.
A dolgozat első része olyan nagykanonikus sokaságon működő iteratív mód- szerek kifejlesztésével és tesztelésével foglalkozik, ami adott megcélzott koncentrá- ciókhoz meghatározza a kémiai potenciálokat. A javasolt algoritmusokat Lennard- Jones elegyeken és különböző elektrolitrendszereken teszteltük. A kétféle javasolt iterációs eljárás közül az egyik különösen hatékonynak bizonyult, amit egy energia- korrekciós faktor segítségével alkalmassá tettünk az individuális ionok kémiai poten- ciáljainak meghatározására. Ezeket a módszereket széles körben használjuk az ion- csatornák szimulációs vizsgálatánál is.
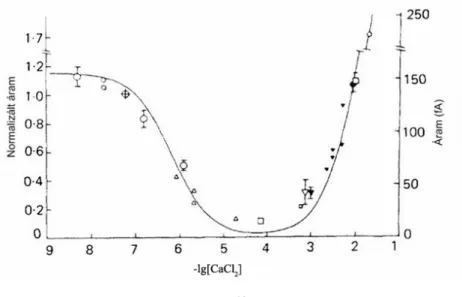
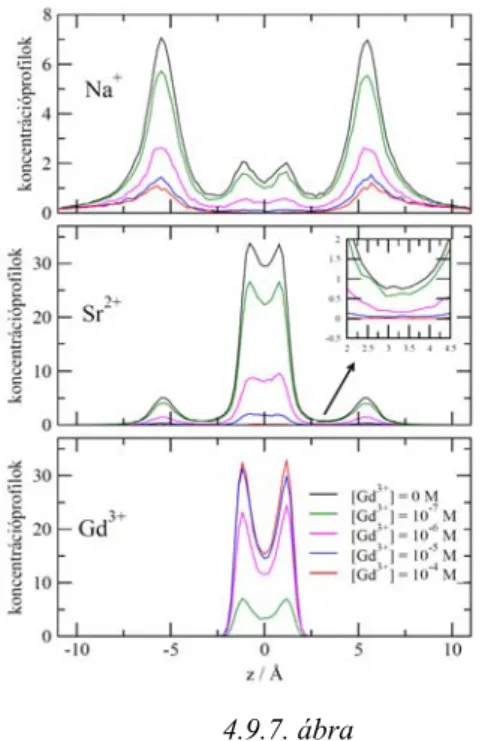
A dolgozat második felében egyrészt megvizsgáltam a csatornamodellünk geometriai paramétereinek hatását az ionszelektivitásra. Azt találtam, hogy a csator- na szelektív szűrőjének térfogata az elsőrendű meghatározója a kalcium versus nátri- um szelektivitásnak. Megvizsgáltam továbbá három különböző töltésű kation ver- sengését a szelektív szűrőben. Az eredményeim azt mutatják, hogy a kísérletekkel megegyező módon a trivalens ionok teljesen blokkolják a monovalens és divalens ionok áramát. Megmutattam továbbá, hogy modellünk megfelelően reprodukálja a szelektivitás változását attól függően, hogy milyen divalens ion van jelen a rendszer- ben (Ca2+, Ba2+ vagy Sr2+). Ezekben a vizsgálatokban a csatornán átfolyó áram nagy- ságára az integrált Nernst-Planck egyenletből vontunk le következtetéseket.
Grand canonical Monte Carlo simulations of bulk electrolytes and calcium channels
The main goal of the thesis is the study of inhomogeneous electrolyte systems - particularly, the L-type calcium channel - with grand canonical Monte Carlo (GCMC) simulations. The electrolyte was modeled in the framework of an implicit solvent model, where the ions were considered as charged hard spheres, while the solvent was represented as a dielectric background. The structure of the L-type calcium channel is unknown, therefore, we used a reduced model based on the minimal structural information that the selectivity filter of the channel contains 4 negatively charged glutamic acids. The carboxyl groups at the ends of the side chains were modeled as structural ions confined to the filter but free to move inside otherwise. In our simulations, the inhomogeneous phase was in equilibrium with a bulk electrolyte of fixed composition. In order to simulate this system in the grand canonical ensemble, we need to know the chemical potentials corresponding to this prescribed composition.
The first part of the thesis deals with the development an testing of iterative methods that use GCMC simulations and determine the chemical potentials that produce a targeted set of concentrations. The suggested algorithms were tested on Lennard-Jones mixtures and various electrolyte systems. One of the two suggested iteration procedure proved to be especially efficient. With the addition of an energy correction factor, we made the method capable of determining the chemical potentials of individual ions. These methods are widely used in our simulation studies for ion channels.
In the second part of the thesis, I studied the effect of changing the geometrical parameters of our channel model to ion selectivity. I found that the first order determinant of calcium versus sodium selectivity is the volume of the selectivity filter. Furthermore, I studied the competition of three cations of different charges in the selectivity filter. My results show that, in agreement with experiments, trivalent ions block the current of monovalent and divalent ions completely. I have shown that our model appropriately reproduces the change in selectivity as a function of the divalent ion present in the system (Ca2+, Ba2+ or Sr2+). In these studies, the current flowing through the channel was estimated from the integrated Nernst-Planck equation.
Simulations grand-canonique d’électrolytes en solution et dans des canaux calciques
L'objectif de cette thèse est l'étude d'électrolytes inhomogènes, en particulier les canaux calciques de type L, par le biais de simulations Monte Carlo dans l'en- semble grand-canonique (GCMC). L'électrolyte est modélisé par un modèle de sol- vant implicite, où les ions sont considérés comme des sphères dures chargées, alors que le solvant est représenté par sa constante diélectrique. La structure des canaux calcique de type L est inconnue, c’est pourquoi j’ai utilisé un modèle simplifié basé sur les informations structurelles minimales connues à savoir que le canal contient quatre groupement acides glutamiques chargés négativement. Les groupes carboxyli- ques en bout des chaines latérales sont modélisés comme des ions structurels confi- nés dans le filtre ionique mais libres de se mouvoir à l'intérieur. Dans notre simula- tion, la phase inhomogène était en équilibre avec la phase volumique de l'électrolyte de composition donnée. Pour simuler ce système dans l'ensemble grand-canonique, nous devons connaître les potentiels chimiques correspondant à la composition im- posée.
La première partie de la thèse est consacrée au développement et au test des méthodes itératives utilisées dans la simulation GCMC ainsi qu'à la détermination des potentiels chimiques de l'électrolyte en équilibre avec le canal ionique et qui permettent d’obtenir les concentrations voulues dans le canal ionique. Les algorith- mes développés ont été testés sur des mélanges de fluides de Lennard-Jones et diffé- rents électrolytes. Une des deux procédures d'itération proposée s'est révélée particu- lièrement efficace. Avec l'ajout d'une correction à l'énergie, j’ai établi une méthode capable de déterminer le potentiel chimique individuel de chaque ion. Ces méthodes sont actuellement largement utilisées dans nos simulations numériques pour l'étude des canaux ioniques.
Dans la seconde partie de ma thèse, j'ai étudié l'effet du changement des pa- ramètres géométriques de du modèle de canal ionique sur la sélectivité ionique. J'ai trouvé, en première approximation, que le paramètre déterminant dans la sélectivité du canal vis à vis de la sélection des ions calcium sur les ions sodium est le volume du filtre. En outre, j'ai étudié la compétition de trois cations de charges différentes dans le filtre de sélectivité. Mes résultats montrent que, en accord avec les expérien- ces, des ions trivalents bloquent complètement le courant des ions monovalents et divalents. J’ai montré que le modèle reproduit le changement de sélectivité en fonc- tion des ions divalents (Ca2+, Ba2+ ou Sr2+) présents dans le système. Dans ces diffé- rentes études, le courant qui passe dans le canal est estimé par l’équation de Nernst- Planck.
1. Bevezetés ... 8
2. Modell ... 11
2.1. Az oldatok primitív modellje ... 11
2.2. Szimulációs módszerek általában ... 13
2.3. Kanonikus sokaságú Monte Carlo ... 16
2.4. Nagykanonikus sokaságú Monte Carlo... 17
3. Kémiai potenciál számítása... 20
3.1. Irodalmi áttekintés... 20
3.2. Sorfejtéses GCMC módszer... 23
3.3. Adaptív-GCMC módszer ... 24
3.4. Töltéskorrekció az A-GCMC eljáráshoz... 26
3.5. A sorfejtett és az adaptív algoritmus összehasonlítása Lennard-Jones elegyek esetén ... 28
3.5.1. A sorfejtéses módszer ... 28
3.5.2. Az adaptív módszer... 31
3.6. Tömbfázisú elektrolitok szimulációja... 34
3.6.1. Sokaságok rendszerméret-függése 1:1 elektrolit esetén ... 34
3.6.2. Az átlagolás hatása az Adaptív GCMC módszer konvergenciájára... 35
3.6.3. Az MGB és a Lamperski módszer konvergenciájának összehasonlítása ... 37
3.6.4. Az MGB/I+av algoritmus korrekciója, individuális részecske behelyezés/kivétel esetén ... 40
3.6.5. Elektrolit elegyek ... 44
4. Az L-típusú kalciumcsatorna szelektivitására vonatkozó vizsgálatok... 47
4.1. Az ioncsatornák: biológiai háttér ... 47
4.2. Az L-típusú kalcium-csatornára vonatkozó kísérleti eredmények... 52
4.3. Az ioncsatornás szimulációk történeti áttekintése ... 59
4.4. A csatornamodellünk ... 64
4.5. Speciális mintavételezési technikák... 66
4.6. Az elektrosztatikus energia számolása a szimulációban... 68
4.7. Az ioncsatorna vezetőképességének számítása... 71
4.8. A csatorna geometriai jellemzőinek hatása a szelektivitásra ... 74
4.8.1. A csatorna térfogatának hatása a szelektivitásra... 75
4.8.2. A csatorna alakjának hatása a szelektivitásra... 78
4.8.3. Az oxigénionok hatása a szelektivitásra ... 82
4.8.4. Összefoglalás ... 85
4.9. Trivalens, divalens és monovalens ionok versengése ... 87
4.9.1. Két kation versengése ... 87
4.9.2. Három kation versengése ... 91
5. Összefoglalás ... 104
6. Köszönetnyilvánítás ... 106
7. Irodalomjegyzék... 107
1. Bevezetés
Az ioncsatornák olyan membránfehérjék, amelyek a különböző élettani szempontból fontos szervetlen ionoknak a sejtmembránon való átjutását szabályoz- ható módon biztosítják. Ezek az ioncsatornák sokszor rendkívül szelektívek, például a kalciumcsatorna nagyobb valószínűséggel engedi át a kalciumiont, mint a nátrium- vagy a káliumiont, még úgy is, hogy a monovalens ionból sokkal több van. Az ion- csatornák viselkedésének befolyásolása révén működő gyógyszerek az orvostudo- mányban alkalmazott gyógykészítmények nagy százalékát teszik ki. Természetes anyagok (íz-, illatanyagok) sokasága is különböző ioncsatornákon fejti ki hatását.
Laboratóriumok százaiban rutinszerűen mérik ezeknek a kis gépezeteknek a tulaj- donságait. A szimulációs módszerek és a számítógépek fejlődésével az ioncsatornák elméleti vizsgálata is rohamos fejlődésnek indult az utóbbi 15 évben.
Egy olyan kutatócsoport munkájába kapcsolódtam be, amely elektrolitok in- homogén rendszereit vizsgálta nagykanonikus sokaságú Monte Carlo szimulációk alkalmazásával. Ezen belül én az L-típusú kalciumcsatorna szelektivitási mechaniz- musával foglalkoztam. Ez egy élettanilag rendkívül fontos ioncsatorna, amely az izomsejtek külső membránjában helyezkedik el, és az izom összehúzódását paran- csoló elektromos ingerület hatására kalciumot bocsát a sejtbe. (Az ioncsatornák je- lentőségéről és osztályozásáról a 4.1 fejezetben olvasható egy összefoglaló.)
Ennek az ioncsatornának az úgynevezett szelektív szűrője egy erősen negatí- van töltött tartomány, ami miatt ez a csatorna a nagyobb töltésű ionokat preferálja a kisebb töltésűvel szemben. Erre az ioncsatornára számos elektrofiziológiai kísérleti munka áll rendelkezésre az irodalomban, ahol általában azt vizsgálták, hogy mikép- pen változik a csatornán átfolyó áram, ha a tömbfázisban változtatjuk az egymással versengő kationok koncentrációit. (Az L-típusú kalciumcsatornára vonatkozó kísérle- tekről a 4.2 fejezetben olvasható egy összefoglaló.)
Az ioncsatorna, a membrán, amiben elhelyezkedik, valamint az ezt a rend- szert körülvevő tömbfázis (a sejten belüli illetve sejten kívüli térrész) egy inhomogén elektrolitikus rendszert képez. Egyensúlyban a hőmérsékleten, a nyomáson és a ké- miai potenciálon kívül bármely fizikai mennyiség lehet helyfüggő (a rendszer inho- mogén). Inhomogén rendszerekben általában a rendszer inhomogén tartománya – azaz ahol valamilyen fal vagy külső kényszer a fizikai állapotjelzők inhomogenitását
okozza – egyensúlyban van egy homogén tömbfázissal, azaz ugyanolyan hőmérsék- lettel, nyomással és kémiai potenciállal bír. Jelen esetben a membrán és maga a fe- hérje (az ioncsatorna) az inhomogenitást okozó tényezők. Nem egyensúlyi esetben a külső tér és/vagy a koncentráció gradiens szintén inhomogenitást okoz.
Általában a rendszer inhomogén részének tulajdonságai, ezen tartomány szer- kezete függ a homogén fázis összetételétől. Például sokszor az a kérdés, hogy az in- homogén rendszer melyik összetevőből mennyit adszorbeál (abszorbeál) a tömbfázis összetételének függvényében. Az ioncsatornák szelektivitásának vizsgálatánál is ez a kérdés: egy adott összetételű elektrolitból melyik kationt engedi át a kalciumcsator- na? Mi ennek a szelektivitásnak a mechanizmusa? Ennek a kérdésnek a megválaszo- lására az a kutatócsoport, amelyhez csatlakoztam, egy egyszerű modellt állított fel a kalciumcsatorna szűrőjére (lásd 4.4 fejezet), és ezt a modellt Monte Carlo szimuláci- ós módszerrel (lásd 2. fejezet) vizsgálták (lásd 4.3 fejezet). Munkájuk során bebizo- nyosodott, hogy erre a célra a legalkalmasabb a nagykanonikus sokaság. Ezen nincs különösebb csodálkoznivaló, mivel közismert hogy a nagykanonikus sokaság külö- nösen alkalmas inhomogén rendszerek vizsgálatára. Ennek az az oka, hogy a homo- gén tömbfázis egyenértékű egy virtuális tömbfázissal, amit a hőmérséklet és a kom- ponensek kémiai potenciáljainak rögzítésével egyértelműen definiálhatunk. Az ezen tömbfázissal való egyensúlyt speciális részecskebehelyezési illetve –kivételi lépé- sekkel biztosítjuk. Emiatt a homogén tömbfázis közvetlen szimulálására nincs is szükség, vagy csak annak egy kis tartományát kell csak közvetlenül belefoglalnunk a szimulációs cellába.
A nagykanonikus sokaságnak azonban az a hátránya, hogy ismernünk kell azokat a kémiai potenciálokat, amelyek egy adott összetételű rendszert állítanak elő.
A kísérleti munkák során is mindig a koncentrációkat állítják be, és nem a kémiai potenciálokat. Felmerül tehát az igény egy olyan módszer iránt, amellyel előírt kon- centrációkhoz meg tudjuk határozni a kémiai potenciálokat. Kanonikus sokaságon a Widom-féle tesztrészecske módszer [1] használatos erre a célra, de pont abban a koncentráció-tartományban, ami minket a kalciumcsatornák miatt érdekel, a használ- hatósága korlátozott. Ez az a tartomány, ahol például egy 100 mM-os NaCl mellett
M-os nagyságrendű koncentrációban van jelen egy másik komponens, jelesül a CaCl2. Az ilyen összetételű elegyeknél a sűrűség-fluktuációk korrekt kezelése elen- gedhetetlen. Ennek szimulálására a kanonikus sokaság a részecskeszámok rögzített volta miatt kevésbé alkalmas, mivel a sokkal kisebb mennyiségben jelen lévő kom-
ponensből is elegendőnek kell lenni, ami túl nagy szimulációs rendszer használatá- hoz vezet. A nagykanonikus sokaság – ahol a részecskeszámok fluktuálnak – viszont nem szenved ettől a hátránytól. Ezért azt a célt tűztük ki magunk elé, hogy a kémiai potenciálok meghatározására szolgáló eljárás alapja a nagykanonikus sokaság le- gyen. Ezt csak iteratív módon érhetjük el, azaz ismételt szimulációkat végzünk, és az iteráció során a kémiai potenciálokat valamilyen algoritmus szerint változtatjuk, egé- szen addig, amíg a nagykanonikus szimuláció a kívánt koncentrációkat nem szolgál- tatja. Azt, hogy ez a cél valós igényt elégít ki, mi sem bizonyít jobban, minthogy velünk párhuzamosan S. Lamperski [2] is ugyanezt a célt tűzte ki maga elé. Az eljá- rás lelke az az algoritmus, amelynek segítségével egy következő iterációban használt kémiai potenciálokat az előző iteráció eredményeiből kiszámítjuk.
Munkánk során két ilyen algoritmust is javasoltunk (lásd 3.2 és 3.3 fejezetek), míg Lamperski egy harmadik, a mieinktől eltérő algoritmust dolgozott ki (lásd 3.1 fejezet). A dolgozatban egy összehasonlító analízisét adjuk ezen algoritmusok- nak, felhasználjuk Lamperski ötletét (mely szerint a végeredményt az iterációkban használt kémiai potenciálok átlagaként kapjuk meg) az eljárásunk hatékonyabbá téte- lére, és egy korrekciós energiatagot vezetünk be, amelynek segítségével nemcsak a közepes ionaktivitási tényezőt (azaz a só kémiai potenciálját), hanem az egyes indi- viduális ionok aktivitási tényezőit (kémiai potenciáljait) is pontosan meghatározhat- juk.
A dolgozat második felében az ezzel a módszerrel számolt kémiai potenciá- lokat használom arra, hogy az L-típusú kalciumcsatorna egy egyszerű modelljének további tulajdonságait tanulmányozzam. Egyrészt megvizsgálom, hogy a szelektív szűrő alakjának megváltoztatása milyen hatással van monovalens és divalens (konk- rétan Na+ és Ca2+) ionok versenyére (lásd 4.8 fejezet), majd kísérleti eredményektől motiválva megvizsgálom, hogy mi történik, ha a rendszerben nemcsak kettő-, hanem háromfajta ion versenyez egymással, azaz a monovalens és a divalens ion mellett egy trivalens ion is jelen van (lásd 4.9 fejezet).
2. Modell
2.1. Az oldatok primitív modellje
Szimulációink során elektrolitok inhomogén rendszereit vizsgáltuk. Az elekt- rolitot az úgynevezett primitív modellel jellemeztük. Ebben a modellben az oldószer- molekulákat implicit módon vesszük figyelembe egy dielektromos kontinuum formá- jában. Az oldószer-molekulák szabadsági fokait tehát kiátlagoljuk, és az általuk adott átlagos, lineáris dielektromos válasz formájában vesszük figyelembe, azaz a Cou- lomb kölcsönhatás nevezőjében megjelenik a dielektromos együttható, ami az oldó- szer árnyékoló hatását reprezentálja. Az ionokat explicit módon, töltött merevgöm- bökként modellezzük. Az i-edik és j-edik ion közötti kölcsönhatás potenciális energi- ája (Vij) a következő formában adható meg:
2 4
2
0 2
j i j
i
j i
ij d d
r r ha
e z z
d r d
ha r
V
, (2.1.1)
ahol és az ionok töltésszáma, az elemi töltés, és zi zj e di dj az ionok átmérője,
0 a vákuum permittivitása, a dielektromos együttható és r a kölcsönható ionok középpontjainak távolsága.
A primitív modell kétségkívül egy elnagyolt modellje az elektrolitoknak, mi- vel az oldószert nem molekuláris szinten modellezi, mégis alkalmasnak bizonyult többféle kísérleti jelenség leírására és értelmezésére, melyekben általában nagy sze- repet játszik a Coulomb kölcsönhatás hosszú távú jellege.
Valamilyen töltött rendszert (egy töltött részecskét, egy töltött határfelületet, elektródot vagy éppenséggel az ioncsatorna töltött szelektív szűrőjét) az elektrolit ionjai semlegesítenek, azaz ez a részrendszer az úgynevezett ellenionokat magához vonzza. Mivel az ionok közben hőmozgást is végeznek, ez az árnyékolás egy ionfel- hő illetve elektromos kettősréteg formájában megy végbe. Ennek a tartománynak a szerkezete nagy fontossággal bír számos kísérleti eredmény magyarázata szempont- jából [3 - 5].
A primitív modell szimulációs eszközökkel tanulmányozva alkalmas olyan jelenségek reprodukálására, amelyek a kettősréteg szerkezetének megváltozásán ala- pulnak divalens ionok hatására. Az úgynevezett túltöltés (overcharging) jelensége például azt jelenti, hogy több multivalens ion vonzódik az elektródhoz, mint amennyi az elektród semlegesítéséhez szükséges. Ez a többlet pozitív töltés egy anionréteg kialakulását eredményezi, amit töltésinverziónak nevezünk [3; 4]. Ez a jelenség az alapja az elektroforetikus mozgékonyság előjel-változásának [6 - 9], azonos töltésű részecskék közötti vonzóerő kialakulásának (a cementet összetartó erő [10; 11], DNS molekulák kisózása [12; 13]), vagy a szelektivitási jelenségeknek nanopórusokban [14; 15]. A primitív modell továbbá rendkívül célravezetőnek bizonyult ioncsatornák szelektivitási mechanizmusainak vizsgálatában (lásd később).
Az alapvető elméletek a Poisson egyenlet megoldásán alapulnak Boltzmann eloszlás feltételezésével. Egy ion árnyékolását a többi által a Debye-Hückel elmélet [16] írja le, az elektrokémiai kettősréteg szerkezetére Gouy-Chapman elméletnek [17; 18] nevezzük ugyanezt, míg a kolloid kémiában a Derjaguin–Landau–Verwey–
Overbeek (DLVO) elmélet [19; 20] használatos. Amikor azonban divalens ion van jelen a rendszerben – mint a fent említett esetekben –, ezek az elméletek csődöt mondanak. Ekkor modernebb statisztikus mechanikai elméletek (integrálegyenletek, sűrűségfunkcionál elmélet) illetve molekuláris szimulációk használata szükséges.
2.2. Szimulációs módszerek általában
A rendezetlen, kondenzált fázisú rendszerek szerkezetének statisztikus me- chanikai alapon történő vizsgálatában kiemelkedő helyet foglalnak el a számítógépes szimulációs módszerek. Ezek a módszerek az anyagi rendszer mikroszkópikus tulaj- donságainak, azaz a molekulák vagy atomok közötti kölcsönhatásoknak ismeretében a sokrészecskés rendszer mikroállapotait közvetlenül modellezik, és a fázistérből ily módon mintát véve a keresett tulajdonságokat sokaság- vagy időátlagként számítják.
Az intermolekuláris potenciálokon kívül szükség van még néhány termodinamikai állapotjelző rögzítésére a használt sokaságtól függően. Két alapvető szimulációs módszer létezik, az egyik a molekuláris dinamikai (MD), a másik a Monte Carlo (MC) módszer. Az MD szimulációk során a rendszer fázistérbeli trajektóriáját a klasszikus newtoni mozgásegyenletekkel határozzák meg. A trajektória mentén szá- mított fizikai mennyiségek átlaga időátlagnak tekinthető.
A Monte Carlo szimuláció ezzel szemben sztochasztikus, a fázistérben nem egyetlen rendszer trajektóriáját követjük végig, hanem véletlenszerűen mintát ve- szünk a konfigurációs tér pontjai közül, így különböző mikroállapotú rendszerek sokaságát állítjuk elő. A módszer nem alkalmas nemegyensúlyi, időben változó rend- szerek vizsgálatára, csak az egyensúlyban levő rendszerek jellemzői határozhatóak meg. A részecskék „mozgása” indeterminisztikus, valószínűségi törvénynek enge- delmeskedik.
Folyadékok egyensúlyi tulajdonságainak szimulációjára Metropolis és mun- katársai [21] alkalmazták először az MC módszert 1953-ban a MANIAC számítógé- pen. Az általuk szimulált kétdimenziós modellrendszer mindössze 108 merev, ko- rong alakú részecskéből állt. Azóta az elektronikus számítógépek viharos fejlődésé- vel és elterjedésével párhuzamosan ez a módszer világszerte használatos, viszonylag egyszerű eljárássá vált, segítségével egyre nagyobb és bonyolultabb rendszerek vizs- gálhatók.
A Monte Carlo módszer sokdimenziós integrálok becslésére is felhasználha- tó, ha véletlen számok segítségével elegendően nagyszámú mintát veszünk. Így egyensúlyi statisztikus mechanikai rendszerek fizikai-kémiai tulajdonságai is számít- hatók a módszer segítségével. Amikor egy rendszert vizsgálunk, rögzíteni kell annak termodinamikai határfeltételeit, azaz hogy a rendszert milyen tulajdonságú falak ha-
tárolják. Eszerint különféle sokaságokat lehet definiálni: megkülönböztetünk például mikrokanonikus (EVN), kanonikus (NVT), nagykanonikus (VT) és izoterm-izobár (NpT) sokaságokat.
Mivel munkám során Monte Carlo szimulációval foglalkoztam, disszertáci- ómban is ezt mutatom be részletesen. A részecskék közötti kölcsönhatást leíró poten- ciálfüggvények ismeretében olyan, különböző mikroállapotú rendszereket állítunk elő, melyek együttese valamilyen statisztikus mechanikai sokaságot (pl. kanonikus, nagykanonikus, stb.) alkot. A különböző mikroállapotú rendszereket ezért úgy kell előállítani, hogy az adott statisztikus mechanikai sokaság termodinamikai állapotát meghatározó extenzív paraméterek (pl. kanonikus sokaság esetén a rendszer térfoga- ta és részecskeszáma) a szimuláció során állandó értéken maradjanak, míg a termo- dinamikai állapotot meghatározó intenzív mennyiségekhez tartozó konjugált extenzív mennyiségek értéke a szimuláció során kapott rendszerekben az adott sokaságnak megfelelő eloszlást mutassa (pl. kanonikus sokaságon az energia a Boltzmann- eloszlást kövesse).
Mind kanonikus és nagykanonikus sokaságon a rendszer térfogata állandó, ezért definiálnunk kell egy a kívánt geometriával rendelkező állandó térfogatú szi- mulációs cellát. Az ioncsatornára vonatkozó szimulációkra a cella felépítését a 4.4 fejezetben ismertetjük. Tömbfázisú szimulációinkban a következőképpen építjük fel a rendszert.
Tekintsünk egy V térfogatú, kocka alakú szimulációs cellát, amely N részecs- két tartalmaz. Amennyiben a cella falakkal határolt, a minta nem tekinthető makroszkópikusnak, mivel a határfelületi jelenségek szerepe jelentős. Tömbfázisú rendszert az inhomogenitásoktól távol szimulálunk. A periodikus határfeltétel alkal- mazásával kiküszöbölhetőek a határfelületi jelenségekből származó hibák, mivel a középpontinak tekintett cella körül ebben az esetben végtelen számú ugyanolyan cella helyezkedik el (2.2.1. ábra).
Ezekben a cellákban a részecskék ugyanúgy mozognak, mint a központi cella részecskéi. Ez azt jelenti, hogy ha egy részecske kilép a kockából egy adott irányban, a szomszéd cellából belép a neki megfelelő „replika részecske” az ellentétes irány- ból.
2.2.1. ábra
Periódikus határfeltétel szemléltetése a szimulációs cellákban: „Ha egy részecske kilép a kockából egy adott irányban, a szomszéd cellából belép a neki megfelelő „replika részecske” az ellentétes
irányból."
A periódikus határfeltételhez az energia számolása szempontjából hozzá tar- tozik az úgynevezett legközelebbi szomszéd eljárás (minimum image convention).
Ennek során egy adott részecske energiáját úgy számítjuk, hogy összeadjuk az ezen részecskének a dobozban lévő többi részecskével való párkölcsönhatását, mégpedig úgy, hogy ezt a részecskét a kocka közepébe helyezzük.
2.3. Kanonikus sokaságú Monte Carlo
A kanonikus sokaság olyan alrendszerek együttesét jelenti, amelyek a kör- nyezettel termikus egyensúlyban vannak, vagyis energiát cserélhetnek vele. Az al- rendszerekben lévő részecskék száma állandó, ahogy a rendszer hőmérséklete és tér- fogata is. Ebben az esetben a rendszer zárt, a fal diaterm, merev és impermeábilis.
Valamely B konfigurációs (a részecskék helyzetétől és orientációjától függő) fizikai mennyiség kanonikus sokaságátlaga gömbszimmetrikus részecskék esetén:
N N
N N
N
NVT d U
U B
B d
r r
r r
r
exp
exp , (2.3.1)
ahol U
rN a rendszer teljes energiája és 1/kBT, amelyben a Boltzmann- faktor éskB
T a hőmérséklet.
A Monte Carlo mintavételi lépések közül a legáltalánosabb a részecskemoz- gatás, mert ez minden sokaságra érvényes. Alapesetben a véletlenszerűen kiválasztott részecske véletlenszerűen kiválasztott helyre történő mozgatása történik. A szimulá- cióban az i állapotból a j állapotba jutás valószínűsége:
iji NVT
j NVT
ij U
U Q
U
P Q
exp
exp exp
1
1
, (2.3.2)ahol QNVT a kanonikus állapotösszeg és Uij Uj Ui a mozgatással együtt járó energiaváltozás.
Ha a Uij0, azaz Pij 1, ezzel a valószínűséggel fogadjuk el a mozgatást.
Ha , akkor mindig elfogadjuk a mozgatást (Metropolis mintavételezés) [21].
Ez a fajta mintavételezés biztosítja a mikroszkópikus reverzibilitást.
0
Uij
2.4. Nagykanonikus sokaságú Monte Carlo
A nagykanonikus (GC) sokaság olyan alrendszerek együttesét jelenti, ame- lyek a környezettel nem csak energiát, hanem részecskét is cserélhetnek, így az egyes alrendszerek hőmérséklete
T
mellett a részecskék kémiai potenciálja
is állandó lesz, miközben az extenzív állapotjelzők közül csak a rendszer térfogatának
ér- téke azonos a sokaság egyes alrendszereiben. Ebben az esetben a rendszer nyitott, a fal diaterm, merev és permeábilis.
V
A Monte Carlo szimulációk statisztikus mintavételt hajtanak végre véletlen- szerű lépésekkel egy ilyen sokaságú rendszeren. A nagykanonikus sokaságátlag
B-re szintén gömbszimmetrikus részecskék esetén egykomponensű rendszerre:
N
N N
N N
N N
N N
VT d U
N e
U B
N d e B
r r
r r
r
exp
!
! exp . (2.4.1)
A nagykanonikus Monte Carlo szimulációk során a részecskék helycseréjén kívül további művelet is megengedett, ez pedig a részecske hozzáadás illetve eltávolítás.
Az ezen a sokaságon működő MC módszert a 60-as – 70-es évek fordulóján fejlesz- tette ki egymástól függetlenül Norman és Filinov [22] illetve Adams [23; 24]. Ennek során az komponens egy véletlenszerűen kiválasztott részecskéjét megpróbáljuk a szimulációs cella egy véletlenszerűen kiválasztott helyére behelyezni, illetve onnan eltávolítani. Ezen behelyezés/eltávolítás elfogadásának a valószínűsége:
i
kT V U
N
P N i
i i i
! exp , !
1
min , (2.4.2)
ahol értéke behelyezéskor +1 kivétel esetén pedig -1, az i komponens ré- szecskeszáma a művelet előtt, V a térfogat,
Ni
U a művelettel együtt járó energiavál- tozás és i az i komponens kémiai potenciálja. A szimulációban azonos valószínű- séggel kíséreljük meg a részecske behelyezést, illetve eltávolítást.
Mielőtt rátérnénk az elektrolitok nagykanonikus szimulációjára, tisztázzunk néhány alapfogalmat. Egy egyszerű elektrolit sztöchiometriai egyenlete a következő:
A Kz Az
K
, (2.4.3)ahol a K és az A jelzi a kationt és az aniont, valamint és jelölik azokat a sztöchiometriai együtthatókat, amelyek kielégítik a töltéssemlegesség feltételét:
0
z z
. (2.4.4)
A só kémiai potenciálja
s kifejezhető az ionok kémiai potenciáljaiból:
s . (2.4.5)
Nagykanonikus sokaságú MC szimulációk esetén az i-edik komponens konfiguráci- ós kémiai potenciálja felírható:
ex3
tot log
log 2 i i
i i
i kT c
m
kT h
, (2.4.6)
ahol a teljes kémiai potenciál, h a Planck állandó, az i-edik részecske tö- mege és a többlet kémiai potenciál. Az utolsó tag az ideális gáztól való többlet, és az ionok közötti kölcsönhatást fejezi ki. A só kémiai potenciálja felírható a követ- kező módon:
tot
i mi
ex
i
ex ex log
exlog s
s kT c c kT c c
. (2.4.7)
Ez az egyenlet egyben definiálja a só többlet kémiai potenciálját is. Az i-edik indi- viduális ion aktivitási együtthatója i exp
iex/kT
, míg a só közepes aktivitási együtthatója
s
.Elektrolitok esetében jobban elterjedt olyan részecske behelyezéssel/kivétellel dolgozni, ahol darab K k ont és z ati darab z aniont helyezünk be/távolítunk el. A 2.4.4 egyenlet értelmében ezek az ionok egy semleges csoportot (sót) alkotnak [25]. A só behelyezés/kivétel elfogadási valószínűsége (amelyet egyébként bármely sóra felírhatunk):
A
kT
V U
! N
! N
! N
! , N
P s
A K
A s K
exp
1
min , (2.4.8)
ahol NK és NA a kation és az anion darabszáma behelyezés/kivétel előtt.
Ez a fajta részecske-mozgatás automatikusan biztosítja a rendszer töltéssem- legességét, míg individuális ionok behelyezése/kivétele esetén a töltéssemlegesség csak átlagosan áll fenn, a szimuláció minden pillanatában nem feltétlenül. Az átlagos
töltéssemlegesség is csak akkor áll fenn, ha olyan kémiai potenciálokkal dolgozunk, amelyek töltéssemleges rendszert eredményeznek, azaz fennáll, hogy:
0
i ii N
z . (2.4.9)
Eszerint tehát attól függően, hogy milyen részecske behelyezést alkalmazunk, két különböző nagykanonikus sokaságról beszélhetünk. Individuális ionbehelyezés esetén a sokaság független változói:
T,V,1,...,m
0
, míg só behelyezés esetén a só kémiai potenciálja mellett a só ionjainak össztöltése a másik független paraméter, ami természetesen zérus (zNzN ).
Ahogy azt már említettük, a nagykanonikus sokaság számos előnnyel rendel- kezik. Hátránya mindenekelőtt az, hogy általában olyan rendszert szeretnénk szimu- lálni, ahol a különböző komponensek koncentrációi rögzítettek a kémiai potenciáljuk helyett. Szükségünk van tehát azokra a kémiai potenciálokra, amelyek egy nagykanonikus szimuláció végén az előírt koncentrációkat szolgáltatják sokaságát- lagként: ci Ni /V. A következő fejezetekben különböző módszereket mutatunk be, amelyekkel a kémiai potenciál meghatározható.
3. Kémiai potenciál számítása
3.1. Irodalmi áttekintés
Ahhoz tehát, hogy alkalmazni tudjuk a nagykanonikus Monte Carlo szimulá- ciót, szükségünk van a rendszerben lévő komponensek adott koncentrációihoz tarto- zó kémiai potenciálokra. Mielőtt kifejteném az általunk kifejlesztett módszereket a kémiai potenciál számítására, ismertetek néhány az irodalomban használt eljárást.
A Widom-féle tesztrészecske beillesztési módszer az egyik legelterjedtebb módszer a kémiai potenciál számolására [1]. Eredetileg kanonikus sokaságra lett ki- fejlesztve, de bármely sokaságon működik. A módszer során elvégzünk egy szimulá- ciót kanonikus sokaságon egy adott összetételű elegyre. Ezután a szimulá- ció során nyert mintakonfigurációkba időnként beillesztünk egy
-edik szel- lemrészecskét és kiszámítjuk annak a többi részecskével létrejövő kölcsönhatásából származó energiáját (jelölése Widom/I). Ezt a részecskét nem hagyjuk a cellá- ban, csak a betételéhez szükséges energiára vagyunk kíváncsiak. Az
-edik szellemrészecske behelyezése után az i-edik komponens többlet kémiai potenciálja am 1...N N
i1 N
N
1
UN
i1
N
i kT
kT U
ex ln exp (3.1.1)
egyenlet szerint a Boltzmann-faktorok sokaságátlagából kapható meg.
A Widom eljárás hátránya, hogy csak semleges molekulákból álló rendszerek (pl. sók) többlet kémiai potenciáljának illetve aktivitási együtthatójának számítására alkalmas, ionok hozzáadása esetén pontatlan eredményeket kapunk, mivel sérülni fog a töltéssemlegesség. Ezért az előző fejezetben – nagykanonikus szimulációk esetén – már taglalt, ionok semleges kombinációját helyezzük be. Ekkor a 3.1.1 egyenletből az adott só többlet kémiai potenciálját kapjuk (jelölése Widom/S). Ha például két tesztrészecskét helyezünk be a rendszerbe, akkor az energiaváltozás
U U U U , (3.1.2)
ahol U a pozitív, U a negatív tesztrészecske és a többi rendszerben lévő ré- szecske közötti kölcsönhatási energia, az pedig a két töltött részecske közötti energia. Ha tehát egy ion kémiai potenciáljára vagyunk kíváncsiak, és a Widom
U
módszert úgy alkalmazzuk, hogy egyetlen iont helyezünk be a rendszerbe, akkor a fenti energiatag hiányozni fog az energiából. Egy töltéssemleges elektrolitban ugyanis mindig jelen vannak egy adott ionhoz tartozó ellenionok is. Ez a hiányzó energia a Widom/I módszernek nagyon erős rendszerméret függést okoz.
U
Ennek ellensúlyozására az irodalomban két módszer ismert. Svensson és Woodward az ionok töltéseinek átskálázásával [26] oldották meg a töltéssemlegesség sérülésének problémáját (jelölése SW/I). Munkánk szempontjából fontosabb volt Sloth és Sørensen módszere [27 - 30], akik a q töltésű tesztrészecske töltését egy
konstans háttértöltéssel semlegesítették (jelölése SS/I). Ekkor a hi- ányzó ellenionokkal való kölcsönhatás becsülhető, mint az ezen háttértöltéssel való kölcsönhatás:
/L3 Q r Q
0 3
4 2 1
L Q
Q Q d
U r
r R
r
. (3.1.3)
Feltételezhető, hogy a tesztrészecske a szimulációs cella középpontjában van . Az integrálást elvégezve:
R0
LK UQ Q
0
2
32
, (3.1.4)
ahol
3 2 log 6 2
1
1 1
1 1
1 x2 y2 z2
dz dy
K dx
. (3.1.5)UQ
egy állandó tag, amely csak a szimulációs cella méretétől, és a behelyezett ion töltésszámától függ.
Nagykanonikus sokaságon a kémiai potenciál a szimuláció paramétere, míg a koncentráció a szimuláció eredményeként áll elő. Korábban már kifejtettük, hogy ez a sokaság alkalmasabb bizonyos rendszerek vizsgálatára, mint a kanonikus sokaság.
Ezért felmerül annak igénye, hogy az adott koncentrációhoz tartozó kémiai potenciá- lokat ezen a sokaságon határozzuk meg, azaz szellemrészecskék behelyezése/kivétele helyett valós részecskéket alkalmazunk, ily módon megengedve a különböző kom- ponensek fluktuációját a rendszerben.
Ez vezette Lamperskit arra, hogy – velünk párhuzamosan – kifejlesszen egy iteratív szimulációs eljárást, adott megcélzott koncentrációkhoz
citarg tartozó többlet kémiai potenciálok
iex meghatározására [2]. Az iteráció során változtatta a kémiai potenciálokat a következő algoritmus szerint (jelölése Lamperski/I+av):Ha ci
n citarg iex
n1
iex
n iex. (3.1.6a) Ha ci
n citarg iex
n1
iex
n iex. (3.1.6b) ahol ci
n egy adott iterációban kapott átlagérték a koncentrációra. Ennek viszonyaa megcélzott koncentrációhoz határozza meg, hogy a többlet kémiai potenciált egy kis értékkel növeljük vagy csökkentjük. Az iteráció során tehát a koncentráció a megcélzott érték körül, míg a többlet kémiai potenciál ezzel párhuzamosan az ennek megfelelő érték körül fluktuál. Lamperski azt javasolta, hogy a kívánt kémiai poten- ciált az iterációk során fluktuáló kémiai potenciálok átlagaként definiáljuk. Ezt az eljárást fordított (inverse) GCMC módszernek (IGCMC) nevezte el, és ezt használta mind individuális, mind pedig só behelyezés/eltávolítás esetén.
3.2. Sorfejtéses GCMC módszer
Egy olyan nagykanonikus sokaságú eljárást javasoltunk [31], amely a parciá- lis sűrűségeknek a kémiai potenciálok szerinti sorfejtésén alapszik (Newton - Raphson módszer vagy érintő módszer).
Egy bináris elegyre:
n
n
n
n
2
n
2
n2 1 1
1 1 1 1
1 1 1 1
, (3.2.1)
n
n
n
n
2
n
2
n2 1 2
1 1 2 2
2 1 1 1
.A sorfejtésben az előző, -edik iterációban a kémiai potenciálok bemenő paraméte- rek, a sűrűségek sokaságátlagként állnak elő (
n
n i
ni
), míg a sűrűségek deri- váltjai fluktuációs formulákból számolhatók:
i j i jj
i N N N N
kTV
1
. (3.2.2)Ha tehát a következő iterációban a sűrűségeket a megcélzott sűrűségekként definiál- juk ( ), akkor a fenti egyenletrendszerben csak a következő iteráció kémiai potenciáljai az ismeretlen mennyiségek. Így ezekre a kémiai potenciálokra egy olyan becslést kapunk, amely egyre közelebb kerül a kívánt értékhez, ahogy az iteráció előre halad. A módszer pontosságának a sokaságátlagok számolásának pon- tossága szab határt.
1
itargi n
A fluktuációs formulák sokkal kevésbé konvergáló mennyiségek egy szimu- lációban, mint a szokásos sokaságátlagok. A fenti algoritmus konvergenciájához nincs szükség pontos értékekre. Még a deriváltak megközelítően pontos értékei is közelebb vezetik az iterációt a kívánt állapothoz.
3.3. Adaptív-GCMC módszer
Munkánk során – Lamperskivel párhuzamosan – kifejlesztettünk egy olyan iteratív, nagykanonikus sokaságú MC eljárást is, amellyel adott megcélzott koncent- rációkhoz tartozó kémiai potenciálokat lehet számolni [31].
Az eljárás során a rendszer a megcélzott koncentráció körül fluktuál, az az el- járás azonban, amellyel a kémiai potenciálokat újraszámoljuk két iteráció között kü- lönbözik attól, amit Lamperski javasolt [2].
Az algoritmus a következő:
I. Az első lépésben kiszámoljuk i
1 -et a megcélzott koncentrációt használva valamilyen kezdeti becslést
iex
0
alkalmazva a többlet kémiai potenci- álra:
1 log
itarg iex
0i kT c
. (3.3.1)
II. Elvégzünk egy GCMC szimulációt a kapott i
1 -et használva, amelynek eredményeként megkapjuk az átlagos koncentrációt ebben az iterációban
ci
1
. Ebből az átlagos többlet kémiai potenciál számolható:
1
1 log
1ex
i i
i kT c
. (3.3.2)
III. Az iteráció kimenő iex-ét használjuk fel a következő iteráció bemenő paramétereként:
2 log itarg iex
1i kT c
. (3.3.3)
Általánosságban a kémiai potenciál a következő formula szerint számolható az előző iterációban használt/kapott adatokból (jelölése A-GCMC/I):
c
nkT c n n
i i i
i
targ
log
1
. (3.3.4)
Amennyiben sót helyezünk be/veszünk ki, akkor a só kémiai potenciálja számolható ki a következő algoritmussal (jelölése A-GCMC/S):
c n c n
c kT c
n
n s
s
targ targ
log
1 . (3.3.5)
Eljárásunk egy praktikus előnye az, hogy egy már létező GCMC kód hasz- nálható, míg az iterációs rész szabadon átírható körülötte. (Ugyanez érvényes Lamperski módszerére is.) Ezt az eljárást egy 2008-as publikációban javasoltuk [31], ahol a végeredményt a kémiai potenciálokra az utolsó iterációban kapott eredmény szolgáltatta. Ezt az tette lehetővé, hogy az algoritmus szerint a kémiai potenciál nem folyamatosan fluktuál az átlagérték körül, hanem ahhoz folyamatosan konvergál (en- nek a konvergenciának természetesen határt szab az egy-egy iterációban elvégzett szimuláció véges hossza, azaz a ci
n értékek statisztikus hibája). Minél pontosabb eredményt akarunk kapni az iteráció végén, annál hosszabb szimulációra van szükség az iterációban.A Lamperski által javasolt átlagolási eljárásra mindazonáltal a mi algoritmu- sunk esetében is lehetőség van. Megmutatjuk, hogy a mi algoritmusunkat az átlago- lási eljárással kombinálva egy robosztus, gyorsan konvergáló eljárást kapunk [32].
Így tehát a mi algoritmusunk és az átlagolási eljárás házasításáról van szó, ezért ké- sőbb esetenként a házasított módszer kifejezést használjuk rá (jelölése MGB/S+av).
Egy tipikus iteráció során azt látjuk, hogy (a kezdeti értékektől függően) a kémiai potenciálok fokozatosan konvergálnak a kívánt érték felé, majd azok körül fluktuálnak. Az átlagolást nyilván erre a második periódusra érdemes elvégezni.
Hogy ne kelljen folyamatosan figyelni, hogy hol van ez a periódus, az átlagolást úgy végezzük el, hogy az iterációk végén kapott értékek sorozatából az első 40%-ot el- dobjuk.
n
n . i
i
i i
n . n n
4 0
ex ex
4 0
1
. (3.3.6)
Ennek a módszernek a nevére az Adaptív GCMC nevet javasoltuk.
3.4. Töltéskorrekció az A-GCMC eljáráshoz
Az előbb ismertetett A-GCMC módszer só behelyezéssel a só kémiai poten- ciáljának meghatározására hatékonyan működött. Amikor azonban individuális iono- kat helyezünk be/veszünk ki, és az ezen komponensek kémiai potenciáljait kívánjuk meghatározni, azt találjuk, hogy az iteráció nagyon lassan konvergál. Ennek ugyanaz a hiányzó ellentöltéssel való kölcsönhatás az oka, mint ami már a Widom módszernél is problémát okozott. Ennek a hibának a kiküszöbölésére egy korrekciót vezetünk be, melynek során a Sloth és Sørensen által javasolt konstans semlegesítő háttértöltést használjuk [30]. Míg azonban a Widom módszernél ez a háttértöltés mindig egy be- helyezett virtuális tesztrészecskét volt hivatott semlegesíteni, addig ebben az esetben ennek az energiatagnak más célja van. Egy adott iterációban a kémiai potenciálok általában nem felelnek meg egy töltéssemleges rendszernek, azaz nem produkálnak olyan koncentrációkat, amelyek kielégítenék a
0i zi ci feltételt. Ezért a többlet kémiai potenciál egy iterációban nem csak azt az energiát jelenti, ami a behelyezett ionnak a rendszerben levő többi ionnal való kölcsönhatásából adódik, hanem azt az energiát is, amely a rendszer nettó töltésével való kölcsönhatást is tartalmazza. Ez kiküszöbölhető úgy, ha ezt a tagot a kémiai potenciálhoz hozzáadjuk. Ezért tehát azt javasoljuk, hogy individuális ionok behelyezése esetén az algoritmust egészítsük ki ezzel a korrekciós taggal:
L K n Q e z n c kT c n
n i
i i i
i
0 targ
log 32
1
, (3.4.1)
ahol az utolsó tag egy behelyezett ion és az -edik iterációban a rendszer nettó tölté- se közötti kölcsönhatás. Ez a nettótöltés egy iterációban sokaságátlagként áll elő:
n
i
i
ie N n
z n
Q . (3.4.2)
Ez a korrekciós tag hozzásegíti az algoritmusunkat, hogy megtalálja a töltéssemleges állapotot.
Az alábbi táblázatban összefoglalva mutatjuk be a különböző általunk vizsgált kano- nikus és nagykanonikus sokaságú eljárásokat:
rövidítések szerző(k) behelyezés/kivétel sokaság átlagolás
Widom/S Widom só kanonikus -
Widom/I Widom individuális kanonikus -
SS/I Sloth és Sørensen individuális kanonikus -
SW/I Svensson és Woodward individuális kanonikus - MGB/S Malasics és munkatársai só nagykanonikus nincs
MGB/I Malasics és munkatársai individuális nagykanonikus nincs
Lamperski/S+av Lamperski só nagykanonikus van
Lamperski/I+av Lamperski individuális nagykanonikus van
MGB/S+av Malasics és Boda só nagykanonikus van
MGB/I+av Malasics és Boda individuális nagykanonikus van MGB/I+av+corr Malasics és Boda individuális nagykanonikus van
1. táblázat
Az általunk vizsgált kémiai potenciál számoló módszerek összefoglaló táblázata
3.5. A sorfejtett és az adaptív algoritmus összehasonlítása Lennard-Jones elegyek esetén
A sorfejtett és az adaptív algoritmusainkat egy Lennard-Jones elegyre hason- lítjuk össze. Lennard-Jones elegy esetén a potenciál:
6 12
4
ij ij
ij
LJ r r r
, (3.5.1)
ahol és i j indexek a molekulákat jelölik, és a komponenseknek felelnek meg, a molekula méretére jellemző paraméter, az a potenciál energiapara- métere, míg a két molekula közötti távolság. A hosszútávú korrekciókat nem vet- tük figyelembe, mivel az algoritmusunk hatékonyságának tesztelését úgynevezett
„cut-off” potenciállal is elég volt elvégezni.
rij
Egy bináris LJ elegyet szimuláltunk, amelynek az energia- és távolságparamé- terei rendre 12 0.707111, 22 0.511, 12 0.7511 és 22 0.511
5 . 1
voltak.
Munkánk során redukált hőmérsékletet alkalmaztunk (kT/11 ), ami a tiszta LJ fluidum kritikus hőmérséklete felett van. Ha az 1 komponens méretét egységnyinek választjuk, akkor a megcélzott parciális sűrűség (ami megfelel a koncentrációnak) értékei: . 1targ113 2targ113 0.4
3.5.1. A sorfejtéses módszer
Az iterációs eljárás elvégzéséhez meg kellett adnunk a kezdeti többlet kémiai potenciálokat az egyes ionokra. Ezek az adatok először ideális gáz értékekre vonat- koztak
ex 1 2ex 1 0
1 ( )/kT ( )/kT
0 / ) 1 ( , 1
/kT 2ex kT
, majd egy másik esetben az iterációs eljárást a adatokkal kezdtük, amely egy durva becslése a több- let kémiai potenciál értékeknek.
) 1
ex(
1
Mivel ebben a technikában viszonylag pontos értékeket kellett kapnunk a de- riváltakra, minden iterációban azonos hosszúságú szimulációt végeztünk.
3.5.1. ábra
A parciális sűrűség és a kémiai potenciál konvergenciája az iterációszám függvényében a sorfejtett módszerrel, különböző kiindulási állapotok esetén
(szaggatott, piros vonal: 1ex(1)/kT1,2ex(1)/kT0, fekete, folytonos vonal: 1ex(1)/kT2ex(1)/kT0)
Itt a konfigurációs kémiai potenciálokat (3.2.1 egyenlet) ábrázoltuk, mert ez az a mennyiség, amit extrapolációval változtatunk az eljárásban. Ha
értékekből (szaggatott, piros vonal) indulunk ki, az iteráció gyorsabb, mintha ideális gáz (folytonos, fekete vonal) értékek lennének kez- detben. Ideális gáz kiindulási esetben először „billeg” a rendszer, majd mikor eléggé közel van a végső állapothoz, elkezd gyorsan konvergálni (3.5.1. ábra). Mivel a
0 / ) 1 ( , 1 /
) 1
( 2ex
ex
1 kT kT
1,2
i függvények monotonok a szuperkritikus hőmérsékleten a mi esetünkben, az eljárás előbb-utóbb megtalálja a konvergencia-területet.
3.5.2. ábra
A parciális sűrűség és a többlet kémiai potenciál konvergenciája az iterációszám függvényében az adaptív módszerrel, különböző kiindulási állapotok esetén
(szaggatott, piros vonal: 1ex(1)/kT1,2ex(1)/kT0, fekete, folytonos vonal: 1ex(1)/kT2ex(1)/kT0)
A kezdeti állapotra vonatkozó jó becslésnek nagyon fontos szerepe van, ha a hőmérséklet a kritikus hőmérséklet alatt van. Ebben az esetben a rendszer a gáz- és folyadékfázis között fluktuál és egy-egy iteráció a metastabil régióba is betévedhet, vagy átbillenhet a másik fázisba.
Ez azt jelenti, hogy az algoritmusunk nem annyira robosztus folyadék fázis- ban a kritikus hőmérséklet alatt, mint gázfázisban, ahol a többlet-tag kicsi az ideális taghoz képest. A kezdőértékeket tehát fokozott óvatossággal kell ilyen esetekben megválasztani. Hasznos lehet előzetes Widom mintavételezéssel kombinált kanoni- kus szimulációk futtatása, mivel kanonikus sokaságon másik fázisba való átcsapás veszélye nem fenyeget.
![4.1.2. ábra A transzport fajtái [38].](https://thumb-eu.123doks.com/thumbv2/9dokorg/873559.46998/48.892.293.660.737.943/ábra-a-transzport-fajtái.webp)