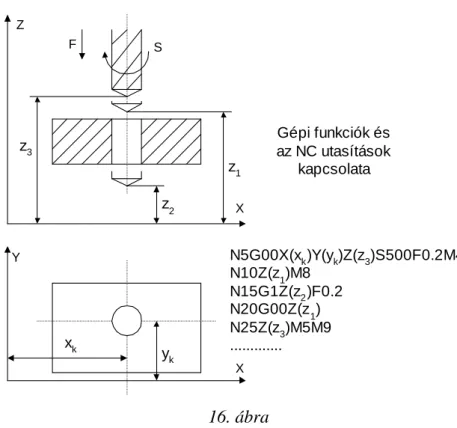
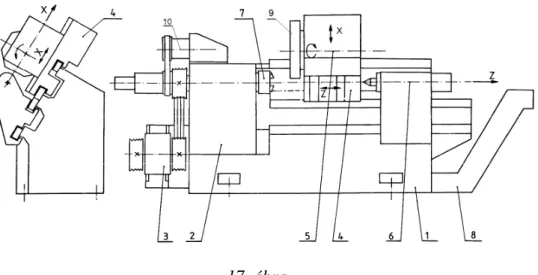
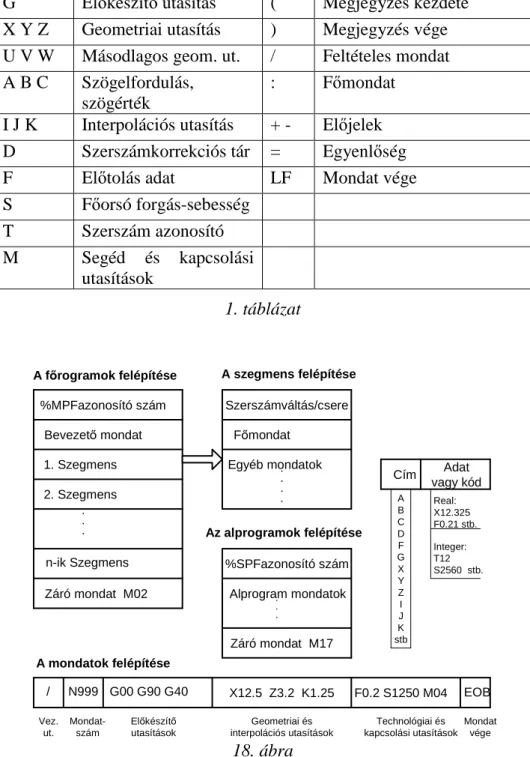
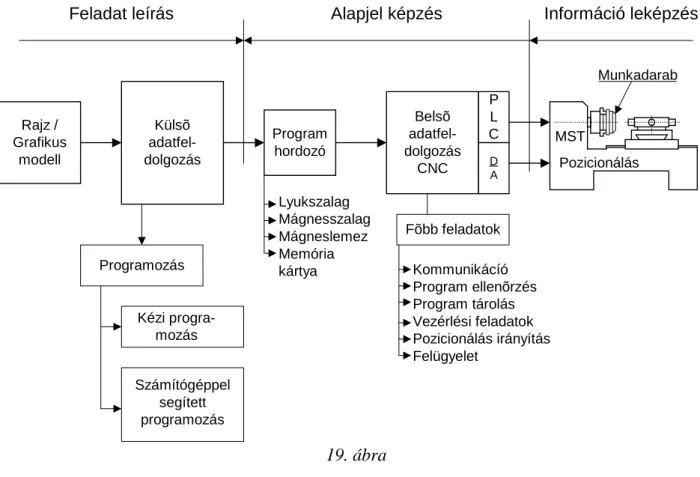
Szerszámgépek elmélete
Szerzık: Dr. Patkó Gyula Dr. Csáki Tibor Dr. Zsiga Zoltán
Dr. Szabóné dr. Makó Ildikó Simon Gábor
Lektor: Dr. Faragó Károly
1 Történeti visszatekintés: az NC kialakulása, fejlıdése ... 5
1.1 Az NC technika fejlıdésének fıbb állomásai ... 5
1.2 A hagyományos és a számítógépes számjegyvezérlés összehasonlítása... 5
2 Szerszámgépek dinamikai kérdései ... 7
2.1 Modellalkotás ... 7
2.2 Szerszámgépek dinamikájának fıbb területei ... 8
2.2.1 Szíjjal hajtott fıorsók csavaró lengései ... 8
2.2.2 Szíjjal hajtott fıorsó csavaró lengéseinek vizsgálata két szíjhajtás esetén... 15
2.3 Mellékhajtómővek dinamikai vizsgálata... 20
3 Gépalapozás dinamikai kérdései ... 23
3.1 A sajátfrekvencia és a statikus süllyedés kapcsolata... 24
3.2 Gépalapok tervezése aktív rezgésmentesítés esetén... 25
3.3 Aktív rezgésmentesítés kiegyensúlyozatlanság okozta gerjesztı erı esetén ... 29
3.4 Passzív rezgésmentesítés... 32
4 A számjegyvezérlés alapelve ... 35
4.1 Az NC fogalma... 35
4.2 Az NC gépek alkalmazási területei ... 36
4.3 Az NC technika elınyei, hátrányai... 36
4.4 Az NC gépek alkalmazásának következményei... 37
4.5 CNC gépek programozásának alapelvei... 38
5 Az információfeldolgozás folyamata ... 42
5.1.1A külsı adatfeldolgozás módszerei, jellemzıi ... 42
5.1.2 A belsı adatfeldolgozás jellemzıi... 46
6 A CNC vezérlések funkciói ... 49
7 Geometriai információs rendszer ... 53
7.1 A koordinátarendszerekkel kapcsolatos általános elıírások ... 55
7.2 Eszterga geometriai rendszere... 55
7.3 Fúró-maró megmunkálóközpont geometriai rendszere... 57
7.4 Eszterga megmunkálóközpont koordinátarendszere ... 59
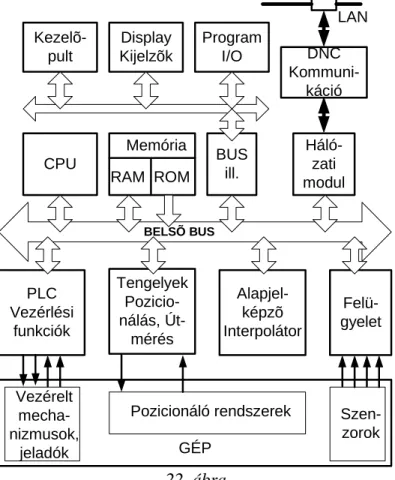
8 CNC vezérlések funkcionális egységei... 60
9 Pozícionálási módok összefoglalása ... 62
9.1 A pozícionálás feladata ... 62
9.2 Pozícionáló rendszer felépítése ... 62
9.3 Pozícionálási módok ... 63
9.3.1 Pontvezérlés jellemzıi, alkalmazása ... 63
9.3.2 Szakaszvezérlés jellemzıi, alkalmazása... 64
9.3.3 Pályavezérlés jellemzıi, alkalmazása... 65
10 A CNC kézi programozásának alapjai ... 67
10.1 CNC programozás nyelvi eszközei ... 67
10.2 Egy ISO NCL utasításrendszer felépítése ... 67
10.2.1 Elıkészítı utasítások fajtái, programozásuk ... 71
10.2.1.1 Pozícionálási módok programozása... 71
10.2.1.1.1 Pontvezérléssel történı mozgás gyorsmenettel:... 71
10.2.1.1.2 Lineáris mozgás programozása elıírt sebességgel... 72
10.2.1.1.3 Körpályán mozgás a fısíkokkal párhuzamos síkban ... 73
10.2.1.1.4 Menetesztergálás, hengeres, kúpos, síkmenet G33 ... 73
10.2.1.2 Várakozás programozása G04 ... 74
10.2.1.3 Méretmegadási módok programozása ... 74
10.2.1.4 szerszámpálya korrekciózás programozása ... 74
10.2.1.6 Célpontra állás módjának programozása ... 77
10.2.1.7 Gépi ciklusok programozása... 77
10.2.1.8 Mértékegység- és funkcióváltás programozása ... 88
10.2.1.9 Egyéb elıkészítı utasítások programozása... 88
10.2.2 Geometriai utasítások fajtái és programozásuk ... 89
10.2.3 A technológiai utasítások fajtái az alábbiak: ... 90
10.2.4 Kapcsolási utasítások és programozásuk... 91
10.2.5 Programtechnikai utasítások és karakterek... 91
10.3 Speciális egyszerősített kontúrleírások a Sinumerik 810T vezérlésnél... 92
11 A CNC számítógéppel segített programozásának alapjai ... 93
11.1 A számítógéppel segített CNC programozás folyamata ... 93
11.1.1 Gép és vezérlés definíció ... 93
11.1.2 Geometria átvétele, feldolgozása, módosítása... 94
11.1.3 Szerszámpályák, mőveletek... 95
11.1.4 Posztprocesszálás... 96
11.2 MASTERCAM rendszer rövid ismertetése... 96
11.2.1 Menü- és ablakrendszer ... 96
11.2.2 Geometriai elemek, felületek, testek ... 103
11.2.2.1 Geometriai elemek, entitások létrehozása, generálása... 104
11.2.2.2 Az entitások szerkesztése... 109
11.2.2.3 Entitások transzformációja ... 110
11.2.2.4 Entitások tulajdonságainak elemzése... 110
11.2.2.5 Felületek létrehozása és módosítása ... 113
11.2.2.6 Testmodellezés... 114
11.2.3 Technológiai mőveletek, kiválasztásuk, paraméterezésük ... 114
11.2.4 Az NC program ellenırzése ... 126
11.2.5 A megmunkálás szimulációja... 129
11.2.6 Posztprocesszálás... 132
12 Az interpoláció elmélete ... 134
12.1 Az interpolátor feladata ... 134
12.2 Az interpoláció 3D-s leírása ... 136
12.3 Interpolációs módszerek... 139
12.3.1 DDA interpolátorok ... 139
12.3.2 Interpoláció a véges növekmények módszerével ... 147
12.3.3 Interpoláció koordináta lépésekkel ... 151
12.3.4 Térbeli görbék interpolációja... 156
13 Irodalomjegyzék... 159
Ezzel a jegyzettel az a célunk, hogy összefoglaljuk a modern szerszámgépek néhány elméleti kérdését, bemutassuk a számjegyvezérlés (NC, Numerical Control) hatását a szerszámgépek fejlıdésére és alkalmazására, felhívjuk a figyelmet néhány dinamikai kérdésre, megismertessük a számjegyvezérlés, az NC technika alapjait, bemutassuk a kézi és számítógépes programozás eszközeit, lehetıségeit, és felvázoljuk az interpoláció elméleti alapjait.
A mérnöki tevékenységet, esetünkben a gépészmérnöki tevékenységet jellemzı négy fı kérdéskör a következıkben foglalható össze (Takács György gondolatai alapján):
A mérnöknek tevékenysége során a következı választ kell megadnia:
• MIT (konstrukció, termék)
• MIBİL (anyag)
• HOGYAN (technológia)
• MIVEL (szerszámgép)
akar létrehozni. A négy kérdés egymástól nem választható el, bár nyilvánvaló, hogy egy adott tevékenység során a mérnök gondolataiban nem egyforma súllyal szerepelnek. Ha a négy kérdést egy egyenlı oldalú gúla csúcspontjaiként képzeljük el, azt mondhatjuk, hogy valamelyik csúcs az adott tevékenység során közelebb állhat hozzánk, valamelyikre koncentrálva dolgozunk, de jó eredményt csak akkor érhetünk el, ha nem hagyjuk figyelmen kívül a többit sem. Ebben a jegyzetben a MIVEL kérdésével foglalkozunk. Szándékaink szerint az alapképzés és a mesterképzés 2-3 tantárgyában is hasznosítható ismereteket foglaltunk össze, amelyek segítik az olvasót, hallgatóinkat a terület áttekintésében, és megalapozzák az elmélyültebb ismeretek megszerzésének lehetıségét.
A 2. és 3. fejezetek Patkó Gyula és Simon Gábor munkájának eredményei. A szerzık munkájuk során felhasználták a Szerszámgépek Tanszékén évtizedek alatt felhalmozott tudást és saját elméleti munkásságukkal kiegészítve mutatják be az olvasónak.
Az 1. és a 4-10. fejezeteket Csáki Tibor, Zsiga Zoltán és Szabóné Makó Ildikó írták. A szerzık köszönetüket fejezik ki Erdélyi Ferencnek, akinek vezetése alatt megismerkedhettek ezzel a nagyon izgalmas és szép területtel, az NC és CNC gépek világával. Erdélyi Ferenc tisztánlátása, világos és rendszerezı gondolkodásmódja nagy segítségükre volt abban, hogy a hallgatóknak érthetı formában tudják átadni ismereteiket.
A 11. és 12. fejezetet Csáki Tibor írta. Az elızı bekezdésben írottak erre a részre is vonatkoznak, mai tudásunkat Erdélyi Ferencnek köszönhetjük.
Az olvasónak, hallgatóinknak sikeres tanulmányokat kívánunk és reméljük, hogy e jegyzet is segítséget nyújt ismereteik fejlesztésében, késıbbi eredményes munkájukban.
A szerzık.
1 Történeti visszatekintés: az NC kialakulása, fejl ı dése 1.1 Az NC technika fejl ı désének f ı bb állomásai
Az NC technika kialakulása a II. világháború utáni idıszakra esett. A fejlesztés elindítója a repülıgépgyártás igénye a szárnyprofilok és a bonyolult monolit alkatrészek elıállítására alkalmas automatizált gyártóeszközök létrehozása iránt. A fejlıdés dinamikáját egyértelmően az irányítástechnika, a számítástechnika, az elektronika, félvezetı-technika fejlıdése határozta meg. A fejlıdés rövid története az alábbi:
1949-52 USA: az elsı NC gép megjelenése
(MIT Massachusetts Institute of Technology) 1950-es évek: Európai megjelenés
1963 Magyarország: MFS-320 marógép,
1965 ERI-250 eszterga, Csepeli Szerszámgépgyár, 1974 mikroprocesszorok: CNC gépek
1981 multiprocesszoros vezérlések, FMS, FMC 1982 CNC fogazógépek, köszörők
1985 CIM rendszerek 1990 OPEN CNC
2000+ hálózatba kapcsolt, együttmőködı vezérlések
1.2 1.2 1.2
1.2 A hagyományos és a számítógépes számjegyvezérlés összehasonlítása A hagyományos és a számítógépes számjegyvezérlés összehasonlítása A hagyományos és a számítógépes számjegyvezérlés összehasonlítása A hagyományos és a számítógépes számjegyvezérlés összehasonlítása
A fejlesztés kezdetén ún. konvencionális (KNC) vezérlések építésére volt mód, a mai értelemben vett CNC vezérlések építése csak a mikroprocesszorok, a nagyintegráltságú félvezetı áramkörök és memóriák megjelenése után vált lehetıvé. A vezérléstípusok legfontosabb jellemzıi az alábbiak:
Az NC (KNC) vezérlés fı jellemzıi
• Rögzített logika,
• Lyukszalagos, mágnesszalagos programbevitel,
• Nincs programtárolás,
• Nincs programjavítási, szerkesztési lehetıség,
• NC funkciók száma korlátozott.
A CNC vezérlések fı jellemzıi
• Szabadon programozható logika (nem a felhasználó által!),
• Számítógépes programbevitel,
• Tárolt alkatrészprogram,
• Programszerkesztés, javítás, helyszíni programírás,
• On-, Off –line szimuláció,
• Rendszerbe kapcsolhatóság FMS, FMC, DNC,
• Nagy számú NC funkció, felügyelet.
A mai gyakorlatban már kizárólag CNC gépeket építenek!
Napjainkban a CNC technikát a gyártóeszközök irányítására rendkívül széleskörően alkalmazzák. A gépek szolgáltatásai igen sokrétőek, a vezérlık jelfeldolgozási sebessége már nem jelent korlátot a gépek tervezıinek.
A komplex alkatrészek pontossági igényei és a megmunkálási idı rövidítésének igénye egyfelıl, a vezérlések teljesítményének növekedése másfelıl, együtt a szerszámgép konstruktırök kreativitásával, az utóbbi évtizedben a „multi-tasking machines”, a sokfunkciós, sok megmunkálási feladatot elvégezni képes szerszámgépek kifejlesztéséhez vezetett. Kezdetben az esztergákat szerelték fel maró fejekkel (eszterga központok), a mai fejlesztések azonban már közvetlenül a komplex több-tengelyes gépek tervezésére és létesítésére irányulnak, amelyek mind a marógépektıl, mind az esztergáktól különböznek.
2 Szerszámgépek dinamikai kérdései
A mőszaki fejlıdés – különösen a nem civil mérnöki területek, például hadiipar, őrkutatás terén tapasztalt – üteme a szerszámgépekkel szemben is egyre szigorúbb követelményeket támaszt.
Ennek következményeként igen sok, sıt egyre több dinamikai feladat megoldását követeli meg egy ilyen berendezés megtervezése. Ráadásul a civil iparban is csak azok a berendezések piacképesek, amelyek – számos egyéb szempont mellett – dinamikai szempontból is kifogástalanok.
Ez a fejezet a szerszámgéptervezıi gyakorlatban elıforduló legfontosabb dinamikai, elsısorban lengéstani problémákat tárgyalja egyszerő modelleken keresztül, egységes elv szerint, a Lagrange- féle másodfajú mozgásegyenletekbıl kiindulva.
2.1 2.1 2.1
2.1 Modellalkotás Modellalkotás Modellalkotás Modellalkotás
Adott gép vagy szerkezet dinamikai vizsgálatának folyamatát az 1. ábra mutatja.
1. ábra
Célszerő elıször a vizsgált szerkezet mechanikai modelljét felrajzolni. Ez rendszerint koncentrált tömegek, a tömegekhez kapcsolódó rugalmas elemek, csillapítások, valamint az imént felsorolt elemek valamelyikéhez, esetleg több elemhez kapcsolódó gerjesztések szimbolikus jelöléseit tartalmazza. Minél egyszerőbb a modell, rendszerint annál könnyebb a dinamikai vizsgálat
elvégzése. Ezért a mechanikai modell megalkotásakor idealizáló feltevéseket, ezzel párhuzamosan pedig elhanyagolásokat engedünk meg: csak lényeges tömegeket veszünk figyelembe; a rugalmas elemek tömegét elhanyagoljuk; a csillapításokat lineárisnak tekintjük, stb. Törekedni kell a valóság minél jobb megközelítésére, ugyanakkor az egyszerőséget is szem elıtt kell tartani. E két ellentétes szempont arányának helyes megválasztásával olyan mechanikai modell nyerhetı, melynek
dinamikai vizsgálata a gyakorlat számára gyors, kielégítı pontosságú eredményeket szolgáltat. A mechanikai modell létrehozására vonatkozó általános szabály nem létezik, döntı a mőszaki probléma lényegének felismerése, melyhez viszont a mérnöki gyakorlat során megszerzett tapasztalat elengedhetetlen.
A vizsgálat szempontjából helyes mechanikai modell felállítását megkönnyíti a vizsgált szerkezet ún. kinematikai modelljének elızetes felrajzolása. A bemutatott problémák tárgyalását – ahol lehetséges – ez a jegyzet is a kinematikai modell felrajzolásával indítja.
A fejezet csak véges szabadságfokú, ún. diszkrét dinamikai modellekkel foglakozik, amelyek véges számú és tömegő merev testet tartalmaznak. Ilyenkor a dinamikai jellemzık (tömegek,
rugóállandók, csillapítási együtthatók, stb) mellé a szabadságfokok számának megfelelı számú helyzetjellemzıt is fel kell venni. Ez lehet például valamely tömeg tömegközéppontjának elmozdulása, valamely merev test szögelfordulása, tömegek egymáshoz képesti elmozdulása, tömegközéppont sebessége, stb. Ezeket a helyzetjellemzıket más néven általánosított
koordinátáknak nevezzük, és a dinamikai problémák, valamint a példák tárgyalásakor x-szel, ϕ- vel, stb. jelöljük.
A vizsgált rendszerek dinamikai viszonyait a mechanikai modell alapján felállított mozgásegyenlet vagy egyenletrendszer írja le, melyeket a dinamikai jellemzık és az általánosított koordináták ismeretében a Lagrange-féle másodfajú mozgásegyenletekbıl kiindulva írhatunk fel. Az így felírt mozgásegyenletek rendszerint differenciálegyenletek vagy egyenletrendszerek, melyeket egyébként a rendszer matematikai modelljének is szokás nevezni. A mozgásegyenletet vagy egyenletrendszert megoldva, a mechanikai modellen keresztül vizsgálhatjuk a valós gép vagy szerkezet viselkedését.
Mivel az egyszerősítı feltételezések és elhanyagolások következtében a modellekre levezetett számítások eltérnek a valóságos értékektıl, ezért a valóságos szerkezet dinamikai viselkedésének mechanikai modellen keresztül történı megítélése szintén komoly mérnöki tapasztalatot igényel.
2.2 Szerszámgépek dinamikájának f ı bb területei
Gyakorló szerszámgéptervezınek munkája során az alábbi – elsısorban forgácsoló szerszámgépek tervezésekor felmerülı – dinamikai problémák valamelyikére, esetleg mindegyikére kell megoldást találnia:
1. Hajtómővek dinamikája 2. Fıhajtómővek lengései 3. Szíj csavaró lengései
4. Fogaskerekes hajtómővek csavaró lengései 5. Fıorsó hajlító lengései
6. Mellékhajtómővek lengései 7. Lemezek lengései (pl. burkolat)
8. Állványok, szánrendszerek dinamikája 9. Forgácsolási folyamat dinamikája 10. Gépalapok dinamikája
A fejezet szabta keretek miatt a fıhajtómővek, valamint a mellékhajtómővek jellemzı dinamikai problémáinak egy-egy jellemzı rész feladatával foglalkozunk. Külön fejezetben mutatjuk be a gépalapok dinamikájának néhány jellegzetes feladatát.
2.2.1 Szíjjal hajtott fıorsók csavaró lengései
A vizsgált géprész kinematikai modelljét a Hiba! A hivatkozási forrás nem található. mutatja.
2. ábra
Az M villanymotor a z fokozatú fıhajtómővön keresztül, az sz szíjhajtással forgatja az o fıorsót.
Ilyen hajtást alkalmaznak például nagyteljesítményő gépek esetén, amikor el szeretnénk érni, hogy a motor és a fıhajtómő jelentıs hıtermelése a nagypontosságú fıorsó egység állapotát ne
befolyásolja.
A vizsgálat során a szíj kivételével a hajtás minden egyes elemét ideálisan merevnek tekintjük. A rugalmas szíjhajtás következtében indításkor, fékezéskor, a forgácsolás megkezdésekor és
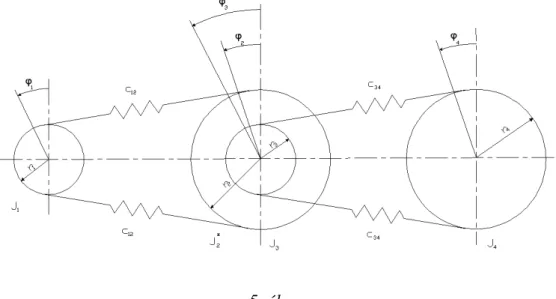
befejezésekor a fıorsó és a hajtómőelemek csavaró lengést végezhetnek. Az alábbiakban elvégzett dinamikai vizsgálat a fıorsó csavaró lengéseinek saját körfrekvenciáit határozza meg, ahol a szíjat lineárisan rugalmas elemként vesszük figyelembe. A hajtás mechanikai modelljét az alábbi ábra mutatja (3. ábra).
3. ábra
Az ábrán r1, r2 a hajtás és a hajtott szíjtárcsák sugarát, J1, J2 az összes mereven forgó tömegnek az 1 és a 2 szíjtárcsák tengelyeire redukált tehetetlenségi nyomatékát, c pedig a lineárisan rugalmasnak tekintett szíjágak rugómerevségét jelenti. Ebben a fejezetben mindenféle csillapító hatástól eltekintünk. A rendszer két szabadságfokú, így a Lagrange-féle másodfajú
mozgásegyenletek felírásához két általános koordinátát kell felvenni. Legyenek ezek a tárcsák ϕ1, ϕ2 szögelfordulásai.
A dinamikai jellemzık, valamint az általános koordináták ismeretében felírhatjuk a két
szabadságfokú lengırendszer mozgásegyenlet-rendszerét, elıállítva ezzel a dinamikai probléma matematikai modelljét. Csillapítás hiányában a Lagrange-féle másodfajú mozgásegyenlet
( )
i
i i
d E E
Q i 1;2
dt ϕ ϕ
∂ − ∂ = =
∂ ∂
ɺ (2.1)
alakját alkalmazzuk, ahol E a mozgási energia, Qi pedig az általánosított erıkoordináta. Ezek a mennyiségek
2
2 2 2
i i 1 1 2 2
i 1
1 1 1
E J J J
2 ϕ 2 ϕ 2 ϕ
=
=
∑
= ɺ + ɺ (2.2)valamint a
i
i
Q U
ϕ
= −∂
∂ (2.3)
alakban írhatók fel, ahol U a potenciális energia. Ez a szíjágak rugalmas alakváltozása következtében jelenik meg, és
( )
22 i i 1
U l
2c
∆
=
=
∑
(2.4)alakú, ahol ∆li az i -edik szíjág rugalmas hosszváltozása. Most az 1 index a felsı, a 2 index az alsó szíjágra vonatkozik. Az egyes szíjágak rugalmas hosszváltozása a
( )
( )
1
1 1 1 2 2 2 1 2 2 1 2
2 1
2 2 2 1 1 2 2 1 2 2 1
2
l r r r r r k
r
l r r r r r k
r
∆ ϕ ϕ ϕ ϕ ϕ ϕ
∆ ϕ ϕ ϕ ϕ ϕ ϕ
= − = − = −
= − = − = −
(2.5)
kifejezésekkel számítható. Az (2.5) összefüggések felírásakor feltételeztük, hogy a szíjtárcsák ϕ1, ϕ2 szögelfordulása elég kicsi, így az egyes szíjágak végpontjainak elmozdulása – melyekbıl a
szíjágak rugalmas hosszváltozása származik – jó közelítéssel megegyezik a ϕ1, ϕ2
szögelfordulásokhoz, mint központi szögekhez tartozó s1 =r1ϕ1 és s2 =r2ϕ2 ívhosszakkal. A (2.5) kifejezésben 1
2
k r
=r a szíjhajtás hajtóviszonya.
Az elızıek alapján a potenciális energia, majd az általános erıkoordináták az
( )
2( )
22 2
2 1 2 2 2 1
1 2
r k r k
U U U
2c 2c
ϕ ϕ− ϕ − ϕ
= + = + (2.6)
és a
( ) ( )( ) ( )
( )( ) ( ) ( )
2 2 2
2 1 2 2 2 1 2 1 2
1
1
2 2 2
2 1 2 2 2 1 2 2 1
2
2
2r k k 2r k k 2r k k
Q U
2c 2c c
2r k 1 2r k 2r k k
Q U
2c 2c c
ϕ ϕ ϕ ϕ ϕ ϕ
ϕ
ϕ ϕ ϕ ϕ ϕ ϕ
ϕ
− − − −
= −∂ = − − = −
∂
− − − −
= − ∂ = − − = −
∂
(2.7)
kifejezésekkel adhatók meg. Vezessük be a 2 2r2
= c
γ
csavarási rugóállandót, így Q1-re és Q2-re az egyszerőbb( )
( )
1 2
1
2 1
2
Q k k Q k
ϕ ϕ γ
ϕ ϕ
γ
= − −
= − −
(2.8)
összefüggések adódnak. A potenciális energiára és az általános erıkoordinátákra kapott (2.6) és (2.8) kifejezéseket (2.2)-vel együtt a (2.1) Lagrange-féle másodfajú mozgásegyenletekbe helyettesítve a
2
1 1 1 2
2 2 1 2
k k
J 0
k 1
J 0
ϕ ϕ ϕ
γ γ
ϕ ϕ ϕ
γ γ
+ − =
− + =
ɺɺ ɺɺ
(2.9)
mozgásegyenlet-rendszert kapjuk, amely egyben a vizsgált rendszer matematikai modellje is. A (2.9) mozgásegyenlet-rendszert a Mqɺɺ+Kq=0 mátrix-egyenletnek megfelelıen
2
1 1 1
2 2 2
k k
J 0 0
0 J k 1 0
ϕ γ γ ϕ
ϕ ϕ
γ γ
−
+ =
−
ɺɺ
ɺɺ (2.10)
mátrixos alakban is felírhatjuk, ahol
1 2 1 2 2
1 2
0 ,
0
,
1 ,
.
M J a tömegmátrix
J
q a gyorsulásvektor
k k
K a merevségi mátrix
k
q az elmozdulásvektor ϕ
ϕ
γ γ
γ γ ϕ ϕ
=
=
−
=
−
=
ɺɺ ɺɺ
ɺɺ
A (2.10) mátrix-egyenlet megoldását
j t 1 j t
2
q φeα φ eα φ
= =
(2.11)
alakban keressük. (2.11) alapján
( )
1 j t
2
1 2 j t 2 1 j t 2
2 2
q j e
q j e e q.
α
α α
φ α φ
φ α α φ α
φ φ
=
= = − = −
ɺ ɺɺ
(2.12)
A (2.11), (2.12) kifejezéseket a (2.10) mátrix-egyenletbe helyettesítve, φ1, φ2-re a 2
2 1
1
2 2
2
k k
J 0
k 1 0
J
α γ γ φ
α φ
γ γ
− + −
=
− − +
(2.13)
lineáris homogén egyenletrendszer adódik. φ φ1 = 2 =0 esetén kapjuk (2.13) triviális megoldását.
Ekkor a hajtás nyugalomban van, és számunkra ez az állapot érdektelen. Triviálistól eltérı
megoldása (2.13)-nek akkor van, amikor az együttható-mátrixból képzett determináns értéke zérus, azaz
2 2
1
2 2
k k
J
k 1 0
J
α γ γ
γ α γ
− + −
=
− − +
. (2.14)
A determinánst kifejtését és matematikai mőveleteket követıen adódik a rendszer
( )
4 2 2
1 2 1 2
J J J k J 0
α γ α− + = (2.15)
karakterisztikus egyenlete. Az egyenletben elıforduló α a csavaró lengımozgást végzı tömegek saját körfrekvenciája. α =0 megoldás esetén a tömegek nyugalomban vannak, vagy a
megmunkálás során elvárt merevtest szerő forgást végzik. Indításkor, fékezéskor, fogásváltás
esetén, vagyis amikor a rendszert impulzusszerő terhelés éri, a szíj rugalmasságának köszönhetıen a szíjtárcsákkal mereven kapcsolódó, forgó tömegek lengésbe jönnek, és csavaró lengéseket
végeznek. Ennek a lengımozgásnak a saját körfrekvenciája (2.15) alapján – a dinamikai jellemzık függvényében – az
2 n
2 1n
1 k
, n 1;2;3;...; z
J J
α = γ + γ = (2.16)
kifejezéssel számítható. Említettük, hogy a J1 tehetetlenségi nyomaték az 1 szíjtárcsa tengelyére redukált érték, amely a motor és a z fokozatú hajtómő tehetetlenségi nyomatékait tartalmazza.
Mivel a hajtómő tehetetlenségi nyomatéka függ a pillanatnyi fokozattól, azaz J1 =J1n, ahol n az éppen mőködésben lévı fokozat sorszáma, és n=1...z, a (2.16)-tal felírt saját körfrekvencia is függ ettıl. A legkisebb saját körfrekvenciát megkapjuk, ha J1 =J1max, és ekkor
2 min
2 1max
1 k
J J
α = γ +γ . (2.17)
Az imént bemutatott elvi alapokat egy számpélda segítségével tesszük szemléletessé Példa:
Tekintsük a Hiba! A hivatkozási forrás nem található. kinematikai modelljét. A jelen feladatban vizsgált fıhajtás abban különbözik az ábrán bemutatott hajtástól, hogy most 3 db szíj vesz részt a hajtásban.
Egyéb adatok:
2
J1max =5 kgm
2
J2 =1,6 kgm
1 2
r = =r 150 mm, azaz k=1.
Az alkalmazott szíj típusa: ékszíj, 11x17 MSZ2532,
2
2
Keresztmetszete : A 143mm
Rugalmassági Modulusza : E 222,5 N mm
=
= 1 szíjág hossza: l=0.7 m=700 mm A szíjágak száma: n=3
Feladat:
Határozzuk meg a csavaró lengések legkisebb saját körfrekvenciáját! αmin =? Egy szíjág ∆l1 megnyúlása esetén a szíjágban
1 1
1
F 1 l
c ∆
= (2.18)
nagyságú erı ébred. Feltételezzük, hogy az F1 erı hatására a szíjág valamely keresztmetszetében ébredı σ1 húzófeszültség a keresztmetszet mentén egyenletesen oszlik meg, azaz írható, hogy
1 1
1 1
l F
E E
l A
σ = ε = ∆ = . (2.19)
(2.19)-bıl F -re az 1
1 1
F AE l l
= ∆ (2.20)
kifejezést kapjuk, melyet (2.18)-cal összevetve egyetlen szíjág rugómerevségére az
1
1 AE
c = l (2.21)
összefüggés adódik, melybıl a rugómerevségre kapjuk, hogy
1
2
2
l 700mm mm
c 0,022
AE 143mm 222,5 N N
mm
= = = . (2.22)
3 szíjág eredı rugómerevségét az alábbi meggondolással számíthatjuk: tegyük fel, hogy a szíjágak azonosak, és egyformán terheltek. Ekkor a szíjágakat feszítı erık eredıje az egyes szíjágakban ébredı erık összege, azaz
e 1 2 3
F =F +F +F . (2.23)
Ez az összefüggés (2.18) alapján az
1 2 3
1 1 1 1
l l l l
c∆ = c ∆ +c ∆ +c ∆ (2.24)
alakban is felírható. Mivel – feltételezésünk szerint – a szíjágak mind geometria, mind terhelés tekintetében megegyeznek, ezért (2.24) helyett
1
3 1
c
c = írható, melybıl a szíjágak eredı rugóállandójára
3 6
1
0,022mm
c N mm m
c 7 ,33 10 7 ,33 10
3 3 N N
− −
= = = ⋅ = ⋅ (2.25)
adódik. Ezt felhasználva számítható a γ csavarási rugóállandó,
6
3
2 2 2
2
7 ,33 10 m
c N 0,163 10 1
2r 2 0,15 m Nm
γ
−
⋅ −
= = = ⋅
⋅ , (2.26)
melyet felhasználva a keresett legkisebb csavarási saját körfrekvenciára (2.17) alapján
2 2 2 2
1max 2
min
2 2
1max 2
J k J 5kgm 1 1,6kgm 1
1 71,1
J J 5kgm 1,6kgm 0,163 s
Nm
α γ
+ + ⋅
= = =
⋅ ⋅ (2.27)
adódik. Ehhez az
55 , 9 60 2 n = n
= π
α összefüggés alapján
perc fodulat
n 680
2 60 ≅
= πα
fordulatszám tartozik. Látható, hogy a viszonylag alacsony értékő minimális csavaró saját körfrekvencia következtében már a hajtás kis fordulatszáma is elıidézheti a forgó tömegek veszélyes mértékő csavaró lengéseit.
2.2.2 Szíjjal hajtott fıorsó csavaró lengéseinek vizsgálata két szíjhajtás esetén
Ekkor az elızı probléma úgy módosul, hogy az M motor és a z fokozatú hajtómő között is rugalmasnak tekintett szíjhajtással valósul meg a teljesítmény átvitel. A hajtás kinematikai modelljét a 4. ábra mutatja.
4. ábra
Ez alapján a vizsgált szerkezet mechanikai modellje az alábbi ábra szerint rajzolható fel (5. ábra).
5. ábra ahol
J a motor, a kihajtó tengely és az 1 szíjtárcsa együttes tehetetlenségi nyomatéka, azaz 1
1 motor tengely szt1
J =J +J +J ,
*
J a z fokozatú hajtómő 2 2 szíjtárcsa tengelyére redukált tehetetlenségi nyomatékának és a 2 szíjtárcsa tehetetlenségi nyomatékának az összege, azaz J*2 =Jh+Jszt 2,
J a 3 szíjtárcsa tehetetlenségi nyomatéka, azaz 3 J3 =Jszt 3,
J a 4 szíjtárcsa, a fıorsó, valamint a fıorsó tokmányába fogott munkadarab együttes 4
tehetetlenségi nyomatéka, azaz J4 =Jszt 4 +JFO+Jmdb.
A merev hajtómő-kinematika következtében ϕ2, ϕ3 szögelfordulások között érvényesek a
3 2 2
h h 3
2 3 h h
k 1 i
k i
ϕ ϕ ϕ ϕ
ϕ = ⇒ϕ = = ⇒ = (2.28)
összefüggések, ahol k a hajtómő éppen bekapcsolt hajtóviszonya, h h
h
i 1
= k pedig az áttétel. (2.28) alapján tehát a vizsgált rendszer 3 szabadságfokú. A szerkezet mozgásegyenlet-rendszerét most is a Lagrange-féle másodfajú mozgásegyenlet
i
i i
d E E
dt ϕ ϕ Q
∂ − ∂ =
∂ ∂
ɺ (2.29)
alakjából kiindulva állítjuk elı. Ehhez elıször a (2.29)-ben szereplı energiamennyiségeket és általános erıkoordinátákat írjuk fel. A mozgási energiára írhatjuk, hogy
2 * 2 2 2
1 1 2 2 3 3 4 4
1 1 1 1
E J J J J
2 ϕ 2 ϕ 2 ϕ 2 ϕ
= ɺ + ɺ + ɺ + ɺ , (2.30)
ahol (2.28) alapján ih
2 3
ϕɺ =ϕɺ , így (2.30) az
2 * 2 2
1 1 2 2 3 2 4 4
h
1 1 1 1
E J J J J
2 ϕ 2 i ϕ 2 ϕ
= + + +
ɺ ɺ ɺ (2.31)
alakban is felírható, ahol 2 2* 12 3 i J J J
h
+
= . Ezt figyelembe véve a mozgási energia függvénye az
(
1 12 2 22 4 42)
E 1 J J J
2 ϕ ϕ ϕ
= ɺ + ɺ + ɺ (2.32)
alakúra adódik.
A potenciális energiát (2.4)-hez hasonlóan írhatjuk fel azzal a különbséggel, hogy most 2 helyett 4 rugalmas szíjágat kell figyelembe venni, így (2.4) most
( ) ( ) ( ) ( ) ( )
2 2 2 2 24 4
i 1 2 3 4
i
i 1 i 1 i 12 12 34 34
l l l l l
U U
2c 2c 2c 2c 2c
∆ ∆ ∆ ∆ ∆
= =
=
∑
=∑
= + + + (2.33)alakúra adódik, ahol 1 1
2 1
r 1
k = =r i , z 3
4 z
r 1
k = r =i , 3 2 ih
ϕ =ϕ . Ebben az esetben is feltételezzük, hogy a forgótömegek ϕi szögelfordulásai kicsik, így a szíjágak rugalmas hosszváltozására érvényesek a
1 1
1 1 1 2 2 2 1 2 2 2
2 1
1 1
2 2 2 1 1 2 2 1 2 2
2 1
3 3 2
3 3 3 4 4 4 3 4 4 4 4 4
4 z h z
3 3
4 4 4 3 3 4 4 3 4 4
4 z
l r r r r r
r i
l r r r r r
r i
l r r r r r r
r i i i
l r r r r r
r i
∆ ϕ ϕ ϕ ϕ ϕ ϕ
∆ ϕ ϕ ϕ ϕ ϕ ϕ
ϕ ϕ
∆ ϕ ϕ ϕ ϕ ϕ ϕ
∆ ϕ ϕ ϕ ϕ ϕ ϕ
= − = − = −
= − = − = −
= − = − = − = −
= − = − = −
2
4 4
h z
r i i
ϕ ϕ
= −
(2.34)
összefüggések. Ennek, valamint a (2.33) összefüggésnek megfelelıen a potenciális energiára az
2 2
2 2
2 2 2
2 1 2 1 2 2 2 1 2
4 4 4 4 4 4
2 2 2 2 2 2
h z h z h z
1 1 1
12 12 34 34 12 34
r r r
r r r
i i i i i i
i i i
U 2c 2c 2c 2c c c
ϕ ϕ ϕ
ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ
− − −
− − −
= + + + = + (2.35)
kifejezést kapjuk, melybıl (2.3) alapján az erıkoordinátákra adódnak a
( )
2 2
2 2
1 2 1 2
1 1 12 1 12
2
2 1 2
4 4
2 2
h z h z
1 2
2 12 34
2 2
4 4
4 2 4
4 h z 34 34
U 2r 2r
Q i c i c
2r 1
2r 1
i i i i U i
Q c c
U 2r 2r
Q i i c c
ϕ ϕ
ϕ
ϕ
ϕ ϕ ϕ
ϕ
ϕ ϕ
ϕ
= −∂ = − +
∂
−
− −
∂
= − = − −
∂
= − ∂ = −
∂
(2.36)
összefüggések. Bevezetve a 122 12
2
c
2r =γ , 342 34
4
c
2r =γ csavarási rugóállandókat, (2.36) a
1 2 1 2
1 12 1 12
2 1 2 2 2 4
1 12 12 h z 34 h z 34
4 2 4
h z 34 34
1 1
Q i i
1 1 1 1
Q i i i i i
1 1
Q i i
ϕ ϕ
γ γ
ϕ ϕ ϕ
γ γ γ γ
ϕ ϕ
γ γ
= − +
= − + +
= −
(2.37)
alakúra módosul. A Lagrange-féle másodfajú mozgásegyenletek
1
1 1
2
2 2
4
4 4
d E E
dt Q
d E E
dt Q
d E E
dt Q
ϕ ϕ
ϕ ϕ
ϕ ϕ
∂ − ∂ =
∂ ∂
∂ − ∂ =
∂ ∂
∂ − ∂ =
∂ ∂
ɺ ɺ ɺ
(2.38)
alakúak, melyekbe (2.32)-t és (2.37)-et behelyettesítve, és elvégezve a matematikai mőveleteket, kapjuk a vizsgált szerkezet
1 1 2 1 2
1 12 1 12
2 2 1 2 2 2 4
1 12 12 h z 34 h z 34
4 4 2 4
h z 34 34
1 1
J 0
i i
1 1 1 1
J 0
i i i i i
1 1
J 0
i i
ϕ ϕ ϕ
γ γ
ϕ ϕ ϕ ϕ
γ γ γ γ
ϕ ϕ ϕ
γ γ
+ − =
− + + − =
− + =
ɺɺ
ɺɺ
ɺɺ
(2.39)
mozgásegyenlet-rendszerét. (2.39)-et (2.10)-hez hasonlóan, Mqɺɺ+Kq=0 mintájára, a
2
1 12 1 12
1 1 1
2 2 2 2 2
1 12 12 h z 34 h z 34
4 4 4
h z 34 34
1 1
i i 0
J 0 0 0
1 1 1 1
0 J 0 0
i i i i i
0 0 J 0
1 1
0 i i
γ γ
ϕ ϕ
ϕ ϕ
γ γ γ γ
ϕ ϕ
γ γ
−
+ − + − =
−
ɺɺ ɺɺ ɺɺ
(2.40)
mátrix-egyenlet alakjában is felírhatjuk, ahol most is
1 2
4 1
2 4
2
1 12 1 12
2 2
1 12 12 34 34
34 34
1 2 4
0 0
0 0 ,
0 0
,
1 1
0
1 1 1 1
,
1 1
0
h z h z
h z
J
M J a tömegmátrix
J
q a gyorsulásvektor
i i
K a merevségimátrix
i i i i i
i i
q a elmo
ϕ ϕ ϕ
γ γ
γ γ γ γ
γ γ
ϕ ϕ ϕ
=
=
−
= − + −
−
=
ɺɺ ɺɺ ɺɺ
ɺɺ
. zdulásvektor
(2.41) (2.40) megoldását az elızı fejezetben bemutatott eljárás szerint végezzük. A csavarási saját
körfrekvenciát a mozgásegyenlet-rendszer megoldásai alapján adódó karakterisztikus egyenlet pozitív valós megoldásai adják.
2.3 Mellékhajtóm ő vek dinamikai vizsgálata
Egy forgácsoló szerszámgép mellékhajtómőve a megmunkáláshoz szükséges mellékhajtásokat, például esztergáló vagy maró megmunkálás esetén az elıtolást és a fogásvételt biztosítja.
Mellékhajtómővek tervezése és dinamikai vizsgálata során az alábbi alapvetı követelményeket vesszük figyelembe:
1. Terheléstıl független, egyenletes elıtolást biztosítson, 2. Megmunkálást befolyásoló káros rezgések ne alakuljanak ki.
A továbbiakban egy golyósorsós, lineáris mozgású mellékhajtómő egyszerősített mechanikai modelljének az 1. követelményhez kapcsolható dinamikai vizsgálatát végezzük el.
A szerkezet kinematikai modelljét a 6. ábra mutatja.
6. ábra
Az M motor az sz szíjhajtáson keresztül hajtja meg a 2 szíjtárcsával egy tengelyen lévı
golyósorsót, amely a golyósmechanizmuson keresztül hozza létre a 3 szán lineáris elmozdulását. A vizsgálat eredményeként meghatározzuk az állandó nagyságú és irányú F
elıtoló erı mellett szükséges M
hajtónyomaték nagyságát.
A mozgásegyenlet elıállítása során az elemek kapcsolatát merevnek tételezzük fel, a szíjak tömegét és a súrlódást elhanyagoljuk. A mozgásegyenletet most is a Lagrange-féle másodfajú
mozgásegyenlet (2.1) alakjából kiindulva állítjuk elı. Az ehhez szükséges általános koordinátákat jelöljük ϕ1, ϕ2-vel és s -mal, ahol 3 ϕ1 és ϕ2 a motor és a fıorsó tengelyeinek a szögelfordulása, s 3 pedig a szán elmozdulása. Jelölje továbbá J a hajtó tengelyen lévı forgó tömegek együttes 1
tehetetlenségi nyomatékát, azaz J1=Jmotor+Jtgk+Jszt1, J a hajtott tengely forgó tömegeinek 2 együttes tehetetlenségi nyomatékát, azaz J2 =Jszt 2+Jorsó, m pedig a szán és a szánon lévı 3 munkadarab együttes tömegét, azaz m3 =mszán+mmdb. Ezek alapján a Lagrange-féle
mozgásegyenletben elıforduló mozgási energiát az
2 2 2
1 1 2 2 3 3
1 1 1
E J J m s
2 ϕ 2 ϕ 2
= ɺ + ɺ + ɺ (2.42)
függvény segítségével írhatjuk fel. Mivel az elemek ideálisan merev kapcsolatát tételezzük fel, vagyis eltekintünk a szíj, valamint a golyósorsó rugalmasságától, érvényesek az alábbi, általános koordináták közötti összefüggések.
A szíjhajtás merevségébıl 2 1 k 1 i
ϕ =ϕ = ϕ adódik, ahol k a hajtásviszony, i pedig az áttételi viszony. A ϕ2 és az s általános koordináták közötti összefüggés felírásához tekintsük az alábbi 3
ábrát (7. ábra).
7. ábra
Az ábra a golyósorsó egyik menetét ábrázolja kiterítve, szimbolikusan. r és h a menet 2 középsugara és menetemelkedése. Az orsó 1 körülfordulása esetén ϕ2 =2π . A hasonló háromszögek tétele alapján írhatjuk, hogy
π ϕ2 2 2
3
2r h r
s = , melybıl 3 2
2 ϕ π
s = h . Ebbıl 2 1 k 1 i ϕ =ϕ = ϕ
felhasználásával 3 1
2 ϕ
πi
s = h adódik. Az 3 2
2 ϕ π
s = h és 2 1 k 1
i
ϕ =ϕ = ϕ általános koordinátákat
egymással összevetve látható, hogy ezek csak ϕ1-tıl függenek, így a ϕ1 általános koordináta a szerkezet bármely helyzetét egyértelmően meghatározza, így a vizsgált rendszer egy szabadságfokú, és ϕ ϕ1= az általános koordináta. Ez alapján (2.42) az
2 2
2 2 2 2 2 2
1 1 2 2 1 3 1 1 2 3 T
1 1 1 1 h 1 J h 1
E J J m J m J
2 ϕ 2 i ϕ 2 2 i ϕ 2 i 2 i ϕ 2 ϕ
π π
= + + = + + =
ɺ ɺ ɺ ɺ ɺ (2.43)
alakban írható fel, ahol
2 2 3
2
1 2
+ +
= i
m h i J J JT
π az összes mereven mozgó tömegnek az 1 szíjtárcsa tengelyére redukált tehetetlenségi nyomatéka. A vonatkozó Lagrange-féle másodfajú mozgásegyenlet
d E E
dt ϕ ϕ Q
∂ −∂ =
∂ ∂
ɺ (2.44)
alakú. A (2.44) egyenlet jobb oldalán álló Q általános erıkoordináta Q=Fβ+Mb
(2.45) alapján számítható, ahol
( )
x 3 3 x
x x
F Fe
v s e h h
e e
2 i 2 i
β ϕ
ϕ ϕ ϕ π π
= −
∂ ∂ ∂
= ∂ = ∂ = ∂ =
ɺ
ɺ
ɺ ɺ ɺ
,
ahol
x x
h h
F Fe e F
2 i 2 i
β = − ⋅ π = − π
.
Mivel
ex
M
M
= 1
és
x
x e
b e
ɺ ɺ
ɺ
∂ =
=∂
∂
=∂
ϕ ϕ ϕ ω1
,
így
1 x x 1
Mb=M e e ⋅ = M , vagyis (2.45) alapján az általános erıkoordinátára
1
Q M F h
2 iπ
= − (2.46)
kifejezés adódik. A (2.43) és (2.46) kifejezéseket behelyettesítve (2.44)-be, elvégezve a matematikai mőveleteket, kapjuk a vizsgált szerkezet
T 1
J M F h
ϕ 2 i
= − π
ɺɺ (2.47)
mozgásegyenletét.
A (2.47) egyenletbıl kiolvasható, hogy állandó irányú és nagyságú eltoló erı és sebesség esetén, vagyis amikor ϕɺɺ =0, a szán mozgatásához 1 h
M F
2 iπ
= nagyságú nyomaték szükséges.
A (2.47) mozgásegyenlet az ideálisan merevnek feltételezett elemekbıl álló, súrlódásmentes mellékhajtómő gyorsuló mozgásait is helyesen írja le.
3 Gépalapozás dinamikai kérdései
A gépalapozás problémaköre szintén a gépek dinamikájának átfogó feladatcsoportjába tartozik, azonban jelentıségénél és tárgyalási módjánál fogva mégis külön fejezetben foglalkozunk vele.
Helyhez kötött megmunkáló berendezéseket általában nem a talajra helyezik, hanem rendszerint rugalmas alátámasztást, ritkábban merevebb gépalapot készítenek számára. A megfelelı támasztás kiválasztásával, vagy a gépalap megfelelı méretezésével elérhetjük, hogy vagy nem jön rezgésbe a gép, és egyúttal a környezet felé sem kelt rezgéseket, vagy pedig a környezetbıl nem vesz fel rezgéseket.
A gépalapozás dinamikájának problémaköre azokkal a rezgéscsökkentési módszerekkel
foglalkozik, amelyek a gépalapnak mint lengırendszernek a megfelelı kialakítását célozzák. E módszerek alkalmazása két alapvetı gépalapozási probléma, az aktív és a passzív rezgésmentesítés kapcsán merülnek fel. Aktív rezgésmentesítéskor a gép rezgéseinek nagyságát és a rezgések
tovaterjedését kívánjuk korlátozni. Passzív rezgésmentesítéskor a környezetbıl származó rezgéseket kívánjuk távol tartani valamely berendezéstıl. Ez utóbbi probléma merül fel például ultraprecíziós megmunkálóberendezések vagy nagypontosságú mérıgépek telepítésekor.
Látni fogjuk, hogy tökéletes rezgésmentességet sohasem lehet elérni, hanem csak tetszıleges kis rezgési amplitúdókat lehet megvalósítani.
Gépalapozás során az alábbi típusok valamelyikét, esetleg kombinációját alkalmazzuk:
1. Tömbalapok: vasbetonból, betonból készült, viszonylag nagytömegő tömbök.
2. Keretalapok: vasbeton- vagy acélszerkezet, fıleg turbináknál alkalmazzák.
3. Falazott alapok: talplemezbıl és arra épített falakból állnak, melyek a gép hossztengelyével párhuzamosak.
4. Cölöpök: alkalmazásával elérhetjük a talaj teherbírásának növelését, vagy a rugózás keményítését.
5. Rugalmas gépalátétek: kisebb gépeket elegendı rugalmas alátétek közbeiktatásával az üzem talaján elhelyezni. Helyesen méretezett vagy kiválasztott alátétekkel elérhetjük, hogy az aktív és passzív rezgésmentesítés feladatát egyszerre lássák el.
3.1 A sajátfrekvencia és a statikus süllyedés kapcsolata
Mielıtt rátérnénk az aktív és passzív rezgésmentesítés jellemzı feladatinak bemutatására,
értelmezzük a statikus süllyedés fogalmát, és megvizsgáljuk a statikus süllyedés mértéke és a gép- gépalap lengırendszer saját körfrekvenciája közötti összefüggést.
Amikor a gépet a rugalmas alátéteken keresztül a talajra helyezik, az alátétek a gép és a gépalap együttes súlyerejébıl adódóan összenyomódnak. Az összenyomódás mértékét nevezzük statikus süllyedésnek. A statikus süllyedés ismeretében – amint azt az alábbiakban látni fogjuk –
meghatározhatjuk a gép-rugalmasgépalátét lengırendszer saját körfrekvenciáját, amelynek ismerete viszont az aktív-passzív rezgésmentesítés elvégzéséhez elengedhetetlen. A vizsgálatokhoz
szükséges mozgásegyenleteket közvetlenül, az impulzus tétel alkalmazásával írjuk fel.
Az alábbi ábra rugalmas gépalátétekre helyezett gép mechanikai – lengéstani – modelljét mutatja (8.
ábra).
8. ábra
ahol m a gép és az esetleges gépalap együttes tömege, c a rugalmas gépalátétek eredı
rugómerevsége, ξ az m tömeg pillanatnyi helyzete, x pedig a statikus süllyedés mértéke. A st csillapításokat most elhanyagoljuk. Az egyszabadságfokú lengı rendszer csak x irányú elmozdulást végezhet, mozgásegyenlete
m 1 mg
ξɺɺ+cξ = (3.1)
alakú. A ξ elmozdulás ξ = xst+x t
( )
alakban is felírható, ahol x t( )
a statikus süllyedés körül végzett rezgés. Ennek következtében (3.1)1 1
mx xst x mg
c c
+ + =
ɺɺ (3.2)
alakúra adódik. A (3.2)-ben elıforduló idıben állandó és idıben változó tagokra a 1
st st
x mg x mcg
c = → = , (3.3)
valamint az
1 1
0 0
mx x x x
c mc
+ = → + =
ɺɺ ɺɺ (3.4)
összefüggések írhatók fel. (3.4) alapján a lengırendszer saját körfrekvenciája az 1 α = mc kifejezéssel számítható, melyet (3.3)-tel összevetve adódik a statikus süllyedés és a saját körfrekvencia közötti
st 2
st
g g
x mcg
α x
= =α → = (3.5)
összefüggés.
3.2 Gépalapok tervezése aktív rezgésmentesítés esetén
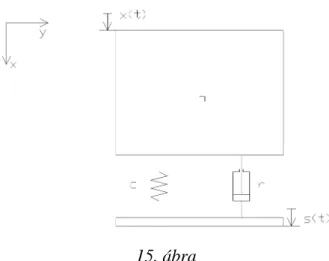
Ennek során a gép tömegét, rugóállandóját, csillapítási tényezıjét úgy választjuk meg, hogy a gépbıl kiinduló lengések kicsik legyenek, így védve a környezetet a géprezgésektıl. A rendszer mechanikai modelljét a 9. ábra mutatja.
9. ábra
Az ábrán m most is a gép-gépalap rendszer együttes tömegét, c a rugalmas gépalátétek eredı rugómerevségét, r az m tömegre ható, lineárisnak feltételezett csillapítások eredı együtthatóját jelölik. x-szel jelöljük az m tömeg pillanatnyi elmozdulását, F t