Purves, Roger Pisani, Robert Freedman, David Statisztika

(1)

Statisztika

Freedman, David

Pisani, Robert

Purves, Roger

(2)

Statisztika

Jerzy Neymannak (1894–1981)

Jerzy Neyman Oroszországban született, Lengyelországban és Angliában dolgozott, mielőtt 1938-ban az USA-ba érkezett.

Korunk nagy statisztikusainak egyike volt.

(3)

iii

Tartalom

ELŐSZÓ ... xx

1. Az olvasóhoz ... xx

1.1. Mi a statisztika? ... xx

1.2. Vázlat ... xx

1.3. Feladatok ... xxi

1.4. Mi változott a harmadik kiadásban? ... xxi

1.5. Köszönetnyilvánítások a harmadik kiadáshoz ... xxi

1.6. Köszönetnyilvánítások a korábbi kiadásokhoz ... xxii

I. KÍSÉRLETEK MEGTERVEZÉSE ... 1

1. Kontrollált kísérletek ... 3

1. 1. A Salk-oltás kipróbálása ... 3

2. 2. A Porta-Cava sönt ... 6

3. 3. Történeti kontrollok ... 7

4. 4. Összefoglalás ... 10

2. Megfigyeléses vizsgálatok ... 11

1. 1. Bevezetés ... 11

2. 2. Egy szívgyógyszer vizsgálata ... 12

3. 3. További példák ... 14

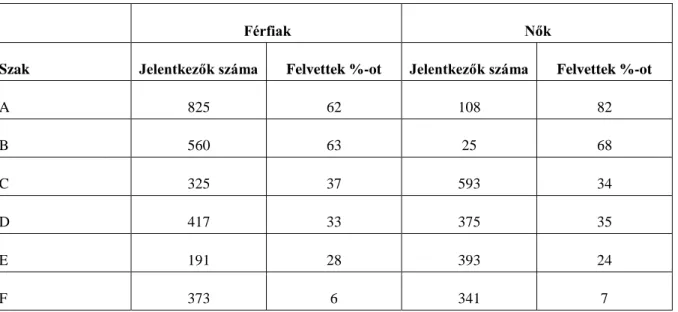
4. 4. Hátrányos nemi megkülönböztetés a posztgraduális felvételiken ... 16

5. 5. Összemosódás ... 19

5.1. „A” feladatsor ... 20

6. 6. Ismétlő feladatsor ... 24

7. 7. Összefoglalás és áttekintés ... 27

II. LEÍRÓ STATISZTIKA ... 29

3. A hisztogram ... 32

2. 2. Hogyan rajzoljunk hisztogramot? ... 35

2.1. „B” feladatsor ... 37

3. A sűrűségskála ... 38

3.1. „C” feladatsor ... 40

4. 4. Változók ... 41

4.1. „D” feladatsor ... 42

5. 5. Kontrollváltozó bevezetése ... 43

5.1. „E” feladatsor ... 45

6. 6. Kereszttáblák ... 45

6.1. „F” feladatsor ... 46

7. 7. Szelektív tenyésztés ... 47

4. Az átlag és a szórás ... 55

2. 2. Az átlag ... 55

3. 3. Az átlag és a hisztogram ... 58

4. 4. A négyzetes középérték ... 63

5. 5. A szórás ... 64

6. 6. A szórás kiszámítása ... 69

7. 7. A számítás statisztikai funkciókkal ellátott számológéppel ... 71

5. Adatok normális közelítése ... 76

(4)

Statisztika

1. 1. A normálgörbe ... 76

2. 2. A normálgörbe alatti területek meghatározása ... 80

3. 3. A normális közelítés adatokon ... 82

4. 4. Percentilisek ... 84

5. 5. Percentilisek és a normálgörbe ... 87

6. 6. A skála megváltoztatása ... 88

6. A mérési hiba ... 93

2. 2. A véletlen hiba ... 93

3. 3. Magányos esetek ... 97

4. 4. Torzítások ... 99

6. 6. Különleges ismétlő feladatsor ... 100

7. Pontok és egyenesek ábrázolása ... 105

1. 1. Pontok a koordináta-rendszerben ... 105

2. 2. Pontok bejelölése ... 107

3. 3. A meredekség és a tengelymetszet ... 108

4. 4. Egyenesek ábrázolása ... 110

5. 5. Az egyenes algebrai egyenlete ... 111

III. KORRELÁCIÓ- ÉS REGRESSZIÓSZÁMÍTÁS ... 114

8. A korreláció ... 117

1. 1. A pontdiagram ... 117

2. 2. A korrelációs együttható ... 123

3. 3. A szórásegyenes ... 130

4. 4. A korrelációs együttható kiszámítása ... 132

9. Kicsit bővebben a korrelációról ... 142

1. 1. A korrelációs együttható tulajdonságai ... 142

2. 2. A változók szórása és a pontdiagram ... 145

3. 3. Kivételek ... 147

4. 4. Ökológiai korrelációk ... 148

5. 5. Az összefüggés még nem jelent oksági kapcsolatot ... 150

10. Regressziószámítás ... 158

1. 1. Bevezetés ... 158

(5)

Statisztika

v

2. 2. Az átlagdiagram ... 161

3. 3. Regressziós becslés az egyénekre ... 164

4. 4. A regressziós tévkövetkeztetés ... 167

5. 5. Két regressziós egyenes van ... 171

6. 6. Ismétlő feladatok ... 173

11. A regressziós egyenes négyzetes középhibája ... 177

1. 1. Bevezetés ... 177

2. 2. A négyzetes középhiba kiszámítása ... 181

3. 3. A maradékok ábrázolása ... 183

4. 4. A függőleges sávok a pontdiagramon ... 185

5. 5. A normális közelítés alkalmazása egy függőleges sávon belül ... 190

12. A regressziós egyenes ... 197

1. 1. Meredekség és tengelymetszet ... 197

2. 2. A legkisebb négyzetek módszere ... 202

3. 3. Van-e értelme a regressziós egyenesnek? ... 206

IV. VALÓSZÍNŰSÉG ... 212

13. Mik az esélyek? ... 214

1. 1. Bevezetés ... 214

2. 2. Feltételes valószínűségek ... 219

3. 3. Szorzási szabály ... 220

4. 4. Függetlenség ... 222

5. 5. A Collins-per ... 225

14. Még mindig a valószínűségről ... 229

1. 1. A kimenetelek felsorolása ... 229

2. 2. Összeadási szabály ... 233

3. 3. Két gyakran feltett kérdés ... 234

4. 4. De Méré lovag paradoxona ... 238

5. 5. Szabályosak-e a valódi dobókockák? ... 243

15. A binomiális formula ... 246

1. 1. Bevezetés ... 246

(6)

Statisztika

2. 2. A binomiális formula ... 249

4. 4. Nagy ismétlő feladatsor ... 253

5. 5. Összefoglalás, áttekintés ... 258

V. VÉLETLEN INGADOZÁS ... 260

16. A nagy számok törvénye ... 262

1. 1. Mit mond a nagy számok törvénye? ... 262

2. 2. Véletlen folyamatok ... 268

3. 3. A húzások összege ... 269

4. 4. Hogyan készül egy dobozmodell ... 271

17. A várható érték és a standard hiba ... 278

1. 1. A várható érték ... 278

2. 2. A standard hiba ... 280

3. 3. A normális eloszlásgörbe használata ... 283

4. 4. Egy számítási képlet ... 287

5. 5. Osztályozás és darabszámok ... 288

7. 7. Utóirat ... 296

18. Elméleti hisztogramok normális közelítése ... 297

1. 1. Bevezetés ... 297

2. 2. Elméleti hisztogramok ... 298

3. 3. Elméleti hisztogramok és a normálgörbe ... 304

4. 4. A normális közelítés ... 305

5. 5. Mikor alkalmazható a normális közelítés ... 308

6. 6. Összefoglalásul ... 315

7. 7. Összefoglaló feladatsor ... 316

VI. MINTAVÉTEL ... 320

19. Nagy mintán végzett felmérések ... 322

1. 1. Bevezetés ... 322

2. 2. A Literary Digest híres közvéleménykutatása ... 323

3. 3. Hogyan kiáltották ki elnöknek Dewey-t a közvéleménykutatók? ... 325

4. 4. A véletlen felhasználása a felmérésekben ... 328

5. 5. Mennyire működnek jól a valószínűségi eljárások? ... 331

6. 6. A Gallup közvéleménykutatás közelebbről ... 332

7. 7. Telefonos felmérések ... 336

8. 8. Véletlen hiba és torzítás ... 336

20. Véletlen hibák mintavételnél ... 343

1. 1. Bevezetés ... 343

2. 2. A várható érték és a standard hiba ... 346

3. 3. Felhasználjuk a normálgörbét ... 349

(7)

Statisztika

vii

4. 4. A korrekciós szorzó ... 352

5. 5. A Gallup közvéleménykutatásai ... 356

21. A százalékarányok pontossága ... 360

1. 1. Bevezetés ... 360

2. 2. Konfidenciaintervallumok ... 364

3. 3. Hogyan értelmezzük a konfidenciaintervallumokat? ... 367

4. 4. Figyelmeztetés ... 370

5. 5. A Gallup intézet közvéleménykutatásai ... 371

22. A foglalkoztatottság és a munkanélküliség mérése ... 377

1. 1. Bevezetés ... 377

2. 2. A rendszeres népességfelmérés mintájának előállítása ... 378

3. 3. A felmérés megvalósítása ... 379

4. 4. A minta súlyozása ... 383

5. 5. A standard hibák ... 383

6. 6. Az adatok minősége ... 386

7. 7. A torzítás ... 386

23. Az átlagok pontossága ... 390

1. 1. Bevezetés ... 390

2. 2. A mintából számolt átlag ... 394

3. 3. Melyik standard hibával kell dolgoznunk? ... 400

4. 4. Amit ne feledjünk ... 402

VII. VALÓSZÍNŰSÉGI MODELLEK ... 415

24. Modell a mérési hibára ... 417

1. 1. Becslést adunk egy átlag pontosságára ... 417

2. 2. Valószínűségi modellek ... 419

3. 3. A Gauss-modell ... 424

4. 4. Következtetések ... 429

25. Valószínűségi modellek a genetikában ... 433

1. 1. Hogyan fedezte fel Mendel a géneket ... 433

2. 2. A modellnek megfelelőek voltak-e Mendel adatai? ... 439

3. 3. A regresszió törvénye (visszatérés az átlaghoz) ... 440

4. 4. A modell értékeléséről ... 443

VIII. SZIGNIFIKANCIAPRÓBÁK ... 447

26. Szignifikanciapróbák ... 449

1. 1. Bevezetés ... 449

(8)

Statisztika

2. 2. Null- és ellen- ... 452

3. 3. Próbastatisztikák és szignifikanciaszintek ... 453

4. 4. Hogyan áll össze egy szignifikanciapróba? ... 455

5. 5. Nulla–egy dobozok ... 457

6. 6. A t-próba ... 461

27. További próbák az átlagra ... 476

1. 1. Az eltérés standard hibája ... 476

2. 2. KÉT MINTAÁTLAG ÖSSZEHASONLÍTÁSA ... 478

3. 3. Kísérletek ... 484

4. 4. Továbbra is kísérletekről ... 489

5. 5. Mikor használhatunk z-próbát? ... 493

28. A χ²-próba ... 499

1. 1. Bevezetés ... 499

2. 2. A χ²-próba felépítése ... 506

3. 3. Hogyan alkalmazta Fisher a χ²-próbát ... 509

4. 4. Függetlenségvizsgálat ... 511

29. Szignifikanciapróbák, közelebbről ... 521

1. 1. Szignifikáns-e az eredmény? ... 521

2. 2. Szignifikanciavadászat ... 522

3. 3. Fontos-e az eredmény? ... 528

4. 4. A modell szerepe ... 530

5. 5. Bizonyítja-e az állítást az eltérés? ... 535

6. 6. Következtetések ... 537

IX. FÜGGELÉK ... 551

30. Feladatmegoldások ... 555

1. I. rész: Kísérletek megtervezése ... 555

1.1. 2. fejezet. Megfigyeléses vizsgálatok ... 555

1.1.1. „A” feladatsor ... 555

2. II. rész: Leíró statisztika ... 557

2.1. 3. fejezet. A hisztogram ... 557

2.1.1. „A” feladatsor ... 557

2.1.2. „B” feladatsor ... 558

2.1.3. „C” feladatsor ... 558

(9)

Statisztika

ix

2.1.4. „D” feladatsor ... 558

2.1.5. „E” feladatsor ... 559

2.1.6. „F” feladatsor ... 559

2.2. 4. fejezet. Az átlag és a szórás ... 559

2.2.1. „A” feladatsor ... 559

2.2.2. „B” feladatsor ... 561

2.2.3. „C” feladatsor ... 561

2.2.4. „D” feladatsor ... 561

2.2.5. „E” feladatsor ... 562

2.3. 5. fejezet. Adatok normális közelítése ... 563

2.3.1. „A” feladatsor ... 563

2.3.2. „B” feladatsor ... 563

2.3.3. „C” feladatsor ... 564

2.3.4. „D” feladatsor ... 564

2.3.5. „E” feladatsor ... 565

2.3.6. „F” feladatsor ... 565

2.4. 7. fejezet. Pontok és egyenesek ábrázolása ... 565

2.4.1. „A” feladatsor ... 565

2.4.2. „B” feladatsor ... 565

2.4.3. „C” feladatsor ... 566

2.4.4. „D” feladatsor ... 566

3. III. rész Korreláció- és regressziószámítás ... 568

3.1. 8. fejezet. A korreláció ... 568

3.1.1. „A” feladatsor ... 568

3.1.2. „B” feladatsor ... 570

3.1.3. „C” feladatsor ... 570

3.1.4. „D” feladatsor ... 571

3.2. 9. fejezet. Kicsit bővebben a korrelációról ... 571

3.2.1. „A” feladatsor ... 571

3.2.2. „B” feladatsor ... 573

3.2.3. „C” feladatsor ... 573

3.2.4. „D” feladatsor ... 574

3.3. 10. fejezet. Regressziószámítás ... 575

3.3.1. „A” feladatsor ... 575

3.3.2. „B” feladatsor ... 576

3.3.3. „C” feladatsor ... 578

3.3.4. „D” feladatsor ... 579

3.3.5. „E” feladatsor ... 580

3.4. 11. fejezet. A regressziós egyenes négyzetes középhibája ... 580

3.4.1. „A” feladatsor ... 580

3.4.2. „B” feladatsor ... 581

3.4.3. „C” feladatsor ... 581

3.4.4. „D” feladatsor ... 581

3.4.5. „E” feladatsor ... 583

3.5. 12. fejezet. A regressziós egyenes ... 583

3.5.1. „A” feladatsor ... 583

3.5.2. „B” feladatsor ... 584

4. IV. rész. Valószínűség ... 584

4.1. 13. fejezet. Mik az esélyek? ... 584

4.1.1. „A” feladatsor ... 584

4.1.2. „B” feladatsor ... 585

4.1.3. „D” feladatsor ... 586

4.2. 14. fejezet. Még mindig a valószínűségről ... 586

4.2.1. „A” feladatsor ... 586

4.2.2. "B" feladatsor ... 587

4.2.3. „C” feladatsor ... 587

4.2.4. „D” feladatsor ... 588

4.3. 15. fejezet. A binomiális formula ... 589

4.3.1. „A” sorozat ... 589

5. V. rész. Véletlen ingadozás ... 590

(10)

Statisztika

5.1. 16. fejezet. A nagy számok törvénye ... 590

5.1.1. „A” sorozat ... 590

5.1.2. „B” sorozat ... 591

5.1.3. „C” sorozat ... 591

5.2. 17. fejezet. A várható érték és a standard hiba ... 591

5.2.1. „A” sorozat ... 591

5.2.2. „B” sorozat ... 592

5.2.3. „C” sorozat ... 593

5.2.4. „D” sorozat ... 594

5.2.5. „E” sorozat ... 595

5.3. 18. fejezet. Elméleti hisztogramok normális közelítése ... 596

5.3.1. „A” sorozat ... 596

5.3.2. „B” sorozat ... 596

5.3.3. „C” sorozat ... 597

6. VI. rész. Mintavétel ... 599

6.1. 19. fejezet. Nagy mintán végzett felmérések ... 599

6.1.1. „A” feladatsor ... 599

6.2. 20. fejezet. Véletlen hibák mintavételnél ... 600

6.2.1. „A” feladatsor ... 600

6.2.2. „B” feladatsor ... 601

6.2.3. „C” feladatsor ... 602

6.3. 21. fejezet. A százalékarányok pontossága ... 602

6.3.1. „A” feladatsor ... 602

6.3.2. „B” feladatsor ... 603

6.3.3. „C” feladatsor ... 604

6.3.4. „D” feladatsor ... 605

6.3.5. „E” feladatsor ... 605

6.4. 22. fejezet. A foglalkoztatottság és a munkanélküliség mérése ... 605

6.4.1. „A” feladatsor ... 606

6.5. 23. fejezet. Az átlagok pontossága ... 606

6.5.1. „A” feladatsor ... 606

6.5.2. „B” feladatsor ... 607

6.5.3. „C” feladatsor ... 608

6.5.4. „D” feladatsor ... 610

7. VII. rész. Valószínűségi modellek ... 610

7.1. 24. fejezet. Modell a mérési hibára ... 610

7.1.1. „A” sorozat ... 610

7.1.2. „B” sorozat ... 611

7.1.3. „C” sorozat ... 611

7.2. 25. fejezet. Valószínűségi modellek a genetikában ... 612

7.2.1. „A” sorozat ... 612

8. VIII. rész.Szignifikanciapróbák ... 613

8.1. 26. fejezet. Modell a mérési hibára ... 613

8.1.1. „A” feladatsor ... 613

8.1.2. „B” feladatsor ... 614

8.1.3. „C”feladatsor ... 614

8.1.4. „D” feladatsor ... 614

8.1.5. „E” feladatsor ... 615

8.1.6. „F” feladatsor ... 617

8.2. 27. fejezet. További próbák az átlagra ... 618

8.2.1. „A” feladatsor ... 618

8.2.2. „B” feladatsor ... 618

8.2.3. „C” feladatsor ... 619

8.2.4. „D” feladatsor ... 620

8.3. 28. fejezet. A χ²-próba ... 623

8.3.1. „A” feladatsor ... 623

8.3.2. „B” feladatsor ... 624

8.3.3. "C" feladatsor ... 624

8.4. 29. fejezet. Szignifikanciapróbák, közelebbről ... 626

8.4.1. „A” feladatsor ... 626

(11)

Statisztika

xi

8.4.2. "B" feladatsor ... 626

8.4.3. „C” feladatsor ... 627

8.4.4. „D” feladatsor ... 628

8.4.5. „E” feladatsor ... 628

31. Táblázatok ... 630

1. NORMÁLIS ELOSZLÁSTÁBLÁZAT ... 630

2. t-TÁBLÁZAT ... 631

3. χ2-TÁBLÁZAT ... 632

(12)

Az ábrák listája

3.1. Hisztogram. Az ábra az amerikai családok jövedelem szerinti megoszlását mutatja 1973-ban. 32

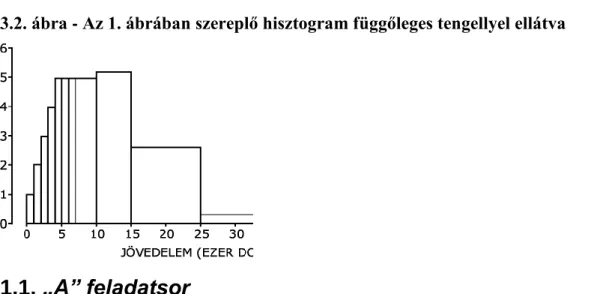
3.2. Az 1. ábrában szereplő hisztogram függőleges tengellyel ellátva ... 33

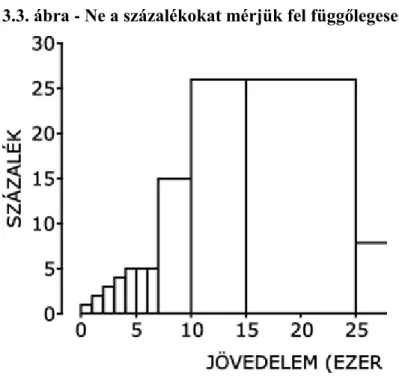
3.3. Ne a százalékokat mérjük fel függőlegesen! ... 36

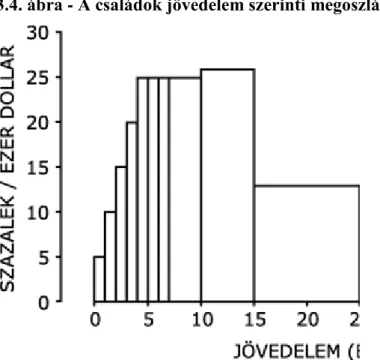
3.4. A családok jövedelem szerinti megoszlása az USA-ban, 1973. ... 37

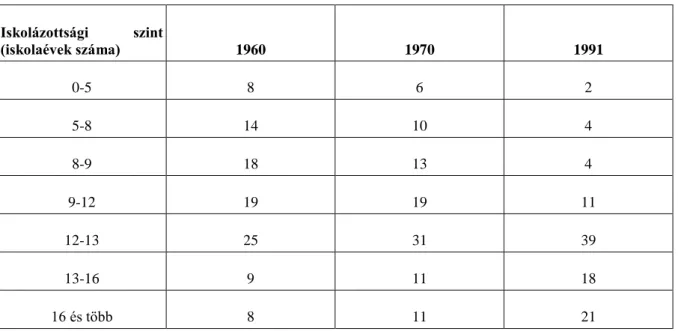
3.5. A 25 éven felüli amerikai népesség eloszlása 1991-ben, iskolázottsági szint szerint. ... 38

3.6. A családlétszám megoszlását ábrázoló hisztogram, 1993. Diszkrét változó esetén a lehetséges értékekre tesszük az osztásközök középpontját. ... 42

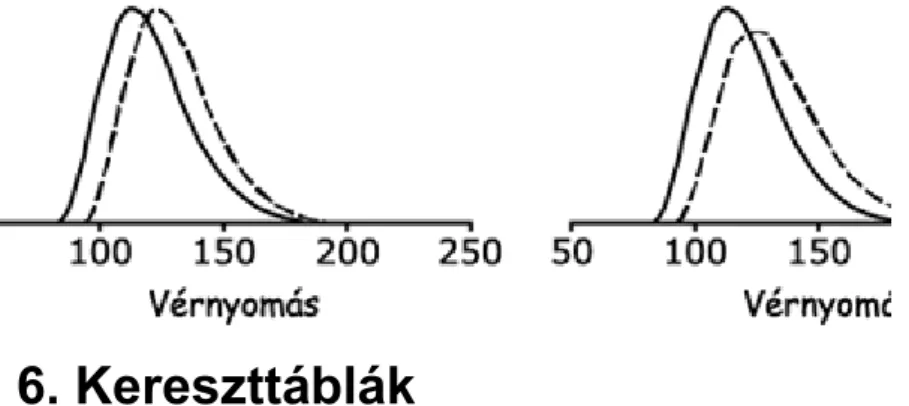
3.7. A fogamzásgátló tabletták hatása. A felső ábra a Contraceptive Drug Studyban résztvevő 1747 tablettaszedő és 3040 nem szedő 25-34 éves nő szisztolés vérnyomását mutatja. Az alsó ábrán a nem szedők hisztogramját 5 hgmm-rel jobbra toltuk. ... 44

3.8. Tyron kísérlete. Az intelligencia megoszlása az eredeti populációban. ... 47

3.9. Tyron kísérlete. Hét generációnyi szelektív tenyésztés után világosan elkülönül az „útvesztőben okos‖ és az „útvesztőben buta‖ törzs. ... 47

4.1. Középérték és szóródás. A két hisztogram középpontja azonos, de a jobboldali jobban szóródik. 55 4.2. A föld felszínének megoszlása a tengerszinthez viszonyított magasság szerint a tengerszint fölött (+), illetve alatt (-). ... 55

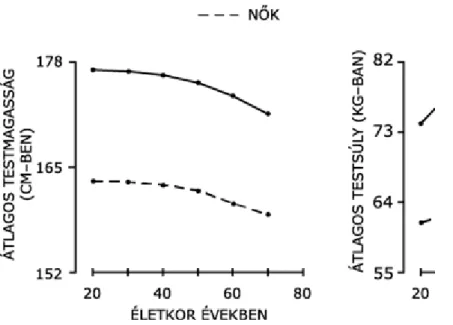
4.3. Az életkorspecifikus testmagasság- és testsúlyátlagok a HANES mintájában szereplő 18-74 éves férfiakra és nőkre. A baloldali ábra a testmagasságokat, a jobboldali a testsúlyokat ábrázolja. (Az eredetileg hüvelykben és fontban mért adatokat itt centiméterben és kilogrammban adjuk meg. A szerk.) 57 4.4. A HANES mintájában szereplő 6.588 18-74 éves nő testsúlyának hisztogramja. A testsúlyátlagot szaggatott vonal jelöli. Csak 41% testsúlya nagyobb az átlagosnál. (Az adatokat átírtuk font helyett kilogrammra. A szerk.) ... 59

4.5. Az 1, 2, 2, 3 számsor hisztogramja. A hisztogram szimmetrikus a 2-es értékre nézve; a teljes terület 50%-a 2-től balra, 50%-a jobbra helyezkedik el. ... 59

4.6. Az átlag. Az ábra felső részében három hisztogram látható, az átlagokat nyilak jelölik. Ahogy a besatírozott téglalap tolódik jobbra, az átlagot is húzza maga után. Az átlagtól balra eső terület aránya felmegy 75%-ra. Az ábra alsó részében ugyanezen hisztogramokat merev súlytalan deszkára erősített fatömbökként ábrázoltuk. A hisztogramok az átlagnál alátámasztva lesznek egyensúlyban. ... 59

4.7. A hisztogram ferdesége ... 61

4.8. A szórás és a hisztogram: a HANES vizsgálatában résztvevő 6588 fő 18-74 éves nő testmagassága. Szaggatott függőleges vonal jelzi az átlagot (161 cm). Az egy szórásnyin belüli területet besatíroztuk: a nők 67%-a tért el legfeljebb egy szórásnyival (legfeljebb 6,3 cm-rel) az átlagtól. (A hisztogram adatait hüvelyk helyett centiméterben adjuk meg. A szerk.) ... 65

4.9. A szórás és a hisztogram: a HANES vizsgálatában részt vevő 6588 fő 18-74 éves nő testmagassága. Szaggatott függőleges vonal jelzi az átlagot (161 cm). A két szórásnyin belüli besatíroztuk: a nők 94%-a tért el legfeljebb két szórásnyival (legfeljebb 13 cm-rel) az átlagtól. ... 65

5.1. A normálgörbe ... 76

5.2. A nők magassághisztogramja a normálgörbével összevetve. A hisztogram alatti terület 155 és 167 cm között (a magasságukat tekintve az átlagtól egy szóráson belüli nők aránya) nagyjából megegyezik a görbe alatti területtel –1 és +1 között – azaz 68%-kal. ... 78

5.3. Normális közelítéskor a normálgörbével helyettesítjük az eredeti hisztogramot a görbe alatti terület kiszámítása előtt ... 83

5.4. Az átlag és a szórás. Az átlag és a szórás a középpont, illetve a középpont körüli szóródás mértékének megadásával összegzi a normálgörbét követő hisztogramot. ... 84

5.5. A családi jövedelmek megoszlása: USA, 1992. ... 84

5.6. ... 85

6.1. Az amerikai kilogramm-etalon, a K20. ... 96

6.2. Magányos esetek. A felső ábra az NB 10-es 100 mérési eredményének hisztogramja; az összehasonlítás kedvéért berajzoltuk a normálgörbét. A görbe nem jól illeszkedik a hisztogramhoz. Az alsó ábra a három magányos eset elhagyása után nyert hisztogramot mutatja. A görbe jobban illeszkedik. Az adatok többsége a normálgörbét követi, ám néhány mérési eredmény sokkal messzebb esik az átlagtól, mint azt a görbe alapján várnánk. ... 98

6.3. ... 101

7.1. ... 105

7.2. ... 105

(13)

Statisztika

xiii

7.3. ... 105

7.4. ... 107

7.5. ... 107

7.6. ... 107

7.7. ... 107

7.8. ... 108

7.9. ... 108

7.10. A meredekség ½. ... 108

7.11. A meredekség 0. ... 108

7.12. A meredekség –1. ... 109

7.13. ... 109

7.14. ... 109

7.15. ... 109

7.16. ... 109

7.17. ... 110

7.18. ... 110

7.19. ... 110

7.20. ... 110

7.21. ... 111

7.22. ... 111

7.23. ... 112

7.24. ... 112

7.25. ... 112

8.1. 1078 apa és fiú testmagasságának pontdiagramja. A diagram pozitív összefüggést mutat az apák és fiaik magassága között. A 45 fokos, y = x egyenesre esnek azok a családok, ahol a fiú magassága megegyezik az apjáéval. A berajzolt függőleges sávban találhatók azok a családok, ahol az apa magassága kerekítve 72 hüvelyk, azaz 183 cm. (Az eredeti, hüvelykben megadott adatokat centiméterben tüntetjük fel. A szerk.) ... 117

8.2. 2.a A pontdiagram egyik pontja; 2.b A pontdiagram elnagyolt vázlata ... 118

8.3. A fiú magassága közel van az apa magasságához ... 119

8.4. A pontdiagram összegzése ... 123

8.5. Pontdiagram összegzése. A korrelációs együttható azt méri, hogy mennyire szorosan csoportosulnak a pontok egy egyenes köré. ... 124

8.6. A korrelációs együttható (r) hat különböző pozitív értéke. Az ábrák úgy készültek, hogy az átlag 3, a szórás pedig 1 legyen mind vízszintesen, mind függőlegesen; 50 pont szerepel mindegyik ábrán. A korrelációs együtthatóval mértük, hogy mennyire tömörülnek a pontok. ... 125

8.7. A korrelációs együttható hat negatív értéke. Az ábrák úgy készültek, hogy az átlag 3, a szórás 1 legyen mind vízszintesen, mind függőlegesen; 50 pont szerepel az egyes ábrákban. A pontok tömörülését a korrelációs együtthatóval mértük. ... 127

8.8. A szórásegyenes megrajzolása ... 131

8.9. Hogyan működik a korrelációs együttható? ... 133

9.1. A napi maximum hőmérsékletek 1993. júniusában New Yorkban és Bostonban. A baloldali ábrán Fahrenheit fokban; a jobboldalin Celsius fokban ábrázoltuk az adatokat. Az r ugyanakkora. ... 142

9.2. Napi legalacsonyabb és legmagasabb hőmérsékletek 1993. júniusában New Yorkban. ... 143

9.3. A szórások és a pontdiagram. Mindkét ábránál ugyanakkora a korrelációs együttható: 0,70. Úgy tűnik azonban, mintha a fölső ábrában szorosabban tömörülnének a pontok a szórásegyenes körül – ez azért van, mert kisebbek a szórások. ... 145

9.4. A korrelációs együttható. Ahogy az r közelít 1-hez, a tipikus pontok függőleges irányú távolsága a szórásegyenestől egyre kisebb lesz a függőleges szóráshoz viszonyítva. ... 146

9.5. Ha előfordulnak magányos pontok, vagy ha az összefüggés nemlineáris, a korrelációs együttható félrevezető lehet. ... 147

9.6. Az arányszámokból vagy átlagokból számolt korreláció rendszerint túlságosan nagy. A bal oldali ábrán három (A, B, illetve C) államban élő személy jövedelmét és iskolázottságát ábrázoltuk. Az egyes embereket lakóhelyük betűjelével jelöltük. Mérsékelt korrelációt találunk. A jobb oldali ábrán az egyes államokra vonatkozó átlagok szerepelnek. Az átlagok közötti korreláció majdnem 1. ... 149

9.7. ... 151

9.8. A mellrák miatti halálozási arány a zsiradékfogyasztással összevetve néhány országra. ... 151 10.1. Pontdiagram. Az egyes pontok egy-egy, a HANES-ben résztvevő 18-24 éves férfi magasságát és testsúlyát mutatják, összesen 988 személyét. A berajzolt függőleges sáv jelenti az átlagnál körülbelül egy szórásnyival magasabb férfiakat. A szaggatott vonallal jelölt szórásegyenesre esnek közülük azok,

(14)

Statisztika

akiknek a testsúlya is egy szórással nagyobb az átlagnál. A sávba eső pontok többsége a szórásegyenes alatt található: a testsúlyok csak a szórás valamekkora részével haladják meg az átlagot. A folytonos vonallal jelölt regressziós egyenes ad becslést az egyes magasságértékekhez tartozó átlagos testsúlyra.

158

10.2. A regressziós eljárás. x egy szórásnyi növekedésekor y átlagos értéke csak r szórásnyival nő. 160 10.3. Az átlagdiagram az egyes testmagasságokhoz tartozó átlagos testsúlyt mutatja a HANES mintájában

szereplő 998 fő 18-24 éves férfi adatai alapján. A regressziós egyenes kisimítja az ábrát. ... 161

10.4. Nemlineáris összefüggés. Nem használható a regressziós egyenes akkor, amikor a változók közötti összefüggés nem egyenesen arányos (azaz nem lineáris). ... 162

10.5. A regressziós effektus. Ha a fiú 1 hüvelykkel nagyobb az apjánál, akkor a család a szaggatott vonalra esik. A 72 hüvelykhez tartozó függőleges sáv azoknak a családoknak felel meg, ahol az apa magassága 72 hüvelyk (hüvelykre kerekítve). Ebben a sávban a pontok többsége a szaggatott vonal alatt van. A 64 hüvelykhez tartozó függőleges sáv azokat a családokat jelenti, ahol az apa magassága kerekítve 64 hüvelyk; itt a pontok többsége a szaggatott vonal fölött található. A folytonos vonallal jelölt regressziós egyenes az összes függőleges sávhoz tartozó középpontokat célozza be; a szórásegyenesnél kevésbé meredek. ... 168

10.6. A regressziós effektus. A szórásegyenest szaggatott, a regressziós egyenest folytonos vonallal jelöltük. A pontok a fiúk magasságátlagait mutatják az apák különböző magasságértékeire. A pontok a szórásegyenesnél kevésbé meredeken emelkednek. Ez a regressziós effektus. A regressziós egyenes a pontokat követi. ... 169

10.7. A regressziós effektus modellje. ... 170

10.8. A bal oldali ábra a testsúly magasság szerinti, a jobb oldali a magasság testsúly szerinti regressziós egyenesét mutatja. A szórásegyenest szaggatott vonallal jelöltük. ... 171

10.9. A két regressziós egyenes ... 172

11.1. Az előrejelzés hibája a regressziós egyenestől való függőleges irányú ( + vagy – előjelű) eltérés. A pontdiagramban a HANES mintájában szereplő 998 fő 18-24 éves férfi magassága és testsúlya szerepel. 177 11.2. Az előrejelzés hibája az egyenestől való függőleges irányú eltéréssel egyenlő ... 178

11.3. Hozzávetőleges becslés. A pontdiagram pontjainak 68%-a beleesik abba a sávba, amelyet a regressziós egyenessel párhuzamos, attól (fölfelé, illetve lefelé) egy négyzetes középhibára lévő egyenesek határolnak. A pontok mintegy 95%-a a regressziós egyenessel párhuzamos, attól két négyzetes középhibára lévő szélesebb sávban található. ... 179

11.4. A regressziós egyenes négyzetes középhibája, valamint az y szórása. ... 181

11.5. A maradékok ábrázolása. ... 183

11.6. A maradékdiagram. A baloldali pontdiagram a HANES mintájában szereplő 988 fő 18-24 éves férfi magasságát és testsúlyát mutatja; az ábrában a regressziós egyenes is szerepel. Jobboldalt a maradékdiagram látható. A maradékok semmiféle tendenciát vagy mintázatot nem mutatnak. .... 184

11.7. Határozott tendenciát mutató maradékdiagram. Alighanem hiba volt regressziós egyenest illeszteni a pontokra. ... 184

11.8. Apák és fiaik. A folytonos vonallal jelölt függőleges sávban találhatók a 64 hüvelyk magas apák családjai; a folytonos vonallal rajzolt hisztogram mutatja a fiaik testmagasságát. A 72 hüvelyk magas apák családjai a szaggatottan jelölt függőleges sávba esnek; a szaggatott vonalas hisztogram az ő fiaik magasságára vonatkozik. A két hisztogram alakja hasonló, és közelítőleg megegyeznek a szórások. 186 11.9. 9. ábra. Heteroszcedasztikus pontdiagram: a jövedelem és az iskolai végzettség (a befejezett osztályok száma) közötti összefüggés a Kalifornia államban élő, 25-29 éves nők egy 426 fős mintájára, 1993. A regressziós egyenes is szerepel az ábrán. ... 187

11.10. ... 188

11.11. Rögbilabda alakú pontdiagram. Egy keskeny függőleges sávba eső pontokat nézünk most. A hozzájuk tartozó y értékek új adatsort jelentenek. Az új átlagot a regressziós eljárással kaphatjuk meg, az új szórást a regressziós egyenes négyzetes középhibája adja meg. A tipikus y érték a sávon belül az új átlag körül lesz – attól egy új szórásnyira fölfelé vagy lefelé. ... 190

11.12. A baloldali ábrán a Secchi-mélység és a teljes klorofill koncentráció pontdiagramja látható; a klorofill koncentráció mértékegysége egymilliárd részecskére eső részecskeszám (ppm). A jobboldali ábrán az adatokat transzformáltuk: a 10-es alapú logaritmusukat vettük. ... 192

12.1. A regressziós egyenes. A jövedelem és az iskolázottság pontdiagramja a kaliforniai 25-29 éves férfiak egy 1993-as, 555 fős mintáján. ... 197

12.2. A meredekség és a tengelymetszet ... 198

12.3. A regressziós egyenes meredekségének és tengelymetszetének meghatározása. ... 198

12.4. A Hook-törvény. A megnyúlás egyenesen arányos a terheléssel ... 203

12.5. Az 1. táblázat pontdiagramja. ... 204

(15)

Statisztika

xv

12.6. 20 téglalap területe és kerülete közötti összefüggés pontdiagramja; a regressziós egyenest is

berajzoltuk. ... 206

12.7. A 20 téglalap ... 206

13.1. De Moivre ajánlása a The Doctrine of Chances elé ... 214

13.2. De Moivre megoldása ... 217

13.3. A visszatevéses és a visszatevés nélküli húzás közötti különbség. Két húzást végzünk, véletlenszerűen, a három lapot tartalmazó dobozból. Tegyük fel, hogy az első húzás a 3-as ... 218

13.4. Szorzási szabály. (Egy figura 100 embernek felel meg.) ... 221

14.1. Dobás két kockával. A két kocka 36-féleképpen eshet – ezt mutatja a táblázat belseje; mind a 36 egyforma esélyű. ... 230

16.1. John Kerrich érmedobálásos kísérlete. A "véletlen hiba" egyenlő (fejek száma) – (dobások számának fele). ... 264

16.2. A véletlen hiba a dobások számának százalékában kifejezve. Amikor a dobások száma növekszik, ez a százalék csökken: a dobások számához viszonyítva a véletlen hiba csökken. A vízszintes tengely nem méretarányos. ... 265

16.3. Rulettasztal (nevadai rulett). ... 272

18.1. Tapasztalati hisztogramok, amint az elméleti hisztogramhoz konvergálnak. Számítógép szimulálta, hogy két dobókockával dob, majd veszi a két pontszám összegét. Ezt megismételte 100-szor, s hisztogramot készített a kapott 100 számról (felső rajz). Ez tapasztalati hisztogram: megfigyelésen alapul. A második rajz 1000 ismétlésre vonatkozik, a harmadik 10 000 ismétlésre. (Egy ismétlés: egyszeri dobás két kockával.) Az alsó rajz eszményi, azaz elméleti hisztogram ugyanerről (pontszámok összege, két dobókockával történő dobásnál). ... 299

18.2. Tapasztalati hisztogramok, amint az elméleti hisztogramhoz konvergálnak. Számítógép szimulálta, hogy két dobókockával dob, s veszi a két pontszám szorzatát. Ezt ismételte 100-szor, s a kapott 100 szorzatról hisztogramot készített (felső rajz). Ez tapasztalati hisztogram: megfigyelésen alapul. A második rajz 1000 ismétlésre vonatkozik, a harmadik 10 000 ismétlésre. (Egy ismétlés: egyszeri dobás két kockával.) Az alsó rajz eszményi, azaz elméleti hisztogram ugyanerről (pontszámok szorzata, két dobókockával történő dobásnál). ... 301

18.3. A 100 érmedobásból kapott fejek számára vonatkozó elméleti hisztogram, a normálgörbével összehasonlítva. A görbét a hisztogramra vonatkozó standard egység skálához igazítva rajzoltuk. 304 18.4. A normális közelítés. Fejek számára vonatkozó elméleti hisztogramok, 100, 400 és 900 érmedobás esetére. Összehasonlításul a normálgörbe is látható. Amint a dobások száma nő, a hisztogramok egyre jobban megközelítik a normálgörbét. ... 305

18.5. A féloldalas, 9 0-t és egy 1-est tartalmazó doboz hisztogramja. ... 308

18.6. Normális közelítés, a 9 0-t és egy 1-est tartalmazó dobozból végzett húzások összegére. A felső rajzon a 25 húzás összegére vonatkozó elméleti hisztogram látható, a középsőn a 100, az alsón a 400 húzás összegére vonatkozó. Összehasonlításul a normálgörbe is látható. Mivel a doboz féloldalas, a hisztogramok baloldalt magasabbak a normálgörbénél, jobboldalt pedig alacsonyabbak. Ahogy a húzások száma nő, a hisztogramok egyre jobban közelítik a normál-görbét. ... 308

18.7. Elméleti hisztogramok az 1-est, 2-est és 3-ast tartalmazó dobozból végzett 25, illetve 50 húzás összegéről. A hisztogramok nagyon szépen követik a normálgörbét. ... 309

18.8. Az 1-est, 2-est és 9-est tartalmazó doboz hisztogramja. Egyáltalán nem hasonlít a normálgörbére. 310 18.9. Összeg normális közelítése. Elméleti hisztogramok, az 1-est, 2-est és 9-est tartalmazó dobozból végzett húzások összegére. A felső rajz 25 húzásra vonatkozik – ez nem igazán követi a normál-görbét. (Figyeljük meg a hullámokat!) A középső rajz 50 húzásra vonatkozik. Az alsó rajz 100 húzásra vonatkozik; ez nagyon szépen követi a normálgörbét. ... 310

18.10. Elméleti hisztogramok, 10 illetve 25 kockadobás szorzatáról. A hisztogramok nem hasonlítanak a normálgörbéhez. Az egyes oszlopok alapja megfelel egy-egy tartománynak a szorzat értékei közül; az oszlop területe egyenlő annak a valószínűségével, hogy a szorzat értéke ebbe a tartományba fog esni. A 10 dobásnál a területnek körülbelül a 6%-a nem látszik; a 25 dobásnál körülbelül 20% nem látszik. A felső rajzon a függőleges lépték: százalék, 10 000-ként; az alsó rajzon: százalék, 10¹¹-enként. ... 312

19.1. Többlépcsős csoportos mintavétel ... 329

19.2. A Gallup Intézet által használt szavazócédula. A kérdezők titkos szavazócédulát használnak a bizonytalanok számának csökkentésére. ... 332

19.3. A Gallup Intézet kérdőíve az 1984-es választáskor ... 333

19.4. A Gallup Intézet kérdőíve az 1984-es választáskor (folytatás) ... 334

20.1. Hisztogram a férfiak számának alakulásáról 100 elemű mintákban. ... 344

20.2. Hisztogram a férfiak arányának alakulásáról 400 elemű mintákban. 250 mintát választottunk ki véletlenszerűen az egészségügyi vizsgálat résztvevői közül. ... 345

(16)

Statisztika

20.3. ... 351 21.1. A konfidenciaintervallumok értelmezése. 100 különböző mintából nyert 95%-os

konfidenciaintervallumokat láthatunk. Az intervallum mintáról mintára változik. A minták körülbelül 95%-ánál beleesik a konfidenciaintervallumba a függőleges vonallal jelölt populációbeli arány. . 368 21.2. ... 370 22.1. A munkanélküliségi ráta alakulása 1929 és 1994 között. ... 377 22.2. A Rendszeres Népességfelmérés elsődleges mintavételi egységei az 1990-es évek felvételeinél. 378 22.3. A foglalkoztatottság és a keresetek c. kiadvány A-26 táblázata (36. oldal), 1994. április. .... 381 23.1. Az ábra felső részében az 1-estől a 7-esig az összes számot tartalmazó dobozból kihúzott 25 szám összegének elméleti hisztogramja látható. Az alsó rész a kihúzott számok átlagának elméleti hisztogramját mutatja. Ha standard egységekben vesszük fel a hisztogramokat, a kettő tökéletesen megegyezik. 391 23.2. ... 392 23.3. ... 393 23.4. Számítógépes szimuláció. Az ábra felső részében az egész város 25 éven felüli lakosainak iskolázottság szerinti megoszlása látható. A középső részben a minta iskolázottság szerinti megoszlását láthatjuk. Ezek adathisztogramok. Az alsó részben a dobozból kihúzott 400 szám átlagának elméleti hisztogramja szerepel, mely közel van a normálgörbéhez. A városban 12,0 év az átlagos iskolázottsági szint, szórása 4,0 év; a mintában 11,6 és 4,1 a megfelelő számok. (Az adathisztogramoknál alkalmazott végpontkonvenció: a 12–13 osztásköz például azokat tartalmazza, akik elvégeztek 12 osztályt, de a 13- adikat nem –középiskolai végzettségűek, akik egy évet sem végeztek főiskolán.) ... 397 24.1. 1.ábra. Hőmérsékletek és dobozmodellek. A felső rajz a San-Fransisco-i repülőtér 1993-as napi hőmérsékletmaximumait mutatja. Éves mintázatot – évszakos ingadozást – látunk az adatokban: nyáron melegebb, télen hidegebb van. Helyi mintázatok is vannak: rövid meleg és hideg időszakok. Nincs alkalmas dobozmodell. Az alsó rajz azt mutatja, milyenek lennének a hőmérsékletek, ha dobozból húzás határozná meg őket. ... 421 24.2. A felső rajz az NB 10-en végzett egymás utáni méréseket ábrázolja (lásd a 6. fejezet 2. szakasz 1.

táblázatát). A középső rajz fiktív adatsorát egy dobozmodellt szimuláló számítógép hozta létre. A két rajz nagyon hasonlít, ami azt mutatja, hogy a dobozmodell igen jól közelíti az adatokat. Az alsó rajz erős időbeli mintázatot mutató adatsor grafikonja. Nem írható le dobozmodellel. ... 422 25.1. Mendel valószínűségi modellje a borsószem magszínének meghatározására: mindkét szülőtől egy- egy gént választunk, véletlenszerűen. Az egyes kombinációk valószínűsége is látható az ábrán. (A spermiumból származó gént írtuk előre; magszín szempontjából a s/z és z/s kombinációk a

megtermékenyítést követően megkülönböztethetetlenek.) ... 435 25.2. Mikroszkópos felvétel. Sejtek egy borsópalánta gyökércsúcsáról, körülbelül 2000-szeres nagyításban. A középen látható sejt épp osztódni készül. Ebben a fázisban mindegyik kromoszóma két egyforma, egymás mellett fekvő darabból áll. Tizennégy kromoszómát látunk, hét homológ párban – I-től VII-ig római számok jelölik a párokat. A borsószem színét meghatározó génpár az I-es kromoszómapáron van – egyik darabja az egyik, másik darabja a másik kromoszómán. ... 437 25.3. A testmagasság örökletes meghatározottságára vonatkozó egyszerűsített Mendel-Fisher modell. A testmagasságot egyetlen génpár határozza meg, tisztán additív genetikai hatással. A gyermek mindkét szülő génpárjából húz egyet véletlenszerűen, így áll össze a gyermek génpárja. ... 441 25.4. A testmagasság örökletes meghatározottságára vonatkozó egyszerűsített Mendel–Fisher modell, három tisztán additív hatású génpárt feltételezve. A gyermek a két szülő mindegyik génpárjából véletlenszerűen húz egyet, így áll össze a gyermek megfelelő génpárja. ... 442 25.5. Ivarsejtek és testi sejtek keletkezése, osztódással. A kromoszómákat itt nagybetűkkel jelöljük, pl.: C.

A kromoszómák homológ párokban fordulnak elő; az egy párhoz tartozó kromoszómákat azonos betűvel jelöljük, az egyikre vesszőt téve. C és C' tehát homológ pár: kémiailag hasonlóak, de nem egyformák. A sejt az osztódás előkészületi fázisában mindegyik kromoszómáját megkettőzi. C-t e megkettőzött

állapotában C-C jelöli. E kettős két darabja kémiailag egyforma; gyenge kötés fogja őket össze. Ugyanígy megkettőződik C' is, amiből C'-C' lesz. ... 443 26.1. Student-görbék. A szaggatott vonal a Student-görbe (fent a négy szabadságfokú, lent a kilenc szabadságfokú). A folytonos vonal a normálgörbe, összehasonlításul. ... 465 27.1. Sorsolt kontrollú kísérlet az A és a B kezelés összehasonlítására. Minden alanyt egy lap képvisel. A lapon két szám van: az egyik az alanynak az A kezelésre adott válasza; a másik a B-re adott válasza. Csak az egyiket lehet megfigyelni. ... 485 27.2. ... 490 28.1. 5 és 10 szabadságfokú χ²-görbe. A görbék jobb felé messzire elnyúlnak. Az egyre nagyobb szabadságfokú görbék egyre laposabbak lesznek, és egyre jobbra tolódnak. (A folytonos vonalú az 5 szabadságfokú görbe, a szaggatott a 10 szabadságfokú.) ... 501

(17)

Statisztika

xvii

28.2. Pearson-közelítés. A felső grafikonon a szabályos kocka 60 dobása nyomán számított χ²-statisztika elméleti hisztogramja látható, és, összehasonlításképpen, az 5 szabadságfokú χ²-görbe. Az alsó grafikonon a valamely értéktől jobbra eső maradékterületek arányai láthatók. Nézzük például a 14,2-t a vízszintes tengelyen. A hisztogramon a terület 1,4382%-a esik 14,2-től jobbra. A görbe alatti megfelelő terület 1,4388%. Az arány 1,4382/1,4388 ≈ 0,9996 – ezt az értéket látjuk az alsó grafikonon 14,2 fölött.

Hasonlóképpen jártunk el a többi arány esetében is. ... 503

(18)

A táblázatok listája

1.1. A Salk-oltás vizsgálatának eredményei, 1954. Csoportméretek, és gyermekbénulási esetek

előfordulási aránya százezer főre, az egyes csoportokban. Kerekített számok. ... 5

1.2. Vizsgálat a porta-cava söntről folytatott 51 vizsgálatról. A jól tervezett vizsgálatok szerint a műtét keveset vagy semmit sem ér. A gyengén tervezett vizsgálatok eltúlozzák a műtét hasznát. ... 6

1.3. Sorsolt kontrollcsoportú kísérletek összehasonlítása olyan kísérletekkel, melyeknél a kontroll nem sorsolt: a hároméves túlélés arányai a májkapuvénai áthidalás vizsgálataiban (kerekített százalékok) 7 1.4. Vizsgálatok vizsgálata. Négy terápia sorsolt kontrollú és történeti kontrollt használó kísérletekkel végzett értékelése. A vizsgálatok összefoglalt végkövetkeztetését ábrázoljuk: pozitívan vélekednek-e a terápiáról (+), vagy negatívan (-). ... 8

1.5. Sorsolt kontrollú kísérletek, illetve történeti kontrollos vizsgálatok: három éves túlélési arányok a szívkoszorúér bypass műtét vizsgálataiban, műtött betegekre és a kontrollcsoportra. A sorsolt kontrollú kísérletek eltérnek a történeti kontrollt használóktól. ... 9

2.1. A clofibrate vizsgálat. A vizsgált személyek száma, és azon személyek százalékaránya, akik az 5 éves nyomonkövetés alatt meghaltak. "Rendesen szedők", akik a felírt szernek legalább 80%-át beszedték. A többiek "a szedést elhanyagolók". ... 12

2.2. Felvételi adatok a Kaliforniai Egyetem hat legnagyobb szakáról. ... 17

2.3. Jelentkezők létszáma összesen, a 2. táblázat szerint. ... 18

3.1. A családok jövedelem szerinti megoszlása az USA-ban, 1973. Az osztásközök a baloldali végpontot tartalmazzák, a jobboldalit nem. ... 35

3.2. A szisztolés vérnyomás életkor és fogamzásgátló tabletta szedése szerint a Contraceptive Drug Study vizsgálatában részt vevő nők körében, a terhes, illetve más hormonkészítményeket szedő nők kivételével. Az osztásközökbe a baloldali végpont tartozik bele, a jobboldali nem, ennek. jelentősége elhanyagolható. A táblázatban százalékban szerepelnek a számok; az oszlopok összege a kerekítés miatt eltérhet a 100-tól. ... 45

5.1. Az 1992-es amerikai családi jövedelmek egyes percentilisei. ... 85

6.1. Az NB 10-en végzett 100 mérés. A méréseket a Nemzeti Mérésügyi Hivatalban Almer és Jones végezték. A mértékegység: mikrogramm, amennyivel kevesebb 10 grammnál. ... 94

8.1. ... 132

8.2. Az r kiszámítása ... 132

12.1. A Hooke-törvényt demonstráló adatok ... 203

14.1. Esélyek, három kockával dobva, 9-es illetve 10-es pontösszegre. ... 231

16.1. John Kerrich érmedobálásos kísérlet ... 262

16.2. A tiszta nyereség. Ez az addigi nyereség–veszteség számok halmozott összege. ... 273

17.1. Számítógépes szimuláció: 25 véletlenszerűen, visszatevéssel végzett húzás összege a 0-s, 2-es, 3-as, 4-es és 6-os lapokat tartalmazó dobozból, 100 esetben. ... 282

17.2. Hatvan dobás egy dobókockával. ... 289

17.3. Kerrich érmedobálós kísérlete: az egymást követő 100 dobásos szakaszok közül melyikben hány fejet kapott. ... 290

18.1. 5 érmedobás sorrendjeinek száma adott számú fejjel. ... 297

18.2. Dobások két kockával. A számítógép szimulálja, hogy két kockával dobunk, majd összeadja a pontszámokat. Ezt a gép 10 000-szer ismétli; ebből itt az első 100 látható. ... 298

19.1. Az 1936-os elnökválasztás ... 324

19.2. Az 1948-as elnökválasztás ... 326

19.3. A Gallup Intézet felméréseinek torzítása a Republikánus Párt irányában, 1936-1949 ... 327

19.4. A Gallup Intézet eredményei az 1948 utáni elnökválasztásoknál ... 331

20.1. Véletlenszerűen kiválasztottunk száz embert és feltüntettük a nemüket. 51 férfi (F) és 49 nő (N) volt közöttük. Az alapsokaságban 46% volt a férfi és 54% a nő. ... 344

20.2. 250 véletlen mintát vettünk egy egészségügyi vizsgálat résztvevői közül. A résztvevők 46%-a volt férfi. A minta elemszáma 100. A férfiak száma az egyes mintákban az alábbiak szerint alakult. .. 345

20.3. A korrekciós szorzó értéke 2500 húzás esetén. ... 354

21.1. A Gallup közvéleménykutatások az egyszerű véletlen mintával összehasonlítva. Az előrejelzési hibák összességében nagyobbak, mint amekkorát azonos nagyságú egyszerű véletlen mintánál várnánk. 371 21.2. A Gallup közvéleménykutatásainak pontossága akkora egyszerű véletlen mintával összehasonlítva, amennyi a valószínű szavazók száma a Gallup mintájában. ... 372

(19)

Statisztika

xix

22.1. A 16 éven felüli népesség, a katonaság és az intézményben élők nélkül. A Munkaügyi Statisztikai

Hivatal becslései, 1994. március. Millió fő. ... 380

22.2. A munkanélküliségi ráta bőrszín, életkor és nem szerint. A Munkaügyi Statisztikai Hivatal becslései, 1994. március. Százalékban. ... 381

22.3. Becsült standard hibák, 1994. március ... 384

24.1. Az Amerikai Egyesült Államok lakossága, 1790–1990. ... 420

26.1. Kivonatos t-táblázat. ... 466

27.1. Eredmények egy, az adatok bemutatásának szerepét vizsgáló kísérletből. ... 489

28.1. Hatvan dobás egy dobókockával, mely talán cinkelt ... 499

28.2. Megfigyelt és várható gyakoriságok, az 1. táblázatbeli adatok alapján. ... 500

28.3. Kicsi χ²-táblázat (részlet a könyv végén található található nagyobból.) ... 502

28.4. A kezesség nemek szerinti megoszlása ... 511

28.5. A kezesség nemek szerinti megoszlása ... 511

28.6. Megfigyelt és várható gyakoriságok ... 512

28.7. Sor- és oszlopösszegek ... 513

29.1. Kivonatos t-táblázat. ... 521

29.2. SRI teljesítmény-pontszámok 20 Far West Laboratory-osztályra. A pontszámok 0-tól 100-ig terjedhetnek. ... 532

(20)

ELŐSZÓ

Hogy milyen dalt énekeltek a szirének, s hogy mi volt Akhilleusz neve, amikor asszonyok között bújkált – rejtelmes kérdések, sejtésünk mégis van róluk.

—Sir Thomas Browne (Anglia, 1605–1682)

1. Az olvasóhoz

Be szeretnénk mutatni néhány érdekes problémát, melyeket statisztikai módszerek segítségével tanulmányoztak, továbbá azt is, hogyan lehet ezeket a módszereket önállóan alkalmazni. Igyekszünk elmagyarázni, melyik módszer mitől működik, s mire jó odafigyelni, ha mások használják őket. Úgy tűnik, hogy a matematikai írásmód sokak elől kifejezetten eltakarja a lényeget – ez a könyv ezért szavakra, ábrákra és táblázatokra épül;

elvétve fordulnak csak elő benne x-ek és y-ok. Amikor szakkönyvet olvas, még a hivatásos matematikus is gyakran átsiklik a képleteken. Voltaképpen arra vágyik, hogy legyen mellette egy megértő barát, aki elmagyarázza, milyen elgondolás vagy milyen elképzelt tevékenység áll az egyenletek mögött. Arra törekszünk, hogy a könyvünk olvasóinak ilyen barátai legyünk.

1.1. Mi a statisztika?

A statisztika annak mestersége, hogyan lehet bizonyos rejtelmes kérdésekkel kapcsolatosan számszerű következtetésekre – vagy inkább sejtésekre – jutni.

• Mik egy új orvosi beavatkozás hatásai?

• Mi okozza a szülők és gyermekeik közötti hasonlóságot – és mennyire erős ez a hatás?

• Mitől van a ruletten haszna a kaszinónak?

• Ki nyeri a soron következő választásokat? Mennyivel?

• Mennyi a foglalkoztatottak száma? Mennyi a munkanélkülieké?

Nehéz kérdések – ha van kedve ilyesmiken gondolkodni, abban a statisztikai módszerek sokat segíthetnek.

Ezeket a módszereket olyan emberek dolgozták ki az évszázadok során, akik különféle, őket foglalkoztató problémákra keresték a megoldást. Közülük is megismerkedünk majd néhánnyal.

1.2. Vázlat

Az I. rész a kísérletek megtervezésével foglalkozik. Ha jó a kísérleti terv, akkor az adatokból megbízható következtetéseket lehet levonni. Néhány rosszul tervezett kísérletet is górcső alá veszünk, hogy kiderüljön, hol lehetnek buktatók, és hogy megmutassuk, milyen kérdéseket érdemes feltenni, mikor az ember vizsgálatokról olvas. Az egész könyvből talán éppen ez, a vizsgálatok tervezése a legfontosabb – azért is kezdjük ezzel. Esetleg úgy látszik majd, hogy minden egyszerű ebben a részben – de a látszat sokszor csal: az I. részben sok a mélység.

Egy vizsgálat során általában olyan sok szám keletkezik, hogy feltétlenül összesíteni kell őket. A II. részben a leíró statisztikával – az adatok összesítésének mesterségével – fogunk ismerkedni. Hisztogramokról, átlagról, szórásról és a normális görbéről esik szó. Ezt a témakört folytatja a III. rész, amelyben az összefüggések elemzéséről fogunk beszélni: például, hogy miképpen függ a jövedelem az iskolázottságtól. A legfontosabb címszavak: korreláció és regresszió.

A statisztikai gondolatmenetek jelentős része a IV. részben tárgyalt valószínűségszámításon alapul; közöttük az V. részben kifejtésre kerülő sorsolásos modellek teremtik meg a kapcsolatot. Érmék, dobókockák, rulettkerekek a fő példák. Megismerkedünk a várható értékkel és a standard hibával; elméleti hisztogramokat készítünk, és tárgyaljuk a normális görbéhez való konvergenciát.

A statisztikai következtetés lesz a VI-VIII. rész témája: hogyan lehet minták alapján érvényesen általánosítani.

A VI. rész a becslésekről szól. Hogyan jelzi például előre a választási eredményt a Gallup felmérés? Mitől jobb egyik mintavételi módszer, mint a másik? A VII. rész sorsolásos modelleket használ a mérési hibák elemzéséhez és egy genetikai elmélet kidolgozásához. A VIII. részben a szignifikancia-próbákkal ismerkedünk – ezek

(21)

ELŐSZÓ

xxi

segítségével lehet eldönteni, összeegyeztethető-e mintánk a populációra vonatkozó feltevéseinkkel. A VI-VIII.

részből ki fog derülni, hogy a statisztikai következtetés sorsolásos modelleken nyugszik: ha rossz a modell, az eredményül kapott következtetés nagyon ingatag lehet.

A szakmabeliek számára mostanában a következtetések elmélete a statisztika legérdekesebb szakterülete. A nem-statisztikusok viszont a leíró statisztikát többnyire jobban tudják használni, és könnyebben is értik. Emiatt a leíró statisztikát a következtetések előtt tárgyaljuk. Mondanivalónk puszta váza az 1-től 6., 13., 16-tól 21., 23. és 26. fejezetben található meg. Az olvasó, ha ezeket elolvasta, utána kedvére tallózhat. Folytatásként mi talán a 8., 10., 27. és 29. fejezeteket ajánlanánk.

1.3. Feladatok

Többé-kevésbé minden fejezet minden szakaszához csatlakozik egy feladatsor (megoldások a könyv végén). Ha az olvasó sorra, ahogy következnek, megoldja őket, és utána ellenőrzi a megoldást, ezzel némi gyakorlatra tehet szert az újonnan elsajátított készségekben – és megtudja, milyen mértékben sikerült elsajátítania őket. Minden fejezet (az 1. és a 7. kivételével) ismétlő feladatokkal zárul. Ezeknek a megoldása nem szerepel a könyvben.

A feladatok megoldása során esetleg majd kísértést érez, hogy visszalapozzon, hátha feltűnik valahol az idevágó képlet. A könyv ilyenfajta visszafelé-olvasása igen frusztráló lehet. Az ismétlő feladatokhoz egy-egy képletnél sokkal több kell. Hozzávetőleges becslésekre és kvalitatív ítéletekre egyaránt szükség lehet. Más szóval:

intuitíve is érteni kell, hogy miről van szó. Ahhoz, hogy ez a megértés kialakuljon, érdemes a könyvet elejétől a vége felé haladva olvasni.

Miért van ebben a könyvben ennyire sok olyan feladat, amiket nem lehet a megfelelő képletbe helyettesítéssel megoldani? Ennek főként az az oka, hogy a valódi világban sem sok probléma oldható meg ezzel a módszerrel.

Viszont abból, amikor emberek úgy alkalmaznak statisztikai formulákat, hogy valójában fogalmuk sincsen arról, amit csinálnak, sokszor származik zűrzavar. Ebben a könyvben egy másik megközelítést javaslunk:

gondolkozzunk.

1.4. Mi változott a harmadik kiadásban?

A sok könyvek írásának nincs vége.

—Prédikátor könyve

Többé-kevésbé ugyanazok a témák, és ugyanabban a sorrendben követik egymást most is, mint a második kiadásban. Az idő azonban a számok fölött sem múlik el nyomtalanul. (Havi 50 dollárért például a negyvenes években nagyszerű lakást lehetett bérelni.) Ezért az adatok egy részét a 90-es éveknek megfelelően korszerűsítettük. A jövedelmi és iskolázottsági statisztikák az amerikai rendszeres népességfelmérés (Current Population Survey) 1993. márciusi adatfelvételéből valók; a harmadik HANES-vizsgálat (National Health and Nutrition Examination Survey, Országos Egészség- és Táplálkozásfelmérés) 1994-es felvételének előzetes eredményei is többször szerepelnek.

A korábbi kiadásokhoz hasonlóan továbbra is sok számítógépes grafikát használunk az adatok bemutatásához.

Viszont a vázlatok mind szabadkézi rajzok; ezzel szerettük volna az olvasót arra ösztönözni, hogy maga is készítsen hasonlókat – nem szerettük volna, hogy a túlzott precizitás elvegye ettől a kedvét. Újra gyönyörködhetünk Dana Fradon (The New Yorker) rajzaiban - van közöttük néhány új is.

Néhány döntő ponton új kifejtő részek is szerepelnek; új szakasz foglalkozik például az összemosódás, illetve a kísérleti kontrasztokra vonatkozó próbák kérdésével. A közel 200 új feladatban számos friss vizsgálatot szerepeltetünk. Egy-egy "Nagy ismétlő feladatsor" zárja a 6., 15., 23. és 29. fejezetet; ezek a teljes addigi anyagrészt átfogják. A bennük szereplő feladatok

megoldásában nem igazít el, hogy mi a környező fejezetek témája. Ezekhez a fejezetekhez "Összefoglalás, áttekintés" rész is tartozik, amely összefoglalja az előző részt, és átvezet a rákövetkezőhöz.

1.5. Köszönetnyilvánítások a harmadik kiadáshoz

Dana Fradon rajzolta a karikatúrákat. Dale Johnson és Laura Southworth az ábrákat. A szöveget az Integre szedte, TEX-ben. A számítógépes grafikát PostScriptbe kódolva integráltuk a végső nyomtatási állományokba; a kódolás jelentős részben Charles Everett (A.A.E.C., Pennington, New Jersey), továbbá Richard és Adele Cutler (Utah State University) munkája.

(22)

ELŐSZÓ

Segítőkész megjegyzéseket sok helyről kaptunk. A harmadik kiadás tekintetében külön köszönetet mondunk Mike Andersonnak (Berkeley), Dick Berknek (UCLA), Jeff Fehminek (Berkeley), David Kaye-nek (Arizona State University), Steve Kleinnek (RAND), Russ Lyons-nak (Indiana), Mike Ostlandnek (Berkeley), Erol Pekoz-nak (UCLA), Diana Petittinek (Kaiser Permanente), Juliet Shaffernek (ETS), Bill Simpsonnak (Winnipeg), Terry Speednek (Berkeley), Philip Starknak (Berkely) és Allan Stewart-Oatennek (Santa Barbara).

Végül, itt mondunk köszönetet azoknak, akik olvasták az első két kiadást (vagy a harmadik kiadás számos előkészítő verzióját), s azoknak is, akik ezekből tanultak.

1.6. Köszönetnyilvánítások a korábbi kiadásokhoz

A könyv megírását a Ford Foundations (1973-1974) és a Regents of the University of California (1974-75) támogatta. Nehéz időkben segítséget és bátorítást kaptunk Earl Cheit-től és Sanford Elberg-től.

Segítőkész hozzászólásokat kaptunk a következőktől: Frank Anscombe (Yale), Diccon Bancroft (Yale), Leo Breiman (Berkeley), John Cairns (Oxford), Merrill Carlsmith (Stanford), Persi Diaconis (Cornell), Fred Katz (Berkeley), David Lane (Modena), Richard Light (Harvard), Peter McCullagh (Chicago), Ludolf Meester (Delft), Gerald Mendelsohn (Berkeley), Lincoln Moses (Stanford), Bill Navidi (Colorado School of Mines), James Robins (Harvard), Thomas Rothenberg (Berkeley), Bruce Rotschild (UCLA), Bernard Saffran (Swarthmore), Shanna Swan (California State Department of Health Services), Amos Tversky (Stanford), Geoff Watson (Princeton), és Hans Zeisel (Chicago). A második kiadás készítésében részt vett Ani Adhikari.

Külön köszönet illeti szerkesztőnket, Donald Lammet azért, hogy az egyre alakuló kéziratból valahogy mégis könyv lett.

(23)

I. rész - KÍSÉRLETEK

MEGTERVEZÉSE

(24)

Tartalom

1. Kontrollált kísérletek ... 3 1. 1. A Salk-oltás kipróbálása ... 3 2. 2. A Porta-Cava sönt ... 6 3. 3. Történeti kontrollok ... 7 4. 4. Összefoglalás ... 10 2. Megfigyeléses vizsgálatok ... 11 1. 1. Bevezetés ... 11 2. 2. Egy szívgyógyszer vizsgálata ... 12 3. 3. További példák ... 14 4. 4. Hátrányos nemi megkülönböztetés a posztgraduális felvételiken ... 16 5. 5. Összemosódás ... 19 5.1. „A” feladatsor ... 20 6. 6. Ismétlő feladatsor ... 24 7. 7. Összefoglalás és áttekintés ... 27

(25)

3

1. fejezet - Kontrollált kísérletek

Mindig cselekedj helyesen. Ez egyeseknek megelégedésére szolgál, a többieket megdöbbenti.

—–Mark Twain (USA,1835–1910)

1. 1. A Salk-oltás kipróbálása

Új gyógyszert vezetnek be. Hatékonyságát kísérletekkel kell ellenőrizni – hogyan tervezzék meg ezeket a kísérleteket? A fő módszer az összehasonlítás.¹ A kísérleti személyek egy részének – ők a kezelt csoportⁱ – beadják a gyógyszert; a többi kísérleti személy lesz a kontrollcsoport – ők nem kapnak a gyógyszerből. Ezután összehasonlítják a két csoport reagálását. Sorsolással (véletlenszerűen, azaz random módon) kell eldönteni, ki kerül a kezelt, ki a kontrollcsoportba, és a kísérletnek kettős - vak módon kell lefolynia: sem a kísérleti személyek, sem a válaszreakciójukat mérő orvosok nem tudhatják, hogy ki tartozik a kezelt, és ki a kontrollcsoportba. E gondolatokat egy gyógyszer kipróbálásának a valóságban megtörtént példáján fogjuk bemutatni.²

Az Egyesült Államokat 1916-ban érte el a járványos gyermekbénulás első hulláma; a következő negyven évben a betegség több százezer áldozatot követelt, főként a gyermekek köréből. Az ötvenes évekre több vakcinát is felfedeztek a gyermekbénulás ellen. A Jonas Salk által kifejlesztett oltás tűnt a legígéretesebbnek. Laboratóriumi vizsgálatok igazolták, hogy veszélytelen, s hogy megindítja a gyermekbénulás elleni antitestek termelődését.

1954-re a Közegészségügyi Szolgálat (Public Health Service) és az Országos Gyermekbénulás Alapítvány (National Foundation for Infantile Paralysis – NFIP) készen állt rá, hogy az oltást a laboratórium falain kívül, az életbenis kipróbálja.

Tegyük fel, hogy az NFIP alapítvány nem tett volna mást, egyszerűen csak beadta volna az oltást nagyszámú gyereknek. Ha aztán a gyermekbénulási esetek száma jelentősen az 1953-as szám alá esik 1954-ben, ez az oltás hatékonysága mellett szóló bizonyítéknak számított volna. Viszont a gyermekbénulási járvány intenzitása évről évre jelentős mértékben ingadozott. 1952-ben körülbelül 60 000 megbetegedést észleltek; 1953-ban csak feleennyit. Ha 1954-ben kevés a gyermekbénulásos megbetegedés, az jelenthette volna az oltás hatékonyságát – de jelenthette volna azt is, hogy 1954 nem járványos év.

Hogy hatásos-e az oltás, az csak úgy derülhetett ki, ha a gyermekek egy részét tudatosan kihagyják az oltásból – kontrollcsoportnak használják őket. Ez kínos orvosetikai kérdést vet fel: kegyetlenségnek tűnhet, ha egyesektől megtagadják a kezelést. Gyakran előfordul azonban, hogy egy új gyógyszerről az ellenőrzésére lefolytatott rengeteg laboratóriumi vizsgálat nyomán sem válik egyértelművé, ellensúlyozzák-e kedvező hatásai az alkalmazásával járó kockázatokat.³ A kérdés csakis jól kontrollált kísérlettel tisztázható megnyugtatóan.

Így is történt: az NFIP kontrollcsoportos kísérlettel igyekezett meggyőződni az oltás hatásosságáról. A kísérleti személyek gyermekek voltak, a gyermekbénulásnak leginkább kitett korosztályokból: elsősök, másodikosok és harmadikosok. A vizsgálat helyszínéül olyan iskolakerületeketválasztottak az ország minden részéből, melyekben magas arányú volt a gyermekbénulás előfordulása. A vizsgálatban kétmillió gyermek vett részt, körülbelül félmilliót oltottak be. Egymilliót szándékosan nem oltottak be; további félmilliónak a szülei nem járultak hozzá az oltáshoz.

Az összehasonlításos módszerre látunk példát: csak a kezelt csoporthoz tartozó személyeket oltották; a kontrollcsoporthoz tartozók nem kaptak oltást. Ezután összehasonlíthatjuk a két csoport reakcióit, hogy lássuk, okoz-e valami eltérést a kezelés. A Salk-féle oltás vizsgálatánáleltérő méretű volt a kezelt, és a kontrollcsoport,

11. Fejezet Kontrollált kísérletek

[i] Az összehasonlításos módszert először feltehetően a XIX. század elején használták, annak kimutatására, hogy az érvágás mégsem annyira hatékony ellenszere a tüdőgyulladásnak. Ld. Pierre Louis; Recherches sur Les Effets de la Saignée dans quelques Maladies inflammatoires: et sur l'Action de l'Emétique et des Vésicatoires dans la Pneumonie (Párizs: J.B. Bailière, 1835; angolul, 1836; újranyomva:

The Classics of Medicine Library, 1986, Birmingham, Alabama.) Részletesebben tárgyalja R.H.Shryock, The Development of Modern Medicine (University of Pennsylvania Press, 1936, 163.o.) Továbbá említenünk kell Lindnek a C-vitamin skorbut-ellenes hatásával kapcsolatos vizsgálatát; ld. K.J. Carpenter, The History of Scurvy and Vitamin C (Cambridge University Press, 1986.)

iA magyar nyelvű irodalomban a kísérleti csoport elnevezés is használatos. (A ford.)

2Thomas Francis, Jr. et al., "An evaluation of the 1954 poliomyelitis vaccine trials – summary report," American Journal of Public Health vol. 45 (1955), 1-63.o. Lásd még P.Meier cikkét, "The biggest public health experiment ever: the 1954 field trial of the Salk poliomyelitis vaccine", in J.M.Tanur et al., Statistics: A Guide to the Unknown, 3rd. ed. (Wadsworth, 1989). Olvasmányosabb összefoglalást találnak Jane S. Smith, Patenting the Sun (Anchor, 1990) c. könyvében.

3Újabb keletű példa: sok halálesetet okoztak szív-aritmia elleni gyógyszerek. Thomas J. Moore, Deadly Medicine (Simon & Schuster, 1995.)