HUNGARIA, EGER
COMMISSIO REDACTORIUM
Sándor Bácsó (Debrecen), Sonja Gorjanc (Zagreb), Tibor Gyimóthy (Szeged), Miklós Hoffmann (Eger), József Holovács (Eger), László Kozma (Budapest), Kálmán Liptai (Eger), Florian Luca (Mexico), Giuseppe Mastroianni (Potenza), Ferenc Mátyás (Eger), Ákos Pintér (Debrecen), Miklós Rontó (Miskolc, Eger),
János Sztrik (Debrecen, Eger), Garry Walsh (Ottawa)
S
TOMUS 32. (2005)
ANNALES
MATHEMATICAE ET INFORMATICAE
ANNALES MATHEMATICAE ET INFORMATICAE 32. (2005)ANNALES MATHEMATICAE ET INFORMATICAE 32. (2005)
Contents
Cruz-Barroso, R., Daruis, L., González-Vera, P. and Njåstad, O., Quadrature rules for periodic integrands. Bi-orthogonality and para-
orthogonality . . . 5
Fazekas, I., Burkholder’s inequality for multiindex martingales . . . 45
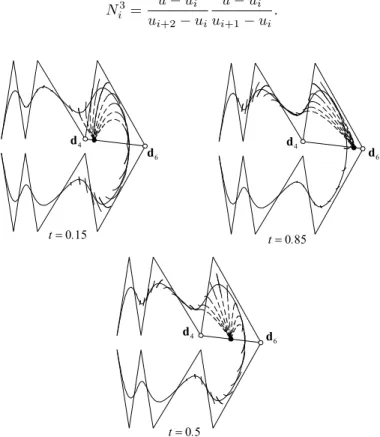
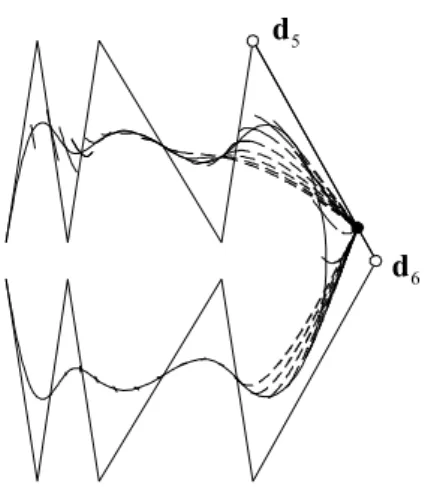
Hoffmann, M. and Juhász I., A limit theorem for one-parameter alter- ation of two knots of B-spline curves . . . 53
Kocsis, I., Solution of a sum form equation in the two dimensional closed domain case . . . 61
Łenski, W., Pointwise very strong approximation as a generalization of Fe- jér’s summation theorem . . . 79
Mathieu, M., Towards a non-selfadjoint version of Kadison’s theorem . . . . 87
Mühlbach, G. W. and Tang, Y., Construction of ECT-B-splines, a sur- vey . . . 95
Nygaard, O., A remark on Rainwater’s theorem . . . 125
Petz, D., Means of positive matrices: Geometry and a conjecture . . . 129
Székelyhidi, L., Discrete spectral synthesis . . . 141
Szilágyi, I., Note on symmetric alteration of knots of B-spline curves . . . . 153
Tómács, T., Some special cases of a general convergence rate theorem in the law of large numbers . . . 159
Weisz, F., Wiener amalgams and summability of Fourier series . . . 167
Methodological papers Burai, P. and Száz, Á., Homogeneity properties of subadditive functions . 189 Geda, G., Solving initial value problem by different numerical methods: Practical investigation . . . 203
Kónya, E., On the fundamental theorem of compact and noncompact sur- faces . . . 211
Krisztin Német, I., Remarks on the concepts of affine transformation and collineation in teaching geometry in teachers’ training college . . . 225
ANNALES
MATHEMATICAE ET INFORMATICAE
VOLUME 32. (2005)
EDITORIAL BOARD
Sándor Bácsó (Debrecen), Sonja Gorjanc (Zagreb), Tibor Gyimóthy (Szeged), Miklós Hoffmann (Eger), József Holovács (Eger), László Kozma (Budapest), Kálmán Liptai (Eger), Florian Luca (Mexico), Giuseppe Mastroianni (Potenza), Ferenc Mátyás (Eger), Ákos Pintér (Debrecen), Miklós Rontó (Miskolc, Eger),
János Sztrik (Debrecen, Eger), Garry Walsh (Ottawa)
INSTITUTE OF MATHEMATICS AND COMPUTER SCIENCE ESZTERHÁZY KÁROLY COLLEGE
HUNGARY, EGER
ISSN 1787-5021
A kiadásért felelős:
az Eszterházy Károly Főiskola rektora Megjelent az EKF Líceum Kiadó gondozásában
Kiadóvezető: Kis-Tóth Lajos Felelős szerkesztő: Tömösközi Péter
Műszaki szerkesztő: Tómács Tibor Megjelent: 2005. december Példányszám: 50
Készítette: Diamond Digitális Nyomda, Eger Ügyvezető: Hangácsi József
Note from the Editor
As you may observed, starting with the present volume our journal changes its name and editors. Formerly known as Acta Academiae Paedagogicae Agri- ensis, Sectio Mathematicae, established in 1974, the journal mainly served as a scientific appearance for the local mathematical community of the Eszterházy Ká- roly College. From this issue, with extended multinational Editorial Board and peer-reviewing process we try to reach a higher international standard of scientific publication. Despite these developments we would like to preserve the traditional values of our journal: consistency and commitment for high quality. The scope of the journal also remains unchanged: original manuscripts from all fields of mathe- matics and computer science are welcome.
Miklós Hoffmann Managing Editor
Annales Mathematicae et Informaticae 32(2005) pp. 5–44.
Quadrature rules for periodic integrands.
Bi-orthogonality and para-orthogonality ∗
Ruymán Cruz-Barroso
a, Leyla Daruis
a, Pablo González-Vera
a, Olav Njåstad
baLa Laguna University ldaruis@ull.es, pglez@ull.es
bNorwegian University of Science and Technology
Abstract
In this paper, the algebraic construction of quadrature formulas for weigh- ted periodic integrals is revised. For this purpose, two classical papers ([10]
and [14]) in the literature are revisited and certain relations and connections are brought to light. In this respect, the concepts of “bi-orthogonality” and
“para-orthogonality” are shown to play a fundamental role.
Key Words: Trigonometric polynomials, Szegő polynomials, quadratures, bi-orthogonality, para-orthogonality.
AMS Classification Number: 41A55, 33C45
1. Introduction
Let the integral In(f) = R
Γf(z)dµ(z) be given with Γ a certain curve in the complex plane and dµ a positive measure on Γ. By an n-point quadrature rule for this integral we mean an expression likeIn(f) =Pn
j=1Ajf(zj)with zj 6=zk
if j 6=k and {zj}nj=1 ⊂ Γ so that the weights or coefficients {Aj}nj=1 and nodes {zj}nj=1 are to be determined by imposing thatIn(f)exactly integrates i.e. In(f) coincides withIµ(f)for as many basis functions as possible in an appropriate func- tion space S where the above integral exists. Two situations have been most widely considered in the literature. Namely, on the one hand, the case when Γcoincides with a subinterval of the real line, that is, Γ = [a, b], −∞6 a < b 6∞ and on the other hand whenΓ is the unit circle, i.e. Γ = T ={z ∈C : |z|= 1}. Ob- serve that the second case is equivalent to dealing with real integrals of the form Rπ
−πf(θ)dµ(θ),f being a 2π-periodic function (here by a slight abuse of notation
∗This work is partially supported by the research project PI-2002-023 of Gobierno de Canarias.
5
6 R. Cruz-Barroso, L. Daruis, P. González-Vera and O. Njåstad we writef(z) =f(θ), dµ(z) =dµ(θ) forz =eiθ). As for the first case, it is well known that the construction of quadrature formulas to approximate integrals like Rb
af(x)dµ(x)represents an interesting research topic which has been exhaustively considered in the last decades and where orthogonal polynomials find one of their most direct and natural applications. Indeed, if {Qk}∞k=0 denotes the sequence of orthonormal polynomials for the measure µ, then In(f) =Pn
j=1Ajf(xj) with {xj}nj=1the zeros ofQn(x)andλj =¡Pn
k=0Q2k(xj)¢−1
forj = 1, . . . , n(Christoffel numbers) satisfiesIn(P) =Rb
aP(x)dµ(x) for any polynomialP of degree 2n−1.
In this case,{In(f) : n= 1,2, . . .}represent the well known sequence of Gaussian or Gauss–Christoffel quadrature formulas (see e.g. [8] for a survey). On the other hand, although quadratures on the unit circle and other related topics such as Szegő polynomials and the trigonometric moment problem have been receiving much re- cent attention because of their applications in rapidly growing fields of pure and applied mathematics (Digital Signal Processing, Operator Theory, Probability The- ory, . . .), there do not exist so many results about quadratures on the unit circle as in the real case. In this respect, the main aim of this paper is to emphasize the role played by certain sequences of orthogonal trigonometric polynomials in- troduced by Szegő [14] in the construction of quadrature rules on the unit circle by carrying out a comparision with the approach given by Jones et. al in [10]. In both approaches, a fundamental tool will be the so-called Szegő polynomials or polyno- mials which are orthogonal on the unit circle in the following sense: given n>1, it is known (see e.g. [13]) that a unique monic polynomial ρn(z)exists such that Rπ
−πρn(eiθ)e−ikθdµ(θ) = 0for k= 0,1, . . . , n−1. Furthermore, if we assume that the support ofµ has infinitely many points, then Rπ
−πρ2n(eiθ)dµ(θ) =k ρn k2µ>0.
Setting ρ0 ≡ 1, then {ρn}∞n=0 is called the orthogonal sequence of monic Szegő polynomials. On the other hand, the sequence {ϕn}∞n=0 with ϕn(z) = kρρn(z)
nkµ rep- resents an orthonormal sequence of Szegő polynomials (observe that such a se- quence is uniquely determined by assuming that the leading coefficient ofϕn(z)for n= 0,1, . . . is positive). Setting D={z ∈ C : |z|<1} (sometimes we will use E={z∈ C : |z|>1}, C=T∪D∪E) a fundamental property concerning the zeros of ρn(z)for n>1 (and apparently rather negative for our purposes) is the following (see e.g. [1]): “For eachn>1, all the zeros ofρn(z)lie inD”. Thus, un- like the Gauss–Christoffel formulas, now the zeros of Szegő polynomials can not be directly used as nodes in our quadratures. Following two initially different paths, throughout the paper we will see how this drawback can be overcome. The paper is organized as follows. In Section 2, some preliminary results concerning trigono- metric polynomials, Laurent polynomials and algebraic polynomials are presented.
Then, in Section 3 the problem of the interpolation by trigonometric polynomials is analyzed whereas in Section 4 the so-called bi-orthogonal systems of trigonometric polynomials are introduced and their most relevant properties studied. The con- struction of quadrature rules exactly integrating trigonometric polynomials with degree as large as possible is considered in Section 5 and a connection with the unit circle presented in Section 6. Finally some illustrative numerical experiments
Quadrature rules for periodic integrands. Bi-orthogonality and para-orthogonality 7 are shown in Section 7.
2. Preliminary results
We will start by fixing some definitions and notations. Thus, for a nonnegative integer n,Πn will denote the space of (in general complex) algebraic polynomials of degreenat most andΠthe space of all polynomials. On the other hand, a real trigonometric polynomial of degreenis a function of the form
Tn(θ) =a0+ Xn
k=1
(akcoskθ+bksinkθ), ak, bk ∈R, |an|+|bn|>0.
Clearly, whena0, ak and bk are in general complex numbers for k= 1, . . . , n, we shall be dealing with trigonometric polynomials with complex coefficients. Thus, when we refer to a trigonometric polynomial we are implicitly meaning with real coefficients. We also denote byTnthe space of trigonometric polynomials of degree nat most, i.e.
Tn=span{1,cosθ,sinθ, . . . ,cosnθ,sinnθ}
and hence, dim(Tn) = 2n+ 1. We occasionally deal with complex trigonomet- ric polynomials, where a0, ak and bk are arbitrary complex numbers. By using the transformation z = eiθ and Euler’s formulas, for any complex trigonometric polynomial one can writeTn(θ) =Ln(eiθ)where
Ln(z) = Xn
k=−n
ckzk. (2.1)
Then
c0=a0, ck =1
2(ak−ibk), k= 1, . . . , n,
and when the trigonometric polynomialTn is real,a0,ak,bk are real andc−k =ck. FunctionsLn(z)as given above are called Laurent polynomials, or more generally, givenpand qintegers such that p6q, a Laurent polynomial is a function of the form
Ln(z) = Xq
j=p
αjzj, αj∈C. (2.2)
We also denote byΛp,q the space of Laurent polynomials (2.2). Observe that Λp,q=span©
zk :p6k6qª .
Hence,dim(Λp,q) =q−p+ 1. Thus,Ln(z)given by (2.1) belongs to Λ−n,n. Now, by recalling that a double sequence{µk}∞k=−∞of complex numbers is said to be “Hermitian” ifµ−k =µk, a Laurent polynomialL∈Λ−n,nis called Hermitian if the sequence of its coefficients is Hermitian. That is, withLn(z)in (2.1) we have ck =ck fork= 0,1, . . . , nand the following trivially holds,
8 R. Cruz-Barroso, L. Daruis, P. González-Vera and O. Njåstad Theorem 2.1. LetTn(θ)be a complex trigonometric polynomial, and setLn(eiθ) = Tn(θ). ThenTn is real if and only ifLn is Hermitian.
Remark 2.2. If we define ΛHn ={L∈Λ−n,n : L Hermitian} then ΛHn is a real vector space of dimension2n+ 1and one can write
Tn =©
T(θ) : T(θ) =L(eiθ)with L∈ΛHnª .
Let us next consider the connection between trigonometric polynomials and certain algebraic polynomials. For this purpose, letP(z)be an algebraic polynomial of degreen, i.e.,
P(z) = Xn
j=0
ajzj, aj∈C, an6= 0.
Then, the reciprocal P∗(z) of P(z) is a polynomial defined by P∗(z) = znP∗(z) where P∗(z) represents the “sub-star” conjugate of P(z), i.e., P∗(z) = P(1/¯z).
Thus,
P∗(z) =znP(1/z) =¯ znP(1/z) =¯ Xn
j=0
an−jzj whereP(z) =Pn
j=0ajzj. Now, a usefull property of the polynomials that we shall work with is the following: fork∈C\{0}, a polynomial P(z)is called “invariant”
or more precisely, “k-invariant” if
P∗(z) =kP(z) ∀z∈C.
Some direct consequences of this definition are:
1. IfP(z)is invariant, thenP(0)6= 0.
2. Letαbe a zero of the invariant polynomialP(z). Then,1/α¯ is also a zero of P(z).
3. LetP(z) be an invariant polynomial of odd degreen. Then, the number of zeros ofP(z)onT (counting multiplicities) is also odd. On the other hand, ifP(z)is an invariant polynomial with even degreen, it has an even number of zeros onT.
4. Let P(z) be invariant and set P(z) = Pn
j=0cjzj = cn
Qn
k=1(z−zk), then
|P(0)|=|c0|=|cn|Qn
k=1|zk| and taking into account thatQn
k=1|zk|= 1 it follows that |c0| =|cn|. Consequently,cn =kc0 with |k|= 1. Setk =eiω, ω ∈R, and define Q(z) =λP(z), λ6= 0. Then, Q∗(z) =λkP(z) = λλkQ(z), that is,Q(z)is λλk-invariant. Set nowλ=Reiγ, then λλk=ei(ω−2γ). Thus, by takingγ∈Rsuch that γ= ω2 +mπ, withm∈Z, then λλk= 1and Q(z) is1-invariant.
Quadrature rules for periodic integrands. Bi-orthogonality and para-orthogonality 9 Remark 2.3. The term “k-invariant” was introduced by Jones et. al. in [10], whereas Szegő in [14] says that a polynomial P(z) is “autoreciprocal” if P∗(z) = P(z)(1-invariant). Hence, we see that “invariant” polynomials are essentially “au- toreciprocal”.
LetP2n(z)be an invariant polynomial of degree2n. Then, there existsλ2n ∈ C\{0} such thatQ2n(z) =λ2nP2n(z)is1-invariant and we can write:
Ln(z) = Q2n(z) zn =
Xn
j=−n
cjzj, c−j =cj, j= 0,1, . . . , n
that is, Ln ∈ ΛHn and by Theorem 2.1, Ln(eiθ) =Tn(θ) withTn ∈ Tn. Thus, we have
e−inθP2n(eiθ) =λ−12nTn(θ).
Conversely, letTn∈ Tn. Then
Tn(θ) =Ln(eiθ), Ln∈ΛHn.
Again, Ln(z) = P2nzn(z), where P2n(z) ∈ Π2n and 1-invariant. Indeed, P2n(z) = znLn(z). Hence,
P2n∗ (z) =z2nP2n(1/z) =¯ z2nz−nLn(1/¯z)
=znPn
j=−ncjz−j=znPn
j=−nc−jz−j =znLn(z) =P2n(z).
Next, we will see how the connection between trigonometric polynomials and invariant algebraic polynomials allows us to recover some classical results about zeros of trigonometric polynomials. Thus, letαandβ be arbitrary constants, then sin¡θ−α
2
¢sin³
θ−β 2
´
represents a trigonometric polynomial of degree one. Further- more, it can be easily proved by induction that the function
T(θ) =C Yn
j=1
sin
µθ−θ2j−1
2
¶ sin
µθ−θ2j
2
¶
, C6= 0 (2.3)
where{θj}2nj=1are given constants, represents a trigonometric polynomial of degree n. We will now show that a converse result also holds, i.e. any trigonometric polynomial can be factorized as (2.3). Indeed, letTn ∈ Tn, thenTn(θ) =Ln(eiθ), Ln∈∆Hn and one can writeLn(z) = P2nzn(z) withP2n(z)an1-invariant polynomial of degree2n. Therefore,P2n(z) =cn
Q2n
k=1(z−zk),cn6= 0(counting multiplicities) withzj 6= 0 and ifzj 6∈T, then1/z¯j is also a root ofP2n(z). Let 2m denote the number of zeros ofP2n(z)onT(06m6n). Then
P2n(z) =cn
Y2m
j=1
(z−zj)
n−mY
k=1
(z−z˜k) µ
z− 1
˜ zk
¶
, cn 6= 0 (2.4)
10 R. Cruz-Barroso, L. Daruis, P. González-Vera and O. Njåstad where zj = eiθj, θj ∈ R for 1 6 j 6 2m, are the zeros of P2m(z) on T and z˜k
and 1/z˜k for 1 6 k 6 n−m are the zeros not on T, so that z˜k = eiωk with ωk ∈C, wich implies that1/˜zk =eiωk. Furthermore, it can be easily checked that eiθ−eiω= 2isin¡θ−ω
2
¢ei(θ+ω2 ). Therefore, P2n(eiθ) = cn
Q2m
j=1
¡eiθ−eiθj¢ Qn−m
k=1
¡eiθ−eiωk¢ ¡
eiθ−eiωk¢
= cn(−1)n22nQ2m
j=1sin³
θ−θj
2
´ ei
hθ−
θj 2
i
×
× Qn−m
k=1 sin¡θ−ω
k
2
¢sin¡θ−ω
k
2
¢ei
h θ+ωk+2ωk
i
. Then, it follows that,
P2n(eiθ) =λneinθ Y2m
j=1
sin
µθ−θj
2
¶n−mY
k=1
sin
µθ−ωk
2
¶ sin
µθ−ωk
2
¶
, λn 6= 0.
Consequently,
Tn(θ) =Ln(eiθ) = P2neinθ(eiθ)
=λn
Q2m
j=1sin³
θ−θj
2
´ Qn−m
k=1 sin¡θ−ω
2k
¢sin¡θ−ω
2k
¢, (2.5) whereλn 6= 0,θj∈Randωk∈Csuch that<(ωk) =ψk+ 2tπ,ψk ∈(−π, π],t∈Z andk= 1, . . . , n−m. Then, we have proved the following
Theorem 2.4. A real trigonometric polynomialTn(θ)of the precise degree nhas exactly 2n real or complex zeros provided that we count them as usual with their multiplicity and we restrict ourselves to the strip −π < <(θ)6 π. Furthermore, the non-real zeros appear in conjugate pairs.
Remark 2.5. The representation (2.3) is of course not unique.
Furthermore, from (2.3) and (2.5) it can be also proved
Theorem 2.6(L.Fejér and F.Riesz). A real trigonometric polynomial T(θ) is nonnegative for all real θ, if and only if, it can be written in the form
T(θ) =|g(z)|2, z=eiθ
whereg(z)is an algebraic polynomial of the same degree as T(θ).
Proof. Assume T(θ) a trigonometric polynomial of degree n such that T(θ) =
P(eiθ)
einθ with P(z) a polynomial of degree 2n. Since T(θ)> 0 for all θ ∈ R, then possible real zeros ofT(θ)must have even multiplicity. Furthermore, if θ=αis a real zero ofT(θ)thenz=eiα is a zero of P(z)onT. Hence, from (2.4),P(z)can be expressed as:
P(z) =λnp2m(z)qn−m(z)q∗n−m(z), λn6= 0
Quadrature rules for periodic integrands. Bi-orthogonality and para-orthogonality 11 wherepm(z)∈Πm for06m6nand qn−m(z)∈Πn−m. SinceT(θ)>0, for any θ∈R,
T(θ) = |T(θ)|=
¯¯
¯P(eeinθiθ)
¯¯
¯=|λn|¯
¯p2m(eiθ)¯
¯¯
¯qn−m(eiθ)¯
¯¯
¯¯qn−m(eiθ)
¯¯
¯
= |λn|¯
¯p2m(eiθ)¯
¯¯
¯qn−m(eiθ)¯
¯2=¯
¯g(eiθ)¯
¯2
whereg(z) =p
|λn|pm(z)qn−m(z)∈Πn.
Conversely, let g(z) be an algebraic polynomial of degree n, then by setting z=eiθ it follows that
|g(z)|2=g(z)g(z) =g(z)g∗(z) = g(z)g∗(z)
zn =P2n(z) zn
whereP2n(z) =g(z)g∗(z)is clearly an1-invariant polynomial of degree2nso that
|g(z)|2 = Ln(z) ∈ ΛHn, and by Theorem 2.1, |g(z)|2 represents a trigonometric polynomial of degreenwhich is clearly nonnegative for anyθ∈R. ¤
3. Interpolation by Trigonometric Polynomials
As it is well known, polynomial interpolation finds in the construction of quadra- ture formulas one of its most immediate applications. On the other hand, when considering quadrature rules based on trigonometric polynomials, similar results on interpolation will be needed. In this respect, some of the already known results will now be proved by means of the close connection between trigonometric poly- nomials and Hermitian Laurent polynomials shown in the preceding section. First we have,
Theorem 3.1. Given(2n+ 1)distinct nodes{θj} ⊂(−π, π], there exists a unique Tn∈ Tn such that
Tn(θj) =yj, j= 1, . . . ,2n+ 1, (3.1) {yj}2n+1j=1 being a given set of real numbers.
Proof. SetT(θ) =a0+Pn
k=1akcoskθ+bksinkθ. We first show that the constants {ak}nk=0∪ {bk}nk=1 are uniquely determined from conditions (3.1). Now, T(θ) = L(eiθ)withL∈Λ−n,n so that (3.1) is equivalent to
L(zj) =yj, zj =eiθk, j= 1, . . . ,2n+ 1. (3.2) NowL(z)∈Λ−n,n implies thatL(z) = P(z)zn ,P(z)∈Π2n so that (3.2) yields
P(zj) =znjyj, j= 1, . . . ,2n+ 1. (3.3) Sincezj 6=zk,P(z)is uniquely determined by (3.3) and henceT(θ)has the desired interpolation properties. It remains to show thatT(θ) has real coefficients. This
12 R. Cruz-Barroso, L. Daruis, P. González-Vera and O. Njåstad will be proved by showing thatP(z)is1-invariant. To see this we will show that alsoP∗(z)satisfies the interpolation conditions (3.3). Indeed,
P∗(zj) =zj2nP(1/z¯j) =zj2nP(zj) =zj2nzjnyj=zjnyj, yj∈R.
Hence, by virtue of the uniqueness of polynomialP(z), it follows thatP∗(z) =P(z)
and the proof is completed. ¤
As for an explicit representation ofTn∈ Tn satisfying (3.1), because of unique- ness, one can write
Tn(θ) =
2n+1X
j=1
lj(θ)yj (3.4)
where lj(θ) = lj,n(θ) ∈ Tn such that lj(θk) = δj,k =
½ 1 if j=k
0 if j6=k . Since lj(θk) = 0fork= 1, . . . ,2n+ 1,k6=j, clearly by (2.5),
lj(θ) =λj 2n+1Y
k=1,k6=j
sin
µθ−θk
2
¶
, λj 6= 0,
λj being a normalization constant such thatlj(θj) = 1. More precisely, setting Wn(θ) =
2n+1Y
k=1
sin
µθ−θk
2
¶
then, it follows that
lj(θ) =λj Wn(θ) sin
³θ−θj
2
´, j= 1, . . . ,2n+ 1.
Thus,
lj(θj) =λj lim
θ→θj
Wn(θ) sin
³θ−θj
2
´ =λj lim
θ→θj
Wn(θ)
θ−θj
2
= 2λjWn0(θj).
Hence, takingλj =2W01
n(θj) one haslj(θj) = 1and we can write lj(θ) = Wn(θ)
2Wn0(θj) sin
³θ−θj
2
´ , j= 1, . . . ,2n+ 1.
Furthermore, when dealing with the construction of certain quadrature formulas exactly integrating trigonometric polynomials of degree as high as possible, the following result will be required:
Quadrature rules for periodic integrands. Bi-orthogonality and para-orthogonality 13 Theorem 3.2. Let θ1. . . θn+1 be (n+ 1) distinct nodes on (−π, π]. Then there exists a unique trigonometric polynomial Hn∈ Tn satisfying
Hn(θj) =Hn(k)(θj) =yj j= 1, . . . , n+ 1 Hn0(θj) =Hn(k)0(θj) =yj0 j= 1, . . . , n+ 1, j6=k
(3.5)
wherek ∈ {1, . . . , n+ 1} is previously fixed and {yj}n+1j=1 ∪ {yj0}n+1j=1,j6=k is a set of (2n+ 1) real numbers.
Proof. SetHn(θ) =Ln(eiθ)∈Λ−n,n. Then (3.5) becomes Hn(θj) =Ln(eiθj) = Ln(zj) =yj with zj =eiθj ∈Tfor all j = 1, . . . , n+ 1and zj 6=zk ifj 6=k. On the other hand, Hn0(θ) =Ln0(eiθ)ieiθ. Hence, Ln0(zj) = −izjHn0(θj) =−izjyj0 for j= 1, . . . , n+ 1andj6=k. SinceLn ∈Λ−n,n, thenLn(z) = P2nzn(z) withP2n(z)∈ Π2n such that P2n(zj) = zjnLn(zj) = zjnyj, yj ∈ R and zj ∈ T. Furthermore, P2n0 (z) =nzn−1Ln(z) +znLn0(z), hence
P2n0(zj) =nzjn−1Ln(zj) +znjLn0(zj) =zjn−1³
nyj−iyj0´
, j= 1, . . . , n+ 1, j6=k.
Thus our Hermite-type trigonometric interpolation problem reduces to finding P2n(z)∈Π2n such that
P2n(zj) =zjnyj j= 1, . . . , n+ 1 P2n0 (zj) =zn−1j
³
nyj−iyj0
´
j= 1, . . . , n+ 1, j6=k
(3.6)
Now, sincezj6=zlforj6=l, it is known that the interpolation problem (3.6) has a unique solutionP2n(z)andTn(θ) =Ln(eiθ) = P2neinθ(eiθ) will be the unique solution to (3.5). As in Theorem 3.1, it remains to prove thatTn(θ)is a real trigonometric polynomial. To do this, we will show thatPn∗(z)is also a solution to (3.6), hence because of uniqueness we haveP2n(z) =P2n∗ (z)and the conclusion follows. Indeed,
P2n∗ (zj) =zj2nP2n(1/zj) =zj2nP2n(zj)
=zj2nzjnyj =zjnyj =P2n(zj), j= 1, . . . , n+ 1.
Furthermore,(P2n∗ )0(z) = 2nz2n−1P2n(1/z) +z2n¡ P2n¢0
(1/z)¡−1
z2
¢, yielding:
(P2n∗ )0(zj) =z2n−2j h
2nzjP2n(zj)−P2n0(zj) i
. (Here we are making use of the fact ¡
P¢0
(z) = (P0)(z)). Therefore, for j = 1, . . . , n+ 1, j6=k:
(P2n∗ )0(zj) = zj2n−2 h
2nzjzjnyj−zj−(n−1)(nyj+iyj0) i
= zjn−1 h
2nyj−nyj−iyj0 i
=zjn−1[nyj−iyj0] =P2n0(zj).
¤
14 R. Cruz-Barroso, L. Daruis, P. González-Vera and O. Njåstad As for an explicit representation of the interpolating trigonometric polynomial Hn(θ)satisfying (3.5), by virtue of uniqueness we can write for anyk∈ {1, . . . , n+ 1},
Hn(θ) =Hn(k)(θ) =t(k)k (θ)yk+
n+1X
j=1,j6=k
h
t(k)j (θ)yj+s(k)j (θ)y0ji
(3.7) wheret(k)j (θ)ands(k)j (θ)are trigonometric polynomials inTn, such that
t(k)j (θr) =δj,r 16j, r6n+ 1
³ t(k)j ´0
(θr) = 0 16j, r6n+ 1, r6=k s(k)j (θr) = 0 16r6n+ 1, j6=k
³ s(k)j
´0
(θr) =δj,r 16j, r6n+ 1, r6=k, j6=k.
(3.8)
Define now Wn(θ) = Qn+1
j=1sin³
θ−θj
2
´
. If we proceed as in the previous case, after some elementary calculations we deduce the following expressions for such trigonometric polynomials for16j6n+ 1, j6=k:
s(k)j (θ) = Wn2(θ) sin
³θj−θk
2
´
2 sin
³θ−θj
2
´
sin¡θ−θ
k
2
¢[Wn0(θj)]2 ∈ Tn, (3.9)
t(k)j (θ) = Wn2(θ)
sin2θ−
θj 2
sin
θ−θk 2
[2Wn0(θj)]2×
× h
sin
³θj−θk
2
´ + cos
³θj−θk
2
´ sin
³θ−θj
2
´i
∈ Tn
(3.10) and
t(k)k (θ) =
"
Wn(θ) 2Wn0(θk) sin¡θ−θ
k
2
¢
#2
∈ Tn. (3.11)
In the rest of the section we shall be concerned with certain interpolation prob- lems using an even number of nodes, say 2n, in subspaces T˜n ofTn of dimension 2n. For instance,T˜n=Tn\span{cosnθ} orT˜n=Tn\span{sinnθ}. In this respect, it should be recalled that a system of continuous functions{f0, . . . , fm}on an in- terval[a, b]represents a Haar system on [a, b]if and only if for any k,16k6m, {f0, . . . , fk} is a Chebyshev system on[a, b]. Clearly,
{1,cosθ,sinθ, . . . ,cosnθ,sinnθ},
can not be a Haar system on[−π, π](check simply that{1,cosθ}is not a Chebyshev system). Hence, we can not initially assume that given2nnodes{θj}2nj=1on(−π, π]
there existsTn∈ Tn\span{cosnθ}or inTn\span{sinnθ}such thatTn(θj) =yj for allj= 1, . . . ,2n. However, we can prove the following
Quadrature rules for periodic integrands. Bi-orthogonality and para-orthogonality 15 Theorem 3.3. Let{θj}2nj=1⊂(−π, π]be2ndistinct nodes, let{yj}2nj=1be arbitrary real numbers, and consider the interpolation problem:
T˜n(θj) =yj, j= 1, . . . ,2n. (3.12) Then the following hold:
1. If P2n
j=1θj 6=kπ for all k∈ Z, then there is a unique solution of (3.12) in Tn\span{cosnθ} and a unique solution of (3.12) inTn\span{sinnθ}.
2. IfP2n
j=1θj=kπfor an odd integerk, then there is a unique solution of (3.12) in Tn\span{cosnθ}.
3. If P2n
j=1θj = kπ for an even integer k, then there is a unique solution of (3.12) in Tn\span{sinnθ}.
Proof. Assume first that we are trying to findT˜n(θ)∈ Tn\span{sinnθ}satisfying (3.12). Thus, we can write:
T˜n(θ) =a0+
n−1X
j=1
(ajcosjθ+bjsinjθ) +ancosnθ=Ln(eiθ)∈Λ−n,n
withLn(z) =Pn
j=−ncjzj, where cj= aj−ibj
2 , c−j=cj, 16j6n−1, c0=a0.
Thus,c−j =cj for all 06j 6n. Setting as usual zj =eiθj for all j = 1, . . . ,2n, (zj6=zk ifj6=k), (3.12) becomes
T˜n(θj) =Ln(eiθj) =Ln(zj) =yj, j= 1, . . . ,2n giving rise to the linear system
n−1X
k=−(n−1)
ckzjk+cn(zjn+zj−n) =yj, j= 1, . . . ,2n. (3.13) Now, the system (3.13) has a unique solution if and only if∆n 6= 0, where
∆n =
¯¯
¯¯
¯¯
¯¯
¯¯
¯¯
¯¯
¯¯
z−(n−1)1 z1−(n−2) · · · 1 · · · z1n−1 ¡
zn1 +z−n1 ¢ z−(n−1)2 z2−(n−2) · · · 1 · · · z2n−1 ¡
zn2 +z−n2 ¢
... ... ... ... ...
z−(n−1)2n z2n−(n−2) · · · 1 · · · z2nn−1 ¡
z2nn +z2n−n¢
¯¯
¯¯
¯¯
¯¯
¯¯
¯¯
¯¯
¯¯ .
16 R. Cruz-Barroso, L. Daruis, P. González-Vera and O. Njåstad By introducing the Vandermonde determinant associated withz1, . . . , z2n, i.e.,
γn=
¯¯
¯¯
¯¯
¯¯
¯
1 z1 · · · z2n−11 1 z2 · · · z2n−12
... ... ... 1 z2n · · · z2n−12n
¯¯
¯¯
¯¯
¯¯
¯
it can be easily checked that
∆n= (z1· · ·z2n)n−1(1−z1· · ·z2n)γn. (3.14) On the other hand, if we consider our interpolation problem in
T˜n(θ) ∈ Tn\span{cosnθ}, the associated determinant ∆˜n of the corresponding system satisfies
∆˜n= (z1· · ·z2n)n−1(1 +z1· · ·z2n)γn. (3.15) Since zj = eiθj, then z1· · ·z2n = eiλn with λn = P2n
j=1θj. If λn 6= kπ for any integer k, then clearly z1· · ·z2n 6= ±1 and from (3.14) and (3.15), both determinants ∆n and ∆˜n are nonzero since γn 6= 0, which means that the in- terpolation problem (3.12) has a unique solution both in Tn\span{sinnθ} and Tn\span{cosnθ}. Next, assume that λn = kπ for some integer k. Thus, if k is even, then eiλn = 1 and (3.15) is different from zero, whereas if k is odd, then eiλn = −1 and (3.14) does not vanish. Thus, for instance, if ∆n 6= 0, we have found a uniqueLn ∈Λ−n,n, Ln(z) =Pn
j=−ncjzj such thatc−n =cn and satisfy- ingLn(zj) =yj forj = 1, . . . ,2n. Therefore, T˜n(θ) =Ln(eiθ)∈ Tn\span{sinnθ}
andT˜n(θj) =yj for j= 1, . . . ,2n. To check that T˜n(θ)is actually a real trigono-
metric polynomial we proceed as in Theorem 3.1. ¤
Next, a Lagrange-type representation for the trigonometric polynomial T˜n(θ) satisfying the conditions of Theorem 3.3 will be given. Indeed, set
ηn= 1 2
X2n
j=1
θj= 1 2λn
and assume that ηn 6= kπ for any integer k so that ∆n 6= 0. Thus, T˜n(θ) ∈ Tn\span{sinnθ}and by virtue of uniqueness, one hasT˜n(θ) =P2n
j=1t˜j(θ)yj where
˜tj ∈ Tn\span{sinnθ}and ˜tj(θk) =δj,k for16j, k62n. Fix j ∈ {1, . . . ,2n} and define αj = P2n
k=1,k6=jθj. Now, we can write s˜j(θ) = ˜lje(einθiθ) where ˜lj(z) ∈ Π2n
such that ˜lj(zk) = znjδj,k where, as usual, zk = eiθk for k = 1, . . . ,2n. Since
˜tj ∈ Tn\span{sinnθ}, the leading coefficient of˜lj(z)must coincide with˜lj(0), and one has ˜lj(z) = cj(z−wj)Q2n
k=1,k6=j(z−zj) = cjz2n+· · ·+ ˜lj(0). But ˜lj(0) = cjwj
Q2n
j=1,j6=kzj, hence
wj = 1
Q2n
j=1,j6=kzj
= Y2n
j=1
zj =e−P2nj=1,j6=kθj =e−iαj.
Quadrature rules for periodic integrands. Bi-orthogonality and para-orthogonality 17 Therefore, by (2.5) it follows that
˜
sj(θ) = ˜cjsin
µθ+αj
2
¶ Y2n
j=1,j6=k
sin
µθ−θj
2
¶
where˜cj is to be determined such that˜sj(θj) = 1. Setting Wn(θ) =
Y2n
j=1
sin
µθ−θj
2
¶
∈ Tn, we have
˜
sj(θ) = ˜cjsin
µθ+αj
2
¶ Wn(θ) sin³
θ−θj 2
´.
Now,
1 = lim
θ→θj
˜ cjsin
µθ+αj
2
¶ Wn(θ) sin
³θ−θj
2
´ = 2˜cjsin
µθj+αj
2
¶
Wn0(θj).
Observe that 12(θj +αj) = 12P2n
j=1θj = ηn 6= kπ for any integer k, so that sin
³θj+αj
2
´
= sinηn6= 0 and hence
˜
sj(θ) = 1
2Wn0(θj) sinηn sin
µθ+αj
2
¶ Wn(θ) sin
³θ−θj
2
´, j= 1, . . . ,2n. (3.16)
When dealing with the interpolantT˜n(θ)∈ Tn\span{cosnθ}it can be easily verified that the fundamental Lagrange-type trigonometric polynomials˜sj(θ)are now given by
˜
sj(θ) = 1
2Wn0(θj) cosηn cos
µθ+αj
2
¶ Wn(θ) sin
³θ−θj
2
´, j= 1, . . . ,2n. (3.17)
withαj andηn as previously given.
4. Bi-orthogonal systems
Let ω(θ) be a weight function on (−π, π], i.e., ω(θ) > 0 on (−π, π] and 0 <
Rπ
−πω(θ)dθ < ∞. The main aim of this section is briefly collecting some results by Szegő (see [14]) concerning properties of an orthogonal basis for the spaceT of real trigonometric polynomials with respect to the inner product onT induced by ω(θ), namely,
hf, giω= Z π
−π
f(θ)g(θ)ω(θ)dθ, ∀f, g∈ T (4.1)