3. FÉLÉVI HÁZI FELADAT
EGYSZERŰEN ALÁTÁMASZTOTT, HIDROSZTATI- KUS TERHELÉSŰ LEMEZ ANALITIKUS ÉS
VÉGESELEM MEGOLDÁSA
Szerző: Dr. Szekrényes András
megoldása
13.
EGYSZER Ű EN ALÁTÁMASZTOTT, HIDROSZTATIKUS TER- HELÉS Ű LEMEZ ANALITIKUS ÉS VÉGESELEM MEGOLDÁSA
Számítsuk ki a 13.1 ábrán látható, az x tengely mentén lineárisan változó megoszló erővel terhelt lemez deformációs felületét, az élnyomatékokat és az ébredő feszültségek eloszlá- sát:
a. analitikus módszerrel a vékony lemezek alapegyenletei segítségével, b. végeselem-módszerrel az ANSYS 12 szoftver felhasználásával,
majd végül hasonlítsuk össze a kétféle számítás eredményét! A lemez anyaga lineárisan rugalmas, homogén és izotrop.
13.1 ábra. Egyszerűen alátámasztott lemez hidrosztatikus terheléssel.
Adatok:
E = 200 GPa, ν = 0,3, a = 500 mm, b = 350 mm, t = 2 mm, p0 = 10 kN/m2. 13.1 Analitikus megoldás
A 12. fejezetben levezettük a következő lemezegyenletet, ami egy parciális differenciál- egyenlet w(x,y)-ra [1] (ld. (12.31)):
1 1 4 4 2 2 4 4
4 ( , )
2 I E
y x p y
w y
x w x
w =
∂ +∂
∂ + ∂
∂
∂ , (13.1)
ahol I1 = t3/12, E1 = (E/(1-ν2), p(x,y) pedig a lemez felületére működő megoszló erő függ- vénye. Egyszerű alátámasztás esetén a lemez peremein az elmozdulás és a hajlító élnyomaték zérus, azaz a peremfeltételek:
0 ) , 0 ( y =
w ,w(a,y)=0,w(x,0)=0,w(x,b)=0, (13.2) 0
) , 0 ( y =
Mx ,Mx(a,y)=0,My(x,0)=0,My(x,b)=0
(13.7) alapján (ld. 12. fejezet) használjuk fel a hajlító élnyomatékok és az elmozdulásfüggvény kapcsolatát:
)
( , ,
1
1 xx yy
x I E w w
M =− +ν ⋅ ,My =−I1E1(w,yy +ν ⋅w,xx), (13.3) xy
xy I E w
M =− 1 1(1−ν) , ,
azaz az élnyomatékokra vonatkozó peremfeltételek is az elmozdulásfüggvényre vonatkoz- nak. A peremfeltételek teljesíthetők, ha mind az x, mind az y koordináta függvényében szinuszos függvénysorral írjuk fel a megoldást. A megoldásfüggvény [1,2]:
∑∑
∞=
∞
=
⋅
=
1 1
) sin(
) sin(
) , (
n m
mn x y
W y
x
w α β , (13.4)
ahol Wmn, α és β a megoldás együtthatói, és:
a mπ α = ,
b nπ
β = . (13.5)
A terhelést leíró függvényt hasonló sor formájában állítjuk elő:
∑∑
∞=
∞
=
⋅
=
1 1
) sin(
) sin(
) , (
n m
mn x y
Q y
x
p α β . (13.6)
ahol Qmn a terhelés közelítő függvényének együtthatója. A megoldáshoz felhasználjuk a következőt [1,2]:
=
= ≠
∫
bsin(nby)⋅sin(lby) b0/,2, haha nn ll0
π
π . (13.7)
Ez alapján szorozzuk meg p(x,y)-t sin(lπy/b)-vel és integráljuk y szerint 0-tól b-ig:
) 2 sin(
) sin(
) , (
0 1 a
x Q m
dy b b
y y l
x p
m ml
b π
∑
π∫
∞=
⋅
=
⋅ (13.8)
Most mindkét oldalt szorozzuk meg sin(kπx/a)-val és integráljuk x szerint 0-tól a-ig:
kl a b
abQ a dydx
x k b
y y l
x
p( , ) sin( ) sin( ) 4
0 0
=
⋅
∫ ∫
⋅ π π , (13.9)és mivel az indexek kicserélhetők, így:
∫∫
⋅ ⋅=
a b
mn dydx
b y n a
x y m
x ab p
Q
0 0
) sin(
) sin(
) ,
4 ( π π
. (13.10) Ezek után számítsuk ki a megoldásfüggvény deriváltjait:
∑∑
∞=
∞
=
⋅
−
∂ =
∂
1 1
2 2
2
) sin(
) sin(
n m
mn x y
x W
w α α β , (13.11)
∑∑
∞=
∞
=
⋅
−
∂ =
∂
1 1
2 2
2
) sin(
) sin(
n m
mn x y
y W
w β α β ,
∑∑
∞=
∞
=
⋅
∂ =
∂
∂
1 1
2
) cos(
) cos(
n m
mn x y
y W x
w αβ α β ,
∑∑
∞=
∞
=
⋅
∂ =
∂
1 1
4 4
4
) sin(
) sin(
n m
mn x y
x W
w α α β ,
∑∑
∞=
∞
=
⋅
∂ =
∂
1 1
4 4
4
) sin(
) sin(
n m
mn x y
y W
w β α β ,
megoldása
(13.12)
amely egyenletnek helytől függetlenül teljesülnie kell, azaz a nem triviális megoldás:
1 1 2 2
2 )
( I E
Wmn α +β = Qmn , (13.13)
és:
2 2 2
4 1 1 2 2 2 1
1 ( ) I E ((m/a) (n/b) )
Q E
I
Wmn Qmn mn
= +
= +
π β
α . (13.14)
Ezt visszatéve a megoldásfüggvénybe a következőt kapjuk:
∑∑
∞=
∞
=
+ ⋅
=
1 1
2 2 2 1 1
) sin(
) ) sin(
) ( , (
n m
mn x y
E I y Q
x
w α β
β
α . (13.15)
A megoldásfüggvény tehát a terhelés függvényének együtthatója alapján számolható. Az együtthatók (13.7) alapján viszonylag egyszerűen előállíthatók a hidrosztatikus terhelés esetére, mivel p(x,y) = p0⋅x/a [1,2]:
) 8 cos(
) sin(
) 4 sin(
2 0 0 0
0 π
π π
π m
mn dydx p
a x m b
y n a p x Q ab
a b
mn =
∫ ∫
⋅ ⋅ =− , m, n = 1, 3, 5..∞.(13.16) Az együtthatókat a 13.1 táblázatban foglaltuk össze.
m n Qmn
1 1 8 20
π p
1 3 02
3 8 π
p
3 1 02
3 8 π
p
3 3 20
9 8 π
p
3 5 02
15 8
π p
5 3 02
15 8
π p
5 5 02
25 8
π p
13.1 táblázat. Egyszerűen alátámasztott lemez terhelési függvényének együtthatói.
Számítsuk ki a megoldásfüggvény Wmn együtthatóit is. Ezeket a 13.2 táblázatban találjuk meg.
m n Wmn
1 1 6 2 2 2
1 1
0
) ) / 1 ( ) / 1 ((
8
b a
E I
p π +
1 3 6 2 2 2
1 1
0
) ) / 3 ( ) / 1 ((
3
8
b a
E I
p π +
3 1 6 2 2 2
1 1
0
) ) / 1 ( ) / 3 ((
3
8
b a
E I
p π +
3 3 6 2 2 2
1 1
0
) ) / 3 ( ) / 3 ((
9
8
b a
E I
p π +
3 5 6 2 2 2
1 1
0
) ) / 5 ( ) / 3 ((
15
8
b a
E I
p π +
5 3 6 2 2 2
1 1
0
) ) / 3 ( ) / 5 ((
15
8
b a
E I
p π +
5 5 6 2 2 2
1 1
0
) ) / 5 ( ) / 5 ((
25
8
b a
E I
p π +
13.2 táblázat. Egyszerűen alátámasztott lemez megoldásfüggvényének együtthatói.
Látható, hogy összesen hét tagig számoltuk ki az együtthatókat, amivel a deformációs felü- let függvénye:
5 ).
sin(
5 ) sin(
3 ) sin(
5 ) sin(
5 ) sin(
3 ) sin(
3 ) sin(
3 ) sin(
) sin(
3 ) sin(
3 ) sin(
) sin(
) sin(
) sin(
) sin(
) sin(
) , (
55 53
35 33
31
13 11
1 1
b y a
W x b
y a
W x
b y a
W x b
y a
W x b
y a
W x
b y a
W x b
y a
W x y x
W y
x w
n m
mn
π π
π π
π π
π π
π π
π π
π β π
α
⋅ +
⋅ +
+
⋅ +
⋅ +
⋅ +
+
⋅ +
⋅
=
⋅
=
∑∑
∞=
∞
=
(13.17)
A lemez középső pontjában a z irányú elmozdulást az együttható számának növelésével kiszámítottuk. Az első esetben csak W11-et, a második esetben W11-et és W13-at vettük fi- gyelembe és így tovább. Az eredményeket a 13.3 táblázatban foglaltuk össze, ahol látható, hogy az elmozdulás gyorsan konvergál egy adott értékhez.
Wmn együtthatók
száma [db]
1 2 3 4 5 6 7
w(a/2,b/2)
[mm] -3.8388 -3.8072 -3.7102 -3.7154 -3.7148 3.7135 3.7138
13.3 táblázat. Téglalap alakú lemez középső pontjának elmozdulása az együtthatók számának növe- lésével.
megoldása
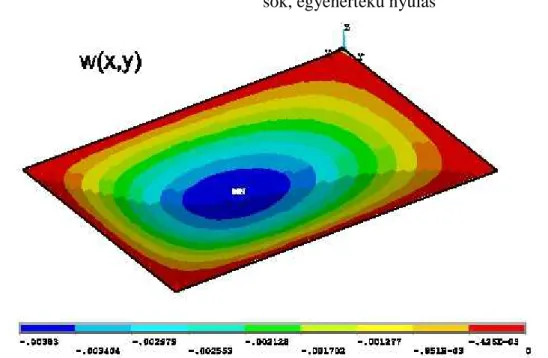
13.2 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemez elmozdulásfüggvénye [m]-ben.
Az elmozdulásfüggvényt a 13.2 ábrán is láthatjuk, ahol mind a hét együtthatót figyelembe vettük. A legnagyobb elmozdulás a lemez középső pontjában jelentkezik. Az élnyomatékok a (13.3) képlet alapján számolhatók:
∑∑
∞=
∞
=
⋅ +
=
⋅ +
−
=
1 1
2 2 1
1 , ,
1
1 ( ) ( )sin( ) sin( )
n m
mn yy
xx
x I E w w I E W x y
M ν α νβ α β ,
(13.18)
∑∑
∞=
∞
=
⋅ +
=
⋅ +
−
=
1 1
2 2 1
1 , ,
1
1 ( ) ( )sin( ) sin( )
n m
mn xx
yy
y I E w w I E W x y
M ν να β α β ,
∑∑
∞=
∞
=
⋅
−
=
−
−
=
1 1
1 1 , 1
1 (1 ) (1 ) cos( ) cos( )
n m
mn xy
xy I E w I E W x y
M ν ν αβ α β ,
ahol Mx az x, My az y tengely mentén értelmezett hajlító élnyomatékok, Mxy pedig a csava- ró élnyomaték. A nyomatékok függvényeit a 13.3-13.5 ábrák mutatják.
13.3 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemezben ébredő Mx hajlító élnyomaték [Nm/m]-ben.
13.4 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemezben ébredő My hajlító élnyomaték [Nm/m]-ben.
13.5 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemezben ébredő Mxy csavaró élnyomaték [Nm/m]-ben.
A nyíróerőket a 13. fejezet (13.19) és (13.20) egyensúlyi egyenletei alapján tudjuk kiszá- molni:
x x
yy xx x xy
x I E w w I E w
y M x
Q M =− 1 1( , + , ), =− 1 1(∆ ),
∂
−∂
∂
= ∂ , (13.19)
y y
yy xx y
yx
y I E w w I E w
y M x
Q M =− 1 1( , + , ), =− 1 1(∆ ),
∂ +∂
∂
= ∂ .
A nyíróerők függvényeit a 13.6 és 13.7 ábrák mutatják.
megoldása
13.6 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemezben ébredő Qy nyíróerő [N/m]- ben.
13.7 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemezben ébredő Qy nyíróerő [N/m]- ben.
A feszültségek az élnyomatékok alapján számolhatók a következő képletekkel [1,2]:
I z Mx
x 1
σ = , z
I My
y 1
σ = , z
I Mxy
xy 1
τ = , (13.20)
ahol I1 = t3/12 a lemez másodrendű nyomatéka. Mivel a feszültségek egy adott z koordiná- tánál az élnyomatékokkal arányosak, ezért azok eloszlásait nem mutatjuk meg. A normál- feszültségek a lemez z = -t/2 koordinátájú középpontjában:
MPa 10 , 2 44 ) 2 / , 2 / (
1
−
=
= t
I b a Mx
σx , (13.21)
MPa 36 , 2 69 ) 2 / , 2 / (
1
−
=
= t
I b a My
σy .
A csúsztatófeszültség legnagyobb értéke az x = a és y = b koordinátájú pontban lép fel, ahol:
MPa 38 , 2 53 ) , (
1
=
= t
I b a Mxy
τy . (13.22)
13.2 Végeselem megoldás
Oldjuk meg a 13.1 ábrán látható lemez feladatot végeselem-módszerrel is! Készítsük el a 13.1 ábrán vázolt lemez végeselem modelljét majd, számítsuk ki a csomóponti elmozdulá- sokat és a feszültségeket! Ábrázoljuk az élnyomatékok, a normál- és csúsztató feszültségek eloszlását a lemez felülete mentén!
A végeselem megoldást ANSYS 12 szoftverrel mutatjuk be. Az egyes parancsok a bal ol- dali, illetve a felső, vízszintes menüből érhetők el. A távolságokat [m]-ben az erőt pedig [N]-ban adjuk meg.
Feladat címének kiírása a képernyőre
File menü / Change Title / Title: “Egyszeruen alatamasztott lemez hidrosztatikus terhelessel”
- képernyő frissítése az egér görgőjével Analízis típusának megadása
PREFERENCES – STRUCTURAL
Elemtípus kiválasztása – 4 csomópontos héjelem (SHELL63)
PREPROCESSOR / ELEMENT TYPES / ADD/EDIT/DELETE / ADD / SOLID / ELASTIC 4NODE 63 / OK /
PREPROCESSOR / REAL CONSTANTS / ADD/EDIT/DELETE / ADD / OK / Shell thickness at node I TH(I) = 0.002 / OK - a vastagság megadása
Anyagjellemzők megadása
PREPROCESSOR / MATERIAL PROPS / MATERIAL MODELS / STRUCTURAL / LINEAR / ELASTIC / ISOTROPIC / EX = 200e9, PRXY = 0.3 / OK Kilépés: Material menü / Exit
A geometria elkészítése
PREPROCESSOR / MODELING / CREATE / AREAS / RECTANGLES / BY 2 CORNERS / WPX = 0, WPY = 0, WIDTH = 0.5, HEIGHT = 0.35
- a koordináták megadása a megnyíló ablakban
A lemez felületét a 13.8 ábra mutatja. A baloldali ikonok közül kattintsunk a 9., „Fit View”
nevű nagyítóra, ezzel mindig az adott objektumhoz méretezzük a képernyőt. Az 1.,
„Isometric View” nevű ikonra kattintva tudjuk 3D-s nézetben megjeleníteni a modellt.
megoldása
13.8 ábra. Egyszerűen alátámasztott lemez kiinduló felülete.
Hálózás
Elemszám beállítása a peremvonalakon
PREPROCESSOR / MESHING / SIZE CNTRLS / MANUALSIZE / LINES / PICKED LINES / PICK / NO. OF ELEMENT DIVISIONS = a megfelelő szám be- írása, a parancs ismétlése
- az x tengellyel párhuzamos peremeken 50 elem - az y tengellyel párhuzamos peremeken 35 elem
PREPROCESSOR / MESHING / MESH / AREAS / MAPPED / 3 OR 4 SIDED / PICK ALL
Plot menü / Multi-Plots - elemek, csomópontok megjelenítése A lemez végeselem hálóját a 13.9 ábra mutatja.
13.9 ábra. Egyszerűen alátámasztott lemez végeselem hálója.
Kinematikai kényszerek
PREPROCESSOR / LOADS / DEFINE LOADS / APPLY / STUCTURAL / DISPLACEMENT / ON LINES
- a négy peremvonal kijelölése / OK / UZ / APPLY
- az x = 0 peremvonal kijelölése / OK / UX / APPLY - az y = 0 peremvonal kijelölése / OK / UY / OK
A kényszereket a megfelelő irányba mutató nyilak szemléltetik, ahogy ezt a 13.10 ábrán láthatjuk.
13.10 ábra. Egyszerűen alátámasztott lemez kinematikai peremfeltételei.
Terhelés megadása, lineárisan változó megoszló erő
A megoszló erő függvényének meredeksége = p0/a = 10000/0,5 = 20000 N/m3
PREPROCESSOR / LOADS / DEFINE LOADS / SETTINGS / FOR SURFACE LD / GRADIENT / SLOPE = - 20000 – a meredekség értéke
SLDIR = X – a lineáris változás iránya SLZER = 0 – a lineáris függvény zérushelye
PREPROCESSOR / LOADS / DEFINE LOADS / APPLY / STUCTURAL / PRESSURE / ON AREAS / VALUE Load PRES Value = 0 (magyarázat: a meredekséget és a
zérushelyet már megadtuk)
A megoszló erő nyilainak megjelenítése
PlotCtrls menü / Symbols / Surface Load Symbols: „Pressures”
Show pres and convect as: „Arrows”
Megoldás
SOLUTION / SOLVE / CURRENT LS
„SOLUTION IS DONE!”
Eredmények kirajzolása, listázása
GENERAL POSTPROC / PLOT RESULTS / DEFORMED SHAPE / Def + undef edge
megoldása
NODAL SOLUTION: csomóponti megoldások
DOF SOLUTION: UX, UY, USUM elmozdulások megjelenítése színskálával STRESS: normál- és csúsztató feszültségek, főfeszültsé-
gek, egyenértékű feszültségek
ELASTIC STRAIN: fajlagos nyúlások és szögváltozások, főnyúlá- sok, egyenértékű nyúlás
13.11 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemez z irányú elmozdulása [m]- ben.
A lemez pontjainak z irányú elmozdulását mutatja a 13.11 ábra, amelyen látható, hogy a legnagyobb elmozdulás a lemez középső pontjában lép fel, értéke: 3,83 mm.
GENERAL POSTPROC / PLOT RESULTS / CONTOUR PLOT / ELEMENT SOLU / ELEMENT SOLUTION: elemre átlagolt megoldások
STRESS: normál- és csúsztató feszültségek, főfeszültsé- gek, egyenértékű feszültségek,
ELASTIC STRAIN: fajlagos nyúlások és szögváltozások, főnyúlá- sok, egyenértékű nyúlás
Élnyomatékok megjelenítése a lemez felülete mentén
Az élnyomatékok megjelenítéséhez ún. elemtáblákat kell definiálni
GENERAL POSTPROC / ELEMENT TABLE / DEFINE TABLE / ADD Lab – User label for item: MX
Item, Comp Result data item: By sequence number / SMISC, 4 / APPLY Lab – User label for item: MY
Item, Comp Result data item: By sequence number / SMISC, 5 / APPLY Lab – User label for item: MXY
Item, Comp Result data item: By sequence number / SMISC, 6 / OK CLOSE
Az elemtáblák tartalmának megjelenítése
GENERAL POSTPROC / ELEMENT TABLE / PLOT ELEM TABLE / Itlab Item to be plotted MX, v. MY, v. MXY Avglab Average at common nodes? Yes - average
Az élnyomatékok eloszlását a 13.12-13.14 ábrák mutatják.
13.12 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemezben ébredő Mx hajlító élnyomaték eloszlása [Nm/m]-ben.
megoldása
13.14 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemezben ébredő Mxy csavaró élnyomaték eloszlása [Nm/m]-ben.
A csomópontokban átlagolt feszültségek alapján számolt feszültségeloszlásokat mutatják a 13.15-13.17 ábrák.
13.15 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemez z = t/2 koordinátájú felületén ébredőσx normálfeszültség eloszlása [Pa]-ban.
13.16 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemez z = t/2 koordinátájú felületén ébredőσy normálfeszültség eloszlása [Pa]-ban.
13.17 ábra. Egyszerűen alátámasztott, hidrosztatikus terhelésű lemez z = t/2 koordinátájú felületén ébredőτxy csúsztatófeszültség eloszlása [Pa]-ban.
A lemez deformációja és az x-irányú feszültség eloszlás kialakulása a mellékelt animáció- kon (pt_anim_13-01.avi, pt_anim_13-02.avi) látható.
megoldása
/ Reaction solution – reakciók listázása
/ Element Table Data – az elemtáblák adatainak listázása Eredmények leolvasása egérrel
GENERAL POSTPROC / QUERY RESULTS / SUBGRID SOLU – komponens kiválasz- tása
Külön ablakban
GENERAL POSTPROC / RESULTS VIEWER – komponens kiválasztása 13.3 Az analitikus és végeselem megoldások összehasonlítása
A kétféle számítás eredményeit a 13.4 táblázatban foglaltuk össze. Az elmozdulást, a hajlí- tó élnyomatékokat és a normálfeszültségeket a lemez középső pontjában, a csavaró élnyomatékot és a csúsztató feszültséget a lemez sarkánál számítottuk ki. A táblázat alap- ján látható, hogy az analitikus és végeselem megoldások nagyon jól egyeznek. Minden esetben a végeselem megoldás ad nagyobb értéket, kivéve a csavaró élnyomaték és a csúsztató feszültség esetén.
Analitikus megoldás
Végeselem megol- dás (SHELL63)
Eltérés [%]
Elmozdulás
w(a/2,b/2) [mm] -3,714 -3,83 -3,03
Élnyomaték
Mx(a/2,b/2) [Nm/m] -29,40 -30,61 -3,95
Élnyomaték
My(a/2,b/2) [Nm/m] -46,24 -47,15 -1,93
Élnyomaték
[Nm/m]Mxy(a,b) 35,59 32,95 8,01
Feszültség
σx(a/2,b/2,t/2) [MPa] -44,10 -46,07 -4,28
Feszültség
σy(a/2,b/2,t/2) [MPa] -69,37 -70,93 -2,20
Feszültség
τxy(a,b,t/2) [MPa] 53,38 49,78 7,23
13.4 táblázat. Az analitikus és végeselem megoldások eredményeinek összehasonlítása.
13.4 Bibliográfia
[1] S. Timoshenko, S. Woinowsky-Krieger. Lemezek és héjak elmélete. Műszaki Könyvkiadó, 1966, Budapest.
[2] J.N. Reddy, Mechanics of laminated composite plates and shells – Theory and applications. CRC Press, 2004, Boca Raton, London, New York, Washington D.C.
[3] ANSYS 12 Documentation. http://www.ansys.com/services/ss-documentation.asp.