MÓDOSÍTOTT GAUSS-FÜGGVÉNYEK ALKALMAZÁSA KROMATOGRÁFIÁS ELÚCIÓS GÖRBÉK LEÍRÁSÁRA
Osváthné Pápai Zsuzsa
Értekezés doktori (PhD) fokozat elnyerése érdekében a Veszprémi Egyetem Anyagtudományok és technológiák
Doktori Iskolájához tartozóan.
Témavezető: Dr. Pap Tamás
VESZPRÉMI EGYETEM ANALITIKAI KÉMIA TANSZÉK
VESZPRÉM 2002
Értekezés doktori (PhD) fokozat elnyerése érdekében a Veszprémi Egyetem Anyagtudományok és technológiák
Doktori Iskolájához tartozóan.
Írta:
Osváthné Pápai Zsuzsa Témavezető: Dr. Pap Tamás
Elfogadásra javaslom (igen/nem)
(aláírás) A jelölt a doktori szigorlaton ... %-ot ért el, ...
Veszprém, ... ………..
a Szigorlati Bizottság Elnöke Az értekezést bírálóként elfogadásra javaslom:
Bíráló neve: ... igen/nem
...
(aláírás) Bíráló neve: ... igen/nem
...
(aláírás) Bíráló neve: ... igen/nem
...
(aláírás) A jelölt az értekezés nyilvános vitáján ...%-ot ért el.
Veszprém, ………
a Bíráló Bizottság elnöke A fentiek alapján a doktori (PhD) oklevél minősítése ...
……….
az EDT elnöke
(KIVONAT)
A dolgozat három új empirikus függvényt, valamint ezek kombinációit mutatja be, melyek a Gauss-függvény módosításán alapulnak. Az egyes egyedi függvények a kromatográfiás csúcsok jellemzőit paraméterként tartalmazzák, melyekből közvetlenül statisztikai momentumok határozhatók meg. A függvények alkalmazhatóságát a különböző kromatográfiás elúciók során nyert digitális pontok illesztésére számos példán keresztül bizonyítja a szerző.
A disszertáció egy kidolgozott, új aszimmetria meghatározási módszert is tartalmaz, melynek során az aszimmetria együttható a kromatográfiás csúcsalakot teljes egészében jellemzi, szemben az eddig alkalmazott módszerekkel, amelyeknél a csúcs egy meghatározott helyén leolvasott (mért) érték jelenti az aszimmetriát.
A vizsgálati eredmények és a kidolgozott módszerek a kromatográfiás elválasztások kiértékelése során közvetlenül felhasználhatók.
(ABSTRACT)
Curve fitting seems to be one of the best methods for the evaluation of chromatographic signals. In this case three new empirical modified Gaussian functions and their combinations are proposed for describing different shapes of chromatographic peaks. The fitted curves are suitable for quick evaluation of chromatographic information, noise filtering and correction of baseline drift. The generated chromatographic curves and the application of the functions for describing real signals are demonstrated in this study.
A new method is demonstrated for the determination peak shape asymmetry, which characterizes the peak completely.
The results obtained and the methods developed can be directly utilised in the evaluation of chromatographic separations.
(AUSZUG)
Die Arbeit stellt drei neue, empirische Funktionen sowie deren Kombinationen vor, die sich auf die Modifizierung der Gauss-Funktion gründen. Die Einzelfunktionen enthalten die Charakteristika der chromatographischen Peaks als Parameter, aus denen statistische Momente unmittelbar ermittelt werden können. Die Anwendbarkeit der Funktionen auf die Anpassung digitaler Punkte, die durch verschiedene chromatographische Elutionen entstanden sind, wird anhand zahlreicher Beispiele nachgewiesen.
Die Dissertation enthält eine neu erarbeitete Methode zur Bestimmung von Asymmetrie, in der die chromatographische Peakform durch den Asymmetrie-Faktor vollständig charakterisiert wird. Insofern unterscheidet sich die Methode von den bisher angewandten, in denen die an einer bestimmten Stelle des Peaks gemessene Asymmetrie für das ganze charakteristisch ist.
Die Untersuchungsergebnisse und die erarbeiteten Methoden können bei der Answertung chromatographischer Abscheidungen unmittelbar angewandt werden.
Köszönetet mondok témavezetőmnek, Pap Tamásnak az évek során nyújtott szakmai útmutatásáért és emberi támogatásáért, mely lehetővé tette, hogy dolgozatom elkészüljön.
Megköszönöm Felinger Attilának hasznos tanácsait és segítségét a munkám során.
Köszönetet mondok Hajós Péternek az ion-kromatogramatográfiás elemzésekért.
Megköszönöm Krivácsy Zoltánnak a kapilláris elektroforézis kísérletek elvégzését.
Szeretnék köszönetet mondani Mink Jánosnak, Kristóf Jánosnak, Horváth Erzsébetnek, Hajba Lászlónak és mindazon munkatársaknak, akik segítettek, emberileg támogattak az elmúlt évek során.
Tartalomjegyzék
Bevezetés 10
I. Irodalmi összefoglaló 11
1. Kromatográfiás csúcsok leírása modellekkel 11
1.1. Elméleti modellek 12
1.1.1. Lineáris kromatográfia 12
1.1.2. Statisztikus modellek 15
1.1.3. Exponenciálisan módosított Gauss-modell 18
1.1.4. Nemlineáris kromatográfia 20
1.2. Empirikus modellek 21
1.2.1. Egyedi csúcsok matematikai leírása 22
1.2.2. Átlapoló csúcsok felbontása 26
2. Kromatográfiás csúcsok jellemzése 27
2.1. A kromatográfiás csúcsot jellemző aszimmetria 30
2.1.1. Az aszimmetria okai 31
2.1.2. A csúcsaszimmetria irodalomból vett meghatározásai 32
II. Kísérleti rész 36
1. Kromatográfiában alkalmazható matematikai függvények vizsgálata 36
1.1. Mérési körülmények 36
1.2. Logaritmikusan módosított Gauss-függvény 38
1.2.1. A függvény alakja 38
1.2.2. Alkalmazások a gázkromatográfiában 42
1.2.3. Alkalmazásoka nagyhatékonyságú folyadék-kromatográfiában 47
1.3. Módosított Hermite-polinomos függvény 48
1.3.1.A függvény alakja 48
1.3.2. Alkalmazások a gázkromatográfiában 52
1.4. Egyszerűen módosított Gauss-függvény 58
1.4.1. A függvény alakja 58
1.4.2. Alkalmazások az ion-kromatográfiában 60
1.5. Függvénykombinációk 65
1.5.1. Erősen elhúzódó csúcsok leírása 66
1.5.1.1. Az összetett függvény alakja 66
1.5.1.2. Alkalmazások a gázkromatográfiában 68 1.5.1.3. Alkalmazások a kapilláris elektroforézisben 69
1.5.2. Lassan emelkedő aszimmetrikus csúcsok 74
1.5.2.1. Az összetett függvény alakja 74
1.5.2.2. Alkalmazások a gázkromatográfiában 75
1.6. A vizsgált függvények összehasonlítása 77
2. Kromatográfiás csúcsaszimmetria meghatározásának új módszere 86
2.1. A módszer elve 86
2.2. A módszer kromatográfiás alkalmazása 89
2.3. Aszimmetria vizsgálatok eredménye 94
III. Összefoglalás 96
Irodalomjegyzék 101
Új tudományos eredmények 105
Bevezetés
Az elmúlt években a matematikai módszerek analitikai kémiai alkalmazása a számítástechnika nagyléptékű fejlődése, valamint az analitikai kémiával való egyre szorosabb kapcsolata következtében jelentősen megnőtt.
A kemometria kifejezést Wold svéd kutató már 1971-ben alkalmazta az analitikai kémiában használatos matematikai módszerek megjelölésére. A kemometria fő célja a megfelelő mérési eljárások kiválasztása és az optimális kísérleti körülmények meghatározása, valamint a mérési adatok információ tartalmának maximális kinyerése.
Legfontosabb területei a statisztikai módszerek és alkalmazásuk, illetve az optimalizálás, faktoranalízis, alakfelismerés, modellezés, paraméterbecslés, görbefelbontás, képfeldolgozás, valamint az azonosítást elősegítő spektrumkönyvtárak létrehozása.
A kromatográfia a kemometriás módszerekkel együtt a modern analitikai kémia egyik legdinamikusabban fejlődő ágát képezi. A kromatográfiás jelfeldolgozás szempontjából talán legfontosabb feladatok közé tartozik az analóg-digitál jelátalakítás; a digitális jel szűrése (mely magában foglalhat görbeillesztéses- vagy mozgó ablakos eljárást is); a jel- transzformáció (pl. Fourier-transzformáció), a deriváltak, integráltak kiszámolása; a digitális jelek tárolása, visszakeresése, azonosítása.
Dolgozatomban a kromatográfiás jel- és adatfeldolgozás területén belül új eljárások kidolgozását és létező programok bővítését tűztem ki célul: három új empirikus függvénnyel, illetve ezek kombinációival foglalkoztam, melyek külön-külön is különböző csúcsalakot képesek leírni. Az általam alkalmazott matematikai modellek különböző típusú kromatográfiás eljárások során kapott "valódi" csúcsok digitális pontjainak illesztésére alkalmasak, ezáltal a csúcsok gyors és pontos jellemzését teszik lehetővé.
Kidolgoztam egy új aszimmetria meghatározási módszer is, mely esetben az aszimmetria faktor a kromatográfiás csúcsot teljes egészében jellemzi.
I. Irodalmi összefoglaló
A analitikai kémiában a digitális jelfeldolgozás célja a műszerek jelének digitális formában történő kiértékelése, azoknak az információknak a kinyerése, amelyek közvetlenül összefüggésbe hozhatók az anyag minőségi vagy mennyiségi jellemzőivel. A digitális jelfeldolgozás tartalmazza az analóg jel digitálissá történő alakításának folyamatát, a digitális zajszűrést, az alapvonalkorrekciót, a jelalakelemzést (peak shape analysis), a görbeillesztést, a jelek tárolásának és visszakeresésének műveletét, a különböző jeltranszformációk végrehajtását és mindazon folyamatokat, amelyek elősegítik a fenti célok megvalósítását.
A kromatogramok számítógépes kiértékelése manapság lehetővé teszi a kromatográfiás csúcs(ok) alakjának alaposabb elemzését, és nem csupán a retenciós idő és a görbe alatti terület kiszámítására korlátozódik. A csúcs alakjának vizsgálata nemcsak a minőségi és mennyiségi elemzést szolgálja, hanem segítségével a kromatográfiás rendszer működésére, a paraméterek megváltozására is következtethetünk. A csúcs alakját közönséges és centrális momentumokkal, a belőlük számítható csúcsossági és aszimmetria együtthatókkal, valamint a csúcs különböző magasságaiban vett csúcsszélességekkel és szélességi adatokból számított különböző aszimmetria faktorokkal jellemezhetjük.
1. Kromatográfiás csúcsok leírása modellekkel
A kromatográfiában a csúcsok matematikai modellekkel történő leírása különösen nagy jelentőséggel bír. A különböző alakú csúcsokat megfelelően leíró rugalmas modellek megkeresése és kidolgozása komoly kihívást jelent a kromatográfus számára.
A kromatográfiás csúcsokat leíró függvények legalább két területen alkalmazhatók a kromatográfiás adatfeldolgozás során: egyrészt az átlapoló csúcsok összetevőkre való felbontásával (dekonvolúciójával) számíthatók a csúcsmagasságok és csúcsterületek;
másrészt egy általános függvény kísérleti adatokra történő illesztése a zaj szűrését és statisztikai momentumok, elsősorban magasabb momentumok meghatározását teszi lehetővé. A függvényillesztés kritikus, mivel a csak kísérleti adatokból történő momentum- meghatározás nagyon érzékeny a kísérleti hibákra (pl. elektromos zajra, alapvonal
elmozdulásra). A görbeillesztéssel történő közelítés jósága a matematikai függvény valódi kromatográfiás görbét leíró képességétől függ. Arra kell törekedni, hogy a modell pontosan leírja a csúcsot, vagyis megfelelően rugalmas legyen a különböző csúcsalakok leírására. A kromatográfiás csúcsok elméleti (fizikai) vagy empirikus modellekkel írhatók le.
1.1. Elméleti modellek
A kromatogramok bonyolult és igen komplex fizikai-kémiai folyamatok eredményeként jönnek létre, ezért egységes, az elválasztó oszlopot elhagyó minta koncentáció-profilját pontosan leíró matematikai függvény felállítása nem lehetséges. Mindig az adott csúcs alakját legjobban leíró függvényt kell kiválasztani és ennek paramétereiből számolni. Az elméleti modellek valós fizikai folyamatokat írnak le, így magyarázatot adhatnak a csúcsok alakjának torzulására. A statisztikai momentumok pontos meghatározása a termodinamikai tulajdonságok és az anyagáramlás kinetikájának meghatározásában is fontos. Így pl. az első momentum az adszorpciós egyensúlyi állandótól függ, míg a részecskék közötti diffúzió és az axiális diszperziós koefficiens a második centrális momentumból vezethető le.
1.1.1. Lineáris kromatográfia
A következőkben lineáris adszorpciós izotermával rendelkező modellekkel foglalkozunk, vagyis az alacsony minta koncentráció miatt a jel intenzitása arányos a minta koncentrációjával. Ez a lineáris viselkedés lehetővé tesz egy igen fontos egyszerűsítést, nevezetesen, mivel nincs versengés a különböző minta-összetevők között, a többkomponensű elválasztás úgy tekinthető, mint a különböző egyedi komponensek elúciójának algebrai összege. Ezért elégséges egyetlen összetevőnek az oszlopban történő mozgását figyelni függetlenül attól, hogy a mintában hány komponens van jelen.
Az ilyen típusú legegyszerűbb elméleti modellek közé sorolható a Martin-Synge [1]
illetve a Craig [2] -féle tányér-modell. Mindkettő úgy tekinti az elválasztó oszlopot, mint véges hosszúságú elméleti tányérok sorozatát. Mindegyik tányér egy-egy cellaként értelmezhető, melyekben az egyes fázisok között pillanatnyi egyensúlyok alakulnak ki.
A Martin-Synge modell elhanyagolja a minta diffúzióját az egyik cellából a másikba.
Kiindulásként egy cella tömegmérlegét az alábbi egyenlettel adja meg:
) ( r 1 r
v r s r
m F c c
dt V dq dt
V dc + = − − (1)
ahol
Vm - az oszlopban levő mozgófázis teljes térfogata, Vs - az állófázis össztérfogata,
Fv - a mozgófázis áramlási sebessége,
cr ,qr - az r-edik cellában rendre a minta mozgó- és állófázisbeli egyensúlyi koncentrációja.
Megoldva az (1) differenciál egyenletet, egy Poisson alakú koncentráció-eloszlást kapunk az oszlop teljes hosszában. Az első momentum egyenlő eloszlású lesz. Felhasználva a Stirling formulát a következő függvényformához jutunk:
−
−
=
−
1 2 exp
) (
1
R N
R R t
N t t
t t t N
f π (2)
ahol N az elméleti tányérszám, tR a retenciós idő, t az idő. Ebben az esetben µ1 = tR, a variancia pedig σ2 = µ2 = tR2/N.
A Craig-féle tányér modell esetén a mozgófázis és a minta egyik cellából a másikba való átmenetekor újabb egyensúlyok állnak be majd bomlanak meg. A minta eloszlása az egyes cellákban, valamint az elúciós profil binomiális eloszlással írható le. Minden egyes átmenetkor az utolsó cellát (Nc-1) elhagyó minta mennyiség eloszlása a következő lesz:
( ) (
1)
( ), 1)
(p =R p RN −1 −R p−N −1 p≥ Nc −
f c c (3)
ahol R a p-edik cellába átmenő minta-arány.
A Craig-modell esetén az első momentum és a variancia összefüggése a következő lesz:
µ1 = nR és σ2 = nR (1-R) , ahol n az anyagátadások száma.
Kis elméleti tányérszám (N = 50) esetén a Martin-Synge- és a Craig-modell még megkülönböztethető egymástól, de már tízszeres tányérszámnál a két modell közötti különbség eltűnik és mindegyikük gyakorlatilag a Gauss-függvénnyel lesz azonos.
A tömegmérleg-modell [3] a tányér-modellekkel ellentétben folytonosan kezeli a minta eloszlását az állófázis és mozgófázis között. A kezdeti és a határfeltételek figyelembe vételé- vel a zóna-profilt a differenciális tömegmérleg-egyenlet integrálásával számolják ki.
A tömegmérleg egyenletében szereplő kifejezések a következők: az oszlop egy zónájában a minta koncentrációjának időbeli változása a mozgófázisban
∂
∂ t c , az állófázisban
∂
∂ t
q , valamint a minta axiális tengely mentén lévő koncentráció gradiense
∂
∂ z
c . Igen kis zónahossz esetén felírhatjuk a következő egyenletet:
2
1 2
z D c z u c t q t
c
a ∂
= ∂
∂ + ∂
∂
− ∂
∂ +
∂ ε
ε (4)
ahol
ε - a töltet porozitása,
u - a mozgófázis lineáris sebessége, Da - az axiális diszperziós koefficiens.
A tömegmérleg megoldásához feltételezték, hogy az elválasztó oszloptöltet radiálisan homogén, a mozgófázis kompresszibilitása elhanyagolható, az axiális diszperziós koefficiens és a hőmérséklet állandó, s az állófázisban nincs diffúzió.
Az un. egyensúly-modellhez jutunk akkor, ha az adszorpciós izotermát lineárisnak tekintjük és a k` retenciós faktor és az izoterma meredeksége között az egyszerű lineáris összefüggést alkalmazzuk. A módosított modell differenciál-egyenletét Guiochon [4] és munkatársai oldották meg. Bár különböző kezdeti és határfeltételeket alkalmazva eltérő eredményekhez jutottak, közös jellemvonása volt a megoldásoknak az, hogy mindegyik jól közelíthető ugyanazzal a Gauss-függvénnyel.
A kromatográfia kinetikus modellje a kinetikai-egyenletet használja fel a zónaszélesedés leírására. Ebben a modellben nincs egy állandó egyensúly az álló- és a mozgófázis között. A kinetikus modellen belül megkülönböztetjük a reakció-diszperzió, valamint a transzport- diszperzió modelljét. Előbbi fejezi ki a lassú adszorpciós/deszorpciós folyamat nem egyensúlyi állapotát, míg az utóbbi modell feltételezi, hogy az adszorpció/deszorpció gyors, de a kinetikai anyagátadás lassú. A modell analitikai megoldása nagyon bonyolult, általánosan Lapidus és Amundson [5] oldotta meg először. Egyszerűbb megoldását Giddings és Eyring [6] adta meg, mely esetben az axiális diszperzió hatását elhanyagolták.
Az általános sebességi modell a kromatográfiás zónaszélesedést okozó valamennyi áramlási és kinetikai jelenség hatását párhuzamosan veszi figyelembe. A legnagyobb mértékű hozzájárulást a részecskék közötti transzport mechanizmus eredményezi (mint pl. a lyuk-diffúzió a folyadékkal töltött pórusokba, a szilárd anyag diffúziója a adszorbeált fázisban, reakció kinetika a fázishatáron, valamint a részecskék közötti transzport és diszperziós mechanizmusok, melyek függnek a külső -póruson kívüli- anyagátadástól és keveredési -axiális diszperziós- hatásoktól). A modell analitikai megoldása néhány egyszerűsítést beleszámítva csak Laplace-tartományban lehetséges [4]. A momentumok meghatározása direkt módon történik a Laplace-transzformációs momentum-elmélet segítségével, majd az első és második momentumból megkapjuk az elméleti tányérmagasság egyenletét.
1.1.2. Statisztikus modellek
A statisztikus vagy mikroszkópikus modellek az elválasztó oszlopban egyetlen molekula véletlenszerű mozgását veszik figyelembe. Ezek közül legfontosabb a véletlenszerű mozgás modellje, a sztohasztikus modell, valamint a karakterisztikus függvény módszere.
A véletlenszerű bolyongás-modell a kromatográfia legegyszerűbb molekuláris modellje, mely -bár nem teljesen reális- a kromatográfiás folyamat viszonylag egyszerű leírását (a vonatkozó egyenlet megoldását) adja. Az egy-dimenziós véletlenszerű mozgás modell szerint a részecske pozitív vagy negatív irányba mozog (az eluens haladási irányának megfelelően ill. azzal ellentétesen) a véletlennek megfelelően. Szimmetrikus esetben a mozgás valószínűsége mindkét irányban 1/2. A részecske várható tartózkodási helye n eset és δ úthossz megtétele után változatlan marad, melynek varianciája σ2 = nδ2 . Időtartományra való kiterjesztés esetén -a diffúziós egyenlet megoldásaként- a következő Einstein-féle összefüggés írható fel:
t D
= 2
σ (5)
ahol D a diffúziós állandó.
Az adszorpciós/deszorpciós jelenségeket molekuláris szinten vizsgálva, levezethető a retenciós idő összefüggése is:
+
= +
=
d a R
R k
t k t t
t 0 ' 0 1 (6)
ahol
tR - a retenciós idő;
t0 - a molekula mozgófázisban eltöltött ideje;
t'R - a korrigált retenciós idő, amit a részecske az állófázisban tölt el;
ka és kd - annak időegységre eső valószínűsége, hogy a molekula az állófázisba illetve a mozgófázisba lép.
A sztochasztikus-modell, mely Giddings és Eyring nevéhez fűződik [6], valószínűségi sűrűségfüggvényt számol a részecske állófázisban illetve mozgófázisban eltöltött idejére.
McQuarrie [7] meghatározta a sztochasztikus-modell elúciós profil momentumait és továbbfejlesztette a modellt úgy, hogy nem egyenletes adszorpciós részeket és különböző injektálási profilokat feltételezett. A sztochasztikus modellből kiszámított első momentum a molekula állófázisban eltöltött átlagos tartózkodási idejét, a korrigált retenciós időt (t'R) adja meg, mely a (6) egyenletből megkapható:
s d a
R n
k t k
t
τ
µ
1 = ' = 0 = (7)A variancia az első két momentumból (µ1, µ2) számítható ki a következő összefüggés szerint:
2 0 2
2 1 2
2 2 2 s
d
a n
k
t k τ
µ µ
σ = − = = (8)
ahol
τs =1/kd - a részecske egy deszorpcióra jutó ideje, n - a deszorpciók átlagos száma,
a többi paraméter pedig azonos a véletlenszerű bolyongás-modellben leírtakkal.
A karakterisztikus függvény-módszer, melyet Dondi [8] és munkatársai dolgoztak ki, a sztochasztikus-modell egy továbbfejlesztett változata. Ebben az esetben is egy részecske véletlenszerű mozgását tekintjük az oszlopon belül. Mivel a szorpciós idő véletlenszerű, eloszlás-függvénnyel írható le. Ha feltételezzük, hogy a molekula átlagosan n-szer adszorbeálódik az oszlopban való vándorlása során, továbbá mivel a szorpciós idők
független véletlenszerű mennyiségek, a teljes szorpciós időt leíró sűrűségfüggvényt az egyes helyeken lévő szorpciós időeloszlások n-szeres konvolúciójával kapjuk meg. A konvolúciós művelet leegyszerűsödik akkor, ha frekvencia tartományban dolgozunk, ahol a konvolúciós műveletnek az egyszerű szorzás felel meg. Ezáltal megkapjuk a teljes szorpciós idő karakterisztikus függvényét frekvenciatartományban, melyet ha inverz-Fourier transzformálunk, az időtartományban kifejezett elúciós profilhoz jutunk. A momentumok, a retenciós idő, a csúcsszélesség és aszimmetria, ferdeség és lapultság közvetlenül meghatározhatók a karakterisztikus függvényből.
Ha a szorpciós lépések Poisson eloszlást követnek (sztochasztikus-modell) és a molekula tartózkodási ideje az egyes fázisokban exponenciális eloszlású, akkor a karakterisztikus függvény megoldása azonos a sztochasztikus-modellével. Az így meghatározott első és második momentum azonos a (7), (8) összefüggésben szereplőkkel, míg a csúcsferdeség (S) és lapultság hasonlóan egyszerű összefüggésekkel adható meg:
2 0
3 2
3
t k S n
a
=
= (9)
0
6 6
t k E n
a
=
= (10)
A Martin-Synge féle tányér-modell szintén levezethető a karakterisztikus függvény- modellből. Ebben az esetben az adszorpciós lépések száma (n) nem véletlenszerű állandó, hanem konstans; míg a szorpciós időeloszlás exponenciális lefutású. Ez esetben a karakterisztikus függvény inverz-Fourier transzformáltja a gamma-eloszlás sűrűségfüggvénye, mely a Martin-Synge modell által definiált csúcsalakot adja meg. Az így kiszámított gamma csúcsalak első momentuma azonos a (7) egyenletben szereplővel, a varianciát a (11) egyenlet, a ferdeséget a (12) összefüggés adja meg, a lapultság pedig a (10) egyenlet alapján számítható ki. Az adszorpciós lépések Poisson-eloszlása feltételezhető:
0 2 2 2
d a
s k
t k
n =
= τ
σ (11)
0
2 2
t k S n
a
=
= (12)
Következtetésként elmondható, hogy a lényegi különbség a két sztochasztikus modell között az, hogy ha az adszorpciók száma Poisson eloszlást követ, akkor a variancia kétszerese az állandó adszorpciós számmal egyenértékű Martin-Synge modell varianciájának. Ez azt jelenti, hogy a szorpciós lépések véletlenszerűségének hozzájárulása azonos a véletlenszerű szorpciós idők hozzájárulásával a csúcs teljes varianciájához.
A karakterisztikus függvényen alapuló módszer ígéretesnek tűnik olyan esetekben, amikor a mozgófázis sebessége nem állandó, vagy az állófázis heterogén adszorpciós részeket tartalmaz.
A sztochasztikus-modell megoldásával kapott lineáris modellek (a tányér-modell, a differenciális tömegmérleg-egyenlet) zóna-profilja nem különböztethető meg a szimmetrikus Gauss-csúcstól még közepes tányérszám esetén sem. Az oszlop túlterheléséből származó csúcsaszimmetria nem magyarázható meg a fenti modellek segítségével, erre a nemlineáris kromatográfia ad választ (ld. I.1.1.4. fejezet).
1.1.3. Exponenciálisan módosított Gauss-modell
Az exponenciálisan módosított Gauss-modell (EMG) a lineáris kromatográfia egyik legelterjedtebb, aszimmetrikus csúcsot is leíró függvénye. Megbízható fizikai modell olyan esetekben, amikor az injektálási profil exponenciális, vagy amikor a mozgófázis keveredése következik be az oszlopon kívüli kromatográf-egységekben.
Az EMG-függvényt a Gauss-görbe és az exponenciálisan lecsengő függvény konvolúciójának eredményeként kapjuk meg:
y(t) = h(t) ∗ f(t) =
∫
∞ −0
) ' ( ) '
(t t f t dt
h (13)
ahol
y(t) - a kromatográfiás csúcsot leíró konvolvált függvény, h(t) – a Gauss-görbét leíró függvény:
( )
− −
= 22
exp 2 ) 2
( π σ σ
tR
t t A
h (14)
f(t) - a lecsengő exponenciális függvény:
f(t) = τ1 ⋅exp
{
−t/τ}
(15)ahol:
A - csúcsterület, V⋅s t - idő, s
tR - retenciós idő, s σ - standard deviáció
τ - időállandó, s.
A konvolúciós integrál és a hibafüggvény meghatározása után, az EMG-függvény végleges alakja a következő lesz:
−
−
−
+
−
−
= τ σ
σ τ
σ τ σ
τ σ
τ exp 2 2 2 2 2
) 2
( 2
2
R R
R t t
t erf t erf
t t A
y (16)
A hibafüggvény manapság már rutin programokkal meghatározható, erre a célra általában polinomos vagy egyéb típusú megközelítéseket alkalmaznak.
A csúcsszélesedés kialakulásában általában egy műszer-effektus dominál, tehát a zavaró hatás egyetlen időállandóval jellemezhető. Ha több különböző domináns oszlopon kívüli hatás is létezik, akkor az EMG-modell kiterjeszthető másodrendűvé vagy magasabb rendűvé. Ebben az esetben a Gauss-függvény és két, illetve több exponenciálisan lecsengő függvény konvolúcióját kell képezni. A magasabb rendű EMG-függvények végleges alakját Felinger [3] táblázatos formában foglalta össze. A másodrendű EMG-függvény jóval elhúzódóbb ("tailing"-esebb) mint az elsőrendű; és a maximumok az elsőrendű EMG- függvény lecsengő ágán helyezkednek el.
A negatív időállandónak (τ) vagy relaxációs időnek nincs fizikai háttere, azonban ezáltal az EMG-függvény empirikus modellként alkalmazható, amely elöl aszimmetrikus ("fronting"-os) csúcsalakot eredményez.
Az EMG-függvény első- és második centrális momentumának (variancia) összefüggése a következő:
2 2 2 1
τ σ µ
τ µ
+
= +
=m
(17) A ferdeség (S) és a lapultság (E) a következő összefüggések szerint határozhatók meg:
( ) (
2 2)
24 2 / 2 3 2
2 3
τ σ
τ τ σ
τ
= +
= +
E S
(18)
Az S és E érték akkor éri el maximumát (Smax = 2, Emax = 1), amikor a τ/σ aszimmetria tényező a végtelenhez tart.
A közelítéseket (hibafüggvény) nem tartalmazó EMG-függvény pontos megoldásához a Fourier-transzformáció vezet. A frekvencia tartományban a konvolúciót a szorzás helyettesíti, és ez jelentősen megkönnyíti a számításokat [9]. Inverz Fourier- transzformációval pedig visszakapjuk az eredeti EMG-függvényt.
Habár az EMG-függvény használata nagyon elterjedt, rugalmassága meglehetősen behatárolt. Alkalmazásának hátrányait a későbbiekben ismertetni fogom (ld. I.1.2.1. fejezet).
1.1.4. Nemlineáris kromatográfia
Nemlineáris kromatográfiában a tömegmegmaradás közelítő analitikai megoldása csak akkor adható meg numerikusan, ha a a minta koncentrációja kicsi és a parabolának feltételezett adszorpciós izoterma csak kis mértékben tér el a lineáristól. A tömegmegmaradás differenciálegyenletét nemlineáris esetben először Houghton [10] oldotta meg (Houghton-modell) feltételezve, hogy a koncentráció igen kicsi és az oszlop végtelen hosszú.
Haarhoff-van der Linde [11] az előzőhöz hasonló módszert használt elúciós profilok meghatározására kissé túlterhelt oszlop esetén. Az ő közelítése abban különbözik a Houghton-modelltől, hogy a diszperziós hatást csak a retenciós idő környezetében számolta ki, mivel a minta koncentrációja csak itt különbözik a nullától. Ez a feltételezés a Houghton- modellel szemben a tömegmegmaradás érvényességéhez vezetett. Mindkét modell esetén a minta koncentráció növekedésével egyre meredekebb felszálló ágú görbét kapunk, tehát a retenciós idő csökken, a leszálló ágak pedig pontosan összeillenek. Ennek az a magyarázata, hogy az injektált minta-koncentráció az izoterma nemlineáris részén nő. Összehasonlítva a két modellt, a Haarhoff-van der Linde-modell előnyösebb, mivel ebben az esetben a
tulajdonítható. Ez esetben az elúciós profilnak (szemben a Houghton modellel) nincs területvesztesége.
A Thomas-modell [12] a nemlineáris kromatográfia egy egyszerűsített modellje, mivel az axiális diszperziót elhanyagolja és csak olyan esetben használható, amikor az adszorpciós/deszorpciós kinetika jóval lassúbb, mint az anyagátadás kinetikája.
1.2. Empirikus modellek
A kromatográfiás elválasztások komplexitása miatt a különböző alakú csúcsok nem írhatók le egyszerű függvényekkel. Egyes modellek fizikai-kémiai információval rendelkeznek (ezekkel foglalkoztunk az előző fejezetekben). Sok esetben azonban a kromatográfus számára elegendő a csúcsparaméterek (retenciós idő, csúcsmagasság, csúcsszélesség), a statisztikus momentumok (csúcsterület, ferdeség, lapultság), valamint az elméleti tányérszám meghatározása és ismerete. Utóbbiak az un. empirikus modellek, melyek sok esetben sokkal jobban illeszthetők a kromatográfiás csúcsok digitális pontjaira, mint az elméleti modellek. Ezáltal a kívánt paraméterek vonatkozásában pontosabb értékekhez jutunk.
Az empirikus modellek nagy előnye, hogy a kromatográfiás csúcs leírására alkalmazott matematikai függvény paraméterként tartalmazza a csúcs jellemzőit, ezáltal a teljes kromatogram memorizálása megvalósítható az illesztett empirikus függvény néhány paraméterének tárolásával, mely jelentős számítógép-memória megtakarítást jelent.
Az empirikus modellek alkalmazási területei közül feltétlenül említésre méltó az átlapoló csúcsok felbontása (I.1.2.2. fejezet). A görbeillesztés során zajszűrés is végrehajtható, mely a csúcs jellemzését jelentősen megkönnyíti.
Az illesztett empirikus függvények lehetővé teszik továbbá az egy, vagy több kísérleti jellemző (pl. eluens áramlási sebessége, a detektor válaszideje, stb.) csúcsalak-módosító hatásának tanulmányozását is.
A szimulált kromatográfiás csúcsok mind oktatási, mind kereskedelmi célok érdekében felhasználhatók, gyakran pedig a kísérleti eljárásra javasolt módszerek validálásához szükségesek.
A fentebb említett célokra nagyszámú empirikus függvényt használnak, javasoltak és javasolnak még ma is az egyre tökéletesebb eredmények elérése érdekében.
1.2.1. Egyedi csúcsok matematikai leírása
Kromatográfiás csúcsok empirikus modellel való leírására az első próbálkozások természetesen Gauss-függvénnyel [13] és annak Baudisch [14] által egyszerűen módosított alakjával történtek:
y = hmax. exp
( )
−
− Dt t t R
.
2
(19) ahol
tR - retenciós idő, s t - idő, s
D - csúcsszélesség, s hmax- csúcsmagasság.
A Poisson-eloszlást leíró függvényt is felhasználták kromatográfiás csúcsok leírására. A függvény alkalmazásával Degen [15] figyelemre méltó eredményeket ért el, aki acetonitril-víz eluens alkalmazásával LiChrosorb RP-8 oszlopon folyadék-kromatográfiás módszerrel elválasztott benzol, naftalin, antracén és benzantracén digitalizált csúcsához Poisson- függvényt illesztett. A relatív eltérés 3-5 % között volt.
Ezek a függvények a szimmetrikus kromatográfiás csúcsokat jól leírják, aszimmetrikus esetben azonban nem adnak kielégítő eredményt.
Aszimmetrikus kromatográfiás csúcsok matematikai leírására többféle módszer létezik, melyek közül legelterjedtebb az EMG-modell. Az EMG-függvény, mint empirikus modell még ma is a legtöbbet használt modell kromatográfiás csúcsok illesztésére. Anderson [16], Foley [17, 18], Davis [19] és Hanggi [20] elméleti szempontból vizsgálta az EMG-függvény alakját, az illesztéssel elkövetett hibákat és alkalmazásának lehetőségeit. Foley [18]
közleményében leírja az EMG-függvény kiszámítására szolgáló BASIC-nyelvű programot is.
Az EMG-függvény segítségével a tiszta Gauss-görbétől (τ = 0) a tiszta exponenciális függvényig (σ = 0) mindenféle átmeneti függvény illeszthető a mért, digitalizált
jelértékekhez. A τ/σ arány aszimmetria faktorként jellemezheti a kromatográfiás csúcs eltérését az ideális szimmetrikus csúcstól.
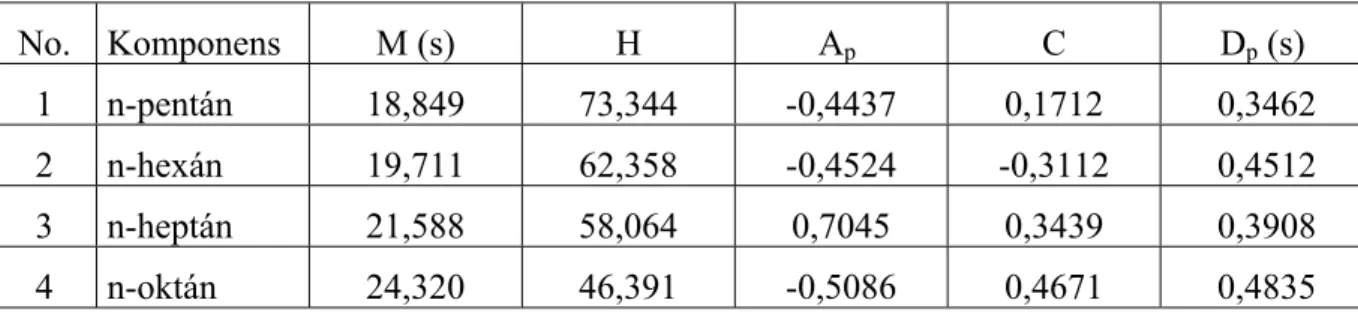
Gladney [21] alkoholok és petróleumpárlatok gázkromatográfiás csúcsaihoz illesztett EMG-függvényt. Li Haochun [22] különböző egyszerű, 5-8 szénatomot tartalmazó szénhidrogének kromatogramjában található csúcsokat ír le.
Az EMG-függvény széleskörű alkalmazása ellenére néhány hátránnyal is rendelkezik:
- A τ és σ paraméterek csak illesztéssel határozhatók meg és az illesztés kiindulási értékei néha rosszul becsülhetők.
- A csúcs élességére (ferdeség, lapultság) egyik paraméter sem ad tájékoztatást.
- τ kis értékeinél, 0 környezetében a számítás bizonytalanná válhat.
- Mivel az EMG-modell paraméterei nem közvetlenül jellemzik a csúcsot és kiértékelése bizonyos közelítéseket tesz szükségessé, gyakorlati alkalmazása ezért nehézkes.
- Az EMG-függvény csak akkor szolgáltat jó illesztést a digitális pontokra, ha a csúcsalak-torzulás oszlopon kívüli hatások eredménye.
A legtöbb empirikus modell a Gauss-függvényből indul ki, bevezetve bizonyos aszimmetriát.
Az egyik széleskörűen alkalmazott, aszimmetrikus csúcsok leírására alkalmas modell a biGauss függvény, mely két különböző szélességű Gauss-csúcsból áll [23]. Habár a biGauss modell igen egyszerű, alkalmazása csak kis csúcs-aszimmetria esetén javasolt. Nem alkalmas hosszan felszálló ágú, vagy hosszan elnyúló csúcsok leírására. A látszólagos aszimmetriát a felszálló- és leszálló ág különböző szélességeinek aránya adja meg (σ2/σ1). Az exponenciálisan elhúzódó aszimmetrikus csúcsok nem jellemezhetők a biGauss modellel.
Papoff [24] és munkatársai összehasonlították az EMG-, a biGauss- (mely dekonvolúciója két fél Gauss-csúcs összegét eredményezi) és a két-Gauss- (mely dekonvolúciójaként két Gauss-csúcs keletkezik) függvényt ionkromatográfiás csúcsok adatainak illesztése során és arra a következtetésre jutottak, hogy torzulásos effektusok fennálltakor a stabilitási állandó pontos meghatározásához az EMG- valamint a két-Gauss-függvény használata az előnyös.
Vayda [25] egy általánosított exponenciális függvényt (GEX) alkalmazott aszimmetrikus csúcsok leírására:
( )
1 0
1 1
0 0 1
0 0
>
>
−
− −
−
−
= −
−
b , a
t t
t t a
exp b t
t t h t t f
a
m b
m (20)
ahol
a és b - konstansok, h - a csúcsmagasság,
tm - a csúcsmaximum helye és t0 - a holtidő.
A GEX függvényt eredményesen alkalmazták kizárásos kromatográfiás görbék felbontásánál.
A Weibull függvény (a = b) a GEX modell egy speciális esete, melynek kromatográfiás csúcsokra való alkalmazása meglehetősen korlátozott, elsősorban a statisztikában (tartózkodási idő, élettartam meghatározására) használják.
Chesler és Cram [26] egy nyolcparaméteres modellt használt aszimmetrikus csúcsok leírására. Ők egy Gauss-függvényt kombináltak egy exponenciális és egy tangens hiperbolikus függvénnyel. A Chlesler-Cram modell kezdeti szakaszán a Gauss-függvény dominál; a hosszan elhúzódó részt az exponenciális és tangens hiperbolikus függvény írja le.
A paraméter értékek megadására különös figyelmet kell fordítani, mivel helytelen megválasztásuk u.n. duzzadásokat okoz a csúcs leszálló ágán.
Sok esetben az aszimmetrikus csúcsok leírására használt modellek a Gauss-csúcs standard deviációjának módosításán alapulnak. Torres-Lapasió [27] a Gauss-függvény standard deviációjának állandó értékét polinom függvénnyel helyettesítette (polinommal módosított Gauss-függvény PMG1), így az erősen aszimmetrikus csúcsok jobb vagy baloldali alakváltozással jól illeszthetővé váltak. Nikitas [28] és munkatársai a PMG1 függvényt tovább módosították azáltal, hogy a Gauss-függvény exponenciális részén kívül bevezették az s0/s arányt:
( ) ( )
...exp )
(
2 2
1 0
2 0
+
− +
− +
=
− −
=
m m
m m
t t s t t s s s
s t t s
s t h
h
(21)
ahol
t - a csúcsmaximum helye,
hm - a csúcsmagasság,
s - a Gauss-csúcstól való standard deviációt jellemző konstans.
Li [29] a Gauss függvényt egy kétlépcsős függvénnyel közelítette; a függvény egyik része a módosított Gauss-csúcs felszálló ágát, a másik része a leszálló ágát jellemzi. Ez az empirikus modell hat paramétert tartalmaz minden csúcsra, mely különösen rugalmassá teszi a függvényt aszimmetrikus csúcsok illesztésére.
Grubner [30, 31] aszimmetrikus csúcsok leírására a Gram-Charlier sor első három tagját használta. A modellt görbeillesztésre alkalmazva gyors becslést kapunk a csúcsok ferdeségének és lapultságának meghatározására.
Kromatográfiás csúcsok matematikai leírására Grushka [32] a Gauss-függvénnyel megszorzott Hermite-polinomot használta, melynek alakja a következő:
h(t)=
π σ 2
1 .exp
− 22 2σ
t
+
∑
∞= σH t i c
i i i 3 !
1 (22)
ahol
t - az idő, s
σ - a standard deviáció, ci - az i-edik momentum,
Hi - a Hermite-polinom i-edik tagja.
Az irodalomban számos más, aszimmetrikus csúcsok leírására alkalmas modell létezik, például a Lorentz-függvény [33], a Fraser-Suzuki modell [34], a Gram-Charlier és az Edgeworth-Cramér sor [35] (melyet Kelly [36, 37] használt gázkromatográfiás csúcsok illesztésére), a Lan-Jorgenson modell [38] (a Gauss- és az EMG- hibridfüggvénye), vagy a generalizált exponenciálisan módosított Gauss-függvény (GEMG) [28]. Di Marco és Bombi [39] a kromatográfiás csúcsokat is leíró empirikus modelleket táblázatos formában foglalta össze.
A kromatográfiás adatsorok illesztésére felhasználható nagyszámú empirikus modell azt bizonyítja, hogy a különböző alakú csúcsokat megfelelően leíró matematikai függvény megtalálása alapvető fontosságú.
1.2.2. Átlapoló csúcsok felbontása
A kromatográfiás gyakorlatban gyakran előfordul, hogy két, vagy több komponens elválasztását a kromatográfiás körülmények változtatása (hőmérséklet, oszlophossz, oszloptöltet, eluens összetétele és áramlási sebessége, stb.) ellenére sem sikerül teljesen megoldani és a kromatogramon többé-kevésbé átlapoló csúcsok keletkeznek. A grafikus eljárások közül a völgypont merőleges levetítése, a háromszög-korrekció és -elnyúló csúccsal való átlapolás esetén- a tangens korrekció terjedt el. Ezeket a módszereket Woerlee [40]
részletesen elemzi közleményében.
Novak [41] és Kishimoto [42] a völgypont levetítésével történő felbontás hibáját elemzi különböző mértékű átlapoltság és eltérő csúcsparaméterek esetén. Megállapításaik szerint a hiba nagymértékben függ az átlapoló csúcsok aszimmetriájától és az átlapoló csúcsok magasságának különbözőségétől.
Mori [43, 44] az átlapoló kromatográfiás csúcsok magasságainak pontos meghatározása céljából számítási módszert dolgozott ki azokra az esetekre, amikor két ill. három csúcs lapol át. Az átlapolt csúcsok jellemző pontjainak megadása után az egyedi csúcsok magasságát matematikai egyenletrendszerek megoldásával határozza meg.
Az átlapoló kromatográfiás csúcsok felbontására gyakran használják a görbeillesztést.
Ekkor az egyedi csúcsok leírására használt egyenletek alkalmazhatók, de természetesen a csúcsok számának megfelelő összegzést el kell végezni.
Metzger [45], Braswell [46], Rosenbaum [47] és Thomas [48] a Gauss-görbe egyenletét használta gázkromatográfiás csúcsok görbeillesztéssel történő felbontására. Grimalt [49]
kromatográfiás csúcsok felbontására különböző matematikai eloszlás-függvényeket (a log- normal-függvényt, a Gamma-, Weibull- és a módosított Gauss-függvényt) próbált ki. A különböző aszimmetriájú csúcsok felbontásánál más-más függvényt talált optimálisnak. A felbontás jóságának meghatározására a maradék szórásnégyzetet és a görbe alatti terület relatív hibáját alkalmazta. D'Allura [50] folyadék-kromatográfiás csúcsok felbontását végezte el számítógép segítségével. Az alkalmazott algoritmus szerint az átlapoló komponensek különböző koncentrációjú egyedi kromatográfiás csúcsaiból számítja ki az átlapolt csúcsot leíró matematikai függvény paramétereit, görbeillesztést alkalmazva.
Crilly [51-53] gázkromatográfiás csúcsok felbontására a Jansson-módszert alkalmazta.
Ez a módszer egy, az átlapoló csúcsok felbontására alkalmazott iteratív nemlineáris
válaszfüggvényére és a maximális csúcsmagasságra van szükség. Az iteráció során az eredeti átlapoló csúcsok görbe alatti területe megegyezik a dekonvolúcióval kapott csúcsok területeinek összegével.
Maeder [54] és Lacey [55] átlapoló kromatográfiás csúcsokat faktoranalízis segítségével bontott fel. A faktoranalízishez előzetes ismeretként az egyedi komponensek infravörös spektruma állt rendelkezésükre.
A hagyományos görbefelbontó módszerek kitűnő és tartalmas összefoglalóját adja meg Fritsch [56] és Felinger [3]. Táblázatos formában megadják az egyes módszerek jellegzetességeit, a módszer által igényelt előzetes információkat, az alkalmazhatóság korlátait és a kapott eredmény felhasználhatóságát.
Átlapoló kromatográfiás csúcsok felbontására az EMG-modellt sokan használják [27, 29, 57-60].
2. Kromatográfiás csúcsok jellemzése
A kromatogram számítógépes kiértékelése lehetővé teszi a kromatográfiás csúcs alakjának alaposabb elemzését és nem korlátozódik a retenciós idő és a görbe alatti terület kiszámítására. A csúcs alakjának vizsgálata nemcsak a mennyiségi és minőségi elemzést szolgálja, hanem segítségével a kromatográfiás rendszer működésére, a paraméterek megváltozására is következtethetünk. A csúcs alakját a közönséges és centrális momentumokkal, a belőlük számítható csúcsossági, ferdeségi és aszimmetria együtthatókkal, a csúcs különböző magasságaiban vett csúcsszélességekkel és a szélességi adatokból számított, különböző aszimmetria együtthatókkal jellemezhetjük [61, 62].
Az utóbbi időben igen megnőtt az érdeklődés a kísérleti kromatográfiás csúcsok jellemzése és leírása iránt. Foley és Dorsey [63] táblázatos formában ismerteti a kromatográfiás csúcsot jellemző paraméterek nevét, szimbólumát és általános összefüggéseiket. Ezeket a paramétereket általánosan kromatográfiás csúcsjellemzőknek (CFOMs) nevezik. Kezdetben kromatográfiás csúcsjellemzők meghatározására kizárólag
"kézi" számítások álltak rendelkezésre, de ezek csak öt paraméter meghatározására voltak pontosak (retenciós idő (tR), empirikus aszimmetria faktor (B/A), csúcsmagasság (hp), bázisszélesség (Wb), csúcsszélesség adott magasságnál (Wα)). Gauss-csúcs esetén a nulladik
momentum a csúcsterülettel (M0) egyenlő, az első momentum megegyezik a retenciós idővel (M1= tR), a második centrális momentum (variancia) a Wb, Wα vagy M0 függvénye. Gauss- csúcs esetén a fennmaradó csúcsjellemzők, mint az aszimmetria faktor, csúcsosság, ferdeség nullával egyenlőek.
Reális kromatográfiás csúcsok esetén Gauss-alakú csúcs feltételezése helytelen. A gyakorlatban az ideális szimmetrikus csúcs nagyon ritka, figyelembe véve a különböző (oszlopon belüli és kívüli) aszimmetria-forrásokat. Pauls és Rogers [64] kimutatta, hogy egy aszimmetrikus csúcs varianciája akár 50%-al is alábecsülhető, ha a csúcs félmagasságában vett Gauss-függvény szélességével számolunk. Kirkland [65] és munkatársai bebizonyították, hogy a tányérszám több mint 100%-al felülbecsült, ha a három általános Gauss-összefüggés bármelyikét használjuk.
Az elmúlt években nagyléptékű fejlődést mutató komputer-technika lehetővé tette, hogy a kromatográfiás kiértékelések a manuális módszerekhez képest sokkal gyorsabban és pontosabban elvégezhetők. Már viszonylag egyszerű algoritmusok használatával is kellő pontossággal meghatározhatók a csúcsparaméterek, bár a második és magasabb centrális momentumok pontosságát erősen befolyásolja az alapvonal zaja [66]. Mivel aszimmetrikus csúcsok esetén az egyszerű Gauss-modell alkalmazása számos hibához vezet (mind az elméleti tányérszám, mind a csúcsfelbontás meghatározásakor), szükségessé vált olyan modellek bevezetése, melyek aszimmetrikus csúcsok leírására is alkalmasak. Egyik legelterjedtebb, aszimmetrikus csúcsok esetén is használható modell az exponenciálisan módosított Gauss-függvény (EMG) [16, 18 - 21, 58, 59, 67, 68].
Az EMG modell
Az EMG függvény alkalmazása új csúcsjellemzők bevezetését jelenti a kromatográfiában, melyek a következők [63]:
• retenciós idő (tG);
• a megfelelő Gauss-csúcstól való standard eltérés (σG);
• az exponenciális módosító (τ);
• az aszimmetriát jellemző hányados (τ/σG);
• az adott aszimmetrikus kromatográfiás rendszer elméleti tányérszáma (NSYS);
• adott rendszer maximális hatékonysága (NMAX), ha az összes aszimmetria forrást kiküszöböltük;
• a relatív rendszerhatékonyság (RSE), mely bizonyítja, hogy a csúcsaszimmetria erőteljesen csökkenti a kromatográfiás hatékonyságot;
• a relatív tányérveszteség (RPL).
Az EMG modellt használva számos empirikus összefüggést találunk kromatográfiás csúcsparaméterek meghatározására [63, 69, 70]. Bidlingmeyer [71] valamint Schudel és Guiochon [72] az elméleti tányérszám kiszámítására vonatkozó módszerek pontosságát vizsgálta. Az oszlop hatékonyságának meghatározása céljából nyolc különböző módszert hasonlítottak össze, melyek közül öt módszer a különböző csúcsmagasságokban vett csúcsszélesség értékek (2σ, félérték szélesség, 3σ, 4σ, 5σ) számolásán alapul. A hatodik módszer a csúcsterületből számolja ki a standard deviációt, a hetedik az első és a második momentum arányát veszi figyelembe. Az utolsó összehasonlító módszer aszimmetrián alapszik, amikor is az elméleti tányérszám kiszámításához a 10%-os csúcsmagasságban vett B/A arányt veszik alapul. Schudel és Guiochon megállapították, hogy a csúcsprofil magasabb részeiben mért szélességgel számoló, illetve az 5σ és az aszimmetria módszerek esetén a hatékonysági értékek jóval magasabbak a momentum-módszerrel számítottnál.
Számítógépes kiértékelés során aszimmetrikus csúcsok, valamint zaj esetén mindenképpen a momentum-módszert javasolják az elméleti tányérszám meghatározására. Manuális módszerként az aszimmetrián, illetve az 5σ kiszámításán alapuló módszereket ajánlják.
Aszimmetrikus és zajos kromatogramok információtartalmának (variancia, ferdeség) kinyerésére Yau és Kirkland [73] az EMG függvény felhasználásával egy új módszert (DuPont-módszer) javasol. Ebben az esetben csupán négy paraméter: a retenciós idő, a csúcsmagasság, a csúcsterület és az első momentum (súlypont) meghatározására van szükség. A javasolt módszer elválasztástechnikai alkalmazhatósága igen széleskörű, így a nagyhatékonyságú folyadékkromatográfiában (HPLC), a gázkromatográfiában és a kizárásos kromatográfiában is felhasználható. Később Yau [60] és munkatársai csúcsparaméterek meghatározása céljából az előbb említett módszerüket másik hárommal (momentum- módszer; James-Martin-; Dorsey-Foley-módszer) hasonlították össze, τ/σ ≤ 1 (csúcsferdeség
≤ 0,71) megszorításokat alkalmazva. A momentum-módszer használata általában nem javasolt valós kromatográfiás csúcsok jellemzésére a nem megfelelően pontos
csúcsfelbontási problémák, valamint az alapvonal levágási pontjainak ("cut-points") nehézkes meghatározása miatt. Bár a James-Martin-féle módszer az elméleti tányérszámot nagyon pontosan számolja, csak erősen szimmetrikus görbék illesztésére használható és ferdeséget sem határoz meg. Mind a Dorsey-Foley-, mind a DuPont-módszer alkalmas elméleti tányérszám és ferdeség meghatározására közel szimmetrikus csúcsok, valamint alacsony háttérzaj esetén. Növekvő alapvonal-zaj vagy erősen elhúzódó („tailing”-es) csúcs esetén a DuPont-módszer a legalkalmasabb.
Szimulált, exponenciálisan módosított Gauss-csúcsok momentumainak meghatározására Anderson és Walters [74] ötféle módszert használt fel. Ezek az összegzési-módszer (mely a momentumok integrálással történő kiszámítását jelenti); a Yau-módszer (mely a τ paramétert iterációval határozza meg); a Gauss-aproximációs módszer (melynél a görbe Gauss- csúcsnak van feltételezve és a második momentum kiszámításához a félérték szélességet veszi alapul); valamint Foley-Dorsey kétféle meghatározási módszere 0,1h (B/A0,1) és 0,5h (B/A0,5) csúcsmagasságokban. Vizsgálták továbbá a momentumok kiszámításának hibáit különböző nagyságú (0,1-10%) alapvonal-zaj jelenlétében is. Arra a következtetésre jutottak, hogy az első három módszer esetén az M1, M2 meghatározásának hibája az alapvonal-zaj és τ/σ (0-6,5) növekedésével egyre nagyobb lesz (4%-83%). A Foley-Dorsey módszereknél, melyek csak τ/σ = 3 értékig alkalmazhatóak, a hibaváltozás tendenciája különbözik az előzőekétől. Ezért Anderson és Walters módosította a momentum kiszámításának összefüggéseit oly módon, hogy a módszer szélesebb τ/σ skálán (0-6,5) is alkalmazható legyen.
2.1. A kromatográfiás csúcsot jellemző aszimmetria
A kromatográfiás csúcsok szimmetriájának ismerete igen fontos a digitális jelfeldolgozás szempontjából. A csúcsalak szimmetrikustól való jelentős eltérése nagyon megnehezíti a kromatográfiás jel információinak (retenciós idő, csúcsszélesség, görbe alatti terület, átlapoltság, stb.) meghatározását.
Mivel a valódi kromatográfiás csúcsok nagy része nem szimmetrikus, ezért szükségessé vált az un. aszimmetria faktor bevezetése, mely jellemzi a csúcsot. Az aszimmetria tényező
vizsgálata előtt szükség van a kromatográfiás csúcsok aszimmetrikusságát okozó tényezők ismeretére.
2.1.1. Az aszimmetria okai
A csúcs alakjában fellépő aszimmetriának számtalan oka van, ezek közül a legfontosabbak az oszlop túlterheltsége (az injektált minta mennyisége nagy), az állófázis felület és/vagy az oszloptöltet heterogenitása, az oszlopon kívüli effektusok és az anyagáramlás hatásai (pl. a mozgófázisnak az állófázis részecskék közötti diffúziója vagy az állófázissal való másodlagos kölcsönhatások).
Az állófázis felületének heterogenitását veszi figyelembe a sztochasztikus modell, melyről az előbbiekben már volt szó (ld. I.1.1.2. fejezet). Ez a modell azonban nem veszi azt figyelembe, hogy a kevés aktív hellyel rendelkező állófázison az aktív centrumok könnyen telítődnek és ezáltal egy nemlineáris hozzájárulást is kap az izoterma. Lineáris izoterma esetén a heterogenitás nem eredményez erős aszimmetriát, a borítottság növekedésével közel Gauss-alakú elúciós profilt kapunk. Erre példa a királis elválasztás, amikor a minta molekulái mind a királisan szelektív, mind a királisan nem szelektív gócokhoz is kötődnek. Általában a királisan szelektív gócok száma jóval kisebb, mint a nem szelektív gócoké, ennek következtében a szelektív gócok már alacsony mintakoncentráció esetén is telítődnek, s ezáltal egy nemlineáris hozzájárulás is keletkezik. Királis állófázis esetén még megemlítendő, hogy az adszorpció/deszorpció sebessége a királisan szelektív gócoknál jóval lassúbb, mint a nem szelektíveknél. Ez a heterogén anyagátadás, valamint a királisan szelektív gócok kis száma magyarázza azt a tényt, hogy enantiomerek elválasztása során kis mintakoncentráció esetén is rendre aszimmetrikus ("tailing"-es) kromatográfiás csúcsok figyelhetők meg [75].
Golshan-Shirazi és Guiochon [76] bebizonyították, hogy az erőteljes aszimmetria a nagyon lassú anyagátadás következménye, melyet az elméleti tányérszám szokatlan kis értéke magyaráz. A lassú anyagátadásból eredő aszimmetria az affinitás-kromatográfiás elválasztások során figyelhető meg, de az általánosan előforduló aszimmetria ("tailing",
"fronting") egyéb tényezőknek is köszönhető.
Dondi [8] és Cavazzini [77] a felület heterogenitásának szerepét a sztochasztikus modell finomításával, a karakterisztikus függvény alkalmazásának módszerével tárgyalta. A
heterogenitás nem okoz erős aszimmetriát, ha az adszorpciós izoterma lineáris. Ilyenkor az elúciós profil közelít a Gauss-görbéhez. A lassú anyagátadás hatásával, a csúcsszélesedést okozó adszorpciós/deszorpciós kinetikával és diszperzióval Felinger [78] foglalkozott, kombinálva a sztohasztikus modellt a mozgófázis diszperziójával.
Az oszlopon kívüli hatás ("műszer-effektus") egy másik jelentős forrásként jelentkezik a kromatográfiás elválasztás során fellépő aszimmetrikus csúcsok esetén. A kromatográfiás berendezés bizonyos egységei (pl. elágazások, csatlakozások, illesztések, detektor) keveredést okoznak, mely megnöveli a csúcs szélességét és aszimmetriáját. A csatlakozó csövekben -melyekben a minta egyenletesen áramlik- egy Gauss-típusú sávszélesedés keletkezik. A nagyobb térfogatokban esetlegesen létrejövő keveredések exponenciális lecsengő ágat eredményeznek. Az utóbbi injektálási profillal találkozhatunk gázkromatográfiás elválasztások során, ha az injektor rész hőmérséklete nem elegendően magas [3].
Hsu és Chen [79] gyors Fourier-transzformációt használva szisztematikus elemzéseket végzett a kinetikus paraméterek kromatográfiás csúcsok aszimmetriájára gyakorolt hatására vonatkozóan. Bár az elméleti elemzést gázkromatográfiás csúcsokra végezték el, az eredmények folyadék-kromatográfiás jelekre is alkalmazhatóak. Az elméleti levezetést gömb alakú szemcsés töltetet tartalmazó izotermikus oszlopra alkalmazták, axiális diszperziójú dugószerű áramlást feltételezve. Táblázatos formában összefoglalták az adszorpciós egyensúlyi állandó (KA), az adszorpciós arány (kads) és a részecskék közötti effektív diffuzivitás nagyságának (Dp) hatását a csúcs aszimmetriájára.
2.1.2. A csúcsaszimmetria irodalomból vett meghatározásai
Az irodalomban számos módszer található az aszimmetria faktor meghatározására.
Általában a harmadik statisztikai momentumot (csúcsossági együttható) használják erre a célra, azonban zajos alapvonal esetén az aszimmetria faktor értéke nagymértékben változhat a figyelembe vett digitális pontok számától függően.
Számos olyan módszer létezik, mely nem kívánja meg a csúcsossági együttható vagy egyéb paraméter pontos meghatározását. Gyakoriak a különböző típusú számítások vagy az egyszerű grafikai módszerek, melyek a csúcs aszimmetriáját egyszerűen és gyorsan
megadják. Az elnyúló csúcsok aszimmetria tényezője legegyszerűbben a csúcs adott magasságában vett félérték szélességével adható meg, mind a felszálló, mind a leszálló ágon.
A leggyakrabban használatos aszimmetria faktor kromatográfiás csúcsok jellemzésére a 0,1h csúcsmagasságban mért b/a arány. Foley és Dorsey [17] hibaszámításokkal bebizonyította, hogy Gauss-, közel Gauss- és EMG görbék esetén a 10%-os csúcsmagasságban számított csúcsparaméterek pontosabb értékeket (alacsonyabb RSD határok) eredményeznek, mint az 5, 30 és 50%-os csúcsmagasságban számítottak.
Az EMG függvény alkalmazásánál a csúcs aszimmetriájának jellemzésére a τ/σG arányt használják. Az arány értékének csökkenésével egyre jobban elhúzódó leszálló ágú görbét kapunk, míg τ/σG végtelenhez tartó értékeinél pedig szimmetrikus Gauss-görbéhez jutunk [80]. Mivel az EMG függvény csúcsossági és ferdeségi együtthatója a τ/σ aránnyal fejezhető ki, igen hasznos a b/a és τ/σ arány között empirikus összefüggéseket keresni, melyek az EMG függvény 0,1h csúcsmagasságban vett paraméterein és aszimmetria faktorán alapulnak.
Az aszimmetrikus csúcs varianciája a következő összefüggéssel adható meg:
(
/)
11,15 / 28 476 ,
1 2
2 1 , 2 0
2 '
2= + = − +
a b a
b τ w
σ
µ (23)
ahol w0,1 = a + b, a csúcsmagasság 10%-ánál vett csúcsszélesség. A szórás kiszámítható a 2
, 1 / 27 , 3
1 , 0
= +
a b
σ w (24)
képlettel. A τ paraméter a (23), (24) összefüggések segítségével meghatározható. A csúcsmaximum tm értékének felhasználásával megkapjuk a retenciós időt (tR):
tR= tm − σ [− 0,19(b/a)2 + 1,16 b/a − 0,55] (25) A csúcsparaméterek (23), (24) képlettel való meghatározásának abszolút relatív hibája kisebb, mint 1,5%, feltéve, hogy b/a ≤ 2,76. A különböző magasságokban mért b/a arányok hasonló tendenciát mutatnak a τ/σ arány függvényében, de kisebb csúcsmagasságokban nagyobb a τ/σ aránytól való függés érzékenysége [26].
McWilliam és Bolton [81] az EMG görbe alatti területet vizsgálta különböző csúcsmagasságoknál és arra a következtetésre jutott, hogy a relatív terület nagyon fontos jellemző az aszimmetria és csúcsalak meghatározása során.
Az aszimmetrikus csúcsok retenciós idejének definíciója nincs kellőképpen tisztázva.
Retenciós időnek vehetjük a csúcsmaximum helyét, a súlypontot, vagy a csúcs első momentumát ("mean"). Súlypontnak megfelel az az idő, amely alatt a minta 50%-a eluálódott az oszlopról; elhúzódó leszálló ágú ("tailing"-es) csúcs esetén a súlypont a görbe leszálló ágára esik. Manapság integrátorral rutinszerűen meghatározható a kromatográfiás csúcs súlypontja, mivel ez a pont megtalálható a görbén a terület 50%-os határánál. Az első momentum ennél távolabb esik. A maximum, a súlypont és az első momentum már mérsékelten aszimmetrikus csúcs esetén is eltér egymástól.
Az US Pharmacopeia (USP) egy másik aszimmetria faktor (T faktor) bevezetését javasolja a csúcs aszimmetriájának jellemzésére. A T faktorra, mely az 5%-os csúcsmagasságban vett a és b félérték szélesség paraméterek mérésén alapszik, a következő összefüggés érvényes:
T a b
= +a
2 (26)
A T faktor értéke nagyon közel van az aszimmetria faktoréhoz, amikor a csúcs aszimmetriája mérsékelt. A két faktor közötti összefüggés függ a görbe alakjától. Ha például az aszimmetrikus csúcs leírható az EMG modell segítségével, akkor a következő összefüggés áll fenn:
T = 0,6 (b/a)0,1 + 0,4 (27)
BiGauss csúcsalak esetén az összefüggés a következőképpen módosul:
T = 0,5 (b/a)0,1 + 0,5 (28)
Farman és munkatársai [82] bevezettek egy olyan aszimmetria faktort, mely független a kromatográfiás adatsorra illesztett modell alakjától és a következőképpen definiálható:
0 1
0
t t tm
−
= −
χ µ (29)
ahol
tm - a csúcsmaximum helye, µ1 - az első momentum, t0 - a holt idő.
Az aszimmetria faktor egységnyi, ha a csúcsmaximum megegyezik az első momentummal, és zérus, ha a csúcsmaximum egyenlő a holt idővel.