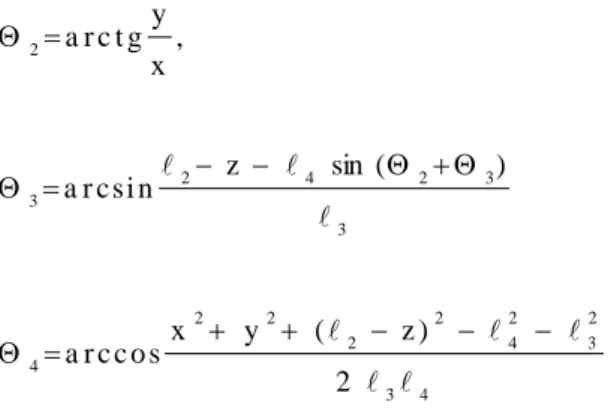TARTALOM
5. ROBOTOK IRÁNYÍTÓ RENDSZERE ... 7
5.1. Robotok belső adatfeldolgozásának struktúrája ... 7
5.2. Koordináta transzformációk ... 10
5.2.1. Forgatás ... 10
5.2.2. R-P-Y szögek ... 12
5.2.3. Homogén transzformációk ... 14
5.2.4. Denavit–Hartenberg-transzformáció ... 15
5.2.5. Jakobi mátrix ... 36
5.3. Robotok dinamikai rendszere és mozgásegyenletei ... 41
5.3.1. Tehetetlenségi tenzor ... 41
5.3.2. Robotok mozgásegyenletei ... 45
5.3.3. Robotok dinamikai modelljei ... 47
5.4. A robotmozgás inverz feladata ... 61
5.5. Hajtónyomatékok számítása aritmetikai processzorral ... 66
5.6. PTP és CP irányítás ... 69
5.6.1. PTP irányítás ... 69
5.6.2. CP irányítás ... 71
5.7. Számított hajtónyomatékok realizálása ... 74
5.8. Robotok hajtásszabályozása ... 76
5.9. Ellenőrző kérdések ... 83
6. ROBOTOK PROGRAMOZÁSA... 84
6.1. Robotok pályagenerálása betanító és világ koordináta-rendszerben való programozás esetén ... 84
6.1.1. Pályagenerálás betanító programozással ... 84
6.1.2. Pályagenerálás világ koordinátarendszerben ... 85
6.2. A CP programozás elve betanító programozással ... 100
6.3. A PTP programozás elve betanító programozás esetén ... 101
6.4. Programszerkesztés betanító programozási rendszerekhez ... 101
6.5. Programszerkesztés elvei világ koordinátarendszerű programozási rendszerekben ... 103
6.6. Ellenőrző kérdések ... 104
7. ROBOTOK ALKALMAZÁSA ... 106
7.1. Robotos anyagkezelő rendszerek ... 106
7.2 Robotos technológiai rendszerek... 109
7.2.1. Gyártócellák ... 109
7.2.2. Robotos festőrendszerek ... 110
7.2.3. Robotos hegesztő rendszerek ... 113
7.2.4. Robotos vágó rendszerek ... 115
7.3. Mobil robotos rendszerek ... 117
7.4. Anyagkezelési és technológiai segédberendezések ... 118
7.5. Robotok alkalmazása az orvostechnikában ... 121
7.6. Ellenőrző kérdések ... 124
8. ROBOTOK VIZSGÁLATA ... 125
8.1. Robotok vizsgálatának elvei, vizsgálati paraméterek ... 125
8.2. Robotok pályakövetési pontosságának vizsgálata ... 127
8.3. Robotok beállási pontosságának és ismétlőképességének vizsgálata . 137 8.4. Robotok munkatér vizsgálata ... 147
8.5. A robotok egyéb jellemzőinek vizsgálata ... 157
8.5.1. Mozgó tárgy követésének pontossága ... 157
8.5.2. Legkisebb programozható lépés ... 158
8.5.3. Merevségi vizsgálatok ... 158
8.5.4. Zajvizsgálatok ... 160
8.6. Ellenőrző kérdések ... 163
9. FELADATOK ... 164
IRODALOMJEGYZÉK ... 177
5. ROBOTOK IRÁNYÍTÓ RENDSZERE
A robotok irányító rendszerének legfontosabb feladata, hogy a TCP pont előírt pályájához a szükséges csuklókoordinátákat (ij (t), sij (t)) megha- tározza, és azokat a hajtórendszerek és a szenzorikai rendszerek segítségével végrehajtsa. Az irányítórendszer ezen túlmenően még több feladatot is ellát,
- kapcsolatot tart a robot környezetével, - felügyeli a hajtásszabályozó rendszert, - biztosítja a programok tárolását,
- felügyeli a különböző egységek közötti adatkommunikációt.
5.1. Robotok belső adatfeldolgozásának struktúrája
A robotok irányító rendszere standard modulokból épül fel, amelyek a robot üzemeltetésében meghatározott részfeladatokat látnak el. Külön-bőző gyártó cégek ezeket a modulokat különféleképpen strukturálják, abban azon- ban megegyeznek, hogy mindegyikben található
- CPU modul, - szervo modul, - memória modul, - input-output modul.
Abban már eltérés van, hogy bizonyos kezelőszervek vagy egységek adat- kommunikációja közvetlenül a fenti modulok valamelyikéhez kapcsolódva, vagy pedig egy illesztőegység közbeiktatásával buszrendszeren keresztül történik.
Az 5.1. ábra egy buszrendszeren keresztül történő adatkommunikációt mutat.
Az 5.2. ábra a TRALLFA TR-400 Mk.2. tip. irányítórendszer felépítését mu- tatja. Az összehasonlításból látható, hogy az utóbbi struktúrában az irányítási feladatnak megfelelően új modulok is megjelennek és a kezelőszervek köz- vetlenül a modulokhoz kapcsolódnak.
RAM ROM EPROM Központi processzor Arithmetikai
processzor
Display - kijelzõ kezelõ egység
Külsõ tároló Disk
Terminál Programfelvétel
PHG
Programkorrekció
Tengely helyzet- szabályozó
Bináris I/O illesztõ egység
Szenzor I/O illesztõ egység Analóg
Digitális párhuzamos Digitális soros
1. Tengely
2. Tengely
n. Tengely
Motor Tachométer
Út/szögadó Végálláskapcsoló
Bemenet Kimenet
Bemenet Kimenet Központi busz
5.1. ábra
RAM ROM EPROM Központi
processzor Arithmetikai
processzor
Display - kijelzõ kezelõ egység
Külsõ tároló Disk
Terminál Programfelvétel
PHG
Programkorrekció
Szenzor I/O illesztõ egység Analóg Digitális párhuzamos Digitális soros
Bemenet Kimenet Központi busz
Merev lemez Szervo modul
Memória modul
Analóg modul
Input-Output modul
Zener
Bináris I/O illesztõ egység
Festékszóró fej (pisztoly) Szelep
vezérl.
Robot
diódák
5.2. ábra
5.2. Koordináta transzformációk
A robotok mozgását felfoghatjuk úgy is mint a robotkarokhoz rögzített koordinátarendszerek (frame koordinátarendszerek) relatív helyzetének vál- tozását. Ennek megfelelően a TCP pont világkoordináta-rendszerbeli helyze- te a karokhoz rögzített koordinátarendszerek transzformációjával előállítha- tó, ha ismerjük a koordinátarendszerek relatív helyzetét meghatározó idő- függvényeket.
A továbbiakban a robotspecifikus koordináta transzformációkat tekint- jük át.
5.2.1. Forgatás
A koordinátageometriából ismert módon a z tengely körüli forgatást (5.3. ábra) az
x
y z1
1
1
y2
x2
z2
1
1
1
5.3. ábra
1 0 0
0 cos
sin
0 sin
cos ) z
( 1 1
1 1
z Rot
R , (5.1)
mátrix segítségével írhatjuk le. Hasonló mátrixok képezhetők az x és y tengelyek körüli forgatásra is, ahol 1 és 1 a koordináta tengelyek körüli elfordulások szöge, így
R xR o t x
( ) co s sin
sin co s
1 0 0
0 0
1 1
1 1
, (5.2)
R yR o t y
( )
co s sin
sin co s
1 1
1 1
0
0 1 0
0
. (5.3)
Ha bármelyik két mátrixot összeszorozzuk, akkor a két tengely körüli együt- tes forgatás mátrixához jutunk:
1 1
1 1 1
1 1
1 1 1
1 1
1 1
1 1
1 1
1 1
x z
cos sin
0
sin cos cos
cos sin
sin sin cos
sin cos
cos sin
0
sin cos
0
0 0
1
1 0 0
0 cos
sin
0 sin cos
) x ( ) z (
Rot
Rot R R
. (5.4)
A három mátrix összeszorzásából a három tengely körüli egyidejű forgatás mátrixa adódik:
1 1 1
1 1
1 1 1 1 1 1
1 1
1 1 1 1
1 1 1 1 1 1
1 1
1 1 1 1
1 1
1 1
1 1
1 1 1
1 1
1 1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
y x z
cos cos sin
sin cos
cos sin cos sin sin cos cos sin
cos cos cos sin
cos sin sin sin cos cos sin sin
sin sin cos cos
cos 0 sin
0 1 0
sin 0 cos
cos sin
0
sin cos cos
cos sin
sin sin cos
sin cos
cos 0 sin
0 1 0
sin 0 cos
cos sin
0
sin cos
0
0 0
1
1 0 0
0 cos sin
0 sin cos
) y ( ) x ( ) z
( Rot Rot
Rot R R R
(5.5)
5.2.2. R-P-Y szögek
Az orientáció jellemzésének egy másik módja a csavarás (Roll), bil- lentés (Pitch) és forgatás (Yaw) szögek használata. Az 5.4. ábrán lévő
z
y
x
R
Y
P
5.4. ábra
szögjelöléseket alkalmazva, és az R-P-Y sorrendnek megfelelően össze- szorozva R (z), R (y), R (x) mátrixokat;
cos cos sin
cos sin
cos sin sin sin cos sin
sin sin cos cos cos
sin
cos sin cos sin
sin sin
sin cos cos sin cos
cos
cos sin
0
sin cos
0
0 0
1
cos 0
sin
sin sin cos
cos sin
sin cos sin
cos cos
cos sin
0
sin cos
0
0 0
1
cos 0 sin
0 1 0
sin 0 cos
1 0 0
0 cos sin
0 sin cos
) x ( ) y ( ) z ( )
, ,
( Rz Ry Rx Rot Rot Rot
RPY
(5.6) forgató mátrixhoz jutunk, amely az 5.5. ábra szerinti forgatást eredményezi.
x
y z1
1
1
y2
x2 z2
z2
y2
x2 z3
y3
x3
z4
y3 z3
x3 y
4
x4
5.5. ábra
5.2.3. Homogén transzformációk
Tekintsük az 5.6. ábrán lévő x1; y1; z1 és x2; y2; z2; koordináta- rendszer P (x1P; y1P; z1P) és P (x2P; y2P; z2P) pontja közötti összefüggést az alábbi bázis független alakban:
r1 = r2 + p. (5.7)
x y
z2
2
2
x1 z1
y1
P
x1P
x2P
y1P y2P
z1P z2P
p r
1
r2
e1 e2 e3
5.6. ábra
Legyenek továbbá e1; e2; e3 az x2; y2; z2 koordinátatengely irányú egység- vektorok az i; j; k bázisában. A fenti bázis független alak e1; e2; e3 ismere- tében az alábbi formában írható fel:
1 1 1
2 2 2
1 3 1 2 1 1
1 3 1 2 1 1
1 3 1 2 1 1
2 2 2
1 3 1 2 1 1
1 3 1 2 1 1
1 3 1 2 1 1
1 1 1
z y x
z z z
y y y
x x x
z z z
y y y
x x x
p p p
z y x
e e e
e e e
e e e
z y x
e e e
e e e
e e e
z y x
p (5.8)
Írjuk fel a fenti mátrixegyenletet az alábbi alakban:
1 1 1
1 0 0 0 1
2 2 2
2 2 2
1 1 3 1 2 1 1
1 1 3 1 2 1 1
1 1 3 1 2 1 1
1 1 1
z y x
z y x
p e e e
p e e e
p e e e
z y x
T z
z z z
y y y y
x x x x
0 p
A , (5.9)
amelyből megállapíthatjuk, hogy az első három egyenlete azonos az előző- ekben felírt mátrixegyenlettel, az utolsó egyenlete pedig az 1 = 1 azonosság, így a két mátrixegyenlet ekvivalens. A fentiek alapján az
x y z
1 1 1
(5.10)
vektor homogén koordinátás alakjának az 1 értékű negyedik koordinátával kiegészített
x y z
1 1 1
1
(5.11)
vektort nevezzük.
5.2.4. Denavit–Hartenberg-transzformáció
A robotkarok csuklóval való kapcsolódása általános kialakítást tekint- ve az 5.7. ábra szerinti kinematikai láncot adja. Az ábrán így általánosan be-
mutatható a karokhoz rögzített koordinátarendszerek egymáshoz viszonyított helyzete, illetve egymásba való transzformációja. Tekintsük a két egymást
ai
si
xi -1 yi -1
zi -1
x i yi z i
i
Kar i +1 Kar i
Kar i -1 Csukló i - 1
Csukló i
Csukló i + 1
i
i+1
5.7. ábra
követő koordináta rendszert az 5.8. ábrán megadott jellemzőkkel adottnak.
Az x2 y2 z2 koordinátarendszer tengelyei 2 és 2 szöggel való elforgatás után x1 y1 z1 koordinátarendszer irányával azonosak lesznek, ezt a transzfor- mációt a
2 2
2 2 2
2 2
2 2 2
2 2
12
cos sin
0
sin cos cos
cos sin
sin sin cos
sin cos
R (5.12)
forgatómátrix hajtja végre. Ahhoz, hogy a két koordinátarendszer
2
2
2 x y
z 2
2
2
x1 z1
y1 s
2
a2
P
x 1P
x2P
y1P
y2P
z1P z2P
5.8. ábra
teljesen fedje egymást még az x2 y2 z2 koordinátarendszer kezdő pontját
2 2 2
2 2
s sin a
cos a
p (5.13)
mértékkel el kell tolni. Az (5.12) mátrix bővíthető az (5.13) vektorral. Ho- mogén koordinátákat alkalmazva az x1 és z1 tengely körüli forgatást és az x1, y1 és z1 tengely menti eltolást együttesen értelmező ún. Denavit–Hartenberg- mátrixhoz jutunk;
1 0
0 0
s cos
sin 0
sin a sin
cos cos
cos sin
cos a sin
sin cos
sin cos
2 2
2
2 2 2 2 2
2 2
2 2 2 2 2
2 2
DH 12
(5.14) Az 1 és 2 koordinátarendszer közötti transzformáció
x1 = DH12 x2 (5.15) mátrixegyenlettel írható le, ahol
x1
1 1 1
1
x y
z , (5.16)
x2
2 2 2
1
x y z
, (5.17)
illetve
1 z y x
1 0
0 0
s cos
sin 0
sin a sin
cos cos
cos sin
cos a sin
sin cos
sin cos
1 z y x
2 2 2
2 2
2
2 2 2 2 2
2 2
2 2 2 2 2
2 2
1 1 1
.
(5.18) A fenti elvek egyenesbe vezetéses kinematikai lánc esetén is alkalmaz- hatók – 5.9. ábra.
5.9. ábra
Több robotkar egymáshoz kapcsolásával létrejövő esetben is értelmez- hető az (5.15) illetve az (5.18) alatti feladat. Ez esetben egyes koordináta- rendszerek transzformációját megvalósító DH mátrixok összeszorzódnak és az (5.15) egyenlet
x1 = DH1n · xn (5.19) egyenletté alakul át.
A robotirányítás gyakorlatában a Denavit–Hartenberg-transzformációnak nem az (5.19) összefüggéssel meghatározott formáját alkalmazzák. Az esetek nagy többségében nem adott forgatási szög és az eltolási mértékhez kell va- lamelyik koordinátát meghatározni, hanem a koordináták és az eltolási mér- ték ismeretében kell előállítani a forgatási szögeket. A koordinátarendszerek célszerű felvételével a forgatási szögek megegyeznek a robot csukló koordi- nátáit megvalósító szögelfordulásokkal.
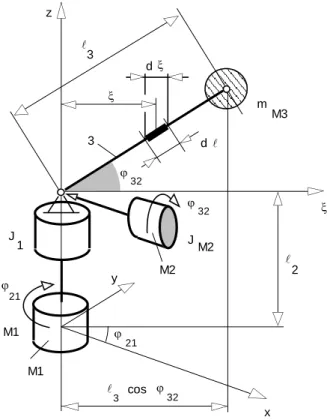
Alkalmazzuk a fenti elvet az 5.10. ábrán lévő robotra.
ai
si
xi - 1
yi - 1
zi - 1
x
i
yi
z i
i
Kar i +1 Kar i
Kar i -1 Csukló i - 1
Csúszka i
Csukló i + 1
i
i+1
= const
P(x;y;z) = TCP
3
4
2
x y
z
x1
x2 x
3
x4
y1
y2 y
3
y4
z1
z2
z 3
z4
3 4
5
2
2
x y
z
5.10. ábra
A robotkarok geometriai méretei alapján az eltolási mértékek:
. 0
, 0
, 90
, a
, a
, 0 a
, 0 s
, 0 s
, s
4 3
o 2
4 4
3 3 2 3 3
2 2
Ennek megfelelően az egyes DH-mátrixok:
1 0
0 0
0 1 0
0 cos
0 sin
0 sin
0 cos
2 2 2
2 2
12
DH , (5.20)
1 0
0 0
0 1
0 0
sin 0
cos sin
cos 0
sin cos
3 3 3
3
3 3 3
3
23
DH , (5.21)
1 0
0 0
0 1
0 0
sin 0
cos sin
cos 0
sin cos
4 4 4
4
4 4 4
4
34
DH . (5.22)
A három mátrix összeszorzásából kapjuk,
D H1 4 D H1 2 D H2 3 D H3 4
mátrixot, amellyel végrehajtható P = TCP pont x4 y4 z4 koordináta- rendszerből x1 y1 z1 illetve xyz világkoordináta-rendszerbe való transzfor- málása. Ha jobban szemügyre vesszük az 5.10. ábrát, megállapíthatjuk, hogy a P = TCP az x4 y4 z4 koordinátarendszer kezdőpontjában van, így az
x4 0 0 0 1
(5.23)
homogén koordinátákkal jellemezhető. A transzformációhoz (5.19) alapján
x1 D H1 4 x4 (5.24.) mátrixegyenlet felhasználásával jutunk, amelyet részletezve
x y z 1
0 0 0 1
1 4
D H (5.25)
összefüggést kapjuk. Az előzőekből ismert, hogy D H1 4 implicite tartal- mazza 2,3 és 4 változókat. (5.25) egyenletrendszer 2,3 és 4 -re való megoldásából
4 3
2 3 2 4 2 2 2 2
4
3
3 2 4
2 3
2
2 ) z ( y sx o c c r a
) (
sin n z
i s c r a
, x gy t c r a
(5.26)
összefüggések adódnak, amely minden összetartó x; y; z értékhez - az 5.10.
ábra koordinátarendszer elhelyezése alapján - kiszámítható. Ha x = x (t), y = y (t) és z = z(t) időfüggvények, akkor i i( )t is időfüggvény lesz.
Példaként határozzuk meg a Denavit–Hartenberg-mátrixok segítségével az 5.11. ábrán látható robotkar P pontjának helyzetét 230-os szög- elfordulás megtétele után az x1, y1, z1 koordinátarendszerben. Az ábrán vázolt helyzet a 2 0o, 3 0o szöghelyzetnek felel meg.
z1
x1
y1 x
2 x
3 z2
a3 s 3
s2
2
3
P = O
x ( t ) 1 y ( t )
1
z ( t ) 1
2= - 90
O2
y2
z3
y3 3
5.11. ábra
A robotkaron három koordinátarendszert helyeztünk el. Látható, hogy a P pont a 3 koordinátarendszer 03 kezdőpontjával egyezik meg. Az egyes koordinátarendszerek eltolásának és elforgatásának mértékét is az ábra mu- tatja.
- Transzformáció az 1-2 koordinátarendszer esetén;
mm .
500 s
, 90
, 0
, mm 0 a
2 2
2 2
(5.14) felhasználásával az 1-2 koordinátarendszer közötti transzformációt megvalósító Denavit–Hartenberg-mátrix általánosan és a kiszámított értékei- vel
1 0
0 0
s cos
sin 0
sin a sin
cos cos
cos sin
cos a sin
sin cos
sin cos
2 2
2
21 2
2 2 2
2 2
2 2
2 2 2
2 2
DH12
(5.27)
1 0 0 0
500 0 1 0
0 1 0 0
0 0 0 1
DH12 (5.28)
- Transzformáció a 2-3 koordinátarendszer esetén;
. 0
, 0
, mm 200 s
, mm 600 a
3 3 3
3
A transzformációs mátrixok (5.14) felhasználásával:
, 1 0
0 0
s cos
sin 0
sin a sin
cos cos
cos sin
cos a sin
sin cos
sin cos
3 3
3
3 3 3 3 3
3 3
3 3 3 3 3
3 3
23
DH
(5.29) illetve a kiszámított értékek:
. 1 0 0 0
200 1 0 0
0 0 1 0
600 0 0 1
23
DH (5.30)
Az 1 és a 3 koordinátarendszer közötti transzformációt megvalósító mátrix:
D H1 3 D H1 2 D H2 3 , (5.31) illetve a számértékeivel
D H1 3
1 0 0 600
0 0 1 200
0 1 0 500
0 0 0 1
. (5.32)
A P pont helyzetét leíró vektor a 3 koordinátarendszerben homogén koordi- nátákkal megadva:
x3 0 0 0 1
. (5.33)
Az 1 koordinátarendszerbe áttranszformált P pont az
x1 D H1 3 x3 (5.34) mátrix szorzás végrehajtásával
x1
1 0 0 6 0 0
0 0 1 2 0 0
0 1 0 5 0 0
0 0 0 1
0 0 0 1
6 0 0 2 0 0 5 0 0 1
, (5.35)
adódnak amelyből a koordinátákra x1 6 0 0, y1 2 0 0; z1 5 0 0 mm adó- dik.
A mátrixokat 230 és 360 értékekre is elvégezve (5.27) és (5.29) mátrixok értékei módosulnak.