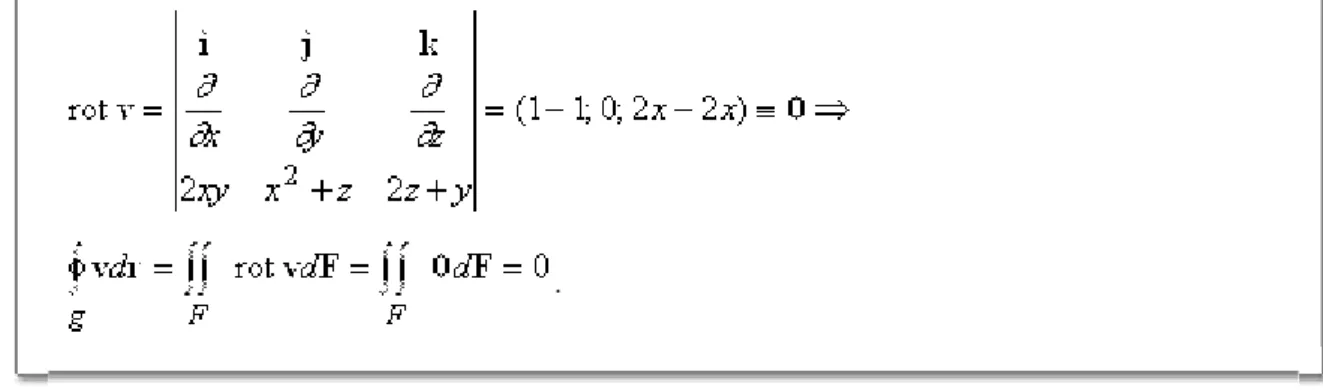M ATEMATIKA II.

K

B

,

M ^ATEMATIKA II.

7

VII. V

1. E

Az u függvényt skalár-vektor függvénynek nevezzük, ha értelmezési tartománya a háromdimenziós tér vektorainak halmaza, a függvényértékek pedig valós számok. Jelölése:

. (1) Ezt a függvényt szokás skalártérnek is mondani.

Az (1) függvény szintfelületei az felületek (C állandó).

Az u függvény deriváltja a

(2)

vektor (gradiens vektor).

Az u függvény e irányban vett iránymenti deriváltja a

(3)

skaláris szorzat (e egységvektor).

A gradiens formális jelölése lehetséges módon (olv. "nábla u"), ahol

(4)

A vektor önmagával vett skaláris szorzata a

(4/a)

Laplace-operátor, és .

Legyen a g görbe egyenlete . Ekkor az u skalár-vektor függvény g

görbe menti, ívhossz szerinti vonalintegrálja:

. (5)

Látható, hogy integrálás előtt az függvénynél elvégeztük az

helyettesítést. Szokás azt mondani, hogy a függvényt lokalizáltuk a görbére. Valójában a függvény leszűkítéséről van szó.

Ha , akkor az (5) integrál értéke a görbe ívhosszával egyenlő. Ha u = f(x, y) kétváltozós függvény, g pedig az (x, y) -síkban fekvő görbe, akkor

. (6)

Ha , akkor ez geometriailag a g vezérgörbéjű, z -tengellyel párhuzamos alkotójú henger palástjából annak a darabnak a felszínével egyenlő, amely a z = 0 sík és a z = f(x, y) felület közé esik.

Az u függvény g görbe menti, x, y, ill. z koordináta szerinti vonalintegrálja:

, , ill. . (7)

Legyen az F felület egyenlete . Ekkor az u függvény F felületre vonatkozó felszíni integrálja:

, (8)

ahol T az F felületdarabnak megfelelő tartomány, a t, v síkon.

Ha az F felület egyenlete z = f(x, y), akkor a (8) integrál a következő alakú lesz:

. (8/a)

Az u függvény F felületre vonatkozó, az (x, y), (x, z), ill. (y, z) koordinátasíkon való vetület szerint vett felületi integrálja:

ill. . (9)

A vektor-vektor függvény értelmezési tartománya is, értékkészlete is vektorokból áll. Jelölése:

. (10)

Ezt a függvényt szokás vektortérnek is mondani.

A v vektor-vektor függvény divergenciája:

, (11)

rotációja:

. (12)

Ha , akkor a vektorteret forrásmentesnek, ha , akkor örvénymentesnek mondjuk.

A v vektor-vektor függvény g görbe menti (skalár értékű) vonalintegrálja:

. (13)

A v függvény F felületre vonatkozó (skalár értékű) felületi integrálja:

, (14)

ahol a felület egyenlete, T pedig a felületdarabnak megfelelő tartomány.

Ha a felület egyenlete z = f(x, y), akkor felfelé mutató normális esetén

dF . (15)

A Gauss-Osztrogradszkij-tétel. Legyen div v folytonos az F sima felülettel határolt zárt V térrészben. Ekkor

, (16)

ahol a dF felületi normálvektor kifelé mutat (külső normális).

A Stokes-tétel. Legyen folytonos a korlátos, sima F felület pontjaiban. Ekkor

, (17)

ahol g az F felület(darab) határgörbéje, amely dF irányából szembenézve, az óramutató járásával ellentétes irányítású.

A Stokes-tétel síkbeli alakjához jutunk, ha v = (P(x, y), pedig az (x, y) - síknak a g görbével határolt T része. Ekkor a Green-formulának nevezett tétel:

. (18)

Ha , vagyis v örvénymentes, akkor az vonalintegrál független a görbe alakjától, annak értéke csak a g görbe kezdőpontjától és végpontjától függ. Ilyenkor a teret potenciálosnak is mondjuk. Ekkor létezik olyan u(r) skalárvektor függvény, ún. potenciálfüggvény, hogy grad u(r) = v (r), és

. (19)

Itt A a g görbe kezdőpontja, B pedig végpontja.

A potenciálfüggvény a grad u = v feltételből határozható meg. Ez a feltétel az alábbi egyenletekre vezet:

. (20)

2. M

Megoldások: láthatók nem láthatók 1. Írjuk fel az függvény szintfelületeinek egyenletét.

Megoldás. A szintfelületek egyenlete u(x, y, z) = C. Tehát formálisan írjunk u helyébe C -t. Ekkor

, azaz . Ez a szintfelületek egyenlete. Ezek a

felületek forgási paraboloidok. C különböző értékeihez különböző felületek tartoznak. Például C = 4

esetben a .

2. Írjuk fel az alábbi függvények gradiensét:

a) ; b) .

Megoldás. Használjuk a (2) képletet:

a) ;

b)

.

3. Számítsuk ki az alábbi függvények adott a irányú iránymenti deriváltját az adott helyen.

a) , ,

b) ; .

Megoldás. Használjuk a (3) formulát.

a) ,

.

Az irányt most az a vektorral adtuk meg, amely azonban nem egységvektor. Vegyük ezért ennek az egységvektorát, és legyen most ez az e egységvektor, azaz

.

Az iránymenti derivált:

.

b) ,

.

Az irány most a grad u vektor iránya. Ennek egységvektora lesz az e vektor, azaz . Ekkor a (3) képlet szerint:

.

4. Számítsuk ki az függvény g görbe menti, ívhossz szerinti vonalintegrálját, ha g az r = (cos t, sin t, t) csavarvonal íve.

Megoldás. Az (5) képletet használjuk. A görbe skaláris egyenletrendszere: x = cos t, y = sin t, z = t. Ekkor

,

.

5. Számítsuk ki az körhenger palástjából annak a résznek a felszínét, amely a z = 0 és a z = 2 – x síkok közé esik (4.8. ábra).

4.8. ábra

Megoldás. A (6) formulát használjuk arra az esetre, amikor u = 2 – x, a görbe paraméteres egyenletrendszere pedig:

x = 2cos t, y = 2sin t.

Ekkor

A palást felszíne:

6. Számítsuk ki az alábbi vonalintegrálokat a megadott görbék mentén:

a) , g : r = (sin t, cos t, t);

b) , g : r = (a(t t), a(1 – cos t), 0), .

c) , g : x = a cos t, y = a sin t, z = bt, .

Megoldás. Használjuk a (7) képleteket.

a) Most zárt görbe mentén kell integrálni, így az integrálás határai 0 és . x = sin t, y = cos t, z = t, dx = cos t dt.

Elvégezve a lokalizálást:

x + y + z = sin t + cos t – sin t = cos t.

Így az integrál:

.

b) x = a(t t), y = a(1 t), dx = a(1 t)dt, dy = a sin t dt. Ezeket a helyettesítéseket elvégezve, az integrál:

.

c) Elvégezve a lokalizálásokat, és figyelembe véve, hogy dx = sin t dt, dy = a cos t dt, dz = b dt, az integrál:

.

7. Számítsuk ki az alábbi felszíni integrálokat:

a) , ahol F az x + y + z = 2 síknak az első térnyolcadba eső része;

b) , ahol F a egyenlőtlenséggel meghatározott test (kúptest) határa.

Megoldás. Használjuk a (8/a) képletet:

a) Itt u = x + y + z, a felület egyenlete pedig . Ekkor

, u leszűkítése a felületre (a lokalizált u):

u = x + y + = 2. Az integrációs tartomány (a felületdarab vetülete vetülete az (x, y) - síkra) a 4.9. ábrán látható.

4.9. ábra

Az integrál:

.

b) A test határa a kúpfelület része ( ), és a z = 1 magasságban lévő körlap ( ). A 4.10. ábra az (x, z) síkkal való metszetet mutatja.

4.10. ábra

Az integrált ennek megfelelően két részletben számítjuk. Az felület esetében

, ,

.

Az felület esetén , . Alaptartomány mindkét esetben

az körlap. Az integrál:

.

8. Számítsuk ki az alábbi, vetület szerint vett felületi integrálokat:

a) , ahol F az x + y + z = 2 síknak az első térnyolcadba eső része;

b) , ahol F a egyenlőtlenséggel meghatározott test (kúptest) határa.

Megoldás. Használjuk a (9) képleteket:

a) Legyen most a felület egyenlete y = . Ekkor u = 2. Az alaptartomány a felület (x, z) - síkon lévő vetülete. Ez a 4.9. ábrán látható háromszög, csak az y tengely szerepét a z tengely veszi át. Az integrál:

.

b) A 7.b) példához hasonlóan az integrált két részletben számítjuk:

.

9. Számítsuk ki az alábbi vektor-vektor függvények divergenciáját és rotációját. Számítsuk ki a divergenciát és rotációt a pontban is:

a) v = r = (x, y, z), (2; ; 5);

b) , ( ; 1; 4);

c) , P(0; 2; );

d) , (1; ; 3).

Megoldás. Használjuk a (11) és (12) képleteket.

a) , .

,

.

b) ,

,

,

.

c) ,

.

.

d) , .

, .

10. Számítsuk ki az alábbi függvények vonalintegrálját a megadott görbék mentén:

a) v = (x – y, y – z, z – x), g : r = (cos t, sin t, cos t), ;

b) , , z = 0, , ;

c) v = (2y, 3z, x), g a , pontokat összekötő szakasz.

Megoldás. Használjuk a (13) képletet úgy, hogy a v függvényt lokalizáljuk a g görbére.

a) A görbe egyenletéből látható, hogy

x = cos t, y = sin t, z = cos t, dx = t dt, dy = cos t dt, dz = t dt. v = (cos t – sin t, sin t – cos t, cos t – cos t).

Az integrandusz:

. Az integrál:

.

b) A görbe origó középpontú, a sugarú kör első síknegyedbeli része. Paraméteres egyenletrendszere: x = a cos t, y = a sin t, z = 0, .

, dx = sin t dt, dy = a cos t dt, dz = 0.

Az integrál:

.

c) Előbb írjuk fel a 1; 1; 2), (2; ; 4) pontokat összekötő görbe (egyenes) egyenletét. Az

irányvektor: . Az egyenes egyenlete:

azaz x = 1 + t, y = 1 – 4t, z = 2 + 2t, ).

Mivel dx = dt, dy = – 4dt, dz = 2dt, az integrál:

11. Számítsuk ki az alábbi függvények felületi integrálját felfelé mutató felületi normális mellett:

a) v = (x + 1; y + z; x + y + z), a felület pedig az x + y + z = 2 síknak az első térnyolcadba eső része (4.11. ábra);

b) v = r = (x, y, z), a felület pedig az , félgömb;

c) v = (2x, x + y, z), a felület pedig az r = (u cos v, u sin v, av) csavarfelület , része.

4.11. ábra

Megoldás. Használjuk a (14) és (15) képleteket.

a) v lokalizálva a z = 2 – x – y felületre:

v = (x + 1; y + 2 – x – y; x + y + 2 – x – y) = (x + 1; 2 – x; 2).

A felfelé mutató dF vektor a (15) szerint:

dF .

Az integrálási tartomány a 4.9. ábrán látható. Az integrál:

.

b) A felső félgömb egyenlete: . Mivel ,

, a felfelé mutató dF vektor

dF .

Az integrandusz:

.

Az alaptartomány az körlap, így az integrál:

.

c) A felület paraméteres egyenletrendszere:

x = u cos v, y = u sin v, z = av.

A felületre lokalizált v vektor:

v = (2u cos v, u cos v + u sin v, av).

A felfelé mutató dF vektor:

.

Az integrandusz:

. Az integrál:

12. Számítsuk ki a Gauss-Osztrogradszkij-tételben szereplő integrálokat, ha , és a V térrészt a paraboloid és a z = 0 sík határolja.

Megoldás. A V térrész (x, z) - síkkal való metszete a 4.12. ábrán látható.

4.12. ábra

Előbb kiszámítjuk a tétel bal oldalán álló hármas integrált.

div v = 1 + 2 + 2 = 5,

.

Itt kihasználtuk azt, hogy a T tartomány az körlap.

A tétel jobb oldalán szereplő integrált két részletben kell számítani, mert a V térrészt határoló felület két részből áll. A kifelé mutató normális miatt a paraboloidhoz tartozó vektor felfelé mutat, a z = 0 síkhoz tartozó pedig lefelé (4.12. ábra). Ennek megfelelően

, .

A paraboloidra lokalizált v vektor és skaláris szorzata:

. A z = 0 síkra lokalizált v vektor és skaláris szorzata:

. A tétel jobb oldalán szereplő integrál:

.

13. Gauss-Osztrogradszkij-tétel felhasználásával számítsuk ki a v = (2x + z, y , x függvény felületi integrálját az gömbfelületre, kifelé mutató normális mellett.

Megoldás. A felületi integrál helyett számítsuk ki div v hármas integrálját. Mivel div v = 2 + 1

= 2, ezért

.

Itt kihasználtuk azt, hogy értéke a V gömbtest térfogatával egyenlő.

14. Számítsuk ki a Stokes-tételben szereplő integrálokat, ha

v = ), a felület pedig a paraboloid része.

Megoldás. A felület és annak határgörbéje a 4.13. ábrán látható. A határgörbe egy 2 sugarú kör.

Paraméteres egyenletrendszere:

x = 2 cos t, y = 2 sin t, z = 0.

A görbére lokalizált v vektor:

v =(4 cos t sin t, 2 sin t, 2 cos t)

4.13. ábra

A bal oldali integrál:

.

A jobb oldali integrálhoz állítsuk elő a rot v vektort.

.

Ez a vektor most nem függ z -től, ezért a lokalizált rot v = (1; 0; 1). A g görbe irányításának megfelelően a dF vektort felfelé kell irányítani, ezért dF = (x, y, 1)dx dy. Így a jobb oldali integrál:

.

15. A Stokes-tétel felhasználásával számítsuk ki a v = (2xy, , 2z + y) vektortér vonalintegrálját a g zárt görbére nézve, ha g az ellipszis.

Megoldás. A vonalintegrál helyett számítsuk ki a a tétel jobb oldalán szereplő integrált:

.

16. Számítsuk ki az

vonalintegrál értékét, ha a g görbe az O(0; 0), A(1; 0), B(1; 1) csúcspontú háromszög (4.14. ábra).

Megoldás. Itt P = 2 + y, Q = 5x y,

A vonalintegrál a (18) felhasználásával:

.

17. Vizsgáljuk meg, hogy van-e potenciája a v = (2xy, , 2z + y) vektortérnek. Ha van, akkor határozzuk meg a potenciálfüggvényt és számítsuk ki v vonalintegrálját az A(2; ; 3), B(1; 0; ) pontokat összekötő tetszőleges görbe mentén.

Megoldás. Potenciál akkor létezik, ha . A 15. példában láttuk, hogy , tehát van potenciál. Az u potenciálfüggvényt abból a feltételből határozzuk meg, hogy grad u = v. Ez a (20) egyenletekre vezet. Jelen esetben

, , .

Látható, hogy az u függvényt annak deriváltjaiból kell előállítani. Az első egyenletet integrálva:

,

ahol nyilván függhet y -tól és z -től. Deriváljuk ezt az u függvényt y szerint. Ekkor .

Ezt felhasználva, . Deriváljuk ezt z szerint. Ekkor

. Ezt felhasználva,

,

ahol tetszőleges állandó. Ellenőrzés:

.

A v vonalintegráljának értéke ekkor nem függ a görbe alakjától, csupán a kezdő- és a végpont helyzetétől. A (19) szerint

.

3. F

1. Írja fel az alábbi skalárvektor függvények szintfelületeinek egyenletét:

a) ; b) u = z y;

c) ; d) u = x + y + z.

2. Írja fel az alábbi függvények gradiensét:

a) ; b) u = z y;

c) ; d) u = x + y + z.

3. Számítsa ki az alábbi függvények a irányú iránymenti deriváltját (adott helyen):

a) , , ;

b) , , .

4. Számítsa ki az alábbi, ívhossz szerinti vonalintegrálokat:

a) , , ;

b) , , ;

c) , ahol g az kör.

5. Számítsa ki az homogén tömegeloszlású csavarvonal íve súlypontjának koordinátáit.

6. Számítsa ki annak a hengerpalástnak a felszínét, amelyet az hengerből a z = xy nyeregfelület és a z = 0 sík az első térnyolcadban kimetsz.

7. Számítsa ki az alábbi vonalintegrálokat:

a) , ha g az görbe íve;

b) , ha g az zárt görbe.

8. Számítsa ki a skalár-vektor függvény felszíni integrálját az r = (u cos v, u sin v, v) csavarfelület

, darabjára nézve.

9. Számítsa ki a függvény felületi integrálját (az (x, y) - síkon való vetület szerint) az r = (u cos v, u sin v, v) csavarfelület , darabjára nézve, felfelé mutató normális mellett.

10. Határozza meg az alábbi vektorterek divergenciáját és rotációját:

a) ;

b) .

11. a) b) div grad

12. Számítsa ki az alábbi vektor-vektor függvények adott g görbe menti (skalár értékű) vonalintegrálját:

a) , g : , ;

b) v = (x , x + y, xyz), g : r = (cos t, sin t, t), .

13. Számítsa ki az alábbi vektorterek (skalár értékű) felületi integrálját felfelé mutató felületi normális mellett:

a) , ahol a felület a 2x + 2y + z = 6 sík első térnyolcadba eső része;

b) v = r = (x, y, z), ahol a felület a kúppalást része;

c) , ahol a felület az gömbfelület első térnyolcadba eső része.

14. Számítsa ki a vektortér felületi integrálját (átáramlási feleslegét) az gömbfelületre, kifelé mutató felületi normális mellett.

15. Számítsa ki a Gauss-Osztrogradszkij-tételben szereplő integrálokat az alábbi v vektortér és V térrész esetén:

a) v = (2 , x + y, ), V : , , ;

b) , , .

16. A Gauss-Osztrogradszkij-tétel alkalmazásával számítsa ki a vektortér felületi

integrálját az , félgömbfelület és az körlap által alkotott zárt felületre

nézve.

17. Számítsa ki a Stokes-tételben szereplő integrálokat az alábbi v vektortér és F felület esetén:

a) , F : 2z = , ;

b) , F : z = , , .

18. A Stokes-tétel alkalmazásával számítsa ki az

vonalintegrált, ahol g az A(a; 0; 0), B(0; a; 0), C(0; 0; a) háromszög.

19. Számítsa ki a Green-formula alkalmazásával az

vonalintegrált, ha a g görbe a , parabolalemez határa.

20. Vizsgálja meg, hogy van-e potenciálja az alábbi vektortereknek. Ha van, akkor állítsa elő a potenciálfüggvényt, majd számítsa ki a vektortér (skalárértékű) vonalintegrálját az adott A, B pontokat összekötő görbe mentén:

a) , A(2; 0; 0), B(0; 1; 2);

b) , A(1; ; 5), B(3; 0; );

c) , A(2; 0; ), B(1; 3; );

d) v = (2x + y; x ; z), A( ; 4; 0), B(2; 1; 3).

Megoldások

1. a) ; b) ;

c) ; d) x + y + z = C.

2. a) grad u = u = 2x i + 2y j + 2z k = (2x, 2y, 2z) = 2r;

b) grad u = u = i j + k = ( , , 1);

c) grad u = u = 2x i + 2y j + k = (2x, 2y, 1);

d) grad u = u = i + j + k = (1; 1; 1).

3. a) grad u = (2x, 2y, 2) = (4; ; 2), ,

;

b) grad u = .

4. a) , ;

b) ; ;

c) x = 2cos t, y= 2sin t, ds = 2dt, .

5. A súlypont koordinátái:

, , ,

ahol s a g görbe ívhossza. Ez jelen esetben , mivel . Az integrálok:

, ,

.

A súlypont koordinátái: , , .

6. Használjuk a (6) képletet: x = 2cos t, y = 2sin t, ds = 2dt, xy = 4cos t sin t, így a palástfelszín (4.15. ábra):

4.15. ábra

.

7. a) x = t, , , dx =dt,

;

b) x = sin t, y = cos t, z = sin t, dy = t dt,

.

8. Alkalmazzuk a (8) formulát. (l. a 11. c) mintafeladatot), így . Az integrál:

.

9. A (9) formulát alkalmazzuk. Ennek a csavarfelületnek Descartes-koordinátás egyenlete: z = arctg . Így az integrál:

.

A feladat megoldható a következőképpen is: dxdy nem más, mint a vektor z tengelyre való vetületének abszolút értéke. Ez jelen esetben u du dv. Ez felhasználva,

.

10. a) div v = v = 2x + 2y + 2z,

;

b) div v = yz + 3 + 2z,

.

11. a) grad u = ,

div grad u = 30 xy + 6z.

De eljárhatunk a következőképpen is:

div grad u = ;

b) div grad .

12. a)

;

b)

.

13. Alkalmazzuk a (14) és (15) formulát.

a) A z = 6 - 2x - 2y felület esetén (a felfelé mutató) dF = (2; 2; 1)dx dy (4.16. ábra).

4.16. ábra

Így

.

b) ,

4.17. ábra

A 4.17. ábrán látható, hogy a kúp palástján támadó vektorok párhuzamosak a támadásponthoz tartozó alkotóval, így merőlegesek dF –re. Ekkor pedig vdF = 0, ezért az integrál értéke is nulla.

c) A gömbfelület vektor egyenlete:

r = (cos u cos v, cos u sin v, sin u).

4.18. ábra

A felfelé mutató normális: . Figyelembe véve, hogy

,

.

14. Az előző feladat mintájára:

.

15. a) Előbb kiszámítjuk a tétel bal oldalán szereplő hármas integrált. A V térrész a 4.19. ábrán látható. A vektortér divergenciája: div v = 4.

.

óA jobb oldali felületi integrált a V térrészt határoló felületek mindegyikére ki kell számítani, ügyelve arra, hogy dF kifelé mutasson.

4.19. ábra

z = 1 , d v = (3x , x + y, ),

,

y = 0, dF = (0; ; 0)dx dz, v = (2x , x, z ),

,

y = 1, dF = (0; 1; 0)dx dz, v = (2x , x + 1, z ),

,

x = 0, dF = ( ; 0; 0)dydz, v = ( , y, z ),

,

z = 0, dF = (0; 0; )dxdy, v = (2x, x + y, ),

.

Tehát a jobb oldali integrál (a fenti öt integrál összege):

,

amely egyezik a bal oldali integrál értékével.

b) .

.

A jobb oldali integrál:

.

Itt kihasználtuk azt, hogy a gömbfelületen .

16. A felületi integrál helyett a tétel bal oldalán álló hármas integrált számítjuk ki . Mivel div v = ,

.

17. a) A felület a paraboloid része. Határgörbéje az , , z = 2 kör (4.20. ábra).

4.20. ábra

E körre lokalizálva a v vektorteret, . A bal oldali integrál:

.

rot v = .

Ez lokalizálva a felületre:

(rot v)

. A jobb oldali integrál:

.

b) A felület és határgörbéje a 4.21. ábrán látható.

4.21. ábra

A határgörbe két részből áll ( és ).

egyenlete: r = (2 cos t, 2 sin t, 4), , egyenlete: r = (t, 0, t ), .

A bal oldali integrál:

.

A felület egyenlete , dF = ( x, y, 1)dx dy.

rot v = , (rot v) = (2y , 1, ).

A jobb oldali integrál:

.

18. A vonalintegrál helyett a tétel jobb oldalán szereplő felületi integrált számítjuk.

4.22. ábra

A három pontra illeszkedő sík (4.22. ábra) egyenlete x + y + z = a, azaz z = a , dF = (1, 1, 1)dx dy, rot v = 2(1, 1, 1). Az integrál:

.

19. A vonaintegrál helyett a (18) formula jobb oldalán szereplő integrált számítjuk ki. A T tartomány a 4.23. ábrán

látható. Jelen esetben , , , . Így

4.23. ábra

.

a)

rot v = ,

tehát van potenciál. Legyen a potenciálfüggvény u. Ekkor

, , .

Az első egyenletet integrálva, . Innen

, és .

Ez utóbbi egyenletből . Végeredményben

.

A vonalintegrál értéke a potenciálkülönbséggel egyenlő, azaz .

b) rot v = ,

tehát nincs potenciál.

c) rot v = v 0 van potenciál.

, ,

.

d) rot v = v = ,

tehát van potenciál. Ha a potenciálfüggvény u, akkor

, , .

Innen . A vonalintegrál:

.

Digitális Egyetem, Copyright © Kovács Béla, 2011