Fizika II.
Szalai, István, Pannon Egyetem
Fizika II.
írta Szalai, István Publication date 2012
Szerzői jog © 2012 Pannon Egyetem
A digitális tananyag a Pannon Egyetemen a TÁMOP-4.1.2/A/2-10/1-2010-0012 projekt keretében az Európai Szociális Alap támogatásával készült.
Tartalom
1. BEVEZETÉS ... 1
2. ELEKTROSZTATIKA ... 2
1. Mikroszkopikus és makroszkopikus elektromos töltés ... 2
1.1. Elektromos töltés, Coulomb-törvény ... 2
1.2. Elektromos térerősség ... 3
1.2.1. Ponttöltés elektromos tere ... 4
1.2.2. Ponttöltés-rendszer elektromos tere ... 4
1.2.3. Térfogati töltéseloszlás ... 5
1.2.4. Felületi töltéseloszlás ... 5
1.2.5. Dipólus elektromos tere ... 6
1.2.6. Elektromos erővonalak ... 6
1.2.7. Töltött részecskék mozgása homogén transzverzális elektromos térben ... 7
1.2.8. Millikan-féle kísérlet ... 8
1.2.9. Dipólus homogén elektromos térben ... 8
1.3. Az elektromos mező fluxusa ... 9
1.4. Gauss-törvény ... 10
1.4.1. Töltött vezetö gömb elektromos tere ... 11
1.4.2. Töltött szigetelö gömb elektromos tere ... 12
1.5. Az elektromos tér munkája és az elektromos potenciál ... 14
1.5.1. Elektromos potenciál, a ponttöltés potenciáltere ... 16
1.5.2. Az elektromos térerősség és a potenciál közti kapcsolat ... 17
2. Kondenzátor, kondenzátor kapacitása ... 18
2.1. Kondenzátorok párhuzamos kapcsolása ... 19
2.2. Kondenzátorok soros kapcsolása ... 20
3. Elektromos tér anyag jelenlétében ... 20
3.1. A Coulomb-törvény dielektrikumokban ... 21
3.2. Gauss-törvény dielektrikumokban ... 21
3.3. Síkkondenzátor dielektrikummal ... 22
3.4. A feltöltött kondenzátor energiája ... 22
4. Az elektromos mező energiasűrűsége ... 22
3. STACIONÁRIUS ELEKTROMOS TÉR ÉS ÁRAM ... 24
1. Áramerősség, stacionárius elektromos áram ... 24
1.1. A töltésmegmaradás törvénye ... 25
1.2. Az elektromos ellenállás és vezetés, Ohm törvénye ... 26
1.2.1. Fajlagos ellenállás és vezetés ... 27
1.2.2. Az Ohm-törvény differenciális alakja ... 28
2. Egyenáramú áramkörök ... 29
2.1. Feszültségforrás, áramforrás ... 29
2.2. Elektromotoros erő, általánosított, differenciális Ohm-törvény ... 29
2.3. Kirchhoff törvényei ... 29
2.3.1. Kirchhoff I. törvénye, vagy csomóponttörvény ... 29
2.3.2. Kirchhoff II. törvénye, vagy huroktörvény ... 30
2.4. Kirchhoff törvényeinek alkalmazásai ... 31
2.4.1. Feszültségforrás belsö ellenállása ... 31
2.4.2. Ellenállások soros kapcsolása ... 31
2.4.3. Ellenállások párhuzamos kapcsolása ... 32
2.4.4. Áram- és feszültségmérö müszerek kapcsolása ... 33
2.4.5. Ideális feszültségosztó, potenciométer ... 33
2.4.6. Az egyenáramú Wheatstone-híd ... 34
2.5. Az áram munkája és teljesítménye ... 35
2.5.1. Joule-törvény ... 37
2.5.2. Feszültségforrás teljesítménye, hatásfok ... 37
4. STACIONÁRIUS ÁRAM ÉS MÁGNESES TERE ... 39
1. Mágneses alapjelenségek ... 39
1.1. Áramjárta vezetö mágneses térben ... 39
1.2. A mágneses mező fluxusa ... 41
1.3. Áramhurok mágneses térben ... 41
1.4. Áramvezetök közti erőhatás ... 43
1.5. A Biot-Savart törvény ... 44
1.6. A Biot-Savart törvény alkalmazásai ... 45
1.7. Az Ampère-féle gerjesztési törvény ... 47
1.8. Az Ampère-féle gerjesztési törvény alkalmazásai ... 50
1.9. A mágnességre vonatkozó Gauss-törvény ... 51
5. Mágneses tér anyagban ... 53
1. Mágneses permeabilitás, mágneses térerősség ... 53
2. Mágnesezettség, mágneses szuszceptibilitás ... 53
3. Az Ampère-féle gerjesztési törvény anyag jelenlétében ... 55
4. Az anyagok osztályozása mágneses tulajdonságaik alapján ... 55
6. Idöben változó elektromágneses tér ... 58
1. Elektromágneses indukció ... 58
2. Az önindukció, önindukciós tényezö ... 60
2.1. Szolenoid önindukciós tényezöje ... 61
2.2. Az önindukció szerepe áram bekapcsolásakor ... 61
2.3. Áram mágneses terének energiája ... 62
2.4. A mágneses tér energiasűrűsége ... 63
2.5. Az elektromágneses tér energiasűrűsége ... 64
3. A kölcsönös indukció ... 64
4. Örvényáramok ... 65
7. Váltakozó áramok ... 67
1. A váltakozó áram és feszültség effektív értéke ... 67
2. R, L és C elemek váltakozó áramú körökben ... 68
3. A váltakozó áram pillanatnyi és átlagos teljesítménye ... 72
8. Maxwell-egyenletek ... 73
9. Irodalomjegyzék ... 75
Az ábrák listája
2.1. 2.1. ábra. Ponttöltések kölcsönhatása ... 2
2.2. 2.2. ábra. Ponttöltések elektrosztatikus tere ... 5
2.3. 2.3. ábra. Pozitív és negatív töltés erovonalképe ... 6
2.4. 2.4. ábra. Negatív töltéspár (A), pozitív töltéspár (B) és elektromos dipólus (C) erovonal eloszlásai 7 2.5. 2.5. ábra. Negatív töltés mozgása transzverzális térben ... 8
2.6. 2.6. ábra. Az elektromos tér fluxusa ... 9
2.7. 2.7. ábra. Ponttöltések fluxusa az felületre ... 10
2.8. 2.8. ábra. Az elektromos térerősség számítása töltött vezetö gömb esetén ... 11
2.9. 2.9. ábra. Az elektromos térerősség számítása töltött szigetelö gömb esetén ... 13
2.10. 2.10. ábra. Az elektromos tér munkája inhomogén mezőben ... 15
2.11. 2.11. ábra. Kondenzátorok párhuzamos kapcsolása ... 19
2.12. 2.12. ábra. Kondenzátorok soros kapcsolása ... 20
3.1. 3.1. ábra. A töltésmegmaradás törvénye ... 25
3.2. 3.2. ábra. Az ellenállás definíciója ... 26
3.3. 3.3. ábra. Egy csomópontba be- és kifutó áramok ... 30
3.4. 3.4. ábra. Áramköri hurok ... 30
3.5. 3.5. ábra. Reális feszültségforrás külső terhelö ellenállással ... 31
3.6. 3.6. ábra. Ellenállások soros kapcsolása ... 31
3.7. 3.7. ábra. Ellenállások párhuzamos kapcsolása ... 32
3.8. 3.8. ábra. Terheletlen (ideális) feszültségosztó és potenciométer ... 33
3.9. 3.9. ábra. Wheatstone-hídas kapcsolás ... 34
4.1. 4.1. ábra. Áramvezetö mágneses térben ... 39
4.2. 4.2. ábra. Áramhurok mágneses térben ... 41
4.3. 4.3. ábra. Párhuzamos áramvezetök kölcsönhatása ... 43
4.4. 4.4. ábra. Az elektromos tér fluxusa ... 44
4.5. 4.5. ábra. Köráram mágneses tere ... 45
4.6. 4.6. ábra. Áramvezetö mágneses tere ... 47
4.7. 4.7. ábra. Több áramvezetö mágneses tere ... 48
4.8. 4.8. ábra. Kiterjedt áramvezetö mágneses tere ... 48
4.9. 4.9. ábra. Szolenoid mágneses indukciójának számítása ... 50
5.1. 5.1. ábra. Domének egy ferromágneses anyagban ... 56
6.1. 6.1. ábra. Az elektromágneses indukció jelensége ... 58
6.2. 6.2. ábra. Elektromágneses indukció tekercsekkel ... 58
6.3. 6.3. ábra. RL áramkör bekapcsolása ... 62
6.4. 6.4. ábra. Áramjárta vezetöhurkok kölcsönhatása ... 64
7.1. 7.1. ábra. Soros RLC áramkör ... 70
1. fejezet - BEVEZETÉS
Ebben a jegyzetben az Elektromosságtan alapjait foglaljuk össze. A jegyzetben leírtak maradéktalan megértéséhez a Fizika I. alapkollégium ismeretei szükségesek. Az elektromosságtan törvényeinek elsajátítását alkalmazási példák kidolgozásával segítjük. A jegyzet az Irodalomjegyzékben hivatkozott művek alapján készült, az alaposabb ismeretekre vágyóknak elengedhetetlen az idézett könyvek -- elsősorban Hevesi Imre Elektromosságtan c. művének -- részletesebb tanulmányozása. A jegyzet anyaga nem teljes, így nem helyettesíti az előadásokon elhangzottakat. Az elektromosságtan alapegyenleteit piros, az alkalmazásokhoz nélkülözhetetlen egyenleteket kék, a mértékegységeket származtató egyenleteket sárga színkóddal láttuk el.
2. fejezet - ELEKTROSZTATIKA
1. Mikroszkopikus és makroszkopikus elektromos töltés
Anyagszerkezeti ismereteinkből tudjuk, hogy a negatív elemi töltés hordozói az elektronok. Az pozitív elemi töltés hordozói a protonok. Az atomok semleges építőkövei a neutronok. A makroszkopikus testek alapállapotban elektromosan semlegesek, ugyanannyi negatív és pozitív töltést tartalmaznak. Két különböző anyagú makroszkopikus test összedörzsölése, majd szétválasztása révén a testek elektromosan töltött állapotba kerülhetnek. A dörzsölés révén az egyik testből elektronok kerülhetnek át a másikba. Az elektrontöbblettel rendelkező test negatívan töltött, míg az elektronhiánnyal bíró test pozitívan töltött lesz. Az elektrosztatikában többnyire a makroszkopikus töltések kölcsönhatásával foglalkozunk.
1.1. Elektromos töltés, Coulomb-törvény
Két pontszerű töltés és között ható (vonzó vagy taszító) erő ( ) az alábbiak szerint adható meg:
(2.1) A (2.1) Coulomb-törvény matematikai alakja megegyezik a mechanikában megismert Newton-féle tömegvonzási törvény matematikai alakjával. (Az egyenletben alkalmazott jelölések a 2.1 ábra alapján egyértelműek.)
2.1. ábra - 2.1. ábra. Ponttöltések kölcsönhatása
Ha az erőt newtonban (N), a töltések közti távolságot méterben (m), a töltések nagyságát pedig coulombban
(C) adjuk meg, úgy , amit a vákuum permittivitása,
, segítségével a
(2.2)
alakba szokásos írni. A rögzítésével a (2.1) egyenlet egyben a töltésmennyiség egységét is definiálja. Az azonos előjelű (nemű) töltések taszítják, a különböző előjelű (nemű) töltések vonzzák egymást. A (2.2) egyenletet is felhasználva vákuumban a Coulomb-törvény az alábbiak szerint adható meg:
(2.3)
amelyben a töltés egysége az 1 C, azaz
(2.4)
1.2. Elektromos térerősség
Egy rögzített -- rendszerűnk szempontjából külsőnek tekintett -- töltés miatt a tér egy adott pontjába helyezett töltésre nagyságú erő hat. Helyezzünk egymás után ugyanabba a pontba különböző nagyságú , ,...
töltéseket, a rájuk ható erőket -el jelölve azt tapasztaljuk, hogy
(2.5)
vagyis az erők és a megfelelő töltések hányadosa a tér pontjára jellemző, állandó mennyiséget (vektort) szolgáltat. Az ilyen módon a pontban definiált vektormennyiséget elektromos térerősségnek nevezzük.
Az előzőek alapján világos, hogy ezt az eljárást a tér tetszőleges pontjában megismételhetjük, és így a tér bármely, helyzetvektorral jellemzett pontjához hozzárendelhetünk egy térerősség vektort. Az így definiált vektorteret elektromos mezőnek nevezzük. A (2.5) egyenlet alapján az adott pontba helyezett töltésre
(2.6)
nagyságú erő hat. Egy adott pontban az elektromos térerősség kizárólag a térre jellemző, és független a pontban lévő töltés nagyságától. Nyilvánvaló, hogy az iránya megegyezik a pontba elhelyezett pozitív töltésre ható erő ( ) irányával. Ha a külső teret egy adott pontban több ( db) töltésből álló töltéselrendezés hozza létre, úgy az erők szuperpozíciójának elvéből a térerősségek szuperpozíciójának elve következik:
(2.7)
Az elektromos térerősség SI egysége newton/coulomb:
(2.8)
1.2.1. Ponttöltés elektromos tere
Határozzuk meg az elektromos térerősséget egy, a vonatkoztatási rendszerűnk origójában lévő töltéstől távolságban lévő pontban. (A töltéstől a pontba mutató helyvektor , és .) A pontba helyezett
töltésre ható erőt a Coulomb-törvény alapján írhatjuk fel:
(2.9)
Az erő ismeretében a töltés által keltett elektromos mező térerőssége a pontban:
(2.10)
(Ne feledkezzünk meg róla, hogy egy vektorok közti egyenlet mindig három skalár egyenlettel ekvivalens, vagyis ebben az esetben
(2.11)
ahol a helyvektor derékszögű koordinátái, pedig a térerősség vektor megfelelő komponensei.)
1.2.2. Ponttöltés-rendszer elektromos tere
A szuperpozíció elvének megfelelően a töltések rendszere által a tér egy pontjában keltett elektromos térerősség:
(2.12)
ahol a töltéstől a pont felé mutató egységvektor, ill. -k a töltések -töl mért távolságai (lásd 2.2.
ábra).
2.2. ábra - 2.2. ábra. Ponttöltések elektrosztatikus tere
1.2.3. Térfogati töltéseloszlás
Ha egy térfogatú test helyvektorral jellemzett térfogatelemében töltés helyezkedik el, akkor a térfogati töltéssűrűség az alábbiak szerint definiálható:
(2.13)
A térfogatú test teljes töltését a test térfogatára vett integrállal számíthatjuk ki:
(2.14)
Homogén töltéseloszlás esetén -- a térfogatban -- konstans.
1.2.4. Felületi töltéseloszlás
Ha egy felületen az helyvektorral jellemzett felületelemen töltés helyezkedik el, akkor a felületi töltéssűrűség az pontban az alábbiak szerint definiálható:
(2.15)
Az felületen lévő teljes töltésmennyiséget egy felületi integrállal számíthatjuk ki:
(2.16)
Homogén felületi töltéseloszlás esetén -- az felületen -- konstans.
1.2.5. Dipólus elektromos tere
Az egymástól távolságban lévő pozitív és egy ugyanolyan nagyságú negatív töltésből álló rendszert elektromos dipólusnak nevezzük. Az elektromos dipólust a
(2.17)
dipólusmomentummal jellemezzük, ahol a negatív ponttöltéstől a pozitív ponttöltéshez húzott vektor ( ). Gyakran bonyolult töltéselrendeződések elektromos tere is egy dipólus elektromos terével helyettesíthető. (Azokat az anyagokat, amelyek molekulái dipólusmomentummal bírnak, poláris anyagoknak nevezzük. Ellentétes esetben apoláris anyagokról beszélünk. A víz és az etil-alkohol poláris, míg a szén- tetraklorid apoláris oldószerek.) A dipólusmomentum SI egysége a (2.17) egyenlet alapján származtatható:
(2.18)
Pontszerű dipólusról beszélünk, ha a töltések távolsága nagyságrendileg kisebb a dipólus középpontja és a megfigyelési pont közötti távolságnál. Be lehet látni, hogy egy dipólusmomentumú pontdipólus elektromos tere a dipólusból mint origóból induló helyvektorral jellemzett pontban az alábbiak szerint adható meg:
(2.19)
Vegyük észre, hogy, míg a ponttöltés elektromos tere a távolság második hatványának reciprokával (lásd (2.10) egyenlet), addig a pontdipólus elektromos tere a távolság harmadik hatványának reciprokával (lásd (2.19) egyenlet) arányos.
1.2.6. Elektromos erővonalak
2.3. ábra - 2.3. ábra. Pozitív és negatív töltés erovonalképe
2.4. ábra - 2.4. ábra. Negatív töltéspár (A), pozitív töltéspár (B) és elektromos dipólus (C) erovonal eloszlásai
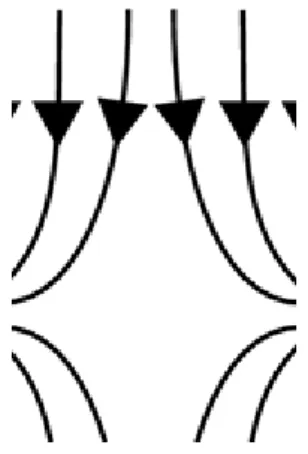
Az elektromos térnek erővonalakkal való szemléltetését Faraday vezette be. Az elektromos erővonalak olyan irányított görbék, amelyek adott pontbani érintöi megadják az ottani elektromos térerősség irányát. Az erővonalak sűrűségével (a térerősségre merőleges egységnyi felületen áthaladó erővonalak számával) az nagyságát szemléltetjük. Az erővonalak irányítása a térerősség irányát adja meg. A 2.3. ábra a különálló pozitív és negatív ponttöltések erővonalait mutatja be. A 2.4. ábrán egy dipólus és különböző töltéspárok erővonalképét mutatjuk be.
1.2.7. Töltött részecskék mozgása homogén transzverzális elektromos térben
Tekintsünk egy töltésü tömegü részecskét, amit nagyságú, -irányú kezdeti sebességgel belövünk egy nagyságú -irányú homogén elektromos térbe (lásd 2.5 ábra). Amennyiben a kezdeti sebességre igaz, hogy , és az elektromos térerősség sem túl nagy, úgy a részecske mozgását a klasszikus mechanika alapján tárgyalhatjuk. Newton második törvénye alapján a gyorsulásra írhatjuk, hogy:
(2.20)
Az irányok és a kezdeti feltételek korrekt figyelembe vételével könnyen beláthatjuk, hogy a (2.20) differenciálegyenlet megoldásaként adódó részecske pálya-egyenlet az alábbiak szerint adható meg:
(2.21)
Az egyenlet alapján látható, hogy a töltött részecske parabolapályán mozog, és a pálya adataiból a fajlagos töltés meghatározható. Elektronok elektromos térben történö pálya-eltérítését vizsgálva fajlagos
töltésükre C/kg adódott.
2.5. ábra - 2.5. ábra. Negatív töltés mozgása transzverzális térben
1.2.8. Millikan-féle kísérlet
Millikan olajcseppeket porlasztott változtatható nagyságú homogén elektromos térbe. (Az elektromos teret síkkondenzátor (lásd késöbb) lemezei között hozta létre.) A porlasztás következtében a cseppek elektromos töltésre tesznek szert. külső tér hiányában egy m sugarú csepp a felhajtóerővel és a Stokes-féle súrlódási erővel kiegyenlített nehézségi erő hatására függöleges irányú állandó sebességgel esik. Egy nagyságú függöleges irányú elektromos tér bekapcsolásával elérhetö, hogy ugyanaz a töltéssel is bíró olajcsepp állandó sebességgel függölegesen emelkedjen. Az erők egyensúlyát mindkét mozgásra felírva, majd a két egyenletet egymással kombinálva az olajcsepp töltésére az adódik, hogy:
(2.22)
ahol a levegö viszkozitása. Millikan megfigyeléseit mikroszkóp segítségével végezte. különböző olajcseppekre is elvégezve a méréseket azt tapasztalta, hogy az egyes cseppek töltései mindig egész számú többszörösei egy legkisebb elemi töltésnek, . Mérései alapján az elemi töltés C-nak adódott. Ez az érték, az elöjelétöl eltekintve az elektron töltése. Mivel az elektron fajlagos töltését az előző fejezetböl már ismerjük, így töltésének ismeretében tömege is meghatározható, és
kg. Millikan eredményeit 1923-ban Nobel-díjjal ismerték el.
1.2.9. Dipólus homogén elektromos térben
Helyezzünk egy dipólust homogén elektromos térbe, olyan módon, hogy a dipólusmomentum vektor a tér irányával szöget zárjon be. A két ellentétes elöjelü töltés miatt a külső tér hatása egy erőpár megjelenésében nyilvánul meg. Belátható, hogy a dipólusra az alábbi forgatónyomaték hat:
(2.23)
Egyéb erőpárok hiányában ez a forgatónyomaték a dipólusokat a külső tér irányába forgatja.
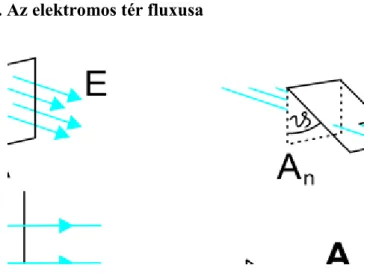
1.3. Az elektromos mező fluxusa
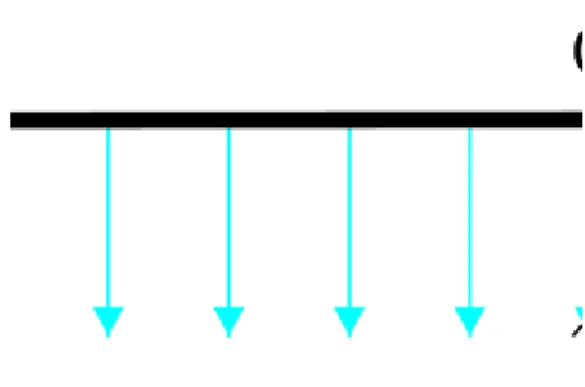
Tekintsünk egy homogén elektromos teret. A térerősségre merőleges felületen átmenö elektromos fluxust ( ) az alábbiak szerint definiáljuk (lásd 2.6 a) ábra):
(2.24)
2.6. ábra - 2.6. ábra. Az elektromos tér fluxusa
Amennyiben az felület normális egységvektora szöget zár be a térerősséggel, úgy a fluxushoz -nak csak az -re merőleges síkra vett vetülete ad járulékot (lásd 2.6.b ábra):
(2.25)
ahol az jelölést használtuk a "vektoriális" felület jelölésére. Ezen definíció általánosításaként, inhomogén térben, görbült felületre a fluxust egy felületi integrál segítségével adhatjuk meg:
(2.26)
Zárt felületre az elektrosztatikus tér fluxusát az alábbiak szerint jelöljük:
(2.27)
Az elektromos tér fluxusának SI egysége:
(2.28)
1.4. Gauss-törvény
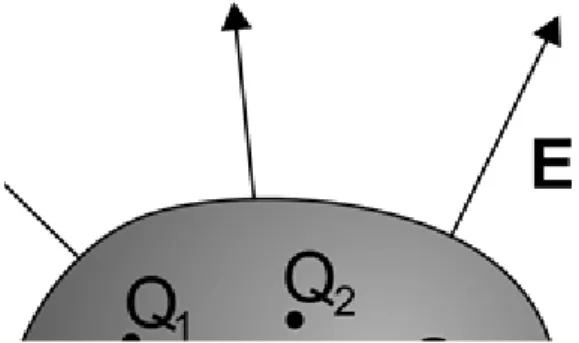
Vegyünk körbe egy, az origóba elhelyezett nagyságú töltést egy sugarú gömbfelülettel. Ha a (2.10) egyenlet alapján a töltés által keltett elektromos tér fluxusát kiszámítjuk a gömb felületére, akkor azt kapjuk, hogy:
(2.29)
ahol kihasználtuk, hogy a térerősség a gömb felületének minden pontjában sugárirányú, azaz merőleges a felületre. Belátható, hogy ha egy -- a töltést körülvevö -- tetszőleges alakú zárt felületre végezzük el a számolást, a fluxusra kapott eredmény nem változik. Ezek alapján a Gauss-törvény kimondja, hogy egy tetszőleges zárt felületen átmenö elektromos fluxus egyenlö a felületen belüli töltésmennyiség - szorosával, azaz
(2.30)
Gauss-törvényét több ponttöltésre is megfogalmazhatjuk. Amenyiben a zárt felületen belül több pontszerű töltés is található (lásd 2.7. ábra),
2.7. ábra - 2.7. ábra. Ponttöltések fluxusa az felületre
úgy az elektromos térerősség zárt felületen átmenö fluxusa egyenlö a zárt felületen belül lévő töltések algebrai összegének -szorosával, azaz
(2.31)
Ha az felületen kívül is helyezkednek el töltések, azokat a (2.31) egyenlet jobb oldalán nem kell figyelembe venni.
Amennyiben az zárt felület által határolt térfogatban a töltések folytonos eloszlásúak, úgy a (2.14) egyenlet alapján a Gauss-törvény az alábbi "integrális" alakba írható:
(2.32)
1.4.1. Töltött vezetö gömb elektromos tere
Ha egy vezetöböl (fémböl) készült gömböt feltöltünk, úgy a töltések a gömb felületén helyezkednek el, mivel a köztük ható taszítóerők miatt így tudnak egymástól a lehetö legtávolabb kerülni. Ebben az esetben tehát egy felületi töltéssűrűséggel van dolgunk, ahol a gömbre felvitt töltés mennyisége, pedig az sugarú gömb felülete.
2.8. ábra - 2.8. ábra. Az elektromos térerősség számítása töltött vezetö gömb esetén
A rendszer szimmetriáját is figyelembe véve a sugárirányú elektromos térerősség (gömbön belüli és kívüli) kiszámítása a Gauss-törvény alapján a legegyszerűbb.
a) , azaz a gömbön kívül ill. a gömb felületén történö számolás
Vegyük körül az sugarú gömböt -- a 2.8.a ábrán látható módon -- egy sugarú koncentrikus Gauss- gömbhéjjal, amelyre szimmetria-meggondolások miatt a fluxust könnyen kiszámíthatjuk:
(2.33)
mivel a térerősség a gömbhéj minden pontjában merőleges a felületre. ( az sugarú gömb felületét jelöli.) A Gauss-törvény értelmében ez a fluxus egyenlö a gömbhéjon belül lévő összes töltés -szorosával, azaz
(2.34)
Az egyenletet átrendezve
(2.35)
vagyis a töltött vezetö gömb elektromos tere a gömbön kívül olyan, mint egy, a gömb középpontjába helyezett - - azonos nagyságú -- ponttöltés elektromos tere.
b) , azaz a gömbön belül történö számolás
Ebben az esetben az sugarú gömbhéjat a 2.8.b ábra alapján kell felvenni. Mivel így az sugarú gömbön belül nincsenek töltések, Gauss törvénye alapján írhatjuk, hogy:
(2.36)
amiböl az következik, hogy a gömbön belül
(2.37)
Az térerősségre kapott (2.35) és (2.37) eredményeket a 2.8.c ábrán foglaltuk össze.
1.4.2. Töltött szigetelö gömb elektromos tere
Az elektromosan feltöltött szigetelö gömbben egyenletes a töltések eloszlása, ami azt jelenti, hogy a töltéssűrűség
(2.38)
Az előző problémának megfelelően itt is két esetet különböztetünk meg:
a) , azaz a gömbön kívül ill. a gömb felületén történö számolás
A számolás megegyezik az előző probléma pontjának megfelelőkkel (lásd 2.9.a ábra) és a végeredmény:
(2.39)
Tehát a gömbön kívül a feltöltött szigetelö gömb is úgy viselkedik, mintha egyenletes eloszlású töltése a centrumába helyezett (azonos töltésü) ponttöltéssel lenne helyettesíthető.
b) , azaz a gömbön belül történö számolás
Ebben az esetben a Gauss-gömbhéjat a 2.9.b ábrának megfelelően kell felvenni.
2.9. ábra - 2.9. ábra. Az elektromos térerősség számítása töltött szigetelö gömb esetén
A gömbhéjon belüli töltésmennyiséget a (2.38) töltéssűrűség térfogati integráljával tudjuk kiszámolni, azaz
(2.40)
Az elektrosztatikus tér fluxusát a térfogatú gömb felületére számolva:
(2.41)
Gauss törvényének megfelelően
(2.42)
amiböl a térerősséget kifejezve
(2.43)
A szigetelö gömbön belül az elektromos térerősség a sugár lineáris függvénye. A szigetelö gömbre vonatkozó összefoglaló ábrát a 2.9.c ábrán mutatjuk be.
1.5. Az elektromos tér munkája és az elektromos potenciál
Homogén elektromos mező munkája
Tekintsünk egy, az térerősséggel leírt homogén elektromos teret, amelyben egy töltés -- elöjelének függvényében -- az erő hatására a térerősségvektor irányában, vagy azzal ellentétes irányban egyenes vonalú pályán mozog. A munka definícióját ismerve, az kezdöponttól a végpontig tartó elmozdulás során a homogén elektromos tér munkája:
(2.44)
ahol pozitív töltés esetén , negatív töltés esetén , és így az erőtér munkája mindkét esetben pozitív.
Amennyiben a mező által kifejtett erő mellett a töltésre valamilyen (mechanikai) kényszererő is hat, úgy elöfordulhat, hogy az elmozdulás és az előzőektöl különböző, tetszőleges nagyságú szöget zárnak be egymással, ebben az esetben a mező munkája:
(2.45)
ami elöjelének megfelelően pozitív és negatív is lehet. Kényszererők hiányában (2.45) visszaadja a (2.44) összefüggést.
Inhomogén elektromos mező munkája
Az inhomogén elektrosztatikus teret egy helyfüggö vektor-vektor függvénnyel jellemezhetjük.
Ebben az esetben a töltésre ható erő , ami egy inhomogén erőteret definiál. Mechanika tanulmányainkra visszautalva, ebben az esetben az és pontokat összekötö, egyenes vonalú elmozdulás során végzett munka:
(2.46)
Az elektrosztatikus tér konzervatív erőtér
Belátható, hogy az elektrosztatikus mező munkája csak kezdeti és végsö pontok megválasztásától függ, és független attól, hogy ezen belül a töltés milyen pályán mozog. Vagyis az elektrosztatikus tér (függetlenül attól, hogy homogén vagy inhomogén) konzervatív erőtér. Ha az pontból a pontba egy görbén mozog a töltés, majd a pontból egy görbén visszajut a kiindulási pontba, akkor a teljes zárt görbén a mező munkája:
(2.47)
Kimondhatjuk, hogy az elektrosztatikus mezőben bármely zárt görbe mentén a tér által végzett munka zérus, azaz:
(2.48)
Tehát az elektrosztatikus tér a gravitációs mezőhöz hasonlóan konzervatív erőtér.
Nyugvó ponttöltés inhomogén terének munkája
Helyezzünk a vonatkoztatási rendszerűnk origójába egy töltést. Ekkor a (2.10) egyenlet szerint a töltés által keltett inhomogén elektromos mező a
2.10. ábra - 2.10. ábra. Az elektromos tér munkája inhomogén mezőben
(2.49)
egyenlettel adható meg. Tekintsük most a töltésnek az helyvektorral jellemzett pontból az helyvektorral jellemzett pontba történö mozgását (lásd 2.10. ábra). (Az egyszerűség végett tételezzük fel, hogy az elmozdulás sugárirányú, azaz és párhuzamosak.) Ekkor a nyugvó töltés elektrosztatikus terének munkája a (2.46) és a (2.49) egyenletek alapján:
(2.50)
ahol felhasználtuk, hogy , mivel az elmozdulás sugárirányú. Az előzőekben elmondottak alapján a végeredmény tetszőleges és helyvektorokkal jellemzett és pontokra is érvényes.
1.5.1. Elektromos potenciál, a ponttöltés potenciáltere
Mechanikai ismereteink alapján elmondhatjuk, hogy egy konzervatív erőtér munkája egyenlö a megfelelő pontokban vett potenciális energiák különbségével. Így a ponttöltés elektromos terének munkájára érvényes (2.50) egyenletet az alábbiak szerint is értelmezhetjük:
(2.51)
ahol
(2.52)
a töltés potenciális energiája a töltés elektrosztatikus terében. A konst. értéke tetszőleges, de logikus választás a konst.=0, mivel esetben a töltések potenciális energiája eltünik ( ). Ennek megfelelően a töltés elektromos terének pontjában lévő töltés potenciális energiája:
(2.53)
Fontos észrevenni, hogy a potenciális energia (2.53) kifejezésében csak az vektor nagysága jelenik meg. A és töltések jelentésétöl elvonatkoztatva, a (2.53) egyenlet alapján két egymástól távolságra lévő és töltés potenciális energiája:
(2.54)
A (2.53) egyenlet szerint a töltés terének ugyanazon pontjába elhelyezett különböző , ,... töltéseknek különböző , , .... nagyságú potenciális energiája van. A (2.53) egyenlet alapján látható, hogy az
, hányadosok értéke csak a töltés terének paramétereitöl függ, így az
(2.55)
egyenlettel definiált elektromos potenciál a töltés elektromos terének jellemzésére alkalmas skalár függvény. A (2.53) egyenlet alapján a ponttöltéstől származó elektromos potenciál:
(2.56)
A (2.51) egyenletnek megfelelően a ponttöltés elektromos terének a töltés -ból -be való mozgatása során végzett munkája:
(2.57)
Az elektrosztatikus tér két pontjában vett potenciálok különbségét feszültségnek nevezzük:
(2.58)
Az elektromos potenciál és a feszültség SI egységét Alessandro Volta (1745-1827) olasz fizikusról 1 voltnak nevezték el. A potenciál egységét -- más alapegységekböl származtatva -- a (2.55) egyenlet alapján kaphatjuk meg:
(2.59)
Azt mondjuk, hogy az elektromos tér két pontja közti feszültség =1V, ha =1C töltés pontok közötti elmozdulása során az elektromos tér =1J munkát végzett.
1.5.2. Az elektromos térerősség és a potenciál közti kapcsolat
A (2.46) egyenlet alapján a potenciálkülönbség és az elektromos térerősség közötti kapcsolatot az alábbiak szerint írhatjuk fel:
(2.60)
Ez az egyenlet a potenciált a térerősséggel fejezi ki. A továbbiakban a térerősséget a potenciál segítségével fejezzük ki. Tegyük fel, hogy az és vektorok csak az koordinátájukban különböznek, s abban is csak egy kicsi távolsággal, azaz és . Ennek megfelelően a potenciálok különbsége is kicsi:
(2.61)
Az előző (2.60) egyenlet integrálját az alábbiak szerint közelíthetjük:
(2.62)
ahol a térerősség vektor komponensét jelöli. A (2.60), (2.61) és (2.62) egyenletek alapján az alábbi közelítö összefüggést kapjuk:
(2.63)
amelyböl a határátmenetet véve egzakt módon adódik, hogy:
(2.64)
A számolást hasonló módon a térerősség és komponensére megismételve azt kapjuk, hogy:
(2.65)
A (2.65) egyenletet a gradiens operátor segítségével az alábbi kompakt alakba írhatjuk:
(2.66)
ahol , és az , és koordinátatengelyek megfelelő egységvektorai.
2. Kondenzátor, kondenzátor kapacitása
Tekintsünk két egymástól elszigetelt vezetö darabot. Ha köztük potenciálkülönbséget (feszültséget) hozunk létre (pl. egy galváncellára kapcsoljuk a vezetö darabokat) úgy az egyiken , a másikon nagyságú töltések halmozódnak fel. Kísérleti tapasztalatok szerint a töltésmennyiség arányos a feszültséggel, vagyis
(2.67)
ahol a vezetö darabok elrendezésére, geometriájára jellemző arányossági tényezö, amit kapacitásnak nevezünk. A kapacitás a töltéstárolóképesség mértéke. Mértékegysége az
(2.68)
1 farad, amit Faraday angol fizikokémikus tiszteletére neveznek így. A két, egymástól elszigetelt vezetöböl álló töltéstároló eszközt kondenzátornak nevezzük.
Síkkondenzátor
A két, egymással párhuzamos, egymástól távolságra lévő, felületü, vezetö lemezekböl álló kondenzátort síkkondenzátornak nevezzük. Be lehet látni, hogy a síkkondenzátor kapacitása:
(2.69)
2.1. Kondenzátorok párhuzamos kapcsolása
Az alábbi 2.11. ábrán kondenzátorok párhuzamos kapcsolását mutatjuk be.
2.11. ábra - 2.11. ábra. Kondenzátorok párhuzamos kapcsolása
Az egyes kondenzátor-elektródákon tárolt azonos elöjelü töltések összeadódnak, s ez alapján a eredö kapacitás:
(2.70)
Általánosítva db párhuzamosan kapcsolt kondenzátorra:
(2.71)
2.2. Kondenzátorok soros kapcsolása
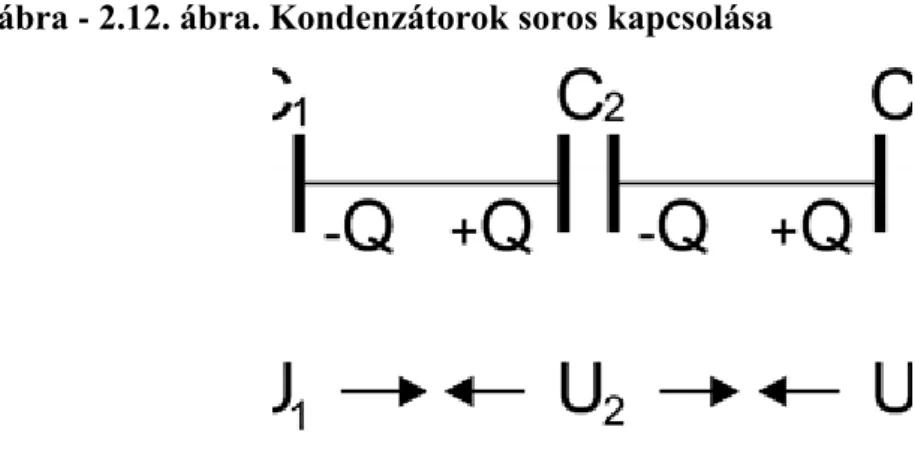
Az alábbi 2.12. ábrán kondenzátorok soros kapcsolását mutatjuk be.
2.12. ábra - 2.12. ábra. Kondenzátorok soros kapcsolása
A sorosan kapcsolt kondenzátorokon esö feszültségek additivitása alapján belátható, hogy az eredö kapacitás:
(2.72)
Általánosítva db sorosan kapcsolt kondenzátorra:
(2.73)
3. Elektromos tér anyag jelenlétében
Tegyük fel, hogy vákuumban az elektromos térerősség . Ha a teret egy szigetelö anyaggal töltjük ki, úgy az anyag belsejében az elektromos térerősség csökken és lesz. A két térerősség viszonyával definiált
(2.74)
az illetö anyagra jellemző mennyiséget relativ permittivitásnak, vagy relatív dielektromos állandónak nevezzük. A vákuum relatív permittivitása . A víz folyadékfázisban mért relatív permittivitása szobahömérsékleten . Az atmoszférikus nyomású levegöre, szobahömérsékleten .
3.1. A Coulomb-törvény dielektrikumokban
Egy relatív permittivitású dielektrikumban a és ponttöltések között ható erő a vákuumban mérhetö erőhöz képest (lásd a (2.1) egyenletet) az -ad részére csökken:
(2.75)
3.2. Gauss-törvény dielektrikumokban
Egy relatív permittivitású dielektrikumban az fluxusa -ad részére csökken, így a megfelelő Gauss- törvény:
(2.76)
Ebben az esetben, folytonos töltéseloszlás esetén a Gauss-törvény az alábbi "integrális" alakba írható:
(2.77)
Dielektrikumok leírására az elektromos térerősség mellett szokásos bevezetni az elektromos indukció (elektromos eltolás) vektorát
(2.78)
amelynek csak a szabad töltések a forrásai. Ezen vektor segítségével a (2.78) egyenlet alapján a Gauss-törvény:
(2.79)
3.3. Síkkondenzátor dielektrikummal
Amennyiben a síkkondenzátor lemezei közti teret egy relatív permittivitású dielektrikummal (szigetelövel) töltjük ki, úgy a kapacitása -szorosára növekszik:
(2.80)
A gyakorlatban használt kondenzátorok kapacitását egyre nagyobb relatív permittivitású szigetelök alkalmazásával növelik.
3.4. A feltöltött kondenzátor energiája
Egy töltött kondenzátor energiáját a feltöltés során végzett elektromos munkával definiáljuk. Ha feszültségkülönbség ellenében elemi töltésmennyiséget mozgatunk, úgy az elemi munka
(2.81)
ahol a kondenzátorokra érvényes összefüggést is felhasználtuk. A feltöltési folyamat teljes munkája az elemi munkák összegzésével (integrálásával) kapható meg:
(2.82)
A (2.82) egyenlet alapján ez más alakba is írható:
(2.83)
4. Az elektromos mező energiasűrűsége
A feltöltött kondenzátor energiája az elektródák közötti térrészben tárolódik. Síkkondenzátort feltételezve a térfogatban tárolt energia (térfogati) sűrűsége:
(2.84)
ahol felhasználtuk, hogy a konderzátorlemezek közti feszültségkülönbség nagyságú homogén elektromos teret hoz létre. Látható, hogy a végeredményben nem szerepelnek a kondenzátor geometriai paraméterei -- azok tetszőlegesen kicsik lehetnek --, így az egyenlet az elektromos mező -beli lokális leírására is alkalmas. Amennyiben a teret egy relatív permettivitású dielektrikum tölti ki, úgy
(2.85)
ahol vektorjelölésre is áttértünk. Az energiasűrűség SI-egysége:
(2.86)
Az elektromos indukció vektorának bevezetésével az elektromos tér térfogati energiasűrűségét kifejezö (2.85) egyenlet az alábbi alakba is írható:
(2.87)
3. fejezet - STACIONÁRIUS ELEKTROMOS TÉR ÉS ÁRAM
Ha egy hosszú fémes vezetö (fémhuzal) két végpontja között elektromos teret hozunk létre, úgy az a szabad töltéshordozók, az elektronok elmozdulását okozza a vezetöben. Gondoskodva a töltések elvezetéséröl és utánpótlásáról az elektromos töltések folytonos áramlása alakul ki a vezetöben. Ezt a "gondoskodást" a fémes vezetö két végének egy feszültségforrás két pólusához történö kapcsolásával biztosíthatjuk.
(Feszültségforrásként galvánelemeket, akkumulátorokat alkalmazhatunk.) Az elektromos töltéseknek ezt az áramát elektromos áramnak nevezzük.
1. Áramerősség, stacionárius elektromos áram
Ha egy vezetö keresztmetszetén idö alatt töltés halad keresztül, úgy az áramerősség átlagát a idöintervallumban az alábbi összefüggés definiálja:
(3.1)
Az áramerősség (a pillanatnyi áramerősség) precízebb definíciójához a fenti egyenlet határértékének képzésével juthatunk:
(3.2)
Fémes vezetökben az elektromos áramot a szabad elektronok (negatív töltések) árama hozza létre.
Természetesen a pozitív töltések árama szintén elektromos áramot hozhat létre. Ezzel az elektrolit oldatokban ill. a félvezetökben találkozhatunk. Az áram irányát -- megállapodás szerint -- a pozitív töltések mozgásirányával definiáljuk. Negatív töltések áramlása esetén az áram iránya ellentétes a töltések mozgásának irányával. Amennyiben az elektromos áram pozitív ( ) és negatív ( ) töltések (ellentétes irányú) áramlása révén alakul ki, úgy az áramerősség az alábbiak szerint számítható:
(3.3)
Ha az áramerősség idöben és a vezetö bármely keresztmetszetén állandó, egyen- vagy stacionárius áramról beszélünk. Ha egy kiterjedt vezetöben az felületen átfolyó áram felületi eloszlása nem egyenletes, akkor az elektromos áramot az áramerősség helyett a áramsűrűséggel jellemezzük. Az áramsűrűség vektormennyiség, vagyis nagysága mellett az irányát is definiálni kell. Az felület egy adott pontjában az áramsűrűség definíciója:
(3.4)
ahol az irányú töltésáramra merőleges felületelem. A vektor mint az függvénye egy vektormezőt határoz meg, amelyet áramvonalakkal szemléltethetünk. Egy felületre számolt teljes áramerősség:
(3.5)
ahol a felületi integrált a teljes felületre ki kell terjeszteni. A (2.26) egyenlettel való analógia alapján elmondhatjuk, hogy az áramerősség nem más, mint a áramsűrűség-vektornak az felületre számolt fluxusa. Az áramerősség SI egysége a (3.2) egyenlet alapján származtatható:
(3.6)
az 1 C/s egységet Ampère tiszteletére 1 ampernek nevezzük, és 1 A-el jelöljük. Az elektro-mosságtanban az áramerősséget alapegységnek tekintjük, így a töltés egysége a coulomb (1C=1As) leszármaztatott mennyiség lesz. (Az áramerősség alapegységét az áramjárta vezetök mágneses kölcsönhatása alapján a késöbbiekben definiáljuk.) Az áramsűrűség SI egységét a (3.4) egyenlet alapján definiáljuk:
(3.7)
1.1. A töltésmegmaradás törvénye
Tekintsünk egy zárt felületet abban a közegben, amelyikben az áram folyik. Az felülettel körbezárt térfogatból kiáramló töltésmennyiséget a (3.5) egyenletnek megfelelően a áramsűrűség felületi integrálja adja. A töltésmegmaradás törvénye értelmében ennek a mennyiségnek egyenlönek kell lennie a térfogatban lévő töltés idöegységre jutó csökkenésével:
(3.8)
3.1. ábra - 3.1. ábra. A töltésmegmaradás törvénye
A térfogatban lévő töltésmennyiséget a (2.14) egyenlet alapján a térfogati töltéssűrűségböl számolva kapjuk, hogy:
(3.9)
Ez az egyenlet nem más, mint a töltésmegmaradás törvényének a és makroszkopikus mennyiségekkel megfogalmazott alakja.
1.2. Az elektromos ellenállás és vezetés, Ohm törvénye
Egy, a 14 ábrán látható homogén fémes vezetö és végpontjai között hozzunk létre különböző feszültségeket, és mérjük meg az egyes feszültségek hatására kialakuló stacionárius áramok erősségét. A kísérletek szerint ugyanannál a fémes vezetönél az egymáshoz tartozó feszültségek és áramok hányadosaira igaz, hogy:
(3.10)
A fémes vezetöt más anyagú, hosszúságú, keresztmetszetü vezetökkel helyettesítve és a kísérletet megismételve az kapjuk, hogy az
(3.11)
3.2. ábra - 3.2. ábra. Az ellenállás definíciója
hányados értéke egy adott fémes vezetöre -- függetlenül a feszültség és így az áramerősség nagyságától -- mindig ugyanaz, de különböző vezetökre más és más érték. A vezetöre jellemző hányadost a vezetö ellenállásának nevezzük. A (3.11) egyenlettel megadott kísérleti eredményt Ohm-törvénynek nevezzük. Ohm törvénye szerint, ha egy homogén vezetöben erősségü áram folyik, akkor a vezetö két vége között
(3.12)
feszültség áll fenn. Megjegyezzük, hogy minden anyagra hömérsékletfüggö, ezért a (3.10) egyenlet hányadosai csak ugyanazon a hömérsékleten adnak azonos, állandó értékeket. Az ellenállás reciprokát vezetésnek ( ) nevezzük, és nyilvánvalóan igaz, hogy:
(3.13)
Az ellenállás SI-egységét a (3.11) Ohm-törvény alapján származtathatjuk:
(3.14)
Az 1 V/A egységet Ohm német fizikus tiszteletére 1 ohm-nak nevezzük. A vezetés egysége -- a (3.13) egyenletnek megfelelően -- a siemens (S):
(3.15)
1.2.1. Fajlagos ellenállás és vezetés
A különböző keresztmetszetü, hosszúságú és anyagi minöségü homogén vezetök ellenállása -- a kísérleti tapasztalatok alapján -- arányos a vezetö hosszával és fordítottan arányos a vezetö keresztmetszetével:
(3.16)
ahol a arányossági tényezöt a vezetö fajlagos ellenállásának nevezzük. Ez utóbbi mennyiség csak a vezetö anyagi minöségétöl függ, és független annak geometriai méreteitöl. (Legtöbb anyag esetén hömérsékletfüggést is mutat.) Hasonló, de a geometriai mennyiségekben fordított arányosságú összefüggés fogalmazható meg a homogén vezetö elektromos vezetésére:
(3.17)
ahol a arányossági tényezöt a vezetö fajlagos vezetésének nevezzük. (Ezt a mennyiséget elsösorban az elektrolit-oldatok jellemzésére szokás alkalmazni.) A (3.16) és (3.17) egyenletekböl és a vezetés definíciójából következik, hogy:
(3.18)
1.2.2. Az Ohm-törvény differenciális alakja
Ha egy hosszúságú és keresztmetszetü homogén vezetö végpontjai között feszültség különbséget hozunk létre, akkor a vezetöben erősségü áram indul. Ohm törvénye alapján írhatjuk, hogy
(3.19)
Felhasználva az áramsűrűség és a térerősség definícióit, a fenti egyenlet az alábbiak szerint írható:
(3.20)
A térerősség és az áramsűrűség vektormennyiségek, izotrop vezetöben a két vektor iránya megegyezik, így a (3.20) egyenletet vektoralakba is felírhatjuk:
(3.21)
A fajlagos ellenállás helyett a fajlagos vezetést használva
(3.22)
Vegyük észre, hogy a (3.22) és a (3.21) egyenletekben a vezetö méretei nem szerepelnek, így azok lokálisan, egy inhomogén vezetöre is érvényesek. Inhomogén vezetö esetén a (3.21) és (3.22) egyenletekben szereplö mennyiségek az helyvektor függvényei. A (3.22) és a (3.21) egyenletek Ohm törvényét differenciális alakban fejezik ki. Megjegyezzük, hogy anizotrop vezetökben az és vektorok iránya különböző, az ilyen anyagokban és tenzormennyiségek.
2. Egyenáramú áramkörök
2.1. Feszültségforrás, áramforrás
Feszültségforrásnak nevezzük azokat a berendezéseket (eszközöket), amelyek valamilyen (nem elektromos) energiát elektromos energiává alakítanak át. Pl. a galvánelemekben és akkumulátorokban kémiai energia, a termoelemekben höenergia, a fényelemekben fényenergia alakul át elektromos energiává. Az elektromos generátorok mechanikai (forgási) energiát alakítanak át elektromos energiává. A feszültségforrások a rájuk kapcsolt terhelésen (pl. ellenálláson) áramot hajtanak át, ezért áramforrásoknak is nevezhetjük ezeket a berendezéseket.
2.2. Elektromotoros erő, általánosított, differenciális Ohm- törvény
A pozitív töltések a nagyobb potenciálú helyröl a kisebb potenciálú hely felé mozognak. Ahhoz, hogy egy áramkörben állandó áram keringhessen, valamilyen "szivattyúnak" vissza kell juttatnia a töltéseket a magasabb potenciálú helyre. (Valóságos áramkörökben többnyire a negatív töltésü elektronok mozognak, az áram irányának azonban -- definíció szerint -- a pozitív töltések látszólagos áramlási irányát nevezzük.) Ezt a visszajuttatást egy ún. generátoros erő végzi. Az egységnyi töltésre ható generátoros erő az ún.
generátoros térerősséget definiálja. A töltésszétválasztó erő munkája az ún. generátoros munka. Az egységnyi töltés szétválasztása során végzett generátoros munkát elektromotoros erőnek vagy elektromotoros feszültségnek nevezzük . Feszültségforrások jelenlétében a (3.22) differenciális Ohm-törvényt az térerősséggel is ki kell egészítenünk:
(3.23)
2.3. Kirchhoff törvényei
Gyakran felmerülö elektrotechnikai probléma ellenálások és feszültségforrások ismert hálózatában a hálózati elemeken átfolyó áramok erősségének számítása. Ezt a feladatot legegyszerűbben Kirchhoff törvényei alapján oldhatjuk meg. A Kirchoff-törvények az elektromosságtan már ismert összefüggéseiböl származtathatók, nem jelentenek új alaptörvényeket.
2.3.1. Kirchhoff I. törvénye, vagy csomóponttörvény
A törvény a töltésmegmaradás törvényéböl származtatható, és kimondja, hogy egy csomópontba befolyó áramok erősségeinek összege egyenlö a csomópontból kifolyó áramok erősségeinek összegével.
3.3. ábra - 3.3. ábra. Egy csomópontba be- és kifutó áramok
A befolyó áramok erősségének elöjelét negatív, a kifolyó áramok erősségét pedig pozitív elöjellel ellátva kimondhatjuk, hogy egy tetszőleges csomópontban az áramerősségek algebrai összege zérus:
(3.24)
2.3.2. Kirchhoff II. törvénye, vagy huroktörvény
A törvény a (3.23) általánosított differenciális Ohm-törvény következménye, és kimondja, hogy egy egyenáramú körben (hurokban) az ellenállásokon esö feszültségek összege egyenlö a hurokban lévő feszültségforrások elektromotoros feszültségeinek összegével:
(3.25)
3.4. ábra - 3.4. ábra. Áramköri hurok
A törvényhez hozzátartozik, hogy a (3.25) egyenletben szereplö és mennyiségeket megfelelő elöjelekkel látjuk el. A hurokban definiálunk egy körüljárási irányt (általában az óramutató járásával megegyezö irányt), s az azzal azonos irányú -ket és -ket pozitív elöjellel, az ellentétes irányúakat pedig negatív elöjellel vesszük figyelembe. Az irányán annak az áramnak az irányát értjük, amit hozna létre (a feszültségforrás negatív sarkától a pozitív felé mutat).
2.4. Kirchhoff törvényeinek alkalmazásai
2.4.1. Feszültségforrás belsö ellenállása
A reális feszültségforrásoknak belsö felépítésük révén ún. belsö ellenállásuk ( ) van. (Ezt pl. galvánelemek esetén nagyrészt az elektrolit oldat ellenállása határozza meg.) Ezért, ha egy reális feszültségforrásra egy külső ellenállást kapcsolunk (lásd 3.5 ábra), akkor az áramkörben folyó áram erősségét a Kirchhoff-féle huroktörvény alapján számíthatjuk ki:
(3.26)
3.5. ábra - 3.5. ábra. Reális feszültségforrás külső terhelö ellenállással
A feszültségforrás külső "kapcsain" (csatlakozási pontjain) mérhetö feszültséget kapocsfeszültségnek nevezzük, amire az előző egyenlet alapján írhatjuk, hogy:
(3.27)
Látható, hogy zárt áramkör esetén ( ) a kapocsfeszültség mindig kisebb, mint az elektromotoros feszültség. Nyitott áramkör esetén ( ) a feszültségforrás kapcsain az ún. üresjárási feszültséget mérjük.
A (3.27) egyenlet alapján nyilvánvaló, hogy az üresjárási feszültség megegyezik a feszültségforrás elektromotoros erejével (elektromotoros feszültségével), azaz .
2.4.2. Ellenállások soros kapcsolása
A 3.6. ábrán ellenállások soros kapcsolását mutatjuk be. A soros kapcsolás jellege következtében az áramerősség -- a csomóponti törvénynek megfelelően -- a kapcsolás minden elemén átfolyik.
3.6. ábra - 3.6. ábra. Ellenállások soros kapcsolása
Ennek megfelelően az egyes ellenállásokon nagyságú feszültségek esnek. Mivel , ezért könnyen belátható, hogy:
(3.28)
A formula kiterjesztéseként db ellenálás soros eredöje az alábbiak szerint számolható:
(3.29)
2.4.3. Ellenállások párhuzamos kapcsolása
A 3.7. ábrán ellenállások párhuzamos kapcsolását mutatjuk be. A csomóponti törvénynek megfelelően a föágban folyó áram erőssége egyenlö a mellékágak áramerősségeinek összegével: . Mivel az ellenállásokon esö feszültségek megegyeznek, könnyen belátható, hogy a párhuzamos eredö ellenállás:
3.7. ábra - 3.7. ábra. Ellenállások párhuzamos kapcsolása
(3.30)
A formula kiterjesztéseként db ellenálás párhuzamos eredöje az alábbiak szerint számolható:
(3.31)
2.4.4. Áram- és feszültségmérö müszerek kapcsolása
Ha egy áramköri elemen ( ellenálláson) átfolyó áram erősségét kívánjuk megmérni, akkor az áramerősséget mérö müszert (amperméröt) az áramköri elemmel sorba kell kapcsolnunk. A müszernek az áramkörbe történö beiktatása nem szabad, hogy megváltoztassa az áramköri elemen átfolyó áram erősségét, ezért a müszer belsö ellenállása ( ) nagyságrendekkel kisebb kell, hogy legyen, mint a vizsgált áramköri elem ellenállása, azaz
. Az ideális árammérö müszer belsö ellenállása zérus ( ).
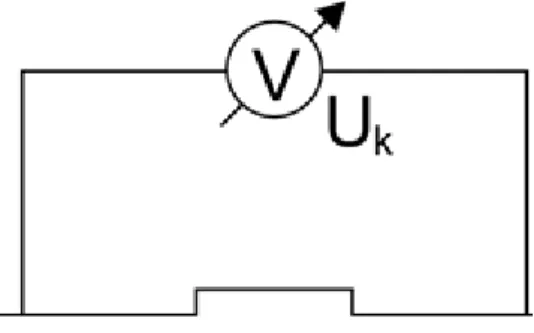
Ha egy áramköri elemen ( ellenálláson) esö feszültséget kívánjuk megmérni, akkor a feszültségmérö müszert (voltméröt) az áramköri elemmel párhuzamosan kell kapcsolnunk. A feszültségmérö müszer áramkörbe történö iktatása nem szabad, hogy megváltoztassa a vizsgált áramköri elemen áthaladó áram erősségét, ezért a párhuzamos kapcsolás jellegge miatt annak belsö ellenállásának ( ) nagyságrendekkel nagyobbnak kell lennie, mint a vizsgált elem ellenállása ( ). Az ideális feszültségmérö müszer belsö ellenállása végtelen ( ).
2.4.5. Ideális feszültségosztó, potenciométer
Ha egy adott feszültséget mértékben ( ) kívánunk leosztani, azt a legegyszerűbben az 20 ábrán látható két, sorosan kapcsolt ellenállás segítségével tehetjük meg. Ohm törvénye és az ellenállások soros kapcsolásánál tanultak értelmében a leosztott feszültség ( ) nagysága
(3.32)
vagyis az alapján kell megválasztani az ellenállások arányát. -t szabadon választva, értékét ismeretében számíthatjuk ki:
(3.33)
3.8. ábra - 3.8. ábra. Terheletlen (ideális) feszültségosztó és potenciométer
A feszültség folyamatos leosztása változtatható ellenállások, vagy más néven potenciométerek segítségével történik. A potenciométerekben egy csúszókontaktus mozgatásával változtatjuk az arányt úgy, hogy
közben .
2.4.6. Az egyenáramú Wheatstone-híd
Az ismeretlen nagyságú ellenállások meghatározásának egyik legpontosabb módszere az ún. Wheatstone-féle hídmódszer. A mérési elvet a 21. ábra szemlélteti. A híd egy ismeretlen nagyságú ellenállásból, egy ismert nagyságú ellenállásból, egy az és pontok közötti hosszúságú, keresztmetszetü, fajlagos ellenállású, homogén méröhuzalból és egy érzékeny galvanométerböl (nagypontosságú áramerősség mérö müszer) áll. A galvanométer egyik kapcsát a csúszókontaktuson keresztül csatlakoztatjuk az huzalhoz, másik kapcsa a ponthoz csatlakozik. A híd áramellátásáról az és pontokra kapcsolt feszültségforrás gondoskodik.
3.9. ábra - 3.9. ábra. Wheatstone-hídas kapcsolás
Az és az hosszúságú méröhuzalok ellenállása a (3.16) egyenlet alapján számolható, azaz:
(3.34)
Mivel nyilvánvaló, hogy
(3.35)
A mérés során a -csúszókontaktus pozícióját addig változtatjuk az vezetö mentén, míg a galvanométer áramot nem jelez. Ebben az esetben a és csomópontokra alkalmazva Kirchhoff I. törvényét írhatjuk, hogy:
(3.36)
Az 1. hurokra alkalmazva Kirchhoff II. törvényét:
(3.37)
A 2. hurokra alkalmazva Kirchhoff II. törvényét:
(3.38)
A (3.37) és (3.38) egyenleteket átrendezve és elosztva egymással, majd az áramok közti (3.36) relációkat figyelembe véve azt kapjuk, hogy:
(3.39)
A méröhuzalok ellenállására vonatkozó (3.34) és (3.35) egyenleteket is figyelembe véve és az ismeretlen ellenállásra kifejezve
(3.40)
A fentiekben ismertetett Wheatstone-hidas mérés az ellenállás mérését hosszúság mérésére vezeti vissza. A gyakorlatban a híd kiegyenlítésére más, ellenállás-változtatáson alapuló módszerek is elterjedtek. A Wheatstone-hidas ellenállásmérés tipikus példája az ún. nullmódszereknek, mivel a mérés során olyan ellenállásváltozást hozunk létre, hogy a mérömüszerűnk áramot detektáljon. Ennek megfelelően a mérömüszernek a nullpontot kell pontosan detektálnia, áramerősségeknél nem kell, hogy hiteles (nagy pontosságú) legyen.
2.5. Az áram munkája és teljesítménye
Tekintsünk egy ellenállású vezetöt, amelyre feszültséget kapcsoltunk, s így az erősségü áramot hajt át a vezetön. Az áramerősség definícióját felhasználva: idö alatt a vezetön töltés halad át. Ennek megfelelően az elektromos mező elemi munkája:
(3.41)
Ohm törvényét felhasználva a (3.41) egyenlet az alábbiak szerint is írható:
(3.42)
Egy véges hosszúságú idöintervallumra a munkát az elemi munkák integrálja adja:
(3.43)
Stacionárius áram esetén az és állandók, ezért a határozott integrál kiszámítása az idöintervallum hosszával történö szorzással ekvivalens, vagyis
(3.44)
ahol . A (3.41) egyenlet alapján a munka SI egysége
(3.45)
azaz, mivel 1Ws=1J megegyezik a mechanikában megismert jule-egységgel. A teljesítmény definícióját felhasználva a (3.41) egyenlet alapján a stacionárius áram teljesítményére azt kapjuk, hogy:
(3.46)
ami az Ohm-törvény felhasználásával az alábbi alakokba írható:
(3.47)
Az elektromos teljesítmény SI egysége a (3.46) egyenlet alapján az 1 watt, azaz
(3.48)
2.5.1. Joule-törvény
Feltételezve, hogy az ellenállású vezetöben az áram hatására semmiféle kémiai reakció sem játszódik le, a idö alatt az áram munkája a vezetöben teljes mértékben hövé alakul, azaz
(3.49)
hömennyiség keletkezik. Ezt a hömennyiséget hasznosítjuk a fütöellenállásokkal való melegítés során (pl.
elektromos vízmelegítökben).
2.5.2. Feszültségforrás teljesítménye, hatásfok
Az egyenáram összteljesítménye
Egy reális feszültségforrást (amelynek véges belsö ellenállása van) és egy külső terhelöellenállást tartalmazó áramkörben az egyenáram teljesítménye a (3.46) és (3.26) egyenletek alapján
(3.50)
Látható, hogy a teljesítményt a feszültségforrás belsö ellenállása csökkenti.
A feszültségforrásból kivehetö teljesítmény
A felhasználó számára csak az ellenálláson az áramkörböl "kivehetö" teljesítmény hasznosítható:
(3.51)
Szélsöérték számítással belátható, hogy a függvénynek a helyen maximuma van, és a maximumra igaz, hogy . Azaz egy feszültségforrásból az külső ellenálláson akkor vehetö ki a maximális teljesítmény, ha annak nagysága megegyezik a feszültségforrás belsö ellenállásával.
Hatásfok
Az áramkör hatásfokán ellenállású fogyasztó által a feszültségforrásból kivett teljesítmény és a feszültségforrás összteljesítményének hányadosát értjük. Ennek megfelelően a (3.50) és (3.51) egyenletek alapján írhatjuk, hogy:
(3.52)
Látható, hogy a hatásfok csak az ideális feszültségforrás ( ) esetén érheti el az értéket.
4. fejezet - STACIONÁRIUS ÁRAM ÉS MÁGNESES TERE
1. Mágneses alapjelenségek
A mágneses alapjelenségeket Thalész (i.e. ) leírásai alapján már az ókori görögök is ismerték.
Megfigyeléseik szerint a kisázsiai Magnesia városa közelében talált vasérc darabok a kisebb vasdarabokat magukhoz vonzották. Ezek az elsö -- magnetit tartalmú -- vasércek voltak az elsö természetes állandó mágnesek.
A permanens mágneses anyagból készült mágnesrudak a legnagyobb mértékben mágneses végeiken -- az ún.
mágneses pólusokban -- fejtik ki mágneses hatásukat. Vasrészecskékkel (vasreszelékkel) történö kölcsönhatás alapján megállapítható, hogy a két pólus "erőssége" egyforma. A mágneses pólusokat egymástól szétválasztani nem lehet, egy mágnesrudat két részre törve ismét két mágneses pólussal rendelkezö mágnesrudakhoz jutunk. A természetben minden mágnes mágneses dipólusként fordul elö. Tapasztalataink szerint mágneses monopólusok nem léteznek. A permanens mágnesek környezetében kialakuló mágneses erőhatás jól szemléltethetö vasrészecskék eloszlásával. A mágneses erőteret az elektrosztatikus térhez hasonlóan erővonalakkal -- mágneses erővonalakkal -- szemléltetjük. A Földnek szintén van mágneses tere. A mágneses dipólusok a Föld mágneses terében orientálódnak, ennek megfelelően megkülönböztetjük a dipólusok északi és déli pólusát. Kísérleti tapasztalat, hogy két rúdmágnes egymáshoz közeli északi és déli pólusa között homogén mágneses tér alakul ki.
Ugyancsak homogén a mágneses tér egy patkó alakúra kialakított permanens mágnes (patkómágnes) északi és déli pólusai között.
1.1. Áramjárta vezetö mágneses térben
A mágneses teret a mágneses indukcióvektorral jellemezzük, amelyre a továbbiakban adunk mérési módszert. Oersted, dán fizikus kísérleti munkája során azt észlelte, hogy egy mágneses iránytü közelébe helyezett, áramjárta vezetö kitéríti az iránytüt. Egy ilyen kísérlet esetén a hatás-ellenhatás törvényének megfelelően az áramjárta vezetöre is erő hat. A mágneses indukció mérésére helyezzünk homogén mágneses térbe (egy patkómágnes pólusai közé) egy hosszúságú vezetöt, amelyben erősségü áram folyik.
4.1. ábra - 4.1. ábra. Áramvezetö mágneses térben
Kísérleti tapasztalatok szerint az egyenes áramvezetöre ható erő arányos a vezetöben folyó áram erősségével és a vezetö hosszával. Az áramvezetöre ható erő akkor a maximális, ha az merőleges az erővonalak irányára, s nem lép fel erőhatás, ha a vezetö párhuzamos az erővonalakkal. Ha az áramjárta vezetö szöget zár be az indukcióvonalakkal, úgy a vezetöre ható erő -val arányos. A kísérleti tapasztalatokat egy egyenletben összegezve:
(4.1)
ahol a tényezöt -- a mágneses indukciót -- használjuk a mágneses tér "erősségének" jellemzésére. Valójában a mágneses indukció vektormennyiség ( ), amit az alábbiak szerint definiálunk: irányának az az irány felel meg, amelyben az áramjárta vezetöre ható erő nulla ( ), nagysága pedig az hosszúságú vezetöre ható maximális erővel ( ) definiálható
(4.2)
Az vektor definiálásával (olyan nagyságú vektor, amelynek iránya megegyezik az áram irányával) az áramjárta egyenes vezetöszakaszra ható erőt (4.1 egyenlet) vektor-egyenlet formájában is megadhatjuk:
(4.3)
A mágneses indukció SI egységét ezen egyenlet alapján származtatva:
(4.4)
amit Nikola Tesla szerb származású amerikai mérnök-feltaláló tiszteletére 1 teslának nevezünk. A vezetö stacionárius áramát az elemi töltések állandó sebességü áramlása hozza létre. Feltételezve, hogy a vezetö keresztmetszetén idö alatt darab nagyságú töltés áramlik át, az áramerősségre azt kapjuk, hogy
(4.5)
Ezen idö alatt a töltések elmozdulása , ezt és a fenti (4.5) egyenletet a (4.3) erőtörvénybe beírva:
(4.6)
majd egyetlen töltésre ható erőre felírva
(4.7)
a mágneses Lorentz-erő kifejezéséhez jutunk. A fémes vezetö szerepétöl eltekinthetünk, a mágneses Lorentz- féle erőtörvény a mágneses indukciójú térben sebességgel mozgó töltésekre érvényes. Ha a sebességgel
mozgó töltésü részecskére a indukciójú mágneses téren kívül még elektromos tér is hat, úgy a részecskére ható teljes Lorentz-féle erő:
(4.8)
ahol az elektromos tér hatását a (2.6) egyenlet alapján vettük figyelembe.
1.2. A mágneses mező fluxusa
A mágneses mező fluxusát az elektromos mező fluxusának megfelelő módon definiáljuk:
(4.9)
A mágneses fluxus SI egysége a (4.9) és (4.4) egyenletek alapján:
(4.10)
azaz 1 weber.
1.3. Áramhurok mágneses térben
Tekintsünk egy mágneses indukciójú térben lévő derékszögű áramjárta vezetökeretet, amely függöleges szimmetriatengelye körül el tud fordulni (lásd 4.2 ábra).
4.2. ábra - 4.2. ábra. Áramhurok mágneses térben
A vezetökeret normális egységvektora a mágneses indukció vektorával szöget zár be. A mágneses tér által az egyenes vezetöszakaszokra kifejtett erőhatásokat a (4.3) egyenlet alapján tudjuk kiszámítani. A vezetökeret hosszúságú oldalaira és párhuzamos, ellentétes irányú erők hatnak. Mivel ezekben a vezetö szakaszokban az áram iránya merőleges -re, írhatjuk, hogy . Az és erőpár függöleges szimmetriatengelyre gyakorolt forgatónyomatéka:
(4.11)
ahol az és hatásvonalainak távolsága, vagyis az erőpár ekkora erőkarral rendelkezik, illetve a téglalap alakú keret felülete. Mivel az és erők a forgástengellyel párhuzamosak, így azok a keretre forgatónyomatékot nem fejtenek ki. Ha a vezetökeret egyetlen menet helyett számú menetböl áll, vagy másképpen mondva menetfelületü tekercset helyezünk a homogén mágneses térbe, úgy a tekercsre ható forgatónyomatékot az
(4.12)
egyenlet alapján számíthatjuk ki. Az felületet a felületi normális egységvektor irányába mutató
vektorként kezelve a vezetökeret (vezetö tekercs) mágneses dipólusmomentumát az alábbiak szerint definiáljuk:
(4.13)