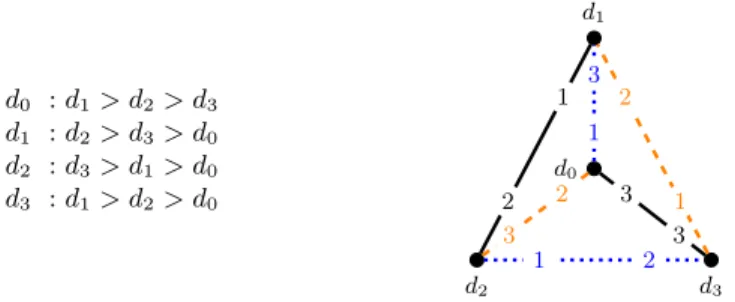CERS-IE WORKING PAPERS | KRTK-KTI MŰHELYTANULMÁNYOK
INSTITUTE OF ECONOMICS, CENTRE FOR ECONOMIC AND REGIONAL STUDIES, BUDAPEST, 2020
Popular Matchings in Complete Graphs ÁGNES CSEH– TELIKEPALLI KAVITHA
CERS-IE WP – 2020/4
January 2020
https://www.mtakti.hu/wp-content/uploads/2020/01/CERSIEWP202004.pdf
CERS-IE Working Papers are circulated to promote discussion and provoque comments, they have not been peer-reviewed.
Any references to discussion papers should clearly state that the paper is preliminary.
Materials published in this series may be subject to further publication.
ABSTRACT
Our input is a complete graph G on n vertices where each vertex has a strict ranking of all other vertices in G. The goal is to construct a matching in G that is “globally stable” or popular. A matching M is popular if M does not lose a head-to-head election against any matching M’: here each vertex casts a vote for the matching in {M,M’} in which it gets a better assignment. Popular matchings need not exist in the given instance G and the popular matching problem is to decide whether one exists or not. The popular matching problem in G is easy to solve for odd n. Surprisingly, the problem becomes NP-hard for even n, as we show here. This seems to be the first graph theoretic problem that is efficiently solvable when n has one parity and NP- hard when n has the other parity.
JEL codes:
C63, C78Keywords: popular matching, NP-completeness, polynomial algorithm, stable matching
Ágnes Cseh
Centre for Economic and Regional Studies, Institute of Economics, Tóth Kálmán utca 4., Budapest, 1097, Hungary
e-mail: cseh.agnes@krtk.mta.hu Telikepalli Kavitha
Tata Institute of Fundamental Research, Mumbai, India
e-mail: kavitha@tifr.res.in
Népszerű párosítások teljes gráfokban ÁGNES CSEH – TELIKEPALLI KAVITHA
ÖSSZEFOGLALÓ
Adott egy teljes gráf, ahol minden csúcs szigorú listában rangsorolja a szomszédjait.
Egy M párosítást akkor nevezünk népszerűnek, ha nincsen olyan M’ párosítás, hogy több csúcs részesíti előnyben M’-t M-mel szemben, mint fordítva. Nem minden inputban létezik népszerű párosítás. Ha a csúcsok száma a gráfban páratlan, akkor könnyű eldönteni, hogy az inputon van-e népszerű párosítás. Meglepő módon ugyanez a probléma NP-teljes olyan gráfokon, amik páros sok csúcsot tartalmaznak.
Ez az első olyan gráfelméleti probléma, ahol a csúcshalmaz paritása ilyen bonyolultságelméleti különbséget indukál.
JEL:
C63, C78Kulcsszavak: népszerű párosítás, NP-teljesség, polinomiális algoritmus, stabil
párosítás
Popular Matchings in Complete Graphs
Agnes Cseh´ 1? and Telikepalli Kavitha2??
1 Centre for Economic and Regional Studies, Institute of Economics, Budapest;cseh.agnes@krtk.mta.hu
2 Tata Institute of Fundamental Research, Mumbai;kavitha@tcs.tifr.res.in
Abstract. Our input is a complete graph G on n vertices where each vertex has a strict ranking of all other vertices inG. The goal is to construct a matching inGthat is “globally stable” orpopular. A matchingMis popular ifM does not lose a head-to-head election against any matchingM0: here each vertex casts a vote for the matching in{M, M0}in which it gets a better assignment. Popular matchings need not exist in the given instanceGand the popular matching problem is to decide whether one exists or not. The popular matching problem inG is easy to solve for oddn. Surprisingly, the problem becomesNP-hard for evenn, as we show here. This seems to be the first graph theoretic problem that is efficiently solvable whennhas one parity andNP-hard whennhas the other parity.
1 Introduction
Consider a complete graphG= (V, E) onnvertices where each vertex ranks all other vertices in a strict order of preference. Such a graph is called a roommatesinstance with complete preferences.
The problem of computing a stable matching in Gis a classical and well-studied problem. Recall that a matchingM is stable if there is noblocking pair with respect toM, i.e., a pair (u, v) where bothuandv prefer each other to their respective assignments inM.
Stable matchings need not always exist in a roommates instance. For example, the instance given in Fig. 1 on 4 verticesd0, d1, d2, d3has no stable matching. (Hered0’s top choice isd1, second choice isd2, and last choice isd3, and similarly for the vertices.)
d0 :d1> d2> d3
d1 :d2> d3> d0
d2 :d3> d1> d0
d3 :d1> d2> d0
d0
d1
d2 d3
1 3
2 3
3 3 1
2
1 2
1 2
Fig. 1.An instance that admits two popular matchings—marked by dotted blue and dashed orange edges—
but no stable matching. The preference list of each vertex is illustrated by the numbers on its edges: a lower number indicates a more preferred neighbor.
Irving [17] gave an efficient algorithm to decide if G admits a stable matching or not. In this paper we consider a notion that is more relaxed than stability: this is the notion ofpopularity. For any vertex u, a ranking over neighbors can be extended naturally to a ranking over matchings as follows: uprefers matching M to matching M0 if (i) u is matched inM and unmatched in M0 or
?Supported by the Cooperation of Excellences Grant (KEP-6/2017), by the Ministry of Human Resources under its New National Excellence Programme ( ´UNKP-18-4-BME-331), the Hungarian Academy of Sci- ences under its Momentum Programme (LP2016-3/2016), its J´anos Bolyai Research Fellowship, and OTKA grant K128611.
?? This work was done while visiting the Hungarian Academy of Sciences, Budapest.
(ii) u is matched in both and u prefers M(u) to M0(u). For any two matchings M and M0, let φ(M, M0) be the number of vertices that preferM toM0.
Definition 1. Let M be any matching in G. M is popular if φ(M, M0) ≥ φ(M0, M) for every matching M0 in G.
Suppose an election is held betweenM andM0 where each vertex casts a vote for the matching that it prefers. So φ(M, M0) (similarly, φ(M0, M)) is the number of votes for M (resp., M0). A popular matchingM never loses an election to another matchingM0 sinceφ(M, M0)≥φ(M0, M):
thus it is a weakCondorcet winner[5, 6] in the corresponding voting instance. This is why popularity can be regarded as a natural notion of “global stability”.
The notion of popularity was first introduced in bipartite graphs in 1975 by G¨ardenfors—popular matchings always exist in bipartite graphs since stable matchings always exist here [10] and every stable matching is popular [11]. The proof that every stable matching is popular holds in non- bipartite graphs as well [4]; in fact, it is easy to show that every stable matching is a min-size popular matching [14]. Relaxing the constraint of stability to popularity allows us to find globally stable matchings that may exist in instances that do not admit stable matchings; moreover, even when stable matchings exist, there may be popular matchings that achieve more “social good” (such as larger size), which might be relevant in many applications.
Observe that the instance in Fig. 1 has two popular matchings: M1 = {(d0, d1),(d2, d3)} and M2 ={(d0, d2),(d1, d3)}. However as was the case with stable matchings, popular matchings also need not always exist in the given instanceG. Just take, for example, the same instance as in Fig. 1, but without vertexd0. Thepopular roommates problemis to decide ifGadmits a popular matching or not. When the graph is not complete, it is known that the popular roommates problem is NP- hard [9, 12]. Here we are interested in the complexity of the popular matching problem when the input instance is complete.
Interestingly, several popular matching problems that are intractable in bipartite graphs become tractable incomplete bipartite graphs. The min-cost popular matching problem in bipartite graphs is such a problem—this is NP-hard in a bipartite graph with incomplete lists [9], however it can be solved in polynomial time in a bipartite graph with complete lists [8]. The difference is due to the fact that while there is no efficient description of the convex hull of all popular matchings in a general bipartite graph, this polytope has a compact extended formulation in a complete bipartite graph.
It is a simple observation (see Section 2) that whennisodd, a matching in a complete graphG onnvertices is popular only if it is stable. Since there is an efficient algorithm to decide ifGadmits a stable matching or not, the popular roommates problem in a complete graphGcan be efficiently solved whennis odd. We show the following result here.
Theorem 1. Let G be a complete graph on n vertices, where n is even. The problem of deciding whether Gadmits a popular matching or not isNP-hard.
So the popular roommates problem with complete preference lists isNP-hard for evennwhile it is easy to solve for oddn. Note that the popular roommates problem is non-trivial for everyn≥5, i.e., there are both “yes instances” and “no instances” of sizen. It is rare and unusual for a natural decision problem in combinatorial optimization to be efficiently solvable whennhas one parity and becomeNP-hard whennhas the other parity. We are not aware of any natural optimization problem on graphs that is non-trivially tractable when the cardinality of the vertex set has one parity, which becomes intractable for the other parity.
1.1 Background and related work
The first polynomial time algorithm for the stable roommates problem was given by Irving [17] in 1985. Roommates instances that admit stable matchings were characterized in [25]. New polynomial time algorithms for the stable roommates problem were given in [24, 26].
Algorithmic questions for popular matchings in bipartite graphs have been well-studied in the last decade [1, 8, 14, 16, 18–20]. Not much was known on popular matchings in non-bipartite graphs.
Bir´o et al. [1] proved that validating whether a given matching is popular can be done in polynomial time, even when ties are present in the preference lists. It was shown in [15] that every roommates instance G= (V, E) admits a matching with unpopularity factorO(log|V|) and that it isNP-hard to compute a least unpopularity factor matching. It was shown in [16] that computing a max-weight popular matching in a roommates instance with edge weights is NP-hard, and more recently, that computing a max-size popular matching in a roommates instance isNP-hard [3].
The complexity of the popular roommates problem was open for several years [1, 7, 15, 16, 22] and two independentNP-hardness proofs [9, 12] of this problem were announced very recently. Interest- ingly, both these hardness proofs need “incomplete preference lists”, i.e., the underlying graph isnot complete. The reduction in [12] is from a variant of the vertex cover problem called thepartitioned vertex cover problem and we discuss the reduction in [9] in Section 1.2 below. So the complexity status of the popular roommates problem in a complete graph was an open problem and we resolve it here.
Computational hardness for instances with complete lists has been investigated in various match- ing problems under preferences. An example is the three-sided stable matching problem with cyclic preferences: this involves three groups of participants, say, men, women, and dogs, where dogs have weakly ordered preferences over men only, men have preferences over women only, and finally, women only list the dogs. If these preferences are allowed to be incomplete, the problem of finding aweakly stable matching is known to beNP-complete [2]. It is one of the most intriguing open questions in stable matchings [22, 27] as to whether the same problem becomes tractable when lists are complete.
1.2 Techniques
The 1-in-3 SAT problem is a well-known NP-hard problem [23]: it consists of a 3-SAT formula φ with no negated literals and the problem is to find a truth assignment to the variables in φ such that every clause has exactly one variable set to true. We show a polynomial time reduction from 1-in-3 SAT to the popular roommates problem with complete lists.
Our construction is based on the reduction in [9] that proved the NP-hardness of the popular roommates problem. However there are several differences between our reduction and the reduction in [9]. The reduction in [9] considered a popular matching problem in bipartite graphs called the
“exclusive popular set” problem and showed it to beNP-hard—when preference lists are complete, this problem can be easily solved. Thus the reduction in [9] needs incomplete preference lists.
The exclusive popular set problem asks if there is a popular matching in the given bipartite graph where the set of matched vertices is S, for a given even-sized subset S. A key step in the reduction in [9] from this problem in bipartite graphs to the popular matching problem in non- bipartite graphs merges all vertices outsideS into a single node. Thus the total number of vertices in the non-bipartite graph used in [9] isodd. Moreover, the fact that popular matchings always exist in bipartite graphs is crucially used in this reduction. However in our setting, the whole problem is to decide ifany popular matching exists in the given graph—thus there are no popular matchings that “always exist” here.
The reduction in [9] primarily uses the LP framework of popular matchings in bipartite graphs from [18, 19, 21] to analyze the structure of popular matchings in their instance. The LP framework characterizing popular matchings in non-bipartite graphs is more complex [21], so we use the com- binatorial characterization of popular matchings [14] in terms of forbidden alternating paths/cycles to show that any popular matching in our instance will yield a 1-in-3 satisfying assignment for φ.
To show the converse, we use a dual certificate similar to the one used in [9] to prove the popularity of the matching that we construct using a 1-in-3 satisfying assignment forφ.
Organization of the paper. We discuss preliminaries in Section 2. Section 3 describes the construction of our complete graph Gcorresponding to a given a 1-in-3 SAT formula φ. Section 4 studies the structure of the graph G and Section 5 shows that any popular matching in G yields a 1-in-3 satisfying assignment forφ. Section 6 completes the reduction by showing how to obtain a popular matching inGfrom any 1-in-3 satisfying assignment for φ.
2 Preliminaries
This section contains a characterization of popular matchings from [14]. We also include a simple proof of the claim stated in Section 1 that when nis odd, every popular matching inG has to be stable.
Let M be any matching in G= (V, E). For any pair (u, v)∈/ M, definevoteu(v, M) as follows:
(hereM(u) isu’s partner inM andM(u) =nullifuis unmatched inM) voteu(v, M) =
(+ ifuprefersv toM(u);
− ifuprefersM(u) tov.
Label every edge (u, v) that does not belong toM by the pair (voteu(v, M),votev(u, M)). Thus every non-matching edge has a label in{(±,±)}. For example, if consider the matching marked by the dashed orange edges in Fig. 1, then (d1, d2) is labeled (+,+), (d2, d3) is labeled (+,−), (d0, d1) is labeled (+,−), and (d0, d3) is labeled (−,−). Note that an edge is labeled (+,+) if and only if it is a blocking edge toM. LetGM be the subgraph ofG obtained by deleting edges labeled (−,−) fromG. The following theorem characterizes popular matchings in G.
Theorem 2 ([14]).M is popular inGif and only ifGM does not contain any of the following with respect to M:
(1) an alternating cycle with a(+,+) edge;
(2) an alternating path with two distinct (+,+) edges;
(3) an alternating path with a (+,+)edge and an unmatched vertex as an endpoint.
Using the above characterization, it can be easily checked whether a given matching is popular or not [14]. Thus ourNP-hardness result implies that the popular roommates problem isNP-complete.
When n is odd.Recall the claim made in Section 1 that whennis odd, every popular matching inGhas to be stable. A simple proof of this statement is included below.
Observation 1 ([13]) LetGbe a complete graph onnvertices, wherenis odd. Any popular match- ing in Ghas to be stable.
Proof. Sincenis odd andGis complete, any popular matching leaves exactly one vertex unmatched.
Let M be a popular matching and letv be the vertex left unmatched in M. Consider a vertex u adjacent tov. We know that (u, w)∈M for somew∈V \ {v}, and due to Part (3) in Theorem 2, no (+,+) edge is incident to w. Sincev is adjacent not only to u, but to all vertices in the graph,
this holds for allw∈V. ThusM is stable. ut
3 The graph G
Recall that φis the input formula to 1-in-3 SAT. The graph G that we construct here consists of gadgets in 4 levels along with 2 special gadgets that we will call theD-gadget andZ-gadget. Gadgets in level 1 correspond to variables in the formula φ while gadgets in levels 0, 2, and 3 correspond to clauses in φ. Variants of the gadgets in levels 0-3 and the D-gadget were used in [9] while the Z-gadget is new.
We will now describe these gadgets: along with a figure, we provide the preference lists of vertices in this gadget. The tail of each list consists of all vertices not listed yet, in an arbitrary order. Even though the preference lists are complete, the structure of the gadgets and the preference lists will ensure that inter-gadget edges will not belong to any popular matching, as we will show in Section 4.
The D-gadget.TheD-gadget is on 4 verticesd0, d1, d2, d3and the preference lists of these vertices are as given in Fig. 1 with all vertices outside theD-gadget at the tail of each list (in an arbitrary order). Recall that this gadget admits no stable matching.
We describe gadgets from level 1 first, then levels 0, 2, 3, and finally, the Z-gadget. The stable matchings within the gadgets are highlighted by colors in the figures. The gray elements in the preference lists denote vertices that are outside this gadget. We will assume thatD in a preference list stands ford0> d1> d2> d3.
Level 1.For each variable Xi in the formulaφ, we construct a gadget on four vertices as shown in Fig. 2. The bottom verticesx0iandy0iwill be preferred by some vertices in level 0 to vertices in their own gadget, while the top verticesxi andyi will be preferred by some vertices in level 2 to vertices in their own gadget. All four vertices in a level 1 gadget prefer to be matched among themselves, along the four edges drawn than be matched to any other vertex in the graph. This gadget has a unique stable matching{(xi, yi),(x0i, yi0)}.
xi :yi> yi0>D> . . . x0i :yi> yi0>D> . . . yi :xi> x0i>D> . . . yi0 :xi> x0i>D> . . .
xi yi
y0i
x0i
1 1
2 2
1 2 2
1
Fig. 2.The variable gadget in level 1.
Level 0.To each clausec=Xi∨Xj∨Xk in the formula φ, we create6 gadgetsin level 0. One of these can be seen in Fig. 3. The top two vertices, i.e.ac1 andbc1, ranky0j and x0k in level 1, as their respective second choices. Recall that indicesjandkare well-defined in the clausec=Xi∨Xj∨Xk. Within this level 0 gadget onac1, bc1, ac2, bc2, both{(ac1, bc1),(ac2, bc2)}and {(ac1, bc2),(ac2, bc1)} are stable matchings. In the preference lists below (and also for gadgets in levels 2 and 3), we have omitted the superscriptcin their lists for the sake of readability.
a1 :b1>y0j> b2>D> . . . a2 :b2> b1>D> . . . b1 :a2>x0k> a1>D> . . . b2 :a1> a2>D> . . .
ac1 bc1
bc2
ac2
1 3
1 2
2 1 3
1
Fig. 3.A clause gadget in level 0.
The gadget on vertices {ac3, ac4, bc3, bc4} is built analogously: the vertexac3 ranks y0k as its second choice, whilebc3 ranks x0i second. In the third gadget, the vertexac5 ranks yi0 second, whilebc5 ranks x0j second. Observe the shift ini, j, k indices as second choices for verticesac1, ac3, ac5 (and similarly, forbc1, bc3, bc5).
The fourth, fifth and sixth gadgets are analogous to the first, second, and third gadgets, respec- tively, but there is a slight twist. More precisely, the preferences ofa0c1, a0c2, b0c1, b0c2 in the fourth gadget are analogous to the preferences in Fig. 3, except thata0c1 ranksyk0 second, whileb0c1 ranksx0j second.
Similarly, the second choice ofa0c3 isyi0, the second choice ofb0c3 isx0k, and finally,a0c5 ranksyj0 second, while b0c5 ranks x0i second. Observe the change in orientation of the indicesi, j, k as second choice neighbors when comparing the first three level 0 gadgets ofcwith its last three level 0 gadgets. This will be important to us later.
Level 2.To each clausec=Xi∨Xj∨Xk in the formulaφ, we create6 gadgetsin level 2. The first gadget in level 2 is on verticespc0, pc1, pc2, qc0, qc1, qc2 and their preference lists are described in Fig. 4.
Note thatpc2 ranksyj from level 1 as its second choice, whileq2c ranksxk from level 1 second.
The second gadget in level 2 is on vertices pc3, pc4, pc5, q3c, q4c, q5c and it is built analogously. That is,pc3 andqc3 are each other’s top choices and similarly,pc4 andqc4 are each other’s top choices, and so on. The preference list of pc5 is q3c > yk > qc4 > q5c > D > . . . and the preference list of q5c is pc4>xi> pc3> pc5>D> . . .
p0 :q0> q2>D> . . . p1 :q1> q2>D> . . .
p2 :q0>yj> q1> q2>D> . . . q0 :p0> p2>D> . . .
q1 :p1> p2>D> . . .
q2 :p1>xk> p0 > p2>D> . . .
pc0 qc0
pc1 qc1
pc2 qc2
1 1
1 1
4 4
2
3 1
2
2 1 3
3
Fig. 4.A clause gadget in level 2.
The third gadget in level 2 is on vertices pc6, pc7, pc8, qc6, qc7, qc8 and it is built analogously. In par- ticular, the preference list of pc8 is q6c > yi > qc7 > q8c > D > . . . and the preference list of q8c is pc7>xj> pc6> pc8>D> . . .
The fourth gadget in level 2 is on verticesp0c0, p0c1, p0c2, q00c, q0c1, q20c and it is totally analogous to the first gadget in level 2. That is,p0c0 andq00care each other’s top choices and similarly,p0c1 andq10care each other’s top choices, and so on. In particular, the preference list ofp0c2 isq00c>yj > q10c> q0c2 >D> . . . and the preference list ofq0c2 isp0c1 >xk > p0c0 > p0c2 >D> . . .
Similarly, the fifth gadget in level 2 is on verticesp0c3, p0c4, p0c5, q30c, q40c, q0c5 and it is totally analogous to the second gadget in level 2. Also, the sixth gadget in level 2 is on verticesp0c6, p0c7, p0c8, q60c, q0c7, q0c8 and it is totally analogous to the third gadget in level 2.
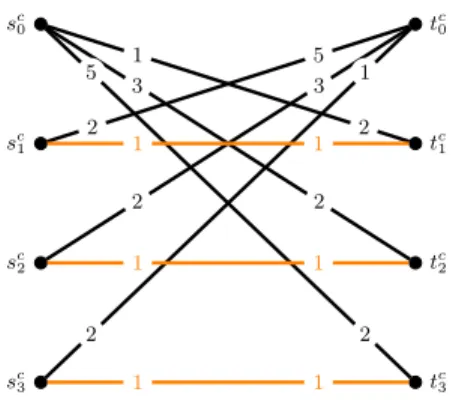
Level 3.To each clausec=Xi∨Xj∨Xk in the formulaφ, we create2 gadgetsin level 3. The first gadget is on verticessc0, sc1, sc2, sc3, tc0, tc1, tc2, tc3 and the preference lists of these vertices are described in Fig. 5.
s0 :t1>q0> t2>q3> t3 >D> t0> . . . t0 : s3>p7> s2>p4> s1>D> s0> . . . s1 :t1> t0>D> . . .
t1 : s1> s0>D> . . . s2 :t2> t0>D> . . . t2 : s2> s0>D> . . . s3 :t3> t0>D> . . . t3 : s3> s0>D> . . .
sc0 tc0
sc1 tc1
sc2 tc2
sc3 tc3
1
2 3
2 5
2 5
2
3
2
1
2
1 1
1 1
1 1
Fig. 5.A clause gadget in level 3.
The second gadget in level 3 is ons0c0, s0c1, s0c2, s0c3, t0c0, t0c1, t0c2, t0c3 and their preference lists are abso- lutely analogous to the preference lists of the first gadget in level 3.
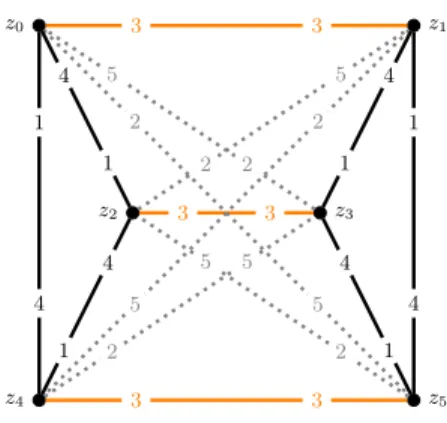
The Z-gadget. The Z-gadget is on 6 vertices z0, z1, z2, z3, z4, z5 and the preference lists of these vertices are given in Fig. 6. The vertices in a set stand for all these vertices in an arbitrary order.
For example,∪i{xi, yi}denotes all the “top” vertices belonging to variable gadgets in an arbitrary order.
Note thatGis a complete graph on an even number of vertices and so every popular matching inGhas to be a perfect matching.
4 Popular edges in G
Call an edgeeinGpopularif there is a popular matchingM inGsuch thate∈M. In this section we identify edges that are not popular and show that every popular edge is an intra-gadget edge, connecting two vertices of the same gadget.
z0 :z4> z5>∪i{xi, yi}>∪c,i{pc3i+1, q3ic, p0c3i+1, q3i0c}>
∪c,i{aci, bci, a0ci, b0ci}> z1 > z2> z3>D> . . . z1 :z5> z4>∪i{xi, yi}>∪c,i{pc3i+1, q3ic, p0c3i+1, q3i0c}>
∪c,i{aci, bci, a0ci, b0ci}> z0 > z3> z2>D> . . . z2 :z0> z1> z3> z4> z5>D> . . .
z3 :z1> z0> z2> z5> z4>D> . . . z4 :z2> z3> z5> z0> z1>D> . . . z5 :z3> z2> z4> z1> z0>D> . . .
z0 z1
z2 z3
z4 z5
3 3
3 3
3 3
2
5 2
5
2
5 2
5
2 5
2 5
1
4 1
4 1 4
1
4 1 4 1
4
Fig. 6.TheZ-gadget.
The following observation, which is straightforward, will be used repeatedly in our proofs.
Observation 2 Let v beu’s top choice neighbor. Ifv is matched inM to a neighbor worse thanu then(u, v)is a blocking edge to M.
Lemma 1. For any clausec, no popular matching in Gcan matchsc0 (similarly, tc0) to a neighbor worse thantc0 (resp.,sc0). An analogous statement holds fors0c0 andt0c0.
Proof. LetM be a popular matching such that (sc0, v)∈M for some vertex v such thattc0> v in sc0’s list, i.e.,sc0 preferstc0 tov. We claim this implies:
– a (+,+) edge reachable fromvvia an alternating path in GM that begins with a non-matching edge incident to vand
– a (+,+) edge reachable fromsc0via an alternating path inGM that begins with a non-matching edge incident to sc0.
If this is the same (+,+) edge then we have an alternating cycle inGM with a (+,+) edge, a contradiction to M’s popularity (by Theorem 2). If these are two different (+,+) edges then there is an alternating path in GM with two (+,+) edges, again a contradiction to M’s popularity (by Theorem 2).
(1) Ifvis a top choice neighbor for some vertex (such aszk, xj, yj, d1, d2, d3, aci, bci, pc0, pc1, and so on) then there is a (+,+) edge incident tov (by Observation 2).
(2) Supposevis one ofsr0, tr0, s0r0, t0r0 for somer. Assume without loss of generality thatv=sr0. Then either (sr0, tr0) is a (+,+) edge ortr0is matched inM to a neighbor better thansr0.
Recall tr0’s preference list: every vertex that tr0 prefers to sr0 is either a top choice neighbor or it is d0. In the former case, there is a (+,+) edge incident to tr0’s partner (by Observation 2) and in the latter case also there is a (+,+) edge incident tod0 since one ofd1, d2, d3is matched to a neighbor worse than d0 and so there is a (+,+) edge between this di and d0. Since the edge (sr0, tr0) is a (+,−) edge, there is a (+,+) edge reachable from sr0 via an alternating path of length 2.
(3) The only case left is whenvis neither a top choice neighbor of some vertex nor one ofsr0, tr0, s0r0, t0r0 for some r. So uis a vertex such asd0 or x0i, yi0 or pc3j+2, qc3j+2, p0c3j+2, q3j+20c (forj = 0,1,2 and some c). It is easy to see that there is a (+,+) edge reachable fromvvia an alternating path of length at most 2. For instance, either (x0i, yi0) is a (+,+) edge or (xi, y0i)∈M which creates the alternating path (sc0, x0i)-(yi0, xi)-(yi,∗), where (xi, yi) is a (+,+) edge.
Similarly, we can argue that there is a (+,+) edge reachable fromsc0 via an alternating path in GM. If tc0 is matched to a neighbor worse thansc0 then the edge (sc0, tc0) is a (+,+) edge. Else tc0 is matched to a neighbor ubetter thansc0 and this means there is a (+,+) edge incident tou, as we argued above in case (2). Hence there is a (+,+) edge reachable fromsc0via an alternating path of
length at most 2 inGM. ut
Lemma 2. Every popular matching matches the vertices in theD-gadget among themselves.
Proof. Let M be a matching that matches di for some i ∈ {0,1,2,3} to a vertex v outside the D-gadget. This means at least 2 verticesdi anddj in theD-gadget are matched to vertices outside the D-gadget. So (di, dj) is a (+,+) edge. We now claim there is a forbidden alternating path or cycle (as given in Theorem 2) toM’s popularity.
Ifv is a top choice neighbor or a vertex such asx0i, y0i orpc3j+2, q3j+2c , p0c3j+2, q3j+20c (forj = 0,1,2 and somec) then there is a (+,+) edgeereachable fromvvia an alternating path of length at most 2 as seen in the proof of Lemma 1. This creates an alternating path in GM with 2 (+,+) edges:
(dj, di) ande.
The other possibility is thatvissc0, tc0, s0c0, t0c0 for some clausec. Assume without loss of generality thatv=sc0. Consider the vertextc0. We know from Lemma 1 thattc0has to be matched to a neighbor at least as good assc0. So we have the following cases:
(1) tc0is matched to a vertexdi0 in theD-gadget: this means there is either an alternating path with 2 (+,+) edges or an alternating cycle with a (+,+) edge:
(sc0, di)(+,+)− (di0, tc0)(+,+)− (sc1,∗) or (sc0, di)(+,+)− (di0, tc0)(+,−)− (sc1, tc1)(−,+)− (sc0, di).
Ifsc1is matched to a neighbor worse thantc0then the former is an alternating path with two (+,+) edges: these are (di, di0) and (tc0, sc1). Elsesc1 is matched to tc1 and the latter is an alternating cycle with a (+,+) edge, which is (di, di0).
(2) tc0 is matched tosci for some i∈ {1,2,3}: this means tci is matched to a neighbor worse thansc0 and so (sc0, tci) is a (+,+) edge and thus we have the following alternating path with two (+,+) edges (tc1, sc0) and (di, dj):
(∗, tc1)
(+,+)
− (sc0, di)
(+,+)
− (dj,∗).
(3) tc0 is matched to eitherpc4 or pc7: we will show that this results in an alternating path with two (+,+) edges. Assume without loss of generality thattc0is matched topc4. Consider the following alternating path:
(∗, sc3)
(+,+)
− (tc0, pc4)
(+,+)
− (qc5,∗) or (∗, dj)
(+,+)
− (di, sc0)(+,−)− (tc3, sc3)(−,+)− (tc0, pc4)
(+,+)
− (q5c,∗).
Recall thatsc3is the top choice neighbor oftc0and the vertexpc4 is the top choice neighbor ofq5c. If the vertex sc3 is matched to a neighbor worse thantc0 then the former path is an alternating path in GM with two (+,+) edges in it: these are (sc3, tc0) and (pc4, qc5). Else (sc3, tc3) ∈ M and recall that the edge (sc0, tc3) is a (+,−) edge as sc0 prefers tc3 to di. This creates the latter path which is an alternating path inGM with 2 (+,+) edges in it: these are (di, dj) and (pc4, q5c). ut The gadgetDadmits 2 popular matchings:{(d0, d1),(d2, d3)}and{(d0, d2),(d1, d3)}. So ifM is a popular matching then either{(d0, d1),(d2, d3)} ⊂M or {(d0, d2),(d1, d3)} ⊂M.
Lemma 3. Let(u, v)be an edge inGwhere bothuandvpreferd0 to each other. Then(u, v)cannot be a popular edge.
Proof. LetM be a popular matching inGthat contains such an edge (u, v). We know from Lemma 2 that either{(d0, d1),(d2, d3)} ⊂M or {(d0, d2),(d1, d3)} ⊂ M. So there is always a blocking edge (di, dj)∈ {(d1, d3),(d1, d2)}to M.
Observe that both uand v cannot belong to the D-gadget as there is no such pair within D.
If exactly one of u, v belongs to the D-gadget then (u, v) is not a popular edge (by Lemma 2).
So neither unor v belongs to theD-gadget and this implies that uprefers d0, d1, d2, d3 to v and symmetrically,v prefersd0, d1, d2, d3 tou.
Consider the following alternating cycleC with respect toM: (u, v)
(+,−)
− (di0, di)
(+,+)
− (dj, dj0)
(−,+)
− (u, v),
where (di0, di) and (dj, dj0) are edges from theD-gadget inM and (di, dj) is a blocking edge. Thus C is an alternating cycle in GM with a (+,+) edge. This contradicts the popularity of M (by
Theorem 2). ut
Corollary 1. The edges (sc0, tc0)and(s0c0, t0c0)are not popular edges for any clausec.
Corollary 1 follows from Lemma 3 by setting u and v to sc0 and tc0 (similarly, s0c0 and t0c0), respectively. Let us callua levelivertex ifubelongs to a level igadget.
Lemma 4. No edge between a levelivertex and a level i+ 1vertex is popular, for0≤i≤2.
The proof of Lemma 4 follows from Claims 1-3 proved below.
Claim 1 There is no popular edge between a level 0 vertex and a level 1 vertex.
Proof. Let M be a popular matching in G with such an edge, say (ac1, y0j). We claim this would create an alternating path inGM with two (+,+) edges in it. Theorem 2 forbids such an alternating path. Consider the vertexbc1. There are 3 possibilities forbc1’s partner inM.
(1) bc1 is matched toac2
So (ac2, bc2) is labeled (+,+). Recall that bc2 is ac2’s top choice and the only neighbor that bc2 prefers toac2 isac1 (matched toyj0). Consider the following alternating path inGM:
(∗, bc2)
(+,+)
− (ac2, bc1)
(−,+)
− (ac1, y0j)
(+,+)
− (x0j,∗).
Ifx0j is matched to a neighbor worse thanyj0 then the above is an alternating path inGM with two (+,+) edges: these are (bc2, ac2) and (yj0, x0j). Else replace (x0j,∗) in the above path with (x0j, yj)−(xj,∗): the (+,+) edges here are (bc2, ac2) and (yj, xj).
(2) bc1 is matched tox0k
Either the edge (x0k, yk0) or the edge (xk, yk) will blockM. Supposey0k is matched to a neighbor worse thanx0k in M. Consider the following alternating path inGM:
(∗, yk0)
(+,+)
− (x0k, bc1)(−,+)− (ac1, yj0)
(+,+)
− (x0j,∗).
Either the above is an alternating path inGM with two (+,+) edges or by replacing (x0j,∗) with (x0j, yj)−(xj,∗) (as done in case (1)), we get an alternating path inGM with two (+,+) edges.
Ify0k is matched to a neighbor better thanx0k in M, i.e., if (xk, y0k)∈M then prefix both these alternating paths with (∗, yk). This will yield an alternating path in GM with (xk, yk) as a blocking edge and either (x0j, y0j) or (xj, yj) as a blocking edge.
(3) bc1 is matched to a neighbor worse thanac1
The edge (ac1, bc1) is labeled (+,+). Consider the following alternating path inGM: (∗, bc1)
(+,+)
− (ac1, yj0)
(+,+)
− (x0j,∗) or (∗, bc1)
(+,+)
− (ac1, y0j)(+,−)− (x0j, yj)
(+,+)
− (xj,∗).
That is, if x0j is matched to a neighbor worse than yj0 then consider the first alternating path above: this is an alternating path in GM with both (bc1, ac1) and (y0j, x0j) as (+,+) edges. Else (x0j, yj) ∈ M and the second alternating path is an alternating path in GM with (bc1, ac1) and (yj, xj) as (+,+) edges.
u t
Claim 2 There is no popular edge between a level 1 vertex and a level 2 vertex.
Proof. Let M be a popular matching in G that contains such an edge, say (pc2, yj). Consider the following alternating path with respect toM:
(pc2, yj)
(+,+)
− (x0j, y0j)
(+,+)
− (xj,∗).
SinceM is a perfect matching,x0j is matched inM. We know that no edge betweenx0j and a level 0 vertex belongs to M (by Claim 1). Also, M cannot match x0j to a neighbor that it regards worse thand0(by Lemma 3). Thusx0jhas to be matched toyj0 inM and so the above alternating path has two (+,+) edges: (x0j, yj) and (xj, yj0). This is a contradiction toM’s popularity (by Theorem 2).