https://doi.org/10.1007/s00224-017-9810-9
The Stable Roommates Problem with Short Lists
Agnes Cseh´ 1,2 ·Robert W. Irving3· David F. Manlove3
© The Author(s) 2017. This article is an open access publication
Abstract We consider two variants of the classical Stable Roommates problem with Incomplete (but strictly ordered) preference lists (SRI) that are degree constrained, i.e., preference lists are of bounded length. The first variant,EGAL d-SRI, involves finding an egalitarian stable matching in solvable instances ofSRI with preference lists of length at mostd. We show that this problem isNP-hard even ifd =3. On the positive side we give a 2d7+3-approximation algorithm ford ∈ {3,4,5}which improves on the known bound of 2 for the unbounded preference list case. In the second variant of SRI, calledd-SRTI, preference lists can include ties and are of
This article is part of the Topical Collection onSpecial Issue on Algorithmic Game Theory (SAGT 2016)
The authors were supported by the Hungarian Academy of Sciences under its Momentum Programme (LP2016-3/2016), its J´anos Bolyai Research Fellowship, OTKA grant K108383, COST Action IC1205 on Computational Social Choice and by EPSRC grant EP/K010042/1.
Agnes Cseh´
cseh.agnes@krtk.mta.hu Robert W. Irving Rob.Irving@glasgow.ac.uk David F. Manlove
David.Manlove@glasgow.ac.uk
1 Institute of Economics, Hungarian Academy of Sciences, Budapest, Hungary
2 Department of Operations Research and Actuarial Sciences, Corvinus University of Budapest, Budapest, Hungary
3 School of Computing Science, University of Glasgow, Glasgow, UK Published online: 30 September 2017
length at mostd. We show that the problem of deciding whether an instance ofd-
SRTIadmits a stable matching isNP-complete even ifd =3. We also consider the
“most stable” version of this problem and prove a strong inapproximability bound for thed=3 case. However ford=2 we show that the latter problem can be solved in polynomial time.
Keywords Stable matching·Bounded length preference lists·Complexity· Approximation algorithm
1 Introduction
In theStable Roommates problem with Incomplete lists(SRI), a graphG =(A, E) and a set of preference listsOare given, where the verticesA= {a1, . . . , an}corre- spond toagents, andO = {≺1, . . . ,≺n}, where≺iis a linear order on the vertices adjacent toaiinG(1≤i≤n). We refer to≺iasai’spreference list. The agents that are adjacent toaiinGare said to beacceptabletoai. Ifajandakare two acceptable agents foraiwhereaj ≺iakthen we say thataiprefersaj toak.
LetM be a matching inG. Ifaiaj ∈ M then we letM(ai)denoteaj. An edge aiaj ∈/ MblocksM, or forms ablocking edgeofM, ifaiis unmatched or prefers aj toM(ai), and similarlyaj is unmatched or prefersaitoM(aj). A matching is calledstableif no edge blocks it. Denote by SR the special case of SRI in which G = Kn. Gale and Shapley [9] observed that an instance of SR need not admit a stable matching. Irving [15] gave a linear-time algorithm to find a stable matching or report that none exists, given an instance ofSR. The straightforward modification of this algorithm to theSRIcase is described in [12]. We call anSRIinstancesolvableif it admits a stable matching.
In practice agents may find it difficult to rank a large number of alternatives in strict order of preference. One natural assumption, therefore, is that preference lists are short, which corresponds to the graph being of bounded degree. Given an inte- gerd ≥ 1, we defined-SRIto be the restriction ofSRI in whichGis of bounded degreed. This special case ofSRIproblem has potential applications in organising tournaments. As already pointed out in a paper of Kujansuu et al. [18],SRIcan model a pairing process similar to the Swiss system, which is used in large-scale chess com- petitions. The assumption on short lists is reasonable, because according to the Swiss system, players can be matched only to other players with approximately the same score.
A second variant ofSRI, which can be motivated in a similar fashion, arises if we allow ties in the preference lists, i.e.,≺i(1 ≤i ≤n) is now a strict weak ordering.
That is,≺i is a strict partial order in which incomparability is transitive. We refer to this problem as the Stable Roommates problem with Ties and Incomplete lists (SRTI) [17]. As in theSRIcase, defined-SRTIto be the restriction ofSRTIin which Gis of bounded degreed. Denote bySRTthe special case of SRTIin whichG = Kn. In the context of the motivating application of chess tournament construction as mentioned in the previous paragraph,d-SRTIis naturally obtained if a chess player has several potential partners of the same score and match history in the tournament.
In theSRTIcontext, ties correspond to indifference in the preference lists. In par- ticular, ifaiaj ∈ Eandaiak ∈ Ewhereaj ≺i ak andak ≺i aj thenaiis said to beindifferent betweenaj andak. Thus preference in theSRIcontext corresponds to strict preference in the case ofSRTI. Relative to the strict weak orders inO, we can define stability inSRTIinstances in exactly the same way as forSRI. This means, for example, that ifaiaj ∈ M for some matchingM, andai is indifferent betweenaj
and some agentak, thenaiak cannot blockM. The termsolvablecan be defined in theSRTIcontext in an analogous fashion to SRI. Using a highly technical reduction from a restriction of 3-SAT, Ronn [23] proved that the problem of deciding whether a givenSRTinstance is solvable isNP-complete. A simpler reduction was given by Irving and Manlove [17].
For solvable instances ofSRIthere can be many stable matchings. Often it is ben- eficial to work with a stable matching that is fair to all agents in a precise sense [11, 16]. One such fairness concept can be defined as follows. Given two agentsai,aj in an instanceI ofSRI, whereaiaj ∈E, let rank(ai, aj)denote the rank ofaj inai’s preference list (that is, 1 plus the number of agents thatai prefers toaj). LetAM
denote the set of agents who are matched in a given stable matchingM. (Note that this set depends only onIand is independent ofMby [12, Theorem 4.5.2].) Define c(M)=
ai∈AMrank(ai, M(ai))to be thecostofM. Anegalitarian stable match- ingis a stable matchingMthat minimisesc(M)over the set of stable matchings inI. Finding an egalitarian stable matching inSRwas shown to beNP-hard by Feder [7].
Feder [7,8] also gave a 2-approximation algorithm for this problem in theSRIset- ting. He also showed that an egalitarian stable matching inSRcan be approximated within a factor ofαof the optimum if and only if Minimum Vertex Cover can be approximated within the same factorα. It was proved later that, assuming the Unique Games Conjecture, Minimum Vertex Cover cannot be approximated within 2−εfor anyε >0 [19].
Given an unsolvable instanceIofSRIorSRTI, a natural approximation to a stable matching is amost-stablematching [1]. Relative to a matchingMinI, definebp(M) to be the set of blocking edges ofM and letbp(I)denote the minimum value of
|bp(M)|, taken over all matchingsMinI. ThenMis amost-stablematching inI if|bp(M)| =bp(I). The problem of finding a most-stable matching was shown to beNP-hard and not approximable withinnk−ε, for anyε >0, unless P=NP, where k= 12ifIis an instance ofSRandk=1 ifIis an instance ofSRT[1].
To the best of our knowledge, there has not been any previous work published on either the problem of finding an egalitarian stable matching in a solvable instance ofSRIwith bounded-length preference lists or the solvability ofSRTIwith bounded- length preference lists. This paper provides contributions in both of these directions, focusing on instances ofd-SRIandd-SRTIford≥2, with the aim of drawing the line between polynomial-time solvability andNP-hardness for the associated problems in terms ofd.
Our Contribution In Section2we study the problem of finding an egalitarian stable matching in an instance ofd-SRI. We show that this problem isNP-hard ifd =3, whilst there is a straightforward algorithm for the case thatd=2. We then consider the approximability of this problem for the case thatd≥3. We give an approximation
algorithm with a performance guarantee of 97 for the case that d = 3, 117 ifd = 4 and137 ifd=5. These performance guarantees improve on Feder’s 2-approximation algorithm for the generalSRIcase [7,8]. In Section3we turn tod-SRTIand prove that the problem of deciding whether an instance of 3-SRTIis solvable isNP-complete.
We then show that the problem of finding a most-stable matching in an instance of d-SRTIis solvable in polynomial time ifd = 2, whilst ford = 3 we show that this problem isNP-hard and not approximable withinn1−ε, for anyε > 0, unless P=NP. Due to various complications, as explained in Section4, we do not attempt to define and study egalitarian stable matchings in instances ofSRTI. Some open problems are presented in Section5. A structured overview of previous results and our results (marked by∗) ford-SRIandd-SRTIis contained in Table1.
Related Work Degree-bounded graphs, most-stable matchings and egalitarian sta- ble matchings are widely studied concepts in the literature on matching under preferences [21]. As already mentioned, the problem of finding a most-stable match- ing has been studied previously in the context ofSRI[1]. In addition to the results surveyed already, the authors of [1] gave anO(mk+1)algorithm to find a matchingM with|bp(M)| ≤kor report that no such matching exists, wherem= |E|andk≥1 is any integer. Most-stable matchings have also been considered in the context ofd-
SRI[4]. The authors showed that, ifd =3, there is some constantc > 1 such that the problem of finding a most-stable matching is not approximable withincunless P=NP. On the other hand, they proved that the problem is solvable in polynomial time ford ≤ 2. The authors also gave a(2d−3)-approximation algorithm for the problem for fixedd ≥ 3. This bound was improved to 2d−4 if the given instance satisfies an additional condition (namely the absence of a structure called anelitist odd party). Most-stable matchings have also been studied in the bipartite restriction ofSRIcalled theStable Marriage problem with Incomplete lists(SMI) [5,14]. Since every instance ofSMIadmits a stable matchingM(and hencebp(M)= ∅), the focus in [5,14] was on finding maximum cardinality matchings with the minimum number of blocking edges.
Regarding the problem of finding an egalitarian stable matching in an instance of
SRI, as already mentioned Feder [7,8] showed that this problem isNP-hard, though approximable within a factor of 2. A 2-approximation algorithm for this problem was also given independently by Gusfield and Pitt [13], and by Teo and Sethuraman [26].
Table 1 Summary of results ford-SRIandd-SRTI
Finding a stable matching finding an egalitarian stable matching
d-SRI in P [12,15] in P ford=2 (∗)
NP-hard even ford=3 (∗)
2d+3
7 -approximation ford∈ {3,4,5}(∗) 2-approximation ford≥6 [7,8]
d-SRTI in P ford=2 (∗)
NP-hard even ford=3 (∗) not well-defined (see Section4)
These approximation algorithms can also be extended to the more general setting where we are given a weight function on the edges, and we seek a stable matching of minimum weight. Feder’s 2-approximation algorithm requires monotone, non- negative and integral edge weights, whereas with the help of LP techniques [25,26], the integrality constraint can be dropped, while the monotonicity constraint can be partially relaxed. Chen et al. [6] study the fixed-parameter tractability of computing egalitarian stable matchings in the setting ofSRTI.
2 The Egalitarian Stable Roommates Problem
In this section we consider the complexity and approximability of the problem of computing an egalitarian stable matching in instances ofd-SRI. We begin by defining the following problems.
Problem 1 EGALd-SRI
Input: A solvable instanceI= G,Oofd-SRI, whereGis a graph andOis a set of preference lists, each of length at mostd.
Output: An egalitarian stable matchingMinI.
The decision version ofEGALd-SRIis defined as follows:
Problem 2 EGALd-SRI DEC
Input: I = G,O, K, whereG,Ois a solvable instanceIofd-SRIandKis an integer.
Question: DoesIadmit a stable matchingMwithc(M)≤K?
In the following we give a reduction from theNP-complete decision version of Minimum Vertex Cover in cubic graphs toEGAL3-SRI DEC, deriving the hardness of the latter problem.
Theorem 1 EGAL3-SRI DECisNP-complete.
Proof ClearlyEGAL 3-SRI DECbelongs toNP. To showNP-hardness, we begin by defining theNP-complete problem that we will reduce toEGAL3-SRI DEC.
Problem 3 3-VC
Input: I= G, K, whereGis a cubic graph andKis an integer.
Question: DoesGcontain a vertex cover of size at mostK?
3-VCisNP-complete [10,20].
Construction of theEGAL3-SRI DECInstance LetG, Kbe an instance of 3-VC, whereG=(V , E),E= {e1, . . . , em}andV = {v1, . . . , vn}. For eachi (1≤i≤n),
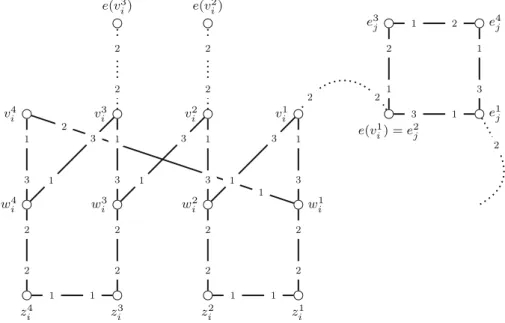
Fig. 1 Notation derived from the 3-VCinstanceG, K
suppose thatvi is incident to edges ej1,ej2 and ej3 in G, where without loss of generalityj1 < j2 < j3. Define ei,s = ejs (1 ≤ s ≤ 3). Similarly for eachj (1 ≤ j ≤ m), suppose thatej =vi1vi2, where without loss of generalityi1 < i2. Definevj,r =vir(1≤r≤2). The use of this notation is illustrated in Fig.1.
We now construct an instanceIof 3-SRIas follows. We define the following sets of vertices.
V = {vir : 1≤i≤n ∧ 1≤r≤4} E = {esj : 1≤j ≤m∧ 1≤s≤2} W = {wir : 1≤i≤n ∧ 1≤r≤4} Z = {zri : 1≤i≤n ∧ 1≤r≤4}
Intuitively,vir ∈ V corresponds to vertex vi and its incident edgeei,r, whilst esj ∈Ecorresponds to edgeejand its incident vertexvj,s. The setV∪E∪W∪Z constitutes the set of agents inI, and the preference lists of the agents are as shown in Fig.2. In the preference list of an agentvir(1≤i≤nand 1≤r≤3), the symbol
Fig. 2 Part of the constructed instance ofEGAL3-SRI DEC
e(vir)denotes the agentejs ∈ Esuch thatej =ei,r andvi =vj,s(that is,ej is the rth edge incident toviandviis thesth end-vertex ofej). Similarly in the preference list of an agentesj (1≤ i≤ mand 1≤ s ≤2), the symbolv(esj)denotes the agent vri ∈ Vsuch thatvi =vj,sandej =ei,r(that is,viis thesth end-vertex ofej and ej is therth edge incident tovi).
Finally we define some further notation inI. Let K = 7m+19n+K. The following edge sets play a particular role in our proof. Addition is taken modulo 4 here.
Vic = {vriwir : 1≤i≤n∧1≤r≤4} Viu = {vriwir+1 : 1≤i≤n∧1≤r≤4} Ej1 = {e1je2j, e3je4j : 1≤j ≤m}
Ej2 = {e1je4j, e2je3j : 1≤j ≤m} MZ = {z1iz2i, z3iz4i : 1≤i≤n}
This finishes the construction of theEGAL3-SRI DECinstanceI. In the remainder of the proof we show thatGhas a vertex coverCwhere|C| ≤Kif and only ifIhas a stable matchingMwherec(M)≤K.
Claim 2 IfGhas a vertex coverC such that|C| = k ≤ K, then there is a stable matchingMinIsuch thatc(M)≤K.
Proof Suppose thatGhas a vertex coverC such that|C| = k ≤ K. We construct a matchingM inI as follows. For eachi (1 ≤ i ≤ n), ifvi ∈ C, addVic toM, otherwise addViutoM. For eachj (1≤j ≤m), ifvj,1∈C, addEj2toM, otherwise addEj1toM. Finally add the pairs inMZtoM.
We now argue thatMis stable. Suppose thatej1e4j ∈Mfor somej (1 ≤j ≤m).
ThenEj2 ⊆ M, sovj,1 ∈ C. Letvi = vj,1. Then by construction, Vic ⊆ M, and hencevirhas his first choice for eachr(1≤r≤4). Thuse1jdoes not form a blocking edge ofMwithv(e1j). The argument is similar ife1jej2∈Mfor somej(1≤j ≤m).
ThenEj1 ⊆ M, sovj,2 ∈ C. Letvi = vj,2. Then by construction, Vic ⊆ M, and hencevri has his first choice for eachr(1≤r≤4). Thuse2j does not form a block- ing edge ofMwithv(e1j). Now suppose thatvirwri+1 ∈ Mfor somei(1 ≤ i ≤n) andr (1 ≤ r ≤ 3). Then Viu ⊆ M, so vi ∈/ C. Let esj = e(vir). If s = 1 then vi =vj,1. Hence by construction ofM,E1j ⊆M. Thene1j has his first-choice part- ner, sovir does not blockM withe(vir). Ifs = 2 thenvi = vj,2. As vj,2 ∈/ C, it follows thatvj,1∈ CasC is a vertex cover. Hence by construction ofM,E2j ⊆M.
Thene2jhas its first-choice partner, sovri does not blockMwithe(vir). It is straight- forward to verify thatMcannot admit any other type of blocking edge, and thusMis stable inI.
Clearly every agent inI is matched inM. We note that Theorem 4.5.2 of [12]
implies that every stable matching inImatches every agent inI– we will use this fact in the next claim. We finally note thatc(M)=4k+12k+9(n−k)+2(n− k)+4(n−k)+7m+4n = 7m+19n+k ≤ K, considering the contributions
from the agents matched inVic,Viu (1 ≤ i ≤ n),Ej1,E2j (1 ≤ j ≤ m) andMZ
respectively.
Claim 3 If there is a stable matchingM inI such thatc(M) ≤ K thenGhas a vertex coverCsuch that|C| =k≤K.
Proof Suppose thatMis a stable matching inIsuch thatc(M)≤K. We construct a set of verticesCinGas follows. AsMmatches every agent inI, then for eachi (1≤i ≤n), eitherVic ⊆MorViu ⊆M. In the former case addvi toC. Also, for eachj (1 ≤ j ≤ m), asMmatches every agent inI, eitherE1j ⊆M orEj2 ⊆M.
Finally, it follows thatMZ⊆M.
We now argue thatCis a vertex cover. Letj (1 ≤j ≤m) be given and suppose thatvj,1 ∈/ C andvj,2 ∈/ C. Suppose firstly that Ej1 ⊆ M. Letvi = vj,2. Then Viu ⊆Mby construction ofC, so thate2jblocksMwithv(e2j), a contradiction. Now suppose thatE2j ⊆M. Letvi=vj,1. ThenViu ⊆Mby construction ofC, so thate1j blocksMwithv(e1j), a contradiction. HenceCis a vertex cover inG.
Moreover ifk = |C|then given the composition ofM, as noted in the previous claim,c(M)=7m+19n+k, and sincec(M)≤Kit follows thatk≤K.
Theorem 1 immediately implies the following result.
Corollary 4 EGAL3-SRIisNP-hard.
We remark thatEGAL2-SRIis trivially solvable in polynomial time: the compo- nents of the graph are paths and cycles in this case, and the cost of a stable matching selected in one component is not affected by the matching edges chosen in another component. Therefore we can deal with each path and cycle separately, minimising the cost of a stable matching in each. Paths and odd cycles admit exactly one sta- ble matching (recall that (i) the instance is assumed to be solvable, and (ii) the set of matched agents is the same in all stable matchings [12, Theorem 4.5.2]), whilst even cycles admit at most two stable matchings (to find them, test each of the two perfect matchings for stability) – we can just pick the stable matching with lower cost in such a case. The following result is therefore immediate.
Proposition 5 EGAL2-SRIadmits a linear-time algorithm.
Corollary 4 naturally leads to the question of the approximabilty ofEGALd-SRI. As mentioned in the Introduction, Feder [7,8] provided a 2-approximation algorithm for the problem of finding an egalitarian stable matching in an instance ofSRI. As Theorems 6, 8 and 10 show, this bound can be improved for instances with bounded- length preference lists.
Theorem 6 EGAL3-SRIis approximable within9/7.
Proof LetIbe an instance of 3-SRIand letMegaldenote an egalitarian stable match- ing inI. First we show that any stable matching inIis a 4/3-approximation toMegal. We then focus on the worst-case scenario when this ratio 4/3 is in fact realised.
Then we design a weight function on the edges of the graph and apply Teo and Sethuraman’s 2-approximation algorithm [25,26] to find an approximate solution Mto a minimum weight stable matchingMopt for this weight function. This weight function helpsM to avoid the worst case for the 4/3-approximation for a signif- icant amount of the matching edges. We will ultimately show thatM is in fact a 9/7-approximation toMegal.
Claim 7 In an instance of EGAL3-SRI, any stable matching approximatesc(Megal) within a factor of4/3.
Proof LetM be an arbitrary stable matching in I. Call an edge uvan (i, j )-pair (i ≤j )ifv isu’sith choice anduisv’sjth choice. By Theorem 4.5.2 of [12], the set of agents matched inMegal is identical to the set of agents matched inM. We will now study the worst approximation ratios in all cases of(i, j )-pairs, given that 1≤i≤j ≤3 in 3-SRI.
• Ifuv∈Megalis a(1,1)-pair thenuandvcontribute 2 toc(Megal)and also 2 to c(M)since they must be also be matched inM(and in every stable matching).
• Ifuv ∈ Megalis a(1,2)-pair thenuandvcontribute 3 toc(Megal)and at most 4 toc(M). Since, ifuv /∈ M, thenvmust be matched to his 1st choice anduto his 2nd or 3rd, because one ofuandvmust be better off and the other must be worse off inMthan inMegal.
• Ifuv∈Megalis a(1,3)-pair thenuandvcontribute 4 toc(Megal)and at most 5 toc(M). Since, ifuv /∈M, thenvmust be matched to his 1st or 2nd choice and uto his 2nd or 3rd.
• Ifuv∈Megalis a(2,2)-pair thenuandvcontribute 4 toc(Megal)and at most 4 toc(M). Since, ifuv /∈ M, then one must be matched to his 1st choice and the other to his 3rd.
• Ifuv∈Megalis a(2,3)-pair thenuandvcontribute 5 toc(Megal)and at most 5 toc(M). Since, ifuv /∈M, thenvmust be matched to his 1st or 2nd choice and uto his 3rd.
• Ifuv ∈Megalis a (3,3)-pair thenuandvcontribute 6 toc(Megal)and also 6 to c(M)since they must be also be matched inM(and in every stable matching – this follows by [12, Lemma 4.3.9]).
It follows that, for every pairuv∈Megal, rank(u, M(u))+rank(v, M(v))
rank(u, Megal(u))+rank(v, Megal(v)) = rank(u, M(u))+rank(v, M(v)) rank(u, v)+rank(v, u)
≤ 4/3.
Hencec(M)/c(Megal)≤4/3 and Claim 7 is proved.
As shown in Claim 7, the only case when the approximation ratio 4/3 is reached is whereMegal consists of (1,2)-pairs exclusively, while the stable matching output by the approximation algorithm contains (1,3)-pairs only. We will now present an algorithm that either delivers a stable solutionM containing at least a significant amount of the (1,2)-pairs inMegal or a certificate that Megal contains only a few (1,2)-pairs and thus any stable solution is a good approximation.
To simplify our proof, we execute some basic pre-processing of the input graph.
If there are any (1,1)-pairs inG, then these can be fixed, because they occur in every stable matching and thus can only lower the approximation ratio. Similarly, if an arbitrary stable matching contains a (3,3)-pair, then this edge appears in all stable matchings and thus we can fix it. Those (3,3)-pairs that do not belong to the set of sta- ble edges can be deleted from the graph. From this point on, we assume that no edge is ranked first or last by both of its end vertices inGand prove the approximation ratio for such graphs.
Take the following weight function on alluv∈E:
w(uv)=
0 ifuvis a (1,2)-pair, 1 otherwise.
We designedw(uv)to fit the necessary U-shaped condition of Teo and Sethura- man’s 2-approximation algorithm [25,26]. This condition on the weight function is as follows. We are given a functionfpon the neighbouring edges of a vertexp. Function fpisU-shapedif it is non-negative and there is a neighbourqofpso thatfpis mono- tone decreasing on neighbours in order ofp’s preference untilq, andfpis monotone increasing on neighbours in order ofp’s preference afterq. The approximation guar- antee of Teo and Sethuraman’s algorithm holds for an edge weight functionw(uv)if for every edgeuv∈ E,w(uv)can be written asw(uv)=fu(uv)+fv(uv), where fuandfvare U-shaped functions.
Ourw(uv)function is clearly U-shaped, because at each vertex the sequence of edges in order of preference is either monotone increasing or it is(1,0,1). Sincew itself is U-shaped, it is easy to decompose it into a sum of U-shapedfvfunctions, for example by settingfv(uv)=fu(uv)= w(uv)2 for every edgeuv.
LetMdenote an arbitrary stable matching, letM(1,2) be the set of (1,2)-pairs in M, and letMoptbe a minimum weight stable matching with respect to the weight functionw(uv). SinceMoptis by definition the stable matching with the largest num- ber of (1,2)-pairs,|Mopt(1,2)| ≥ |Megal(1,2)|. We also know thatw(M) = |M| − |M(1,2)| for every stable matchingM.
Due to Teo and Sethuraman’s approximation algorithm [25,26], it is possible to find a stable matchingMwhose weight approximatesw(Mopt)within a factor of 2.
Formally,
|M| − |M(1,2)| =w(M)≤2w(Mopt)=2|M| −2|Mopt(1,2)|. This gives us a lower bound on|M(1,2)|.
|M(1,2)| ≥2|Mopt(1,2)| − |M| ≥2|Megal(1,2)| − |M| (1)
We distinguish two cases from here on, depending on the sign of the term on the right. In both cases, we establish a lower bound onc(Megal)and an upper bound onc(M). These will give the desired upper bound of 9/7 onc(Mc(M)
egal). 1) 2|Megal(1,2)| − |M| ≤0
The derived lower bound for|M(1,2)|is negative or zero in this case. Yet we know that at most half of the edges inMegalare (1,2)-pairs, andc(e) ≥ 4 for the rest of the edges inMegal. Let us denote|M| −2|Megal(1,2)| ≥ 0 byx. Thus,
|Megal(1,2)| = |M2|−x.
c(Megal)≥ |M| −x
2 ·3+|M| +x
2 ·4=3.5|M| +0.5x (2) We use our arguments in the proof of Claim 7 to derive that an arbitrary stable matching approximatesc(Megal)on the |M2|−x (1,2)-edges within a ratio of43, while its cost on the remaining |M2|+x edges is at most 5. These imply the following inequalities for an arbitrary stable matchingM.
c(M)≤ |M| −x 2 ·3·4
3+|M| +x
2 ·5=4.5|M| +0.5x (3) We now combine (2) and (3). The last inequality holds for allx≥0.
c(M)
c(Megal) ≤ 4.53.5||MM|+|+0.5x0.5x ≤ 97
2) 2|Megal(1,2)| − |M|>0
Let us denote 2|Megal(1,2)| − |M|byx. Notice thatˆ |Megal(1,2)| = xˆ+|2M|. We can now express the number of edges with cost 3, and at least 4 inMegal.
c(Megal) ≥ 3·xˆ+ |M| 2 +4·
|M| − xˆ+ |M| 2
=3.5|M| −0.5xˆ (4)
Let|M(1,2)| =z1. Then exactlyz1edges inMhave cost 3. It follows from (1) thatz1≥ ˆx. Suppose thatz2≤z1edges inM(1,2)correspond to edges inMegal(1,2). Recall that|Megal(1,2)| = xˆ+|2M|. The remaining |M2|+ ˆx −z2edges inMegal(1,2) have cost at most 4 inM. This leaves|M| − |Megal(1,2)| −(z1−z2)= |M2|− ˆx−z1+z2
edges inMegalthat are as yet unaccounted for; these have cost at most 5 in both MegalandM. We thus obtain:
c(M) ≤ 3z1+4
|M| + ˆx 2 −z2
+5
|M| − ˆx
2 −z1+z2
=4.5|M| −0.5xˆ−2z1+z2
≤ 4.5|M| −1.5xˆ (5)
Combining (4) and (5) delivers the following bound.
c(M)
c(Megal) ≤ 4.53.5||MM|−|−1.50.5xxˆˆ < 97 The last inequality holds for everyx >ˆ 0.
We derived thatM, the 2-approximate solution with respect to the weight function w(uv)delivers a 97-approximation in both cases.
Using analogous techniques we can establish similar approximation bounds for
EGAL4-SRIandEGAL5-SRI, as follows.
Theorem 8 EGAL4-SRIis approximable within11/7.
Proof We start with a statement analogous to Claim 7.
Claim 9 In an instance of EGAL4-SRI, any stable matching approximatesc(Megal) within a factor of5/3.
Proof As earlier, we can fix all (1,1)-pairs and eliminate all (4,4)-pairs from the instance. Table2contains all cases foruvedges inMegaland the corresponding costs in an arbitrary stable matching.
We define the same weight functionw(uv) as in the proof of Theorem 6. We remark here thatw(uv)remains U-shaped for preference lists of length 4, because at each vertex the sequence of edges in order of preference is either monotone increas- ing or it is (1,0,1,1). Since we derived Inequality (1) without using the bounded degree property, it holds forEGAL4-SRIas well. We distinguish two cases based on the sign of 2|Megal(1,2)| − |M|.
1) 2|Megal(1,2)| − |M| ≤0
Table 2 uvedges and the corresponding costs inEGAL4-SRI
uv Worst case cost atu Worst case cost atv Cost ratio
(1,2) 4 1 5/3
(1,3) 4 2 6/4
(1,4) 4 3 7/5
(2,2) 4 1 5/4
(2,3) 4 2 6/5
(2,4) 4 3 7/6
(3,3) 4 2 6/6
(3,4) 4 3 7/7
Let us denote|M|−2|Megal(1,2)| ≥0 byx. Thus,|Megal(1,2)| = |M2|−x. Furthermore, letydenote the number of edges with cost at least 5 inMegal.
c(Megal)≥ |M| −x 2 ·3+
|M| +x
2 −y
·4+5y
= 3.5|M| +0.5x+y c(M)≤ |M| −x
2 ·3·5 3+
|M| +x
2 −y
·6+7y=5.5|M| +0.5x+y
c(M)
c(Megal) ≤ 5.53.5||MM|+|+0.5x0.5x++yy ≤ 117 2) 2|Megal(1,2)| − |M|>0
Letxˆ denote 2|Megal(1,2)| − |M|andythe number of edges with cost at least 5 inMegal. Due to Inequality (1), we know that at leastx (1,ˆ 2)-pairs inMegal
correspond to edges of cost 3 inM. The remaining |M2|− ˆx (1,2)-pairs inMegal
correspond to edges of cost at most 5 inM. c(Megal)≥ xˆ+ |M|
2 ·3+4·(|M| − ˆx
2 −y)+5y=3.5|M| −0.5xˆ+y c(M)≤3xˆ+5·|M| − ˆx
2 +6·(|M| − ˆx
2 −y)+7y=5.5|M| −2.5xˆ+y
c(M)
c(Megal) ≤ 5.53.5||MM|−|−2.50.5xxˆˆ++yy < 117
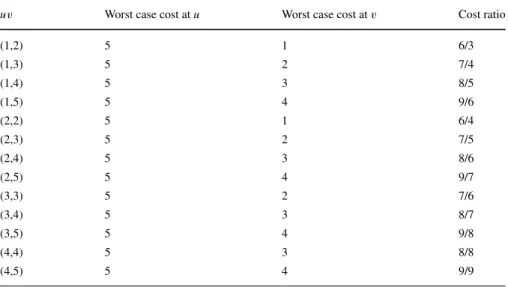
Theorem 10 EGAL5-SRIis approximable within13/7.
Proof Again we start with a statement analogous to Claim 7.
Claim 11 In an instance of EGAL5-SRI, any stable matching approximatesc(Megal) within a factor of 2.
Proof As earlier, we can fix all (1,1)-pairs and eliminate all (5,5)-pairs from the instance. Table3contains all cases foruvedges inMegaland the corresponding costs in an arbitrary stable matching.
We remark thatw(uv)remains U-shaped for preference lists of length 5, because at each vertex the sequence of edges in order of preference is either monotone increas- ing or it is (1,0,1,1,1). We observe that Inequality (1) holds forEGAL5-SRIas well.
Thus we distinguish two cases based on the sign of 2|Megal(1,2)| − |M|. 1) 2|Megal(1,2)| − |M| ≤0
Table 3 uvedges and the corresponding costs inEGAL5-SRI
uv Worst case cost atu Worst case cost atv Cost ratio
(1,2) 5 1 6/3
(1,3) 5 2 7/4
(1,4) 5 3 8/5
(1,5) 5 4 9/6
(2,2) 5 1 6/4
(2,3) 5 2 7/5
(2,4) 5 3 8/6
(2,5) 5 4 9/7
(3,3) 5 2 7/6
(3,4) 5 3 8/7
(3,5) 5 4 9/8
(4,4) 5 3 8/8
(4,5) 5 4 9/9
Let us denote|M|−2|Megal(1,2)| ≥0 byx. Thus,|Megal(1,2)| = |M2|−x. Furthermore, letybe the number of edges with cost 5 andzthe number of edges with cost at least 6 inMegal.
c(Megal)≥ |M| −x 2 ·3+
|M| +x
2 −y−z
·4+5y+6z
= 3.5|M| +0.5x+y+2z c(M) ≤ |M| −x
2 ·3·6 3+
|M| +x
2 −y−z
·7+8y+9z
= 6.5|M| +0.5x+y+2z
c(M)
c(Megal) ≤ 6.53.5||MM|+|+0.5x0.5x++yy++2z2z ≤ 137 2) 2|Megal(1,2)| − |M|>0
Letxˆ denote 2|Megal(1,2)| − |M|,ythe number of edges with cost 5 andzthe number of edges with cost at least 6 inMegal.
c(Megal)≥ xˆ+ |M|
2 ·3+4·(|M| − ˆx
2 −y−z)+5y+6z=3.5|M|−0.5xˆ+y+2z c(M)≤3xˆ+6·|M| − ˆx
2 +7·(|M| − ˆx
2 −y−z)+8y+9z=6.5|M|−3.5xˆ+y+2z
c(M)
c(Megal) ≤ 6.53.5||MM|−|−3.50.5xxˆˆ++yy++2z2z < 137
Using a similar reasoning for each d ≥ 6, our approach gives a cd-approxi- mation algorithm forEGALd-SRIwherecd >2. In these cases the 2-approximation algorithm of Feder [7,8] should be used instead.
3 Solvability and Most-stable Matchings ind-SRTI
In this section we study the complexity and approximability of the problem of decid- ing whether an instance of d-SRTI admits a stable matching, and the problem of finding a most-stable matching given an instance of d-SRTI.
We begin by defining two problems that we will be studying in this section from the point of view of complexity and approximability.
Problem 4 SOLVABLEd-SRTI
Input: I = G,O, whereGis a graph andOis a set of preference lists, each of length at mostd, possibly involving ties.
Question: IsIsolvable?
Problem 5 MIN BPd-SRTI Input: An instanceIofd-SRTI.s
Output: A matchingMinIsuch that|bp(M)| =bp(I).
We will show thatSOLVABLE3-SRTIisNP-complete andMIN BP3-SRTIis hard to approximate. In both cases we will use a reduction from the following satisfiability problem:
Problem 6 (2,2)-E3-SAT
Input: I =B, whereB is a Boolean formula in CNF, in which each clause com- prises exactly 3 literals and each variable appears exactly twice in unnegated and exactly twice in negated form.
Question: Is there a truth assignment satisfyingB?
(2,2)-E3-SATisNP-complete, as shown by Berman et al. [2]. We begin with the hardness ofSOLVABLE3-SRTI.
Theorem 12 SOLVABLE3-SRTIisNP-complete.
Proof ClearlySOLVABLE3-SRTIbelongs toNP. To showNP-hardness, we reduce from (2,2)-E3-SATas defined in Problem 6. LetBbe a given instance of (2,2)-E3-
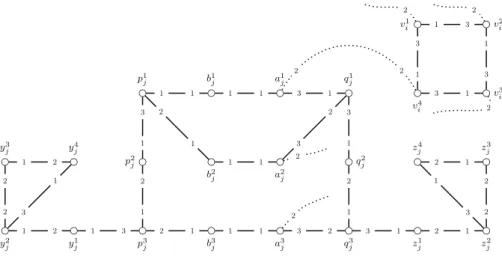
SAT, whereX = {x1, x2, . . . , xn}is the set of variables andC = {c1, c2, . . . , cm} is the set of clauses. We form an instanceI =(G,O)of 3-SRTIas follows. Graph Gconsists of avariable gadgetfor eachxi (1 ≤ i ≤ n), aclause gadgetfor each cj (1≤ j ≤ m)and a set of interconnecting edgesbetween them; these different parts of the construction, together with the preference orderings that constituteO, are shown in Fig.3and will be described in more detail below.
When constructingG, we will keep track of the order of the three literals in each clause ofBand the order of the two unnegated and two negated occurrences of each
Fig. 3 Clause and variable gadgets for 3-SRTI. The dotted edges are the interconnecting edges. The nota- tion used for edgeaj1v4iimplies that the first literal of the corresponding clausecjis the second occurrence of the corresponding variablexiin negated form
variable inB. Each of these four occurrences of each variable is represented by an interconnecting edge.
A variable gadget for a variablexi (1 ≤ i ≤ n) of B comprises the 4-cycle vi1, vi2, vi3, v4iwith cyclic preferences. Each of these four vertices is incident to an interconnecting edge. These edges end at specific vertices of clause gadgets. The clause gadget for a clausecj (1 ≤ j ≤ m) contains 20 vertices, three of which correspond to the literals incj; these vertices are also incident to an interconnecting edge.
Due to the properties of (2,2)-E3-SAT,xioccurs twice in unnegated form, say in clausescj andck ofB. Its first appearance, as the rth literal ofcj (1 ≤ r ≤ 3), is represented by the interconnecting edge between vertexvi1in the variable gadget corresponding toxiand vertexajrin the clause gadget corresponding tocj. Similarly the second occurrence ofxi, say as thesth literal ofck(1≤s≤3) is represented by the interconnecting edge betweenv3i andaks. The same variablexialso appears twice in negated form. Appropriatea-vertices in the gadgets representing those clauses are connected tovi2andvi4. We remark that this construction involves a gadget similar to one presented by Bir´o et al. [4] in their proof of theNP-hardness ofMIN BP3-SRI.
Now we prove that there is a truth assignment satisfyingBif and only if there is a stable matchingMinI.
Claim 13 For any truth assignment satisfying B, a stable matching M can be constructed inI.
Proof In Fig.4, we define two matchings,MiT andMiF, on the variable gadgets and three matchings,Mj1, Mj2andMj3, on the clause gadgets.
Fig. 4 The matchings corresponding to variablexiif it is set to betrueandfalse, respectively, and to the first, second or third literal beingtruein a fixed clausecj
If a variablexi (1≤i ≤n)is assigned to betrue,MiT is added toM, otherwise MiF is added. Similarly, since at least one literal incj (1 ≤ j ≤ m)is true, letr (1≤ r ≤3)be the minimum integer such that the literal at positionrofcj istrue; addMjrtoM. The intuition behind this choice is that if a literal istrue, then the vertex representing it in the variable gadget is matched to its best choice. On the other hand, if some literals in a clause aretrue, then the vertex representing the appearance of one of them in that clause is matched to its last-choice vertex.
We claim that no edge blocksM. Checking the edges in the clause and variable gadgets is easy. The five special matchings were designed in such a way that no edge within the gadgets blocks them. More explanation is needed regarding the intercon- necting edges. Suppose one of them,ajrvis,(r ∈ {1,2,3}, s ∈ {1,2,3,4})blocksM.
SinceMis a perfect matching,ajr needs to be matched to its last choice, aq-vertex.
Similarly,vsi has to be matched to its worst partner. While the partner ofajr indi- cates that the literal represented byvsi (xiorx¯i) istruein the clause, the partner ofvis means that the literal isfalse.
Claim 14 For any stable matchingMinI, there is a truth assignment satisfyingB.
Proof In the next three paragraphs we show that the restriction ofMto any variable or clause gadget is one of the above listed special matchings, and no interconnecting edge is inM.
First of all, if a vertexuis the only first choice of another vertex, thenucertainly needs to be matched inM. This property is fulfilled for all vertices of all clause gadgets except foryj3 andz3j for each cj (1 ≤ j ≤ m). Let us first study clause gadgetcj. Ifyj4 is matched toyj2, thenyj2yj3blocksM. Thus,yj3yj4, and similarly, z3jz4j are part ofMfor all clause gadgets.
Our proof for clause gadgets from this point involves considering matchings cov- ering all twelve remaining vertices. We differentiate two possible cases, depending on the partner ofp3j. In the first case,p3jbj3∈M. Therefore,pj2pj1∈Mtoo, because p2jhas to be matched. For similar reasons,{b1jaj1, b2ja2j, qj1qj2, qj3aj3} ⊆M. This gives us matchingMj3. In the second case, ifp3jis matched top2j, then{bj3aj3, qj3qj2} ⊆M.
There are two possible matchings on the remaining six vertices:{pj1b1j, aj1qj1, bj2aj2} and{p1jb2j, qj1aj2, b1ja1j}. These two matchings together with the lower part of the gadget formMj1andMj2.