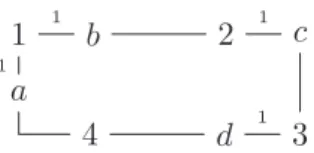European Journal of Operational Research xxx (xxxx) xxx
ContentslistsavailableatScienceDirect
European Journal of Operational Research
journalhomepage:www.elsevier.com/locate/ejor
Complexity of finding Pareto-efficient allocations of highest welfare R
Péter Biró
a,b, Jens Gudmundsson
c,∗aInstitute of Economics, Research Centre for Economic and Regional Studies, Hungarian Academy of Sciences, Budapest, Hungary
bDepartment of Operations Research and Actuarial Sciences, Corvinus University of Budapest, Hungary
cDepartment of Food and Resource Economics, University of Copenhagen, Denmark
a rt i c l e i n f o
Article history:
Received 30 January 2019 Accepted 4 March 2020 Available online xxx Keywords:
Assignment Pareto-efficiency Welfare-maximization Complexity Integer programming
a b s t r a c t
Weallocateobjectstoagentsasexemplifiedprimarilybyschoolchoice.Welfarejudgmentsoftheobject- allocatingagency areencodedas edgeweightsintheacceptabilitygraph.The welfareofanallocation isthesum ofitsedgeweights.Weintroducetheconstrained welfare-maximizingsolution,whichisthe allocationofhighestwelfareamongthePareto-efficientallocations.Weidentifyconditionsunderwhich thissolutioniseasilydeterminedfromacomputationalpointofview.Fortheunrestrictedcase,wefor- mulateanintegerprogramandfindthistobeviableinpracticeasitquicklysolvesareal-worldinstance ofkindergartenallocationandlarge-scalesimulatedinstances.Incentivestoreportpreferencestruthfully arediscussedbriefly.
© 2020TheAuthor(s).PublishedbyElsevierB.V.
ThisisanopenaccessarticleundertheCCBYlicense(http://creativecommons.org/licenses/by/4.0/)
1. Introduction
Weconsidertheallocationofobjectstoagents,suchasschool seats to students,in the absence ofmonetary transfers. We take as given that the assignment should reflect the agents’ prefer- ences andoperationalize thisby restrictingto Pareto-efficiental- locations.1 Typically, not all agents can receive their first choice and the more popular objects have to be rationed. How they are rationedreflects a welfare judgmentonbehalf of theobject- allocatingagency,sayintermsofwhat isfairorsocially optimal.
Forinstance,costsoftransportationmayprohibit admittingastu-
R We are grateful to the anonymous reviewers for their constructive suggestions.
We thank participants at the Lisbon Meetings (2017), the Conference on Mechanism and Institution Design (Durham, 2018), Frontiers of Market Design (Lund, 2018), Matching in Practice (Mannheim, 2018), the EAADS Workshop (Kosice, 2018), the Conference on School Choice and Reform (Lisbon, 2019), the Conference on Eco- nomics Design (Budapest, 2019), and the seminar participants at Corvinus Univer- sity for valuable comments. Péter Biró acknowledges the support of the Hungarian Academy of Sciences under its Momentum Programme (LP2016-3/2018) and Coop- eration of Excellences Grant (KEP-6/2018), and the Hungarian Scientific Research Fund , OTKA, Grant No. K128611 . Jens Gudmundsson acknowledges the financial sup- port of the Jan Wallander and Tom Hedelius Foundation.
∗ Corresponding author.
E-mail addresses: peter.biro@krtk.mta.hu (P. Biró), jg@ifro.ku.dk (J. Gudmunds- son).
1An allocation is Pareto-efficient if no other allocation leaves each agent at least as well off and some agent better off. As an example, if we order the agents and let them sequentially select their preferred object (among those that remain), then the final allocation will be Pareto-efficient. This procedure is known as Serial Dicta- torship .
denttoahighlypreferredbutremoteschoolortheremaybeben- efits to sending children on the samestreet to the same kinder- garteneventhough thefamilies’preferencesdiffer.Wemodelthis ina simpleyetsurprisinglyflexible way:assigningagenti object a creates welfare w(i,a),and the welfare of an allocation is the sumoftheseterms.Weusetoolsofeconomics,computerscience, andoperational research to address the followingquestions: Un- der which conditions doesa Pareto-efficientallocation maximize welfare? Whenthere isatrade-off between Pareto-efficiency and welfare-maximization, how should the objects be allocated? And finally,giventhat the problemcanencompass a large numberof agentsinpractice,canwefindadesirablesolutionefficientlyfrom acomputationalpointofview?
In addressing these questions, we refer for the most part to school choice (Abdulkadiro˘glu andSönmez, 2003; Shi, 2016), but theproblemextends to awide range ofapplications,some well- knownandsome new within thefield of OR.Theseinclude uni- versity admission, resident allocation (Bronfman, Hassidim, Afek, Romm,Shreberk, Hassidim, &Massler, 2015),dormitory room al- location(Perach,Polak,& Rothblum,2008),deceased organdona- tion, social housing, and refugee allocation (Andersson & Ehlers, 2017; Moraga & Rapoport, 2014; Delacrétaz, Kominers, & Teytel- boym, 2016; Trapp, Teytelboym, Martinello, Andersson, & Ahani, 2018).Presentineachoftheseapplicationsisacentralizedobject- allocatinginstitution(a“planner”)withitsownobjectivefunction thatshouldbetakenintoconsiderationinparallelwiththeagents’
preferences.Wereferto Section2 formoredetailedexamples on
https://doi.org/10.1016/j.ejor.2020.03.018
0377-2217/© 2020 The Author(s). Published by Elsevier B.V. This is an open access article under the CC BY license ( http://creativecommons.org/licenses/by/4.0/ ) Please cite thisarticleas:P. Biró and J.Gudmundsson,Complexity offinding Pareto-efficientallocationsof highestwelfare,European
howthewelfarelevelsw(the “edgeweights”)canbesetinorder tocoverawidevarietyofobjectives.
For theparticular applicationofschool choice,we propose an alternative to the priority-based approach that is most used in practice (see Section 1.1). Essentially, whereas our edge weights can be encoded with cardinal information, the ordinal priorities cannot.2 Ifone student isprioritized overanother, then thismay showthattheformerlivesclosertotheschool—butnothowclose, orhow muchcloser.Toillustrate further,saytwo studentsprefer school a to b andthat student1 lives next to b but alsoclosest to(butsomedistanceaway from)a.Anallocation isthenPareto- efficientaslongasbothstudentsareassignedaschool.Byrespect- ingthe distance-basedpriorities, student 1is admittedto a, stu- dent2tob,andbothstudents requiretransportation. Incontrast, bysettingtheedgeweightbetween1andb high,ouroptimalso- lutionwill swapthe assignment andthus reduces transportation costswhileretainingPareto-efficiency.
For ourfirst result, we rely ona recent finding by Sabanand Sethuraman(2015).Theystudythecomplexityofdeterminingthe outcome obtainedby Random Serial Dictatorshipand derive, asa byproduct, results on the decision problem termed SD Feasibil- ity. This asks:For a givenprofile of preferences,an agenti, and an object a, does there exist a serial dictatorship that assigns a to i? Saban and Sethuraman (2015) show that SD Feasibility is NP-completeeven ina restrictedenvironment.3 Using thisresult, ourTheorem1showsthatdecidingwhetherthereexistsaPareto- efficient, welfare-maximizing allocation is NP-complete with the samerestrictions imposed asinthe resultofSabanandSethura- man(2015).Forthesehardproblems,relaxingtherestrictionsonly makestheproblemsyetharder:they remainNP-hard,butthere- sultsgetweaker.
Unless thepreferences ortheedge weightstake on aparticu- larform, thereislittlereasontobelievethat thereactuallyexists aPareto-efficientallocationthatmaximizeswelfare.Whenthereis a conflict betweenthese desiderata, we propose to select a con- strainedwelfare-maximizingallocation.ThisisaPareto-efficiental- locationofhighestwelfare amongthePareto-efficientallocations.
Welabeltheproblemoffinding suchan allocationConstrained- WelfareMax. This is harder than deciding whether there exists aPareto-efficient,welfare-maximizing allocation,soConstrained- WelfareMaxiscomputationally tractableonlyunderyetstronger conditions. As a first step, we restrict attention to object-based weights. Such weights w(i,a) depend only on the object a. For school choice, this can be interpreted as the planner promoting a particular school or topic of study. In Theorem 2, we show thatConstrainedWelfareMaxisNP-hardevenunderobject-based weightsandcompletepreferences.
The next result pertains to the case in which all agents rank theobjectsacceptabletotheminthesameway.Thisisaplausible restrictionwhen there is an objectivemeasure ofquality onthe objects,such assome schoolsproviding objectivelybetter educa- tionthanothers.Ifallagentsranktheobjectsacceptabletothem inthesameway,thentheconditionofcommonpreferencesissatis- fied.Theorem3showsthatdecidingwhetherthereexistsaPareto- efficient, welfare-maximizing allocation is NP-complete even for balanced problemswithobject-based weights andcommonpref- erences.Inaddition, wederive a resultthat complements(Saban
&Sethuraman,2015)onSDFeasibility.
2The same argument applies to preference intensity, which again is cardi- nal information that cannot be encoded in ordinal preferences. On this topic, Abdulkadiro ˘glu, Che, and Yasuda (2015) introduce Choice-Augmented Deferred Accep- tance , which allows agents to express richer preference information. In particular, their agents report both a ranking over schools and a “target” school.
3Specifically, it is NP-complete when agents have complete and strict preferences and the problem is “balanced” with an equal number of agents and objects.
We then proceed to identify computationally tractable cases.
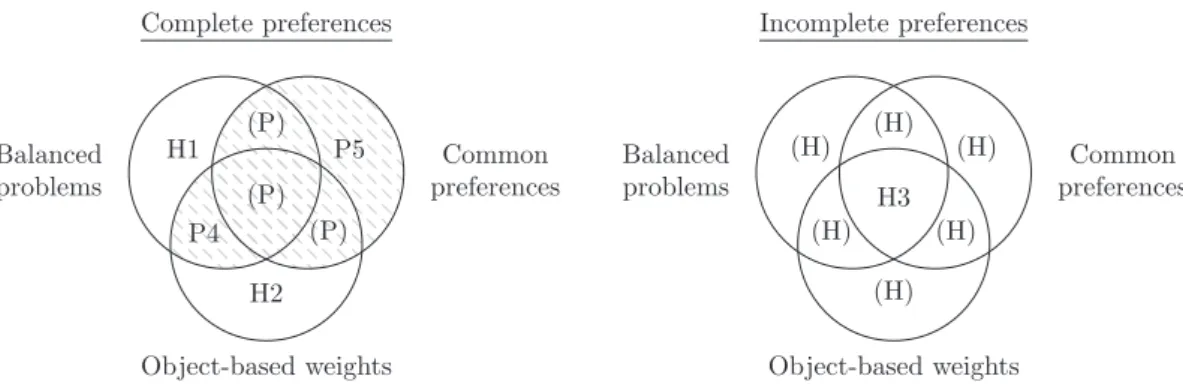
Theorem 4 shows that, forbalanced problems withobject-based weights and complete preferences, all serial dictatorships yield constrainedwelfare-maximizingallocations.Theorem5showsthat ConstrainedWelfareMaxispolynomial-timesolvableundercom- mon and complete preferences using (Kuhn, 1955) Hungarian method.Thereareotherwaysofcombiningthefourconditionsin- troducedthusfar,buttheremainingcasescanallbeinferredfrom Theorem1through5assummarizedinFig.1.
We introduce three additional conditions, each on its own is strong enough to make ConstrainedWelfareMax tractable. The first of these restricts to dichotomous preferences in which all agentsareindifferentbetweenallobjectsacceptabletothem.This domainrestrictionisrelevantwhenallobjectsaresimilarinqual- ity. Under this condition, an allocation is Pareto-efficient if and onlyifitisofmaximumcardinality.Theorem6showsthat,under dichotomous preferences, a constrained welfare-maximizing allo- cationcanbefoundusingtheHungarianmethod.
Thenext conditionisalignedinterests andimpliesthat assign- inganagentamorepreferredobjectleadstohigherwelfare.That is,theinterests ofthe planner,toassign higher-valuedobjects,is alignedwiththeinterestsoftheagents,tobe assignedmorepre- ferredobjects.Theorem7showsthat,underalignedinterests,each welfare-maximizing allocation is Pareto-efficient. In consequence, there exists a Pareto-efficient, welfare-maximizing allocation,and wefinditefficientlyusingtheHungarianmethod.
The final restriction is to agent-based weights, which are such thattheweightw(i,a)onlydependsontheagenti.Suchweights areplausibleforinstanceinmerit-baseduniversityadmissions:the objectiveis toadmit thestudents withthe highestgrades,butit is less important whereto they are admitted. Theorem 8 shows that, under agent-based weights, there exists a Pareto-efficient, welfare-maximizing allocation. Again, we find it efficiently using the Hungarian method. We emphasize also that, for each of the positive results of Theorem 4 through 8, we permit indifference inthepreferences,whereasthehardnessresultsofTheorems1,2, and3 are obtained whenrestricting to strict preferences. Gener- alizingby permitting indifferenceonly makes theseproblemsyet harder.Therefore,ourpolynomial-timealgorithmsremainefficient forstrictpreferenceswhileourNP-hardnessresultsstillholdwhen weallowindifferences.
Movingawayfromthecomputational aspects,Theorem9pro- vides a still related finding: under positive and object-based weights,eachconstrainedwelfare-maximizingallocationisofmax- imum cardinality.That is,there existsno wayof allocatingmore objects even if the constraints of Pareto-efficiency and welfare- maximizationareremoved.
Wealsoformulateanintegerprogram(IP)tosolvethegeneral, unrestrictedproblem.Todoso,weuseanovelcharacterization,in theformoflinearconstraints,ofPareto-efficiencyinthepresence of preference ties. Theorem 10 provides a link between Pareto- efficiencyand competitive equilibriumthrough a variationof the well-knownsecond welfaretheorem.Theorem11summarizesthe IPformulation.
Finally,weconsiderthestrategicpropertiesofoursolutioncon- cept. Theorem 12 establishes a positive result when the prob- lemissufficientlyrestricted.Thatis,withsomeconditionsonthe preferences and the weights, we can select constrained welfare- maximizingallocationsinawaythatincentivizestheagentstore- port preferences truthfully. However, we also show that relaxing eitheroftheconditionsmayallowformanipulation.
Thepaperisstructuredasfollows.Next,wedescribetherelated literature.WeintroducethemodelinSection2togetherwithase- ries of examples and applications. In Section 3,we examine the complexityoffinding constrainedwelfare-maximizing allocations, first through hardness results and then through tractable cases.
Pleasecite thisarticleas:P. Biró and J.Gudmundsson, Complexityoffinding Pareto-efficientallocations ofhighestwelfare,European
P. Biró and J. Gudmundsson / European Journal of Operational Research xxx (xxxx) xxx 3
Common preferences Balanced
problems
Object-based weights (P)
P5 H1
H2 (P)
P4 (P)
Complete preferences
Common preferences Balanced
problems
Object-based weights H3
(H) (H)
(H) (H)
(H) (H)
Incomplete preferences
Fig. 1. Complexity of ConstrainedWelfareMax. Numbers refer to theorems, “H” to NP-hardness, and “P” to polynomial-time solvable cases. Parentheses indicate that the case is covered by a stronger result.
In Section 4, we formulate theIP to solveConstrainedWelfare- Max.InSection5,weexaminethe2016kindergartenallocationin Harku,Estonia,withafocusoncomparingtheconstrainedwelfare- maximizing allocationwithothersolutions.We discussincentives issuesinSection6.WeconcludeinSection7.AppendixAdefines all solutions referred to throughout the papermore formally. Fi- nally, AppendixBcontainsasimulation studythat serves bothto contrastthedifferentsolutions andtoshow thattheinteger pro- grammingapproachisviableinsolvinglargerproblemsquickly.
1.1. Relatedliterature
A focal point in the literature are the stable (also known as justified envy-free and non-wasteful) allocations. Stable alloca- tions refusean agenta preferred object only ifthe object is as- signedahigher-priorityagent.Suchanallocationcanbecomputed through the Deferred Acceptance algorithm (DA; Gale & Shapley, 1962), which maybe adapted to handlepriority ties(Erdil& Er- gin, 2008).4 Thesesolutions havea particularstructure asshown throughthesocalledRuralHospitals’theorem(Roth,1984a;1986;
Gale &Sotomayor,1985).First,thesamestudentsare allocatedin everystableallocation.Second,aschoolthatfailstofillitsseatsat onestableallocationisassignedthesamestudentsateverystable allocation.Nowadays,DAmaybethemostusedprocedureincol- lege admissionandschoolchoiceprograms aroundtheworld(for specificcases,seeAbdulkadiro˘glu,Pathak,&Roth,2005a;Abdulka- diro˘glu,Pathak, Roth, & Sönmez, 2005b; fora recent survey,see Biró, 2017). NotonlyisDA stable,butit alsoselectsthestudent- optimal allocation among the stableallocations and it givesstu- dents incentives to report preferences truthfully. A recent devel- opmentistoallow agentstoreportpreferencesonlyover awell- designed“menu” ofschools(Ashlagi&Shi,2016;Shi,2015).Inthis way,theoutcomeofDAbecomesclosertooptimalfromthepoint of view oftheplanner (inthis case, thecity ofBoston) inasfar ascutting down busingcosts. Takento its extreme, ifthemenus onlycontainasingleschool,thentheplannercanimplementany allocation.
The second leading procedure is Top Trading Cycles (TTC;
Shapley & Scarf, 1974; Abdulkadiro˘glu and Sönmez, 2003), for instance usedinNew Orleans(Abdulkadiro˘glu,Che,Pathak, Roth,
&Tercieux,2017).LikeDA,TTCcannotbemanipulated,butincon- trasttoDA,TTCisPareto-efficientbutnotstable.SerialDictatorship is another non-manipulable way of achieving a Pareto-efficient
4The problem with ties is quite different from the strict case and there are sev- eral different notions of stability, such as weak, strong, and super stability. In the economics literature, focus has mainly been on weak stability. Weakly stable allo- cations always exist, but they may differ in size. Moreover, the problem of finding a weakly stable allocation of maximum size is NP-hard ( Manlove, Irving, Iwama, Miyazaki, & Morita., 2002 ).
allocation, used in Amsterdam’s school choice (de Haan, Gautier, Oosterbeek,& Vander Klaauw,2018)andforresidenceallocation inIsraeluntil2014 (Bronfmanetal.,2015).ItisequivalenttoTTC whenschools sharepriorities. AnotherPareto-efficientsolution is Immediate Acceptance,which wasusedin Boston(Abdulkadiro˘glu andSönmez, 2003)andisstillusedinmanyapplications.Its ma- nipulabilityisconsidereditsmainissue,althoughithasstillsome desirablepropertiesin regardsto theexpectedutilitarian welfare (Abdulkadiro˘glu, Che, & Yasuda, 2011). Finally, simple first-come first-served systems are sometimes used for course allocation, for example in almost every university in Hungary. Fig. 2 sum- marizes these approaches; see also Appendix A for more formal definitions.
The modelof matchingwith contractsis an importantexten- sionthatiswell-studiedfortwo-sidedmatchingproblemssuchas thematchof doctorsto hospital residencyprograms (see, forin- stance,Cechlárová & Fleiner, 2005;Fleiner, 2003; Hatfield& Mil- grom, 2005). The extension is meaningful also in our allocation settingasitallowstoassignobjectstoagentsunderdifferentcon- tractualterms.Toillustrate,considertheHungariancollegeadmis- sions. Most programs can be attended under two possible con- tracts:eitherthestudentpaysafeeorthestatefinancesthestud- ies(seeBiró,2011).Thereisstill atrade-off asstricterrulesapply tothestate-fundedcontracts:thestudenthastograduateinacer- taintimeandworkinHungaryforsometimethereafter.Ifshefails tomeettheserequirements,shehastopaybackthefundingwith interest.Therefore,somestudentsprefertopaythetuitionfeeover takingpartinthe“free” state-fundedprograms(seealsoShorrer&
Sóvágó,2018). Forour purposes,contracts are easy toinclude in the model butactually add very little. This is due to the strong implicationofPareto-efficiency: eachagentisassignedher object underher mostpreferredcontract.Otherwise,changingtheterms of her contract is a Pareto-improvement. In particular, if we, for eachagentandobject,removeallcontractsbutthepreferredone, thenthesetofPareto-efficientallocationsisunchanged.Thus,find- ing a constrainedwelfare-maximizing allocation in amodel with contractsisnomoredifficultthan findingonewhen thereisjust asinglecontractforeachagent-objectpair,whichisequivalentto thesimplermodelwithoutcontracts.
A new application of operational research, receiving consid- erable attention following the 2015 European migrant crisis, is refugeeallocation.Whilethelargerproblemofassigningrefugees to countriesis likely to be resolved using other criteria (Bansak, Hainmueller&Hangartner,2017;MoragaandRapoport,2014),the assignmentwithin countriescanbe viewedasan allocationprob- leminlinewithourstylizedmodel.Specifically, wemaythinkof therefugees asour agentsandofthe variouslocationsthat they canberesettledtoasourobjects(Delacrétazetal.,2016)orturn thingsaroundandviewcitizenslookingtohostrefugeesasagents whiletreatingthe refugeesasobjects(Andersson&Ehlers,2017).
Please cite thisarticleas:P. Biró and J.Gudmundsson,Complexity offinding Pareto-efficientallocationsof highestwelfare,European
Social welfare
Linear welfare function Priorities on objects
CWM TTC DA
Pareto-efficient allocations Stable allocations
Preferences
Fig. 2. The most common ways of taking preferences into account is by selecting a stable or a Pareto-efficient allocation. In parallel, welfare factors can be accounted for through priorities, or, as we are proposing, a linear welfare function. Here, “CWM” denotes the constrained welfare-maximizing solution.
Our edge weights can then encode, as Bansak, Ferwerda, Hain- mueller, Dillon, Hangartner, Lawrence, and Weinstein (2018) put it,that“there aresynergiesbetweenplaces andpeople” andthat
“certaincharacteristics will make a refugee a better match fora particularlocation”. Forinstance, the edgeweights canbe deter- mined usingthe data-drivenalgorithm provided by Bansak etal.
(2018) to represent the probability that a refugee will find em- ploymentwithinalocation(seealsoMossaad,Ferwerda,Lawrence, Weinstein,& Hainmueller, 2018;Bansak,Hainmueller,& Hangart- ner,2016;Trapp etal., 2018). Once theinfrastructure is in place toallowrefugees toexpresstheir preferencesina safeandcred- ibleway,ourIPcanreadilybe usedtofindawelfare-maximizing refugeeresettlement.
Lastly, we summarizesome ofthe existing complexityresults.
Abraham, Cechlárová, Manlove,and Mehlhorn (2005) provide the firstNP-hardnessresultsbyshowingthatfindingaminimumsize Pareto-efficientallocation is computationally hard. For two-sided matching,Irving, Leather, andGusfield (1987) showed that find- ing an optimalstablematching fora linear welfare function isa tractableproblem.Incontrast,iftheobjectiveistofindanoptimal allocation(saywithrespecttosizeorwelfare)thatis“asstableas possible” inthat itminimizesthe numberofblockingpairs,then theproblemisNP-hard(Biró,Manlove,&Mittal,2010).Wereferto Manlove(2013) fora comprehensivesurveyofrelatedcomplexity results.
Regardingtheoptimizationtechniquesusedtotackletheabove describedcomputationally hard cases, integer programs havere- ceivedsignificant attention inrecent years.Theyhave beenused inmore generalsettings such as allocation of papers to review- ers(Garg,Kavitha,Kumar,Mehlhorn,&Mestre,2010)orforcourse allocation(Othman,Sandholm,&Budish,2010),laterimplemented atWhartonCollege(Budish,Cachon,Kessler,&Othman,2016).Fur- therexamples include the resident allocation problemwith cou- plesmotivatedbytheUSandScottishapplications(Biró,Manlove,
& McBride,2014) andthe collegeadmission problem withlower andcommon quotas (Ágoston, Biró, & McBride, 2016). Other OR techniques,based on Scarf’s lemma (Scarf, 1967), have also been proposedfortheproblemofmatchingwithcouples(Biró,Fleiner,
&Irving,2016)andinothermany-to-onestablematchingsettings suchasNguyen,Nguyen,andTeytelboym(2019).
There aredifferentreasonsforwhyintegerprogrammingtech- niqueshadnot been usedto solvethese problemsuntil recently.
First, the heuristic algorithms based on DA perform relatively well in practice,as illustrated by the US resident allocation pro- gram with couples (Roth & Peranson, 1999). Secondly, the prob- lemsizesare relativelylarge (around40,000residents inthe US, and100,000 students inthe Hungarian highereducation admis- sionscheme),andthislarge inputsizecan bechallengingforthe IPsolvers.However,newstudieswithincomputer scienceandOR showthat even suchlarge problemscan be tractable withtheIP approach(see,forinstance,Firat,Briskorn,&Laugier,2016).Asan example,the NP-hardproblemofhavinglower quotasforuniver- sityprogramswassolvedforareal2008instanceoftheHungarian collegeadmissionsafter acarefulpreprocessingandby usingad- vancedIPtechniques(Ágostonetal.,2016).WebelievethatourIP formulationforaspecialproblemsettingcan beequallyusefulin
1
a
b 2
2.2 3.2
.65 .9
Fig. 3. Students and schools for Example 1 . Edge weights represent distances.
practiceandserveasastartingpointwhenconsideringmoregen- eralproblems.
2. Model
There is a finite set of agents N=
{
1,2,...}
and objects A={
a,b,...}
. A problem is balanced if there are as many agents asthere are objects. Agent i has preference Ri over objects accept- able to her,Ai⊆A, andnot beingassigned an object,∅.She finds a atleastasgood asb wheneveraRib.The strict relationis de- notedPiandtheindifferencerelationIi.Foreacha∈Ai,aPi∅.The bipartite acceptabilitygraph (N∪A,E) hasan edge(i,a)∈Ewhen- everaisacceptabletoi.Anallocationx⊆Eisanindependentedge set (matching).If(i, a)∈x, then i is assignedobject xi=a. Ifi is notassignedan object,then xi=∅.The setofallocations isX.An allocation is Pareto-efficient if no allocation leaves each agent at leastas well off andsome agent betteroff. Thus, x∈X isPareto- efficientif thereis noy∈X such that, foreach i∈N, yiRixi, and, forsomej∈N,yjPjxj.Thesocialwelfare ofassigningagenti ob- jecta∈Aiis representedbythe weightw(i,a)≥0on theedge (i, a)∈E.The welfareofx∈X isW(x)=
(i,a)∈xw(i,a). Anallocation x∈X iswelfare-maximizingifitcreatesthehighestwelfareamong allallocations:foreachy∈X,W(x)≥W(y).APareto-efficientalloca- tionisconstrainedwelfare-maximizingifitcreatesthehighestwel- fareamongthePareto-efficientallocations.
Next,weillustratethemodelthroughtwoexamplesinthecon- textofschoolchoice.
Example 1 (Distance-based school choice). In a school choice problem, the agents are students and the objects are seats at schools.Aschool withseveralseatsisthustreatedasseveraldis- tinctobjectswhichweassumestudentstobeindifferentbetween.
Typically, the student assignment hasto respect some priorities, saytofavorstudentsclosertotheschool.Weofferadifferentim- plementation of thisthrough the edge weights inspired by a re- centcourtcaseinLund,Sweden(see Andersson,2017,“Perceived issues”).
Morestudentstop-ranked schoolathan ithadseatsfor,soits seatswere assigned tothe students livingclosest. Student 1had 2.2kilometerswalkingdistancetoher preferredschool a and3.2 kilometertoherassignedschoolb.Hence,thewalkingdistancefor 1increasedbyonekilometerwhenshewasplacedatbratherthan ata.Incontrast,student2wasassignedtoabutwouldonlyhave hadtowalk250metersfurtherhadshebeenplacedatb.SeeFig.3 foranillustration.
Theparents arguedthat student1shouldbe givenhigherpri- orityataas1wouldlosemorefrombeingplacedelsewhere.Two courts (FörvaltningsrättenandKammarrätten)haveruled infavor Pleasecite thisarticleas:P. Biró and J.Gudmundsson, Complexityoffinding Pareto-efficientallocations ofhighestwelfare,European
P. Biró and J. Gudmundsson / European Journal of Operational Research xxx (xxxx) xxx 5
a
1 b 2 c
d 3 4
1
1 1
1
Fig. 4. Students and schools in Example 2 . An edge weight of 1 represents walk- zone priority. For the sake of readability, we have left out the remaining zero- weight edges.
oftheparents.Oneinterpretationisthatthejudgesconsideredthe rejectionof1atafairfromtheperspective ofthedistance-based priorities,butthattheallocationsuggestedbytheparentswasbet- terfromtheplanner’sperspectiveasitreducedthetotaltraveldis- tance.
Example 2 (Walk zones in school choice). School choice priori- tiesare typicallycoarsewithmanyties. Forinstance,all students withintheschool’swalkzonemaybeequallyprioritized.Asanex- ample,saythattherearefourstudentsandfourschools,eachwith a singleseat. Eachstudentprefersschool ato bto cto d,so any completeallocation isPareto-efficient.Walk-zonepriorityisgiven tostudent1atschoolsaandb,to2atc,andto3atd;seeFig.4. Before running an algorithm like Deferred Acceptance or Top Trading Cycles, the priority ties are often broken randomly. This maygive student2priorityatschoolb (over3and4) and3pri- orityatc.Thenbothalgorithmsselecttheallocation{(1,a),(2,b), (3, c), (4, d)},which sends onlystudent 1to a walk-zoneschool.
Ontheotherhand,ifweusetheedgeweightstoindicatewhether the student iswithin the school’s walk zone,then the allocation {(1,b),(2,c),(3,d),(4,a)}iswelfare-maximizing.Itassignsallbut student4toawalk-zoneschool.Hence,thisreducestransportation costswhileretainingPareto-efficiency.
To finish this section, we want to stress that we can take manydifferent objectivesinto accountthrough theedge weights.
In Example 1, we showed how one can minimize total walking distance, while we in the introduction discussed having weights represent theprobabilities that refugees find employment at dif- ferentlocations. Next,wewillseethat manymoreobjectivescan beachievedthroughoursolutionconcept.
Maximizingthenumber ofagentsassigned acceptableobjects. As in Example 2, we may want to maximize the number of agents assigned to suitable places. Further examples are refugee alloca- tion (Andersson & Ehlers, 2017), kindergarten allocation (Veski, Biró,Põder,&Lauri,2017),andtimetablescheduling.Inourmodel, this objective can be achieved through uniform weights (see Theorem9).
Assigning important agentsor positions. We maywantto guar- antee the allocation of a particularly important group of agents or objects. A practical example is (re-)allocation in the US Navy (Yang,Giampapa, &Sycara, 2003). Thisobjectivecan be achieved byputtinglargeweightsontheedgesincidentwiththeimportant nodesinthegraph(comparethesetA◦ inTheorem5).
Reallocationwithinitiallyassignedobjects. Inmanyapplications agents either own or are initially assigned objects and the task is toreallocate theobjects ina desirable way.Twoexamples are teacher reallocation in France (Combe, Tercieux, & Terrier, 2018) andkidneyexchange(Roth,Sönmez, &Ünver,2004).Intheseset- tings, one typically has to ensure that no agent receives an ob- ject lesspreferred than the one she is initially assigned. This is achievedinourmodelbyputtinglargeweightsontheedgeslink- ingtheagentstotheirinitialassignmentsandtheirmorepreferred objects.
Affirmative actioninschoolchoicebyminorityreserves.In many school choice and college admission systems, there are distribu- tional goals over the composition of the students. This is some-
timesenforced by so-called minority reserves, meaning that stu- dents witha particular background orethnicity havepriority for some school seats. Real-world examples includeschool choice in theUS(Abdulkadiro˘gluandSönmez,2003)andcollegeadmissions in India (Aygün & Turhan, 2017; Sönmez & Yenmez, 2019) and Brazil (Aygün & Bó, 2017). This objectivecan be achievedin our modelbyputtinglargeweightsontheedgeslinkingminoritystu- dentstotheschoolseatsreservedfortheminoritystudents.Asan example,aschoolwith100 seatsthatwantstoadmit20students withaparticularsocio-economicbackgroundcanlink20copiesof itsseatswithhigh-weightedges tostudentsqualifyingfortheaf- firmativeactionpolicy.
3. Complexityofconstrainedwelfare-maximization
In this section, we study the complexity of finding a con- strained welfare-maximizing allocation. We denote this problem ConstrainedWelfareMax, and we show that it is NP-hard even understrongconditions.However,wealsoidentifyrestrictionsun- der which the problemis tractable. Throughout, all hardness re- sultsrestricttostrictpreferenceswhereasthepositiveresultsper- mitindifference. Moreover, thehard problems arestated intheir mostrestrictedformandimplyNP-hardnessforalllessrestricted settings.
3.1. Hardnessresults
For our first result, suppose that a single edge has non-zero weight. That is, there is an agent i and an object a such that w(i,a)>0 and otherwise the weights are zero. An allocation is then welfare-maximizing ifand only ifit assignsa to i. Further- more,saypreferences arestrict andcomplete (Ai=A);an alloca- tion is then Pareto-efficient ifand only if it is obtained through a serial dictatorship (Abdulkadiro˘glu and Sönmez, 1998). Hence, thereexistsaPareto-efficient,welfare-maximizingallocationifand only if there exists a serial dictatorship that assigns a to i. This problem, deciding whether such a serial dictatorship exists, is known as SD Feasibility and shown by Saban and Sethuraman (2015), Theorem 2) to be NP-complete for balanced problems.
Theorem1followsimmediately.
Theorem1. DecidingwhetherthereexistsaPareto-efficient,welfare- maximizing allocation is NP-complete even for balanced problems withcompletepreferencesinwhichasingleedgehasnon-zeroweight.
Proof. Checking Pareto-efficiency (Manlove, 2013, Section 6.2.2.1) andwelfare-maximalityofanallocation(theHungarianmethodof Kuhn,1955)canbedoneinpolynomialtime(evenforunbalanced problems withindifferences and incomplete preferences). Hence, the problem is in NP. To show NP-hardness of our problem, we reducefromSDFeasibilityasdescribedabove.
Corollary1isanimmediateimplicationofTheorem1. Corollary1. CONSTRAINEDWELFAREMAX is NP-hardevenforbalanced problemswithcompletepreferences.
Proof. By contradiction, if we easily could find a constrained welfare-maximizingallocation,thenwejustneedtocheckwhether it assigns a to i. If it does, then there exists a Pareto-efficient, welfare-maximizingallocation.Ifitdoesnot,thennosuch alloca- tionexists.ButTheorem1showsthatthisisNP-complete.
This construction shows that a polynomial-time approxima- tionalgorithmthatfinds a“good” butnotnecessarilyconstrained welfare-maximizing allocation cannot give a meaningful worst- casewelfare-guarantee.Thatis,thewelfare-differencebetweenthe constrainedwelfare-maximizingallocationandasecond-bestallo- cation can be arbitrarily large, w(i,a)−0. Indeed, neither of the Please cite thisarticleas:P. Biró and J.Gudmundsson,Complexity offinding Pareto-efficientallocationsof highestwelfare,European
cases shown to be NP-hard in Theorems 1, 2 and 3 permits a meaningfulpolynomial-timeapproximation.5
We proceedto deriverelatedresultsby imposingdifferent re- strictions.Generally, edgeweights can depend on boththe agent and the object, but for the upcoming results it suffices to re- strict attention to object-based weights. That is, the social wel- fareofassigninganobjecttoanagentdependsonlyontheobject.
Theorem2showsthattheNP-hardnessresultextendstothecase ofobject-basedweightsandcompletepreferences.
Definition 1 (Object-based weights). For each {i, j}⊆N and a∈Ai∩Aj,w(i,a)=w(j,a).
Theorem2. CONSTRAINEDWELFAREMAX isNP-hardevenunderobject- basedweightsandcompletepreferences.
Proof.We reduce from the problem of assigning objects in a Pareto-efficientwaybuttoasfewagentsaspossible.Findingsuch a minimum size Pareto-efficient allocation is NP-hard (Abraham etal.,2005).
Extend an arbitrary instance I=(N,A,E,R,w) to I∗=(N,A∪ A∗,E∗,R∗,w∗) such that the properties required inthe statement ofTheorem2aresatisfiedforI∗.Inparticular,
• AddobjectsA∗suchthat
|
A∗|
=|
N|
;• Complete the preferences through a complete acceptability graph:E∗=N×(A∪A∗);
• NewpreferenceR∗i extendsRi:theacceptableobjectsAiatIare inthesameorderatthetopofR∗i,followedbyA∗inanyorder, followedbytheunacceptableobjectsofI;
• The object-based weights are w∗(i,a)=0 for a∈A and w∗(i,a)=1fora∈A∗.
In thisway,I∗ isguaranteed tohaveatleast asmanyobjects asagents.
Letx∗beaconstrainedwelfare-maximizingallocationinI∗.By Pareto-efficiency,aseach ofthe|N|agentsiprefersatleast
|
A∗|
=|
N|
objectsinI∗tothoseunacceptableinI,x∗i ∈Ai∪A∗.Definethe correspondingallocationxinIsuchthatxi=x∗i ifx∗i ∈Aiandxi=∅ifx∗i ∈A∗.Asx∗isPareto-efficientinI∗,xisPareto-efficientinI. ThewelfareW(x∗)isthenumberofassignedA∗-objectinx∗,sothe numberofunassignedagentsin x.Therefore,ifwe can efficiently findtheconstrainedwelfare-maximizingx∗inI∗—thatis,aPareto- efficientallocationthat assignsthemostA∗-objects—then wecan efficientlyfindaminimumsizePareto-efficientallocationinI.But thisisNP-hard.
In some applications, there mayexist an objective ranking of theobjects(Alpern&Katrantzi,2009).Thatis,agents’preferences arederived fromacommonpreference onA andwheneveran agentcompares two objects,she doesso in accordancewiththe commonpreference.
Definition2 (Commonpreference on A). Foreach i∈N and{a, b}⊆Ai,aRib ⇐⇒ ab.
Even if preferences are common in the sense that acceptable objectsarecompared inthesame way,anobject maybeaccept- abletosomeagentsbutnottoothers.Theorem3anditsimmedi- atecorollaryshowthatConstrainedWelfareMaxremainsNP-hard evenwithobject-basedweightsandcommonpreferences.
Theorem3. DecidingwhetherthereexistsaPareto-efficient,welfare- maximizing allocation is NP-complete even for balanced problems withobject-based weightsand commonpreferences in whicha sin- gleedgehasnon-zeroweight.
5For Theorem 3 , this follows by the same logic as for Theorem 1 as there again is only one non-zero weight. For Theorem 2 , inapproximability can be shown through a construction similar to the one used in the proof of Theorem 2 .
Table 1
Preferences over acceptable objects.
i 1 i 2 i 3 i 4 i 5 i 6 i 7 i 8 i 9
a 1 a 2 a 3 a 1 a 2 a 3 a 4 a 5 a 7
c 1 c 2 c 3 a 4 a 5 a 6 a 5 a 6 a 8
a 7 a 8 a 9
c1 c2 c3
i1 i2 i3
a1 a2 a3
i4 i5 i6
a4 a5 a6
i7 i8
a7
a8 i9 a9
Fig. 5. Acceptable pairs are connected by an edge.
Proof. We reduce from the NP-complete Exact-3-Cover decision problem(Garey&Johnson,1979).AninstanceofExact-3-Coveris asfollows.We are givenC=
{
c1,...,c3n}
andB={
B1,...,Bm}
suchthat, for each B∈B, B=
{
c1,c2,c3}
⊆C. We wish to determine whetherthereis B⊆B such thateach objectinC isincludedin exactly one B∈B. That is,is there a partition of C into n ele- ments of B? Next, we transform this instance of Exact-3-Cover intoits corresponding objectallocation problemwithpreferences in whicha singleedge has non-zeroweight. The size ofthe lat- ter problemis notmuchlarger thantheoriginal one(polynomial sizeinm+n).WeshowthattheinstanceofExact-3-Coverhasa feasiblesolutionifandonlyifthenon-zeroweightededgecanbe includedinaPareto-efficientallocation.Definethetotalorder ≥C onCand,withoutloss,assume that eachB=
{
c1,c2,c3}
islabeledaccordingly:c1>Cc2>Cc3.Foreach B={
c1,c2,c3}
∈B,wecreateasubproblem(“gadget”)G thatin- cludes objects B and A={
a1,...,a9}
and agents N={
i1,...,i9}
.Fork=,Nk∩N=Ak∩A=A∩C=∅.Moreover,no objectinAk isacceptabletoanagentinN.WelabeltheobjectsinA“gadget- specific”—theyare onlypartofone gadget, andthey are onlyac- ceptabletoagentswithinthisgadget.Incontrast,theobjectsinC can be partofmultiple gadgetsandacceptable to anyagent. We labelthem“common” objects. Preferencesforanarbitrarygadget G are inTable1(as allgadgets aresymmetric,we dropthe’s).
Fig.5showstheassociatedacceptabilitygraph.
LetA0=
{
a19,...,am9}
be theobjectsof“type”a9 anddefinethe totalorder≥A0 onA0. Addfurtheraset N0 ofnagentswho top- ranktheobjectsinA0 accordingto≥A0 followedbytheobjectsin Caccordingto ≥C.Addalsoaspecialagenti∗andaspecialobject a∗ such that i∗ top-ranks A0 accordingto ≥A0, then C according to ≥C, andlast a∗. Hence, a∗ is only acceptable to i∗. All in all, the object allocation problem contains agents N=N0∪N1∪· · · ∪ Nm∪{
i∗}
and objects A=C∪A1∪· · · ∪Am∪{
a∗}
. (To ensure thattheproblemisbalanced,add2nagentswhofindnoobjectaccept- able.) Observethat there isa common preference onA: let rankthe gadget-specificobjects asa1 · · · a9 inorder ≥A0 and abovethecommonobjects,andthenrankthecommonobjectsas in ≥C, andlast rank a∗. The object-based weights are such that the onlynon-zero weightis w(i∗,a∗)>0. Hence,we wish to de- cidewhetherthere existsaPareto-efficientallocationthatassigns a∗toi∗.
Inordertoassign a∗ toi∗ina Pareto-efficientway,all objects inA0andCmustalsobeassigned.ConsideranarbitrarygadgetG. ThereisonlyonePareto-efficientwayofassigninga9toi9:namely, through x=
{
(i1,a1),...,(i9,a9)}
.Alternatively,we can assignthe commonobjectsc1,c2,c3throughy:y=
i1,c1
,
i2,c2
,
i3,c3
,
i4,a1
,...,
i8,a5
,
i9,a7
. Wecanthenassigna9 toanagentinN0.
Pleasecite thisarticleas:P. Biró and J.Gudmundsson, Complexityoffinding Pareto-efficientallocations ofhighestwelfare,European
P. Biró and J. Gudmundsson / European Journal of Operational Research xxx (xxxx) xxx 7
Suppose that there exists a solutionB⊆B to the instanceof Exact-3-Cover.Defineitscorrespondingallocationxasfollows.For each B∈B, include theedges ofy in xtogether withan edge (j,a9) for some j∈N0. For each B∈B, include x in x. Finally, include the edge (i∗, a∗) in x. Then x is a constrained welfare- maximizing allocation.It coversthecommonobjectsC andn ob- jects inA0inngadgets,andthencovers theremaining m−nob- jects in A0 in the remaining m−n gadgets. In this way, we can assigna∗toi∗inaPareto-efficientway.
In contrast,ifthere isno solutionto theinstance ofExact-3- Cover, then we requiremore than n gadgets to cover C, leaving toofewagentstocoverA0.
Corollary 2. CONSTRAINEDWELFAREMAX is NP-hardeven forbalanced problemswithobject-basedweightsandcommonpreferences.
Corollary3isimmediatefromtheproofofTheorem3andcom- plements(Saban&Sethuraman,2015))resultonSDFeasibilityfor thecaseofcommonbutincompletepreferences.
Corollary 3. SD FEASIBILITY is NP-complete even forbalanced prob- lemswithcommonbutincompletepreferences.
3.2. Tractablecases
We proceed to conditions underwhich ConstrainedWelfare- Maxistractable.Theorem4showsthat,inasufficientlyrestricted setting, we can use a Serial Dictatorship to find a constrained welfare-maximizingallocation.
Theorem 4. CONSTRAINEDWELFAREMAX is polynomial-time solvable forbalanced problemswith object-basedweightsandcomplete pref- erences.
Proof. As the problem is balanced and the preferences com- plete, all objects are assigned at every Pareto-efficient alloca- tion.As weightsareobject-based,everyPareto-efficientallocation creates the same welfare. The problem of finding a constrained welfare-maximizingallocationisthenreducedtofindingaPareto- efficient allocation. This can be done efficiently through Serial Dictatorship.
Anaturalcounterpart tocommonpreferences is“commonac- ceptability”:anobjectisacceptabletooneagentwheneveritisac- ceptabletoallagents.However,anobjectthatisnotacceptableto anyoneaddslittletotheproblem,soweconsideronlythespecial caseofcomplete preferences.When bothcommonandcomplete, preferencesare “thesame” forall agents.Next,Theorem5 shows that the Hungarian method can be used to find a constrained welfare-maximizingallocationwhenallagentshavethesamepref- erence.ComparedtoTheorem4,thereisnowatrade-off between Pareto-efficiency andwelfare-maximization as the highest-valued objectsmaybetheleastliked.
Theorem 5. CONSTRAINEDWELFAREMAX is polynomial-time solvable undercommonandcompletepreferences.
Proof. Let A◦⊆A be the maximal set of at most |N| objects such that abandb∈A◦ implya∈A◦.Pareto-efficiency impliesthat all objectsinA◦mustbeassigned.Toensurethatthisisdone,firstad- justtheweightsbyaddingalarge-enoughconstantK>0tow(i,a) foreachi∈Nanda∈A◦.
If |A◦|<|N|<|A|, then we need to assign some of the objects outside A◦ as well. Let A∗⊆A be the minimal set of at least |N| objects suchthat abandb∈A∗implya∈A∗.Intheacceptability graph,cutalledgestoobjectsnotinA∗.Thisensuresthatonlyob- jectsinA∗areassignedinthereducedproblem.ApplytheHungar- ianmethodtofindamatchingofmaximumweightinthereduced
graph.Thisis a constrainedwelfare-maximizing allocation in the originalproblem.
In addition, ConstrainedWelfareMax is also tractable when all agentsare indifferentbetweenall objects acceptable to them.
Suchdichotomouspreferencesareaspecialcaseofcommonpref- erences.
Definition 3 (Dichotomous preferences). For each i∈N and {a, b}⊆Ai,aIib.
Theorem 6. CONSTRAINEDWELFAREMAX is polynomial-time solvable underdichotomouspreferences.
Proof. It is immediate that an allocation of maximum cardinal- ityisPareto-efficientunderdichotomouspreferences.Toshowthe converse,supposeforcontradictionthatx∈XisPareto-efficientbut thaty∈Xisoflargercardinalitythanx.Then,inthesymmetricdif- ferencebetweenxandy,(xࢨy)∪(yࢨx),thereisanalternatingpath that startsand ends withan edge in y. Updatingx by assigning the objects along thepath as iny allows one more agentto re- ceivean objectwithoutanotheragentbecoming unassigned.This is a Pareto-improvement, contradicting that x is Pareto-efficient.
Next,add a constant K>0 to all edge weights. For a sufficiently largeK,theweightsaresuchthat anallocationoflargercardinal- ityhashigherwelfarethanasmallerallocation.Hence,awelfare- maximizing allocationin thenewproblemmust be ofmaximum cardinalityandthereforePareto-efficient. Inparticular,the alloca- tionisconstrainedwelfare-maximizingintheoriginalproblem.
Furthermore, ConstrainedWelfareMax is tractable when as- signingamorepreferredobjectleadstohighersocialwelfare.Un- der this condition, the planner’s interests are aligned with the agents’ and the edge weights numerically represent the prefer- ences.
Definition 4(Alignedinterests). Foreach i∈N and{a,b}⊆Ai,aRi b ⇐⇒ w(i,a)≥w(i,b).
Theorem7. Underalignedinterests,eachwelfare-maximizingalloca- tionisPareto-efficient.
Proof. Suppose that x∈X is welfare-maximizing but Pareto- dominated by y∈X. Hence, for each i∈N, yiRixi, and, for somej∈N,yjPjxj.Underalignedinterests, yiRixi ⇐⇒ w(i,yi)≥ w(i,xi)andyjPjxj ⇐⇒ w(j,yj)>w(j,xj).ButthenW(x)<W(y), contradictingthatxiswelfare-maximizing.
Hence, under alignedinterests, finding a constrained welfare- maximizingallocation isreducedto findingawelfare-maximizing allocation. This can be done efficiently using the Hungarian method.
Given the weights w, let M(w)⊆X be the set of welfare- maximizingallocations.Therecanbeseveralsuchallocationsfrom whichwecanmakeaparticularselectionthroughasmall-enough perturbation of the edge weights. To do so, let >0 be the welfare-differencebetweenthewelfare-maximizing x∈M(w)and asecond-bestallocation:
=W
(
x)
− maxy∈X\M(w)W
(
y)
.Define the perturbed weights
π
such thatπ
(i,a)=w(i,a)+δ
(i,a),δ
(i, a)≥0, and (i,a)∈Eδ
(i, a)<. It is immediate that M(π
)⊆M(w): the welfare of an allocation outside M(w) has increased by less than , so its welfare must remain smaller than that ofthose in M(w).This intuition will be used to prove Theorem8.Theorem 8shows that there exists a Pareto-efficient, welfare- maximizingallocationwhentheedgeweightsdependonlyonthe Please cite thisarticleas:P. Biró and J.Gudmundsson,Complexity offinding Pareto-efficientallocationsof highestwelfare,European