Sztochasztikus modellezés

Sztochasztikus modellezés

Szerzı: Dr. Raisz Péter

Dr. Fegyverneki Sándor

Lektor: Dr. Kálovics Ferenc

Tartalomjegyzék

1. Valószínűség-számítási alapok 5

1.1. Eseménytér, műveletek eseményekkel . . . 5

1.2. A valószínűség fogalma . . . 6

1.3. Klasszikus valószínűségi mező . . . 7

1.4. Geometriai valószínűségi mező . . . 9

1.5. Feltételes valószínűség, függetlenség . . . 10

1.6. A relatív gyakoriság . . . 13

1.7. Valószínűségi változó . . . 14

1.8. Várható érték, transzformáció . . . 17

1.9. Medián, kvantilis . . . 20

1.10. Néhány diszkrét eloszlás és jellemzői . . . 21

1.11. Néhány folytonos eloszlás és jellemzői . . . 23

1.12. Generátor-, karakterisztikus függvény . . . 31

1.13. A kétdimenziós véletlen vektor . . . 34

1.14. Néhány többdimenziós folytonos eloszlás és jellemzői . . . 38

1.15. Az n-dimenziós véletlen vektor . . . 39

1.16. Valószínűségi változók összege . . . 40

1.17. Egyenlőtlenségek . . . 43

1.18. Nagy számok gyenge törvényei . . . 46

1.19. Polinomiális eloszlás . . . 46

1.20. Transzformáció n-dimenzióban . . . 47

1.21. Centrális határeloszlás-tétel . . . 49

1.22. Vegyes valószínűség-számítási feladatok . . . 49

2. Matematikai statisztikai alapok 55

2.1. Minta, mintavétel . . . 55

2.2. A statisztikai minta jellemzői . . . 57

2.3. Rendezett minták . . . 58

2.3.1. Minimumok és maximumok eloszlása . . . 59

2.3.2. Rendezett mintaelemek eloszlása . . . 60

2.4. Becsléselmélet . . . 64

2.4.1. Pontbecslés . . . 65

2.4.2. Maximum likelihood becslés . . . 67

2.4.3. A momentumok módszere . . . 70

2.4.4. Intervallumbecslések . . . 70

2.5. Hipotézisvizsgálat . . . 74

2.5.1. A likelihood hányados próba . . . 76

2.5.2. Néhány általánosított likelihood hányados próba . . . . 79

2.5.3. A Pearson-féleχ² statisztika és alkalmazásai . . . 83

2.6. Rendezett mintás próbák . . . 86

2.6.1. Az előjelpróba . . . 88

2.6.2. A Wilcoxon próba . . . 90

2.6.3. A Kolmogorov-Szmirnov kétmintás próba . . . 91

2.6.4. A Kolmogorov-próba . . . 92

2.6.5. Azω²-próba . . . 93

2.7. Minta példák . . . 95

2.8. Vegyes matematikai statisztikai feladatok . . . 100

3. Többdimenziós normális eloszlás 103 3.1. Többváltozós normális eloszlás fogalma . . . 103

3.1.1. Többváltozós elemzések . . . 104

3.1.2. Elemi tulajdonságok . . . 105

3.1.3. Jellemzők . . . 106

3.2. A paraméterek becslése . . . 107

3.3. Hipotézis vizsgálat, konfidencia intervallum . . . 110

3.4. Normalitás vizsgálat . . . 112

3.4.1. Perem normalitás vizsgálat . . . 113

3.4.2. Egydimenziós vizsgálaton alapuló módszerek . . . 113

3.4.3. Együttes normalitás vizsgálat . . . 114

3.5. Példák . . . 115

3.5.1. Kétváltozós normális eloszlás . . . 115

3.5.2. T² próba . . . 116

3.5.3. Konfidencia intervallum meghatározása . . . 117

4. Feltételes várható érték, folyamatok 119 4.1. Bevezetés . . . 119

4.2. Feltételes várható érték . . . 122

4.3. A feltételes várható érték tulajdonságai . . . 124

4.4. Martingál . . . 126

4.5. Sztochasztikus folyamatok . . . 131

4.6. Stacionárius folyamatok . . . 132

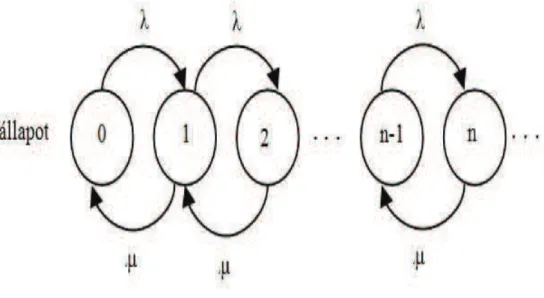
5. Markov-láncok, folyamatok 138 5.1. Markov-láncok . . . 138

5.2. Állapotok osztályozása . . . 146

6. Sorbanálláselmélet 155 6.1. Poisson folyamat . . . 155

6.2. Születési-halálozási folyamatok . . . 160

6.3. A sorbanállási elmélet elemei . . . 164

6.4. M/M/1 sorbanállási-kiszolgálási rendszer . . . 167

6.4.1. A várakozási idők paradoxona . . . 171

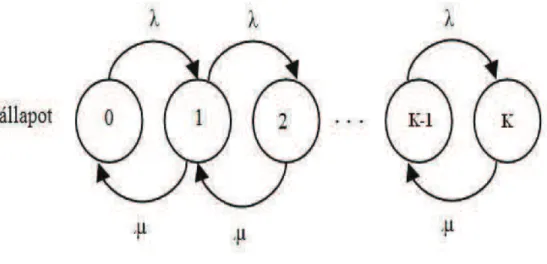
6.5. Az M/M/1/K rendszer . . . 172

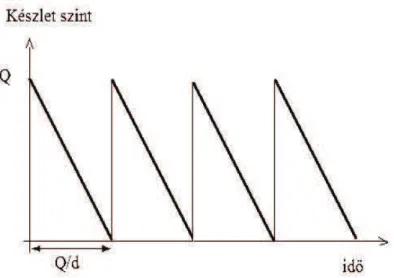
7. Készletgazdálkodási modellek, véletlen ütemezés 175 7.1. Bevezetés . . . 175

7.2. Determinisztikus készletgazdálkodási modellek . . . 176

7.2.1. Az optimális tételnagyság modellje . . . 176

7.3. Sztochasztikus készletgazdálkodási modellek . . . 178

7.3.1. Megbízhatósági típusú sztochasztikus készletmodell . . 178

7.3.2. Véletlen ütemezésű rész-szállítmányok esete . . . 179

8. A szimuláció alapjai 182 8.1. Monte Carlo módszerek . . . 182

8.2. Pszeudovéletlen számok . . . 183

8.2.1. Inverzfüggvény módszer . . . 184

8.2.2. Az elfogadás-elvetés módszere . . . 184

8.2.3. Normális eloszlás generálása . . . 186

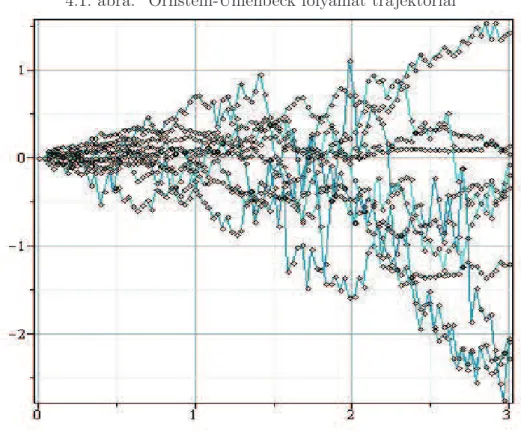
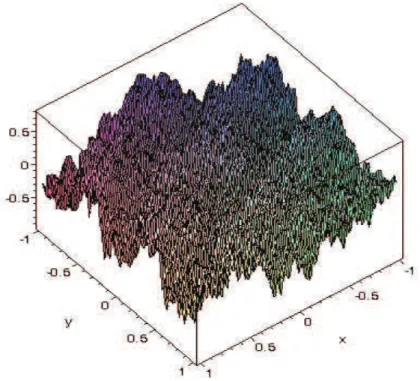
8.3. A Brown-mozgás . . . 187

8.4. A közelítő integrálás hibája . . . 188

9. Alkalmazások 193 9.1. Geometriai Brown-mozgás . . . 193

9.2. Cox-regresszió . . . 196

Irodalomjegyzék 208

1. fejezet

Valószínűség-számítási alapok

1.1. Eseménytér, műveletek eseményekkel

1.1. Definíció. Egy véletlen kísérlet lehetséges eredményeinek összességét eseménytérnek (mintatér) nevezzük. Jele: Ω. Az Ω elemeit elemi esemé- nyeknek nevezzük.

1.2. Definíció. AzΩrészhalmazainak egyFrendszerétσ-algebrának nevez- zük, ha

(1)Ω∈ F,

(2)A∈ F,akkor A∈ F,

(3)A, B ∈ F,akkor A∪B∈ F,

(4)A₁, A₂,· · · ∈ F,akkor A₁∪A₂∪ · · · ∈ F. Az F elemeit pedigeseményeknek nevezzük.

1.3. Megjegyzés. Ha csak (1), (2), (3) teljesül, akkor azF halmazrendszert algebrának nevezzük. Ha A, B ∈ F, akkor A∩B ∈ F.

1.4. Definíció. AzΩhalmazt szokásbiztos eseménynek, az∅halmazt pedig lehetetlen eseménynek nevezni. Továbbá, az A esemény bekövetkezik, ha a kísérlet eredménye eleme azA halmaznak.

1.5. Megjegyzés. Az A∪B esemény bekövetkezik, ha legalább az egyik közülük bekövetkezik, míg azA∩B esemény akkor következik be, ha mind a kettő bekövetkezik.

1.2. A valószínűség fogalma

1.6. Definíció. AP :F →Rnemnegatív leképezéstvalószínűségnek nevez- zük, ha

(1)P(Ω) = 1,

(2)A∩B =∅,akkor P(A∪B) =P(A) +P(B), (3)A₁, A₂, . . . egymást kölcsönösen kizáró események (azazA_i∩A_j =∅, hai < j és i, j= 1,2, . . .), akkor

P

∞

[

i=1

A_i

!

=

∞

X

i=1

P(A_i). (1.1)

1.7. Megjegyzés. Az (1)-(3) tulajdonságokat szokás a valószínűség axió- máinak nevezni.

1.8. Következmény. (1) P(A) = 1−P(A).

(2)P(∅) = 0.

(3)P(B\A) =P(B)−P(A∩B).

(4)P(A∪B) =P(A) +P(B)−P(A∩B).

(5) Ha A⊂B, akkor P(A)≤P(B).

(6) Ha B_n+1 ⊂B_n és

∞

\

i=1

B_n =∅, akkor lim

n→∞P(B_n) = 0.

1.9. Megjegyzés. Az (5) következményt szokás a valószínűség monotoni- tásának is nevezni. Ennek fontos következménye, hogy ha A∈ F, akkor

0≤P(A)≤1,

mert∅ ⊂A⊂Ω.Hasonlóan a (6) következmény a valószínűség folytonossága.

1.10. Definíció. Az (Ω,F, P)hármastvalószínűségi mezőnek nevezzük.

1.11. TÉTEL. (Poincaré) Az A₁, A₂, . . . , A_n eseményekre P

n

[

i=1

A_i

!

=

n

X

k=1

(−1)^k−1 X

i1<i2<···<ik

P

k

\

j=1

A_ij

!

, (1.2)

ahol az összegzést az összes lehetséges{i₁, i₂, . . . , i_k} ⊂ {1,2, . . . , n} esetre tekintjük.

1.12. Megjegyzés. A formula a (4) következmény általánosítása. Teljes indukcióval könnyen bizonyítható.

1.3. Klasszikus valószínűségi mező

1.13. Definíció. Ha az elemi események száma véges és valószínűségük meg- egyezik, akkor a valószínűségi mezőt klasszikusnak nevezzük.

1.14. Megjegyzés. A definíció nagyon rövidnek tűnik, ha arra gondolunk, hogy egy speciális helyzetben megadja a teljes matematikai modellt (a való- színűségi mezőt). Felmerül a kérdés, hogy a modell minden része szerepel-e benne. A válasz igen. Ha az elemi eseményeknek van valószínűsége, azt úgy kell értelmezni, hogy az alaphalmaz minden egy elemű részhalmaza esemény.

Ekkor viszont

F = 2^Ω, azaz F a hatványhalmaz.

Legyen |Ω|=n és jelölje az elemi eseményeket ω_i (i= 1,2, . . . , n).Ekkor 1 =P(Ω) =P

n

[

i=1

{ω_i}

!

=

n

X

i=1

P({ω_i}) =nP({ω_i}).

TehátP({ω_i}) = 1

n (i= 1,2, . . . , n).

Legyen A⊂Ω tetszőleges, ekkor felírható

A={ω_i1, ω_i2, . . . , ω_ik} alakban. Ekkor

P(A) =P

k

[

j=1

{ω_ij}

!

=

k

X

j=1

P({ω_ij}) =kP({ω_i}) = |A|

|Ω|.

Ezzel minden részhalmaznak meghatároztuk a valószínűségét. Tehát az ún.

klasszikus képlet:

valószínűség= kedvező esetek száma

összes esetek száma .⊓⊔ (1.3) VISSZATEVÉSES MINTAVÉTEL: Adott N darab különböző objektum, amelyek közül s darab rendelkezik egy bizonyos tulajdonsággal, például se- lejt. Visszatevéssel kiveszünk n darabot. Legyen a kivett selejtek száma ξ.

Mennyi a valószínűsége, hogy ξ =k, ahol 0≤k ≤n.

p_k =P(ξ =k) = n

k

s^k(N −s)^n−k

Nⁿ . (1.4)

Legyen p= s

N, akkor

P(ξ = k) = n

k

p^k(1−p)^n−k. (1.5) Tehát csak a selejtaránytól függ a valószínűség.⊓⊔

VISSZATEVÉS NÉLKÜLI MINTAVÉTEL: Adott N darab különböző ob- jektum, amelyek közüls darab rendelkezik egy bizonyos tulajdonsággal, pél- dául selejt. Visszatevés nélkül kiveszünkn darabot. Legyen a kivett selejtek számaξ. Mennyi a valószínűsége, hogy ξ =k, ahol 0≤k ≤min{n, s}.

p_k =P(ξ =k) = s

k

N−s n−k

N

n

. (1.6)

1.15. Megjegyzés. Az n elemű sokaságból n^k számú visszatevéses és

n(n−1). . .(n−k+ 1) = n!

(n−k)!

visszatevés nélkülik elemű minta vehető.

Ap_k valószínűségek definíciójából következik, hogy p₀+p₁+· · ·+p_n = 1, amelyből

n

X

k=1

n k

s^k(N −s)^n−k =Nⁿ, illetve

s 0

N −s n

+

s 1

N −s n−1

+· · ·+ s

n

N−s 0

= N

n

.⊓⊔

1.4. Geometriai valószínűségi mező

A geometriai valószínűségi mező bevezetése, a valószínűség definíciója a klasz- szikus valószínűségi mező analógiájára történik. Bevezetése, alkalmazása so- rán kiderül, hogy a szükséges elméleti alapokat majd csak a valószínűségi változóknál illetve a véletlen vektoroknál definiáljuk.

A következő definíciót fogadjuk el a szemlélet alapján a klasszikus valószínű- ségi mező mintájára.

1.16. Definíció. Legyen Ω ⊂ Rⁿ, amelynek létezik és véges a nagysága (jelölje m(Ω)). Továbbá legyen Ω minden eleme (pontja) azonos "esélyű" és A⊂Ω,amelynek szintén létezik az m(A) nagysága. A

P(A) = m(A)

m(Ω) (1.7)

mennyiséget azA valószínűségének nevezzük.

1.17. Megjegyzés.

P(A) = m(kedvező esetek)

m(összes eset) . (1.8)

1.18. Megjegyzés. Egy halmaz nagyságán a hosszát, területét, térfoga- tát(mértékét) értjük. LegyenΩ = [0,1]ésmpedig a hosszúság, ekkor minden Q∈ [0,1] pontra csak az m({Q}) = 0 lehetséges. Ebből rögtön következik, hogy minden legfeljebb megszámlálhatóan végtelen halmaz nagysága (hossza) 0.

1.19. Megjegyzés. Létezik halmaz, amelynek nincs Lebesgue-mértéke.

Nem mérhető halmaz konstrukciója: Legyen Ω = [0,1] és mpedig a hosszú- ság. Az a, b∈Ω relációban van, ha a−b ∈Q,azaz racionális. Ez a reláció reflexív, szimmetrikus, tranzitív. Tehát ekvivalenciareláció, amely osztályo- zást hoz létre. Definiáljuk azE halmazt oly módon, hogy minden osztályból kiveszünk egy elemet. Ez lehetséges a halmazelmélet kiválasztási axiómája szerint. Legyen

Ω∩Q={r₁, r₂, . . .}, En :={x+rn −[x+rn]|x∈E},

ekkor az E_n halmazok páronént diszjunktak és

∞

[

n=1

E_n = Ω. Ha E mérhető, akkor E_n is és nagyságuk megegyezik. Továbbá

∞

X

n=1

m(E_n) = 1,

ami lehetetlen, mert a sor tagjai mind egyenlőek. Ez azt jelenti, hogyE nem mérhető.

1.20. Megjegyzés. Létezik kontinuum számosságú halmaz, amelynek 0 a Lebesgue-mértéke.

A Cantor-féle triadikus halmaz: Legyen E₁ a középső része a [0,1] interval- lumnak, azaz E₁ =

1 3,2

3

. Tehát x ∈ [0,1]\E₁ akkor és csak akkor, ha hármas számrendszerben az első jegy (a 0 után) a0 vagy a 2. Legyen E₂ a középső részek uniója a [0,1]\E₁ halmazból, azaz E₁ =

1 9,2

9

∪ 7

9,8 9

. Tehát x∈[0,1]\(E₁∪E₂)akkor és csak akkor, ha hármas számrendszerben az első két jegy (a0után) a 0vagy a2.Folytassuk a konstrukciót: legyenE_n a középső részek uniója a[0,1]\(E₁∪E₂∪ · · · ∪E_n−1)halmazból. Cantor-féle triadikus halmaznak nevezzük a

C = [0,1]\

∞

[

n=1

E_n

halmazt. Tehát x ∈ C akkor és csak akkor, ha hármas számrendszerben a számjegyei csupán a 0vagy a 2.

AC halmaz nemmegszámlálható. A konstrukció alapján m(E_n) =

1 3

2 3

n−1

, m(C) = 1−

∞

X

n=1

1 3

2 3

n−1

= 0.⊓⊔

1.5. Feltételes valószínűség, függetlenség

1.21. Definíció. AzAeseményBfeltétel mellettifeltételes valószínűségének nevezzük a

P(A|B) = P(A∩B)

P(B) (1.9)

mennyiséget, haP(B)>0.

1.22. Megjegyzés. AP(·|B) :F →Rleképezés tényleg valószínűség, azaz teljesíti a valószínűség axiómáit, ha rögzítjük aB eseményt

1.23. TÉTEL. (szorzási szabály) Ha P(A)>0, P(B)> 0, akkor

P(A∩B) =P(A)P(B|A) =P(B)P(A|B). (1.10) 1.24. TÉTEL. (szorzási szabály általánosítása) Ha az A₁, A₂, . . . , A_n eseményrendszerre P(

n−1

\

i=1

A_i)>0, akkor

P(

n

\

i=1

A_i) =P(A₁)P(A₂|A₁)· · ·P(A_n|A₁∩A₂∩ · · · ∩A_n−1). (1.11) 1.25. Definíció. Az A₁, A₂, . . . eseményrendszert teljes eseményrendszer- nek nevezzük, haA_i∩A_j =∅, hai < j és i, j= 1,2, . . . , és

∞

[

i=1

A_i = Ω.

1.26. TÉTEL. (teljes valószínűség)HaA₁, A₂, . . . teljes eseményrendszer és P(A_i)>0, ha i= 1,2, . . . , akkor tetszőleges B esemény esetén

P(B) =

∞

X

i=1

P(B|A_i)P(A_i). (1.12) Bizonyítás.

P(B) =P(B∩Ω) =P(B∩

∞

[

i=1

A_i) =P(

∞

[

i=1

(B∩A_i)) = (1.13)

=

∞

X

i=1

P(B∩A_i) =

∞

X

i=1

P(A_i)P(B|A_i). (1.14) Felhasználva a teljes eseményrendszer tulajdonságait, a valószínűség 3. axi-

ómáját és a szorzási szabályt.

1.27. Megjegyzés. A és A teljes eseményrendszert alkot. A∩B, A∩B, A∩B,és A∩B teljes eseményrendszert alkot.

1.28. TÉTEL. (Bayes)HaA₁, A₂, . . . teljes eseményrendszer ésP(A_i)>0, ha i= 1,2, . . . , akkor tetszőleges pozitív valószínűségű B esemény esetén

P(A_k|B) = P(B|A_k)P(A_k)

∞

X

i=1

P(B|A_i)P(A_i)

. (1.15)

Bizonyítás.

P(A_k|B) = P(A_k∩B)

P(B) = P(B|A_k)P(A_k)

∞

X

i=1

P(B|A_i)P(A_i)

(1.16)

Felhasználva a teljes valószínűség tételét és a szorzási szabályt.

1.29. Megjegyzés. A Bayes-tételhez kapcsolódóan bevezethetjük a követ- kező elnevezéseket: P(A_i) az ún. a-priori valószínűség és P(A_i|A) az ún.

a-posteriori valószínűség.

1.30. Definíció. Az A és B eseményt sztochasztikusan függetlennek nevez- zük, ha

P(A∩B) =P(A)P(B). (1.17)

1.31. Megjegyzés. Ha az A és B események függetlenek, akkor A és B, A és B és A és B is függetlenek. Ha 0 < P(A) < 1, akkor A és A nem függetlenek.

1.32. TÉTEL. HaA∩B =∅,ésP(A)P(B)>0,akkor azAés aB esemény nem lehetnek függetlenek.

Bizonyítás.

P(A∩B) = 0, P(A)P(B)>0.

Tehát nem lehetnek egyenlőek.

1.33. Definíció. AzA₁, A₂, . . . , A_n eseményeketpáronként sztochasztikusan függetlennek nevezzük, ha

P(A_i∩A_j) =P(A_i)P(A_j) (1≤i < j ≤n). (1.18)

1.34. Definíció. Az A₁, A₂, . . . , A_n eseményeket teljesen sztochasztikusan függetlennek nevezzük, ha

P(A_i1 ∩ · · · ∩A_ik) =P(A_i1)· · ·P(A_ik), (1.19) ahol 1≤i₁ <· · ·< i_k ≤n, 2≤k≤n.

1.35. Megjegyzés. Ha megvizsgáljuk a feltételrendszert, akkor látható, hogy a teljes függetlenség feltételeinek a száma

n 2

+

n 3

+· · ·+ n

n

= 2ⁿ− n

0

− n

1

= 2ⁿ−1−n,

amely nagyon gyorsan nő. Már n = 3 esetén megadható példa, amely azt mutatja, hog egyik feltétel sem elhagyható.

1.36. Definíció. Az{A₁, A₂, . . . , A_n, . . .}és{B₁, B₂, . . . , B_m, . . .}esemény- rendszereketsztochasztikusan függetlennek nevezzük, ha∀i, j esetén

P(A_i∩B_j) =P(A_i)P(B_j) (1≤i≤n, 1≤j ≤m). (1.20) 1.37. Megjegyzés. Ha az A és B események függetlenek, akkor A és B, A és B és A és B is függetlenek, azaz az {A, A} és {B, B} eseményrend- szerek is függetlenek. Kétσ−algebra független, ha mint eseményrendszerek függetlenek.

1.38. TÉTEL. Ha A₁, A₁, . . . , A_n független események és

P(A_i)<1, (i= 1,2, . . . , n), (1.21) akkor

P(

n

[

i=1

A_i)<1. (1.22)

1.6. A relatív gyakoriság

1.39. Definíció. Bernoulli kísérletsorozatnak nevezzük azt, ha adottA∈ F és egymástól függetlenül, azonos körülmények között elvégezzük ugyanazt a kísérletet, s "csak" azt figyeljük, hogy az A esemény bekövetkezett-e vagy sem.

1.40. Megjegyzés. A visszatevéses mintavétel egy ilyen kísérletsorozatot valósít meg.

1.41. Definíció. Adott egy valószínűségi mező. Vizsgáljuk az A esemény bekövetkezését. Végezzünk el egy Bernoulli-kísérletsorozatot, amelynek a hossza n. Jelölje az A esemény bekövetkezéseinek a számát k_A. Ezt az A eseménygyakoriságának nevezzük. Míg az

r_A = k_A

n (1.23)

mennyiséget pedigrelatív gyakoriságnak nevezzük.

1.42. Megjegyzés. Mivel 0≤k_A ≤n,ezért 0≤r_A ≤1.

k_Ω=n, tehátr_Ω= 1.

Ha A∩B =∅, akkor k_A∪B =k_A+k_B,ezért r_A∪B =r_A+r_B.

Jól látható, hogy a relatív gyakoriság tulajdonságai megegyeznek a valószí- nűségével és mégsem igazán jó mérőszám, hiszen minden újabb kísérlettel változhat.

1.7. Valószínűségi változó

1.43. Definíció. A X : Ω → R leképezést valószínűségi változónak nevez- zük, ha

{X < x}={ω|ω ∈Ω, X(ω)< x} ∈ F ∀x∈R. (1.24) 1.44. Definíció. Legyen

σ(X) ={A∈ F|A=X⁻¹(B),∀B ∈ B(R)}. (1.25) Ezt a halmazt a valószínűségi változó által generáltσ−algebrának nevezzük.

1.45. Definíció. Az

F(x) =P(X < x) (1.26)

formulával meghatározott valós függvényt az X valószínűségi változó elosz- lásfüggvényének nevezzük.

1.46. TÉTEL. Az F valós függvény akkor és csak akkor lehet eloszlásfügg- vény, ha

1. lim

x→−∞F(x) = 0, 2. lim

x→∞F(x) = 1,

3. F(a)≤F(b), ha (a < b), azaz monoton növekvő, 4. lim

x→x0−0F(x) =F(x₀), ∀x₀ ∈R, azaz balról folytonos.

1.47. Megjegyzés. Az F teljesíti az előző tételben szereplő tulajdonsá- gokat. Ha ezenkívül szigorúan nő és folytonos, akkor létezik F⁻¹. Legyen Ω = [0,1], F = a nyílt intervallumok által generált σ−algebra és P pedig egy halmaz hossza. Legyen mindenω∈Ω esetén

X(ω) =F⁻¹(ω), (1.27)

ami folytonos és szigorúan monoton növekvő.

P(X < x) =m({ω|F⁻¹(ω)< x}) =m({ω|ω < F(x)}) =F(x).

1.48. TÉTEL. Legyen F az X valószínűségi változó eloszlásfüggvénye és a, b∈R, ekkor

1. P(a≤X < b) =F(b)−F(a), 2. P(X =a) =F(a+ 0)−F(a).

1.49. Definíció. Az X valószínűségi változót diszkrétnek nevezzük, ha a lehetséges értékek X(Ω) halmazának számossága legfeljebb megszámlálha- tóan végtelen.

1.50. Megjegyzés. Diszkrét valószínűségi változó esetén a lehetséges érté- kek felírhatók egy sorozatként.

1.51. Definíció. Legyen az X valószínűségi változó lehetséges értékeinek sorozatax₁, x₂, . . . . A

p_i =P(X =x_i), (i= 1,2, . . .) (1.28) valószínűségek sorozatáteloszlásnak nevezzük.

1.52. TÉTEL. Ha p₁, p₂, . . . eloszlás, akkor p_i ≥0 (i= 1,2, . . .) és

∞

X

i=1

p_i = 1. (1.29)

1.53. Definíció. Ha létezikf nemnegatív valós függvény, melyre F(x) =

x

Z

−∞

f(t)dt, ∀x∈R, (1.30)

akkor f azF eloszlásfüggvényhez tartozó sűrűségfüggvény.

1.54. Megjegyzés. A sűrűségfüggvény nem egyértelmű. A sűrűségfüggvény létezése azt jelenti, hogy az F eloszlásfüggvény abszolút folytonos.

1.55. TÉTEL. Az f valós függvény akkor és csak akkor lehet sűrűségfügg- vény, ha nemnegatív és

+∞

Z

−∞

f(t)dt= 1. (1.31)

1.56. Definíció. A valószínűségi változótfolytonosnak nevezzük, ha létezik a sűrűségfüggvénye.

1.57. TÉTEL. Legyen az X folytonos valószínűségi változó f sűrűségfügg- vénnyel és a, b∈R, ekkor

P(X =a) = 0 (1.32)

és

P(a≤X < b) = Zb

a

f(x)dx. (1.33)

1.58. Megjegyzés. Tetszőleges eloszlásfüggvény előállítható

p₁F₁+p₂F₂+p₃F₃ (1.34) alakban, aholp₁+p₂+p₃ = 1, p₁ ≥0, p₂ ≥0, p₃ ≥0, F₁diszkrét,F₂ abszolút folytonos ésF₃ folytonos és szinguláris eloszlásfüggvény a Lebesgue-mértékre nézve.

A P és a P^∗ valószínűségek szingulárisak egymásra, ha ∃A ∈ F úgy, hogy P(A) = 0 és P^∗(A) = 0. Általában egy diszkrét és egy abszolút folytonos szinguláris egymásra nézve.

Folytonos és szinguláris eloszlásfüggvény a Lebesgue-mértékre nézve az ún.

Cantor-függvény: A Cantor-féle triadikus halmaz elkészítésekor (l. 1.20 meg- jegyzés) az n-edik lépésben éppen 2ⁿ −1 intervallumot vettünk ki a [0,1]

intervallumból. Jelölje ezeket sorbanA₁, A₂, . . . , A₂ⁿ₋₁. Ekkor legyen

F_n(x) =











0, ha x= 0, k

2ⁿ, ha x∈A_k, k= 1,2, . . . ,2ⁿ−1, 1, ha x= 1.

Az

F(x) = lim

n→∞F_n(x), x∈R

függvényt Cantor-függvénynek nevezzük. F monoton növekvő,F^′ = 0majd- nem mindenütt és nem abszolút folytonos.

1.8. Várható érték, transzformáció

1.59. Definíció. 1. Ha az X diszkrét valószínűségi változó lehetséges érté- keinek a száma véges, azaz a lehetséges értékek

x₁, x₂, . . . , x_n és p_i= P(X =x_i) (i= 1,2, . . . , n), akkor a

n

X

i=1

xipi (1.35)

mennyiségetvárható értéknek nevezzük.

2. Ha az X diszkrét valószínűségi változó lehetséges értékeinek számossága megszámlálhatóan végtelen, azaz a lehetséges értékek

x₁, x₂, . . . , és p_i=P(X =x_i) (i= 1,2, . . .), akkor a

∞

X

i=1

x_ip_i (1.36)

mennyiségetvárható értéknek nevezzük, ha

∞

X

i=1

|x_i|p_i <+∞.

3. Ha X folytonos valószínűségi változó f sűrűségfüggvénnyel, akkor a Z+∞

−∞

xf(x)dx (1.37)

mennyiségetvárható értéknek nevezzük, ha Z+∞

−∞

|x|f(x)dx <+∞. (1.38)

Az X valószínűségi változó várható értékének a jelölése: E(X).

1.60. TÉTEL. 1. E(aX+b) =aE(X) +b, ∀a, b∈R.

2. Ha m≤X ≤M, akkor m≤E(X)≤M.

1.61. Definíció. Legyen X valószínűségi változó és g valós függvény. Ha az Y =g(X) függvény valószínűségi változó, akkor azX transzformáltjának nevezzük.

1.62. Megjegyzés. A transzformált eloszlásfüggvénye F_Y(y) =P({ω|g(X(ω))< y}).

1.63. TÉTEL. Hag differenciálható ésg^′(x)6= 0,akkorX folytonos valószí- nűségi változó esetén Y =g(X) folytonos valószínűségi változó, melynek sű- rűségfüggvénye

f_Y(y) =







f_X(g⁻¹(y))

d

dyg⁻¹(y)

, ha a < y < b,

0, egyébként,

(1.39)

ahol

a= min( lim

x→−∞g(x), lim

x→+∞g(x)), b = max( lim

x→−∞g(x), lim

x→+∞g(x)). (1.40)

1.64. TÉTEL. Ha Y = g(X) az X valószínűségi változó transzformáltja és létezik E(Y), akkor

E(Y) =











∞

X

i=1

g(x_i)P(X =x_i), ha X diszkrét,

+∞R

−∞

g(x)f_X(x)dx, ha X és Y folytonos.

(1.41)

1.65. Definíció. Az

E((X−E(X))²) (1.42)

mennyiséget azX valószínűségi változó szórásnégyzetének nevezzük.

Jele: D²(X).

1.66. Definíció. Ap

E((X−E(X))²)mennyiséget azX valószínűségi vál- tozó szórásának nevezzük.

Jele: D(X).

1.67. Definíció. Az E(X^k)mennyiséget az X valószínűségi változó k-adik momentumának nevezzük.

1.68. Definíció. Az E((X −E(X))^k) mennyiséget az X valószínűségi vál- tozó k-adik centrális momentumának nevezzük.

1.69. Definíció. Az

X −E(X) D(X)

transzformáltat azX valószínűségi változó standardizáltjának nevezzük.

1.70. Definíció. Az

E

X −E(X) D(X)

3!

mennyiséget azX valószínűségi változó ferdeségének nevezzük.

1.71. Definíció. Az E

X −E(X) D(X)

4!

−3

mennyiséget azX valószínűségi változó lapultságának nevezzük.

1.72. TÉTEL. 1. D(aX+b) =|a|D(X), ∀a, b∈R.

2. D²(X) =E(X²)−E²(X).

3. D²(X) =E((X−a)²) + (a−E(X))². 4. min

a∈RE((X−a)²) =D²(X), és ekkor a=E(X).

1.73. Megjegyzés. Az utóbbi két állítás hasonló (sőt formailag azonos) a tehetetlenségi nyomatékra vonatkozó közismert Steiner-tétellel, amely azt mondja ki, hogy egy egyenesen lévő tömegeloszlás tehetetlenségi nyomaté- ka valamely az egyenesre merőleges forgástengelyre vonatkozólag egyenlő a súlyponton áthaladó tengelyre vonatkozó tehetetlenségi nyomatéknak és a tengely súlyponttól mért távolsága négyzetösszegével, ha az össztömeg egy- ségnyi; következésképpen a tehetetlenségi nyomaték akkor minimális, ha a forgástengely a súlyponton megy át.

1.9. Medián, kvantilis

1.74. Definíció. Azmvalós számot azXvalószínűségi változómediánjának nevezzük, ha

P(X < m) =P(X ≥m) = 1

2, (1.43)

azaz

F_X(m) = 1

2. (1.44)

1.75. Megjegyzés. A medián általában nem egyértelmű. Viszont ha létezik a sűrűségfüggvény, illetve létezik az eloszlásfüggvény deriváltja, akkor

mina∈RE(|X−a|) (1.45) pontosan aza= mesetén adódik. Ez a tulajdonság hasonlít a várható érték és szórásnégyzet kapcsolatához. Az E(|X−m|) értéket a mediántól való várható eltérésnek nevezzük.

Bizonyítás.

I =

+∞

Z

−∞

|x−m|f(x)dx= (1.46)

=−

m

Z

−∞

(x−m)f(x)dx+

+∞

Z

m

(x−m)f(x)dx. (1.47)

Alkalmazzuk a következő Leibniz formulát:

d dy

q(y)

Z

p(y)

f(x, y)dx=

q(y)

Z

p(y)

∂

∂yf(x, y)dx+f(q(y), y)q^′(y)−f(p(y), y)p^′(y), (1.48) akkor azt kapjuk, hogy

dI dm =

Zm

−∞

f(x)dx− Z∞

m

f(x)dx. (1.49)

Tehát akkor kapunk minimumot, ha ez nulla, azaz F(m) =

Zm

−∞

f(x)dx= 1

2. (1.50)

Ez pedig éppen az eloszlás mediánjával egyezik meg.

1.76. Definíció. Azx_p valós számot azX valószínűségi változóp-kvantilisé- nek nevezzük, ha

F_X(x_p) =p. (1.51)

1.77. Megjegyzés. Tehát például a medián az 1

2-kvantilis.

1.10. Néhány diszkrét eloszlás és jellemzői

1. BINOMIÁLIS ELOSZLÁS

Legyen n ∈N, A∈ F, és végezzünk el egy n hosszúságú Bernoulli-kísérlet- sorozatot. Továbbá, legyen X az A esemény bekövetkezéseinek a száma.

Ekkor X eloszlása

P(X =k) = n

k

p^kq^n−k, (k= 0,1, . . . , n), (1.52) ahol P(A) = p és q = 1 − p, és az X valószínűségi változót binomiális eloszlásúnak nevezzük. Jelölés: X ∼B(n, p).

1.78. TÉTEL. E(X) =np, D²(X) =npq.

1.79. Megjegyzés. A visszatevéses mintavétel binomiális eloszláshoz vezet.

Továbbá a gyakoriság is binomiális eloszlású.

2. POISSON-ELOSZLÁS

Legyen λ >0rögzített konstans ésλ=np_n, ekkor

n→∞,λ=nplim n

n k

p^k_n(1−pn)^n−k =e^−λλ^k

k!, ahol k = 0,1, . . . . (1.53) AX valószínűségi változót Poisson-eloszlásúnak nevezzükλ >0 paraméter- rel, ha eloszlása

P(X =k) =e^−λλ^k

k!, ahol k= 0,1, . . . . (1.54) Jelölés: X ∼P oisson(λ).

1.80. TÉTEL. E(X) =λ, D²(X) =λ.

3. GEOMETRIAI ELOSZLÁS

A binomiális eloszlás bevezetésekor használt jelölések mellett azX valószínű- ségi változó jelentse azAesemény első bekövetkezéséhez szükséges kísérletek számát. azX eloszlása

P(X =k) =pq^k−1, ahol k= 1,2, . . . . (1.55) 1.81. TÉTEL. E(X) = 1

p, D²(X) = q p².

1.82. Megjegyzés. Az Y = X−1valószínűségi változót is szokás geomet- riai eloszlásúnak nevezni. Az Y eloszlása

P(Y =k) =pq^k, ahol k= 0,1,2, . . . . 1.83. TÉTEL. E(Y) = q

p, D²(Y) = q p². 1.84. Megjegyzés.

P(Y =k+m|Y ≥m) = P({Y =k+m} ∩ {Y ≥m})

P(Y ≥m) .

Viszont

{Y =k+m} ∩ {Y ≥m}={Y =k+m} és

P(Y ≥m) =pq^m"

1 +q+q²+. . .

= pq^m

1−q =q^m. Tehát

P(Y =k+m|Y ≥m) = pq^m+k

q^m =pq^k = P(Y =k). (1.56) Ezzel beláttuk a geometriai eloszlás emlékezet nélküli tulajdonságát.

1.11. Néhány folytonos eloszlás és jellemzői

1. EGYENLETES ELOSZLÁS

Legyen a, b∈Rés a < b. Az X egyenletes eloszlású az(a, b)intervallumon, ha a sűrűségfüggvénye

f(x) =





 1

b−a, ha a < x < b,

0, egyébként. (1.57)

Jelölés: X ∼U(a, b).Az eloszlásfüggvény

F(x) =











0, ha x≤a, x−a

b−a, ha a < x≤b, 1, ha x > b.

(1.58)

1.85. TÉTEL. E(X) = a+b

2 , D²(X) = (b−a)² 12 .

1.86. Megjegyzés. Az egyenletes eloszlás adja a geometriai valószínűségi mező elméleti alapját.

1.87. TÉTEL. Ha F szigorúan monoton növő eloszlásfüggvény és X F el- oszlású, akkorY =F(X) egyenletes eloszlású a [0,1] intervallumon. Fordít- va, ha X ∼U(0,1), akkor Y =F⁻¹(X) éppen F eloszlású.

2. EXPONENCIÁLIS ELOSZLÁS

Az X exponenciális eloszlású λ >0paraméterrel, ha a sűrűségfüggvénye f(x) =

(λe^−λx, ha x≥0,

0, egyébként. (1.59)

Jelölés: X ∼Exp(λ).Az eloszlásfüggvény F(x) =

(0, ha x≤0,

1−e^−λx, ha x >0. (1.60) 1.88. TÉTEL. E(X) = 1

λ, D²(X) = 1 λ². 1.89. Megjegyzés. Örökifjú tulajdonság:

P(X ≥a+b|X ≥a) =P(X ≥b), (1.61) ahol a >0, b >0.

3. NORMÁLIS ELOSZLÁS

Legyen m∈R, σ >0.Az Y normális eloszlású, ha a sűrűségfüggvénye f(x) = 1

σ√ 2πexp

−(x−m)² 2σ²

, x∈R. (1.62)

Jelölés: Y ∼N(m, σ²).

Ha m = 0 és σ = 1, akkor a valószínűségi változót standard normális elosz- lásúnak nevezzük. Jelölje a sűrűségfüggvényétϕ és az eloszlásfüggvényét Φ.

Ha X standard normális eloszlású, akkor az

Y =σX +m (1.63)

valószínűségi változó F eloszlásfüggvényére jellemző, hogy F(x) = Φ

x−m σ

. (1.64)

1.90. TÉTEL. E(X) =m, D²(X) =σ².

1.91. Megjegyzés. Aϕ függvény írja le a Gauss-görbét (haranggörbét).

1.92. Megjegyzés. Φ(0) = 0.5ésΦ(−x) = 1−Φ(x).Ezzel meghatározható táblázatból az eloszlásfüggvény értéke, hiszen általában aΦfüggvény értékeit csak a[0,4) intervallumon szokás megadni.

Néhány standard normális eloszlás érték

x_p Φ(x_p) =p P(m−x_pσ < Y < m+x_pσ) 1 0.8413447460 0.682689492

1.96 0.9750021049 0.950004210 2 0.9772498680 0.954499736 3 0.9986501020 0.997300204 4 0.9999683288 0.999936658

6 0.9999999990 0.999999998 .

1.93. Megjegyzés. A normális eloszláshoz kapcsolódik a hibafüggvény erf(x) = 2

√π Zx

0

e^−u2du

erfc(x) =1−erf(x), (1.65)

azaz

Φ(x) = 1 2

1 +erf

x

√2

. (1.66)

erf(x) = 2

√π

∞

X

n=0

(−1)ⁿx²ⁿ⁺¹ (2n+ 1)n!

= 2

√π

x− x³ 3 + x⁵

10− x⁷ 42+ x⁹

216− · · ·

. (1.67)

erfc(x) = e^−x2 x√

π

# 1 +

∞

X

n=1

(−1)ⁿ 2n!

n!(2x)²ⁿ

%

= e^−x2 x√

π

1− 1 2x² + 3

4x⁴ − 15

8x⁶ + 105 16x⁸ − · · ·

. (1.68)

1.1. ábra.

Az eloszlásfüggvény közelítésére egy 10⁻⁷ pontosságú polinomiális közelítést alkalmazhatunk. A közelítő polinom:

p(x) =c₀+c₁x+c₂x²+· · ·+c₈x⁸. (1.69)

A közelítő polinom együtthatói

intervallum [0,1.5] (1.5,3] (3,6]

c₀ 0.4999999853197 0.5300774546729 -0.1621966195471 c₁ 0.3989437251038 0.2799241265723 1.8137844596010 c₂ -0.0000232473822 0.2005701987176 -1.2430841874817 c₃ -0.0663495262607 -0.2504062323459 0.4883401215203 c₄ -0.0004071645564 0.0949343858651 -0.1201986229749 c5 0.0105643510048 -0.0131657278224 0.0189705569006 c₆ -0.0003504976933 -0.0009270280158 -0.0018738388405 c₇ -0.0012947802876 0.0004671302299 0.0001058586660 c₈ 0.0002619054865 -0.0000383458376 -0.0000026175074 Az eloszlásfüggvény inverzének a közelítésére egy10⁻¹⁴ pontosságú racionális törtfüggvény közelítést alkalmazhatunk.

Standard normális eloszlás inverze (Pascal részlet)

function Invphi(var x:extended):extended;

var szi,ni,ui:extended;

begin ui:=x; if (ui<0) or (ui>1) then Halt; if ui>=0.5 then ui:=1-ui; if ui<(2*1e-15) then ui:=2*1e-15;

ui:=sqrt(-2*ln(ui))-sqrt(ln(4)); if 0.01<ui then begin szi:=0.2385099062881218351e-3;

szi:=szi*ui+0.7748014532123519149e-2;

szi:=szi*ui+0.9433047102597236601e-1;

szi:=szi*ui+0.5906175347671242813e0;

szi:=szi*ui+0.2052429201482605360e1;

szi:=szi*ui+0.3926527220876257871e1;

szi:=szi*ui+0.3827787912267809326e1;

szi:=szi*ui+0.1475664626635605795e1;szi:=szi*ui+0.0;

ni:=0.2384667219100680462e-3;

ni:=ni*ui+0.7472090148248391360e-2;

ni:=ni*ui+0.8675117268832776800e-1;

ni:=ni*ui+0.5155497927835685221e0;

ni:=ni*ui+0.1685386828574926342e1 ; ni:=ni*ui+0.3019304632408607270e1 ; ni:=ni*ui+0.2757985744718406918e1 ; ni:=ni*ui+1;end

else begin

szi:=0.1389671822546715525e-4;

szi:=szi*ui+0.9933095513250211212e-3;

szi:=szi*ui+0.2132223881469308687e-1;

szi:=szi*ui+0.1971184884114817024e0;

szi:=szi*ui+0.9208235553699620741e0;

szi:=szi*ui+0.2302486886454418763e1;

szi:=szi*ui+0.2934913383940946604e1;

szi:=szi*ui+0.1475663066897793476e1;

szi:=szi*ui+0.2236640681757362082e-6;

ni:=0.1389640654034188922e-4;

ni:=ni*ui+0.9770522217813339426e-3;

ni:=ni*ui+0.2025571989491669521e-1;

ni:=ni*ui+0.1775558927085441912e0;

ni:=ni*ui+0.7785719242838022205e0;

ni:=ni*ui+0.1819506588454068626e1;

ni:=ni*ui+0.2152916059924272000e1;

ni:=ni*ui+1.0;end;

if x<0.5 then szi:=-szi; Invphi:=szi/ni; end;

1.94. TÉTEL. (Moivre-Laplace) Legyen azX valószínűségi változó bino- miális eloszlásún és pparaméterrel és 0≤a < b≤n egész, akkor

P(a≤X ≤b) =

b

X

k=a

n k

p^kq^n−k ≈ (1.70)

≈Φ







b−np+1

√npq 2





−Φ







a−np−1

√npq 2





. (1.71) Szemléltetésül tekintsük az 1.1 és az 1.2 ábrát.

4. CAUCHY ELOSZLÁS

Legyen c∈R, s >0.Az Y Cauchy eloszlású, ha a sűrűségfüggvénye

f(x) = 1

πs

"

1 +

x−c s

2#, x∈R. (1.72)

1.2. ábra.

1.95. Megjegyzés. Nem létezik a várható érték és ebből adódóan nem lé- tezik az E(X^α) momentum, ha α≥1.

Az eloszlásfüggvény

F(x) = 1 2+ 1

πarctan

x−c s

. (1.73)

1.96. Megjegyzés. Szokás ac= 0, s= 1esetet (standard) Cauchy-eloszlásnak nevezni.

5. WEIBULL ELOSZLÁS

A Weibull-eloszlás paramétereire többféle elterjedt jelölésrendszer van. Az el- térő jelölések használatát egyértelműen magyarázza, hogy a Weibull-eloszlás

1.3. ábra.

igen széles körben, a legkülönfélébb tudományterületeken alkalmazták, vala- mint a paramétereknek sokféle meghatározási módja is ismeretes és az egyes megoldásoknál a változók átírása jelentős egyszerűsítéseket eredményez. Mi a következőkben az

F_c(x) =

(1−exp(−x^c), ha x≥0,

0, ha x <0, (1.74)

jelölést alkalmazzuk a standard Weibull-eloszlás jelölésére. Ebből a lineáris transzformáltak eloszlása

F_c(x−a

b ). (1.75)

Tehát ez az eloszláscsalád háromparaméteres, amelyből ac az ún. alakpara- méter (típusparaméter). Viszont lényeges, hogy aszimmetrikus eloszlás.

1.4. ábra.

1.97. Megjegyzés. Az eloszlásc= 1esetén az exponenciális eloszlást,c = 2 a Rayleigh eloszlás adja, míg c = 3.57 közelében az eloszlás közel szimmet- rikussá válik és jól közelíti a normális eloszlást. Megfelelő paraméter válasz- tással az is elérhető, hogy a Weibull-eloszlás jól közelítse a lognormális és Γ-eloszlásokat. Tekintsük az 1.3, 1.4, 1.5, 1.6 ábrákat.

1.12. Generátor-, karakterisztikus függvény

1.98. Definíció. Legyen X egy nemnegatív egész értékű valószínűségi vál- tozó és legyen p_j =P(X =j),(j = 0,1,2, . . .). A

G_X(z) =

∞

X

j=0

p_jz^j =E(z^X) (1.76)

1.5. ábra.

függvényt az X generátorfüggvényének nevezzük.

1.99. TÉTEL. LegyenX ésY nemnegatív egész értékű valószínűségi változó, ekkor

(a)G_X(z) konvergens, ha |z| ≤1.

(b) X és Y eloszlása akkor és csak akkor egyezik meg, haG_X(z) =G_Y(z).

(c) p_n = 1 n!

dⁿG_X(z) dzⁿ

z=0

, n= 0,1,2. . . .

(d)E(X) =G^′_X(1) és D²(X) =G^′′_X(1) +G^′_X(1)−(G^′_X(1))². 1.100. Definíció. Legyen X valószínűségi változó a

ϕ_X(t) =E(e^itX), t∈R (1.77) függvényt az X karakterisztikus függvényének nevezzük.

1.6. ábra.

1.101. TÉTEL. Legyen X és Y valószínűségi változó, ekkor (a)F_X =F_Y akkor és csak akkor, ha ϕ_X =ϕ_Y.

(b) |ϕ_X(t)| ≤ϕ_X(0) = 1, ∀t∈R.

(c) ϕ^(k)_X =i^kE(X^k), ha E(X^k)létezik.

1.102. TÉTEL. Ha a ϕ karakterisztikus függvény abszolút integrálható, ak- kor azX valószínűségi változónak létezik a sűrűségfüggvénye, és

f_X(x) = 1 2π

Z∞

−∞

e^−iuxϕ_X(u)du. (1.78)

1.13. A kétdimenziós véletlen vektor

1.103. Definíció. A (X, Y) : Ω → R² leképezést (kétdimenziós) véletlen vektornak nevezzük, ha

{X < x, Y < y}={ω|ω∈Ω, X(ω)< x, Y(ω)< y} ∈ F ∀x, y∈R.

(1.79) 1.104. Definíció. Az F(x, y) = P(X < x, Y < y) formulával meghatáro- zott valós értékű függvényt a (X, Y) véletlen vektor együttes eloszlásfüggvé- nyének nevezzük. Az

F_X(x) = lim

y→+∞F(x, y), F_Y(y) = lim

x→+∞F(x, y) (1.80) függvényeketperemeloszlásfüggvénynek nevezzük.

1.105. TÉTEL. Az F függvény akkor és csak akkor lehet együttes eloszlás- függvény, ha

1. lim

x→−∞F(x, y) = 0, lim

y→−∞F(x, y) = 0, 2. lim

x→∞

y→∞

F(x, y) = 1,

3. F mindkét változójában balról folytonos,

4. F(b, d)−F(b, c)−F(a, d) +F(a, c)≥0, ∀a < b, c < d esetén, azaz teljesül az ún. "téglalap" tulajdonság.

1.106. Megjegyzés. A téglalap tulajdonságból következik, hogy mindkét változójában monoton növekvő.

1.107. Definíció. A (X, Y) véletlen vektort diszkrétnek nevezzük, ha a le- hetséges értékek számossága legfeljebb megszámlálhatóan végtelen.

1.108. Definíció. Legyen az X, illetve Y valószínűségi változó lehetséges értekeinek sorozata x₁, x₂, . . . , illetve y₁, y₂, . . . . A P(X = x_i, Y = y_j) =p_ij (i, j = 1,2, . . .)valószínűségek sorozatát együttes eloszlásnak nevezzük. A

q_i =

∞

X

j=1

p_ij, (i= 1,2, . . .), (1.81)

r_j =

∞

X

i=1

p_ij, (j = 1,2, . . .) (1.82) valószínűség sorozatokat peremeloszlásnak nevezzük. Minden r_j > 0 esetén azX feltételes eloszlása adott Y =y_j mellett

P(X =x_i|Y =y_j) = p_ij

r_j. (1.83)

Az

E(X|Y =y_j) =

∞

X

i=1

x_ip_ij

r_j (1.84)

mennyiségetfeltételes várható értéknek nevezzük. Az

E(X|Y = y_j) =m₂(y_j) (1.85) függvényt az X-nek azY-ra vonatkozó regressziós függvényének nevezzük.

1.109. TÉTEL. Ha p_ij (i, j = 1,2, . . .) együttes eloszlás, akkor p_ij ≥0 (i, j = 1,2, . . .) és

∞

X

i=1

∞

X

j=1

p_ij = 1. (1.86) 1.110. Definíció. Ha létezik f nemnegatív valós értékű függvény, melyre

F(x, y) = Zx

−∞

y

Z

−∞

f(u, v)dvdu, ∀x, y∈R, (1.87) akkor f azF eloszlásfüggvényhez tartozó együttes sűrűségfüggvény. Az

f_X(x) = Z+∞

−∞

f(x, y)dy, f_Y(y) = Z+∞

−∞

f(x, y)dx (1.88) függvényeketperemsűrűségfüggvénynek nevezzük.

1.111. TÉTEL. Az f függvény akkor és csak akkor lehet együttes sűrűség- függvény, ha nemnegatív és

Z+∞

−∞

Z+∞

−∞

f(x, y)dydx = 1. (1.89)

1.112. Definíció. Az (X, Y)véletlen vektort folytonosnak nevezzük, ha lé- tezik az együttes sűrűségfüggvénye.

1.113. Definíció. Az X ésY)valószínűségi változótfüggetlennek nevezzük, ha

F(x, y) =F_X(x)F_Y(y), ∀x, y∈R. (1.90) 1.114. Megjegyzés. A függetlenség megfelelői diszkrét illetve folytonos esetben:

p_ij =q_ir_j, (i, j = 1,2, . . .), (1.91) f(x, y) =f_X(x)f_Y(y) ∀x, y ∈R. (1.92) 1.115. Definíció. Legyen (X, Y) véletlen vektor. Az F(x|y) az feltételes eloszlásfüggvénye az X-nekY =y esetén, ha

F(x|y) =P(X < x|Y = y) = lim

h→0+0P(X < x|y≤Y < y+h). (1.93) 1.116. Megjegyzés. Ha léteznek a feltételes valószínűségek.

1.117. Definíció. Ha létezikf_X|Y nemnegatív valós értékű függvény, melyre F(x|y) =

Zx

−∞

f_X|Y(u|y)du, ∀x, y∈R, (1.94) akkor f_X|Y az X-nek azY-ra vonatkozó feltételes sűrűségfüggvénye.

1.118. Megjegyzés.

f_X|Y(x|y) = f(x, y)

f_Y(y) . (1.95)

1.119. Definíció. A feltételes sűrűségfüggvény segítségével meghatározott feltételes várható értéketregressziós függvénynek nevezzük, azaz az

+∞

Z

−∞

xf_X|Y(x|y)dx=m₂(y) (1.96) függvényt az X-nek az Y-ra vonatkozó regressziós függvényének nevezzük, illetve az

+∞

Z

−∞

yf_Y|X(y|x)dy =m₁(x) (1.97) függvényt az Y-nak az X-re vonatkozó regressziós függvényének nevezzük.

1.120. Megjegyzés. A min_gE((X −g(Y))²) értékét, akkor kapjuk, ha g megegyezik a regressziós függvénnyel.

1.121. TÉTEL. Ha (X, Y) véletlen vektor és g : R² → R olyan függvény, hogyg(X, Y) valószínűségi változó, akkor

E(g(X, Y)) =













 X

i,j

g(x_i, y_j)p_ij, ha (X,Y) diszkrét, Z+∞

−∞

Z+∞

−∞

g(x, y)f(x, y)dydx, ha (X,Y) folytonos.

(1.98)

1.122. Definíció. A

cov(X, Y) =E((X−E(X))(Y −E(Y))) (1.99) mennyiségetkovarianciának nevezzük. Az

r(X, Y) = cov(X, Y)

D(X)D(Y) (1.100)

mennyiséget pedigkorrelációs együtthatónak nevezzük.

1.123. Megjegyzés. A korrelációs együttható az összefüggést próbálja meg mérni. Ha X és Y független, akkor r(X, Y) = 0, fordítva nem igaz. Pl. ha X ∼N(0,1), Y =X², akkor r(X, Y) = 0.

1.124. Definíció. Legyen g valós függvény. Az I(X, Y) =

s

1−D²(Y −g(X))

D²(Y) (1.101)

mennyiségetkorrelációs indexnek nevezzük.

1.125. TÉTEL. 1. E(X+Y)) =E(X) +E(Y).

2. D²(X+Y)) =D²(X) +D²(Y) + 2cov(X, Y).

3. E(E(X|Y =y)) =E(X).

4. |cov(X, Y)| ≤D(X)D(Y), azaz |r(X, Y)| ≤1.

5. 0≤I(X, Y)≤1.

1.14. Néhány többdimenziós folytonos eloszlás és jellemzői

1. EGYENLETES ELOSZLÁS

Az (X, Y) véletlen vektor egyenletes eloszlású az A⊂R² tartományon, ha f(x, y) =





 1

|A|, ha (x, y)∈A, 0, egyébként.

(1.102)

2. NORMÁLIS ELOSZLÁS

Az (X, Y) véletlen vektor normális eloszlású, ha f(x, y) = 1

2πσ₁σ₂p

1−ρ²exp[−Q], (1.103)

Q= 1

2(1−ρ²)

(x−m₁

σ₁ )²−2ρ(x−m₁

σ₁ )(y−m₂

σ₂ ) + (y−m₂ σ₂ )²

, (1.104) ahol σ₁ >0, σ₂ >0,−1< ρ <1.

Q= 1

2σ₁²(1−ρ²)

x−m₁−ρσ₁

σ₂(y−m₂) 2

+ (y−m₂)²

2σ₂² . (1.105)

f_Y(y) =

+∞

Z

−∞

f(x, y)dx= 1

√2πσ₂ exp

−(y−m₂)² 2σ₂²

× Z+∞

−∞

√ 1

2πσ₁p

1−ρ²exp

"

− 1

2σ₁²(1−ρ²)

x−m₁−ρσ₁

σ₂(y−m₂) 2#

dx=

= 1

√2πσ₂exp

−(y−m₂)² 2σ₂²

, (1.106)

mert az integrál értéke1,hiszen egy olyan valószínűségi változó sűrűségfügg- vénye, amely eloszlása

N

m₁+ρσ₁

σ₂(y−m₂), σ₁²(1−ρ²)

. (1.107)

1.126. Megjegyzés. Rögtön látható, hogy a két perem eloszlásaN(m₁, σ₁²) és N(m₂, σ₂²), valamint

m₁(x) =m₂+ρσ₂

σ₁(x−m₁), m₂(y) =m₁+ρσ₁

σ₂(y−m₂).

(1.108) Tehát a regressziós függvények egyenesek.

1.127. Megjegyzés. Hasonló integrálással adódik, hogy éppenρa korrelá- ciós együttható.

1.15. Az n-dimenziós véletlen vektor

A véletlen vektor és a hozzákapcsolódó fogalmak definícióját csak kétdimen- ziós esetben adtuk meg, de nagyon egyszerűen kiterjeszthetőek véges sok valószínűségi változó esetére. Például, az X₁, X₂, . . . , X_n valószínűségi vál- tozókat függetlennek nevezzük, ha

F(x₁, x₂, . . . , x_n) =F_X1(x₁)F_X2(x₂)· · ·F_Xn(x_n) ∀x₁, x₂, . . . , x_n ∈R.

(1.109) 1.128. TÉTEL. AzF(x₁, x₂, . . . , x_n)függvény akkor és csak akkor együttes eloszlásfüggvény, ha minden változójában balról folytonos, és

xilim→−∞F(x₁, x₂, . . . , x_n) = 0, (i= 1,2, . . . , n), (1.110)

xi→+∞(i=1,2,...,n)lim F(x1, x2, . . . , xn) = 1, (1.111) X

K=e1+e2+···+en

(−1)^KF(e₁a₁+ (1−e₁)b₁, . . . , e_na_n+ (1−e_n)b_n)≥0 (1.112)

∀a_i ≤ b_i (i = 1,2, . . . , n) és az összegzést ∀K esetében vesszük, ahol az e₁, e₂, . . . , e_n értéke 0és 1 lehet.

1.129. TÉTEL. Legyenek X₁, X₂, . . . , X_n független valószínűségi változók, melyeknek rendre F_X1, F_X2, . . . , F_Xn az eloszlásfüggvénye. Ekkor

(a) azY(ω) = max{X₁(ω), . . . , X_n(ω)} (∀ω∈Ω) valószínűségi változó elosz- lásfüggvénye

F_Y(y) =F_X1(y)F_X2(y)· · ·F_Xn(y). (1.113) (b) azY(ω) = min{X₁(ω), . . . , X_n(ω)}(∀ω∈Ω) valószínűségi változó elosz- lásfüggvénye

F_Y(z) = 1−(1−F_X1(z))(1−F_X2(z))· · ·(1−F_Xn(z)). (1.114)

1.16. Valószínűségi változók összege

1.130. TÉTEL. (konvolúció)Legyen (X, Y)véletlen vektor ésZ =X+Y, ekkor teljesülnek a következő állítások:

(a) HaX ésY független diszkrét valószínűségi változók, amelyek mindegyiké- nek lehetséges értékei0,1,2, . . . ,akkorZértékeik=i+j (i, j = 0,1,2,3, . . .) és

P(Z =k) = X

i+j=k

P(X = i)P(Y =j) =

k

X

i=0

P(X =i)P(Y =k−i). (1.115) (b) Ha X és Y független valószínűségi változók, akkor

P(Z < z) = Z+∞

−∞

f_X(x)F_Y(z−x)dx= Zz

−∞

f_Z(x)dx, (1.116) aholZ sűrűségfüggvénye

f_Z(z) = Z+∞

−∞

f_X(x)f_Y(z−x)dx= Z+∞

−∞

f_X(z−y)f_Y(y)dy. (1.117)

1.131. TÉTEL. Ha X és Y független nemnegatív egész értékű valószínűségi változó, akkor

G_X+Y(z) =G_X(z)G_Y(z), (1.118) aholG a generátorfüggvényt jelöli.

1.7. ábra.

1.132. TÉTEL. Ha X és Y független valószínűségi változó, ekkor

ϕ_X+Y(t) =ϕ_X(t)ϕ_Y(t), ∀t∈R, (1.119) aholϕ a karakterisztikus függvényt jelöli.

1. χ²_n–ELOSZLÁS

1.133. Definíció. Legyen X₁, X₂, . . . , X_n ∼ N(0,1), amelyek teljesen füg- getlenek, akkor

X =X₁²+X₂²+· · ·+X_n² (1.120) valószínűségi változót n szabadságfokú χ²_n-eloszlásúnak nevezzük. Jelölés:

X ∼χ²_n.

1.134. TÉTEL. E(X) =n, D²(X) = 2n.

1.135. Megjegyzés. Ha n= 2,akkor X exponenciális eloszlású, azaz X ∼ Exp(0.5).

1.8. ábra.

2. Γ-ELOSZLÁS

Legyen α >0, λ > 0. Az X Γ-eloszlású, ha a sűrűségfüggvénye f(x) =





 1

Γ(α)λ^αx^α−1e^−λx, hax >0,

0, hax≤0.

(1.121) Jelölés: X ∼Γ(λ, α).

1.136. TÉTEL. E(X) = α

λ, D²(X) = α λ².

1.137. Megjegyzés. Haα= 1,akkor éppen az exponenciális eloszlást kap- juk.

1.138. Megjegyzés. Független exponenciális eloszlású valószínűségi válto- zók összegeΓ-eloszlás.

1.9. ábra.

1.139. Megjegyzés. Ha azX χ²_n-eloszlású valószínűségi változó akkorα= n

2, λ = 1

2 paraméterű Γ-eloszlású, azaz X ∼Γ(1

2,n

2). (1.122)

1.17. Egyenlőtlenségek

1.140. TÉTEL. (Markov-egyenlőtlenség) Legyen azY nemnegatív valószí- nűségi változó, melynek létezik a várható értéke, ekkor ∀c >0 esetén

P(Y ≥c)≤ E(Y)

c . (1.123)