https://doi.org/10.1007/s11083-019-09511-5
Generalized Forbidden Subposet Problems
D ´aniel Gerbner1·Bal ´azs Keszegh1·Bal ´azs Patk ´os1
Received: 5 June 2018 / Accepted: 11 October 2019
©The Author(s) 2020
Abstract
A subfamily{F1, F2, . . . , F|P|} ⊆ Fof sets is a copy of a posetP inF if there exists a bijectionφ : P → {F1, F2, . . . , F|P|} such that wheneverx ≤P xholds, then so does φ(x)⊆φ(x). For a familyFof sets, letc(P ,F)denote the number of copies ofPinF, and we say thatFisP-free ifc(P ,F)=0 holds. For any two posetsP , Qlet us denote byLa(n, P , Q)the maximum number of copies ofQover allP-free familiesF ⊆ 2[n], i.e. max{c(Q,F) :F ⊆ 2[n], c(P ,F) =0}. This generalizes the well-studied parameter La(n, P ) = La(n, P , P1)whereP1is the one element poset, i.e.La(n, P )is the largest possible size of aP-free family. The quantityLa(n, P )has been determined (precisely or asymptotically) for many posetsP, and in all known cases an asymptotically best construc- tion can be obtained by taking as many middle levels as possible without creating a copy of P. In this paper we consider the first instances of the problem of determiningLa(n, P , Q).
We find its value whenP andQare small posets, like chains, forks, theNposet and dia- monds. Already these special cases show that the extremal families are completely different from those in the originalP-free cases: sometimes not middle or consecutive levels max- imizeLa(n, P , Q)and sometimes the extremal family is not the union of levels. Finally, we determine (up to a polynomial factor) the maximum number of copies of complete multi-level posets ink-Sperner families. The main tools for this are the profile polytope method and two extremal set system problems that are of independent interest: we maxi- mize the number ofr-tuplesA1, A2, . . . , Ar ∈Aover all antichainsA⊆2[n]such that (i)
∩ri=1Ai = ∅, (ii)∩ri=1Ai = ∅and∪ri=1Ai = [n].
Keywords Extremal set systems·Forbidden subposet problems
Bal´azs Patk´os patkos@renyi.hu D´aniel Gerbner gerbner@renyi.hu Bal´azs Keszegh keszegh@renyi.hu
1 Alfr´ed R´enyi Institute of Mathematics, Hungarian Academy of Sciences, P.O.B. 127, Budapest, H-1364, Hungary
/Published online: 10February2020
1 Introduction
The very first theorem of extremal finite set theory is due to Sperner [25] and states that if Fis a family of subsets of[n] = {1,2, . . . , n}such that no two sets inFare comparable, then|F| ≤ n
n/2
holds, and equality is achieved if and only ifFconsists of all then/2- element or all the n/2-element subsets of[n]. For 0 ≤ k ≤ nthe family consisting of all the k-element subsets of[n]are called (full) levelsand we introduce the notation [n]
k
= {F ⊆ [n] : |F| =k}for them. Sperner’s theorem was generalized by Erd˝os [6] to the case whenFis not allowed to containk+1 mutually comparable sets, i.e. a(k+1)-chain.
He showed that among such families the ones consisting ofkmiddle levels are the largest.
In the early eighties, Katona and Tarj´an [21] introduced a generalization of the problem and started to consider determining the size of the largest family of subsets of[n]that does not contain a configuration defined by inclusions. Such problems are known as forbidden subposet problems and are widely studied (see the recent survey [15] or Chapter 7 of [14]).
In this paper, we propose even further generalizations: we are interested in the maximum number of copies of a given configurationQin families that do not contain a forbidden subposetP. Before giving the precise definitions, let us mention that similar problems were studied by Alon and Shikhelman [1] in the context of graphs. They considered the problem of finding the most number of copies of a graphT that anH-free graph can contain.
Definition LetP be an arbitrary poset andFa family of sets. We say thatG⊆Fisa copy ofP inFif there exists a bijectionφ :P →Gsuch that wheneverx≤P xholds, then so doesφ(x)⊆φ(x). In this case we also say thatP is asubposetofF. Letc(P ,F)denote the number of copies ofPinFand for any pair of posetsP , Q,let us define
La(n, P , Q)=max{c(Q,F):F⊆2[n], c(P ,F)=0}, and for families of posetsP,Qlet us define
La(n,P,Q)=max
⎧⎨
⎩
Q∈Q
c(Q,F):F⊆2[n],∀P ∈P c(P ,F)=0
⎫⎬
⎭. We denote byPkthe chain of lengthk, i.e. the completely ordered poset onkelements. In particular,P1 is the poset with one element. Let us state Erd˝os’s above mentioned result with our notation.
Theorem 1.1(Sperner [25] fork=1, Erd˝os [6] for generalk) For every positive integerk the following holds:
La(n, Pk+1, P1)= k i=1
n n−k2 +i
.
The main conjecture of the area of forbidden subposet problems was first published by Griggs and Lu in [16] and by Bukh [3], although it was already folklore by that time in the extremal finite set theory community.
Conjecture 1.2 For a posetPlet us denote bye(P )the largest integermsuch that for any n, any familyF⊆2[n]consisting ofmconsecutive levels isP-free. Then
n→∞lim
La(n, P , P1) n
n/2 =e(P )
holds.
In other words, Conjecture 1.2 states that to obtain an asymptotically largestP-free fam- ilyF⊆2[n], one has to consider as many middle levels of 2[n]as possible without creating a copy ofP.
There are not many results in the literature where other posets are counted. Katona [19]
determined the maximum number of 2-chains (copies ofP2) in a 2-Sperner (P3-free) family F ⊆2[n]. This was reproved in [24] and generalized by Gerbner and Patk´os in [13].
Theorem 1.3([13]) For anyl > kthe quantityLa(n, Pl, Pk)is attained for some family F that is the union ofl−1levels. Moreover, La(n, Pk+1, Pk) = n
ik
·ik
ik−1
· · · · ·i2
i1
, wherei1 < i2 <· · ·< ik < nare chosen arbitrarily such that the valuesi1, i2−i1, i3− i2, . . . , ik−ik−1, n−ikdiffer by at most one.
Theorem 1.3 shows that to make Conjecture 1.2 valid in this more general context one has to remove at least the word consecutive. But there are cases when all families consisting of full levels are very far from being optimal. Let the generalized diamond posetDkbe the poset onk+2 elementsa, b1, b2, . . . , bk, cwitha < b1, b2, . . . , bk < c. Let us consider La(n, D2, P3), which is the maximum number of 3-chains in diamond-free families. Every family that contains at least three full levels of 2[n]contains a copy ofD2, while a family that is the union of at most two levels, does not contain any copy ofP3. Therefore, ifF is D2-free and is the union of full levels, thenc(P3,F)=0, while there areD2-free families with lots of copies ofP3. Note thatD2is the smallest poset for which Conjecture 1.2 has not been proved.
Theorem 1.4 For the generalized diamond posets and integersk > lthe following holds:
k−1 l
La(n−k+1, P3, P2)≤La(n, Dk, Dl)≤
k+1 2
−k k−1 l
La(n, P3, P2).
Note that Theorem 1.4 impliesLa(n, Dk, Dl)=θk,l(La(n, P3, P2))for any fixedkand l. So it is a natural question whether the limitdk,l = limn→∞La(n,DLa(n,Pk,Dl)
3,P2) exists and if so, what its value is. In the simplest casek=2, l=1 the above inequalities and Theorem 1.3 imply 1/3≤d2,1≤1.
Let us examine what version of Conjecture 1.2 may hold in our setting. Letl(P )be the height of a posetP, i.e. the length of the longest chain inP. Clearly, ifFis the union of anyl(P )−1 full levels, it must beP-free. On the other hand ifFn= ∪l(Q)j=1
[n]
ij
is the union ofl(Q)full levels withij+1−ij ≥cnfor some constantcfor allj =1,2, . . . l(Q)−1, thenFncontains many copies ofQ. Therefore we propose the following.
Conjecture 1.5 For any pairP , Qof posets withl(P ) > l(Q)there exist an integermand a sequence ofP-free familiesFn⊆2[n]that are of the formFn= ∪mj=1
[n]
ij
such that La(n, P , Q)=(1+o(1))c(Q,Fn)
holds.
As we will see, this conjecture often holds even ifl(P ) ≤l(Q). We say that for a pair P , Qof posets Conjecture 1.5strongly holdsif for large enoughnwe haveLa(n, P , Q)= c(Q,Fn) andalmost holds ifLa(n, P , Q) = O(nkc(Q,Fn))for some k that depends
only onP andQ. In both cases we also assume the familyFnisP-free and is the union of full levels, but we do not assume anything aboutl(P )andl(Q). Note that the value of La(n, P , Q)typically grows exponentially inn.
In this paper, we address the first instances of the general problem. Let us note that since the first version of this paper, Gerbner, Methuku, Nagy, Patk´os and Vizer [12] studied the special case whenQis a chain. We will consider the following posets (see Fig.1): let
r
denote the poset onr+1 elements 0, a1, a2, . . . , ar with 0≤aifor alli=1,2, . . . , rand we write
for
2. Similarly, let
rdenote the poset onr+1 elementsa1, a2, . . . , ar,1 withai ≤ 1 for alli = 1,2, . . . , r and we write
for
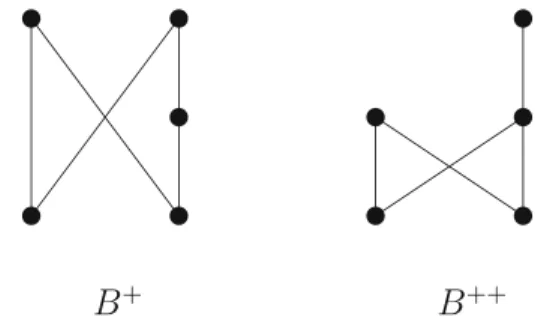
2. The posetN contains four elementsa, b, c, dwitha≤candb≤c, d. The butterfly posetBconsists of four elements a, b, c, dwitha, b≤c, d.
A family that does not containP2is called an antichain. A familyFthat does not contain Pkcan be easily partitioned intok−1 antichainsF1, . . . ,Fk−1the following way: letFi
be the set of minimal elements ofF\ ∪i−1j=1Fj. We call this thecanonical partitionofF. The proof of the next theorem (and of the other theorems) will follow in later sections.
Theorem 1.6 (a) La(n,
, P2)=La(n,
, P2)= n
n/2
. (b) La(n,{
,
}, P2)= n−1
(n−1)/2 . (c) La(n, B, Dr)=(n/2n )
r
. (d) La(n,
,
r)=La(n, ,
r)=(n/2n )
r
.
Parts(a) (c), and(d)of Theorem 1.6 show that Conjecture 1.5 strongly holds for those pairs of posets.
The proof of our next theorem uses the notion of profile vectors (ordinary andl-chain profile vectors) that we will describe later. Here and throughout the paperh(x)denotes the binary entropy function, i.e.h(x)= −xlog2x−(1−x)log2(1−x).
Theorem 1.7 (a) La(n, P3,
r)= La(n, P3,
r)=n
ir
(ir /2ir )
r
for someir withir = (1+o(1))2r2+1r n.
(b) La(n, P4, Dr)=n
jr
jr
ir
((jrjr−ir−ir )/2)
r
for someir =(1+o(1)) n
2r/2+2 and eitherjr = n−irorjr =n−ir−1.
(c) 2(c+o(1))n≤La(n, P3, N )≤o(23n),
wherec = h(c0)+3c0h(c0/(1−c0)) ≈ 2.9502...withc0 being the real root of the equation0=7x3−10x2+5x−1.
Fig. 1 The Hasse diagrams of the posetsN,B,
rand
r
In the above theorem we dealt withLa(n, Pl(Q)+1, Q)for different posetsQ. We knew the place of every element of every copy ofQin the canonical partition. In the following we deal with these kind of problems. We introduce the following binary operations of posets:
for any pairQ1,Q2of posets we defineQ1⊗rQ2by adding an antichain of sizerbetween Q1andQ2. More precisely, let us assumeQ1 consists ofq11, . . . , qa1 andQ2 consists of q12, . . . , qb2. ThenR = Q1⊗r Q2 consists ofq11, . . . , qa1, m1, m2, . . . , mr, q12, . . . qb2. We haveqi1<Rqj1if and only ifqi1<Q1 qj1and similarlyqi2 <Rqj2if and only ifqi2<Q2 qj2. Also we haveqi1 <Rmk <Rqj2for everyi,k, andj. Finally, themk’s form an antichain.
Note thatl(Q1⊗r Q2) =l(Q1)+l(Q2)+1. LetQ⊕rdenote the poset obtained from Q by adding r elements that form an antichain and that are all larger than all elements ofQ. Similar operations of posets were considered first in the area of forbidden subposet problems by Burcsi and Nagy [4].
We will obtain bounds on La(n, Pl(Q1⊗rQ2)+1, Q1 ⊗r Q2) involving bounds on La(n, Pl(Q1)+1, Q1) and La(n, Pl(Q2)+1, Q2). For this, first we need to introduce the notions of profile vectors and profile polytopes. For a family F ⊆ 2[n] of sets, let α(F)=(α0, α1, . . . , αn)denote theprofile vectorofF, whereαi = |{F ∈F : |F| =i}|. Many problems in extremal finite set theory ask for the largest size of a family in a class A⊆22[n]. This question is equivalent to determining maxF∈Aα(F)·1, where1is the vector of lengthn+1 with all entries being 1, and·denotes the scalar product.
More generally, consider a weight functionw: {0,1, . . . , n} →R, and assume we want to maximize w(F) :=
F∈Fw(|F|). Then this is equivalent to maximizingα(F)·w, wherew=(w(0), w(1), . . . , w(n)). AsA⊆22[n]holds, we have{α(F):F∈A} ⊆Rn+1 and therefore we can consider its convex hullμ(A), that we call the profile polytopeof A. It is well known that any weight function with the above property is maximized by an extreme pointofμ(A)(a point that is not a convex combination of other points ofμ(A)), moreover if such a weight function is non-negative, then it is maximized by anessential extreme point, i.e. an extreme point which is maximal with respect to the coordinate-wise ordering. First results concerning profile polytopes were obtained in [8–11,20] and the not too recent monograph of Engel [7] contains a chapter devoted to this topic.
Using this we can determineLa(n, P3, P2), and using induction with this as the base case, one can determineLa(n, Pk+1, Pk), but in other cases we will need a more powerful tool than ordinary profile vectors. The notion ofl-chain profile vectorαl(F)of a family F ⊆2[n]was introduced by Gerbner and Patk´os [13] and denotes a vector of lengthn+1
l
. The coordinates are indexed byl-tuples of[0, n], andαl(F)(i1, i2, . . . , il)is the number of chainsF1 F2 · · · Flsuch thatFj ∈Fand|Fj| = ij for all 1≤j ≤l. For a set A⊆22[n]one can define thel-chain profile polytopeμl(A), its extreme points and essential extreme points analogously to the above. Note that forl =1 we get back the definition of the original profile polytope.
Here we introduce two new types of profile vectors. For a familyF ⊆2[n]of sets, let βr(F) = (β0r, β1r, . . . , βn−1r ) denote ther-intersection profile vectorofF, where βir = βir(F)= |{{F1, F2, . . . , Fr} :Fj ∈F, these arerdifferent sets, and |r
j=1Fj| =i}|. For a familyF⊆2[n]of sets, letγr(F)=(γ0,1r , γ0,2r , . . . , γ0,nr , γ1,2r , . . . , γnr−1,n)denote the r-intersection-union profile vector ofF, whereγi,jr = γi,jr (F) = |{{F1, . . . , Fr} : F1, . . . , Fr∈F,these arerdifferent sets,|F1∩ · · · ∩Fr| =i, and|F1∪ · · · ∪Fr| =j}|. Note that ifA⊆ 2[n]is an antichain, thenγi,jr (A) > 0 impliesj−i ≥ 2, therefore the number of non-zero coordinates inγr(A)is at mostn+1
2
−n=n
2
≤n2.
Let us illustrate with two examples why these profile vectors can be useful in count- ing copies of different posets. LetKr1,r2,...,rs denote thecompletes-level posetons
i=1ri
elements
a11, a21, . . . , ar11, a21, a22, . . . , a2r2, . . . , as1, a2s, . . . , asrs withahi < ajl if and only ifi < j. Observe that
r =K1,r,B=K2,2andDr=K1,r,1. Let F be a P3-free and G be a P4-free family. We will estimate c(Kp,r,F) and c(Kp,r,s,G). If we consider the canonical partitions ofF=F1∪F2andG=G1∪G2∪G3, then a copy ofKp,rinFcontainspsets fromF1andrsets fromF2. If we fixF1, . . . , Fr ∈ F2, then thep“bottom” sets of the copies ofKp,r inF containingF1, . . . , Fr form an antichain in{F ∈F1 :F ⊆ r
j=1Fj}. Therefore, by Theorem 1.1, the number of these copies is at most(||rrj=1Fj|
j=1Fj|/2)
p
, so summing up for all possibler-tuples ofF2 we obtain c(Kp,r,F)≤βr(F)·wp, and consequently
La(n, P3, Kp,r)≤max{βr(A)·wp:A⊆2[n]is an antichain}, where thejth entry of the vectorwpis(j/2j )
p
.
Similarly, if we consider the canonical partition ofG=G1∪G2∪G3, then a copy ofKp,r,s inGcontainspsets fromG1,rsets fromG2andssets fromG3. If we fixG1, . . . , Gr ∈G2, then the bottompand topssets of copies ofKp,r,s containingG1, . . . , Gr form antichains in{G ∈ G1 : G ⊆ r
j=1Gj}and{G ∈ G3 : G ⊇ r
j=1Gj}. Therefore, using again Theorem 1.1, we obtainc(Kp,r,s,G)≤γr(G2)·wp,sand consequently
La(n, P4, Kp,r,s)≤max{γr(A)·wp,s:A⊆2[n]is an antichain}, where the(i, j )th entry of the vectorwp,s is(i/2i )
p
((n−j )/2n−j )
s
. Therefore determining the convex hull (and more importantly its extreme points) of ther-intersection profile vectors andr-intersection-union profile vectors of antichains would yield upper bounds onLa- functions of complete multi-level posets.
We are not able to determine these convex hulls, we will only obtain upper bounds on the coordinates of these profile vectors.
Theorem 1.8 (a) For everyr ≥3and antichainA⊆ 2[n],γ0,nr (A) ≤n2rγ0,nr ( [n]
n/2
).
Ifr=2andnis even, thenγ0,n2 (A)≤γ0,n2 ([n]
n/2
), while ifr=2andnis odd, then γ0,n2 (A)≤ n−1
n/2−1
.
(b) For everyr there exists a sequenceln such that ifA ⊆ 2[n] is an antichain, then β0r(A)≤n2r+1β0r([n]
ln
).
(c) IfA⊆2[n]is an antichain, thenβ02(A)≤12 n
n/32n/3 n/3
and this is sharp as shown by [n]
n/3
ifn≡0,1mod 3 and by [n]
n/3
ifn≡2mod 3.
Ther=2 part of Theorem 1.8(a)was proved by Bollob´as [2]. Using the above theorem, we can give bounds onLa(n, Pl(Q1⊗rQ2)+1, Q1⊗rQ2).
Theorem 1.9 LetQ1, Q2be two non-empty posets.
(a) Ifr≥2, then we have
La(n, Pl(Q1)+l(Q2)+1, Q1⊗rQ2)≤ n2r+2 max
0≤i<j≤n
n
j
j
i
γ0,j−ir
[j−i] (j−i)/2
La(i, Pl(Q1)+1, Q1)La(n−j, Pl(Q2)+1, Q2)
. Furthermore, ifr≥3and Conjecture 1.5 almost holds for the pairsPl(Q1)+1, Q1and Pl(Q2)+1,Q2, then so it does for the pairPl(Q1⊗rQ2)+1, Q1⊗rQ2.
(b) Ifr=1, then we have
La(n, Pl(Q1)+l(Q2)+1, Q1⊗1Q2)≤ max
0≤j≤n
n
j
La(j, Pl(Q1)+1, Q1)La(n−j, Pl(Q2)+1, Q2)
. Furthermore, if Conjecture 1.5 strongly/almost holds for the pairs Pl(Q1)+1, Q1 and Pl(Q2)+1,Q2, then so it does for the pairPl(Q1⊗1Q2)+1, Q1⊗1Q2.
Theorem 1.10 LetQbe a non-empty poset.
(a) Ifr≥2andn∈N, then there exists ani=i(r, n)such that La(n, Pl(Q)+2, Q⊕r)≤ max
0≤j≤n
n i
β0r
[n−i] j−i
La(j, Pl(Q)+1, Q)
. Furthermore, if Conjecture 1.5 almost holds for the pairPl(Q)+1, Q, then so it does for the pairPl(Q)+2, Q1⊕r.
(b) Ifr=1, then we have
La(n, Pl(Q)+2, Q⊕1)≤ max
0≤j≤n
n j
La(j, Pl(Q)+1, Q)
.
Furthermore, if Conjecture 1.5 strongly/almost holds for the pairPl(Q)+1, Q, then so it does for the pairPl(Q)+2, Q⊕1.
We can apply Theorem 1.9 and Theorem 1.10 to complete multi-level posets (Fig.2).
Corollary 1.11 For any complete multi-level posetKr1,r2,...,rs, Conjecture 1.5 almost holds for the pairPs+1, Kr1,r2,...,rs.
Fig. 2 The Hasse diagrams of multi-level posets
Corollary 1.12 Conjecture 1.5 strongly holds for the pairPs+1, Kr1,r2,...,rs if for every i < sat least one ofriandri+1is equal to 1.
Corollary 1.12 does not tell us anything about the set sizes in the family containing the most number of copies ofKr1,r2,...,rs. The next theorem gives more insight for an even more special case.
Theorem 1.13 The value of La(n, Pl+3, Kr,1,...,1,s) (where there are l copies of 1 in Kr,1,...,1,s) is attained for a familyF= ∪lj=1+2[n]
ij
, wherei1= i2/2,il+2= (n+il+1)/2 andi3−i2,i4−i3, . . . , il+1−ildiffer by at most 1.
Finally observe that Conjecture 1.2, if true, and Theorem 1.1 would have another con- sequence: the asymptotics of La(n, P ) = La(n, P , P1) would equal that of La(n, Pj) for some integerj. This is not true in our more general context in the following stronger sense that even the order of magnitude ofLa(n, P , Q)can be different from any function La(n, Pj, Q).
Theorem 1.14 There does not exist any integerjwithLa(n, B, P2)=(La(n, Pj, P2)).
The rest of the paper is organized as follows: we prove Theorem 1.4 and Theorem 1.6 in Section2. We prove Theorem 1.7 in Section3. Theorem 1.8, Theorem 1.9, Theorem 1.10, and their corollaries are proved in Section4, Theorem 1.14 in Section5, while Section6 contains some concluding remarks.
2 Proofs of Theorem 1.4 and Theorem 1.6
Proof of Theorem 1.4 We start by proving the upper bound. LetF ⊆ 2[n] be aDk-free family. As for any posetP, the canonical partition of aP-free family can consist of at most
|P|−1 antichains, we can assume that the canonical partition ofFisk+1
i=1Fi. In any copy ofDlinF, the sets corresponding to the top and bottom element ofDl come fromFi and Fj withi−j ≥ 2. The number of such pairs of indices isk+1
2
−k. Let us bound the number of copies ofDlwith top element fromFiand bottom element fromFj. AsFi∪Fj
isP3-free, there are at mostLa(n, P3, P2)many ways to choose the top and the bottom elementsFB ⊂FT. AsFisDk-free, there can be at mostk−1 sets inFlying betweenFB
andFT, so the number of copies ofDlwithFB, FT being top and bottom is at mostk−1
l
. The upper bound onLa(n, Dk, Dl)follows.
For the lower bound we need a construction. LetF1∪F2 ⊆ 2[n−k+1]be the canon- ical partition of the P3-free family F with c(P2,F) = La(n− k+ 1, P3, P2). For j = 3,4, . . . , k+1 letFj = {F ∪ [n−k+2, n−k+j −1] : F ∈ F2}, where for i ≤ j,[i, j]denotes the set{i, i+1, . . . , j −1, j}. We claim thatG = ∪k+1i=1Fi isDk- free withc(Dl,F) ≥k−1
l
La(n−k+1, P3, P2). Indeed, every setG ∈Gis contained in a setFk+1 ∈Fk+1and contains a setF1 ∈F1, therefore if there was a copy ofDk, we could assume that its bottom element is fromF1and its top element is fromFk+1. But any Fk+1∈Fk+1contains exactly one element from eachFiwherei=2,3, . . . , k, so there is no space for a copy ofDk. On the other hand, for every pairF1 ⊂F2inF1∪F2we can addlsets from{F2∪ [n−k+2, n−k+j−1] :j =3,4, . . . , k+1}to form a copy of Dl. For each such pair we will obtaink−1
l
such copies.
Proof of Theorem 1.6 To prove (a), by symmetry, it is enough to showLa(n, , P2) = n
n/2
. Consider any
-free familyF ⊆2[n]. As the
-free property implies theP3-free property, the canonical partition ofFisF1∪F2. By the
-free property ofF, elements ofF1 are contained in at most one copy ofP2. Also, every copy ofP2 inFmust contain a set fromF1. Sperner’s theorem yields c(P2,F) ≤ |F1| ≤ n
n/2
. On the other hand F := {F ⊆ [n] : |F| = n/2} ∪ {[n]}is
-free and everyn/2-element set forms a copy ofP2with[n].
We continue with proving(b). We will need the following definition. For any family F, thecomparability graph ofFhas vertex setFand two setsF, F ∈F are joined by an edge ifF ⊆ F orF ⊆ F holds. The connected components of the comparability graph of F are said to be thecomponents ofF. If a familyF is both
-free and - free, then its components are either isolated vertices or isolated edges in the comparability graph. Thereforec(P2,F)is the number of components that are isolated edges. It follows thatLa(n,{
,
}, P2) ≤ 12La(n,{ ,
}, P1) = n−1
(n−1)/2
where the result in the last equation was proved by Katona and Tarj´an [21]. The construction (given also in [21])F:=
[n−1]
(n−1)/2
∪ {{n} ∪F :F ∈ [n−1]
(n−1)/2
}shows that the above upper bound can be attained.
To prove(c), let us consider aB-free familyF ⊆2[n]and letM= {M∈F : ∃F, F∈ F such thatFM F}. AsB-free impliesP4-free, we obtain thatMis an antichain, thus|M| ≤ n
n/2
, by Theorem 1.1. Moreover, ifM ∈ M, then there do not exist two elementsF1, F2∈FwithMF1, F2. Indeed, by the definition ofMthere existsF∈F withF M, andF, M, F1, F2would form a copy ofB. Similarly, for everyM ∈M there exists exactly one elementF ∈F withF M. Therefore, a copy ofDr containsr elements ofM, and they determine the remaining two elements, which impliesc(Dr,F)≤ |M|
r
≤(n/2n )
r
. The constructionF:= {∅,[n]} ∪ [n]
n/2
shows that this upper bound can be attained.
To prove (d), by symmetry, it is enough to showLa(n, ,
r) = (n/2n )
r
. IfF is -free, then it is in particularP3-free. Consider its canonical partitionF = F1 ∪F2. Then a copy of
r containsrelements fromF1 and one fromF2. Moreover, anr-tuple fromF1 may form a copy of
r with at most one element fromF2, otherwise there is a copy (actually rcopies) of
inF. AsF1 is an antichain, by Theorem 1.1, the upper boundLa(n,
,
r) ≤ (n/2n )
r
follows andF := {[n]} ∪ [n]
n/2
shows that this can be attained.
3 The profile polytope method
In this section we prove Theorem 1.7 after stating a result concerningl-chain profile vectors, due to Gerbner and Patk´os [13].
LetSn,kbe the class of allk-Sperner (i.e.Pk+1-free) families on[n].
Lemma 3.1(Gerbner, Patk´os, [13]) The essential extreme points ofμl(Sn,k)are thel-chain vectors ofk-Sperner families that consist of the union ofkfull levels.
Let us state the immediate consequence of the above lemma that we will use in our proofs in the remainder of this section.
Corollary 3.2 Let l ≤ k and w : 2[n]
l
→ R+ be a weight function such that w({F1, F2, . . . Fl})depends only on|F1|,|F2|, . . . ,|Fl|. Then the maximum of
F1F2···Fl,Fi∈F
w({F1, F2, . . . , Fl})
over all familiesF∈Sn,kis attained at some family that consists ofkfull levels.
Proof of Theorem 1.7. To prove(a), we showLa(n, P3,
r) = n
ir
(ir /2ir )
r
as the other statement follows by symmetry. Let us consider the canonical partitionF1∪F2of aP3-free familyF. Note that a copy of
r contains exactly one elementF fromF2andrelements F1, F2, . . . , Fr ∈F1 withFi F for all 1,2, . . . , r. Let us consider a setF ∈ F2. The sets ofF1contained inF form an antichain, thus by Theorem 1.1, their number is at most |F|
|F|/2
. Therefore, the number of copies of
r that containF is at most(|F|/2|F| )
r
and we obtain
c(
r,F)≤
F∈F2
|F|
|F|/2
r
≤ max
A∈Sn,1
A∈A
|A|
|A|/2
r
. Therefore, if we setw(i):= (i/2i )
r
, then we can apply Corollary 3.2 withl =k =1 to obtainc(
r,F)≤max0≤i≤nn
i
w(i). On the other hand, the familiesF(i)=[n]
i
∪[n]
i/2
areP3-free andc(
r,F(i)) =n
i
w(i)showingLa(n, P3,
r)= max0≤i≤nn
i
w(i). To obtain the value ofirwe need to maximizef (i):=n
i
w(i). We have
f (i)
f (i+1) = i+1 n−i ·
r−1
j=0 i
i/2
−j r−1
j=0 i+1
(i+1)/2
−j =(1+o(1)) i+1 2r(n−i)
wheni tends to infinity withn. For constant values ofi, the ratiof (i)/f (i+1)is easily seen to be smaller than 1 (ifnis big enough), therefore the maximum off (i)is attained at ir =(1+o(1))2r2+1r nas stated.
To prove(b), we consider the canonical partition of a P4-free familyF ⊆ 2[n]. Any copy of Dr in F must contain one set from F1,F3 each and r sets fromF2. For any F1∈F1, F3 ∈F3withF1⊂F3, the number of copies ofDrcontainingF1andF3ism
r
, wherem= |MF1,F3|withMF1,F3 = {F ∈F2:F1 ⊂F ⊂F3}. AsMF1,F3 = {M\F1 : M∈MF1,F3}is an antichain inF3\F1, we havem≤ |F3|−|F1|
(|F3|−|F1|)/2
. Therefore, we obtain
c(Dr,F)≤
F1∈F1,F3∈F3,F1⊂F3
|F3|−|F1|
(|F3|−|F1|)/2 r
≤ max
0≤i<j≤n
n j
j i
j−i
(j−i)/2 r
, where to obtain the last inequality we applied Corollary 3.2 withl=k=2 andw(i, j )= ((j−i)/2j−i )
r
. Observe that ifir andjr are the values for which this maximum is taken, then for the familyF=[n]
ir
∪[n]
jr
∪ [n]
(ir+jr)/2
we havec(Dr,F)=n
jr
jr
ir
((jr−ir )/2jr−ir )
r
. To obtain the value ofir andjrlet us fixx=j−ifirst. Note thatn
j
j
i
=n
x
n−x
i
, so we have
n
i+1+x
i+1+x
i+1
(x/2x )
r
n
i+x
i+x
i
(x/2x )
r
= n
x
n−x
i+1
(x/2x )
r
n
x
n−x
i
(x/2x )
r
= n−x−i i+1 , which implies thatir+jr=norir+jr =n−1 holds.