MŰHELYTANULMÁNYOK DISCUSSION PAPERS
INSTITUTE OF ECONOMICS, CENTRE FOR ECONOMIC AND REGIONAL STUDIES, HUNGARIAN ACADEMY OF SCIENCES - BUDAPEST, 2019
MT-DP – 2019/15
Optimal Kidney Exchange with Immunosuppressants
HARIS AZIZ – ÁGNES CSEH
Discussion papers MT-DP – 2019/15
Institute of Economics, Centre for Economic and Regional Studies, Hungarian Academy of Sciences
KTI/IE Discussion Papers are circulated to promote discussion and provoque comments.
Any references to discussion papers should clearly state that the paper is preliminary.
Materials published in this series may subject to further publication.
Optimal Kidney Exchange with Immunosuppressants
Authors:
Haris Aziz senior lecturer
at the School of Computer Science and Engineering, UNSW and the team leader
of the Algorithmic Decision Theory group haris.aziz@unsw.edu.au
Ágnes Cseh research fellow Institute of Economics
Centre for Economic and Regional Studies Hungarian Academy of Sciences
cseh.agnes@krtk.mta.hu
September 2019
Optimal Kidney Exchange with Immunosuppressants
Haris Aziz - Ágnes Cseh
Abstract
Potent immunosuppressant drugs suppress the body’s ability to reject a transplanted organ up to the point that a transplant across blood- or tissue-type incompatibility becomes possible. In contrast to the standard kidney exchange problem, our setting also involves the decision about which patients receive from the limited supply of immunosuppressants that make them compatible with originally incompatible kidneys. We firstly present a general computational framework to model this problem. Our main contribution is a range of efficient algorithms that provide flexibility in terms of meeting meaningful objectives. We also show that these algorithms satisfy desirable axiomatic and strategic properties.
Keywords: kidney exchange, immunosuppressant drugs, matching, complexity
JEL classification: C63, C78
Optimális vesecsere immunszupresszáns gyógyszerek segítségével
Haris Aziz – Cseh Ágnes
Összefoglaló
Bizonyos erős immunszupresszáns gyógyszerek olyan mértékben képesek befolyásolni az emberi test idegen szervvel szemben tanúsított befogadókészségét, hogy a vércsoport szerinti vagy szövettani inkompatibilás áthidalhatóvá válik.
A szokványos vesecsereproblémával ellentétben modellünkben döntést kell hoznunk, hogy mely betegek kapják ezeket a korlátozott számban rendelkezésre álló, erős gyógyszereket. Először építünk egy általános, számítástudományi alapokon nyugvó modellt a problémához. Ezen a modellen később konstruálunk egy sokféleképpen módosítható, hatékony algoritmust, ami különböző célok elérését szolgálhatja.
Azt is megmutatjuk, hogy ez az algoritmus vonzó aximomatikus és stratégiai tulajdonságokkal is rendelkezik.
Tárgyszavak: vesecsere, immunszupresszáns gyógyszerek, párosítások, komplexitás
JEL kódok: C63, C78
Optimal Kidney Exchange with Immunosuppressants
Haris Aziz
∗and Agnes Cseh ´
†Abstract
Potent immunosuppressant drugs suppress the body’s ability to reject a transplanted organ up to the point that a transplant across blood- or tissue-type incompatibility becomes possi- ble. In contrast to the standard kidney exchange problem, our setting also involves the decision about which patients receive from the limited supply of immunosuppressants that make them compatible with originally incompatible kidneys. We firstly present a general computational framework to model this problem. Our main contribution is a range of efficient algorithms that provide flexibility in terms of meeting mean- ingful objectives. We also show that these algorithms satisfy desirable axiomatic and strategic properties.
Introduction
The deployment of centralized matching algorithms for effi- cient exchange of donated kidneys is a major success story of market design (Bir´o et al. 2019). The standard model for kidney exchange involves information about patients’ com- patibility with kidneys in the market. A patient can only be given a kidney that is compatible with the patient. The goal is to enable exchanges of kidneys via a centralized algorithm to satisfy the maximum number of patients.
We consider a new kidney exchange model which has an interesting feature that is informed by significant technolog- ical advances in organ transplant. The technology concerns immunosuppressants which if given to a patient can make her receptive to kidneys which she is not receptive to by de- fault (Montgomery et al. 2011). We will refer to the model as Kidney Exchange with Immunosuppressants (KEI). Im- munosuppressants (abbreviated as suppressants from here onwards) have been successfully used in Japan and Korea and increasingly being considered in other countries (Chun, Heo, and Hong 2017), even though they are costly and may have side effects.
In this paper, the fundamental research problem that we explore is that of designing mechanisms for kidney ex-
∗UNSW Sydney and Data61 (CSIRO), Australia, haris.aziz@unsw.edu.au
†Hungarian Academy of Sciences, Centre for Economic and Regional Studies, Institute of Economics, Hungary cseh.agnes@krtk.mta.hu
change with immunosuppressants that satisfy desirable com- putational, incentive and monotonicity properties. A naive way of using suppressants is to clear the classic kidney ex- change market without using them and then give suppres- sant to the patients who are left. However, there can be more efficient ways of giving suppressant to particular patients and then implementing exchanges of kidneys to facilitate as many transplants as possible. At first sight, the two-stage and connected process of using foresight to first giving suppres- sants to suitable patients and then finding a matching that satisfies suitable social objectives appears to be a complex problem. We design a flexible algorithmic approach for the problem.
Our contributions are as follows.
• We formalize a general model of kidney exchange with immunosuppressants that features compatible, half- compatible, and incompatible kidneys, and which allows for allocations as a result of multi-way exchanges. We then initiate a computational study of kidney exchange with immunosuppressants. Prior mechanism design work on the subject either only allows pairwise exchanges or focuses on a restricted model.
• Our central contribution is modeling important KEI prob- lems in terms of graph algorithms involving minimum cost perfect matchings. Depending on how we set the edge costs in the graph problem, we can find in poly- nomial time, allocations corresponding to several impor- tant objectives. The objectives include maximizing the to- tal number of transplants and given that maximizing the number of compatible transplants. Among the list of ob- jectives captured by our algorithmic framework, we defer the choice of the exact objective to the policy-makers.
• We then focus on the problem where there is an upper bound on the number of suppressants that can be used. We present a polynomial-time algorithm for maximizing the number of transplants for a restricted model that we refer to as the silver bullet model. In the model, once a patient has been given a suppressant, then the patient can take any kidney. For our general model in which certain kidneys are inherently incompatible, we show that the problem of maximizing the number of transplants polynomial-time
reduces to an interesting generalized matching problem whose complexity has been open for years.
• We also study axioms for our model. If patients prefer a transplant without potent suppressants and there is a central budget for these suppressants, then we show that strategyproofness, individual rationality, and a very weak form of efficiency called unanimity are incompatible. We also show that this impossibility disappears if we consider coarse preferences or do not impose hard upper bounds on the number of suppressants used.
Some of the techniques that we use such as to capture strong individual rationality, achieve strategyproofness, han- dle pairwise exchanges etc. are of independent interest and can be applied to a host of other problems in matching mar- kets.
Related Work
Kidney exchange is one of the major research topics in matching market design (S¨onmez and ¨Unver 2011; Abra- ham, Blum, and Sandholm 2007; Hatfield 2005; Roth, S¨onmez, and ¨Unver 2005a; Bir´o, Manlove, and Rizzi 2009).
In many of the papers, the algorithms only allow exchange cycles of limited size due to logistical and other constraints.
In this paper, we allow exchange cycles of any size. Note that for any exchange cycle bounds that are three or more, even the kidney exchange problem in the traditional model without immunosuppressants is NP-hard (Abraham, Blum, and Sandholm 2007).
The use of suppressants to facilitate more efficient kid- ney exchange has been discussed in medical circles (see, e.g. Abramowicz et al. (2018)). The two market design pa- pers directly relevant to our work are ones where kidney ex- change with immunosuppressants has been mathematically modeled (Chun, Heo, and Hong 2017; Andersson and Kratz 2019). Chun, Heo, and Hong (2017) prove a couple of im- possibility results as well as an exchange mechanism with some desirable monotonicity properties. They assume that once suppressants are administered to a patient, she can take a kidney from any donor. We consider a more general model in which half-compatibility is specific to particular patient- donor pairs.
Andersson and Kratz (2019) consider a more general model in which only certain donor-patient pairs can be made compatible after giving suppressants to the patient. They fo- cus onpairwisekidney exchange (Roth, S¨onmez, and ¨Unver 2005b) and provide some properties of half-compatibility priority matchings and present an efficient computational method for finding them. They also analyze the welfare im- plications of pairwise kidney exchange over the blood group barrier, both theoretically and via a simulation study. Our pa- per goes beyond the pairwise exchange model and presents results that can use longer cycles. We also show how our general results that do not impose restrictions on the ex- change cycles can be adapted for the case of pairwise ex- change.
Model and Concepts
A kidney exchange market is a tuple(P, D, C, H, I)where P ={p1, p2, . . . , pn}is a set ofnpatients (agents) andDis the set of donors. Some patients and donors come in pairs;
others come single. If a patientpienters the market together with her donor, then the donordiwill be equipped with the same indexi.
Each patientpi partitions the donorsDinto setsCi,Hi, andIi. The setCi is the set of donors whom patientpi is compatible with. The setHiis the set of donorspiis half- compatible with. Half-compatibility means that if a sup- pressant is givenpi, thenpi can accept a kidney from any donor inHi. Donors in the setIiare incompatible with pa- tientpieven ifpiis given a suppressant. These partitions at each patient form the collections of setsC= (C1, . . . , Cn), H = (H1, . . . , Hn), andI = (I1, . . . , In)in the input. For simplicity, we assume that compatible patient-donor pairs are not present, because their transplant is arranged outside of the system.
Anallocationassigns each patientpi at most one donor who is either in Ci or inHi. Patients who are assigned a half-compatible donor receive suppressants.
We consider three models.
1. BM (Baseline model): for eachpi∈P,Hi=∅.
2. SBM (Silver bullet model): for eachpi∈P,Ii=∅.
3. GM (General model).
The baseline model coincides with the traditional kidney exchange model in which immunosuppressants are not con- sidered. SBM is the model in which we assume that if a pa- tient is given a suppressant then she will be able to receive any kidney in the market. GM is the general model that also allows for some kidneys being inherently incompatible for a patient even if she has been given suppressants. Unless spec- ified, we will focus on GM. In some cases, we will present some results that hold for the silver bullet model.
As far as a patient or the social designer is concerned, there are two types of preferences. We will treat matching with incompatible donors to be infeasible.
1. Coarse preferences: a patient is indifferent between a compatible donor and a half-compatible donor along with a suppressant, and prefers both options over no transplant at all.
2. Refined preferences: a patient prefers compatible donors over half-compatible donors along with a suppressant, which are preferred over no transplant at all.
Coarse preferences have the underlying assumption that a patient has no significant cost (in terms of money or side- effects) when receiving a half-compatible kidney.
Based on the preference relation one can define concepts such as Pareto optimality. Chun, Heo, and Hong (2017) con- sidered SBM and coarse preferences. They also consider re- fined preferences when defining a monotonicity property.
Andersson and Kratz (2019) considered GM and refined preferences.
A patient who is assigned a compatible donor or a half- compatible donor along with a suppressant is referred to as
satisfied. Our general goal is to satisfy the maximum number of patients while minimizing the need of suppressants. We will consider the following feasibility condition for all al- locations, which captures a natural individual rationality re- quirement: either a patient donates her donor’s kidney to the market and gets a strict improvement or she and her donated kidney are not part of any allocation. We will refer to this condition asstrong individual rationality (S-IR).Notice that a patient who enters the market with a half-compatible donor improves her situation if she is assigned her own or another half-compatible donor along with a suppressant. Also, S-IR implies that a donor assigned to a patient will only donate a kidney if her patient also receives one. A weaker require- ment isindividual rationality (IR)whereby no patient who has a compatible kidney donor ends up with no transplant.
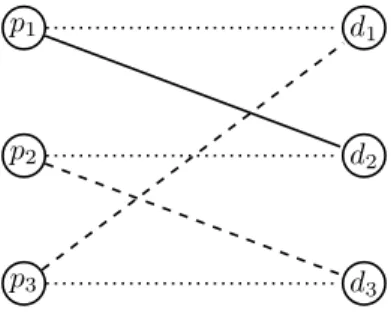
Example 1. Consider a kidney exchange problem in which there are three patientsp1, p2, p3with corresponding donors d1, d2, d3. No patient’s donor has a kidney compatible with the patient. Patient p1 finds the kidney of d2 compatible, whiled3 ∈ H2 and d1 ∈ H3. The problem is captured in Figure 1.
If immunosuppressants are not allowed, then no patient will be able to get a kidney without violating S-IR. Suppose the system has 2 suppressants available. In that case, one suppressant can be givenp2and another top3. Thenp1can take a compatible kidney ofd2,p2takes a half-compatible kidney ofd1andp3takes a half-compatible kidney ofd3.
p1
p2
p3
d1
d2
d3
Figure 1: A bipartite matching view of KEI. The dashed lines indicate half-compatible edges. Solid edges indicate compatibility edges. Dotted edges indicate a patient-donor pair.
A general graph theoretic approach
We construct a general bipartite matching based model cap- turing the most basic features of kidney exchange markets.
It guarantees that each donor gives at most one kidney, each patient receives at most one kidney, and the donor in a pair is only part of the exchange if her patient receives a kid- ney. This framework gives us a set of feasible solutions for the problem. Then, by adding edge weights to the graph and finding a maximum weight matching, an optimal solution can be calculated. We specify a set of possible edge weights that can serve a large variety of goals of the decision maker, such as cost-efficiency or saving as many lives as possible.
Matching model
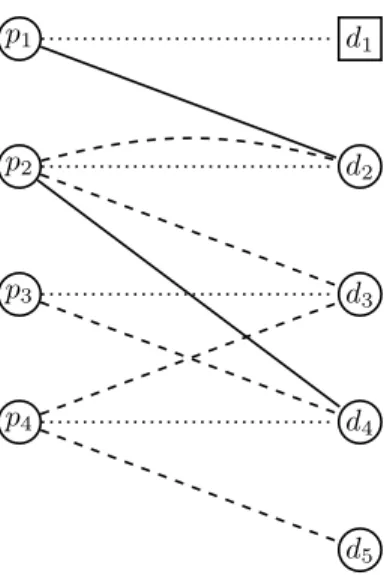
We build a bipartite graph to the instance (P, D, C, H, I), see Figure 2. For convenience, we distinguish between pa- tients with and without a related donor, who will form the setsP2andP1, respectively. Analogously,D1is the set of altruistic donors, while donors inD2enter the market along with their related patient inP2. The vertices of our graph are of three types.
• To each patientpi ∈P, we construct a patient vertexpi.
• To each donordi∈D, we construct a donor vertexdi.
• We construct a dummy donor vertexdj for each patient pj∈P1.
If a donor-patient pair who applies for the scheme to- gether, then the patient and donor and given the same index:
we refer to them aspianddifor some fixedi. Patients with- out a donor share the same index with their dummy donor vertex. Altruistic donors in the system do not have such a fixed-index pair.
The edges of the graph are as follows.
• Each patientpi ∈ P2 is connected to her related donor di∈D2via aprivate edge.
• Each patientpj ∈ P1is connected to her dummy donor djvia a private edge.
• A donordihas acompatibleedge to a patientpj, wherei might be equal toj, ifdi∈Ci.
• A donor di has a half-compatible edge to a patientpj, whereimight be equal toj, ifdi∈Hi.
The three kinds of edges will play distinct roles when assigning weights to them. Private edges represent no transplant, while compatible and half-compatible edges stand for compatible and half-compatible transplants taking place. Notice that a patient and her donor forming a half- compatible pair are connected by two parallel edges, one private and one half-compatible.
Our goal is to calculate a P-complete matching in the constructed graph. ByP-complete, we mean that each pa- tient needs to be matched in the matching. A matching and the corresponding allocation are in trivial one-to-one corre- spondence with each other. A patient matched to her dummy donor or to her incompatible donor represents no transplant.
The matching property ensures that each patient receives one kidney at most, and each donor also donates one kid- ney at most. Since a patient pi ∈ P2 is only connected to di∪Ci∪Hi, and we restrict our attention to P-complete matchings only, pi is either satisfied or she remains un- matched, together withdi.P-completeness ensures the fol- lowing natural consequence of S-IR: either a patient uses her donor’s kidney and gets a strict improvement, or she and her donated kidney are not part of any allocation.
With coarse preferences assumed, there might be restric- tions on the compatibility of a kidney given to a patient in a patient-donor pair who enter the market together. To en- sure that a half-compatible pair only participates in a cross- donation or a cycle if and only if the patient receives a com- patible kidney, we only need to delete the edges running from the patient to all half-compatible donors.
p1
p2
p3
p4
d1
d2
d3
d4
d5
Figure 2: Example instance for our bipartite graph. Here, P1={p1}, and thus,d1is a dummy donor. The only altru- istic donor isd4, forming setD1. Dotted edges are private, dashed edges mark half-compatible donations, and finally, solid edges mark compatible donations.
Objectives
We offer a variety of different weight functions defined on the edges of our graph. Each weight function serves a justi- fiable goal, as we argue later.
Table 1 summarizes the options for defining the weight function on each edge (pi, dj), depending on the type of the edge. We assume N to be a sufficiently large integer.
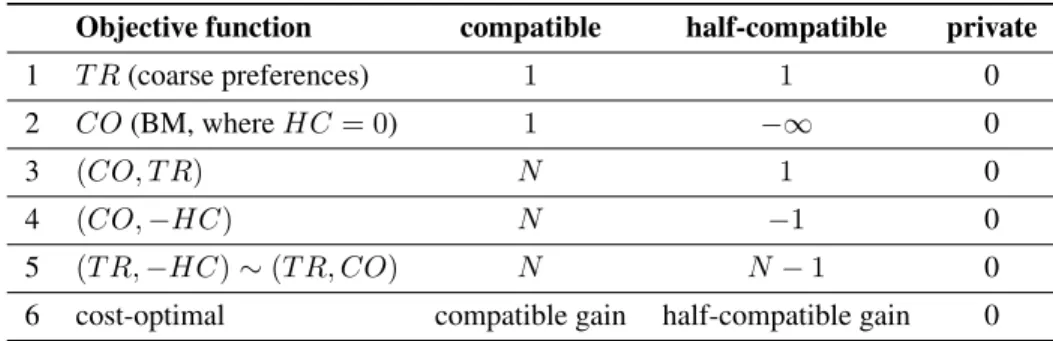
In an allocation, we denote the number of patients receiv- ing a kidney from a compatible donor byCO, the number of patients receiving a kidney from a half-compatible donor byHC, while the total number of patients receiving a kid- ney byT R = CO+HC. Our objective functions are to be maximized in the lexicographic sense, e.g.(T R,−HC) maximizes the number of transplants in total, and subject to this, it minimizes the number of half-compatible transplants.
Our objective functions can achieve the following.
1) The number of transplants is maximized if each pair cho- sen for surgery contributes weight1, while no transplant adds no weight to the matching.
2) The number of transplants is maximized in the baseline model, if half-compatible donations are forbidden due to their infinitely large negative weight, and each compati- ble donation contributes weight1.
3) If a compatible transplant carries a larger weight than the weight of all half-compatible transplants that can be car- ried out, then the main goal is to maximize the number of compatible donations. Since half-compatible donations do carry some small weight, their number will be maxi- mized, but only subject to the first objective.
4) Since half-compatible donations now carry a small nega- tive weight, they are only to be planned if they enable ex- tra compatible transplants. However, any number of half-
compatible donations are welcome if they make only one more compatible donation happen, because we gain a lot in our objective function by addingNjust one more time to it.
5) If compatible and half-compatible donations both carry a large weight, but the latter ones are somewhat less prof- itable, then the maximum number of donations will be calculated, and subject to this, as few half-compatible do- nations will be planned as possible.
6) The most general version is when we set an arbitrary weight to each transplant. This weight can express the expected utility in terms of life expectancy, risks, health- care savings, and it can differ for each pair. A max weight solution corresponds to a maximum utility allocation.
Our goal is to compute a maximum weight P-complete matching in the graph. A maximum weight matching can be computed in strongly polynomial time (Munkres 1957).
To take care ofP-completeness, or equivalently, maximum size, one only needs to apply the standard weight modifica- tion, in which each edge gets an additional uniform weight that is larger than the sum of the original weights. As a re- sult, we obtain the following central result.
Theorem 1. For each of the objectives 1) to 6), there exists a strongly polynomial-time algorithm to find an allocation achieving those objectives.
Fix upper bound on HC
Immunosuppressants are highly useful to allow half- compatible kidneys to be allocated. However, they are not only extremely expensive but they also have undesirable side-effects. Given these issues, the market designer may wish to specify a fixed upper quota onHC=h, and wishes to maximize transplants subject toh. We show that even with an upper bound, we can solve the following central problem.
h-ALLKEI
Input: KEI instanceG = (N, O, e, A)and integer m.
Question:Is there an allocation satisfying all the patients with at mosthpatients using immunos?
Theorem 2. h-ALLKEI can be solved in polynomial time even for the general model.
Proof. Construct the corresponding graph as defined in the previous section, but only keep compatible or half- compatible edges. We want to check whether there exists aP-complete matchingMsuch that|M∩E0| ≤hand each patient gets a compatible or half-compatible allocation. This question can be answered by solving a simple weightedP- complete matching problem. In the graph with compatible or half-compatible edges only, we give each half-compatible edge weight 0 and each compatible edge weight 1. The weight of any P-complete matchingM isn− |M ∩E0|.
The maximum weight matching in this instance has weight at leastn−hif and only if there is an allocation using at mosthimmonosuppressants.
Objective function compatible half-compatible private
1 T R(coarse preferences) 1 1 0
2 CO(BM, whereHC= 0) 1 −∞ 0
3 (CO, T R) N 1 0
4 (CO,−HC) N −1 0
5 (T R,−HC)∼(T R, CO) N N−1 0
6 cost-optimal compatible gain half-compatible gain 0 Table 1: The variety of possible cost functions serving different goals.
A more general version ofh-ALLKEI is the following problem.
h-MAXKEI
Input: KEI instance (P, D, C, H, I) and integers t andh.
Question:Is there an allocation giving at leasttpatients a compatible donor with at mosthpatients us- ing immunos?
Our next result is thath-MAXKEI can be solved in poly- nomial time in the Silver Bullet Model.
Theorem 3. h-MAXKEIcan be solved in polynomial time in the Silver Bullet Model.
Proof. If we have a model that excludes incompatibility, as the Silver Bullet Model, then a modification of the built graph solves this problem. The modification of the graph is as follows. The goal is to decompose each half-compatible edge into a set of paths, and then lead these paths through a gadget that will regulate the maximum number of used half-compatible edges through its size. First we add this gad- get, which consists of 2h new vertices in sets A and B, and a set of h disjoint edges of weight 0 between them:
{(a1, b1),(a2, b2). . . ,(ah, bh)}. Then we replace each edge (pi, dj)in the half-compatible class by a set of edges con- necting pi to each of a1, a2, . . . , ah, and dj to each of b1, b2, . . . , bh. The weight on these edges are set to be half of the original weight of the replaced half-compatible edges.
The rest of the graph remains unchanged. For an example, see Figure 3, which is a transformed version of our example instance from Figure 2, withh= 2.
Claim 1. A maximum weight(P∪A∪B)-complete match- ing in the above-described graph corresponds to an allo- cation maximizing the weight subject toHC ≤ h, if half- compatible donations are less desirable than compatible do- nations according to the weight function.
Proof. Due to the size of the gadget, no (P ∪ A∪ B)- complete matching allows more thanhvertices inP to be matched along their edges to the gadget. Moreover, the num- ber of vertices inPthat are matched to a vertex inAequals the number of vertices inDthat are matched to a vertex in B, because a (P ∪A∪B)-complete matching covers all vertices in the gadget. These vertices inP andD will be
p1
p2
p3
p4
d1
d2
d3
d4
d5
a1
a2
b1
b2
Figure 3: Substituting all half-compatible edges by a gadget allowing at mosth= 2half-compatible donations.
the agents participating in half-compatible donations. Due to the assumptions of the Silver Bullet Model, any perfect matching on them is a set of executable transplants. The rest of the transplants are chosen based on the maximum weight matching criterion.
Notice that it is possible that a donor and a patient are connected via a 3-path through the gadget and via a direct compatible edge as well, but for all weight functions where half-compatible donations are less desirable than compatible donations (all our weight functions except for 1 and possi- bly 6), the path will carry the lower weight. Therefore, no (P ∪A∪B)-complete matching using such edges in the gadget can be of maximum weight.
One can calculate a maximum weight matching among all(P∪A∪B)-complete matchings using the usual weight transformation of adding a large uniform weight to all edges incident to any vertex in P ∪A∪B. This completes the proof.
This construction in the proof of Theorem 4 answers a question more general thanh-MAXKEI. It actually decides
whether there is an allocation of weight at leasttwhile using at mosthsuppressants.
Theorem 4. In the silver bullet model, a minimum cost S-IR allocation can be computed in polynomial-time even if there is an upper bound on the number of suppressants that can be used.
Next, we identify connections ofh-MAXKEI with a spe- cial case of budgeted matching, a well-studied graph prob- lem of unknown complexity.
UNIT-COSTBUDGETEDMATCHING
Input: Bipartite graphG = (A∪B, E),E0 ⊆ E, edge weights, and an integerh.
Question:Find a maximum weight matching M such that|M∩E0| ≤h.
UNIT-COST BUDGETED MATCHING admits a PTAS (Berger et al. 2011; Mastrolilli and Stamoulis 2012). Berger et al. (2011) observe that for polynomial weights and costs (here we set the costs to be 1), BUD-
GETEDMATCHINGis very unlikely to be NP-hard, because it would imply RP=NP. However, after several decades, the problem of finding a deterministic algorithm to solve this problem is still open.
We now show howh-MAXKEI reduces to UNIT-COST
BUDGETEDMATCHING.
Lemma 1. h-MAXKEIpolynomial-time reduces toUNIT- COSTBUDGETEDMATCHING.
Proof. We set E0 to be the set of half-compatible edges, while G and the upper bound h are identical in the two problems. To make sure that the maximum weight matching in UNIT-COSTBUDGETEDMATCHINGisP-complete, we modify the edge weightsw(e)fromh-MAXKEI as follows.
w0(e) :=w(e) +n
The weight of matchingM is thusw0(M) := w(M) + n· |M|. Sincew(e)≤1, matchings of larger size are bound to have a larger weight as well, thusw0(M)is maximized by a P-complete matching. Within the set ofP-complete matchings,w0is maximized in the maximum weight match- ing according tow.
Notice that the weight transformation can be extended to other objective functions as well:
w0(e) :=w(e) +n·wmax(e).
Regarding parametrized complexity, our trivial parameter ish, the number of suppressants available. Ifhis small, then one can try which h half-compatible edges are used, and then search for a maximum weight allocation in the rest of the instance built out of compatible and private edges only.
Axioms
We consider some natural axioms for allocation algorithms (mechanisms). A mechanism isutilitarian (UTIL)if it max- imizes the total number of transplants (satisfied patients). A
mechanism isPareto optimal (PO)if it returns a Pareto opti- mal allocation among the set of feasible outcomes. A mech- anism isstrategyproof (SP), if no patient can misreport her compatibility relation to obtain a more preferred allocation.
An extremely weak form of Pareto optimality is calleduna- nimity (UNAN) that requires that a mechanism returns an allocation that gives each agent a fully compatible kidney whenever such an allocation exists. We discuss that our flex- ible objective-based algorithmic approach satisfies many of these properties.
Utilitarianism and Pareto optimality
Only objective functions 1, 2, and 5 reach UTIL, since they are the only ones that maximize the number of transplants in total.
PO (under coarse preferences) means that no inclusion- wise larger allocation exists. Only objective functions 1, 2, and 5 satisfy this.
PO (under refined preferences) means that no other allo- cation keeps the set of compatible donations, while extend- ing the set of donations or upgrading a half-compatible do- nation to a compatible one. Only objective function 1 fails this: PO (under refined preferences) is defined for refined preferences, while objective function 1 is defined for coarse preferences.
UNAN is implied by both PO (under refined preferences) and PO (under coarse preferences), and thus all objective functions satisfy it.
Strategyproofness
Next, we consider strategic properties. We identify a funda- mental incompatibility between strategyproofness and una- nimity when agents have refined preferences and there is an upper bound on the number of suppressants.
Theorem 5. Even for 3 patients, the combination SP (under-refined-preferences), UNAN, and IR are incompati- ble. Even for 3 patients, the combination SP (under-refined- preferences), UNAN, and S-IR are incompatible.
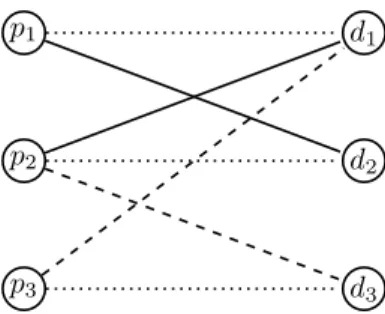
Proof. Consider the problem instance depicted in Figure 4.
Suppose there is exactly 1 suppressant available. Then PO requires that all three patients are matched: 1 getsd2, 2 gets d3and3getsd1. Suppose patient 2 misreports and reportsd3
as imcompatible. In that case, IR and PO imply that patient 2 getsd1 and patientp1 getsd2, which is an improvement forp2with respect to refined preferences.
Since UTIL implies PO (under coarse preferences), we also derive the following statements.
Corollary 1. The combination SP (under-refined- preferences), PO (under refined preferences), and IR (or S-IR) are incompatible. The combination SP (under- refined-preferences), PO (under coarse preferences), IR (or S-IR) are incompatible.
If there is no upper bound on the number of suppres- sants available, then PO, IR, and SP are compatible under refined or coarse preferences. This can be proved by reduc- ing our problem to that housing markets with trichotomous
p1
p2
p3
d1
d2
d3
Figure 4: A KEI instance for the proof of Theorem 5. The dashed lines indicate half-compatible edges. Solid edges in- dicate compatibility edges. Dotted edges indicate a patient- donor pair.
preferences. Even for general weak preferences, suitable ex- tensions of TTC achieve all the axioms(see, e.g. Saban and Sethuraman (2013)). The agents have trichotomous prefer- ences: fully compatible kidneys are most preferred, half- compatible kidneys are second most preferred, and incom- patible kidneys are least preferred.
Theorem 6. If there is no upper bound on the number of suppressants available, then there exists an algorithm that is PO, IR, and SP.
Our next insight is that as long as we consider strat- egyproofness with respect to coarse preferences, we can achieve all the objectives in conjunction with strategyproof- ness. The key is to overlay the priority mechanism over the algorithm that optimizes one of the global objectives while constrained to S-IR. The result follows from similar insights as that of Aziz (2019) and Hatfield (2005). The desirabil- ity of the overlay of the priority mechanism is that it can take as a black box any given algorithm that optimizes some criterion over the set of feasible allocations. In the overall algorithm, first, an optimal valueW of a feasible matching is computed. Then, we go over an order of agents and check whether the agent in question can be satisfied in some opti- mal allocation which still satisfying all the preceding agents who could also be satisfied in some optimal allocation. It can be proved that an agent has no incentive to misreport her preferences in the Coarse preference model.
Theorem 7. For all the objectives in the paper, there ex- ists an algorithm that is SP (under coarse preferences) and meets the objective subject to S-IR and upper bound on the number of suppressants.
Pairwise exchanges
In this section, we restrict our attention to pairwise ex- changes. In many countries, the organ exchange programs only consider pairwise exchanges (Andersson and Kratz 2019). In this case, a simpler model suffices. The only pos- sible transplants are cross-donations between two patient- donor pairs, and an altruistic donor donating a kidney to a patient, who might come with or without a donor.
We build a simple graph for these sorts of donations. First, we represent each patient-donor pair, each altruistic donor,
Algorithm 1Priority Overlay
1 Construct graphGwith appropriate edge weights.
2 Compute a maximum weightA-complete matching of G. Let the weight of the matching beW.
3 Take a permutation (ordering)πof the elements inN.
Denote byπ(i)thei-th element in the ordering.
4 fori=1 tondo
5 whiletarget=falsedo
6 Remove fromGeach ofpπ(i)’s edges except the most preferred. Compute the maximum weightA- complete matching ofG. If the weight is less than W or if there does not exist aA-complete match- ing, then put back the removed edges but remove most preferred edges in the graph. Otherwise set target to true.
7 end while 8 end for
9 Compute a maximum weight complete matchingM of G. Consider the allocationxin which each patientpi∈ P gets a donor that it is matched to inM. Ifpi ∈P is matched to a dummy donor, its allocation is null.
10 return (x(1), . . . , x(n))
and each patient without a donor as a vertex. Then we con- nect two of these vertices if a cross-donation or an altruistic donation, as described above, is possible, because all donors are either compatible or half-compatible to the prospective recipient of the kidney. The edge carries the weight of the two transplants altogether, where transplant weights are cal- culated based on the relevant row of Table 1. We look for a not necessarily perfect maximum weight matching.
Conclusions
Immunosuppressants constitute one of the major develop- ments in the transplant of organs. We have studied a gen- eral model of kidney exchange that also models the use of immunosuppressants. We envisage further work on both al- gorithmic as well as market design aspects of the problem.
The most striking open question is undoubtedly to determine the complexity of MAXKEI in the general model. By solv- ing that problem, one might even reach progress in budgeted matching, a long-standing open problem in matching theory.
Finally, we note that some of our insights may be usable for other organ markets that involve lungs (Luo and Tang 2015), livers, or even a combination of these and other or- gans (Dickerson and Sandholm 2017).
References
Abraham, D.; Blum, A.; and Sandholm, T. 2007. Clear- ing algorithms for barter exchange markets: Enabling na- tionwide kidney exchanges. InProceedings of the 8th ACM Conference on Electronic Commerce (ACM-EC), 295–304.
ACM Press.
Abramowicz, D.; Oberbauer, R.; Heemann, U.; Viklicky, O.;
Peruzzi, L.; Mariat, C.; Crespo, M.; Budde, K.; and Oniscu, G. C. 2018. Recent advances in kidney transplantation: a
viewpoint from the Descartes advisory board. Nephrology Dialysis Transplantation33(10):1699–1707.
Andersson, T., and Kratz, J. 2019. Pairwise kidney exchange over the blood group barrier.The Review of Economic Stud- ies.
Aziz, H. 2019. Strategyproof multi-item exchange un- der single-minded dichotomous preferences. arXiv preprint arXiv:1905.10778.
Berger, A.; Bonifaci, V.; Grandoni, F.; and Sch¨afer, G. 2011.
Budgeted matching and budgeted matroid intersection via the gasoline puzzle. Mathematical Programming 128(1- 2):355–372.
Bir´o, P.; Haase-Kromwijk, B.; Andersson, T.; ´Asgeirsson, E. I.; Baltesov´a, T.; Boletis, I.; Bolotinha, C.; Bond, G.;
B¨ohmig, G.; Burnapp, L.; et al. 2019. Building kidney exchange programmes in European overview of exchange practice and activities.Transplantation103(7):1514–1522.
Bir´o, P.; Manlove, D. F.; and Rizzi, R. 2009. Maxi- mum weight cycle packing in optimal kidney exchange pro- grams. Discrete Mathematics, Algorithms and Applications 1(4):499–517.
Chun, Y.; Heo, E. J.; and Hong, S. 2017. Kidney exchange with immunosuppressants. Technical report, Vanderbilt Uni- versity Department of Economics.
Dickerson, J. P., and Sandholm, T. 2017. Multi-organ ex- change. Journal of Artificial Intelligence Research60:639–
679.
Hatfield, J. W. 2005. Pairwise kidney exchange: Comment.
Journal of Economic Theory125:189–193.
Luo, S., and Tang, P. 2015. Mechanism design and imple- mentation for lung exchange. InIJCAI, 209–215.
Mastrolilli, M., and Stamoulis, G. 2012. Constrained match- ing problems in bipartite graphs. InInternational Sympo- sium on Combinatorial Optimization, 344–355. Springer.
Montgomery, R. A.; Lonze, B. E.; King, K. E.; Kraus, E. S.;
Kucirka, L. M.; Locke, J. E.; Warren, D. S.; Simpkins, C. E.;
Dagher, N. N.; Singer, A. L.; et al. 2011. Desensitization in hla-incompatible kidney recipients and survival. New Eng- land Journal of Medicine365(4):318–326.
Munkres, J. 1957. Algorithms for the assignment and trans- portation problems.Journal of the Society for Industrial and Applied Mathematics5(1):32–38.
Roth, A. E.; S¨onmez, T.; and ¨Unver, M. U. 2005a. A kidney exchange clearinghouse in New England. American Eco- nomic Review95(2):376–380.
Roth, A. E.; S¨onmez, T.; and ¨Unver, M. U. 2005b. Pairwise kidney exchange.Journal of Economic Theory125(2):151–
188.
Saban, D., and Sethuraman, J. 2013. House allocation with indifferences: a generalization and a unified view. InPro- ceedings of the 14th ACM Conference on Electronic Com- merce (ACM-EC), 803–820. ACM Press.
S¨onmez, T., and ¨Unver, M. U. 2011. Matching, allocation, and exchange of discrete resources. In Benhabib, J.; Jack-
son, M. O.; and Bisin, A., eds., Handbook of Social Eco- nomics, volume 1. Elsevier. chapter 17, 781–852.