Stability and Hopf bifurcation of a diffusive

Stability and Hopf bifurcation of a diffusive

Gompertz population model with nonlocal delay effect

Xiuli Sun

, Luan Wang

and Baochuan Tian

1College of Mathematics, Taiyuan University of Technology, Taiyuan, 030024, China

2Faculty of Economics, Shanxi University of Finance & Economics, Taiyuan, 030006, China

3Beijing Polytechnic, Beijing, 100176, China

Received 12 September 2017, appeared 4 May 2018 Communicated by Ferenc Hartung

Abstract. In this paper, we investigate the dynamics of a diffusive Gompertz popula- tion model with nonlocal delay effect and Dirichlet boundary condition. The stability of the positive spatially nonhomogeneous steady-state solutions and the existence of Hopf bifurcations with the change of the time delay are discussed by analyzing the distribution of eigenvalues of the infinitesimal generator associated with the linearized system. Then we derive the stability and bifurcation direction of Hopf bifurcating peri- odic orbits by using the normal form theory and the center manifold reduction. Finally, we give some numerical simulations.

Keywords: reaction–diffusion, nonlocal delay, Hopf bifurcations, stability.

2010 Mathematics Subject Classification: 35B32, 35B35, 35B10, 37K50, 37G10, 37G15.

1 Introduction

The Gompertz equation is one of the models that are often used to describe the dynamics of the populations, including cellular populations of tumour growth, see [18,26,28–30,37]. The basic Gompertz model has the following form

V˙(t) =−rV(t)lnV(t)

K , V(0) =V0,

where V is simply the number of cells/individuals and K is the plateau number of cells/in- dividuals. It was proposed by Benjamin Gompertz in 1825 for the first time (see [18]). Since Laird et al. [30] showed that the Gompertz model could describe the normal growth of an organism such as the guinea pig over an incredible 10000-fold range of the growth in [26], the Gompertz equation is often used in the formulation of equations describing the population dy- namics and to describe the inner growth of tumour. In order to better describe the investigated

BCorresponding author. Email: sxl891123@163.com

phenomena, the time delays are often introduced into models [1–4,7,12–17,31,33,34,36]. Lit- erature [35] introduced the discrete time delay to the classical Gompertz model in different ways and obtained the following four models with delays:

V˙(t) =−rV(t)lnV(t−τ)

K ;

V˙(t) =−rV(t−τ)lnV(t−τ)

K ;

V˙(t) =−rV(t−τ₁)lnV(t−τ₂)

K ;

and it also introduced another model with two delays in which it separated two right-hand side terms describing two different processes, namely, the term rlnKV(t)(with K 6= 1) de- scribing the growth of the population and the term−rV(t)lnV(t)describing the competition between individuals, and by using such biological interpretation, it proposed the model with two delays :

V˙(t) =rlnKV(t−τ₁)−rV(t−τ₂)lnV(t−τ₂),

where τ₁ and τ₂ reflect the delay of growth and competition, respectively. In [35], it showed that the model’s dynamics depend crucially on the place where the delay/delays are included.

As the placement of delays in the models reflects the delays of different biological processes to their stimuli, so this conclusion is not surprising from the biological point of view. The mathe- matical and numerical analysis presented in it could help researchers who want to incorporate the Gompertz equation with delays into their models to choose the most appropriate version of the equation.

Moreover, in mathematical biology, many models of population dynamics can be described by the delayed reaction–diffusion equations [6,8,9,20]. In recent years, some researchers [27,32,39,41] have worked on the following reaction–diffusion equations with delay effect:







∂u

∂t =_d∆u+u f(u(x,t−τ),v(x,t−τ)),

∂v

∂t =_d∆v+vg(u(x,t−τ),v(x,t−τ)).

In a reaction–diffusion model with time-delay effect, the individuals which located at x in previous times may not be at the same point in space presently. So the diffusion and time delay are always not independent of each other for a delayed reaction–diffusion model (see References [5,10,11,19,21,22,24,40]). Thus, it is more reasonable to consider the diffusive type model with nonlocal delay. For instance, Britton [5] introduced the following model:

∂u(x,t)

∂t =_d∆u(x,t) +λu(x,t)(1+αu−(1+α)g∗ ∗u), where

g∗ ∗u=

Z _t

−_∞ Z

Ωg(x,y,t−s)u(y,s)dyds,

and analyzed the traveling waves on unbounded domain. Then Gourley and Britton [19] pro- posed a predator–prey system with spatiotemporal delay. In [10], Chen and Yu analyzed the following reaction–diffusion equation with spatiotemporal delay and homogeneous Dirichlet boundary condition:







∂u

∂t = d∂²u

∂x² +λuF(u, Z _∞

0

Z _π

0 G(x,y,s)f(s)u(y,t−s)dyds), x∈(0,π), t>0, u(x,t) =0, x =0,π, t >0,

where

G(x,y,t) = ² π

∑

e^−dk2tsinkxsinky, and f(t)is the delay kernel, satisfying f(t)≥0, fort≥0, andR∞

0 f(t)dt=1. It is shown that a positive spatially nonhomogeneous equilibrium can bifurcate from the trivial equilibrium.

Moreover, the stability of the bifurcated positive equilibrium was investigated. And they also proved that, for the given spatiotemporal delay, the bifurcated equilibrium is stable under some conditions, and Hopf bifurcation cannot occur. Chen and Yu [11] studied the following general form:







∂u(x,t)

∂t =d∆u+λu(x,t)F

u(x,t), Z

ΩK(x,y)u(y,t−τ)dy

, x ∈_Ω, t >0, u(x,t) =0, x∈ _∂Ω, t>0.

Guo and Yan [24] investigated the following diffusive Lotka–Volterra type population model with nonlocal delay effect:











∂u(x,t)

∂t =d∆u+λu[1−(A₁₁∗u)(x,t−τ)−(A₁₂∗v)(x,t−τ)],

∂v(x,t)

∂t =_d∆v+λv[1−(A₂₁∗u)(x,t−τ)−(A22∗v)(x,t−τ)], for all x∈_Ωandt>0, where A_ij,i,j= 1, 2, are kernel functions and

(A_ij∗f)(x,t) =

Z

ΩA_ij(x,y)f(y,t)dy, i,j=1, 2.

The existence and multiplicity of spatially nonhomogeneous steady-state solutions are ob- tained by using Lyapunov–Schmidt reduction. Through analyzing the distribution of eigen- values of the infinitesimal generator associated with the linearized system, we show the stabil- ity of spatially nonhomogeneous steady-state solutions and the existence of Hopf bifurcation with the changes of the time delay. The stability and bifurcation direction of Hopf bifurcating periodic orbits are derived by the normal form theory and the center manifold reduction.

In this paper, we investigate the following diffusive Gompertz population model with nonlocal delay effect:















∂w(x,t)

∂t =d∆w(x,t) +λw(x,t)

1−ρ(λ)

Z

ΩK(x,y)w(y,t−τ)_lnw(y,t−τ)dy

, x∈ _Ω, t >_0, w(x,t) =0, x∈_∂Ω, t >0,

where w(x,t) is the population density at time t and location x, d > 0 is the diffusion coef- ficient, τ ≥ 0 is the time delay, λ > 0 is a scaling constant, Ωis a connected bounded open domain in Rⁿ (n ≥ 1), with a smooth boundary ∂Ω, and Dirichlet boundary condition is imposed so the exterior environment is hostile, ρ(λ)is the function of λ, K(x,y)is a kernel function which describes the dispersal behavior of the population. The nonlocal growth rate per capita incorporates the possible dispersal of the individuals during the maturation period, hence it is a more realistic model.

We first introduce some notations. Denote X = H²(_Ω)∩H¹₀(_Ω), Y = L²(_Ω), where H₀¹(_Ω) ={u∈ H¹(_Ω)|u(x) =0,x∈∂Ω}. For a spaceZ, we also define the complexification of Z to be Z_C , ^ZLiZ = {x₁+ix₂ | x₁,x₂ ∈ Z}. Denote by C([−τ, 0],Y) the Banach space of continuous mappings from[−τ, 0]intoYequipped with the supremum normkφk= sup_{−τ≤θ≤0}{kφ(θ)k_Y}forφ∈ C([−τ, 0],Y). For a linear operatorL: Z₁ →Z2, we denote the domain ofLbyD(L). For the complex-valued Hilbert spaceY²_C, we use the standard inner producthu,vi=R

Ωu¯^T(x)v(x)dx.

Letλ∗ be the principal eigenvalue of the linear operator−_d∆subject to the homogeneous Dirichlet boundary conditionw = 0 on ∂Ω, and let φbe the corresponding eigenfunction of λ∗ such thatφ(x)>0 for all x∈_Ω.

Throughout the paper, we assume that the kernel functionK(x,y)is a continuous and non- negative function on ¯Ω×_{Ω, and}^¯ R

ΩK(x,y)ϕ(y)dy>0 for all positive continuous functionsϕ onΩ, andρ(λ) =λ−λ∗. Whenρ(λ) =λ−λ∗, the above model becomes















∂w(x,t)

∂t = _d∆w(x,t) +λw(x,t)

×

1−(λ−λ∗)

Z

ΩK(x,y)w(y,t−τ)lnw(y,t−τ)dy

, x∈ _Ω, t >0, w(x,t) =0, x ∈_∂Ω, t>0.

(1.1)

We consider system (1.1) with the following initial condition:

w(x,s) =η(x,s), x∈ _Ω, s ∈[−τ, 0], (1.2) where η ∈ C([−τ, 0],Y). From [25], we know that the operator d∆ generates an analytic strongly positive semigroupT(t)onYwith the domainD(_d∆) =_X.

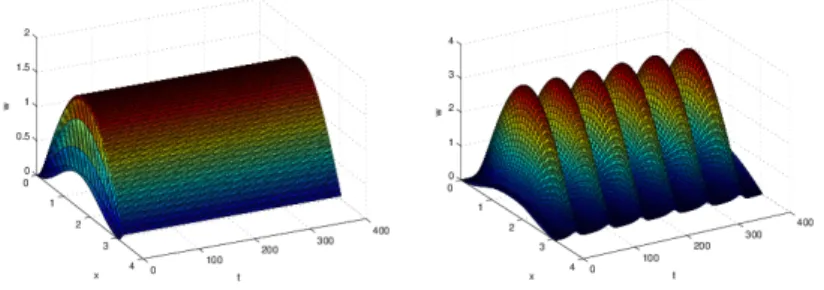
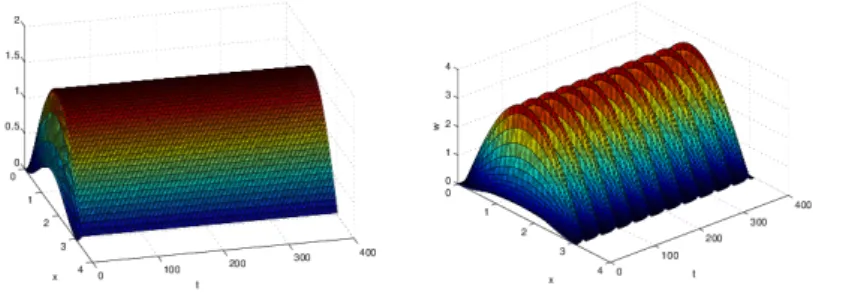
The rest of the paper is organized as follows. In Section 2, we study the existence of the positive spatially nonhomogeneous equilibrium of system (1.1). In Section 3, we consider the eigenvalue problems. In Section 4, we show the stability of the bifurcated positive equilibrium and the occurrence of Hopf bifurcation. In Section 5, the direction of the Hopf bifurcation is given by using normal form theorem and the center manifold theorem. Some numerical simulations are given in Section 6.

2 The existence of the positive spatially nonhomogeneous equilib- rium

In this section, we study the existence of the spatially nonhomogeneous positive steady state solutions of system (1.1), which satisfies the following boundary value problem:







d∆w(x) +λw(x)

1−(λ−λ∗)

Z

ΩK(x,y)w(y)lnw(y)dy

=0, x∈_Ω, w(x) =0, x ∈_∂Ω.

(2.1)

Firstly, we have the following decompositions:

X= N(d∆+λ∗)⊕_X1, Y= N(_d∆+λ∗)⊕_Y1,

where

N(_d∆+λ∗) =span{φ}, X1=

ψ∈ _X|

Z

Ωφ(x)ψ(x)dx=0

, Y1=

ψ∈ _Y|

Z

Ωφ(x)ψ(x)dx=0

.

Then we can obtain the following theorem about the existence of the positive equilibrium solutions of Eq. (2.1) by using the implicit function theorem.

Theorem 2.1. There exist λ^∗ > λ∗ and a continuously differential mapping λ → (ξ_λ,β_λ) from [λ∗,λ^∗]toX1×_R⁺, such that(1.1)has an equilibrium solution

w_λ= β_λ[φ+ (λ−λ∗)ξ_λ], (2.2) whereβ_λ∗ >0satisfies

λ∗β Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)ln(βφ(y))dxdy =

Z

Ωφ²(x)dx, (2.3) andξ_λ∗ is the unique solution of the equation

(_d∆+λ∗)ξ+φ

1−λ∗β_λ∗ Z

ΩK(x,y)φ(y)ln(β_λ∗φ(y))dy

=0. (2.4)

Proof. Sinced∆+λ∗is bijective fromX1toY1andφ

1−λ∗β_λ∗R

ΩK(x,y)φ(y)(_lnβ_λ∗φ(y))dy

∈ Y1, we haveξ_λ∗ is well defined.

Next, we provew_λ is the solution to (2.1). Define g:X1×_R×_R→_Yby g(ξ,β,λ) = (_d∆+λ∗)ξ+φ+ (λ−λ∗)ξ

−λβ[φ+ (λ−λ∗)ξ]

Z

ΩK(x,y)[φ+ (λ−λ∗)ξ]_lnβ[φ+ (λ−λ∗)ξ]dy.

From Eqs. (2.3) and (2.4), we see thatg(ξ_λ∗,β_λ∗,λ∗) =0, and D_(ξ,β)g(ξ_λ∗,β_λ∗,λ∗)[_γ,e] = (d∆+λ∗)γ−λ∗φ

Z

ΩK(x,y)φ(y)(_lnβ_λ∗φ(y) +₁)dye.

HereD_(ξ,β)g(ξ_λ∗,β_λ∗,λ∗)[γ,e]is theFréchetderivative ofgwith respect to(ξ,β).

As _Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)(_lnβ_λ∗φ(y) +₁)dxdy6=_0, we have

φ Z

ΩK(x,y)φ(y)(lnβ_λ∗φ(y) +1)dy6∈_Y1.

SoD_(ξ,β)g(ξ_λ∗,β_λ∗,λ∗)is bijective fromX1×_RtoY. Then from the implicit function theorem, there exist aλ^∗ >λ∗and a continuously differentiable mappingλ7→ (ξ_λ,β_λ)∈_X1×_R⁺such that

g(ξ_λ,β_λ,λ) =0, λ∈[λ∗,λ^∗], which implies thatw_λ solves Eq. (2.1).

3 Eigenvalue problems

Letλ∈ (λ∗,λ^∗], andw_λ be the positive equilibrium solution of (2.1) obtained in Theorem2.1.

Linearizing system (2.1) atwλ, we have















∂v(x,t)

∂t =d∆v(x,t) +λ

1−(λ−λ∗)

Z

ΩK(x,y)w_λ(y)lnw_λ(y)dy

v(x,t)

−λ(λ−λ∗)w_λ(x)

Z

ΩK(x,y)(lnw_λ(y) +1)v(y,t−τ)dy, x∈_Ω, t>0, v(x,t) =0, x∈ _∂Ω, t>0,

(3.1)

Define a linear operatorB(λ):D(B(λ))→_Yby B(λ) =d∆+λ

1−(λ−λ∗)

Z

ΩK(x,y)w_λ(y)_lnw_λ(y)dy

,

with domainD(B(λ)) = X. From [38], the semigroup induced by the solutions of (3.1) has the infinitesimal generatorB_τ(λ)_{given by}

Bτ(λ)ϕ= ϕ,˙ (3.2)

where

D(Bτ(λ)) =

ϕ∈C_C∩C_C¹ : ϕ(0)∈_XC,

˙

ϕ= B(λ)ϕ(0)−λ(λ−λ∗)w_λ Z

ΩK(·,y)(lnw_λ(y) +1)ϕ(−τ)(y)dy

, andC¹_C=C¹([−τ, 0],Y_C).

The spectral set ofB_τ(λ)is

σ(B_τ(λ)) ={µ∈_C:∆(λ,µ,τ)ψ=0, for someψ∈_XC\{0}}, where

∆(λ,µ,τ)ψ:= B(λ)ψ−λ(λ−λ∗)w_λ Z

ΩK(·,y)(lnw_λ(y) +1)ψ(y)dye^−µτ−µψ.

ThenBτ(λ)has a purely imaginary eigenvalueµ=iω(ω6=0)for someτ≥0 if and only if

B(λ)ψ−λ(λ−λ∗)wλ

Z

ΩK(·,y)(lnwλ(y) +1)ψ(y)dye^−iθ−iωψ=0. (3.3) is solvable for some ω > 0, ψ 6= 0 and θ ∈ [0, 2π). So if there exists a pair (ω,θ)such that (3.3) has a solutionψ, then

∆(λ,iω,τn)ψ=0, τn= ^θ+2nπ

ω , n=0, 1, 2, . . .

Next, we will show that for λ ∈ (λ∗,λ^∗], there exists a unique pair (ω,θ) which solves (3.3). Assume that(ω,θ,ψ)is a solution of (3.3) with ψ(6=0)∈_XC. Ignoring a scalar factor,ψ can be represented as

ψ=αφ+ (λ−λ∗)z, hφ,zi=0, α≥0, kψk²_Y

C =α²kφk²_Y

C+ (λ−λ∗)²kzk²_Y

C =kφk²_Y

C. (3.4)

Substituting (2.2), (3.4) andω= (λ−λ∗)hinto (3.3), we obtain the following equation equiv- alent to (3.3):



























f₁(z,α,h,θ,λ):= (d∆+λ∗)z

+ [αφ+ (λ−λ∗)z]

1−λ Z

ΩK(·,y)w_λ(y)lnw_λ(y)dy−ih

−λβ_λ[φ+ (λ−λ∗)ξ_λ]

×

Z

ΩK(·,y)[αφ+ (λ−λ∗)z](lnβ_λ[φ+ (λ−λ∗)ξ_λ] +1)dye^−iθ, f₂(z,α,λ):= (α²−1)kφk²_Y

C+ (λ−λ∗)²kzk²_Y

C.

(3.5)

Note that whenλ=λ∗,

f₂(z,α,λ) =0⇔α=α_λ∗ =1.

We have

f₁(z,α_λ∗,h,θ,λ∗) = (_d∆+λ∗)z+φ

1−λ∗β_λ∗ Z

ΩK(·,y)φ(y)lnβ_λ∗φ(y)dy−ih

−λ∗β_λ∗φ Z

ΩK(·,y)φ(y)(lnβ_λ∗φ(y) +1)dye^−iθ. Hence

f₁(z,α_λ∗,h,θ,λ∗) =_0,

is solvable for some value ofz∈ (_X1)_C,h≥0 andθ ∈[0, 2π)if and only if there exists a pair (h,θ)_withh≥0 andθ ∈[_{0, 2π})_satisfying













 λ∗β_λ∗

Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)(lnβ_λ∗φ(y) +1)dxdycosθ

=

Z

Ωφ²(x)dx−λ∗β_λ∗ Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)lnβ_λ∗φ(y)dy, h

Z

Ωφ²(x)dx =λ∗β_λ∗ Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)(_lnβ_λ∗φ(y) +₁)dxdysinθ.

Solving the above equation, we have

θ_λ∗ =arccos Z

Ωφ²(x)dx−λ∗β_λ∗ Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)lnβ_λ∗φ(y)dy λ∗β_λ∗

Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)(lnβ_λ∗φ(y) +1)dxdy ,

h_λ∗ = λ∗β_λ∗

Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)(_lnβ_λ∗φ(y) +₁)dxdysinθ_λ∗ Z

Ωφ²(x)dx

,

andz_λ∗ ∈(_X1)_C is the unique solution of the following equation (_d∆+λ∗)z+φ

1−λ∗β_λ∗ Z

ΩK(·,y)φ(y)lnβ_λ∗φ(y)dy−ih_λ∗

−λ∗β_λ∗φ Z

ΩK(·,y)φ(y)(lnβ_λ∗φ(y) +1)dye^−iθλ∗ =0.

DefineF: (_X1)_C×_R³×_R→_YC×_RbyF= (f₁,f₂). Then we have the following theorem on the solvability of F=_0.

Theorem 3.1. There exists a continuously differentiable mappingλ7→ (z_λ,α_λ,h_λ,θ_λ)from[λ∗,λ^∗] toX_C×_R³such that F(zλ,α_λ,hλ,θ_λ,λ) =0. Moreover,

(F(z,α,h,θ,λ) =0, α,h≥0, θ ∈[0, 2π). has a unique solution(z_λ,α_λ,h_λ,θ_λ).

The proof is similar to Theorem 2.5 of [8] and we omit it here.

To summarise, we have the following result about the eigenvalue problem.

Corollary 3.2. Forλ∈ (λ∗,λ^∗], the eigenvalue problem

∆(λ,iω,τ)ψ=0, ω≥0, τ≥0, ψ(6=0)∈_XC, has a solution if and only if

ω =ω_λ = (λ−λ∗)h_λ, τ=τn= ^θλ+2nπ

ω_λ , n=0, 1, 2, . . . , (3.6) and

ψ= cψ_λ, ψ_λ =α_λφ+ (λ−λ∗)z_λ,

where c is a nonzero constant, and zλ,α_λ, hλ,θ_λ are defined as in Theorem3.1.

Next, we consider the adjoint operator ofBτ(λ)for later application. Similar as in [8], we see that the adjoint operator is

∆˜(λ,iω,τ)ψ^˜ =B(λ)ψ^˜−λ(λ−λ∗)

Z

ΩK(y,·)w_λ(y)(lnw_λ(x) +1)ψ^˜(y)dye^iωτ+iωψ,˜ which satisfies

hψ,˜ ∆(λ,iω,τ)ψi=h_∆^˜(λ,iω,τ)ψ,˜ ψi, Its point spectrum is the same as that of∆(λ,iω,τ):

σ_p(_∆(_λ,iω,τ)) =σ_p(_∆^˜(_λ,iω,τ))_. We conclude that if the corresponding adjoint equation

B(λ)ψ˜−λ(λ−λ∗)

Z

ΩK(y,·)w_λ(y)(lnw_λ(x) +1)ψ˜(y)dye^iθ˜+iω˜ψ˜ =0, ψ˜(6=0)∈_XC, (3.7) is solvable for some value of ˜ω>0, ˜θ∈ [0, 2π), then

∆˜(_λ,iω, ˜˜ τ_n)ψ˜ =_0, τ˜_n= ^θ˜+2nπ

˜

ω , n=0, 1, 2, . . .

Similarly, for λ∈ (λ∗,λ^∗], there is a unique (ω, ˜˜ θ, ˜ψ)which is the solution to (3.7), ˜ψ(6= 0)∈ X_C. ˜ψcan be represented as

ψ˜ =αφ˜ + (λ−λ∗)z,˜ hφ, ˜zi=0, α˜ ≥0, kψ^˜k²_Y

C =α˜²kφk²_Y

C + (λ−λ∗)²kz˜k²_Y

C =kφk²_Y

C. (3.8)

Substituting (3.8) and ˜ω = (λ−λ∗)h^˜ into (3.7), we obtain the following equation equivalent to (3.7):































f˜₁(z, ˜˜ α, ˜h, ˜θ,λ):= (_d∆+λ∗)z˜+ [αφ˜ + (λ−λ∗)z˜]

×

1−λ Z

ΩK(x,y)w_λ(y)lnw_λ(x)dy+ih˜

−λβ_λ Z

ΩK(y,x)[φ(y) + (λ−λ∗)ξ_λ(y)][αφ˜ + (λ−λ∗)z˜]

×(lnβ_λ[φ(x) + (λ−λ∗)ξ_λ(x)] +1)dye^iθ˜, f˜₂(z, ˜˜ α,λ):= (α˜²−1)kφk²_Y

C+ (λ−λ∗)²kz˜k²_Y

C.

(3.9)

Similarly to (3.5), we obtain

˜

α_λ∗ =1, θ˜_λ∗ =arccos

Z

Ωφ²(x)dx−λ∗β_λ∗ Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)lnβ_λ∗φ(y)dy λ∗β_λ∗

Z

Ω

Z

ΩK(y,x)φ(x)φ²(y)(lnβ_λ∗φ(x) +1)dxdy ,

h˜_λ∗ = λ∗β_λ∗

Z

Ω

Z

ΩK(y,x)φ(x)φ²(y)(lnβ_λ∗φ(x) +1)dxdysin ˜θ_λ∗ Z

Ωφ²(x)dx

,

and ˜z_λ∗ ∈(_X1)_C is the unique solution of the following equation (_d∆+λ∗)z˜+φ

1−λ∗β_λ∗ Z

ΩK(·,y)φ(y)lnβ_λ∗φ(y)dy+ih˜_λ∗

−λ∗β_λ∗φ Z

ΩK(y,·)φ(y)(lnβ_λ∗φ(x) +1)dye^−iθλ∗ =0.

Define ˜F : (_X1)_C×_R³×_R → _YC×_R by ˜F = (f^˜₁, ˜f2). Then we have the following result which can be proved similarly as in Theorem3.1and Corollary3.2.

Theorem 3.3.

(1) There exists a continuously differentiable mappingλ7→ (z˜_λ, ˜α_λ, ˜h_λ, ˜θ_λ)from[λ∗,λ^∗]toX_C× R³ such thatF˜(z˜_λ, ˜α_λ, ˜h_λ, ˜θ_λ,λ) =0. Moreover,

(F˜(z,α,h,θ,λ) =_0, α,h≥0, θ ∈[0, 2π). has a unique solution(z˜_λ, ˜α_λ, ˜h_λ, ˜θ_λ).

(2) Forλ∈(λ∗,λ^∗], the eigenvalue problem

∆˜(λ,iω, ˜˜ τ)ψ^˜ =0, ω˜ ≥0, ˜τ≥0, ˜ψ(6=0)∈_XC, has a solution if and only if

˜

ω=ω˜_λ = (λ−λ∗)h^˜_λ, τ˜ = τ˜_n= ^θ˜λ+2nπ

˜

ω_λ , n=0, 1, 2, . . . (3.10) and

ψ˜ =cψ˜_λ, ψ˜_λ =α˜_λφ+ (λ−λ∗)z˜_λ, where c is a nonzero constant.

Remark 3.4. From the above discussion, we can see that h_λ = h^˜_λ and θ_λ = θ^˜_λ, and conse- quentlyω_λ = ω˜_λ and τ_n = τ˜_n. Therefore, in the following, we will only use (hλ,θ_λ,ω_λ,τ_n) and not the ones with tilde. But the corresponding eigenfunctions of ∆(λ,iω_λ,τ_n) may be different from the ones for the adjoint operator ˜∆(λ,iω_λ,τ_n).

4 Stability and Hopf bifurcations

In this section, we first give the stability of the positive equilibrium w_λ of (1.1) whenτ = 0 and then discuss the existence of Hopf bifurcations.

Proposition 4.1. For eachλ ∈ (λ∗,λ^∗], all the eigenvalues of Bτ(λ)have negative real parts when τ=0, therefore the positive equilibrium w_λof (1.1)is locally asymptotically stable whenτ=0.

Proof. Otherwise, there exists a sequence{λ_n}^∞_n=1, such that λ_n > λ∗ forn ≥1, limn→_∞λ_n= λ∗, and forn≥1, the corresponding eigenvalue problem

(B(λn)ψ−λn(λn−λ∗)w_λnR

ΩK(·,y)(lnw_λn(y) +1)ψ(y)dy=µψ, x∈_Ω,

ψ(x) =0, x∈ ∂Ω, (4.1)

has an eigenvalueµ_λn ≥0, Reµ_λn ≥0 and the eigenfunctionψ_λn,kψ_λnk=1.

For n ≥ 1, we write ψ_λn as ψ_λn = c_λnw_λn +φ_λn , where c_λn ∈ _C and c_λn = hw_λn,ψ_λni/ hw_λn,w_λni. w_λn is the positive solution of (1.1) when λ = λn, and φ_λn ∈ _XC satisfies hφ_λn,w_λni = 0. If φ_λn ≡ 0, then we substitute ψ_λn = c_λnw_λn and µ = µ_λn into the first equation of (4.1) and obtain

−µ_λnw_λn = λ_n(λ_n−λ∗)w_λn Z

ΩK(·,y)(lnw_λn(y) +1)w_λn(y)dy, which is a contradiction. Henceφ_λn 6≡0 for eachn≥1. Since

hB(λ_n)φ_λn,w_λni=hφ_λn,B(λ_n)w_λni, B(λ_n)w_λn =0,

multiplying the first equation of (4.1) byψ_λn =c_λnw_λn+φ_λn whenµ= µ_λn, we can get hB(λ_n)φ_n,φ_λni=λ_n(λ_n−λ∗)

w_λn

Z

ΩK(·,y)(lnw_λn(y) +1)ψ_λn(y)dy, ψ_λn

+µ_λn. (4.2) Asw_λnis the principal eigenfunction ofB_λnwith principal eigenvalue 0, sohB_λnφ_λn,φ_λni<0.

Then

0≤Re(µ_λn)≤Re

−λ_n(λ_n−λ∗)

w_λn Z

ΩK(·,y)(lnw_λn(y) +1)ψ_λn(y)dy, ψ_λn

→0, asn→∞, hence limn→_∞Re(µ_λn) =0.

From (4.2), we have

|Im(µ_λn)|=

Im

−λn(λn−λ∗)

w_λn Z

ΩK(·,y)(lnw_λn(y) +1)ψ_λn(y)dy, ψ_λn

→0, asn→_∞. Similar to the proof of Lemma 2.3 of [8], we get

|λ₂(λ_n)| · kφ_λnk²_Y

C≤ |hB(λ_n)φ_λn,φ_λni|_{, (4.3)}

whereλ₂(λ_n)is the second eigenvalue ofB(λ_n). Then

|λ₂(λn)| · kφ_λnk²≤

λn(λn−λ∗)

w_λn Z

ΩK(·,y)(lnw_λn(y) +1)ψ_λn(y)dy, ψ_λn

+|µ_λn|. Since

λ₂(λ_n) =λ₂−λ∗ >0, so lim_n→_∞kφ_λnk_YC =0.

DenoteE_λn =λ_n(λ_n−λ∗)hw_λnR

ΩK(·,y)(lnw_λn(y) +1)ψ_λn(y)dy,ψ_λni, then Eλ_n =λ_n(λ_n−λ∗)|cλ_n|²

wλ_n

Z

ΩK(·,y)(lnwλ_n(y) +1)wλ_n(y)dy, wλ_n

+λ_n(λ_n−λ∗)_cλn

wλ_n

Z

ΩK(·,y)(_lnwλn(_y) +₁)_wλn(_y)_dy, φ_λn

+λ_n(λ_n−λ∗)c_λn

w_λn Z

ΩK(·_,y)(_lnw_λn(y) +₁)φ_λn(y)dy, w_λn

+λ_n(λ_n−λ∗)

w_λn Z

ΩK(·,y)(lnw_λn(y) +1)φ_λn(y)dy, φ_λn

. Since

nlim→_∞

w_λn

Z

ΩK(·_,y)(_lnw_λn(y) +₁)w_λn(y)dy, w_λn

= β³_λ∗ Z

Ω

Z

ΩK(x,y)φ²(x)φ(y)(lnβ_λ∗φ(y) +1)dxdy >0,

and limn→_∞kφ_λnk_YC = 0, then there exists N∗ ∈ _Nsuch that for each n ≥ N∗, Re(E_λn)> 0, which implies that

Re(µ_λn) =hB(λ_n)φ_λn,φ_λni −Re(E_λn)<0.

This is a contradiction with Re(µ_λn) ≥ 0 for n ≥ 1. So all the eigenvalues of B_τ(λ) have negative real parts whenτ=0.

Theorem 4.2. Assume that λ ∈ (λ∗,λ^∗], then µ = iω_λ is a simple eigenvalue of B_τn for n = 0, 1, 2, . . .

Proof. Suppose that there existsφ₁ ∈ D(B_τn)∩ D([B_τn]²)_{such that}[B_τn(λ)−iω_λ]²φ₁=_{0, then} [B_τn(λ)−iω_λ]φ₁∈ N[B_τn(λ)−iω_λ] =Span{e^iωλ·ψ_λ}.

So there exists a constant a such that

[B_τn(λ)−iω_λ]φ₁ =ae^iωλ·ψ_λ. Hence

φ˙₁(θ) =iω_λφ₁(θ) +ae^iωλθψ_λ, θ ∈[−τ_n, 0], φ˙₁(0) =B(λ)φ₁(0)−λ(λ−λ∗)w_λ

Z

ΩK(·,y)(lnw_λ(y) +1)φ₁(−τn)(y)dy. (4.4)

From the first equation of (4.4), we have

φ₁(θ) =φ₁(₀)e^iωλθ+aθe^iωλθψ_λ,

φ˙₁(0) =iω_λφ₁(0) +aψ_λ. (4.5) Then from Eqs. (4.4) and (4.5), we can obtain

∆(λ,iω_λ,τ_n)φ₁(0) = [B(λ)−iω_λ]φ₁(0)−λ(λ−λ∗)w_λ Z

ΩK(·,y)(lnw_λ(y) +1)φ₁(0)(y)dye^−iθλ

=aψ_λ+λ(λ−λ∗)w_λ Z

ΩK(·,y)(lnw_λ(y) +1)φ₁(−τn)(y)dy

−λ(λ−λ∗)w_λ Z

ΩK(·,y)(lnw_λ(y) +1)φ₁(0)(y)dye^−iθλ. Sinceφ₁(−τn) =φ₁(0)e^−iωλτn−aτne^−iωλτn, then we have

∆(λ,iω,τ_n)φ₁(0) =a

ψ_λn−λ(λ−λ∗)τ_nw_λ Z

ΩK(·,y)(lnw_λ(y) +1)ψ_λ(y)dye^−iθλ

. Hence

0= h_∆^˜(λ,iω, ˜˜ τ_n)ψ^˜_λ,φ₁(0)i

= h_∆^˜(λ,iω,τ_n)ψ^˜_λ,φ₁(0)i

= hψ^˜_λ,∆(λ,iω,τn)φ₁(0)i

= a^Z

Ωψ¯˜_λ(y)ψ_λ(y)dy

−λ(λ−λ∗)τ_nw_λ Z

Ω

Z

ΩK(x,y)w_λn(x)(lnw_λ(y) +1)ψ^¯˜_λ(x)ψ_λ(y)dxdye^−iθλ

. Whenλ→λ∗,

Z

Ωψ¯˜_λ(y)ψ_λ(y)dy−λ(λ−λ∗)τ_nw_λ Z

Ω

Z

ΩK(x,y)w_λn(x)(lnw_λ(y) +1)ψ¯˜_λ(x)ψ_λ(y)dxdye^−iθλ

→

Z

Ωφ²(y)dy>0.

Soa=0. Thusφ₁∈ N[Bτn(λ)−iω_λ]. By induction, we obtain

N[B_τn(λ)−iω_λ]^j =N[B_τn(λ)−iω_λ], j=1, 2, . . . , n=0, 1, 2, . . . Therefore,µ=iω_λ is a simple eigenvalue of B_τn forn=0, 1, 2, . . .

Since µ = _iωλ is a simple eigenvalue of Bτn , then from the implicit function theorem, there are a neighborhoodO_1n×O_2n×O_3n ⊂ _R×_C×_XC of(τn,iω_λ,ψ_λ)and a continuously differential function(µ,ψ):O_1n →O_2n×O_3nsuch that for eachτ∈O_1n, the only eigenvalue ofBτ(λ)inO2n isµ(τ), and

µ(τn) =iω_λ, ψ(τn) =ψ_λ,

∆(λ,µ(τ),τ) = [B(λ)−µ(τ)]ψ(τ)

−λ(λ−λ∗)w_λ Z

ΩK(·_,y)(_lnw_λ(y) +₁)ψ(τ)(y)dye^−µ(τ)τ

=0, τ∈O_1n.

(4.6)

Then we have the following transversality condition.