Analízis lépésről - lépésre

(1)

Analízis lépésről - lépésre

interaktív tananyag

Dr. Stettner Eleonóra

Klingné Takács Anna

(2)

Analízis lépésről - lépésre: interaktív tananyag

írta Dr. Stettner Eleonóra és Klingné Takács Anna

(3)

Tartalom

Előszó ... vi

1. Sorozatok ... 1

1. Definíció, alapfogalmak ... 1

2. Konvergens, divergens sorozatok ... 10

3. Nevezetes sorozatok határértékei ... 17

4. Műveletek konvergens sorozatokkal ... 20

5. Kritikus határértékek, rendőr-elv ... 21

6. Egy pénzügyi alkalmazás ... 23

7. Részletesen kidolgozott feladatok a sorozatok témaköréből ... 24

7.1. Monotonitás, korlátosság ... 24

7.1.1. 1. feladat ... 24

7.1.2. 2. feladat ... 27

7.1.3. 3. feladat ... 29

7.1.4. 4. feladat ... 30

7.2. Két (egyváltozós) polinom hányadosának határértéke ... 32

7.2.1. 1. feladat ... 33

7.2.2. 2. feladat ... 35

7.2.3. 3. feladat ... 36

7.2.4. 4. feladat ... 37

7.2.5. összefoglalás ... 38

7.2.6. 5. feladat ... 38

7.2.7. 6. feladat ... 39

7.2.8. 7. feladat ... 40

7.3. A qⁿ sorozat határértékére visszavezethető feladatok ... 41

7.3.1. 1. feladat ... 41

7.3.2. 2. feladat ... 43

7.3.3. 3. feladat ... 44

7.3.4. 4. feladat ... 45

7.3.5. 5. feladat ... 46

7.4. Néhány "∞-∞" típusú kritikus határérték kiszámítása ... 47

7.4.1. 1. feladat ... 47

7.4.2. 2. feladat ... 48

7.4.3. 3. feladat ... 49

7.5. Az (1+1/n)ⁿ sorozat határértékére visszavezethető határértékszámítási feladatok . 50 7.5.1. 1. feladat ... 50

7.5.2. 2. feladat ... 51

7.5.3. 3. feladat ... 53

7.5.4. 4. feladat ... 54

7.5.5. 5. feladat ... 55

7.5.6. 6. feladat ... 56

7.6. Feladatok önálló megoldásra ... 57

8. Függelék -- Számhalmazok ... 58

2. Sorok ... 62

1. Sorok, bevezető példák ... 62

2. A sor matematikai fogalma ... 64

3. A mértani sor ... 65

4. Konvergencia kritériumok ... 67

5. Egyéb sorokra vonatkozó összefüggések ... 69

6. Szemléltetés ... 70

7. Feladatok önálló megoldásra ... 71

3. Függvények ... 73

1. Függvény definíciója ... 73

1.1. Az értelmezési tartomány ... 74

2. Függvénytulajdonságok ... 76

2.1. Zérushely ... 76

(4)

2.3. Periodikusság ... 79

2.4. Monotonitás ... 80

2.5. Korlátosság ... 82

2.6. Szélsőérték ... 84

2.7. Konvexitás ... 85

3. Elemi függvények és függvénytranszformációk ... 87

4. Összetett függvények ... 93

5. Inverz függvények ... 96

6. Néhány további függvény ... 97

4. Függvény határértéke, folytonosság ... 101

1. Függvény határértéke ... 101

2. A határérték típusai ... 104

2.1. Véges helyen vett végtelen határérték ... 104

2.2. Végtelenben vett végtelen határérték ... 106

2.3. Végtelenben vett véges határérték ... 109

2.4. Véges helyen vett véges határérték ... 111

2.5. Mikor nem létezik a határérték? ... 113

3. Nevezetes függvény határértékek ... 115

4. Folytonosság ... 118

4.1. Függvény pontban való folytonossága ... 118

4.2. Féloldali folytonosság ... 119

4.3. Intervallumon folytonos függvények ... 119

4.4. Folytonos függvények tulajdonságai ... 125

4.5. Szakadási helyek fajtái ... 127

5. A határérték és a folytonosság feladatokban ... 128

5.1. Szemléleten alapuló feladatmegoldás ... 129

5.2. Algebrai átalakításokon alapuló feladatmegoldás ... 134

5.3. Maple gyakorló panel a határérték meghatározására ... 135

6. Megoldásra javasolt feladatok ... 135

5. Differenciálszámítás ... 137

1. A differenciálszámítás elemei ... 137

1.1. Differenciahányados, differenciálhányados, derivált függvény ... 137

1.2. Differenciálhatóság és folytonosság ... 142

1.3. Differenciálási szabályok ... 143

1.4. Maple ellenőrző panel a deriváláshoz ... 144

1.5. Maple gyakorló panel a deriváláshoz ... 144

1.6. Középérték tételek ... 145

1.7. Kidolgozott feladatok ... 147

6. A differenciálszámítás alkalmazásai ... 152

1. Alkalmazások ... 152

1.1. Monotonitás ... 152

1.2. Szélsőérték ... 152

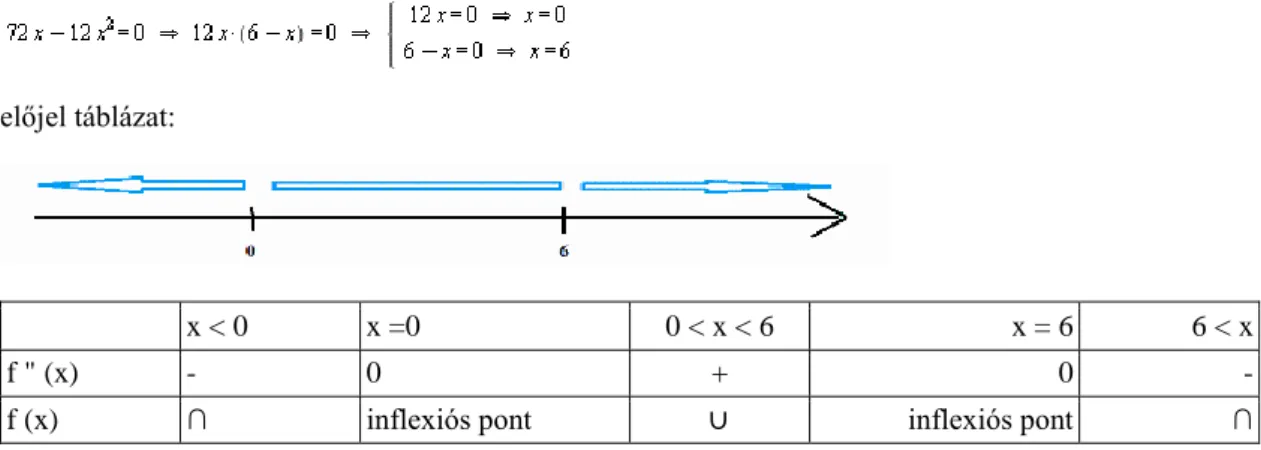
1.3. Konvexitás, inflexiós hely ... 154

1.4. Függvényvizsgálat ... 154

1.5. Példák függvényvizsgálatra ... 155

1.6. Érintő ... 169

1.7. Közelítés ... 170

1.8. Gazdasági feladatok megoldása ... 172

7. Integrálszámítás ... 178

1. Definíciók, az integrálás és deriválás kapcsolata ... 178

2. Integrálási típusok ... 180

3. Maple gyakorló-ellenőrző panel az integráláshoz ... 182

4. Határozott integrál ... 182

8. Az integrálszámítás alkalmazásai ... 187

1. Az integrálás alkalmazásai ... 187

(5)

1.2. Függvénygörbék közti terület ... 188

1.3. Függvény átlaga ... 191

1.4. Görbe ívhossza ... 192

1.5. Forgástest térfogata, palástjának felszíne ... 193

1.6. Súlypont ... 195

9. Kétváltozós függvények I. ... 198

1. Bevezetés ... 198

2. Kétváltozós függvények definíciója, szemléltetése ... 198

3. Értelmezési tartomány ... 204

4. Határérték ... 210

5. Parciális deriváltak ... 212

6. Iránymenti derivált ... 215

7. Megoldott feladatok ... 217

10. Kétváltozós függvények II. ... 220

1. Szélsőérték ... 220

1.1. Fogalmak ... 220

1.2. Szükséges feltétel ... 220

1.3. Elégséges feltétel ... 224

2. Érintősík ... 230

3. Megoldott feladatok ... 233

Irodalomjegyzék ... 236

(6)

Előszó

"Én nem csak azért szeretem a matematikát, mert alkalmazni lehet a technikában, hanem fõleg azért, mert szép.

Mert játékos kedvét is belevitte az ember, és a legnagyobb játékra is képes: megfoghatóvá tudja tenni a végtelent. Végtelenségrõl, ideákról hiteles mondanivalói vannak. És mégis annyira emberi, korántsem az a bizonyos kétszerkettõ: magán viseli az emberi alkotások soha le nem zárt jellegét." Péter Rózsa

Tapasztalatunk szerint a felsőoktatásban tanuló hallgatók számára a matematikai tanulmányaik során az első féléves analízis a legnehezebben legyőzhető akadály. Ennek oka véleményünk szerint az új oktatási szinthez való alkalmazkodáson kívül az, hogy a végtelen fogalma oly sokszor és különböző formában felbukkan a tananyagban. Az "Analízis lépésről - lépésre" című tananyag főleg a több éve - sokszor több évtizede - érettségizett levelező hallgatóknak szól, akiknek szükséges apró lépésekre bontani a matematikai gondolatmeneteket és fel kell idézni a rég elfeledett matematikai fogalmakat is. Reméljük, hogy ez a tananyag sok hallgató életét teszi könnyebbé, és ahogy Péter Rózsa matematikus szép bevezető idézetében olvashatjuk, sikerül megfoghatóvá tenni a végtelent.

Tananyagunk Maple programmal készült. A rövid elméleti összefoglalók után a kidolgozott feladatokra általában két különböző megoldást mutatunk. Az egyik a hagyományos utat választja, a másik azt mutatja meg, hogy Maple utasítások segítségével hogyan kapjuk meg az eredményt. Sok animációval, szemléltetéssel szeretnénk az elmélet meértését és a feladatmegoldást segíteni. Minden fejezet végén önálló megoldásra javasolt feladatokat is közlünk. A nagyon részletesen kidolgozott, sokszor az általános iskolai ismeretekig visszanyúló feladatmegoldások kifejezetten a több éve végzett levelező szakos hallgatóknak szólnak. Ezek a feladatok főként az első fejezetben találhatók, itt ismételjük át a legfontosabb matematikai fogalmakat és ööszefüggéseket, a későbbiekben a részletezés ilyen mélységeire már nincs szükség.

Kaposvár, 2014

(7)

1. fejezet - Sorozatok

1. Definíció, alapfogalmak

Eddigi tanulmányainkra visszaemlékezve általában a sorozatokról a számtani és a mértani sorozat jut az eszünkbe. A sorozatok azonban ennél a két típusnál sokkal változatosabbak lehetnek. A sorozatok általános definíciója a következő:

Definíció:

A sorozat egy olyan függvény, amelynek értelmezési tartománya a pozitív természetes számok halmaza , értékkészlete pedig a valós számok egy részhalmaza.

(8)

Természetesen a fenti ábrán az értelmezési tartománynak és az értékkészletnek is csak egy részhalmaza látható.

A hozzárendelés szabálya például lehet az ábra alapján az, hogy minden pozitív természetes számhoz a négyzetét rendeljük.

Ha képletben írjuk fel: a1=1 a2=4 a3=9 a4=16 ... an=n²

Látható, hogy az értelmezési tartomány elemei, a pozitív egész számok az alsó indexben, a hozzárendelt értékek, az értékkészlet elemei pedig az egyenlőségjel után vannak.

A fenti halmazábrával bonyolult a sorozatokat szemléltetni. A szokásos ábrázolás, szemléltetés számegyenesen és koordináta -rendszerben történik. Minden sorozatnak végtelen sok tagja van, de ábrázolni természetesen csak véges sokat tudunk.

Ábrázoljuk a fenti sorozatot a számegyenesen:

A sorozatokat Maple programban is ábrázolhatjuk számegyenesen és koordináta-rendszerben is.

[ > pointplot({seq([n², 0], n = 1 .. 10)}, color = red, symbol = solidcircle, symbolsize = 12)

(9)

[ > pointplot({seq([n, n²], n = 1 .. 30)}, color = blue, symbol = solidcircle, symbolsize = 12);

Sorozat megadása:

Hogyan adhatunk meg egy sorozatot?

(10)

, például: ,

an = 5 + 2 n , például: a3 = 5 + 2 ⋅ 3 =11 , a80 = 5 + 2 ⋅ 80 = 165

Ha képlettel adunk meg egy sorozatot bármely elemét gyorsan ki tudjuk számolni úgy, hogy n helyére a sorozat sorszámát helyettesítjük. Nem ütközik sokkal nagyobb nehézségbe a sorozat 100. elemének kiszámolása, mint az 1. Ugyanezt nem mondhatjuk el, ha a sorozatot rekurzióval adjuk meg.

2.rekurzióval

A rekurzióval való megadás úgy történik, hogy megadjuk a sorozat első elemét, vagy néhány első elemét, ezután még egy képzési szabályt is megadunk arról, hogy egy sorozatelem hogyan, milyen műveletekkel képezhető az előző elemből, vagy elemekből. Legyen például a sorozat első eleme a1 = 5 , és a további elemek képzési szabálya an = an-1 + 2 , n = 2, 3, ... , vagyis a sorozat minden elemét (az elsőt kivéve) úgy kapjuk meg, hogy az előző elemhez hozzáadunk 2-t. Ekkor a2 = a1+ 2 =5+2=7, a3 = a2+ 2 = 7+2= 9 , ezzel a módszerrel a nagyobb indexű tagok kiszámítása hosszú ideig tart.

A legismertebb rekurzív sorozat a Fibonacci-sorozat. Képzési szabálya a következő: a1 = 1, a2 = 1, an = an-1 + an-2, n > 2

A sorozat első és második eleme 1, minden további elemet úgy kapunk meg, hogy összeadjuk a sorozat előző két elemét. A Fibonacci-sorozathoz nagyon sok érdekesség kapcsolódik. Egészen hihetetlen, hogy hány helyen fordul elő a természetben, alkalmazzák szabályait építészek, képzőművészek, költők, zeneszerzők. Még a tőzsde árfolyammozgásainak leírására is használják, bár ez az alkalmazás sokak által vitatható.

A rekurzív sorozatokkal az a probléma, hogyha pl. a 100. elemét szeretném kiszámítani, akkor minden elemét meg kell határozni egészen a 99.-ig. Nem lehetséges az 1. pontbeli képlethez hasonló, csak n-től függő képletet megadni a rekurzív sorozatokra is? A matematikának külön fejezete foglalkozik a rekurzív sorozatok explicit képletének megadásával. Milyen típusú sorozatokhoz tudunk megadni képletet, és ha lehetséges a megadás hogyan?

3. Szöveges utasítással

Ha így adunk meg egy sorozatot nagyon fontos, hogy vigyázzunk a pontos fogalmazásra, hogy egyértelműen reprodukálható legyen az általunk megadott sorozat. A világ bármely pontján, a különböző előképzettséggel rendelkező emberek mind ugyanarra a sorozatra gondoljanak, ha hallják a megfogalmazásunkat. Mikor használjuk ezt a módszert? Ha más módszer nem alkalmas a sorozat megadására, például a sorozat n. eleme legyen a π n. jegye. Erre valóban nem alkothatunk sem képletet, sem rekurziót.

4. A sorozat néhány elemének felsorolásával

Például a felsorolt elemek legyenek az 5, 7, 9, 11, 13, ... . Ekkor észrevehetjük, hogy a an = 2 n + 3 alkalmas képzési szabály. Ennek a megadási módnak az a veszélye, hogy a folytatás nem mindig egyértelmű.

5. A függvény értelmezési tartományának leszűkítésével

Legyen például a függvény az . Az f(x) függvény értelmezési tartománya a valós számok halmaza, kivéve a 0-t, ha az értelmezési tartományt leszűkítjük a pozitív természetes számok halmazára az

sorozatot kapjuk. Ábrázoljuk a függvényt és a sorozatot egy koordináta-rendszerben:

[ >

(11)

[ >

[ > plot([l, f], n = -10 .. 10, style = [point, line], color = [blue, red], symbol = solidcircle, symbolsize = 20, thickness = [4, 2]);

A következő példa ugyanerre a megadási módra az függvény és az sorozat.

Az első ábrán csak a sorozat, a másodikon a sorozat és a függvény együtt látható

[ >

(12)

[ >

[ > plot([l, f], n = 0 .. 10, style = [point, line], color = [blue, red], symbol = solidcircle, symbolsize = 20, thickness = [4, 2]);

(13)

A sorozatok legfontosabb tulajdonságai:

Korlátosság:

Az an sorozat felülről korlátos, ha van olyan szám, hogy minden -ra.

Megadható egy valós szám, az úgynevezett felső korlát (K), amelynél minden sorozatelem kisebb, vagy egyenlő (más szóval nem nagyobb).

Az an sorozat alulról korlátos, ha van olyan szám, hogy minden -ra.

Megadható egy valós szám, az úgynevezett alsó korlát (k), amelynél minden sorozatelem nagyobb, vagy egyenlő (más szóval nem kisebb).

Az an sorozat korlátos, ha alulról és felülről is korlátos.

A sorozatelemek a két - alsó és felső - korlát között "mozoghatnak".

A következőkben néhány sorozatot szemléltetünk korlátaikkal együtt, ha vannak.

A sorozat felülről korlátos, alulról nem Felső korlát: K

= 1

A sorozat alulról korlátos, felülről nem Alsó korlát: k

= 3

A sorozat korlátos Alsó korlát k = 2 , felső korlát

K = 2, 25

A sorozat sem alulról, sem felülről nem korlátos

(14)

Monotonitás:

Az an sorozat szigorúan monoton nő, ha an < an+1 minden -ra.

Minden sorozat elem nagyobb az őt megelőzőnél. Számításokban gyakran az an+1 - an > 0 egyenlőtlenségnek kell teljesülni.

Az an sorozat monoton nő, ha an ≤ an+1 minden -ra.

Minden sorozat elem nagyobb, vagy egyenlő az őt megelőzőnél. Számításokban gyakran az an+1 - an ≥ 0 egyenlőtlenségnek kell teljesülni.

Az an sorozat szigorúan monoton csökken, ha az an > an+1 minden -ra.

Minden sorozat elem kisebb az őt megelőzőnél. Számításokban gyakran az an+1 - an < 0 egyenlőtlenségnek kell teljesülni.

Az an sorozat monoton csökken, ha an≥ an+1 minden -ra.

Minden sorozat elem kisebb, vagy egyenlő az őt megelőzőnél. Számításokban gyakran az an+1 - an ≤ 0 egyenlőtlenségnek kell teljesülni.

A korlátosság példáit tartalmazó táblázat első cellájában a sorozat szigorúan monoton csökken, a másodikban szigorúan monoton nő, a harmadikban újra szigorúan monoton csökken, a negyedik cella példája nem monoton.

Példa:

Mit mondhatunk a következő sorozatról monotonitás és korlátosság szempontjából?

Monotonitás vizsgálata:

Mielőtt a bizonyításhoz kezdünk, számítsuk ki a sorozat néhány első elemét!

Sejtés: a sorozat szigorúan monoton csökken. (Vigyázat! Az első néhány elem kiszámítása nem mindig alkalmas a helyes sejtés megfogalmazására. Egyes sorozatok néhány első eleme monoton nő, de lehetséges, hogy a további elemek monoton csökkennek.)

(15)

an+1 - an=

, mert a számláló negatív és a nevező pozitív.

Tehát a sorozat szigorúan monoton csökken. Ha egy sorozat szigorúan monoton csökken, az első eleme, vagy bármely annál nagyobb szám alkalmas lesz felső korlátnak, legyen pl. a felső korlát K = 0, 6 . Hogyan határozzuk meg az alsó korlátot? Számítsuk ki a sorozat egy nagy indexű tagját, abból talán megsejthetjük az alsó korlátot.

, ha nagyon szoros alsó korlátot akarunk megadni, úgy tűnik, hogy az 1/2 alkalmas lesz, ezt be kellene bizonyítani. Van most egy egyszerűbb módszer is. Látjuk, hogy a sorozat minden tagja pozitív, így a k = 0 biztosan jó lesz alsó korlátnak, és ez nyilvánvaló, bizonyítanunk sem kell.

Nézzük végig a fenti gondolatmenetünket a Maple utasításokkal:

[ >

[ > a(1) # A sorozat 1. elemének kiszámítása

[ > evalf(a(1(,3) # A sorozat elemeit tizedestörtté alakítjuk, mert így könnyebben össze tudjuk hasonlítani a tagokat, és sejtést tudunk megfogalmazni a sorozat monotonitására.

Hasonlóan további elemeket is kiszámítunk és tizedestörtté alakítunk.

Sejtés: A sorozat szigorúan monoton csökken.

[ > a(n+1) # A sorozat n+1. eleme

[ > a(n+1)-a(n) # Az n+1. és az n. elem különbsége

[ > simplify(a(n+1)-a(n)) # A különbség lehető legegyszerűbb alakra hozása

[ > solve(a(n+1)-a(n) < 0, [n]) # Megvizsgáljuk, hogy a sorozat szigorúan monoton csökkenő-e? Ez azt jelenti, hogy n-re megoldjuk az a(n+1)-a(n)<0 egyenlőtlenséget

[ > s := solve({n > 0, a(n+1)-a(n) < 0}, [n]) # Azt kaptuk, hogy minden pozitív n-re teljesül az egyenlőtlenség, tehát a sorozat valóban szigorúan monoton csökken. Ezért a felső korlát a sorozat első eleme lesz.

[ > a(1000) # A felső korlátot a sorozat elég nagy indexű eleme segít megsejteni.

[ > # Megnézzük, hogy sejtésünk

helyénvaló-e?

Igen, minden pozitív n-re igaz a fenti egyenlőtlenség, tehát valóban jó alsó korlát az 1/2.

[ > l : = [[n, a(n)], $n = 1 .. 10)]; # A sorozat első tíz elemének kiszámítása:

[ > plot([l, k, K], n = 0 .. 10, style = [point, line, line], color = [blue, red, green], symbol = solidcircle, symbolsize = 20, thickness = [4, 2, 2], view = [0 .. 10, 0 .. 1]); # Szemléltetés a koordináta-rendszerben az alsó és felső korláttal együtt.

(16)

2. Konvergens, divergens sorozatok

A konvergencia és a divergencia a sorozatokkal kapcsolatos legfontosabb fogalmak. Egyes sorozatok szép nagy, egyenletes léptekkel gyalogolnak a +∞, vagy a -∞ felé, míg mások egy, vagy több pontba "sűrűsödnek".

Vizsgáljuk először ezeket a néhány pont köré besűrűsödő sorozatokat. Hogy tudjuk ezt a szemléletes képet matematikailag pontosan megfogni? Először meghatározzuk a környezet fogalmát:

Környezet

Az "a" pont ε > 0 sugarú környezete az ]a- ε,a+ ε[ nyílt intervallum, ahol ε tetszőleges pozitív, valós szám.

Torlódási pont

Az an sorozat torlódási pontja "a", ha a tetszőleges ε > 0 környezetén belül a sorozatnak végtelen (∞) sok eleme van. Nagyon fontos kihangsúlyozni, hogy a definíció bármilyen kis ε sugarú környezet esetében igaz, és a kérdés ekkor érdekes igazán.

A következő táblázatban három sorozatot szemléltetünk, amelyeknek rendre 1, 2 illetve 3 torlódási pontjuk van.

A szemléltetés nem egy egyszerű ábra, hanem animáció. Maple-ben a képre kattintva megjelenik az animáció menü, ahol, ha az FPS: utáni számot kicsire 1, vagy 2 értékre állítjuk az animáció lassabb lesz, és jobban meg tudjuk figyelni a sorozatok viselkedését. A harmadik sorozat esetében úgy tűnik, hogy csak három elemet ábrázolunk, ez azért látszik így, mert ez a három elem (-1, 0, 1) ismétlődik, mindegyik végtelen sokszor.

A sorozatnak egy torlódási pontja A sorozatnak két torlódási pontja A sorozatnak három torlódási pontja

(17)

van és az a 0. van a 2 és a - 2. van a - 1, 0, és az 1.

Konvergencia

Konvergens csak az a sorozat lehet, ami egyetlen pontba "sűrűsödik", nem lehet több torlódási pontja. Ekkor a torlódási pontot a sorozat határértékének nevezzük.

Ha a határérték bármilyen kicsi ε > 0 sugarú környezetét vesszük, a sorozatelemek egyszercsak beugranak ebbe a környezetbe és utána mindig benn is maradnak. Legyen a sorozatnak N db eleme a környezeten kívül. Ekkor az utolsó elem, ami még nincs a megadott környezetben az aN . Pontosabban ezt így fogalmazhatjuk meg: a sorozat konvergens és határértéke "a", ha bármely pozitív ε- hoz található egy N ( ε - tól függő) küszöbindex, hogy ha a sorozat N-nél nagyobb sorszámú elemeit tekintjük, akkor azok a határértékhez, "a"-hoz ε -nál közelebb lesznek. (A konvergencia 1. definíciója)

Matematikai jelekkel így írható fel a definíció: Az an sorozat konvergens és határértéke "a", ha

(A jelek magyarázata: "∀" , az ún. univerzális kvantor, jelentése minden, bármely. "∃" , egzisztenciális kvantor, jelentése van olyan, létezik) A fenit megfogalmazással ekvivalens definíció a következő: Az an sorozat konvergens és határértéke "a", ha "a" bármilyen "kis" ε > 0 sugarú, ]a- ε,a+ ε[ környezetén kívül a sorozatnak véges sok eleme van. (A konvergencia 2. definíciója)

Jelölések: vagy,

Tekintsük újra az sorozatot. Mi lehet a sorozat határértéke? A monotonitás vizsgálatnál kiszámoltuk a sorozat 1000. elemét, ami elég közel van az 1/2-hez. Nézzük meg, hogy az 1/2 jó lesz-e határértéknek? Legyen először ε = 0,05. Számítsuk ki, hogy a sorozat hány eleme lesz az 1/2- nek az ε = 0,05 sugarú környezetén kívül, illetve hányadik elemtől lesznek a sorozatelemek a megadott környezetben?

(18)

Az abszolútérték "elhagyható", mert pozitív számot tartalmaz. < 0,05 Vegyük mindkét oldal reciprokát, ekkor az egyenlőtlenség iránya megfordul. 2 ⋅ (2n + 3) > 20 ⇒ 4n + 6 > 20 ⇒ 4n > 14 ⇒ n > 3,5

Tehát n = 4, 5, ... adódott, vagyis a sorozatelemek a 4. elemtől kezdve vannak az 1/2 -nek az ε = 0,05 sugarú környezetében. Ezért a küszöbindex N = 3, a sorozatnak csak az első három eleme van a megadott intervallumon kívül. Általában N, a küszöbszám az egyenlőtlenség megoldása során kapott eredmény egész része. Ugyanezt az egyenlőtlenséget ε = 0,01, ε = 0,001 esetében is oldjuk meg. A kapott küszöbszámok rendre N = 23, N = 248. Az alábbiakban a Maple utasításokkal történő számolást, majd a kapott eredmények szemléltetését láthatjuk.

[ > e : = | a(n) - 0.5 |# Az egyenlőtlenség bal oldalának felírása [ > f := simplify(e) # Az egyenlőtlenség bal oldalának leegyszerűsítése [ > solve({(e < 0.5 and n > 0)}, n); # a megoldás 0,05-re

[ > solve({ e < 0.01 and n > 0 },n); a #megoldás 0,01-re [ > solve({ e < 0.001 and n > 0 },n); a #megoldás 0,001-re

[ > # Az egyenlőtlenség általános

megoldása

[ > érték := eval(küszöb, [ε = 0.05])

[ > N := floor(érték) # a küszöbszám megadása 0,05 sugarú környezet esetén [ > érték := eval(küszöb, [ε = 0.01])

[ > N := floor(érték) # a küszöbszám megadása 0,01 sugarú környezet esetén [ > érték := eval(küszöb, [ε = 0.001])

[ > N := floor(érték) # a küszöbszám megadása 0,001 sugarú környezet esetén

(19)

A Maple limit utasítása megadja a sorozat határértékét:

[ >

Divergencia

A nem konvergens sorozatokat divergens sorozatoknak nevezzük.

A divergens sorozatok is többfélék lehetnek.

A divergens sorozatok típusai:

• + végtelenhez tartó sorozatok (→ + ∞)

• - végtelenhez tartó sorozatok (→ - ∞)

• oszcillálva ("ide-oda ugrálva") divergens sorozatok

Akkor tart a +∞-hez egy sorozat, ha bármilyen (nagy) M számot adunk meg, mindig található egy sorozatelem, ami ennél a számnál nagyobb lesz és onnantól kezdve az összes sorozatelem nagyobb lesz M-nél. Az utolsó elem, ami még nem nagyobb M-nél az N. elem. Matematikai jelekkel leírva: an → ∞, ha ∀ M-hez ∃ N úgy, hogy an > M, ha n > N

(20)

Akkor tart a - ∞-hez egy sorozat, ha bármilyen M számot adunk meg, mindig található egy sorozatelem, ami ennél a számnál kisebb lesz és onnantól kezdve az összes sorozatelem kisebb lesz M-nél. Az utolsó elem, ami még nem kisebb M-nél az N. elem. Matematikai jelekkel leírva: an → - ∞, ha ∀ M-hez ∃ N úgy, hogy an < M, ha n > N

Jelölés:

oszcillálva divergens,

korlátos sorozat oszcillálva divergens, nem korlátos sorozat

Mit mond a Maple limit utasítása divergens sorozatok esetén?

[ > limit(n², n = infinity) ; # +∞-hez tartó sorozat [ > limit(-2⋅ n+1, n = infinity); # -∞-hez tartó sorozat

[ > limit((-1)ⁿ⋅ n, n = infinity); # oszcillálva divergens sorozat Néhány példa különböző tulajdonságú sorozatokra:

A fenti példákat nézzük meg Maple-ben szemléltetve is. Az első oszlopban számegyenesen ábrázoltuk a sorozatokat animálva, a második oszlopban koordináta - rendszerben ábrázoltunk, a harmadik oszlopban összefoglaltuk a legfontosabb tulajdonságokat:

(21)

Alulról korlátos k = 1, monoton növekvő, nincs torlódási pontja,

divergens,

limit(1/n, n = infinity) = 0

Korlátos k = -1, K = 1/2, nem monoton, torlódási pontja 0,

konvergens, határértéke 0

Korlátos k = -1, K = 1, nem monoton, torlódási pontjai:-1, 0, 1,

oszcillálva divergens

Nem korlátos, nem monoton, nincs torlódási pontja, oszcillálva

divergens

(22)

Felülről korlátos K = -1, monoton csökkenő, torlódási pontja nincs,

divergens

Korlátos k = -2, K = 2, nem monoton, torlódási pontjai: -2, 2,

Korlátos k = -1, K = 1, nem monoton, torlódási pontjai: -1, 1,

Észrevehetjük, hogy a példaként szereplő sorozatokban többször előfordul a (-1)ⁿ és a (-1)⁽ⁿ⁺¹⁾ kifejezés. n értékétől függően ezeknek a kifejezéseknek a számértéke, - 1, és +1 felváltva. Ezért szerepük a váltakozó előjel biztosítása. Ha (-1)ⁿ -nel szorozzuk meg a képletet, akkor a sorozat első eleme negatív lesz, a második pozitív és így tovább, minden páratlan sorszámú elem negatív és minden páros sorszámú pozitív. Ha (-1)⁽ⁿ⁺¹⁾-nel szorozzuk meg a sorozat képletét, akkor a páratlan sorszámú elemek lesznek pozitív előjelűek és a páros sorszámú elemek negatívok. A divergens sorozatok határértékét az előbb már megnéztük a Maple limit utasításával. Most nézzük meg a táblázatban szereplő konvergens sorozatok határértékét:

[ >

A fenti táblázatban szerepelnek monoton és nem monoton, korlátos és nem korlátos, konvergens és divergens sorozatok. Tegyünk rendet, vizsgáljuk meg, hogy ezek a sorozat tulajdonságok milyen kapcsolatban vannak egymással.

A konvergencia, a monotonitás és a korlátosság kapcsolata

Tétel: Ha az an sorozat konvergens, akkor korlátos. A bizonyítás vázlatosan a következőképpen szól. Ha egy sorozat konvergens, akkor a konvergencia 2. definíciója értelmében a határérték tetszőleges ε sugarú környezetén kívül a sorozatnak véges sok eleme van. Az 1. definíció azt mondja, hogy pontosan N db elem van az ε sugarú környezeten kívül. De a véges sok elem között mindig van legnagyobb és legkisebb, ami alkalmas felső ill. alsó korlátnak. Előfordulhat az is , hogy a sorozatnak a környezeten kívül egyáltalán nincs eleme, vagy csak a + ε - nál nagyobb, vagy a - ε -nál kisebb eleme nincs. Ezért a felső korlát K = maximum{a1, a2, ...aN, a + ε}, az alsó korlát k = minimum{a1, a2, ...aN, a - ε}. Az ábra egy olyan esetet mutat, ahol a sorozatnak a N db ε sugarú környezeten kívüli elemei között van a + ε -nál nagyobb, és a - ε -nál kisebb eleme is.

(23)

Ha az an sorozat korlátos, akkor nem szükségképpen konvergens. Ilyen sorozatok például a táblázat dn, gn, hn

sorozatai. Ezt úgy is szoktuk fogalmazni, hogy a korlátosság a konvergencia szükséges, de nem elégséges feltétele.

an konvergens ⇒ an korlátos an korlátos ⇏ an konvergens Halmaz ábrával:

Tudunk-e a konvergenciára elégséges feltételt megfogalmazni? Igen, ez a következő tétel, amit bizonyítás nélkül közlünk:

Tétel: Ha az an sorozat korlátos és monoton, akkor konvergens.

DE!

Ha az an sorozat konvergens, akkor nem szükségképpen korlátos és monoton. Ilyen például a cn sorozat, ami konvergens, de nem monoton.

Ezért: A korlátosság és monotonitás a konvergencia elégséges, de nem szükséges feltétele.

an konvergens ⇏ an korlátos és monoton an korlátos és monoton ⇒ an konvergens Halmaz ábrával:

3. Nevezetes sorozatok határértékei

A következőkben néhány nevezetes sorozat határértékét vizsgáljuk meg. Az an=1/n sorozat már többször előfordult, tudjuk, hogy határértéke 0.

(24)

A második nevezetes sorozat a qⁿ sorozat. Ez különböző alapok esetében másképpen viselkedik. Az alábbi táblázatban láthatjuk a lényegesen különböző eseteket.

összefoglalva:

Különben osszillálva divergens a sorozat.

Ezután tekintsük az sorozatot, mivel n értéke páros és páratlan szám is lehet fontos az a > 0 kikötés (páros gyök alatt negatív szám nem állhat!). (A sorozat határértékét különböző a értékekre úgy is megsejthetjük, hogy a számológépünkbe beírunk egy tetszőleges pozitív számot, és elkezdjük "nyomogatni" a gyök billentyűt. Ha sokszor megismételjük a gyökvonás műveletet, akármilyen nagy, vagy akármilyan kicsi számból is indultunk ki egyszer 1 érték adódik, ami azt jelenti, hogy a sorozat elemek a számológép pontosságánál már jobban megközelítik az 1-et.)

Szemléltessük ezt a sorozatot is néhány a érték esetében.

Láthatjuk és bebizonyítható, hogy az sorozat határértéke minden pozitív n -re 1. Ha n > 1 , akkor a sorozat szigorúan monoton csökkenve tart 1-hez, ha n < 1 , akkor szigorúan monoton növekedve, n = 1 esetén a sorozat természetesen a konstans 1 sorozat lesz.

A következő nevezetes sorozat az , láthatjuk, hogy itt a gyökkitevőn kívül a gyök alatti mennyiség sem állandó, hanem a változó n érték. Mivel n mindig pozitív a gyök alatti mennyiségre nem kell kikötést tennünk, csak a gyökkitevő miatt kell n > 1 -re vizsgálnunk a sorozatot, mivel a legkisebb gyökkitevő a 2, más szóval a négyzetgyök. Először kiszámítjuk a sorozat határértékét, majd megnézzük a századik elem közelítő értékét 20 tizedes jegyig, végül ábrázoljuk a sorozat néhány elemét:

[ >

(25)

[ > Közelítés := evalf(c, 20)

[ >

A sorozat szigorúan monoton csökken az első két elemet kivéve, határértéke 1. Tehát a 4. nevezetes sorozat határértéke:

A következő nevezetes sorozat egy olyan hatvány, ahol az alap és a kitevő is változik. A pénzügyi számításokban is előfordul, ahogy egy további fejezetben látni fogjuk.

A sorozat:

Számoljuk ki a sorozat néhány elemét:

...

[ >

[ > közelítés : = evalf (b, 20);

(26)

A határértékre most "nem szám" adódott, hanem azt írta ki a program, hogy e. Mi az e szám és mennyi az értéke? Az e egy irracionális szám (végtelen nem szakaszos tizedestört), ezért csak közelítő értékét tudjuk megadni, ezt számolta ki a program 20 tizedesig. Milyen irracionális számokat ismerünk még? A π, a biztosan mindenkinek eszébe jut.

Ha egy kicsit megváltoztatjuk a sorozatot és a zárójelben szereplő tört számlálója tetszőleges való szám lesz a határérték így változik:

, ahol

4. Műveletek konvergens sorozatokkal

Az előbbi részben öt nevezetes sorozat határértékével ismerkedtünk meg, de nyilvánvaló, hogy nem csak ennek az öt sorozatnak a határértékére vagyunk kíváncsiak. Hogyan tudjuk más sorozatok határértékeit meghatározni ezekre a nevezetes sorozatokra építve? Erre ad választ a műveletek konvergens sorozatokkal fejezet. Ha adott két konvergens sorozat an és bn és ismerjük mindkettő határértékét, vagyis tudjuk, hogy és

, akkor sorozatok is konvergensek és

(27)

, ahol b ≠ 0 és bn ≠ 0 , ahol c konstans és a > 0

, ahol a > 0

Mit jelent ez? Nézzünk meg néhány példát.

Mit alkalmaztunk? A 2. műveleti azonosságot:

Mit alkalmaztunk? A 3. műveleti azonosságot:

A fenti két művelet egy más utáni alkalmazásával azt kapjuk, hogy ha egy számot n tetszőleges pozitív egész kitevős hatványával elosztjuk, akkor 0-hoz taró sorozatot kapunk, képletben: , ahol , és

További részletesen kidolgozott feladatok a tananyag 2. fejezetében találhatók.

5. Kritikus határértékek, rendőr-elv

Ez előző pontban megismert műveleti szabályok mindig alkalmazhatók sorozatok határértékének kiszámítására?

Sajnos nem, vannak ún. kritikus határértékek, ekkor mindig valami "trükköt " kell alkalmazni a határérték kiszámítására a műveleti szabályok egyszerű alkalmazásával nem érünk célba. Melyek ezek a kritikus határértékek? És mit értünk azalatt pontosan, hogy kritikus határérték?

Ha egy tört számlálója és nevezője is 0-hoz tart, hova tart a tört? Ez az egyik leggyakrabban előforduló kritikus határérték. A műveleti szabály azért sem alkalmazható, mert az említett hányadost nem tudjuk értelmezni, de ha megnézünk néhány ilyen példát láthatjuk, hogy a hányados sorozat határértéke bármi lehet.

Az első példában a számláló , a nevező , mindkettő (a számláló és a nevező is) 0-hoz tart, ha n tart ∞- hez. Ha felhasználjuk a törtek osztásának szabályát (a számlálót az osztó reciprokával szorozzuk), akkor n adódik, tehát a határérték ∞.

A következő példában cseréljük meg a tört számlálóját és nevezőjét. Ekkor is igaz, hogy a tört számlálója és nevezője is a 0-hoz tart, de az eredmény most , aminek a határértéke 0.

(28)

Végül nézzünk egy olyan példát, ahol a számláló és a nevező is 0-hoz tart, a hányados pedig egy véges számhoz, mondjuk 2-höz.

Láthatjuk, hogy mi is a probléma ezzel a határérték típussal, nem tudjuk megmondani, hogy mi lesz a hányados határértéke, mert a konkrét sorozatoktól függően bármi lehet. A többi kritikus határérték esetében is ez okozza a gondot, az eredmény lehet akármi, 0, ∞, tetszőleges valós szám.

összefoglalva a kritikus határértékek:

Ha és , akkor sorozat határértékéről nem tudunk semmit sem mondani.

A következőben még egy módszert ismertetünk egy sorozat határértékének kiszámítására, ez a Rendőr-elv

Adott három sorozat an, bn és cn , és tudjuk, hogy b1 az a1 és c1 között helyezkedik el a számegyenesen, vagyis a1

≤ b1 ≤ c1, hasonlóan a2 ≤ b2 ≤ c2, és így tovább minden n-re. Továbbá a bn-et közrefogó két sorozat an és cn

határértéke megegyezik, és ez a közös határérték A , akkor bn sorozatnak "sincs más választása, kénytelen lesz"

A -hoz konvergálni.

Matematikai jelőlésekkel:

Adott három sorozat an, bn és cn

Egy sorozat határértékét rendőr-elvvel meghatározni azért nem könnyű, mert kell keresnünk egy, a sorozatunknál elemenként nagyobb és egy, elemenként kisebb sorozatot és még annak is teljesülnie kell, hogy a két sorozatnak ugyanaz legyen a határértéke.

Nézzünk egy példát!

Számítsuk ki a határértéket! A számláló és a nevező is ∞-hez tart, ez egy "kritikus" határérték.

(29)

Találtunk a sorozatunkhoz elemenként kisebb és nagyobb sorozatot. Most már csak azt kell megnézni, hogy mi a két közrefogó sorozat határértéke. Tudjuk a 2. nevezetes sorozat határértékét:

, ezért , így a keresett határérték

Szemléltessük eredményünket, ábrázoljuk a három sorozat néhány elemét koordináta - rendszerben:

[ >

6. Egy pénzügyi alkalmazás

Pénzügyi számítások során gyakran találkozunk sorozatokkal, de ez általában egy sorozat néhány értékének kiszámítása. Például a kamatoskamat számításnál, hitel törlesztőrészletének, betét értékének meghatározásánál.

Ezekben a feladatokban a sorozat néhány elemét, vagy néhány elemének összegét kell kiszámítanunk.

Határértéket, a sorozat viselkedését a végtelenben általában nem vizsgáljuk, pedig a matematikai analízis

(30)

Az e-hez és e hatványaihoz tartó nevezetes sorozat "pénzügyes " háttere:

"Az e talán nem mindenkinek tűnik annyira "természetesnek ". Nevét onnan kapta, hogy többek között olyan alapvető életfolyamatok modellezésében is találkozhatunk vele, mint a növekedés és a fogyás. Nem is beszélve arról a szintén alapvető dologról, amely (Erdőst leszámítva) gyakran foglalkoztatja az embereket nevezetesen a pénzről. Az e központi szerepet játszik a kamatos kamat számításánál. Tegyük fel, hogy 1 dollárt teszünk egy olyan bankba, ami 100% tőkésített kamatot ígér egy évre. Egy másik pénzintézet a tőkésítést fél évre vállalja.

Utóbbi esetben jobban járunk, mivel a hat hónap letelte után a befektetett összeg 50%-ának megfelelő kamatot kapunk, azaz 50 centet. Év végére persze már a kamat is kamatozik, így tizenkét hónap elteltével a teljes összeg 2 dollár 25 centre nő. Na és mi van akkor, ha az évi 100%-os kamat negyedéves bontásban értendő? Egy év után ebben az esetben már 2 dollár 44 centünk lesz. Ha pedig évente nyolcszor számolunk kamatot, 2 dollár 57 centet tehetünk zsebre. Végül mi történik, ha a túlságosan is nagylelkű Erdős Bank folyamatosan kínálja az évi 100%

kamatot? Vajon Erdős szavaival élve "végtelenül gazdagok " lennénk-e 12 hónap elteltével? Nem egészen. Az összeg, amelyre ily módon szert tehetünk, nem lenne több, mint e, vagyis 2,718 - dollár. " Paul Hoffman: A PRÍM ember ERDőS PÁL kalandjai a matematika végtelenjében

Számoljunk végig egy olyan példát, ahol a kamat hozzáadása a tőkéhez (tőkésítés) nem év végén történik, hanem félévente, negyedévente, stb.:

Számoljuk ki 1 Ft felnövekedett értékét, ha az éves kamatláb 12% és a tőkésítés arányos kamatlábakkal félévente, negyedévente, havonta, illetve naponta történik.

Félévente: , vagyis a növekedés 12,36%

Negyedévente: , vagyis a növekedés 12,55%

Havonta: azaz , vagyis a növekedés 12,68%

Naponta: az arányos kamatláb ekkor ,azaz , a növekedés 12,70%

Folytonos kamatozás esetén: , ahol m az évi tőkésítések száma, i pedig a kamat, , ami közelítőleg 12,75%-os növekedés.

A folytonos kamatozásnál nyert érték a különböző kamatozási folyamatok felső határa. Ha nem 1 Ft, hanem C0; és nem egy év, hanem n szerepelt volna a példában, akkor az éves kamattényezőt még n-dik hatványra kellene emelni és a C0-lal szorozni.

7. Részletesen kidolgozott feladatok a sorozatok témaköréből

7.1. Monotonitás, korlátosság

7.1.1. 1. feladat

(31)

Mielőtt a bizonyításhoz kezdünk, számítsuk ki a sorozat néhány első elemét!

Sejtés: a sorozat szigorúan monoton nő

Számítsuk ki az an+1 - an különbséget, ha pozitív eredményt kapunk, akkor bebizonyítottuk a sejtést.

an+1 felírása: az an képletébe n helyére (n+1)-et írunk, fontos, hogy mindig tegyük zárójelbe! (A zárójel néha elhagyható, de ha nem vagyunk benne biztosak, hogy mikor, azt javaslom, mindig írjunk zárójelet, mert akkor biztos nem követünk el hibát.)

A fenti sorban felbontottuk a zárójeleket és összevontunk. Ezután közös nevezőre hozzuk a két törtet, mivel a nevezőknek nincs közös tényezője (a legnagyobb közös osztójuk 1) a közös nevező a két nevező szorzata lesz:

Látható, hogy a közös nevezőre hozás mindkét törtnél lényegében törtbővítés volt. Az első tört számlálóját és nevezőjét is megszoroztuk n + 3 -mal, a második törtet n + 4 -gyel bővítettük. Most közös a nevező, ezért a kifejezésünket egy törtként is felírhatjuk, majd a számlálóban felbontjuk a zárójeleket, ezután összevonunk. A nevezőben soha ne végezzük el a szorzást!

A nevező második tagjánál vigyázzunk, a zárójel előtt negatív előjel van, ez azt jelenti, hogy ha felbontjuk a zárójelet minden tag ellentétes előjelű lesz.

A számláló összevonása után kapott tört előjelét már könnyen megvizsgálhatjuk. A számláló 5, ez pozitív, a nevezőben n+4 > 0 és n+3 > 0, mert n > 0, ezért a szorzatuk is, így a nevező is pozitív. Ha egy tört számlálója és nevezője is pozitív, akkor a tört is az, tehát bebizonyítottuk az állítást, a sejtés igaz, a sorozat szigorúan monoton nő.

Korlátosság vizsgálata:

Ha egy sorozat szigorúan monoton nő, vagy monoton nő, akkor első eleme mindig alkalmas alsó korlátnak, k = a1 A felső korlát keresése előtt célszerû kiszámítani a sorozat határértékét.

A sorozat szigorúan monoton növekedve tart 2-höz. Ezért a 2 (de bármely 2-nél nagyobb szám is) alkalmas lesz felső korlátnak. Nézzük meg, hogy valóban igaz-e, hogy minden sorozat elem (ehhez a sorozat általános elemével kell elvégezni a vizsgálatot) kisebb, mint 2.

(32)

Vonjunk ki az egyenlőtlenség mindkét oldalából kettőt, majd hozzuk a bal oldali kifejezést közös nevezőre:

Vigyázat, negatív előjel a zárójel előtt!!!

Igaz egyenlőtlenséget kaptunk, mert a bal oldali tört számlálója negatív (-5), nevezője pozitív, mert n > 0, így a tört is negatív. Tehát a sorozat egy felső korlátjának K = 2 valóban megfelel.

összefoglalva: sorozatunk szigorúan monoton nő és korlátos, alsó korlátja k = a1=3/4, felső korlátja K = 2, konvergens, határértéke is 2. (Az alábbi ábra azt mutatja, hogy a sorozatok korlátaikkal együtt Excel programban is szemléltethetők.)

Most nézzük meg, hogy ugyanennek a feladatnak a megoldásában, hogyan segítenek a Maple utasítások?

[ > restart [ > with(plots):

[ > a(n):=(2*n+1)/(n+3) [ > a(1)

[ > a(2) [ > a(3) [ > a(n+1) [ > a(n+1)-a(n)

[ > simplify(a(n+1)-a(n))

[ > solve({n > 0, a(n+1)-a(n) > 0}, [n])

(33)

[ > limit(a(n), n = infinity) [ > K := limit(a(n), n = infinity) [ > l := [`$`([n, a(n)], n = 1 .. 10)]

[ > plot([l, k, K], n = 0 .. 10, style = [point, line, line], color = [blue, red, green], symbol = solidcircle, symbolsize = 20, thickness = [4, 2, 2], view = [0 .. 10, 0 .. 2])

7.1.2. 2. feladat

Sejtés: a sorozat szigorúan monoton csökkenő

(34)

Milyen előjelű a kapott tört? Számlálója negatív (-8), de vajon a nevező előjele mi lesz? Mindkét szorzótényező negatív a nevezőben, mert n > 0, azért szorzatuk pozitív. A tört negatív lesz, mert a számlálója és a nevezője különböző előjelű.

ezért a sorozat szigorúan monoton csökken.

Minden szigorúan monoton csökkenő és monoton csökkenő sorozat első eleme alkalmas lesz felső korlátnak, K = a1 = 6

Az alsó korlát kiszámítása előtt nézzük meg a határértéket:

Alsó korlátnak megfelelő lesz a -2, vagy bármely nála kisebb szám. Az alsó korlátnál minden sorozatelemnek nagyobbnak kell lennie, ezért a következő egyenlőtlenségnek kell teljesülnie:

an > - 2

Az egyenlőtlenség igaz, mert a számláló és a nevező is negatív, ezért a tört pozitív. A sorozat szigorúan monoton csökken, felső korlátja 2, alsó korlátja -2, tehát korlátos a sorozat, és így konvergens is, határértéke -2.

Ezt a feladatot is végigkísérhetjük Maple-ben az előző feladatnál felsorolt utasításokkal. A kapott ábra:

(35)

7.1.3. 3. feladat

n ≠ 5

Kikötést kell tennünk, mert a nevező nem lehet 0. Miért nem tettünk kikötést az előző feladatokban, hiszen ott is tört tagú sorozataink voltak? Ha tettünk volna kikötést ez az első feladatban n ≠ -3, a másodikban n ≠ 0,5 lett volna, de ezek az n értékek a sorozatoknál sohasem fordulnak elő, mert az n csak pozitív, egész szám lehet.

a5 nincs értelmezve

Mit mondhatunk ennek a sorozatnak a monotonitásáról, először csökken, majd felugrik egy nagyot, és újra csökkenni kezd. Ha valaki csak az első három tagot számolja ki az a sejtése támadhat, hogy ez a sorozat szigorúan monoton csökkenő. Nézzük meg, hogy a szokásos számolásból kiderül-e a sorozat „renitens

(36)

Vizsgáljuk meg a kapott tört előjelét, a számláló mindig negatív, tehát a tört előjelét a nevező fogja meghatározni. Ha n < 4 mindkét tényező negatív, a nevező pozitív, a tört negatív, tehát 4-nél kisebb n-ekre a sorozat szigorúan monoton csökken. Ha n > 5, akkor mindkét tényező pozitív, szorzatuk pozitív, a tört negatív, ekkor is szigorúan monoton csökken a sorozat. A fenti törtből a sorozat 4 és 5 közötti viselkedésére nem kapunk választ, ki kell számítanunk a megfelelő sorozatelemeket (amelyiket lehet).

Mondhatjuk azt, hogy a sorozat szigorúan monoton csökken, ha n > 5, általában is elmondhatjuk, hogy a sorozat viselkedése „nagy” n-ekre érdekel bennünket, a sorozat elején néhány „nem jól viselkedő taggal” nem kell törődnünk.

Hasonlóan az előzőekhez gyakorlásként meg lehet határozni a határértéket, a felső korlát K = 7, az alsó korlát k

= -5 lesz. összefoglalva a sorozat szigorúan monoton csökken, ha n > 5, felső korlátja K = 7, az alsó korlátja k = -5, tehát korlátos, ezért konvergens is, határértéke 1.

A megoldás lépései Maple utasításokkal is végigvihetők. A kapott grafikon a korlátokkal:

7.1.4. 4. feladat

an = - 2 n + 5

(37)

a1 = - 2 ⋅ 1 + 5 = 3 a2 = - 2 ⋅ 2 + 5 = 1 a3 = - 2 ⋅ 3 + 5 = -1

Sejtés: a sorozat szigorúan monoton csökken.

Bizonyítás:

an+1 - an = ( -2(n + 1) + 5) - ( -2n + 5) = -2n -2 + 5 +2n - 5 = -2 < 0 Tehát a sorozat valóban szigorúan monoton csökken.

Mivel a sorozat szigorúan monoton csökkenő a sorozat első eleme alkalmas lesz felső korlátnak, K = a1 = 3

A sorozat alulról nem korlátos.

Bizonyítás indirekt:

Tegyük fel, hogy van egy m szám, ami alkalmas alsó korlátnak, vagyis a sorozatnak nincs m-nél kisebb eleme.

Ezt képletben a következőképpen írhatjuk fel:

an > m minden n ∈ ℕ⁺ esetén -2n + 5 ≥ m

-2n ≥ m - 5

Vigyázat! Negatív számmal való osztás, az egyenlőtlenség irány megfordul!

A kapott végeredmény nyilvánvaló lehetetlenség, hiszen n bármilyen nagy pozitív természetes szám lehet. Az ellentmondást csak úgy oldhatjuk fel, hogy eredeti állításunk hamis volt, vagyis a sorozatnak nincs alsó korlátja.

összefoglalva a sorozat szigorúan monoton csökken, felülről korlátos, felső korlátja K = a1 = 3 , alulról nem korlátos.

Maple-ben:

(38)

[ > a(1) [ > a(2) [ > a(3) [ > a(n+1)-a(n)

[ > limit(a(n), n = infinity) [ > solve({a(n)-m >= 0}, [n]) [ > K := a(1)

[ > l := [`$`([n, a(n)], n = 1 .. 10)]

[ > plot([l, K], n = 0 .. 10, style = [point, line], color = [blue, red], symbol = solidcircle, symbolsize = 20, thickness = [4, 2], view = [0 .. 10, -16 .. 4])

7.2. Két (egyváltozós) polinom hányadosának határértéke

Az an = 1/n sorozat határértékére visszavezethető feladatok

A polinomok határértéke mindig ±∞ , ha n → ∞ , tehát ha két polinom hányadosának határértékét szeretnénk kiszámítani, az mindig egy ± ∞ / ± ∞ típusú kritikus határérték. Ezért ki kell találni valami olyan módszert, amivel azonos átalakítások segítségével addig formáljuk a kifejezéseket, amíg a határérték már nem lesz kritikus.

Mi a polinom? Egy változó, jelen esetben „n” hatványai számokkal szorozva és összeadva, csökkenő hatványok szerint rendezve. Pl.:

4n³ + 5n² - 2n + 11, ez n változó harmadfokú egyváltozós polinomja.

A definíció szerint összeadásnak kell szerepelni a hatványok között, a fenti példában azonban van egy kivonás

(39)

4n³ + 5n² + (- 2)⋅ n + 11 formába is írható.

Az „n” hatványok előtti szám-szorzókat együtthatóknak szoktuk nevezni.

A legnagyobb kitevőjű hatvány előtti együttható a főegyüttható.

7.2.1. 1. feladat

Számítsuk ki a következő határértéket:

Láthatjuk, hogy a számlálóban és a nevezőben is elsőfokú polinom van (n = n¹). A számlálót és a nevezőt is elosztjuk tagonként n-nel. Megtehetjük-e ezt anélkül, hogy megváltozna a tört értéke? Ez azonos átalakítás, nevezetesen tört egyszerûsítés, hasonlóan

átalakításhoz, (ahol a törtet 3-mal egyszerűsítettük) tehát a tört értéke nem változik.

Tudjuk, hogy , vagy másképp , ha

Ezután a szürke keretben levő műveleti azonosságokat alkalmazzuk:

(40)

A számláló határértékére az 1. azonosság alkalmazható (kivonás), a számláló határértéke:

an = 2 (konstans 2 sorozat: 2, 2, 2, ), a = 2, b = 0, 2 – 0 = 2

A nevező határértékére szintén az 1. azonosság alkalmazható (összeadás), a nevező határértéke:

, bn = 5 a = 0, b = 5, 0 + 5 = 5

A tört határértékéhez már csak a 4. azonosságot kell felhasználni, és adódik, hogy ha a számláló határértéke 2, a nevezőé pedig 5, akkor a tört határértéke 2 / 5 lesz.

Tehát:

Maple-ben a limit utasítás azonnal megadja a sorozat határértékét.

[ >

[ > plot([l, h], n = 0 .. 10, style = [point, line], color = [blue, red], symbol = solidcircle, symbolsize = 20, thickness = [4, 2], view = [0 .. 10, 0 .. .5])

(41)

7.2.2. 2. feladat

A számláló és a nevező fokszáma megegyezik, mindkettő másodfokú polinom. A legnagyobb kitevőjû hatvány az n², ezzel osztjuk el a számlálót és a nevezőt is. A következő adódik:

Az egyszerűsítések után:

a szürke táblázat 2. és 3. azonosságát alkalmaztuk.

(42)

Általánosan is elmondhatjuk, hogy a (a számlálóban c egy állandó szám, a nevezőben n pozitív, egész kitevőjû hatványa az (n^k) típusú határérték mindig 0.

Az előző feladatban megnéztük, hogy és ugyanígy igazolható az is, hogy Ezután az 1. és 4. azonosság alkalmazásával adódik, hogy a határérték

A szemléltetést a Maple segítségével végezzük el. Az ábrára pillantva, észrevehetjük, hogy a sorozat csak a 2.

elemtől kezdődően szigorúan monoton növekvő és azt is, hogy ennek a sorozatnak a konvergenciája sokkal

„lassúbb” az előzőnél. Ott már a 10. elem 0,05-nél kevesebbel tér el a határértéktől, itt még a 20. elem eltérése is csaknem 10-szer annyi (0,5).

7.2.3. 3. feladat

A következőben egy olyan tört határértékét számítsuk ki, ahol a számláló fokszáma nagyobb a nevező fokszámánál:

(43)

Magyarázat: A legnagyobb hatvány n³, tehát ezzel osztjuk el a számlálót és a nevezőt is. Felhasználva az ismert azonosságokat azt kapjuk, hogy a számláló 1-hez, a nevező 0-hoz tart. A nem kritikus határértékek között felsoroltuk a szám/0 típusú határértéket, ami végtelen. Azt, hogy +, vagy végtelent kapunk-e a számlálóban és a nevezőben is a legnagyobb kitevőjû tagok előjele határozza meg. Ez a számlálóban az n³, a nevezőben a 3 n², mivel mindkettő pozitív szám, az eredmény +∞ lesz.

...

7.2.4. 4. feladat

Számítsuk ki a következő határértéket, a számláló fokszáma most legyen kisebb a nevező fokszámánál:

(44)

7.2.5. összefoglalás

7.2.6. 5. feladat

Mit tegyünk, ha gyök is szerepel a feladatban? Először azt az esetet vizsgáljuk, amikor csak a nevezőben, vagy csak a számlálóban van gyök. n > 1 kikötést azért kell megtennünk, hogy a nevezőben ne legyen a gyök alatt negatív szám.

, mert 2n > 0.

Magyarázat: A számlálóban levő kifejezést bevisszük a gyök alá. Gyök alá úgy viszünk be egy (nem negatív) kifejezést, hogy négyzetre emeljük. (Általában, ha n. gyök alá visszük be, akkor n. hatványra emeljük.)

(45)

7.2.7. 6. feladat

Ha a számláló és a nevező is azonos kitevőjű gyök alatt van. Ekkor közös gyök alá visszük és a gyök alatt a két polinom hányadosára vonatkozó szabály szerint járunk el.

Felhasznált azonosság:

(46)

7.2.8. 7. feladat

Ha a számláló és a nevező gyökének fokszáma különböző, Azért, hogy a feladat nevezője ne legyen 0, az n > 1 kikötést kell tennünk.

A felhasznált azonosságok:

Azt is mondhatjuk, hogy a számláló fokszáma (a legnagyobb kitevőjű hatványának fokszáma) 3/2, harmadik hatvány a második gyök alatt, a nevező fokszáma (a legnagyobb kitevőjű hatványának fokszáma) 2/3 , második hatvány a harmadik gyök alatt. Mivel a számláló fokszáma nagyobb, mint a nevezőé, a határérték ∞.

(47)

7.3. A q

ⁿ

sorozat határértékére visszavezethető feladatok

A feladatok megoldása során gyakran felhasználjuk a középiskolában tanult hatványozás azonosságokat.

7.3.1. 1. feladat

Ebben a feladatban egy olyan törtet vizsgálunk, amelynek a nevezője egytagú (nincs a tört nevezőjében összeadás, kivonás) Az azonosságokat ebben a leckében kicsit szokatlan módon visszafelé alkalmazzuk.

Mindenki előtt ismert, hogy két azonos nevezőjû törtet így adunk össze:

(48)

„Fordítva” alkalmazva ez azt jelenti, hogy ha egy tört számlálójában összeg van, akkor két azonos nevezőjű tört összegévé bontható.

, feladatunkban:

Most nézzük az összeg két tagját külön, hogyan alakíthatók tovább. Az első tag számlálójában az 1. hatványozás azonosságot alkalmazzuk, ezt is „fordítva” jobbról balra olvassuk most: összeget látunk a kitevőben és azt azonos alapú hatványok szorzatává alakítjuk.

Ezután 3ⁿ -nel egyszerûsítünk és megkapjuk az összeg első tagját, ami 9. A második tag átalakítása: Tudjuk, hogy 1 minden hatványa 1, vagyis 1ⁿ = 1 bármely n-re. Így

Az utóbbi egyenlőség a hatványozás 5. azonosságát használta fel (jobbról balra visszafelé) Foglaljuk össze az átalakításokat és számoljuk ki a határértéket:

A határérték kiszámításánál azt használtuk fel, hogy mert az alap abszolút értéke kisebb egynél, azaz számokkal és jelekkel:

Az ábrán nyomon követhető a "villámgyors" konvergencia.

(49)

7.3.2. 2. feladat

Most egy olyan határértéket számítsunk ki, ahol a nevező többtagú és a hatványalapok is különbözők:

Először alkalmazzuk az 1. és 2. hatványozás azonosságot:

Próbáljuk a tagokat külön alakítani. A számláló 1. tagja

Mit használtunk itt fel? Az egész számok törtekkel való szorzásának szabályát.

Általánosan ezt így is írhatjuk:

a számlálót az egész számmal megszorozzuk, a nevező változatlan marad.

A számláló 2. tagja: 4⋅ 3ⁿ⋅ 3² = 4⋅ 3²⋅ 3ⁿ = 4⋅ 9⋅ 3ⁿ = 36⋅ 3ⁿ

Mit használtunk fel? A szorzás tényezői tetszés szerint felcserélhetők. Idegen szóval a szorzás kommutatív:

a⋅ b = b⋅ a

természetesen nemcsak két, hanem több tényezőre is igaz, hogy a tényezők tetszés szerinti sorrendbe írhatók. Mi a feladatban 3 tényezőre alkalmaztuk a kommutativitást.

Hasonlóan alakítható a nevező 2. tagja is: 5⋅ 2ⁿ⋅ 2 = 5⋅ 2⋅ 2ⁿ = 10⋅ 2ⁿ

Gyakori hiba, hogy az eredmény 20ⁿ. Ez miért nem jó? Az n. hatvány csak a 2 alapra vonatkozik a 10-re nem.

10⋅ 2ⁿ≠20ⁿ 10ⁿ⋅ 2ⁿ = (10⋅ 2)ⁿ = 20ⁿ Hol tartunk most a fenti átalakítások után?

A hatványalapok közül (2, 3) válasszuk ki a nagyobb abszolút értékût, ez (3) és annak n. hatványával (3 ) osszuk el tagonként a számlálót és a nevezőt is:

Az 5. hatványozás azonosság és a lehetséges egyszerűsítések után a következő adódik:

(50)

A határérték kiszámításánál azt használtuk fel, hogy , mert az alap

Szép példát látunk egy nem monoton sorozatra.

7.3.3. 3. feladat

Számítsuk ki a következő határértéket, az újdonság ebben a feladatban az előzőekhez képest, hogy az egyik kitevőben szorzat van.

Ez a számláló 1. tagja a 2²ⁿ. Hogyan alakítjuk át?

Az átalakításhoz a 3. hatványozás azonosságot használtuk fel.

1. megjegyzés: ha a kitevőben a 2 és az n között nincs műveleti jel, ez mindig szorzást jelent, 2n = 2⋅ n 2. megjegyzés:

és is helyes átalakítás, de most a 2. számunkra a célravezető.

A további átalakítások az 1. és 2. hatványozás azonosság szerint az előző feladatoknál ismertetett módon végezhetők el.

(51)

Kiválasztjuk a legnagyobb abszolút értékû hatványalapot, ez most 4, 4ⁿ -nel osztjuk el a számláló és a nevező minden tagját. A nevező harmadik tagját így alakítjuk át:

Az osztások, az 5. hatványozás azonosság és a fenti átalakítás alkalmazása után kapjuk:

A határérték kiszámításánál azt használtuk fel, hogy

mert mindhárom alap abszolút értéke egynél kisebb szám.

7.3.4. 4. feladat

Eddig nem használtuk még a 4. hatványozás azonosságot és nem vizsgáltunk negatív alapot sem. Nézzünk most egy olyan feladatot, ami ezeket is tartalmazza.

A számláló 2. tagjában alkalmazzuk a 4. hatványozás azonosságot:

2ⁿ⋅ 5ⁿ = (2⋅ 5)ⁿ = 10ⁿ

(52)

A legnagyobb abszolút értékű hatványalap most a 10, ezzel osztjuk a tört számlálóját és nevezőjét, természetesen most is felhasználjuk az 5. hatványozás azonosságot.

A határérték kiszámításánál azt használtuk fel, hogy , mert mindkét alap abszolút értéke egynél kisebb szám.

7.3.5. 5. feladat

Változtassuk meg a feladatot úgy, hogy a legnagyobb abszolút értékű alap csak a nevezőben szerepeljen, a számlálóba 10 helyett írjunk egy kisebb számot, például 5-öt.

A határérték számításnál azt kaptuk, hogy a tört számlálója 3-hoz, nevezője 0-hoz tart. Ezt a matematikailag

„csúnya” felírást idézőjelbe tettem a 0-val való osztás miatt, de a határérték számítás elméletéből tudjuk, hogy ez nem ún. „kritikus határérték”, hanem tudjuk, hogy a sorozat a ∞-be tart. Hogyan tudjuk eldönteni, hogy +, vagy – végtelen lesz-e a határérték? A számlálóban és a nevezőben is el kell dönteni, hogy melyik tag a legnagyobb. Ez a számlálóban és a nevezőben is a 2. tag. Ezek egyikének előjele pozitív, (számlálóban a 3), a másiké negatív (a nevező 2. tagja), így hányadosuk negatív lesz, ezért a határérték -∞.

(53)

Ha a 20. tagot kiszámoljuk az már -752,132, a sorozat gyorsan "vágtat" a -∞ felé.

7.4. Néhány "∞-∞" típusú kritikus határérték kiszámítása

7.4.1. 1. feladat

Ha n → ∞, akkor n + 3 → ∞és , hasonlóan , tehát valóban a felírt kifejezés határértéke

"∞ - ∞" típusú kritikus határérték.

Ha egy kifejezést 1-gyel szorzunk, az értéke nem változik. Minden olyan tört értéke 1, amelynek a számlálója és nevezője megegyezik

Emlékezzünk az azonosságra is.

Szorozzuk meg a kifejezést 1-gyel, amit formában írunk fel.

Törtet egész számmal úgy szorzunk, hogy az egész számot a tört számlálójával összeszorozzuk, a nevezőt változatlanul leírjuk, ugyanígy járunk el tetszőleges egész és törtkifejezésekkel is.

(54)

Felhasználtuk az átalakítás során a azonosságot, a összefüggést, ami minden a≥0 esetére igaz.

A következő lépésnél vigyázzunk a zárójelfelbontásra különösen, ha a zárójel előtt negatív előjel áll! A folytatás:

Miért lett 0 a határérték? A számláló 4, a nevező határértéke +∞, a „nem kritikus határértékek között felsoroltuk, hogy a

Lassan konvergál a sorozat a 0-hoz, még 20. tagnál is legalább 0,4 az eltérés a határértéktől.

7.4.2. 2. feladat

Nem mindig lesz a számlálóban állandó szám az átalakítás után. Nézzünk erre is egy példát:

Eddig a szokásos átalakításokat végeztük el. A határértéket "∞-∞" típusú kritikus határértékből típusú, szintén kritikus határértékké alakítottuk.

Most osszuk el a számlálót és a nevezőt is n -tel. A gyök alá n-et négyzetre emelve n² formában vigyük be.

(55)

Nagyon gyorsan konvergál a sorozat 1-hez, már a 3. tagnál az ábrán szinte alig látható az 1-től való eltérés.

7.4.3. 3. feladat

Nézzünk még egy az előzőhöz hasonló példát:

Eddig a szokásos átalakításokat végeztük el. A határértéket "∞-∞" típusú kritikus határértékből típusú, szintén kritikus határértékké alakítottuk. Most osszuk el a számlálót és a nevezőt is n² -tel. A gyök alá n²-et négyzetre emelve (n²)² = n⁴ formában vigyük be.

A számláló 1-hez a nevező 0-hoz tart, az idézőjelbe tett osztásnak a számok körében nincs értelme, de mint határérték létezik és nem is kritikus, értéke ∞, mégpedig +∞, mert a nevező pozitív, ahogy a számláló nagyobbik tagja is az.

(56)

7.5. Az (1+1/n)

ⁿ

sorozat határértékére visszavezethető határértékszámítási feladatok

7.5.1. 1. feladat

Először a zárójelben levő kifejezést alakra kell hoznunk.

Az átalakításhoz a következőket használjuk fel: a + (-b) = a - b, vagy számokkal: 10 + (-3) = 10 - 3 , ha egy kifejezéshez (vagy számhoz) egy negatív kifejezést (vagy számot) hozzáadunk, az ugyanazt eredményezi, mintha a hozzáadott értéket kivontuk volna.

Törtet egész számmal úgy osztunk, hogy ha lehetséges elosztjuk a számlálót az egész számmal, ha nem a nevezőt szorozzuk meg vele. Ugyanígy végezzük el az említett műveletet algebrai kifejezésekre is. Algebrai kifejezéseknél általában a 2. módszer alkalmazható, ezért a számpélda és a „betűs” példa is arra vonatkozik.

,

Hogyan lehet eldönteni a felírásból, hogy törtet osztunk egész számmal, vagy egész számot törttel? Az egyenlőségjel helye mutatja meg. A kétféle felírást tilos összekeverni, mert egész más eredményre vezet.

Nézzünk mindkettőre ugyanazokkal a számokkal 1-1 példát és hasonlítsuk össze az eredményt:

Egész számot törttel osztunk: