Nemlineáris hőterjedés és hőképanalízis

(1)

Nonlinear Extension of the Heat Equation and Infrared Imagery

Nemlineáris Hőterjedés és Hőképanalízis

Ildikó Jancskárné Anweiler

Supervisors Dr. László Czúni

and

Dr. Amália Iványi

University of Pannonia

Faculty of Information Technology

Information Science & Technology PhD School

2009

(2)

Nemlineáris Hőterjedés és Hőképanalízis Értekezés doktori (PhD) fokozat elnyerése érdekében

a Veszprémi Egyetem Informatikai Tudományok Doktori Iskolájához tartozóan

Írta:

Jancskárné Anweiler Ildikó

Témavezető: Dr. Czúni László és Dr. Iványi Amália Elfogadásra javaslom (igen / nem)

(aláírás)**

A jelölt a doktori szigorlaton …... % -ot ért el,

Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: …... …... igen /nem ……….

(aláírás) Bíráló neve: …... …...) igen /nem

……….

(aláírás) ***Bíráló neve: …... …...) igen /nem

……….

(aláírás) A jelölt az értekezés nyilvános vitáján …...% - ot ért el

Veszprém/Keszthely, ……….

a Bíráló Bizottság elnöke A doktori (PhD) oklevél minősítése…...

………

Az EDT elnöke

(3)

I want to express my thank to the supervisors, Dr. Lászó Czúni PhD and Dr-Habil.

Amália Iványi DsC PhD for all help and support of my PhD work. I want to thank her/him for taking time and having patience during the research and for giving motivation for continued efforts.

I wish to thank to my colleagues at the University of Pécs, Department of Information Technology, Pollack Mihály Faculty of Engeenering, who assisted in direct or indirect way to my thesis. In particular I give my gratitude to Dr. Lajos Szakonyi, the head of Department, for his support to carry out this research and to Zoltán Sári for interesting discussions and good collaboration. Finally, I wish to thank my family for all support over the last years.

(4)

Kivonat

A jelen PhD értekezés első témaköre a nemlineáris parabolikus hőegyenlet megoldására dolgoz ki numerikus eljárást. A mérnöki gyakorlatban használatos szimulációs modellrendszerek jelenleg még nem tartalmazzák beépített elemként a hőmérsékletvezetési együttható (hődiffuzivitás, hőmérséklet-eloszlási tényező) hiszterézises hőmérsékletfüggését kezelni képes paraméter-beállítás lehetőségét, ezért az ilyen jellegű vizsgálatokhoz elengedhetetlen saját elvek kidolgozása. Az értekezésben egy, az erőforrás és számítási idő igény csökkentésének céljából, a multigrid módszer adta lehetőségeket kiaknázó, megfelelő pontosságú és jó konvergencia tulajdonságú, a nemlineáris parabolikus hőegyenlet szemi-implicit, hierarchikus megoldórendszerének kifejlesztésére kerül sor. A disszertáció értékeli a kifejlesztett nemlineáris diffúziós együttható hőterjedésre gyakorolt speciális hatását.

Kifejlesztésre kerül egy speciális, a szakirodalomban publikált módszerektől eltérő, fuzzy szabálybázis alapú nemlineáris diffúziós képsimító eljárás. A cél olyan jellegű hőképek feldolgozása, amelyek a vizsgált jelenségből kifolyólag elmosódott éleket, diffúz hőmérsékleti foltokat, félig-átlátszó turbulens szabad gőzáram sugárzási mintáit tartalmaznak, és a klasszikus módszerekkel feldolgozásuk nem hatékony, vagy nem szolgáltat olyan jó eredményt, mint a kidolgozott nemlineáris szűrővel.

A második témakörben kidolgozásra kerül egy, a homogén, kétfázisú, fáziátalakulással járó áramlási modellekben alkalmazható, hőmérsékletfüggő fázisváltozási modell. A kifejlesztett modell a fázisátmenetet jellemző paraméter hőmérsékletfüggését egy hiszterézis operátor segítségével veszi figyelembe, lehetővé téve metastabil fázisátmenetek vizsgálatát is. Az új fenomenológikus hiszterézis modell az állapotegyenlet típusú fázisátmeneti modellek kiterjesztett változatának tekinthető. A kidolgozott modell előnye, hogy szakember által viszonylag könnyen paraméterezhető, numerikusan jól kezelhető, a mérlegegyenletekhez csatolható és áramló folyadékokban lezajló fázisváltozást is képes leírni, amelyet a bemutatott végeselemes modellezőrendszerben megoldott feladat is igazol.

A harmadik témakör szabadba kilépő gőzáram infravörös sugárzási képeire eddig még nem alkalmazott, minőségi és mennyiségi képfeldolgozási eljárást vezet be. A disszertációban kidolgozott eljárás bizonyítja, hogy a kondenzálódott vízcseppek hősugárzási képe megfelelő előkészítés után lehetőséget ad a turbulens áramlás pillanatnyi és átlagolt jellemző paramétereinek meghatározására. A kifejlesztett új, iteratív, inverz eljárás segítségével a keresztmetszeti hőmérséklet és abszorpciós együttható eloszlása függvénnyel közelíthető, amelyből megfelelő megfontolásokkal a gőzáramban lévő cseppfolyós vízmennyiség megbecsülhető.

(7)

Abstract

This thesis concerns with two direct and one inverse heat transfer problems coupled to infrared image processing. In the first part a new, coarse level iterating multigrid algorithm is developed for solving 2D nonlinear parabolic heat equations including hysteretic type diffusion coefficients. The developed hysteretic and fuzzy-rule based nonlinear diffusion models are applied for smoothing of thermal images.

In the second part a new, phenomenological, temperature dependent hysteresis model of vapour-liquid phase transitions is developed in order to improve the accuracy of the existing equation-of-state type phase transition models.

In the third part a thermal image based new inverse algorithm is developed for estimating qualitative and quantitative properties in free steam jets.

(8)

Zusammenfassung

Die Arbeit beschäftigt sich mit zwei direkten und einem inversen Problem im Bereich der nichtlinearen Erweiterungen der Wärmeleitungsgleichung und Wärmebildverarbeitung. In dem ersten Themabereich wird eine multigride Lösungsmöglichkeit für solche nichtlinearen Wärmeleitaufgaben entwickelt, wo die Wärmediffusivität oder die Temperaturleitfähigkeit temperaturabhängigen Hysteresis- Charakter hat. Die ausgeführten nichtlinearen Diffusionsvorgänge werden auch als Glättungsverfahren in der Bildverarbeitung der Wärmebilder angewendet.

In dem zweiten Themabereich wird ein neues, temperaturabhängiges Hysteresis-Modell von Typ Zustandsgleichung für die Lösung des durch die Dampf-Wasser- Zustandsänderung hervorgerufenen numerischen Problems entwickelt.

In dem dritten Themabereich wird aufgrund des Dampffreistrahls ein neues inverses Wärmestrahlungsverfahren entwickelt, um die durchschnittliche Temperatur und den Absorptionskoeffizienten zu definieren.

(9)

Aim of the Research

Numerical solutions of parabolic heat equations with variable thermal properties in more than one dimension require extensive resources and are time-consuming. Efforts to take into account the temperature dependence of thermal diffusivity, the primary material property in heat equations, recently tend towards polynomial or exponential approximations. The experimentally proved hysteresis of diffusivity for composite materials is yet to be included in numerical modelling systems applied in common engineering applications. In view of the experimental results, I introduced a correctly parameterized Preisach hysteresis operator to model heat diffusion in these composites using numerical simulations. The semi-implicit finite difference scheme with a high spatial resolution leads to a large system of equations with parameters that vary in time and space and have hysteresis memories at each mesh point. However, the required so- called inner iteration, because of hysteresis like temperature dependence of the diffusivity, could dramatically increase the computational cost by handling the local hysteresis at each grid point. In my research I set out to prove that by utilizing the potential of the full multigrid method, both the solution time and memory demands can be reduced. I would like to verify that stable and rapid convergence can be provided by the evaluated coarse level iterating multigrid method even in cases of hysteresis. Using test examples, I proved that due to the hysteretic character of diffusivity, heat transfer processes become non-symmetric which can be very different from constant (linear) processes.

Vapour-liquid phase transformation is an important phenomenon in many technological applications, since boiling and condensation are associated with high heat transfer efficiency. The heat transfer and fluid flow accompanied by liquid-vapour phase change processes have all the complexity of single-phase convective transport, plus additional elements resulting from motion of the interface, metastable phase stability, and dynamic interactions between the phases. Establishing accurate, numerically easy to handle models of these complex processes have recently been the focus of many scientific and engineering research projects. Mathematical models for vapour-liquid phase transformations can be divided into two classes: diffuse interface models and sharp interface models. With the diffuse interface method, all governing equations can be solved over the entire computational domain without any priori knowledge of the location of the interfaces, therefore using the diffuse interface is a popular tool for simulations of two-phase flows in engineering applications. Generally the diffuse interface model consists of three conservation equations of mass, momentum and energy, and of an evolution equation of the order parameter that represents the transition between the phases, i.e. the so-called four-equation model. In my research, I focused on the governing equation of the phase transition. The goal was to state a hysteresis function that describes the temperature dependence of the order parameter. The

(10)

wanted to develop a more easily parameterized model than the kinetic type phase transition models and to connect it to the governing equations of a homogeneous fluid flow model in which thermally induced phase transition can be expected with a predefined degree of supersaturation. I want to develop a permissible supersaturation limit for investigation in the thermodynamic aspect and to validate the evaluated model with a 2D finite element model of a fluid flow.

Thermal images represent special cases in gray-scale imaging because of the fact that their edges are blurred and the signal-to-noise ratio is worse than in normal (visible- domain) images. Infrared images can be degraded not only through errors in the imaging processes but also by the non-uniform properties of the surface where data have been collected and by the semitransparent character of the observed phenomenon.

In my research I focused on the infrared images of a semitransparent free jet flow. I set out to introduce special techniques that are not included in common image processing software for visualization and for qualitative and quantitative analyses. I investigated how the nonlinear extended parabolic heat equation, as a diffusion filter, can improve the visualization of thermal images. I also aimed to evaluate a new fuzzy rule-based extension to the diffusion filter, in which the diffusion coefficient is controlled by human knowledge based linguistic rules. My aim was to establish an efficient method of determining a flexible diffusion coefficient function for thermal images so that the result is more suitable for specific applications than the original image. I realized that thermal images of a free steam jet may be suitable for both qualitative and quantitative analyses. In qualitative analysis the characteristics of instantaneous turbulence flow fields is investigated with the fuzzy extended diffusion filter and with reconstruction from high frequencies and from thresholded wavelet modes. In quantitative analysis the summarized images are used and a new iterative inverse method is developed for both simultaneous estimation of temperature and absorption coefficient distributions and for approximating the liquid water content in the jet stream.

So, ultimately the aims of my research are: developing thermally induced, easy to parameterize, nonlinear (diffusion and phase transition) extensions of recently used numerical heat transfer models together with the appropriate discretization schemes, which support numerical simulations effectively in engineering applications;

introducing new image processing methods for infrared images which contain blurred edges or diffuse temperature regions and smooth signatures of semitransparent fluid flow; enhancement of visualization by smoothing the thermal images with the nonlinear extended heat equation and performing a quantitative analysis of free turbulent flow field with the newly developed inverse method.

(11)

1 New Multigrid Technique for Solving Nonlinear Heat Equations and its Application to the Smoothing of Thermal Images

1.1 Introduction

The purpose of this thesis is two-fold. Firstly, to develop a new, computational efficient multigrid algorithm for solving 2D nonlinear parabolic heat equations including hysteretic type diffusion coefficients. The second purpose is to prove the effectiveness of special smoothing effects of the hysteretic and fuzzy-rule based nonlinear diffusion models on thermal images.

The analyses of transient thermal responses in composite materials, for instance in chalcogenide glass, could be of great importance in various engineering and scientific fields. These materials have received a lot of attention over the past several years due to their wide range of applications both in engineering and scientific fields [36].

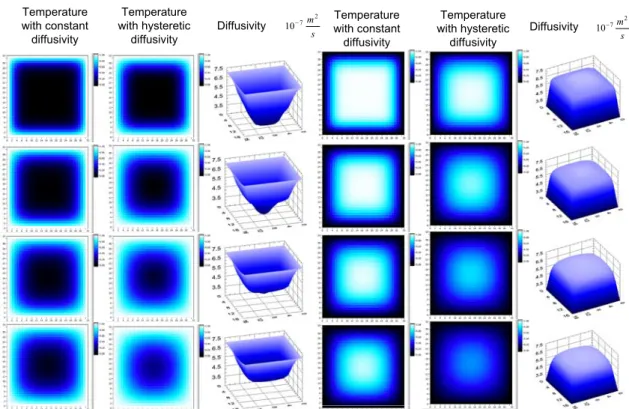
Experiments prove that thermal diffusivity of composite materials shows hysteresis like behaviour [113], [119]. For example hysteresis of thermal diffusivity of silica based materials used in coke oven linings is reported in [113]. The thermal conductivity of chalcogenide semiconductor glass has been studied in [133] and hysteresis properties appearing in certain compositions of Se-Te-Cu alloys have been proved. Measured hysteresis of thermal conductivity under an applied electromagnetic field can be found in [80]. The hysteresis is related to microstructure changes such as phase transitions, micro-cracking induced by thermal expansion anisotropy, interfacial decohesion between particles and so forth. In this study, I aim to prove that with an appropriate numerical model, transient thermal responses could be very different with constant and hysteretic diffusivity. With the proposed numerical method these differences could be analysed qualitatively.

Several numerical methods have been developed for the analysis of heat transfer problems in solids [56], [59], however solutions of transient problems with variable thermal properties in more than one dimension are very resource demanding and time- consuming, therefore most existing models have been developed under constant coefficient conditions. Efforts to take into account the temperature dependence of thermal diffusivity tend towards polynomial or exponential approximations [29], [44], [46]. Simulation of heat diffusion with hysteresis requires improvements to the presently applied numerical procedures. In this study I propose a semi-implicit numerical method that includes a hysteresis operator to describe the local temperature dependence of the diffusivity.

The parabolic heat equation with hysteretic diffusivity can only be solved numerically.

(12)

equations. In the last few years, the multigrid technique has become one of the most popular numerical solvers of large systems [18], [49], [50], [142]. The multigrid technique can produce very good convergence rates. It can solve a problem with N unknowns in O

( )

N time [121], however the required so-called inner iteration, because of hysteresis like temperature dependence of the diffusivity, can dramatically increase the computational cost by handling at each grid point the local hysteresis memory. In this study I propose a so-called coarse level iterating multigrid method to reduce the solution time and memory demands. When the exact solution of the problem is sufficiently smooth, which in diffusion processes is a reasonable assumption, this type of problem reduction does not cause considerable deviations in results. It will be stated that stable and rapid convergence can be provided by the proposed method even in cases of hysteresis, and both the memory demand and the computational time can be reduced by using the introduced hierarchical iteration technique.

I have presented the differences between the constant and hysteretic diffusions with transient 2D test examples. Results are provided by uniform and non-uniform initial conditions and constant or periodically changing first order type boundary conditions.

Transient nonlinear diffusion with a non-uniform initial condition leads to another possible interpretation of the heat diffusion problem in processing thermal images.

PDE-based diffusion models are widely used for image enhancement and denoising [109], [134]. In this study I focused on the special smoothing effects of the hysteretic diffusion coefficient in thermal images. Thermal images represent special cases of gray- scale images, where the pixel-intensity is proportional to the temperature of the surface where the data were collected. This results in edges which are blurred in thermal images and the signal-to-noise ratio is worse than in the normal (visible-domain) images [96]. I can verify that the enhancement of images can be achieved by using the proposed nonlinear diffusion algorithms, but there is no general rule to declare the intensity dependence of the diffusion coefficient even less so in hysteresis form. Therefore I replaced the hysteresis operator by a fuzzy decision system with intensity and/or gradient as input(s) and the local diffusion coefficient as output. Membership functions and fuzzy rules reflect the image enhancement demands defined by an expert. The proposed fuzzy diffusion technique is a novel approach to thermal image processing and could be very useful not only in enhancing visual inspection but also for pre-processing of images for thresholding or clustering by removing noise and/or smoothing only the predefined intensity region(s) without blurring or moving edges.

1.2 The Coarse Level Iterating Multigrid Method

In this section I developed a new iteration method for speeding up the numerical solution of a large nonlinear system of equations involving hysteresis of parameters.

This type of problems arises, for example, in numerical modelling of transient thermal responses in composite materials with variable thermal properties. This analysis could

(13)

be of great importance in various engineering and scientific fields. Several experiments prove that over a broad temperature range, the thermal diffusivity behaviour of ceramic composites can be hysteretic [80], [113], [133]. The hysteresis behaviour of the thermal diffusivity has to be approximated using an appropriate numerical model. In this study the scalar Preisach hysteresis model [57] is employed. In this section I focused on the potential of the multigrid technique where a material parameter shows hysteresis property. Thermodynamic aspects of phenomenological hysteresis modelling the temperature driven phase transitions are presented in the next point.

Multigrid is a technique rather than a fixed prescribed method and therefore there are no general rules about the method that is best to use for its subroutines. Accordingly, the multigrid algorithm has to be conditioned to the problem to be solved. I analysed the components of the Full MultiGrid method (FMG) on a simple steady-state heat conduction problem in Appendix A. My aim with this analysis was to select the appropriate multigrid components that were suitable for conductive heat transfer problems.

1.2.1 Model Definition with Hysteresis

In this study a 2D transient heat transfer problem is assumed with temperature- dependent thermal diffusivity κ (it is assumed that the temperature dependence of the volumetric heat capacity c_v can be neglected and the expression of thermal diffusivity

cv

λ

κ = is valid, where λ is the thermal conductivity). The heat equation is written with a dimensionless temperature θ in the form

( ) ( )

s

( )

t,

y y

x x

t κ θ θ κ θ θ θ

θ ₊

⎥⎦

⎢ ⎤

⎣

⎡

∂

∂ + ∂

⎥⎦⎤

⎢⎣⎡

∂

= ∂

∂

∂ , (1)

where the thermal diffusivity κ

( )

θ is a function of the temperature, the spatial coordinates x,y∈Ω, Ω=

[ ] [ ]

0,L × 0,L are held. The source term s

( )

θ t, is not detailed in this study. The initial condition of θ

(

x,y,0

)

=θ_init, x,y∈Ω and the first order boundary conditions θ

(

x,y t,

)

=θ_w, x,y∈∂Ω are assumed. The nonlinearity of the system originates from the composite material properties, since the diffusivity shows hysteresis like temperature-dependence. The thermal diffusivity as a function of the temperature is shown in Fig. 1 and corresponds to the measured data presented in [113].

Santos et al. [113] observed that during a heating cycle, in the range of lower temperatures, there is a sudden change in the thermal diffusivity, according to the microstructure modification, in the referred case, the phase transition of α →β cristobalite. Furthermore the thermal diffusivity upon heating remains relatively unaltered until a higher temperature range, where it presents another steep increase.

During cooling a reverse process takes place, but higher diffusivity values can be

(14)

expected. Furthermore, experiments showed that thermal cycling can reduce the hysteresis of diffusivity in composites.

In the following, I assumed that the temperature dependent diffusivity hysteresis could be modelled with a temperature dependent hysteresis operator [61], [69]. This assumption, i.e. that hysteresis of diffusivity has been invariably present, has been established by a series of steady state measurements in [113]. In this study an appropriate parameterized Preisach-type hysteresis model is introduced. Preisach-type of hysteresis models have been widely used to describe the ferromagnetic hysteresis [57].

0 0.2 0.4 0.6 0.8 1

25 30 35 40 45 50 55 60 65 70 75

θ κ ( 10-8 m2 /s)

cycle 2 cycle 1

cycle 3

Fig. 1. Hysteresis of thermal diffusivity with experimentally observed damping effects of thermal cycling [113]

The main assumption of the Preisach model is that the material can be modelled by a parallel summation of weighted elementary (bistable) hysteresis relays. Each relay is represented mathematically by a hysteresis operator γ_αβ , where α , β represent the state of relay ‘0’ and ‘1’. The Preisach hysteresis model can be applied as a general hysteresis function that has single-input single-output. When modelling the diffusivity hysteresis, the input is the temperature θ and the thermal diffusivity κ

( )

θ is the output.

In this macroscopic analysis, the physical interpretation of the elementary relay is unnecessary. A detailed microscopic explanation of the hysteresis phenomena in composites can be referred to in [19]. It can generally be considered that a relay corresponds to a homogeneous cluster of material, which has commonly changing physical properties, two states of an elementary bistability (cluster) corresponding to two different solid phases, at a low temperature stable phase and at a high temperature stable phase, respectively, and the hysteresis function represents the statistics on the probability of the state of those clusters. It has to be mentioned that in the referred literature [113] it is explained that there are some other microcrystal changes with changing temperature, for instance opening and closing of the internal flaws that could cause diffusivity variations as well.

(15)

The Preisach plane with coordinates of θ_α, θ_β are shown in Fig. 2a. Considering that each elementary hysteresis relay has a weight factor μ

(

θα,θβ

)

, by knowing the input history θ

( )

t , the output κ

( )

θ can be obtained by counting how many relays are in state

‘1’. Mathematically this counting process can be written as

( ) ( ) ( )

( )

∫∫

1

=

t S

, t d d

t μθ_αθ_β γ_αβθ θ_α θ_β

κ ,

(2) where S¹

( )

t is the plane that over the relays are in state ‘1’. Since γ_αβθ

( )

t =1 if

(

θ_α,θ_β

)

∈S¹

( )

t so (2) yields

( ) ( )

∫∫

( )

=

t S

, d d

t

1

β α β

αθ θ θ

θ μ

κ . To adapt the model to the right

scale, a bias thermal diffusivity κ₀ is added to the model.

θα

θβ k+1

θ θk

Fig. 2. a) The Preisach triangle with symbolic relays and b) the corresponding weight function interpreted over the discretized triangle

Repeated heating-cooling cycles can decrease the magnitude of the thermal diffusivity and decrease the area of the hysteresis loops as well. This can be introduced into the model through a cycle factor, ν . So, the continuous form of the modified Preisach operator is

( )

( ) ( )

( ) ^α ^β ^α ^β

ν

ν μθ θ θ θ

κ

θ t b d d

H

t S

∫∫

,

+

=

1

0 ,

(3) where ν is the heating-cooling cycle number, the bias thermal diffusivity κ^ν₀ depends on ν , b^ν is an appropriate multiplier that can vary with ν as well.

The numerical implementation of the Preisach scalar model is based on the Preisach triangle of elementary hysteresis relays. The normalized distribution function

(

^θ ^θ

)

¹ ₂

(

₁ ₂ ^σ₁² ^σ₂²

)

μ _α, _β = / N _D m ,m , , is discretized on a 500×500 grid, N₂_D represents the

(16)

variances σ₁², σ₂². The graphical representation of the applied distribution function can be seen in Fig. 2b. The diffusivity at grid points ^κ

( )

^θ^k⁺¹ is calculated by a recursive formula provided by discretization of the Preisach operator in (3)

( ) ( ) ( ) ( )

^, ⁱ ^j ^m^, ⁱ^,^j ^P

m b T H

j i ,

k P k

k

j

i ⎟⎟ ⋅ = ∈

⎠

⎜⎜ ⎞

⎝

±⎛

=

= ⁺

∑∑

+¹ θ ¹ κθ ^ν μθ_α θ_β

θ

κ , (4)

where T_P is the area of the domain over which in the last input step the hysteresis relays have changed their state and m is the number of relays in the domain P. The sign of the second part of the right-hand side depends on the direction of the temperature change.

The hysteresis cycles in Fig. 1 can be provided by the following parameters:

525

2 0

1 m .

m = = , σ₁ =σ₂ =0.18, in first thermal cycle κ¹₀ =28⋅10⁻⁸ m² s, b¹=1, in the second cycle κ₀² =27⋅10⁻⁸m² s, 57b² =0. and in the third and the other cycles

s m 10

26 ⁸ ²

0 = ⋅ −

κν , b^ν =0.43, ν =3,4,L. 1.2.2 Discretization of the Nonlinear Model

The solution domain Ω has been discretized by a Cartesian mesh with a uniform mesh size h=L n. Time differentiation is discretized by the Crank-Nicholson method that is second-order accurate [121]. The right hand side of (1) is discretized in two steps. First the thermal flux differences are calculated, considering cell interfaces at the distance of

2

±h from grid points, for example between points

( )

ij and

(

i+1,j

)

, the assumed flux is ^Ji₊₁₂,j =κi₊₁₂,j

(

θi₊₁,j−θij

)

^h, where κ_i₊₁₂_,_j is a space averaged diffusivity,

(

i,j i ,j

)

j ,

i₊₁₂ =0.5κ +κ₊₁

κ .

Depending on the time averaging of the diffusivity, various approaching methods can be obtained to (1). The Crank-Nicholson method with space averaged, time-instantaneous diffusivity has the form of

( ) ( ) ( )

(

1 1 12 12

)

¹²

2 1 1

1 2 1 1

1

1 1 ₊

± + ±

+± +

±+ +

+

+ Δ

− + Δ

+ Δ

Δ =

− _k _k

j , i k

j , i l,

k j , i l,

k j , i k

ij l, k

ij J J J J s

h

t θ σ σ

θ , (5)

where the first superscript k refers to the time step and the second superscript l refers to the iteration cycle. The weighting factor is σ =0.5 for the Crank-Nicholson method, J is the heat flux and ΔJ denotes the flux differences. Each flux difference has been computed in the same manner, for example

1 1

2 1 1 1

2

1 + +

+ − ++ +

±+ = −

ΔJ_i^k ^l,_,_j J_i^k ^l,_,_j J_i^k ^l,_,_j . (6)

(17)

The thermal fluxes in the iteration step l+1 and at time step k+1 are determined by the diffusivity hysteresis model k⁺¹l,⁺¹⁼

(

ij^k⁺¹^l,⁺¹

)

ij Hθ

κ . At time step k, the diffusivity hysteresis ^κ_ij ⁼^H

( )

^θ_ij^k is not involved in the inner iteration marked by l.

Another approaching scheme can be evaluated using time-averaged temperatures to determine the diffusivity hysteresis. In this case the discretized form of (1) is

( ) ( ) ( )

(

1¹2

)

¹²

1 2 1 1

1

1 1 ₊ ₊

± +

+

± +

+

± +

+

+ Δ

− + Δ

+ Δ

Δ =

− _k_l, _k

j , i l,

k j , i l,

k j , i k

ij l, k

ij J J J J s

h

t θ σ σ

θ . (7)

Grid points at time levels k and k+1 have the same values of diffusivity,

( )

(

ij^k

)

l, k ij l,

k

ij H . θ θ

κ ⁺¹² ⁺¹ = 05 ⁺¹ ⁺ . Graphical interpretation of the time centred diffusivity calculation is shown in Fig. 3.

( )

⎟

⎠

⎜ ⎞

⎝

= ⎛ ⁺ ⁻ ⁺

+ k

ij l, k ij l,

k

ij H θ θ

κ ¹² ¹ ¹

2

1 θ_ij^k⁺¹^l,

k

θij

k j , i+1

θ

k j , i−1

θ k l,

j , i

1 1 +

θ+ l, k

j , i

1 1 +

θ−

k j , i +1 k θ

j , i −1

θ

l, k

j ,

i 1

1 +−

θ θ_i^k_,_j⁺₊¹₁^l,

(

ij^k ^l

)

l k

j i l k

j i

, 2 1 , 2 1

1 , , 2 1

2 1

, 2

1 +

+ + + +

+ = κ κ

κ

Fig. 3. Semi-implicit finite difference method, diffusivity calculation with hysteresis operator at grid points of half time steps. Intergrid averaged diffusivities are used for the calculation of fluxes

Diffusivity at cell interfaces is interpolated linearly by

(

1¹² ¹ ¹² ¹

)

1 2 1

2

1 ⁺ 05 ₊⁺ ⁺ ⁺ ⁺ ⁺

++ ^l, = _i^k _,_j ^l, _ij^k ^l,

k j ,

i . κ κ

κ . (8)

The thermal flux across the cell interfaces at time level k+1 and in iteration cycle l+1 is calculated according to

( )

^h

J_i^k₊⁺₁¹₂^l,_,⁺_j¹=κ_i^k₊⁺₁¹₂²_,_j^l,⁺¹θ_i^k₊₁⁺¹_,_j^l,⁺¹−θ_ij^k⁺¹^l,⁺¹ . (9) At time level k the thermal flux is ^J

(

k ij^k

)

^h

j , i l, k

j ,

i₊₁⁺₂¹ =κ₊⁺₁¹₂² ⁺¹θ₊₁ −θ . All the other thermal fluxes could be derived in the same manner.

Substituting thermal fluxes (9) into (7) produces the so-called time-centred discretization scheme

(18)

( ) ( )

^s ^t^,

h p t

k ij k

j , i l, k

j , i k

j , i l, k

j , i k

ij

l, k

j , i l, k

j , i l,

k ij

Δ + Δ +

+

−

= Δ +

− +

+

± + +

±

± + +

±

+ +± + +± +

±+ +

+

2 1 1 1 2 1

2 1 1

1 2 1

2 2 1

1 1

1 1 2 1

2 1 1 1 1 1 2 1

2 2 1 1 1

1 2 1 2

θ κ

θ

θ κ

θ

(10)

where κ_i^k_±⁺₁¹₂²_,_j^l,⁺¹θ_i^k_±⁺₁¹_,_j^l,⁺¹ is an abbreviation of κ_i^k₊⁺₁¹₂²_,_j^l,⁺¹θ_i^k₊⁺₁¹_,_j^l,⁺¹+κ_i^k₋⁺₁¹₂²_,_j^l,⁺¹θ_i^k₋⁺₁¹_,_j^l,⁺¹ and so on and

( )

2

1 2 1

2 1 1 2 1

2 2 1

+ +

+ + +

− + + + + +

− + + +

= Δ _i^k _,_j^l, _i^k _,_j^l, _i^k_,_j ^l, _i^k_,_j ^l, h

p t κ κ κ κ . (11)

Assembling (10) for each interior node, it yields a system of equations

2 1 1

1 1 1 1

1 + + + + + +

+ ^l, ^k_h ^l, = ^k_h ^l, ^k_h + ^k_h

k

h θ B θ S

A , (12)

where A^k_h⁺¹^l,⁺¹ is the matrix of the coefficients on the left-hand side of (10), θ^k_h⁺¹^l,⁺¹ is the vector of unknown temperatures, B^k_h⁺¹^l,⁺¹ is the coefficients on the right-hand side, θ^k_h is the solution temperature vector at time step k, S^k_h⁺¹² is the vector of the source terms multiplied by Δt. Subscript h refers to the level of the spatial resolution.

The semi-implicit finite difference method (10) resembles the 2D variation of the DuFort-Frankel scheme, which is consistent with the original PDE only if

2 <<1

Δtκ_max h , where κmax=max

( )

κij , 1i,j=1,L,n− [121]. To avoid solutions that do not satisfy the physical nature of the modelled system, the upper limit to the time step can be evaluated from the following inequalityΔt≤h²

(

2

(

1−σ

)

κ_max

)

.

1.2.3 The Coarse Level Iterating Multigrid Solver

The nonlinearity of κ in method (10) needs iteration. The Newton iteration is very expensive in CPU time because of the large set of unknown variables [121]. Hysteresis- like temperature dependence of the diffusivity dramatically increases the computational cost by handling, at each grid point, the local memory in the discretized model (12).

Treatment of this memory is very resource and time consuming. The finer the resolution, the more hysteresis memory has to be treated. Using coarser resolution decreases the computational costs, but produces a coarser solution as well. In this study I suggest using a coarse level iterating multigrid algorithm, in which the fine resolution of the temperature field is preserved, but the hysteresis of diffusivity is reduced to a coarser grid, by utilising the multigrid algorithm that works on several resolutions [61], [65].

In a general case, the multigrid solver assumes an initial guess on the fine resolution for the diffusivity k ,

( )

^kh

h H θ

κ ⁺¹²⁰ = and for the temperature field θ^k_h⁺¹^,⁰ =θ^k_h. In every iteration cycle the diffusivity coefficients have to be re-calculated for all fine grid

(19)

points. To reduce the solution time, before the iteration, problem (12) should be reduced to the next coarser grid, with mesh size H =2h, in the form of

2 1 1

1 1 1 1

1 + + + + + +

+ ^l, ^k_H ^l, = ^k_H ^l, ^k_H+ ^k_H

k

H θ B θ S

A , (13)

where the initial temperature θ^k_H⁺^1,⁰ of time step k+1 has been determined by the restriction of the fine grid solution at time step k, θ^k_H⁺¹^,⁰ =θ^k_H =Rθ^k_h. The initial diffusion coefficient field has been defined with the hysteresis operator as κH⁰ =H

( )

θ^kH . The source term S^k_h⁺¹² has been restricted to S^k_H⁺¹², or S^k_H⁺¹² could be calculated directly as well. The temperature field approximation for time step k+1 and mesh size

H could be evaluated by iteration (13) with the new values of diffusivity

( )

(

¹ ¹⁰

)

1 2

1 ^l, 05 ^k_H ^l, ^k_H ^,

k

H⁺ ⁺ =H . θ ⁺ +θ ⁺

κ , until the absolute difference decreases below a

preliminarily defined ε limit, θ^k_H⁺¹^l,⁺¹−θ^k_H⁺¹^l, <ε. After this so-called inner-iteration, the diffusivity and the temperature are interpolated to the fine grid. By denoting P as the prolongation operator and I^h_H as the interpolation operator, the fine grid diffusivity is κ^k_h⁺¹² =S_GSPκ^k_H⁺¹²^l,⁺¹, the initial temperature is θ^k_h⁺¹^,⁰ =I^h_Hθ^k_H⁺¹^l,⁺¹. The prolonged diffusivity needs smoothing, S_GS denotes the Gauss-Seidel smoothing operator corresponding to ( A-14) in Appendix A. The interpolated temperature could be seen as a good initial solution to the grid level h. To evaluate the fine grid solution θ^k_h⁺¹, some multigrid V-cycles are applied, until the convergence criterion is reached. During the fine grid V-cycles the diffusivity field remains unaltered. The graphical scheme of the iteration method can be seen in Fig. 4.

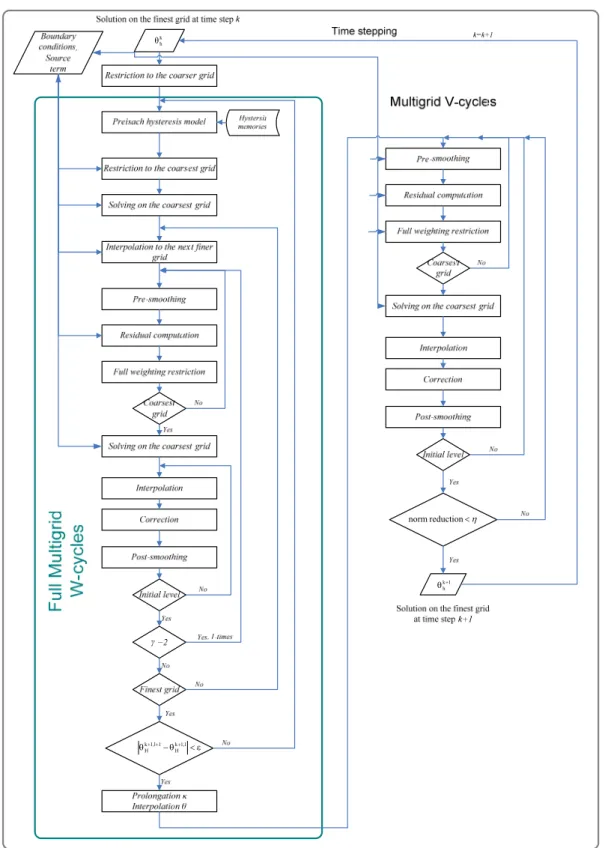
Fig. 4. Schematic representation of the coarse level iterating multigrid method

This proposed coarse level iterating hierarchical algorithm consists of two types of multigrid methods. The inner-iteration is on the coarser grid, the solver is the so-called full multigrid algorithm. The advantages of this FMG method are the exact initial

Nemlineáris hőterjedés és hőképanalízis

Nonlinear Extension of the Heat Equation and Infrared Imagery