A diklór-metán képlete CH2Cl2. A négy ligandum tetraéderesen rendeződik a szénatom körül. A klóratomoknak nagyobb a térigényük, mint a hidrogéneké, ezért a szerkezet libikóka alakú vagy torzult tetraéder.
C Cl Cl
H H
A molekula poláris, mivel a C−Cl kötések polárisak, és a dipólusvektorok eredője nem zérusvektor. (Megjegyzés: a molekula szimmetrikus, ám mégis poláris. Gyakran tévesen azt nevezik dipólusmolekulának, melyben a poláris kötések aszimmetrikusan helyezkednek el. Itt látható, hogy a kötések szimmetrikusan helyezkednek el, viszont a dipólusvektorok nem oltják ki egymást.)
Formaldehid:
A formaldehid összegképlete H2C=O. A központi szénatomhoz három ligandum kapcsolódik, ez háromszög alakban rendeződnek a szén köré. A molekula mind a négy atomja egy síkban helyezkedik el, a szén és oxigén atomok között kettős kötés van.
C O H
H
A molekulában a C−H kötés pedig apoláris, a C−O kötés poláris, ezért a formaldehid egy dipólusmolekula.
3.2.5. Összetett ionok szerkezete
Az összetett ionok alakját ugyanazok a hatások befolyásolják, mint a semleges molekulák esetében.
Az összetett ionok rendszerint delokalizált elektronrendszerrel rendelkeznek, ezért a ligandumok száma határozza meg az alakjukat.
Ammóniumion (NH4 +)
Mint korábban már említettük, az ammóniumion úgy keletkezik, hogy az ammóniához adunk egy H+-iont (protont), mely datív kötést létesít a nitrogénatom magános párjával. A négy hidrogén teljesen egyenértékű (minden N−H kötés egyenlő hosszú), ezért az ammóniumion szabályos tetraéder szerkezetű (a metánhoz hasonlóan).
N H H H H
Oxóniumion (H3O+)
Az oxóniumion a vízmolekula protonálásával keletkezik, a víz egyik magános párja és a H+-ion között létesül datív kötés, a három O−H kötéshossz egyforma. Mivel van egy magános elektronpárja is, a négy elektronpár tetraéderesen rendeződik el, így az oxóniumion szerkezete trigonális piramis (háromszög alapú piramis).
O H H H
Karbonátion (CO32−)
A karbonátion a szénsavból vezethető le úgy, hogy két H+-ionját (protonját) eltávolítjuk:
H2CO3 → 2 H+ + CO32−
.
A keletkező karbonátion delokalizált elektronrendszerrel rendelkezik, szerkezete szabályos háromszög vagy trigonális planáris alakú (így kerülnek a lehető legtávolabb egymástól az oxigének):
O C
O O 2
Nitrátion (NO3−
)
A salétromsavból (HNO3) egy H+-ion eltávolításával keletkező nitrátion a karbonátionhoz hasonlóan szintén szabályos háromszög vagy trigonális planáris alakú, elektronrendszere delokalizált:
O N
O
O
Szulfátion (SO42−)
A kénsav (H2SO4) kétértékű sav, mely azt jelenti, hogy két protont tudunk eltávolítani belőle, ekkor szulfátion keletkezik (SO42−). A szulfátionban a négy oxigén úgy tud egymástól a legtávolabb elhelyezkedni, ha szabályos tetraéderesen rendeződnek, így az ion szerkezete szabályos tetraéder. A szulfátionban a π-elektronok delokalizálódnak.
2
S O
O O
O Foszfátion (PO43−
)
A foszforsav (H3PO4) háromértékű sav, belőle három H+-iont (protont) lehet eltávolítani. Így keletkezik a foszfátion (PO43−
). Négy egyenértékű oxigénatom szabályos tetraéderesen rendeződik a foszforatom körül, a foszfátion szerkezete így szabályos tetraéder, elektronszerkezete delokalizált.
3
P O
O O
O
3.2.6. Gyakorlókérdések, -feladatok
19. Hogyan állapítja meg egy adott egyszerű molekula felírását AXnEm alakban?
20. Mit nevezünk ligandumnak?
21. Definiálja a kötéshosszt és a kötésszöget!
22. Milyen szempontokat kell figyelembe venni, ha egy molekula alakját szeretnénk meghatározni?
23. Milyen esetben apoláris egy molekula?
24. Milyen feltételeknek kell teljesülniük ahhoz, hogy egy molekulát dipólusmolekulának nevezhessünk?
25. A szén-tetrakloridban (CCl4) a C−Cl kötések polárisak, ám a kísérleti tapasztalatok szerint molekula mégis apoláris. Miért?
26. Mikor mondjuk egy molekulára, hogy az lineáris szerkezetű?
27. Mikor mondjuk egy molekulára, hogy az sík szerkezetű?
28. Milyen esetekben lehet egy molekula szerkezete lineáris? Soroljon fel néhány példát!
29. Milyen esetekben lehet egy molekula sík szerkezetű? Ismertessen néhány példát is!
30. Egy molekula központi atomjához két másik atom kapcsolódik, a központi atomnak lehet(nek) magános elektronpárja(i) is. Milyen lehet ennek a molekula szerkezete? Említsen mindegyik esetre egy-egy példát!
31. Állapítsa meg a következő vegyületek molekuláinak szerkezét! Apoláris, vagy dipólusmolekulákról van szó?
a. nitrogén (N2), b. metán (CH4), c. klórmetán (CH3Cl), d. etilén (C2H4), e. acetilén (C2H2), f. ammónia (NH3), g. víz (H2O),
h. kén-hidrogén (H2S), i. klór (Cl2),
j. szén-dioxid (CO2), k. kén-dioxid (SO2), l. kén-trioxid (SO3),
m. foszfor-pentaklorid (PCl5).
32. Állapítsa meg a következő összetett ionok szerkezét!
a. oxóniumion (H3O+), b. ammóniumion (NH4
+), c. karbonátion (CO32−), d. foszfátion (PO43−), e. nitrátion (NO3−), f. szulfátion (SO42−).
4. HALMAZOK, HALMAZÁLLAPOTOK
Ebben a fejezetben az anyagok összetételével, megjelenési formáikkal, a különböző halmaz- állapotokkal és halmazállapot-változásokkal foglalkozunk.
4.1. Alapfogalmak: elemek, vegyületek, keverékek
Kémiai elemek: azonos rendszámú atomokból felépülő anyagok. Vegyjellel jelöljük őket.
Példák: foszfor (P), réz (Cu), kálium (K), oxigén (O), bróm (Br) stb.
Az elemek az atomokat összetartó kölcsönhatások alapján lehetnek:
○ atomos: a nemesgázok – lezárt elektronhéjuk következtében – atomos felépítésűek. A nemesgázatomok között legfeljebb diszperziós kölcsönhatás jöhet létre.
Például: hélium (He), neon (Ne), argon (Ar) stb.
○ kovalens kötéssel összekapcsolva:
molekuláris: két vagy több azonos atomból felépülő elemmokekulák. Az ilyen molekulákat homonukleáris molekuláknak is nevezzük (homonukleáris: azonos atommagokból felépülő). Az elemmolekulák ezért mindig apolárisak.
Néhány példa elemmolekulára: O2, Cl2, N2, P4, S8, C60 stb.
atomok háromdimenziós rendeződése erős kovalens kötéssel összekötve.
Például: gyémánt (C), vörösfoszfor (P), szilícium (Si) stb.
○ fémes kötéses elemek:
Például: nátrium (Na), ólom (Pb), réz (Cu) stb.
Vegyületek: elemeket meghatározott arányban tartalmazó anyagok, az egyes elemek arányát egész számokkal fel lehet írni. A vegyületeket képletükkel jellemezzük. A képlet vegyjelek kombinációja, melyben az arányokat kifejező számokat az adott vegyjel jobb alsó indexébe írjuk:
AaBbCc…
Példák: HCl (sósav), CH3OH (metanol), MgCl2 (magnézium-klorid), Al2(SO4)3 (alumínium- szulfát), Na3PO4 (trinátrium-foszfát) stb.
A vegyületek atomjait is többféle kötés tarthatja össze:
○ kovalens kötés:
molekuláris: két vagy több különböző atomból épülnek fel, heteronukleáris molekuláknak nevezzük (heteronukleáris: különböző atommagokból felépülő).
Lehetnek polárisak, vagy apolárisak.
Néhány példa: CO2 (szén-dioxid), HCl (hidrogén-klorid), SO3, (kén-trioxid) P4O6, (tetrafoszfor-hexaoxid) stb.
atomok háromdimenziós rendeződése erős kovalens kötéssel összekötve.
Például: SiO2 (szilícium-dioxid) stb.
○ ionos kötés:
Például: nátrium-klorid (NaCl), kálium-szulfát (K2SO4), kalcium-oxid (CaO) stb.
○ esetleg fémes kötés: viszonylag ritka, de vannak olyan fémekből felépülő anyagok, melyek pontos összetétellel rendelkeznek.
Például: Ni3Al stb.
○ Gyakran a részecskéket összetartó erő átmenet a különböző fajta kötések között (például átmenet a kovalens és ionos kötés között, erre példa az ezüst-klorid, AgCl).
Keverék vagy elegy: elemekből és/vagy vegyületekből felépülő halmaz, melyben az egyes alkotóelemeknek nincs megkötött aránya. A keverék komponenseit (alkotóelemeit) fizikai módszerekkel rendszerint szét lehet választani. Fizikai változás: az anyag tulajdonságai úgy változnak meg, hogy közben új anyag nem keletkezik. Például átkristályosítás, szublimálás, desztillálás stb. Az elegy kifejezést általában nem alkalmazzuk szilárd keverékekre.
Az oldatok is tulajdonképpen keverékek vagy elegyek, általában folyékony halmazállapotúak, de ritkábban beszélhetünk szilárd oldatokról is. Az oldat fogalmának definiálásakor gyakran azt olvashatjuk, hogy az oldatban van egy kitüntetett komponens, melyet oldószernek nevezünk, ennek a részaránya nagyobb, mint a többi komponensé. Ez többnyire igaz is, ám vannak kivételek: tömény oldatok esetén lehetséges, hogy az oldott anyag mennyisége nagyobb, mint az oldószeré.
Fázis: azon térrész, melynek minden pontjában megegyeznek mind a kémiai, mind a fizikai tulajdonságok.
Például: olajat vízzel összekeverve, azok gyakorlatilag nem elegyednek, két elkülönülő fázist kapunk. A felső (felülúszó) fázis az olaj, az alsó (alulúszó) pedig a víz. Egy „jég–víz” keverékben pedig a szilárd fázis a jég, a folyadék fázis pedig a cseppfolyós víz.
Homogén egy anyagi halmaz, ha nincsenek benne határfelületek, és minden pontjában megegyezik a kémiai összetétel.
Például egy jól összekevert cukoroldat homogén fázist képez, ha mindenhol egyforma a cukor koncentrációja.
Inhomogénnek nevezünk egy anyagi halmazt, ha pontról pontra változik az összetétele, de nincsenek benne határfelületek.
Például inhomogén fázist kapunk, ha a következőképp készítjük a cukoroldatot: a cukorra ráöntjük a vizet, és keverés nélkül magára hagyjuk a rendszert. A cukor feloldódik, és az oldat alján nagyobb lesz a cukor koncentrációja, mint az oldat tetején, egészen addig, amíg a diffúzió hatására homogénné nem válik az oldat.
A heterogén rendszerek több fázist tartalmaznak, bennük határfelületek találhatók.
Például: olaj és víz keveréke.
4.1.1. ábra: Homogén, inhomogén és heterogén rendszerek
A különféle (homogén, inhomogén, heterogén) rendszerek időben változhatnak. A különféle fázisokat alkotó részecskék mozgása (diffúzió) az inhomogén rendszereket – az anyagi minőségtől függően hosszabb vagy rövidebb idő alatt – homogén rendszerré alakíthatják. Például az inhomogén folyadékok idővel homogenizálódhatnak. Ezzel ellentétben az inhomogén szilárd anyagok spontán (külső behatás nélkül) ritkán alakulnak át homogén rendszerré, mivel a szilárd anyagok részecskéit összetartó erők meggátolják a részecskék szabad mozgását.
Természetesen heterogén rendszer is átalakulhat inhomogénné vagy homogénné, és fordítva.
Például ha a fentiekhez hasonlóan egy pohár vízhez egy evőkanál cukrot adunk, először egy heterogén (kétfázisú) rendszer jön létre, majd a só feloldódásával megszűnik a fázishatár. Ha az oldatot az oldódás során nem keverjük folyamatosan, akkor az oldat inhomogén lesz, az edény alján nagyobb lesz a cukor koncentrációja, mint az edény felső részében. Az oldatot magára hagyva egy idő után homogenizálódik.
A gáz vagy gőz fázis még gázkeverékek esetén is egy idő után homogénné válik (a gázok hőmozgásuk következtében összekeverednek). Heterogén fázisú rendszerek nem alakulhatnak ki két
homogén inhomogén heterogén
légnemű fázisból, ám lehetségesek gáz(gőz)–folyadék, gáz(gőz)–szilárd, folyadék–folyadék, folyadék–szilárd és szilárd–szilárd rendszerek. Az alábbiakban néhány példa:
Gáz–folyadék: például oxigéngáz és víz.
Gáz–szilárd: például platina és hidrogéngáz.
Folyadék–folyadék: egymással nem elegyedő vagy korlátozottan elegyedő folyadékok. Például benzin és víz keveréke.
Folyadék–szilárd: lehet például oldott anyag és oldószer vagy szilárd anyag és olvadéka.
Szilárd–szilárd: például egy elem két módosulata (sárga foszfor és vörös foszfor, grafit és gyémánt).
A magára hagyott rendszer mindig az egyensúly elérésére törekszik.
Standard állapot: a jelenlegi konvenciók szerint a standard állapot egy konkrét nyomásértéket jelöl, még pedig vagy a 105 Pa-t, vagy a normál légköri nyomást (101 325 Pa), függetlenül a hőmérséklettől. Régebben elterjed volt a standard állapot definíciója mint normál légköri nyomás és 25,00 °C (298,15 K) hőmérséklet kombinációja.
4.2. Az anyagi halmazok csoportosítása
A környezetünkben előforduló anyagokat többféleképpen csoportosíthatjuk:
Összetétel alapján:
– Egyszerű anyagok: csak azonos rendszámú atomokat tartalmaznak: elemek.
– Összetett anyagok: többféle rendszámú anyagból épülnek fel. Ezek lehetnek vegyületek, vagy keverékek.
Komponensek száma szerinti csoportosítás:
– Tiszta anyagok: elemek vagy vegyületek, egyetlen komponensből állnak.
– Keverékek: többféle komponensből állnak.
Halmazállapot szerinti csoportosítás (az egyetemi tanulmányok során szó lesz még egy negyedik halmazállapotról is):
– szilárd anyag – folyadék
– légnemű anyagok vagy gázok.
4.3. Halmazállapotok, halmazállapot-változások
Elméletileg minden elem és vegyület három halmazállapotban fordulhat elő, a gyakorlatban azonban nem minden elem és vegyület veszi fel mindhárom halmazállapotot. Például azért, mert az anyag olvadása vagy forrása során elbomlik.
Egy anyag halmazállapota alapvetően a hőmérséklettől, a nyomástól és az anyagi minőségtől függ.
4.3.1. Halmazállapot-változások:
Olvadás: az anyag szilárd halmazállapotból folyadékká válik.
Szublimáció: a szilárd anyag közvetlenül légnemű halmazállapotba kerül anélkül, hogy folyadék halmazállapotot venne fel.
Forrás: folyadékból légnemű anyag keletkezik.
Fagyás: folyadék állapotból légnemű halmazállapotba kerül az anyag.
Kondenzáció vagy lecsapódás: légnemű halmazállapotból szilárd vagy folyadék halmazállapotba kerül az anyag.
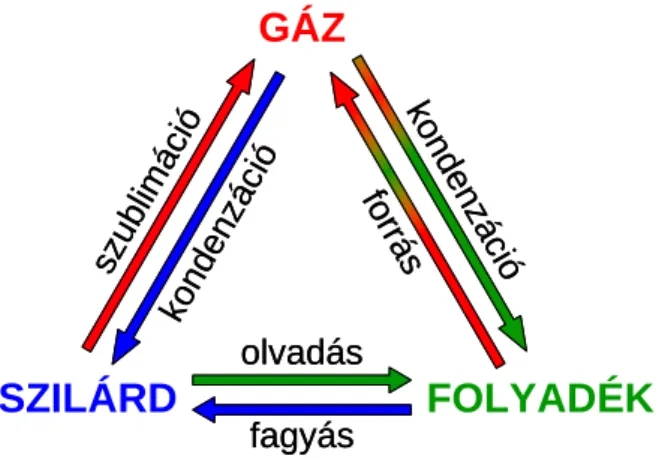
4.3.1.1. ábra: Fázisátalakulások
Tiszta anyagok (elemek vagy vegyületek) halmazállapot-változásai adott nyomás esetén jól meghatározott hőmérsékleten mennek végbe, az anyagra jellemző fizikai állandók. A következőkben ezen kitüntetett hőmérsékleteknek az elnevezésével ismerkedünk meg. Ezek mértékegysége a hőmérséklet szokásos mértékegysége (Celsius-fok: °C, kelvin: K).
Olvadáspont: az a hőmérséklet, melyen az anyag normál légköri nyomáson szilárd halmazállapotból folyadékká alakul.
Fagyáspont vagy dermedéspont: azon hőmérséklet, melyen az anyag normál légköri nyomás mellett folyadékból szilárd halmazállapotúvá alakul.
Tiszta anyagok olvadás- és fagyáspontja megegyezik.
Forráspont: az a hőmérséklet, melyen az anyag normál légköri nyomáson folyadékból légnemű halmazállapotúvá válik.
Kondenzációs vagy lecsapódási pont: azon a hőmérséklet, melyen az anyag normál légköri nyomáson légneműből folyadék vagy szilárd halmazállapotúvá válik.
Szublimációs pont: az a hőmérséklet, melyen az anyag normál légköri nyomáson szilárdból közvetlenül légnemű halmazállapotúvá válik.
Tiszta anyagok forrása esetén azok forráspontja és kondenzációs pontja megegyezik, hasonlóan a szublimáció esetén a szublimációs pont és a kondenzációs pont azonos.
Jogos kérdés, hogy miért hangsúlyozzuk, hogy tiszta anyagok esetén egyezik meg például az olvadáspont és a fagyáspont. Természetesen a keverékeknek (elemek és/vagy vegyületek keveréke) is van olvadáspontja és fagyáspontja, ám ezek esetén azonban az olvadáspont és fagyáspont csak ritkán egyezik meg. Ez természetesen igaz a többi halmazállapot-változásra is. Az elegyek halmazállapot- változásairól részletesebben az egyetemi tanulmányok során esik majd szó.
Megjegyzés: mint fentebb említettük, nemcsak a hőmérséklettől, de a nyomástól is függ, hogy milyen halmazállapotú egy tiszta anyag. A nyomásfüggés igaz azon kitüntetett hőmérsékletekre is, melyeken a halmazállapot-változások végbemennek. A fizikai állandókat mindig normál légköri
GÁZ
SZILÁRD FOLYADÉK
kondenz áció szub
lim áció
kondenz áció szub
lim
áció kondenz
áci ó forr
ás kondenz
áci ó forr
ás
olvadás fagyás olvadás
fagyás
nyomásra adjuk meg, melynek értéke 101 325 Pa. Ez természetesen konvenciók kérdése, és bizonyos újabb ajánlások nem a normál légköri nyomást, hanem a hozzá igen közeli 105 Pa (100 kPa, 1 bar) nyomást adják meg referenciapontnak. Amennyiben nem normál légköri nyomáson mérjük a halmazállapothoz tartozó hőmérsékletet, a „pont” (olvadáspont, forráspont stb.) helyett „hőmérséklet”- et mondunk. Például, ha egy anyag forrásának hőmérsékletét nem normál légköri nyomáson mérjük, a kapott értéket szabályosan nem mondhatjuk forráspontnak csak forráshőmérsékletnek. Az olvadáshőmérsékletet a külső nyomás nem nagyon befolyásolja, ám a szublimációs és forráshőmérséklet nyomásfüggése viszonylag nagy.
Egy tiszta szilárd anyagot állandó nyomáson melegítünk. Hogyan változik az anyag hőmérséklete eközben?
A hőközlés hatására növekszik a szilárd anyag hőmérséklete, az anyag hőkapacitása adja meg, hogy egy adott hőmennyiség hatására mekkora hőmérséklet-növekedést tapasztalunk. A hőmérséklet egészen addig növekszik, míg az anyag elkezd megolvadni. Az olvadás folyamata közben azonban nem növekszik a hőmérséklet: a hőmérséklet mindaddig állandó marad, amíg az összes szilárd anyag folyadékká nem alakul. A hőmennyiség nem a hőmérséklet növelésére, hanem az olvadásra fordítódik.
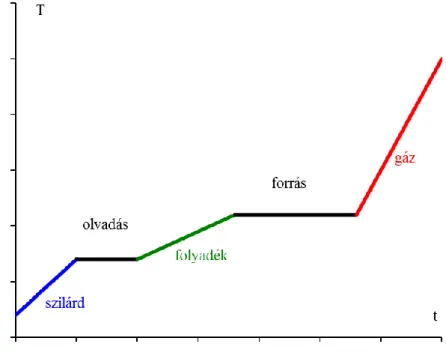
A hő ahhoz szükséges, hogy a szilárd anyagban lévő kötéseket felbontsuk, így az anyag folyadékká alakuljon. További hőközlés hatására a folyadék hőmérséklete folyamatosan növekszik, míg a forrás meg nem indul. Az olvadáshoz hasonlóan forrás során is állandó a hőmérséklet mindaddig, amíg folyadék is található a gőz mellett. Miután az összes folyadék elforrt, a gőz hőmérséklete növekszik. A folyamatot az alábbi ábrán szemléltethetjük.
4.3.1.2. ábra: Hőmérséklet–idő diagram állandó nyomás mellett A halmazállapot-változások során a hőmérséklet állandó.
Vegyünk egy másik példát: a jég olvadása 0 °C hőmérsékleten megy végbe (normál légköri nyomáson). Mi történik, ha egy hőszigetelt edényben nagy mennyiségű −10 °C hőmérsékletű jeget és +5 °C hőmérsékletű folyékony vizet összekeverünk? Mivel a jég olvadáspontja (víz fagyáspontja) 0 °C, a jég ennél alacsonyabb hőmérsékleten nem tud megolvadni. Ahhoz, hogy a jég elkezdjen olvadni, a hőmérsékletének 0 °C-ra kell emelkednie. Mivel hőszigetelt edényben dolgozunk, a felmelegedéshez szükséges hőmennyiség csak a melegebb folyékony víztől származhat. A víznek tehát le kell hűlnie, a jégnek pedig fel kell melegednie 0 °C-ra ahhoz, hogy a halmazállapot-változás végbemehessen! Sejthető, hogy a folyamat végére a hőmérsékletek kiegyenlítődnek. A rendszer véghőmérséklete függ a jég és a víz mennyiségétől (és további fizikai állandóktól is).
Szélsőséges esetben olyan is előfordulhat, hogy az összes jég felolvad, és a hőmérséklet 0 °C vagy annál magasabb. Ez akkor lehetséges, ha kis mennyiségű jeget sok vízbe helyezünk.
Egy másik eset, hogy csak jég marad az edényben, az összes víz megfagy. Ez akkor lehetséges, ha nagyon sok jéghez adunk kevés vizet.
Tehát a fenti esetben mindenképpen hőmérséklet-kiegyenlítődésnek kell történnie, melynek során beáll a termikus egyensúly. Termikus egyensúly esetén a rendszer minden pontjának azonos a hőmérséklete.
Tiszta anyagok esetén az olvadás, forrás stb., azaz a halmazállapot-változások során a két különböző halmazállapotú fázisoknak egymással egyensúlyban kell lenniük, ezért a halmazállapot- változás – adott nyomás esetén – csak egy konkrét hőmérsékleten mehet végbe.
Fontos megjegyezni, hogy a halmazállapot-változás hőmérsékletét mindig úgy kell kísérletileg meghatározni, hogy közben az anyag mindkét halmazállapotban jelen legyen, tehát egyensúlyi hőmérsékletet mérjünk!
A halmazállapot-változásokat kísérő hőváltozások
Mint fentebb említettük, egy éppen olvadó anyagot melegítve, a hő arra fordítódik, hogy végbemenjen a halmazállapot-változás. A szilárd anyagban lévő kötőerőket fel kell szakítanunk, hogy kialakuljon a folyékony halmazállapot, melyben a részecskék el tudnak mozdulni. Forrás esetén szintén energiát kell befektetnünk ahhoz, hogy a folyadék részecskéit eltávolítsuk egymástól annyira, hogy létrejöjjön a légnemű halmazállapot. A helyzet hasonló a szublimációnál is, energiabefektetés szükséges ahhoz, hogy a szilárd anyagban lévő kötéseket megszüntessük, és az anyag így légnemű halmazállapotúvá váljék.
Tehát az olvadás, a forrás és a szublimáció esetén energiát kell befektetnünk, így ezek endoterm folyamatok. Az ellentétes irányú folyamatok, azaz a fagyás és kondenzáció során energia szabadul fel, ezek exoterm folyamatok.
Endoterm folyamat: hőelnyeléssel járó folyamat.
Például: olvadás, forrás, szublimáció.
Exoterm folyamat: hőfelszabadulással járó folyamat.
Például: fagyás, kondenzáció.
Nézzünk egy hétköznapi példát a folyadékok párolgására!
Nyári forró napokon nagyobb városokban gyakran locsolják vízzel az utakat. A víz (és a többi folyadék) azonban nemcsak a forráspontján párolog, hanem alacsonyabb hőmérsékleteken is. A párolgás, a forráshoz hasonlóan endoterm folyamat, tehát hőt von el a környezetétől. Az elpárolgó víz így valamelyest lehűti az aszfaltot.
Az elnyelődő, illetve felszabaduló hő arányos az anyag tömegével és így anyagmennyiségével. Az ilyen fajlagos vagy moláris hőmennyiségek már függetlenek az anyag mennyiségétől (tömegétől, illetve anyagmennyiségétől), ezért anyagi jellemzők, megfelelő táblázatokban összegyűjtve megtalálhatóak.
Fajlagos olvadáshő: egységnyi tömegű szilárd anyag megolvasztásához szükséges hő.
m Lolv Q
Moláris olvadáshő: egységnyi anyagmennyiségű szilárd anyag megolvasztásához szükséges hő.
n Lolv,m Q
A két mennyiség között a moláris tömeg (M = m / n) teremt kapcsolatot, melynek segítségével könnyen átválthatjuk őket egymásba:
M
Lolv Lolv,m , illetve Lolv,m MLolv.
Mivel az olvadás endoterm folyamat, a fajlagos, illetve moláris olvadáshő előjele – konvenció szerint – pozitív.
Hasonlóan definiálható fajlagos/moláris fagyáshő, forráshő (vagy párolgáshő), szublimációs hő és kondenzációs hő. Azon hőfajtákat, melyek során nem tapasztalható hőmérséklet-változás, látens hőnek nevezzük gyűjtőnéven.
Minden endoterm folyamat esetén a hő előjele pozitív, exoterm folyamatok esetén pedig negatív.
Így az egyes fajlagos/moláris hők előjele:
Pozitív előjel:
– olvadáshő,
– forráshő (párolgáshő), – szublimációshő.
Negatív előjel:
– fagyáshő,
– kondenzációshők.
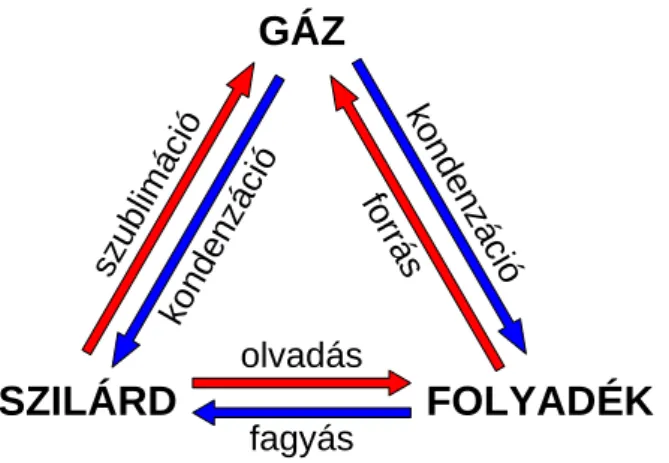
Az alábbi ábrán a piros nyíl az endoterm (hőelnyelő) folyamatot jelöli (a hő előjele pozitív), a kék nyilak pedig az exoterm (hőtermelő) folyamatokat mutatják (a hő előjele negatív).
4.3.1.3. ábra: Fázisátalakulások hőváltozásai
Az olvadás és fagyás ellentétes folyamatok, egy adott mennyiségű anyag megolvasztásához ugyanannyi hőt kell befektetni, mint amennyi hő felszabadul annak megfagyásakor. Ebből adódik, hogy a fajlagos olvadáshő és a fajlagos fagyáshő nagysága ugyanakkora, csak előjele ellentétes.
Tehát a fajlagos, illetve moláris mennyiségekre:
Lfagyás = −Lolvadás
Lkondenzáció = −Lforrás
Lkondenzáció = −Lszublimáció
GÁZ
SZILÁRD FOLYADÉK
kondenz áció szub
lim
áció kondenz
áci ó forr
ás
olvadás fagyás
A szublimációs hő megegyezik az olvadáshő és forráshő összegével:
Lszublimáció = Lolvadás + Lforrás
4.3.2. A szilárd halmazállapot
Szilárd halmazállapotban a részecskéket összetartó erők igen nagyok, a részecskék csak külső erőhatásra tudnak elmozdulni, akkor csak kis mértékben.
A szilárd anyagok alakja és térfogata is állandó, csak viszonylag nagy erőbehatásokra változtatható meg.
A szilárd anyagokat két csoportra oszthatjuk szerkezetük alapján:
Amorf anyagok: nem szabályos (kristály)szerkezetű anyagok.
Példák: üveg, gumi, a legtöbb műanyag, viasz, szurok stb.
Kristályos anyagok: a szilárd anyagot alkotó részecskék a tér minden irányában szabályos elrendeződésben helyezkednek el.
Példák: nátrium-klorid, elemi jód, magnézium stb.
A kristályos anyagokra jellemző a kristályrács, melynek legkisebb ismétlődő egysége az elemi cella.
(Moláris) rácsenergiának nevezzük azt az energiát, mely felszabadul, mikor egymástól végtelen távolságban lévő részecskékből 1 mól anyag kristályrácsa létrejön. (Másképp megfogalmazva, ugyanennyi energiát kell befektetnünk, hogy 1 mól anyag kristályrácsát megbontsuk, azaz az alkotórészecskéket végtelen távolságba távolítsuk egymástól.
A kristályos szerkezetű anyag a részecskéket összetartó erők alapján lehet:
– fémrácsos, – ionrácsos, – molekularácsos, – atomrácsos.
Fémrács: az anyagot erős fémes kötés tartja össze. A kristály rácspontjaiban pozitív töltésű fémionok találhatók, a vegyértékelektronok közöttük delokalizálódva helyezkednek el.
A fémrácsban kristályosodó anyagok változatos olvadásponttal rendelkeznek, például a higany olvadáspontja −39 °C, míg a volfrám olvadáspontja 3695 °C.
A fémek mechanikai tulajdonsági szintén nagyban függenek az elemtől. Vannak egészen lágy, könnyen megmunkálható és kemény, rideg fémrácsos anyagok is.
A fémrácsos anyagok a hőt és az elektromos áramot általában igen jól vezetik.
Fémeket és fémrácsban kristályosodó vegyületeket többnyire csak kémiai átalakulással lehet oldatba vinni, mely rendszerint a fém oxidációját jelenti. (Ez alól kivétel például az amalgámképzés, mely egy fém higannyal alkotott ötvözetének, oldatának tekinthető.) A fém kémiai tulajdonságaitól függően oldódhat vízben, híg, nem oxidálósavakban, tömény oxidálósavakban, illetve lúgokban.
Példa: vas (Fe), magnézium (Mg), réz (Cu) stb.
A fémek leggyakrabban az alábbi három rácstípus valamelyikében kristályosodnak:
Elnevezés Térben középpontos kockarács
Lapon középpontos kockarács
Hatszöges (hexagonális) rács Koordinációs
szám 8 12 12
Mechanikai tulajdonságok
Általában nem túl jól meg- munkálható fémek (nem elég szoros az illeszkedés, vagy ridegek, vagy túl lágyak)
Puha, könnyen megmun- kálható (a siklási síkokon el tudnak csúszni egymáson a rétegek)
Többnyire kemény fémek
Példák: Na, K, V, Cr, Fe Au, Ag, Al, Cu, Pb Mg, Ti, Zn, Cd, Zr Ionrács: az anyagot erős ionos kötés tartja össze, mely az ellentétes töltésű ionok elektrosztatikus vonzásából adódik. A kristály rácspontjaiban felváltva kationok és anionok helyezkednek el.
Az ionrácsos vegyületek olvadáspontja (és forráspontja) általában magas.
Az ionrácsos vegyületek szigetelők, ám megolvasztva vezetik az áramot.
Azon vegyületek, melyek ionrácsban kristályosodnak, általában jól oldódnak poláris oldószerekben, például vízben.
Gyakran előfordul, hogy a vegyület a kristályrácsban az oldószer (például víz) molekuláival együtt kristályosodik. (A víz mellett természetesen más oldószer – például alkoholok, ammónia – esetén is lehetséges szolvátburok kialalkulása.) Ha egy só vizes oldatból kristályosodik ki, akkor a kristályrácsban található vízmolekulákat kristályvíznek nevezzük. Ezt a képletben a következőképpen jelöljük: például a kristályos nátrium-szulfát esetén Na2SO4 · 10 H2O, mely azt jelenti, hogy egy mól nátrium-szulfát mellett 10 mól kristályvíz található. A fenti jelölés azonos a következővel:
Na2SO4(H2O)10.
Példák ionrácsos vegyületekre: nátrium-klorid (NaCl), kálium-nitrát (KNO3), kristályos réz(II)- szulfát (CuSO4 · 5 H2O), kristályos magnézim-klorid (MgCl2 · 6 H2O) stb.
Molekularács: a kristály rácspontjaiban molekulák találhatók, ezeket (gyengébb) másodrendű kölcsönhatások tartják össze.
A molekularácsos anyagokra jellemző a viszonylag alacsony olvadáspont (és forráspont is), mivel a molekulákat csak másodrendű kötések tartják össze, emellett ezen anyagok általában illékonyak.
Az apoláros molekulákból felépülő molekularácsos anyagok apoláros oldószerben jól oldódnak, ezzel ellentétben a dipólusmolekulákból felépülő molekularácsos anyagok poláros oldószerben oldódnak jól. Például az elemi jód (a kristályrácsban apoláris I2 molekulák) kiválóan oldódik az apoláris szén-tetrakloridban és szénhidrogénekben. A szintén molekularácsban kristályosodó, ám dipólusmolekula hidrogén-klorid (HCl) pedig poláris oldószerekben (például víz) oldódik jól.
Általában jó elektromos szigetelők.
A molekularácsos anyagok közé tartoznak a nemesgázok is, noha atomos szerkezetűek. Éppen ezért a nemesgázokat szokták egyatomos molekuláris szerkezetűnek is nevezni.
Példák: víz (H2O), ammónia (NH3), jód (I2), hélium (He), sárgafoszfor (P4), rombos kén (S8) stb.
Atomrács: a kristály rácspontjaiban atomok találhatók, melyeket erős kovalens kötés tart össze.
Az atomrácsos anyagok olvadáspontja rendszerint igen magas, ennek magyarázata a kristályrácsot összetartó kovalens kötés erősségében keresendő.
Az atomrácsos elemek és vegyületek általában kemény, mechanikailag igen ellenálló anyagok (például gyémánt).
Rendszerint nem vezetik jól a hőt és az elektromos áramot.
A rácsot összetartó kovalens kötések következtében az atomrácsos elemek és vegyületek általánosságban igen oldhatatlanok közönséges oldószerekben (például víz, aceton stb.). Az atomrácsos anyagokat többnyire csak igen erélyes körülmények mellett lehet feloldani (például tömény lúgokban, erős oxidálósavak tömény oldataiban stb.).
A nemesgázok nem atomrácsos, hanem molekularácsos vegyületek!
Példák: gyémánt (C), bór (B), szilícium-dioxid (SiO2) stb.
A különböző rácstípusok (fémrács, ionrács, molekularács, atomrács) összehasonlítása
Tulajdonság Fémrács Ionrács Molekularács Atomrács
Kristályrácsot összetartó kölcsönhatás
fémes kötés ionos kötés másodrendű kötőerők
kovalens kötés
Olvadáspont változó magas alacsony magas
Oldhatóság csak kémiai reakcióval
poláris oldószerekben
poláris vagy apoláris oldószerekben
csak kémiai reakcióval Mechanikai
szilárdság
általában jó, a fém fajtájától
függően
változó általában törékenyek vagy
puhák
általában kifejezetten jó Elektromos
vezetőképesség
általában kifejezetten jó
szigetelők, felolvasztva
vezetők
szigetelők szigetelők
Jellemző anyagok fémes elemek, ötvözetek
kizárólag vegyületek
nemfémes elemek nemfémes és félfémes elemek
Példák nátrium (Na),
cink (Zn)
kálium-klorid (KCl), nátrium-szulfát
(Na2SO4)
argon (Ar), hidrogén-klorid
(HCl)
bór (B), szilícium-dioxid
(SiO2)
4.3.3. A folyadék halmazállapot
A folyadék halmazállapotú anyagok részecskéi viszonylag könnyen el tudnak mozdulni egymás mellett, ezért felveszik a tárolóedény alakját (különbség a szilárd anyagoktól). Azonban a folyadékok térfogata külső nyomás hatására csak kismértékben változik (különbség a légnemű anyagoktól). Ennek oka, hogy nemcsak vonzó-, hanem taszítóerő is fellép a folyadékokban. Ez a – kis távolságoknál fellépő – taszítóerő akadályozza meg, hogy a folyadékokat nagymértékben összenyomjuk.
Tehát a folyadékokra jellemező, hogy nincs önálló alakjuk, de van önálló térfogatuk.
Felületi feszültség
Amennyiben a folyadék határfelülete fölött egy másik fázis (például gáz) található, a folyadék felszínén található részecskékre a folyadék belseje felől sokkal erősebbek a kölcsönhatások, mint a
gázfázis felől, a folyadék belseje befelé „húzza” a felszínen lévő részecskéket. A felületi feszültségnek nevezzük a folyadék felületét csökkentő erőhatást. (A felületi feszültséget megadja, hogy mekkora munkával tudjuk a folyadék felületét egységnyivel megnövelni.) A felületi feszültség következménye, hogy a folyadékok a lehető legkisebb felületűre húzódnak össze. Például a szappanbuborék gömb alakú, a nyugvó folyadékok felszíne sík.
Oldódás és elegyedés
A folyadékokra jellemző a diffúzió, melynek nagy szerepe van a különféle anyagok oldódásában.
Oldódás során az oldószer-molekulák körülveszik az oldott anyag részecskéit, ezt a folyamatot szolvatációnak nevezzük. Az egyik legfontosabb oldószer, a víz esetén hidratációról szoktunk beszélni.
A folyadékokat gyakran oldószerként alkalmazzuk, ismerünk poláris és apoláris oldószereket. Az oldódással vagy elegyedéssel kapcsolatban alapvető fontosságú a „hasonló hasonlót old”-elv, mely alapján a dipólusmolekulákból felépülő oldószer elsősorban ionokból álló sókat és dipólusmolekulákat oldanak, míg az apoláris oldószerek apoláris anyagokat oldanak jól.
Néhány példa: a poláris molekulákból álló szőlőcukor (C6H12O6) vagy az ionrácsos nátrium- hidroxidot (NaOH) a víz – mint poláris oldószer – igen jól oldja, ám az apoláris molekulákból álló szénhidrogénekkel gyakorlatilag nem elegyedik. Az apoláris szén-tetrakloridban (CCl4) viszont nem oldódnak a sószerű és dipólusmolekulákból álló anyagok, ellenben az apoláris jódot (I2), brómot (Br2) és szénhidrogéneket jól oldja.
A folyadékok nemcsak szilárd anyagokat, hanem gázokat is oldhatnak. Például a poláris molekulájú hidrogén-klorid- (HCl), kén-dioxid- (SO2) vagy az ammóniagáz (NH3) kiválóan oldódik a dipólusmolekulákból álló vízben. Ezt a következő, úgynevezett szökőkútkísérlettel is szemléltethetjük:
4.3.3.1. videó: A szökőkútkísérlet
Ezzel ellentétben a víz rosszul oldja az apoláris molekulájú anyagokat, így például az elemi oxigént (O2), nitrogént (N2), a metánt (CH4) vagy a nemesgázokat. Az apoláris oldószerek pedig jól oldják az apoláris molekulákból álló gázokat, például a metánt.
Beszélhetünk fizikai és kémiai oldódásról: a fizikai oldódás során az oldószer-molekulák úgy veszik körül az oldott anyagot, hogy annak összetétele nem változik meg, tehát az oldószer és az oldott anyag molekulái között másodrendű kötőerők lépnek fel.
Kémiai oldódás során viszont az oldott anyag reagál az oldószerrel, így új anyag keletkezik.
Például, ha hidrogén-kloridot oldunk vízben, a beoldódott molekulák ionosan disszociálnak
Megjegyzés: a szén-dioxid apoláris molekulájú, ám viszonylag jól oldódik vízben. Ennek oka, hogy az oldódás során kémiai változás történik, a szén-dioxid részlegesen szénsavvá alakul, mely ezután – szintén részlegesen – ionosan disszociál az oldatban.
Az alábbi videón két egymással nem elegyedő folyadékkal mutatunk be egy érdekes kísérletet:
4.3.3.2. videó: Az „ugráló” nátrium Gőztenzió
A folyadékok párolognak, mely során a felszíni részecskék elszakadnak a folyadékfázistól.
(Megjegyzés: elvileg a szilárd anyagok is párolognak, viszont ennek mértéke általában olyan csekély, hogy gyakorlatilag nem is tapasztalható. Viszont bizonyos illékony szilárd anyagok jelentős mértékben szublimálhatnak/párologhatnak akár szobahőmérsékleten is. Gondoljuk az „elillan, mint a kámfor”
mondásra.)
Vizsgáljuk meg a következő gondolatkísérletet!
Egy lezárt, levákuumozott edénybe viszonylag nagy mennyiségű folyékony vizet spriccelünk, majd a hőmérsékletet állandó T1 értéken tartva mérjük az edényben a nyomást (a gőztér nyomását mérjük). Azt tapasztaljuk, hogy a víz párolog, és a nyomás folyamatosan növekszik. Viszont egy idő után lelassul a nyomás növekedésének sebessége, végül beáll egy telítési értékre. Ekkor a folyadék térfogata sem változik már tovább. A nyomást az időben ábrázolva a következő grafikont kapjuk:
4.3.3.1. ábra: A gőztenzió kialakulása
Az egyensúly beálltakor mérhető p° nyomást a folyadék telített gőznyomásának vagy gőztenziójának nevezzük.
Gőztenzió: folyadékkal vagy szilárd anyaggal egyensúlyban lévő telített gőz nyomása adott hőmérsékleten.
Mi történik, ha a fenti kísérletet sokkal kisebb mennyiségű vízzel ismételjük meg, azaz csak pár cseppnyi vizet spriccelünk az edénybe?
p
idő p°
Ekkor a víz teljes mennyisége elpárolog, és a mérhető parciális nyomás az előző kísérletben tapasztaltnál sokkal kisebb. A jelenség magyarázata a következő: a víz mennyisége kevés volt ahhoz, hogy a telített gőznyomást biztosítsa, tehát a gőztér telítetlen maradt.
Relatív páratartalom: a folyadékból keletkezett gőz nyomásának és az adott anyag azonos hőmérsékletén vett gőztenziójának a hányadosa. Általában százalékban fejezzük ki az értékét.
) T ( p
) T ( p
Például ha a nyomás p° / 2, akkor a relatív páratartalom értéke 50%, ha a nyomás p° / 4, akkor a relatív páratartalom 25%-os.
A gőztenzióval kapcsolatban nagyon fontos megjegyezni, hogy csak akkor alakul ki a telített gőznyomás, ha a gőz és folyadék között egyensúly jön létre, azaz folyadék is és gőz is van a rendszerben. (Az egyensúly itt azt jelenti, hogy a párolgás sebessége megegyezik a kondenzáció sebességével, a nyomás beáll egy állandó értékre.) Tehát a telített gőznyomás csak úgy jöhet létre, ha megfelelő mennyiségű folyadék áll rendelkezésre!
Most ismételjük meg a kísérletet magasabb állandó hőmérsékleten!
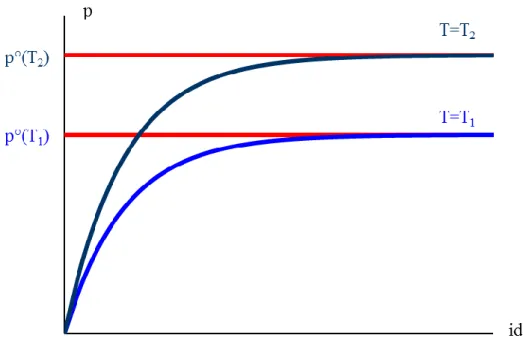
Nagyobb T2 hőmérsékleten a folyadékok illékonyabbak, ezért a görbe nagyobb nyomásértéknél telítődik. Ez azt jelenti, hogy a folyadék feletti gőztenzió függ a hőmérséklettől, méghozzá magasabb hőmérsékleten nagyobb a gőznyomás értéke [ha T2 > T1, akkor p°(T2) > p°(T1)].
4.3.3.2. ábra: A gőztenzió különböző hőmérsékleteken
Most vizsgáljuk meg, mi történik, ha nagy mennyiségű vizet nem levákumozott, hanem levegővel töltött tartályba spriccelünk állandó T1 hőmérsékleten!
A nyomás már a t = 0 időpontban sem nulla, mivel a levegőnek eleve van egy bizonyos nyomása.
Ám a nyomás ebben az esetben is növekszik. Egy arra alkalmas berendezéssel mérjük a levegő és a vízgőz nyomását, és azt tapasztaljuk, hogy a vízgőz telítődési nyomására éppen az előző gőztenzióértéket kapjuk! Ebből arra következtethetünk, hogy a gőztenzió nem függ a gőz melletti egyéb komponensektől.
(Megjegyzés: amikor a folyadékot bejuttatjuk a levegővel telt edénybe, a levegő összenyomódik.
A víz párolgása során a folyadék mennyisége folyamatosan csökken, így a levegő nyomása is változik valamelyest. Tehát az össznyomás értéke nem pontosan egyezik meg a kiindulási nyomásnak a gőztenzióval megnövelt értékével. Azonban ha a folyadék mennyisége nagy, és a hőmérséklet nem túl magas, akkor ez a térfogatváltozás, és a belőle származó levegő nyomásváltozása gyakorlatilag elhanyagolható.)
A fenti kísérleteket megismételhetjük különféle folyadékokkal is, ekkor azt tapasztalnánk, hogy a folyadék gőztenziója függ a folyadék anyagi minőségétől.
Összefoglalva a fenti kísérletek eredményeit:
Tiszta anyagok gőztenziója:
– függ a hőmérséklettől: magasabb hőmérsékleten nagyobb a gőztenzió, mint alacsonyabb hőmérsékleten,
– függ az anyagi minőségtől: az illékonyabb anyagok gőztenziója egy adott hőmérsékleten nagyobb, mint a kevésbé illékonyaké,
– független a folyadék feletti egyéb anyagok (például levegő) nyomásától és annak összetételétől, értéke a külső nyomással nem befolyásolható.
Megjegyzés: a legutolsó jellemző szigorúan nem igaz, extrém nagy külső nyomás esetén a tiszta anyag gőztenziója csekély mértékben függ a külső nyomástól.
Ahogy növeljük a hőmérsékletet, a gőztenzió növekszik. Azon a hőmérsékleten, melyen a gőztenzió értéke megegyezik a légköri nyomás (külső nyomás) értékével, a folyadék belsejében is megindul a párolgás, a buborékok képződése, és az anyag elkezd forrni. Tehát a forráshőmérséklet az a hőmérséklet, melyen a folyadék gőztenziója éppen megegyezik a külső nyomással.
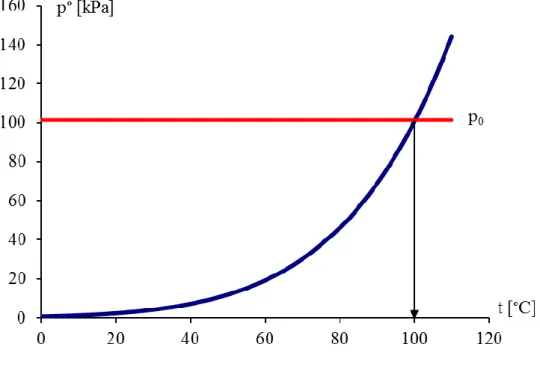
4.3.3.3. ábra: A forráspont
A fenti ábrán kék görbével a víz gőztenzióját ábrázoltuk a hőmérséklet függvényében, a piros vízszintes vonal pedig a normál légköri nyomást jelenti (p0 = 101,325 kPa). Az ábrát megvizsgálva kiderül, hogy a gőztenziógörbe 100 °C hőmérsékleten metszi a vízszintes vonalat, tehát a víz forráspontja a jól ismert 100 °C.
Megjegyzés: Mi történik, ha a Himalája tetején melegítünk folyékony vizet? A Himalája tetején a nyomás sokkal kisebb, mint a tengerszinten, mintegy 40 kPa. Ha behúzunk egy vízszintes vonalat ehhez az értékhez, az 77 °C-nál metszi a gőztenzió görbéjét, azaz a Himalája tetején már 77 °C-on forr a tiszta víz!
Fontos megjegyezni a következőket: a tiszta folyadék gőztenziója független a külső nyomástól, viszont a folyadék forráspontja a külső nyomás függvénye!
Természetesen nemcsak folyadékoknak, hanem szilárd anyagoknak is van gőztenziója, mivel a szilárd anyagok felszínéről is elszakadhatnak részecskék, melyek így a gőz fázisba kerülnek. A szilárd anyagok feletti, a szilárd anyaggal egyensúlyban lévő telített gőznyomást is gőztenziónak nevezzük. A szilárd anyag feletti gőztenzió is függ a hőmérséklettől és az anyagi minőségtől.
A Clausius–Clapeyron-egyenlet
A fent bemutatott ábra alapján sejthető, hogy a gőztenzió és a hőmérséklet között exponenciális összefüggés áll fenn. A tiszta anyag feletti gőztenzió és az abszolút hőmérséklet közötti kapcsolatot a Clausius–Clapeyron-egyenlet jelenti, mely a következő formában írható fel:
T R
L
e C ) T (
p .
A képletben L egy moláris látens hőt jelent, mely szilárd anyag szublimációja esetén a szublimációs hő, míg egy folyadék párolgása esetén a moláris párolgáshő, C az adott anyagra jellemző konstans, R az egyetemes gázállandó (R = 8,314 J/(mol∙K)), T pedig az abszolút hőmérséklet.
Az egyenletet szokás az alábbi logaritmusos formában is felírni:
T R C L ln ) T ( p
ln .
Fontos megjegyezni, hogy a Clausius–Clapeyron-egyenlet közelítőleg érvényes csak, ám ennek ellenére rendszerint igen jól alkalmazható. A közelítő jelleg abból adódik, hogy az egyenletben szereplő látens hő hőmérsékletfüggését általában elhanyagoljuk, illetve a termodinamikai összefüggésekből történő levezetések során más elhanyagolásokat is teszünk. A Clausius–Clapeyron- egyenlet segítségével egy adott hőmérsékleten megmért gőznyomás és a látens hő ismeretében egy közeli hőmérsékletre át tudjuk számítani a gőznyomást.
A gőztenzióval kapcsolatos számítási feladatokkal a fejezet végén ismerkedünk meg.
4.3.4. Tiszta anyagok fázisdiagramja
A fázisdiagramok a különböző anyagok fázisegyensúlyait szemléltetik. Az alábbiakban a tiszta anyagok fázisdiagramjaival foglalkozunk, mely a nyomás és a hőmérséklet függvényében jeleníti meg az egyes fázisokat. A fázisátmeneteket görbékkel, a fázisokat tartományokkal jellemezhetjük. A fentiek alapján megállapíthatók a tenziógörbék, azaz a tiszta szilárd anyag vagy folyadék feletti egyensúlyi gőznyomások, melyek exponenciális függvényekkel közelíthetők. Egy tiszta anyag gőznyomása a hőmérséklet függvényében az alábbi görbével jellemezhető.
4.3.4.1. ábra: A gőznyomás a hőmérséklet függvényében
Jól megfigyelhető, hogy a függvénynek töréspontja van: két közel exponenciális lefutású görbére bontható a függvény. Ennek oka, hogy alacsonyabb hőmérsékleteken a gőz szilárd fázissal, magasabb hőmérsékleteken pedig cseppfolyós halmazállapotú anyaggal tart egyensúlyt. A Clausius–Clapeyron- egyenlet, mely szilárd–gőz és folyadék–gőz egyensúlyokra is alkalmazható, a két esetben azonban más látens hőt kell behelyettesítenünk. A fentiekben már tárgyaltuk, hogy a szublimációs hő nagyobb, mint a párolgáshő. Ennek következtében egy adott tiszta anyag esetén a szublimációhoz tartozó görbe meredeksége nagyobb, mint a párolgáshoz tartozó görbéé.
Az abszolút nulla fok (T=0 K) tetszőlegesen megközelíthető, ám nem érhető el kísérletileg, ezért ezt a pontot nem tudjuk értelmezni ezen a görbén. Azonban a gőztenzió értéke 0-hoz közeledik, ha a hőmérsékletet 0 K-hez közelítjük.
A tenziógörbe egyrészt megadja a szilárd anyaggal vagy folyadékkal egyensúlyban lévő gőz nyomását adott hőmérsékleten, vagy fordítva: az adott nyomáshoz tartozó fázisátalakulás (halmazállapot-változás) hőmérsékletét. Így a görbe azon szakasza, mely a töréspontnál alacsonyabb hőmérsékleteken jellemző, az szublimációs görbe (szilárd–gőz átalakulás), míg a magasabb hőmérsékletekhez tartozó a párolgási görbe. A szublimációs görbéről leolvashatók az adott nyomáshoz tartozó szilárd–gőz fázisátalakulások hőmérsékletei, míg a párolgási görbéről az adott nyomáshoz tartozó forráshőmérsékletek értékei. Felmerülhet a kérdés, hogy a szilárd–folyadék fázisátalakulást milyen görbe jellemzi. A szilárd és a folyadék halmazállapotot (fázist) az úgynevezett olvadáspontgörbe választja szét. Mivel az olvadáspont rendszerint csak csekély mértékben függ a nyomástól, a nyomás–hőmérséklet diagramban az olvadáspontgörbe csaknem függőleges. A három görbe az úgynevezett hármaspontban találkozik. Ez jól megfigyelhető a tiszta anyagok fázisdiagramján:
4.3.4.2. ábra: Tiszta anyagok fázisdiagramja
(Megjegyzés: az, hogy az olvadáspontgörbe „jobbra” vagy „balra” dől-e, a szilárd anyag és a folyadék moláris térfogatának különbsége adja meg. Tehát a szilárd anyag és a folyadék sűrűsége alapján megállapítható, hogy a görbe növekszik vagy csökken a hőmérséklet növelésével. Abban az esetben, ha a szilárd anyag moláris vagy fajlagos térfogata kisebb, mint a folyadéké – tehát ξszilárd > ξfolyadék – az olvadáspontgörbe „jobbra dől”. Ez igen gyakori a tiszta anyagok között, egy példa a szén-dioxid. Előfordul azonban, hogy a folyadék moláris vagy fajlagos térfogata kisebb a szilárdénál, azaz ξszilárd < ξfolyadék, ekkor a görbe balra dől. Erre egy igen fontos példa a víz.)
A hármaspontban a folyadék, a gőz és a szilárd fázisok egyensúlyban vannak egymással, az ekkor mérhető nyomás és a hőmérséklet (hármasponti nyomás és hőmérséklet) az adott tiszta anyagra jellemző mennyiségek, és így függetlenek a mérési körülményektől.
A hármaspont hőmérséklete feletti hőmérsékleten nem lehet a szilárd anyagot elszublimáltatni, ehhez hasonlóan a hármasponti hőmérséklet alatti hőmérsékleten a folyadék nem párologhat.
Megjegyzés: bizonyos anyagoknak lehet több hármaspontjuk is. Ez elsősorban akkor lehetséges, ha szilárd fázisban lehetőség van különböző, egymással egyensúlyban lévő fázisok kialakulására. Ilyen fázisok lehetnek például a szén esetén a grafit és a gyémánt, ezeket allotróp módosulatoknak nevezzük.
A hármaspont mellett a fázisdiagram egy másik fontos pontja a kritikus pont (K). A kritikus pont a párolgásgörbe végpontja, jellemző rá a kritikus nyomás és a kritikus hőmérséklet. A kritikus nyomás feletti nyomáson nem lehetséges légnemű halmazállapot, a gáz vagy gőz kondenzálódik. Ezzel ellentétben a kritikus hőmérsékletnél magasabb hőmérsékleten nem lehet folyadék fázis. Ez lehetőséget ad a gőz és a gáz fogalmak definíciójára:
Gőz: olyan légnemű anyag, mely a tiszta anyagra jellemző kritikus hőmérsékletnél alacsonyabb hőmérsékletű. A kritikus hőmérséklet felett nem lehet gőzről beszélni.
Gáz: rendszerint magában foglalja a gőz fogalmát is, tehát a légnemű halmazállapot szinonimájának tekinthető.
Ha a hőmérséklet nagyobb a kritikus hőmérsékletnél, a nyomás pedig a kritikus nyomásnál, egy negyedik fázishoz jutunk: a (szuperkritikus) fluid vagy szuperfluid fázis. A fluid állapot tulajdonságaiban a folyadék és légnemű halmazállapot között helyezkedik el: jellemző rá a kiváló oldóképesség, a kis viszkozitás. (Szuperkritikus szén-dioxidot alkalmaznak koffeinmentes kávé előállítására ipari méretekben is. Emellett növényi hatóanyagok kinyerésére is használnak szuperkritikus állapotú anyagokat, sőt szennyvizek és talajok károsanyag-tartalmának csökkentésére is alkalmazhatóak.
Ha egy kísérletben egy gőz–folyadék kétfázisú rendszer hőmérsékletét lassan a kritikus hőmérséklet fölé emeljük, a két fázis közötti fázishatár eltűnik, egy homogén fázis keletkezik. A kritikus pont elérésekor rendszerint zavarosodást, opálosodást figyelhetünk meg.
A fázishatár eltűnése azt jelenti, hogy a folyadék feszültsége nullává válik. Ehhez hasonlóan más tulajdonságokban is történik változás:
– a moláris párolgáshő nullává válik (eltűnik), – a felületi feszültség eltűnik,
– a folyadék és gáz sűrűsége azonossá válik, – a két fázis viszkozitása azonossá válik.
Megjegyzés: a felületi feszültség hőmérsékletfüggését az Eötvös-törvény írja le:
V . ) T T ( k
3 / 2 m k
Az egyenletben γ a folyadék felületi feszültsége (N/m), k az Eötvös-állandó, melynek értéke 2,1 ∙ 10−7 J/(K∙mol2/3), Tk a kritikus hőmérséklet (K), T az abszolút hőmérséklet, Vm pedig a folyadék moláris térfogata (m3/mol).
Az alábbi ábrán a szén-dioxid felületi feszültségének hőmérsékletfüggését figyelhetjük meg:
4.3.4.3. ábra: A szén-dioxid felületi feszültségének a hőmérsékletfüggése
A következő diagramokon a cseppfolyós és légnemű szén-dioxid sűrűségét és a szén-dioxid moláris párolgáshőjét ábrázoltuk a hőmérséklet függvényében:
4.3.4.4. ábra: A szén-dioxid sűrűségének a hőmérsékletfüggése
4.3.4.5. ábra: A szén-dioxid moláris párolgáshőjének a hőmérsékletfüggése 4.3.5. A légnemű halmazállapot
A gázok sem önálló alakkal, sem önálló térfogattal nem rendelkeznek. A gázok – a folyadékokhoz hasonlóan – kitöltik a rendelkezésre álló teret, és a térfogatuk függ a nyomástól. A gázokban általában igen gyenge a részecskék közötti kölcsönhatás, gyakorlatilag elhanyagolható.
Ideális gáz: az alkotórészecskék pontszerűek és a közöttük nincsen kölcsönhatás.
Megjegyzendő, hogy az ideális gáz egy modell, mivel a gázokat alkotó részecskék sosem tekinthetők szigorúan pontszerűnek és közöttük kialakulhatnak gyenge kölcsönhatások is. A valóságban a legtöbb gáz reális gázként viselkedik. A reális gázokra nem érvényesek szigorúan az alábbiakban tárgyalt, az ideális gázok viselkedését leíró törvényszerűségek. A problémát elsősorban az alacsony hőmérséklet és nagy nyomás együttes alkalmazása jelentheti, mivel ekkor a gáz (gőz) már közel van a kondenzációhoz, ahol a részecskék között viszonylag jelentős a kölcsönhatás. A reális gázok leírására számos elmélet született, ám ezekkel itt nem foglalkozunk. Az alábbiakban az ideális gázok nyomása, hőmérséklete, térfogata és anyagmennyisége közötti összefüggéseket ismertetünk.
Felmerülhet a kérdés, hogy van-e olyan gáz, mely közel ideálisnak tekinthető. Például a hélium igen széles hőmérséklet- és nyomástartományban ideális gázként viselkedik, tehát az ideális gáz törvényei
igen jó közelítéssel érvényesek rá. Emellett számos hétköznapi gáz is nem túl nagy nyomáson és nem túl alacsony hőmérsékleten közel ideálisnak tekinthető, azaz nem követünk el jelentős hibát, ha ideális gázok leírására szolgáló összefüggéseket alkalmazunk számításaink során.
4.3.5.1. Összefüggések az ideális gáz nyomása (p), térfogata (V) és hőmérséklete (T) között:
Boyle–Mariotte-törvény: a gáz nyomása (p) és térfogata (V) között fordított arányosság áll fenn, ha a gáz anyagmennyisége és a hőmérséklet állandó. A hőmérsékletet állandó értéken tartva adott anyagmennyiségű gáz térfogatának és nyomásának szorzata állandó:
p · V = állandó.
Ha egy adott anyagmennyiségű, nyomású és térfogatú gáz nyomását vagy térfogatát a következő összefüggéssel kiszámíthatjuk:
p1 · V1 = p2 · V2.
A gáz térfogatát a nyomásának függvényében ábrázolva jól látható, hogy a mennyiségek közt fordított arányosság áll fenn:
4.3.5.1.1. ábra: Boyle–Mariotte-törvény
Charles-törvény (Gay-Lussac I. törvénye): állandó anyagmennyiség és nyomás esetén a gáz térfogata (V) és abszolút hőmérséklete (T) között egyenes arányosság áll fenn:
. állandó T
V
A kelvinben (K) mért abszolút hőmérséklet a Celsius-fokban (°C) mért hőmérsékletnél 273,15 egységnyivel nagyobb:
T[K] = t[°C] + 273,15.
A törvény megadja az ideális gázok hőtágulását. Például V1 térfogatú és T1 hőmérsékletű gázt lezárt edényben, állandó külső nyomás mellett T2 hőmérsékletre melegítve (vagy hűtve) a gáz V2
térfogata számítható:
2 2 1 1
T V T
V .
Az egyenes arányosság következtében az ideális gáz térfogatát a hőmérsékletének függvényében ábrázolva egyenest kapunk (a gáz anyagmennyisége nem változik – az edény zárt, illetve a külső nyomás állandó):
4.3.5.1.2. ábra: Charles-törvény (Gay-Lussac I. törvénye)
Gay-Lussac-törvény (Gay-Lussac II. törvénye): adott anyagmennyiségű gáz nyomása (p) és abszolút hőmérséklete (T) között egyenes arányosság van, ha a térfogat állandó. Másképp megfogalmazva a nyomás és az abszolút hőmérséklet hányadosa állandó:
. állandó T
p
Ha ismert egy adott anyagmennyiségű gáz nyomása és hőmérséklete, akkor egy ettől eltérő hőmérsékleten számítható a gáz nyomása, ehhez hasonlóan ismert nyomáshoz kiszámítható a hőmérséklete. (Természetesen a gáz anyagmennyisége és térfogata állandó eközben.)
2 2 1 1
T p T p
Grafikusan ábrázolva:
4.3.5.1.3. ábra: Gay-Lussac-törvény (Gay-Lussac II. törvénye) A fenti három törvény egyesítésével kapjuk az általános vagy egyesített gáztörvényt:
Egyesített gáztörvény: adott anyagmennyiségű gáz esetén állandó értéket kapunk, ha a gáz nyomásának és térfogatának a szorzatát elosztjuk az abszolút hőmérsékletével:
. állandó T
V p
Az előzőekhez hasonlóan két állapot között is felírható, ha a gáz anyagmennyisége nem változik:
T . V p T
V p
2 2 2 1
1
1
Az egyesített gáztörvényből könnyen megkaphatjuk a fenti három gáztörvényt: behelyettesítve például a T1 = T2 feltételt, adódik a Boyle–Mariotte-törvény.
Avogadro-törvény: különböző anyagi minőségű ideális gázok térfogata és anyagmennyisége megegyezik, ha nyomásuk és térfogatuk azonos. Tehát a gáztörvények függetlenek a gáz anyagi minőségétől, ha a gáz ideálisnak tekinthető.
Az Avogadro-törvény következménye, hogy adott nyomáson és hőmérsékleten az ideális gázok térfogata csak a gáz anyagmennyiségétől függ, az anyagi minőségétől nem függ. Így a moláris térfogat (1 mól gáz térfogata adott hőmérsékleten és nyomáson) is független az anyagi minőségtől:
n Vm V.
Például 0 °C-on (273,15 K-en) és normál légköri nyomáson (101 325 Pa) az ideális gázok moláris térfogata 22,41 dm3/mol, függetlenül anyagi minőségüktől.
Az ideális gázok állapotegyenlete:
p · V = n · R · T, ahol
p: a gáz nyomása Pa-ban, V: a gáz térfogata m3-ben,
n: a gáz anyagmennyisége molban,
R: egyetemes gázállandó vagy Regnault-állandó, melynek értéke: 8,314 J/(mol·K), T: a gáz hőmérséklet K-ben.
A gáztörvény alkalmazásakor nagyon fontos, hogy a fenti mértékegységekben helyettesítsük be a mennyiségeket, különben félrevezető eredményeket kapunk!
Érdemes megjegyezni, hogyha a nyomást kPa-ban, a térfogatot pedig dm3-ben (literben) írjuk be az ideális gáztörvénybe, az eredményben nem okoz változást:
(1 kPa) · (1 dm3) = (103 Pa) · (10−3 m3) = (1 Pa) · (1 m3).
A gáztörvény szigorúan véve ideális gázokra teljesül, ám nem túl alacsony hőmérsékleten a legtöbb reális gáz tulajdonságait is
Honnan származik az egyetemes gázállandó (R)?
A kísérletek alapján 1 mól gáz térfogata normál légköri nyomáson (p = 101 325 Pa) és 0 °C hőmérsékleten (T = 273,15 K) 22,41 dm3 (V = 0,02241 m3), így a Regnault-állandó:
K mol 314 J , K 8 mol
m 314 N , K 8 mol m m
N 314 , K 8
15 , 273 mol 1
m 02241 , 0 Pa 325 101 T n
V R p
3 3 2
.
Az ideális gáztörvény segítségével a gázok sűrűségét is ki tudjuk számítani, ha ismerjük a gáz moláris tömegét:
T R
M p p
T R
M p
T R n
n M V d m
.
Tehát az ideális gáz sűrűsége a nyomástól, a moláris tömegtől, és a hőmérséklettől függ.
Gázok relatív sűrűsége: két gáz sűrűségének aránya, dimenziómentes szám.
Ha a két gáz ugyanabban az állapotban van (azonos nyomásuk és hőmérsékletük), akkor a relatív sűrűség megegyezik a moláris tömegek arányával:
2 1 2 1
2 1
rel M
M T R
M p
T R
M p d
d d
.
4.3.5.2. Gázelegyek
A gázelegyeket tömegszázalékos, mólszázalékos vagy térfogatszázalékos összetételükkel szoktuk jellemezni.
Tömegtört vagy tömegszázalék: az i-dik komponens tömegének (mi) és a keverék össztömegének (∑ mi) a hányadosa. A tömegszázalék a tömegtört százalékban kifejezett értéke. Az i- dik komponens tömegtörtje:
i i
i m
w m
A tömegszázalékra szokták az alábbi jelölést is alkalmazni: (m/m)%.
Móltört vagy mólszázalék: az i-dik komponens anyagmennyiségének (ni) és a keverék össz- anyagmennyiségének (∑ ni) a hányadosa. A mólszázalék a móltört százalékban kifejezett értéke. Az i- dik komponens móltörtje:
i i
i n
x n .
A mólszázalékra az alábbi jelölés is használatban van: (n/n)%.
Térfogattört vagy térfogatszázalék: az i-dik komponens térfogatának (Vi) és a keverék össz- térfogatának (∑ Vi) a hányadosa. A térfogatszázalék a térfogattört százalékban kifejezett értéke. Az i- dik komponens móltörtje:
i i
i V
V .
A definíció alapján a térfogatszázalékra a következő jelölés is ismert: (V/V)%.
Az Avogadro-törvény értelmében ideális gázok esetén a móltört és a térfogattört megegyezik.
i i x
Parciális nyomás: az a nyomás, melyet az adott komponens egyedül fejtene ki, ha a rendelkezésre álló térfogatot – azonos hőmérsékleten – egyedül töltené ki. Az i-dik komponens parciális nyomása:
pi = xi · pössz.
Parciális térfogat: az a térfogat, melyet az adott komponens egyedül töltene be a gázkeverék össznyomásán.
Vi = xi · Vössz
A parciális mennyiségek közötti összefüggések:
Dalton-törvény: egy adott gázelegyben a komponensek parciális nyomásának összege megadja a gázelegy össznyomását (pösszes). N-komponens esetén:
össz N
1 i
i N
2
1 p p p p
p
.