Connected Floer homology of covering involutions

https://doi.org/10.1007/s00208-020-01992-9

Mathematische Annalen

Connected Floer homology of covering involutions

Antonio Alfieri¹·Sungkyung Kang^2,3·András I. Stipsicz¹

Received: 30 July 2019 / Revised: 27 March 2020 / Published online: 28 April 2020

© The Author(s) 2020

Abstract

Using the covering involution on the double branched cover of S³ branched along a knot, and adapting ideas of Hendricks–Manolescu and Hendricks–Hom–Lidman, we define new knot (concordance) invariants and apply them to deduce novel linear independence results in the smooth concordance group of knots.

1 Introduction

Concordance questions of knots have been effectively studied by 4-dimensional topo- logical methods by several authors. For a knot K in the three-sphere S³ one can consider the double branched cover(K)of S³branched along K. IfK is a slice knot (i.e. it bounds a smoothly embedded disk in the 4-diskD⁴) then(K)bounds a four-manifoldX having the same rational homology asD⁴: thisX can be chosen to be the double branched cover of D⁴along the slice disk. The existence of such four- manifold then can be obstructed by various methods, leading to sliceness obstructions of knots. For example, Donaldson’s diagonalizability theorem applies in case(K)is known to bound a negative definite four-manifold with intersection form which does not embed into the same rank diagonal lattice. This line of reasoning was used by Lisca in his work about sliceness properties of 2-bridge knots, see [8,17,21]. A numerical

Communicated by Jean-Yves Welschinger.

B

alfieriantonio90@gmail.com Sungkyung Kang

sungkyung38@icloud.com András I. Stipsicz stipsicz.andras@renyi.hu

1 Rényi Institute of Mathematics, Reáltanoda utca 13-15, Budapest 1053, Hungary 2 Mathematical Institute, University of Oxford, Oxford, UK

3 Institute of Mathematical Sciences, The Chinese University of Hong Kong, Shatin, Hong Kong

invariant (in the same spirit) was introduced by Manolescu–Owens [22] utilizing the Ozsváth–Szabó correction term of the unique spin structure of(K).

Different knots might admit diffeomorphic double branched covers, though; for example, ifK andKdiffer by a Conway mutation, then(K)and(K)are dif- feomorphic. This implies that if K is slice, all slice obstructions coming from the above strategy must vanish forKas well. A long-standing problem of this type was whether the Conway knot is slice; it admits a mutant (the Kinoshita–Terasaka knot) which is slice, hence merely considering the double branched cover will not provide sliceness obstruction. (The fact that the Conway knot is not slice has been recently proved by Piccirillo [36], relying on four-dimensional topological methods and results from Khovanov homology.)

The information we neglect in the above approach is that the three-manifold (K)(viewed as the double branched cover of S³ along K) comes with a self- diffeomorphismτ, where pairs of points in(K)mapping to the same point of S³ are interchanged byτ. In this paper we introduce modifications of the usual Heegaard Floer homology groups of(K)which take thisZ/2Z-action into account, leading to new knot invariants.

Heegaard Floer homology associates to a closed, oriented, smooth three-manifold a finitely generatedF[U]-module HF⁻(Y)(whereF[U]is the polynomial ring over the fieldFof two elements): it is the homology of a chain complex(CF⁻(Y), ∂)(defined up to chain homotopy equivalence) and the homology naturally splits according to the spin^cstructures ofY as

HF⁻(Y)=

s∈Spin^c(Y)

HF⁻(Y,s).

IfY is a rational homology sphere (i.e.,b1(Y)=0) then HF⁻(Y,s)admits a natural Q-grading, and the gradedF[U]-module HF⁻(Y,s)is a diffeomorphism invariant of the spin^cthree-manifold(Y,s), while the local equivalence class of(CF⁻(Y,s), ∂) (for the definition of this notion see Definition3.2) provides an invariant of the rational spin^chomology cobordism class of(Y,s). In this case the local equivalence class of CF⁻(Y,s)can be characterised by a single rational number d(Y,s), theOzsváth–

Szabó correction termof the spin^cthree-manifold(Y,s).

More recently, exploiting a symmetry built in the theory, Hendricks and Manolescu in [13] introduced involutive Heegaard Floer homology. The main idea of their con- struction is that, by making use of naturality, one can construct geometrically a grading-preserving chain map ι:CF⁻(Y) → CF⁻(Y)which is (up to homotopy) an involution. The mapping cone of the mapι+id leads to involutive Floer homol- ogy HFI(Y), a module over the ringF[U,Q]/(Q²). This group is interesting only for those spin^cstructures which originate from a spin structure, and provides a new and rather sensitive diffeomorphism invariant of the underlying spin three-manifold.

A further application of the above involution appeared in the work of Hendricks, Hom and Lidman [11], where (through the appropriate use ofι) connected Heegaard Floer homology HF⁻_conn(Y), a submodule of HF⁻(Y)was defined. This submodule turned out to be a homology cobordism invariant.

Similar constructions apply for any chain complex equipped with a homotopy involution. In this paper we will define thebranched knot Floer homologyof K as HFB⁻(K)=H_∗(Cone(τ#+id)), whereτ:(K)→(K)is the covering involution, τ#is the map induced byτ on the Heegaard Floer chain complex CF⁻((K),s0), withs0the unique spin^cstructure on(K), and Cone is the mapping cone of the map τ#+id. (Related constructions have been examined in [12]; cf. also [2].)

Theorem 1.1 The groupHFB⁻(K), as a gradedF[U,Q]/(Q²)-module, is an isotopy invariant of the knot K ⊂S³.

A simple argument shows that, as anF[U]-module, HFB⁻(K)is isomorphic to F[U]_(δ(K))⊕F[U](δ(K))⊕ A, whereδ(K), δ(K)∈ QandAis a finitely generated, gradedU-torsion module overF[U].

Theorem 1.2 The rational numbersδ(K)andδ(K)are knot concordance invariants.

Adapting the method of [11] for defining new homology cobordism invariants of rational homology spheres, we define the connected branched Floer homol- ogy HFB⁻_conn(K)of a knot K ⊂ S³ as follows. Consider a self-local equivalence fmax:CF⁻((K),s0)→CF⁻((K),s0)which commutes (up to homotopy) with τ#and has maximal kernel among such endomorphisms. Then take HFB⁻_conn(K)= H_∗(Im fmax).

Theorem 1.3 The module HFB⁻_conn(K)(up to isomorphism) is independent of the choice of the map fmaxwith maximal kernel, and the isomorphism class of the graded moduleHFB⁻_conn(K)is a concordance invariant of the knot K .

It follows from the construction that HFB⁻_conn(K) is an F[U]-submodule, indeed a direct summand of HF⁻((K),s0). As a finitely generated F[U]-module, HFB⁻_conn(K)is the sum of cyclic modules, and since it is of rank one, it can be written as

HFB⁻_conn(K)=F[U] ⊕HFB⁻_red-^conn(K),

where the second summand (the U-torsion submodule) is the reduced connected homology ofK.

It is not hard to see that if HF⁻((K),s0)=F[U]holds—for example if(K) is anL-space, which is the case whenK is a quasi-alternating knot—thenτ#is chain homotopic to the identity map, implying the following.

Theorem 1.4 If K is concordant to a quasi-alternating knot, then the reduced group HFB⁻_red-^conn(K)vanishes.

Somewhat more surprisingly, the same vanishing holds for torus knots (a behaviour similar to the one presented by the analogue of the upsilon-invariant defined in the seeting of Khovanov homology by Lewark and Lobb [19,27]):

Theorem 1.5 For the torus knot Tp,qwe have thatHFB⁻_red-conn(Tp,q)=0.

Finally we use lattice cohomology of Némethi [23] to get a computational scheme for the above invariants in the case of Montesinos knots. This second class of compu- tation is based on results by Dai and Manolescu [4] and applies in particular to pretzel knots.

1.1 Topological applications

In [20] Lidman and Moore showed that a pretzel knot P(a1, . . . ,ak)is anL-space knot (i.e. it hasL-space surgeries) if and only if it is a torus knot of the formT2,2n+1, or a pretzel knot of the formP(−2,3,q)for someq ≥7 odd. In [39] the question of which linear combinations ofL-space knots is concordant to a linear combination of algebraic knots was studied. In [1, Theorem 1.1] the first author showed that pretzel knots of the formP(−2,3,q)are not concordant to positive sums of algebraic knots.

It is conjectured that these knots are linearly independent in the quotient of the knot concordance group modulo algebraic knots. Note that for the pretzel knotsP(−2,3,q) the obstruction found in [39, Corollary 3.5] vanishes.

Our calculations for the connected homologies of pretzel knots in combination with the vanishing theorem above allow us to prove certain independence results in the smooth concordance group going in this direction. To state the results, let us introduce the following notations: letC denote the (smooth) concordance group of knots inS³andQA(respectivelyT) those subgroups ofCwhich are generated by all quasi-alternating (respectively torus) knots. In addition,QA+T is the subgroup generated by quasi-alternating knots and torus knots.

Theorem 1.6 Let K be the connected sum of pretzel knots of the form P(−2,3,q), with q ≥7odd. Then K is not concordant to any linear combination of torus knots.

Indeed,[K]is a nonzero in the quotientC/(T +QA).

Furthermore, relying on computations from [4,15], and ideas and results from [3], we prove the following.

Theorem 1.7 The pretzel knots{P(−2q−1,4q+1,4q +3)| q ≥1}are linearly independent in the quotient groupC/(T +QA). Indeed,Z^∞is a direct summand of C/(T +QA).

Note that P(−2q −1,4q +1,4q +3)has trivial Alexander polynomial, thus is topologically slice. It was previously known that there exists an infinte family of topologically slice knots which is linearly independent inC/QA. Our result proves that we can also find such a family, not just up to quasi-alternating knots, but up to connected sums of quasi-alternating knots and torus knots. For independence from L-space knots, see [40].

1.2 Organization of the paper

The paper is organized as follows. In Sect.2we introduce branched knot Floer homol- ogy, and in Sect. 3 we discuss the details of the definition of the connected Floer

homology group HFB⁻_conn(K)of a knotK ⊂S³. Section4is devoted to the proof of the vanishing results above, while in Sect.5we give a way to compute the invariants for Montesinos knots. Finally in Sect.6we derive some independence results in the smooth concordance group.

We would like to thank András Némethi for numerous highly informative discus- sions. We specially thank the anonymous referee for providing a number of suggestions and advises which greatly improved the paper. The first and the third authors acknow- eldge support from the NKFIH Élvonal project KKP126683. The second author was partially supported by the European Research Council (ERC) under the Euro- pean Union Horizon 2020 research and innovation programme (grant agreement No 674978).

2 Definition of branched knot Floer homology

Let H = (,α,β,z)be a pointed Heegaard diagram which represents a rational homology sphereY, and letJsbe a generic path of almost-complex structures on theg- fold symmetric product Sym^g()(compatible with a symplectic structure constructed in [35]). Heegaard Floer homology [31] assigns to the pair(H,Js)a finitely generated, Q-graded chain complex CF⁻(H,Js)over the polynomial ringF[U], graded so that degU= −2. This chain complex is defined as the freeF[U]-module generated by the intersection points of the Lagrangian toriT_α =α1× · · · ×αgandT_β =β1× · · · ×βg

in Sym^g(), and is equipped with the differential

∂x=

y∈Tα∩Tβ

{φ∈π2(x,y)|μ(φ)=1}

#

M(φ) R

U^nz(φ)·y (1)

where #(M(φ)/R)is the (mod 2) number of points in the unparametrized moduli space M(φ)/Rof Js-holomorphic strips with indexμ(φ)=1 representing the homotopy classφ ∈π2(x,y), andnz(φ)is the intersection number ofφwith the divisorVz = {z} ×Sym^g−1(). For more details about Heegaard Floer homology see [30–33].

For a knotK ⊂S³, let(K)denote the double branched cover ofS³branched along K. The three-manifold(K)comes with a natural mapτ:(K)→(K)(called the covering involution) which interchanges points with equal image under the branched covering mapπ:(K)→ (K)/τ S³. The fixed point set Fix(τ) = Kmaps homeomorphically toKunderπ. As the notation suggests (sinceH1(S³\K;Z)∼=Z), the branched cover(K)in this case is determined by the branch locusK ⊂S³.

Pulling back the Heegaard surface, as well as theα- and theβ-curves of a doubly- pointed Heegaard diagram D = (,α,β, w1, w2)representing K ⊂ S³, we get a pointed Heegaard diagram

HD =

=π⁻¹(),α=π⁻¹(α),β=π⁻¹(β),z=π⁻¹(w1)

of the double branched cover(K). The covering projectionπ:(K)→ S³restricts to a double branched cover of Riemann surfaces π|: → with branch set

{w1, w2}. The restrictionτ|:→of the covering involutionτrepresents the cov- ering involution ofπ|: →, andτ|: →induces a self-diffeomorphism of the symmetric product

σ:Sym^g˜() →Sym^g˜(), (2) leavingT_αandTβ, as well as the divisorVz = {z} ×Sym^g˜−1()invariant.

Pick a generic path of almost-complex structures Js ∈ J(Sym^g˜())(satisfying the usual compatibility conditions with the chosen symplectic form on the symmetric product) and consider the Heegaard Floer chain complex CF⁻(HD,Js)associated to (HD,Js). Recall that there is a direct sum decomposition of CF⁻(HD,Js)indexed by spin^cstructures:

CF⁻(HD,Js)=

s∈Spin^c((K))

CF⁻(HD,Js;s) .

The first (singular) homology group of the double branched cover(K)can be presented by θ +θ^t, where θ is a Seifert matrix for K. Thus, |H1((K),Z)| = det(θ +θ) = det(K), which is an odd number. In particular,(K)has a unique spin structures0. We will focus on CF⁻(HD,Js;s0), the summand of CF⁻(HD,Js) associated tos0.

Note that if the path of almost-complex structures Js ∈ J(Sym^g˜())is chosen generically, transversality is achieved for both Js and the push-forwardσ_∗Js (where σ is given in Equation (2)). For such a choice of almost-complex structures we have well-defined Heegaard Floer chain complexes CF⁻(HD,Js)and CF⁻(HD, σ_∗Js), and we can consider the map

η:CF⁻(HD,Js)→CF⁻(HD, σ_∗Js) (3) sending a generatorx =x1+ · · · +xg_˜ ∈ Tα∩Tβ⊂Sym^g˜() toσ (x)=τ(x1)+

· · · +τ(xg_˜).

Lemma 2.1 The mapηis an isomorphism of chain complexes. Furthermore,ηmaps the summandCF⁻(HD,Js;s0)of the spin structures0intoCF⁻(HD, σ_∗Js;s0).

Proof It is obviously an isomorphism of freeF[U]-modules; indeed,η²=id sinceτ is an involution. To see thatηcommutes with the differential, notice thatu →σ◦u provides a diffeomorphism between the moduli space ofJs-holomorphic representa- tives of a homotopy classφ ∈ π2(x,y)and the moduli space ofσ∗Js-holomorphic representatives ofσ◦φ∈π2(σ(x), σ(y))).

To show that η preserves the spin structure we argue as follows. According to [31, Sect. 2.6] the choice of a basepointzofHDdetermines a mapsz:Tα∩Tβ → Spin^c((K))and

CF⁻(HD,Js;s)=

sz(x)=s

F[U] ·x.

It follows from the definition ofsz thatτ∗(sz(x))=sz(τ(x)). Thus ifsz(x)=s0, we have that

sz(τ(x))=τ_∗(sz(x))=τ_∗(s0)=τ_∗(s0)=τ_∗(s0)=sz(τ(x))

proving that sz(τ(x)) is a self-conjugate spin^c structure, i.e. spin. The claim now follows from the fact that(K)has a unique spin structure.

We define τ#: CF⁻(HD,Js;s0) → CF⁻(HD,Js;s0) as the map η:CF⁻(HD,Js;s0)→CF⁻(HD, σ_∗Js;s0)followed by the continuation map

⁻_Js,t:CF⁻(HD, σ∗Js;s0)→CF⁻(HD,Js;s0)

from [31, Sect. 6], induced by a generic two-parameter familyJs,tof almost-complex structures interpolating betweenJs andτ_∗Js:

τ#=⁻_Js,t ◦η.

Lemma 2.2 τ_#²id, wheredenotes chain homotopy equivalence.

Proof Consider

⁻_Js,t(x)=

y∈Tα∩Tβ

{φ∈π2(x,y)|μ(φ)=0}

# MJs,t(φ)

U^nz(φ)·y

whereMJ_s,t(φ)denotes the moduli spaces ofJs,t-holomorphic strips.

Givenx∈T_α∩Tβone computes η◦⁻_Js,t(x)=

y∈Tα∩Tβ

{φ∈π2(x,y)|μ(φ)=0}

# MJs,t(φ)

U^nz(φ)·τ(y)

=

y∈Tα∩Tβ

{φ∈π2(x,τ(y))|μ(φ)=0}

# MJs,t(φ)

U^nz(φ)·y

=

y∈Tα∩Tβ

{φ∈π2(τ(x),y)|μ(φ)=0}

# MJ_s,t(τ◦φ)

U^nz(σ◦φ)·y

=

y∈Tα∩Tβ

{φ∈π2(τ(x),y)|μ(φ)=0}

# MJs,t(φ)

U^nz(φ)·y

=⁻_τ∗Js,t(τ(x)) ,

hence the identityη◦⁻_Js,t =⁻_σ∗Js,t ◦ηfollows. Thus,

τ_#²=⁻_Js,t ◦η◦⁻_Js,t ◦η=⁻_Js,t ◦⁻_σ∗Js,t ◦η²=⁻_Js,t ◦⁻_σ∗Js,t ,

where the last identity holds because η² = id (a consequence of the fact that τ:(K)→(K)is an involution).

By concatenating Js,t andσ∗Js,t we obtain a one-parameter family of paths of almost-complex structures describing a closed loop based at the path Js. Since the space of almost complex structures (compatible with the fixed symplectic structure) is contractible, we can find a three-parameter family of almost complex structuresJs,t,x

interpolating between the juxtaposition ofJs,t andσ_∗Js,t, andJs,t,1≡Js. As pointed out in [31, Sect. 6], a generic choice ofJs,t,xproduces smooth moduli spaces

MJs,t,x(φ)=

c∈[0,1]

MJs,t,c(φ) φ∈π2(x,y)

of dimensionμ(φ)+1. These can be used to produce a chain homotopy equivalence H_J⁻

s,t,x(x)=

y∈Tα∩Tβ

{φ∈π2(x,y)|μ(φ)=−1}

# MJs,t,x(φ)

U^nz(φ)·y

between⁻_Js,t ◦⁻_σ∗Js,t and id, concluding the argument.

In summary, for a knotK ⊂S³there is a homotopy involutionτ#:CF⁻((K),s0)

→CF⁻((K),s0)associated to the covering involutionτ:(K)→(K). In order to derive knot invariants from the pair(CF⁻(H,s0), τ#), we follow ideas from [13]

and form the mapping cone ofτ#+id:CF⁻((K),s0)→CF⁻((K),s0), written equivalently as

CFB⁻(K)=

CF⁻((K),s0)[−1] ⊗F[Q]/(Q²), ∂cone=∂+Q·(τ#+id) , where degQ = −1. Recall that CF⁻((K),s0)admits an absoluteQ-grading, and τ#preserves this grading, hence CFB⁻(K)also admits an absoluteQ-grading. Taking homology we get the group HFB⁻(K)=H_∗(CFB⁻(K)), which is now a module over the ringF[U,Q]/(Q²). We call HFB⁻(K)thebranched Heegaard Floer homology of the knot K ⊂ S³. Now we are ready to turn to the proof of the first statement announced in Sect.1:

Proof of Theorem1.1 The proof is similar to the one of [13, Proposition 2.8]. Indepen- dence from the chosen path of almost-complex structures is standard Floer theory.

For independence from the chosen doubly pointed Heegaard diagram of K, we argue as follows: A doubly pointed Heegaard diagram D =(,α,β, w1, w2)rep- resenting the knot K ⊂ S³can be connected to any other doubly pointed diagram D =(,α,β, w₁, w₂)of K by a sequence of isotopies and handleslides of the α-curves (orβ-curves) supported in the complement of the two basepoints, and by stabilizations (i.e., forming the connected sum ofwith a torusT²equipped with a new pair of curvesαg+1andβg+1which meet transversally in a single point). A sequence of these moves lifts to a sequence of pointed Heegaard moves of the pull- back diagramsHDandHDwith underlying three-manifold the double branched cover

(K). According to [16] the choice of such a sequence of Heegaard moves yields a natural chain homotopy equivalenceψ: CF⁻(HD)→CF⁻(HD)which fits into the diagram

CF⁻(HD) ^τ#

ψ

CF⁻(HD)

ψ

CF⁻(HD) ^τ# CF⁻(HD)

(4)

that commutes up to chain homotopy. Let :CF⁻(HD) → CF⁻(HD)be a map realizing the chain homotopy equivalence. Then the map f: Cone(τ# +id) → Cone(τ_#+id)defined by f =ψ+Q·(ψ+)is a quasi-isomorphism. Indeed, f is a filtered map with respect to the two step filtration of the mapping cones, and since it induces an isomorphism on the associated graded objects, it is a quasi-isomorphism.

Notice that the mapping cone exact sequence associated to CFB⁻(K)=Cone(τ#+ id)reads as an exact triangle

HF⁻((K),s0) HF⁻((K),s0) HFB⁻(K)

τ∗+id

j_∗

p_∗ (5)

in which j_∗preserves the grading, and p_∗drops it by one. In particular, ifτ_∗=id, the horizontal map in the above triangle is zero, and in that case HFB⁻(K)is the sum of two copies of HF⁻((K),s0)(with the grading on one copy shifted by one).

A close inspection of the exact triangle above reveals that, asF[U]-modules, we have

HFB⁻(K)=F[U]_(δ)⊕F[U]_(δ+1)⊕(F[U]−torsion) .

We setδ(K)=δandδ(K)=δ, which (by the above discussion) are knot invariants.

Notice thatδ(K), δ(K) ∈ Q,δ(K)≡ δ(K)≡ δ(K)mod 2, andδ(K)≤ δ(K) ≤ δ(K), whereδ(K)is the Ozsváth-Szabó correction term of((K),s0), i.e.δ(K)is half the Manolescu-Owens invariant ofK introduced in [22].

3 Concordance invariants from(CF⁻(6(K),s0),#)

Adapting ideas from [11], the chain complex CF⁻((K),s0), equipped withτ#, pro- vides concordance invariants of the knotKas follows. First, recall [11, Definition 2.5]

regardingι-complexes:

Definition 3.1 Anι-complex(C, ι)is a finitely generated, free,Q-graded chain com- plexCoverF[U]together with a mapι:C →CwhereCis supported in degreed+Z

for somed ∈Q(multiplication byUdrops theQ-grading by two), the homology of the localizationU⁻¹H_∗(C)=H_∗(C⊗F[U]F[U,U⁻¹])is isomorphic toF[U,U⁻¹] via an isomorphism preserving the relativeZ-grading, andιis a grading preserving, U-equivariant chain map which is a homotopy involution.

We will considerι-complexes up tolocal equivalence(see [11, Definitions 2.6 and 2.7]).

Definition 3.2 Alocal equivalence f:C→Cof twoι-complexes(C, ι)and(C, ι) is a grading preserving,U-equivariant chain map f:C →Csuch that

• ι◦ f f ◦ι, i.e. the two compositions are chain homotopy equivalent, and

• f induces an isomorphisms flocon the localizationU⁻¹H_∗(C).

Definition 3.3 Twoι-complexes(C, ι)and(C, ι)arelocally equivalentif there exist local equivalences f:C → C andg:C → C. If in addition we have f ◦g id andg◦ f id, then(C, ι)and(C, ι)arechain homotopy equivalentι-complexes.

Given an ι-complex (C, ι), we can look at the set Endloc(C, ι) of its self-local equivalences f:C →C. This can be partially ordered by defining f gif and only if Ker f ⊂Kerg. We say that f ∈Endloc(C)is amaximal self-local equivalenceif it is maximal with respect to this ordering. Since we assumedCto be finitely generated, maximal self-local equivalences always exist. The following lemma summarises the results of [11, Section 3].

Lemma 3.4 Let(C, ι)be anι-complex. Then

(1) if f ∈Endloc(C, ι)is a maximal self-local equivalence, thenιinduces a homotopy involutionι^Imf :Imf →Im f . Furthermore,(Im f, ι^Imf)is locally equivalent to(C, ι);

(2) if f,h ∈ Endloc(C, ι) are two maximal self-local equivalences, then there is a chain homotopy equivalence(Imf, ι^Imf)(Imh, ι^Imh)ofι-complexes;

(3) if(C, ι)is anι-complex locally equivalent to(C, ι)and f ∈Endloc(C, ι), and h ∈ Endloc(C, ι)are self-local equivalences then there is a chain homotopy equivalence(Im f, ι^Imf)(Imh, ι^Imh)ofι-complexes.

Since

H_∗(CF⁻((K),s0)⊗_F[U]F[U,U⁻¹])=HF^∞((K),s0)=F[U,U⁻¹], the pair (CF⁻((K),s0), τ#)of the Heegaard Floer chain complex of the double branched cover(K)of a knot K ⊂ S³ (equipped with the homotopy involution τ# induced by the covering involution) is an ι-complex associated to K. Given a maximal self-local equivalence fmax:CF⁻((K),s0)→CF⁻((K),s0)we define HFB⁻_conn(K), theconnected Floer homologyof the knot K ⊂ S³as H_∗(Im fmax). As an application of Lemma3.4, it is then easy to see that the resulting group, up to isomorphism, is a knot invariant:

Theorem 3.5 The chain homotopy type of Im fmax is independent of the choice of the maximal self-local equivalence fmax ∈ Endloc(CF⁻((K),s0), τ#), hence

HFB⁻_conn(K)is a knot invariant.

We now turn to the proof of the concordance invariance of the groups HFB⁻_conn(K).

The following naturality statement will be crucial in the proof.

Lemma 3.6 (Ozsváth & Szabó [34], Zemke [41])Let Y and Ybe two three-manifolds equipped with self-diffeomorphisms τ: Y → Y and τ: Y → Y. Suppose that W:Y →Yis a cobordism and that there exists a self-diffeomorphism T: W →W restricting toτ andτon the two ends of W . Then

τ#◦F_W⁻_,t=F_W⁻_,T

∗t◦τ#

mapsCF⁻(Y,t|Y)→CF⁻(Y,t|Y)for everyt∈Spin^c(W).

Proof of Theorem1.3 Suppose that K ⊂ S³ is concordant to K, i.e. there exists a smoothly embedded annulusC ⊂ S³× [0,1]with∂C = C∩S³× [0,1] = K × {1} ∪K× {0}. By taking the double branched cover(C)ofS³× [0,1]branched alongC we get a smooth rational homology cobordism from(K)to(K). By adapting [10, Lemma 2.1] forn=2, we get that the four-manifold(C)comes with a distinguished spin structuretrestricting to the canonical spin structure on the two ends. In addition, this spin structure is invariant under the covering involution of the double branched cover(C). Let F_C⁻: CF⁻((K),s0)→CF⁻((K),s0)denote the cobordism map induced by((C),t).

Since(C)is a rational homology cobordism, it follows that F_C⁻:CF⁻((K),s0)→CF⁻((K),s0) and

F₋⁻_C:CF⁻((K),s0)→CF⁻((K),s0) ,

are local equivalences. (Recall that according to [34], a rational homology cobordism induces an isomorphism on HF^∞ = U⁻¹HF⁻.) The fact that F_C⁻ and F₋⁻_C both homotopy commute with the homotopyZ/2Z-actions follows from Lemma3.6and the fact that (in the notations of that lemma) we have T_∗t = t. Then Lemma3.4

concludes the argument.

Proof of Theorem1.2 Let f ∈ Endloc(CF⁻((K),s0), τ#) be a maximal self-local equivalence. As a consequence of Lemma3.4, the chain homotopy type of the mapping cone of the restrictionτ_#^Imf +id:Im f →Im f is a concordance invariant ofK. On the other hand,

H_∗

Cone(τ_#^Imf +id)

=F[U]_δ(K)⊕F[U]_δ(K)+1⊕(F[U]−torsion),

implying the claim.

Since HF⁻((K),s0)is of rank one (as an F[U]-module), and fmaxis a local equivalence, it follows that the summand HFB⁻_conn(K)⊂HF⁻((K),s0)is also of rank one. TheU-torsion submodule of HFB⁻_conn(K)is thereduced connected Floer homologyof K, and it will be denoted by HFB⁻_red-^conn(K). The following simple adaptation of [11, Proposition 4.6] allows us to prove triviality of HFB⁻_red-^conn(K).

Proposition 3.7 HFB⁻_red-^conn(K)=0if and only ifδ(K)=δ(K)=δ(K).

Given a knotK ⊂S³we denote by−K its mirror image.

Lemma 3.8 For a knot K ⊂S³we have thatδ(K)= −δ(−K).

Proof The double branched cover of−Kis−(K). The argument of [13, Proposition

5.2] provides the claimed identity.

Lemma 3.9 If K =K1#K2for two knots K1and K2⊂S³, then

δ(K1)+δ(K2)≤δ(K)≤δ(K)≤δ(K1)+δ(K2). (6) Proof Suppose thatDiis a doubly pointed Heegaard diagram forKi ⊂S³(i =1,2).

Then a doubly pointed Heegaard diagramDcan be constructed forK by taking the connected sums of Di (along w₂¹ in D1 andw²₂ in D2). Then a simple argument shows that the Heegaard diagramHD of(K)originating from Dcan be given as the connected sum ofHD₁ andHD₂, implying that CF⁻(HD)is the tensor product of CF⁻(HD₁)and CF⁻(HD₂). It follows that the mapηDof Equation (3) forHDis the tensor product of the similar mapsηD₁ andηD₂ forHD₁ andHD₂. Since the map induced on CF⁻by Heegaard moves onHD₁ andHD₂splits as the tensor product of maps induced on CF⁻(HD1)and CF⁻(HD2)respectively (note that this fact was also used by Hendricks–Manolescu–Zemke in the proof of [14, Theorem 1.1]), we see that (τD)#and(τD1)#⊗(τD2)#are chain homotopic maps, from which a simple adaptation of the proof of [14, Proposition 1.3] implies the result.

4 Vanishing results

In some cases HFB⁻(K)and HFB⁻_conn(K)can be easily determined. As is customary in Heegaard Floer theory, these invariants do not capture any new information for quasi-alternating knots. It is a more surprising (and as we will see, very convenient) feature of HFB⁻_conn that it is rather trivial for torus knots as well. In this section we show some vanishing results about the group HFB⁻_red-conn(K), while the next section provides methods to determine our invariants for Montesinos (and more generally for arborescent) knots. We start with a simple motivating example.

4.1 An example

Consider the Brieskorn sphere (2,3,7); it can be given as(−1)-surgery on the right-handed trefoil knotT2,3. It is an integral homology sphere with Heegaard Floer

homologyHF((2,3,7))=F²₍₀₎⊕F(−1)and HF⁻((2,3,7))=F[U](−2)⊕F(−2)

in its unique spin^c(hence spin) structure, see [28, Eq. (25)].

This three-manifold can be presented as the double branched cover of S³either along the torus knotT3,7, or along the pretzel knotP(2,−3,−7). The two presenta- tions provide two involutions on(2,3,7), which potentially provide two different maps on the Heegaard Floer chain complex. Indeed, let φ1 denote the involution (2,3,7)admits as double branched cover alongT3,7and letφ2denote the involu- tion it gets as double branched cover alongP(2,−3,−7). Through direct calculation, the actions of these maps on Heegaard Floer homology has been identified in [12, Propositions 6.26 and 6.27].

Theorem 4.1 ( [12])The map(φ1)∗induces the identity map onHF((2,3,7))(and hence on HF⁻((2,3,7)), while the map (φ2)_∗ is different from the identity on

HF((2, 3,7)).

This allows us to compute the invariants HFB⁻ and HFB⁻_conn for T3,7 and P(2,−3,−7), showing that

• HFB⁻(T3,7)=F[U]₍₋2)⊕F[U]₍₋3)⊕F₍₋2)⊕F₍₋3), or, as anF[U,Q]/(Q²)- module (and ignoring gradings) HFB⁻(T3,7)=(F[U,Q]/(Q²))⊕F²,

• HFB⁻_conn(T3,7)=F[U]₍₋2), hence HFB⁻_red-conn(T3,7)=0;

• HFB⁻(P(2,−3,−7))=(F[U,Q]/(Q²))⊕F,

• HFB⁻_conn(P(2,−3,−7))=F[U](−2)⊕F(−2), hence HFB⁻_red-conn(P(2,−3,−7))

=F(−2)=0.

These calculations generalize to show that any torus knot has trivial reduced con- nected Floer homology HFB⁻_red-conn, while for pretzel knots there is a combinatorial method to determine this quantity. In particular, the above results will be reproved in Sect.4.3and in Sect.6.

4.2 Quasi-alternating knots

Proof of Theoem1.4 IfK is a quasi-alternating knot, then the double branched cover (K)is anL-space, and hence HF⁻((K),s0)=F[U]; in particular the homology is only in even degrees. Results of [4] imply thatτ#is determined (up to homotopy) by its action on homology, which (as a grading preserving map) forF[U]must be equal to the identity. Thereforeτ#is homotopic to the identity, and soτ#+id=0, hence the exact triangle of Eq. (5) determines HFB⁻(K)as the sum of two copies of HF⁻((K),s0) (one with shifted grading). Furthermore, since the homotopy commuting assumption of a self-local equivalence in this case is vacuous, we get that HFB⁻_conn(K)=F[U](=

HF⁻((K),s0)), HFB⁻_red-conn(K)=0, and the only invariant we get from this picture is thed-invariant of((K),s0), which is (half of) the Manolescu–Owens invariant of

the knotK from [22].

4.3 Torus knots

Next we turn to the discussion of Theorem1.5. Thanks to the observation below, the proof of this result is significantly easier whenpq is odd.

Proposition 4.2 Suppose that pq is odd. Then the covering involutionτon the double branched cover(Tp,q)is isotopic toid.

Proof The double branched cover of the torus knotTp,qis diffeomorphic to the link of the complex surface singularity given by the equationz²=x^p+y^q, which is the Brieskorn sphere(2,p,q). The covering involutionτ:(2,p,q)→(2,p,q)of Tp,qacts as(z,x,y)→(−z,x,y).

Fixt∈ S¹and consider the diffeomorphism

(z,x,y)→(t^pqz,t^2qx,t^2py).

Clearly we get anS¹-family of diffeomorphisms, wheret =1 gives id, whilet= −1 (under the condition pqodd) givesτ, concluding the proof of the proposition.

The case when exactly one of p andq is even, however, requires some more preparation from lattice homology. (For a more thorough introduction to this subject see [23,25]).

4.4 Lattice homology

This theory was motivated by computational results of Ozsváth and Szabó (for mani- folds given by negative definite plumbing trees of at most one ’bad’ vertex) in [29] and extended by Némethi [23] to any negative definite plumbing trees. The isomorphism of lattice homology with Heegaard Floer homology was established for almost-rational graphs by Némethi in [23], which was extended in [26] to graphs with at most two

’bad’ vertices. Below we recall the basic concepts and results of this theory.

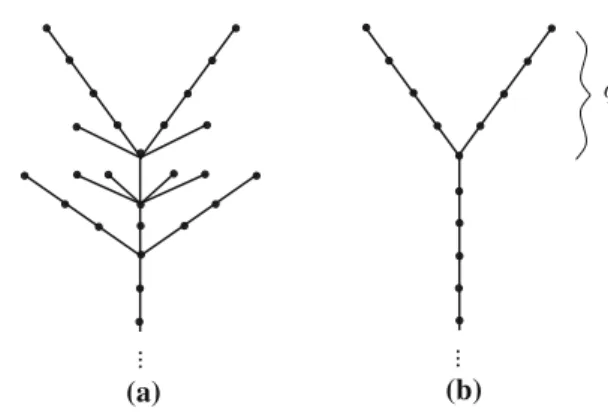
Agraded rootis a pair(R, w)where

• Ris a directed, infinite tree with a finite number of leaves and a unique end modelled on the infinite stem • • • · · ·, subject to the condition that every vertex has exactly one successor (see Fig.1for an example),

• andw: R →Qis a function associating to each vertexxof Ra rational number w(x)∈Qsuch thatw(x2)=w(x1)−2 if(x1,x2)is an edge ofR.

A graded root(R, w) specifies a gradedF[U]-module H⁻(R, w) as follows: As a graded vector space,H⁻(R, w)is generated overFby the vertices ofR, graded so that gr(x)=w(x)for allx∈ R. Multiplication byUis defined on the set of generators by saying thatU·x=yif for the vertexxofRthe vertexyis its successor.

Manolescu and Dai showed in [4] that the lattice homologyH⁻(R, wk)correspond- ing to the graded root(R, wk)can be represented as the homology of amodel complex C(R), which is defined as follows. LetC(R)be generated (as anF[U]-module), by

• the leaves{vl}ofR(with gradingw(vl)), called theeven generators, and

• by theodd generatorsdefined as follows: for a vertexaofRwith valency greater than 2, letV = {v1, . . . , vn}be the set of all vertices ofRsatisfyingUv=a. Then we take the formal sumsv1−v2, . . . , vn−1−vnof vertices ofRas generators of C(R)at degreew(a)+1.

Fig. 1 A graded root

...

TheU-action in this module lowers degree by 2. The differential∂onC(R)vanishes on all even generatorsv, while for an odd generatora the definition is slightly more complicated. Letv andwbe two even generators (i.e. leaves of R) such that a = U^mv−Uⁿwas formal sums of vertices ofR, for some nonnegative integersmandn.

Then set∂(a)=U^m+1v−Uⁿ⁺¹w. In this case we say that the odd generatorais an anglebetween the even generatorsv andw(For pictorial descriptions ofC(R), see [4]).

A negative definite plumbing tree(with associated plumbed four-manifoldX) and a characteristic vector k of H²(X,Z)determines a graded root (R, wk) as follows. LetLbe the non-compact 1-dimensionalC W-complex having the points of H2(X,Z)=Z^||as 0-cells and a 1-cell connecting two vertices, ∈ H2(X;Z) if = +v for some v ∈ . The characteristic vector k ∈ H²(X,Z) = Hom(H2(X),Z)determines a quadratic functionχk: H2(X;Z)→Zthrough the formula

χk()= −1

2(k()+²). (7)

For eachn ∈ ZletSn be the set of connected components of the subcomplex of L spanned by the vertices satisfyingχk≤n. We defineRto be the graph with vertex set

n≥0Sn, in which two verticesx1andx2are connected by a directed edge if and only if the elementsx1∈ Snandx2∈Sn+1(corresponding to components of the sublevel setsχk ≤nandχk ≤n+1, respectively) satisfyx1⊂x2. We definewk: R →Q forx∈Snby the formula

wk(x)= k²+ ||

4 −2n.

A negative definite plumbing graph is rational if it is the resolution graph of a rational singularity, i.e. a singularity with geometric genus pg=0. According to [24, Theorem 1.3] a negative definite graph is rational if and only if the boundaryYof the