A new approach to fuzzy control using the distending function Journal of Process Control

ContentslistsavailableatScienceDirect

Journal of Process Control

journalhomepage:www.elsevier.com/locate/jprocont

A new approach to fuzzy control using the distending function

József Dombi, Abrar Hussain

^∗

Institute of Informatics, University of Szeged, 6720, Szeged, Hungary

a rt i c l e i nf o

Article history:

Received 13 July 2019 Revised 23 October 2019 Accepted 5 December 2019

Keywords:

Fuzzy arithmetic Adaptive fuzzy control Distending function Membership function

Continuously stirred tank reactor

a b s t ra c t

Here, wedevelopafuzzycontrollerusingfuzzyarithmetics andanew typeofmembershipfunction.

Theproposednewfuzzycontroltechniqueissimple,fastandcomputationallyefficient,comparedtothe classicaltechniques(Mamdani,TakagiSugeno)anditcanalsoadapttotheprocessdynamics.Theunique featuresare:1)AnewclassofparametricmembershipfunctioncalledtheDistendingFunction(DF)isin- troduced;2)Ageneralparametricoperatorsystemisused.Itutilizesmostofthefuzzyoperatorsystems forevaluatingtheknowledgebase;3)Inferenceisbasedonfuzzyarithmeticoperations;4)Thisleadsto acomputationallyefficientsingle-stepdefuzzification.Withtheseconcepts,theparadigmoffuzzycontrol designchangesradically.Usingthistechniquewithanoptimizationmethod,anadaptivefuzzycontroller is designed.Thisadaptive controlleradjuststo thechanging dynamicsofthe non-linearprocessesby tuningournewtypeofmembershipfunction.Theeffectivenessoftheproposedmethodologyisdemon- stratedontwoindustrialprocesses(awatertanksystemandcontinuouslystirredtankreactorsystem).

© 2019TheAuthors.PublishedbyElsevierLtd.

ThisisanopenaccessarticleundertheCCBYlicense.(http://creativecommons.org/licenses/by/4.0/)

1. Introduction

Fuzzytheoryhasbeenanareaofextensiveresearchsinceitsin- ception,nearly halfacentury ago,byLotfi A.Zadeh[1,2]anditis providingapplicationsinvariousareasofdailylife[3–6].Todesign control systems for complex ill-defined non-linear processes (for whichadequateanalyticalmodelsarenotavailable),isachalleng- ingtask.Novelcontroltechniquesareproposedtosolvesuchprob- lems [7–10]. However, if a knowledge base is available for these systems,fuzzytheoryprovidesanadequatesolutionforcontroller design[11].Forsomenon-linearprocesses,themodelparameters varywithtime orthey mayhaveuncertaininitial conditions.The control of such non-linear dynamic processes is called adaptive control, where the control lawadapts itself to the changing dy- namicsinorder tomeet thecontrol objectives[12–14].An adap- tivefuzzycontrollerorganizestherulebase(typeandnumberof rules)and it tunes the parameters of the membership functions ifthe process dynamics changes over time [15,16]. Now,we will presentsome basicsofconventional fuzzycontrol techniquesand brieflymentionourcontributions:

The design of fuzzylogic control (FLC) is based onthe set of

’If then’ rules forminga rule base.The multi-input singleoutput (MISO)fuzzyrulebasehasthefollowingform:

Ifx1isAⁱ₁and......andxnisAⁱ_nthenyisBⁱ, (1)

∗ Corresponding author.

E-mail address: hussain@inf.u-szeged.hu (A. Hussain).

wherex₁,x₂,...,xn,yarethelinguisticvariablesthattakethelin- guisticvaluesfromthefuzzysetsA₁,A₂,...,An,Bandi=1,...,lis thenumberoffuzzyrules.Thepartoftheruleafter’If’is alogi- calexpression,calledtheantecedent(relatedtotheinput)andthe part after ’then’ is calledthe consequent (related to the output).

TheFuzzyRuleInference(FRI)appliesafuzzyrelationtomapthe input and output space. Based on the FRI, various types ofcon- troltechniqueshavebeendeveloped.Thetwo bestknownarethe Mamdani [17] and model-based Takagi Sugeno (TS) [18,19] type fuzzycontrolsystems.

IntheMamdaniinferencesystem(alsocalledtheType-ITSsys- tem), the output of a rule is a fuzzy set. The operation of the Mamdaniinferencesystemconsistsoffivesteps.Theseare:1)The fuzzificationofcrispinputsinordertogetfuzzyinputs;2)Thean- tecedent parts of the rules are based on fuzzy logic operators.

Thesefuzzylogicalexpressionsareevaluatedtodeterminetheap- plicability ofthe fuzzyrules; 3) Implication iscarried out to get fuzzyoutputs;4)Aggregatingthefuzzyoutputsofalltherules;5) Defuzzificationoftheaggregatedoutputiscarriedouttogetthefi- nalcrispoutput.TheMamdanifuzzycontrollerdirectlytransforms theoperatorimplicitknowledgeorexpertexplicitviewsintofuzzy rules and generates a control law. The Mamdaniapproach is in- tuitive, works well with direct human input andvarious control taskscanbeperformed[20,21].Thestabilityofaclosedloopcon- trolsystemisoneofthemainobjectivesthat shouldbemet.Fre- quencydomainmethodsaremostlyusedforthestabilityanalysis ofMamdanifuzzy controllers,such asPopov’s method,thecircle stabilitycriterionandhyperstabilitytheory[22].

https://doi.org/10.1016/j.jprocont.2019.12.005

0959-1524/© 2019 The Authors. Published by Elsevier Ltd. This is an open access article under the CC BY license. ( http://creativecommons.org/licenses/by/4.0/ )

In the case ofthe TS(Type-II / Type-III) fuzzy controller, the consequent partofthe rule(Eq.(1)) is afunction (mostlylinear) of the inputs or (as a special case) a crisp value i.e. it is not a fuzzysetasintheMamdanicase.TheTSfuzzymodelconsistsof amembershipfunctionandasetoflinearmodelstoformaglobal nonlinearmodel.TheTSfuzzycontrolleralsohasanonlinearfunc- tionapproximationproperty[23].

There are some drawbackswiththesetwo controltechniques.

Theseare:

1. Theinputspaceisnotcompletelycoveredbythetriangular(or trapezoidal) membership functions i.e.they cover only a lim- itedsubspace.Forexampleifwehavetwoinputs, eachwith7 categories,then49rulesarerequiredtocoverthewholeinput space.Usuallyafewrulesareappliedtodecreasethecomputa- tionload,soalargeareaoftheinputspaceisnotcovered.Ifthe inputvalue fallsinthearea whichisnot coveredby anyrule, thennoactionisgenerated.Ifthenumberofinputvariablesin- creasesfromtwo(workinginahigherdimensionalspace),then theproblemgrowsexponentially.Someeffortstoovercomethis problemhavebeenmadebyL.KoczyandK.Hirota[24],butall theseproceduresincreasethecomputationalcost.

2. Most of the membership functions are not analytical i.e. the derivative isnot definedatevery pointandhigherderivatives donotexist.Thisisadrawbackbecausethegradient-basedop- timization techniques cannot be used to tune the parameters ofthesemembershipfunctionsastheyworkonlyonanalytical functions.However inthiscase, thegradient-freeoptimization techniquescan still beused butthesearenot very fast,accu- rateandcomputationallyefficientcompared togradient-based methods.

3. It isnot clear howto choose a fuzzyoperator systemforthe antecedentpart.Various fuzzyoperators can bechosen. Using differentfuzzyoperators produces differentresults.Hence the choice of membership function and operator system is com- pletelyarbitraryandwecannotgetaproperefficientdesign.

4. Differentimplicationoperatorsareintroduced.Surprisingly,the productoperatorismainlyused.Theproductoperatorisastrict t-normanditisnotanimplicationoperator.

5. Theresultofanevaluationoftheconsequentpartoftheruleis not amembershipfunction (it isan

α

^{-cut ofthemembership}

function). For every input value, each rule isevaluated to get theaggregatedoutput.The aggregationofconsequentpartsof alltherulesisamembershipfunctionwhichdoesnotbelongto thesameclassofthe antecedentandconsequentmembership functions.

6. Centreofgravity(COG)defuzzificationusuallyinvolvesthein- tegralevaluation of the aggregatedfunction and it iscompu- tationallyexpensive. Althoughtherearevarious defuzzification methods that do not require integral calculations, in general thesearelessaccuratethanCOG-basedmethods.

Usingthesetechniques,designinganadaptivefuzzycontrollerisa challengingtask.Aswementionedabove,bothofthesetechniques havesomeadvantagesanddisadvantages.Thereisaneedtocom- binetheseadvantagesintoasingledesignapproach.Weattempted tosolvetheseissuesusinganewapproach,whichhasthefollow- inggoodfeatures:

1. AnewtypeofparametricmembershipfunctioncalledtheDis- tending Function (DF) is introduced. With a few rules, it can coverthewholeinputspace.Ithasthreeparametersandeach hasasemanticmeaning.Thevaluesofthetwoparametersare usuallyfixed andone parametervalueistunedduringthede- signprocess.Ithastwotypes,namelythesymmetricandasym- metricDFandbothcanbeutilizedforcontrolsystemdesign.

2.The DF isanalytical i.e.higherderivatives existat each point.

This property is used in optimization procedures to tune the parametersoftheDF.

3.The generalparametricfuzzyoperatorsystemisusedforeval- uatingtheantecedentpartoftherule.Theoperatorsystemand theDFarebasedontheDombioperator. Hence,botharecon- sistentwitheachother.

4.Ourapproachdoesnotinvolvetheimplicationstep.Insteadthe activationstrengthofeachruleismultipliedbytheconsequent DFtogetthefuzzyoutputofeachrule.

5.TheconsequentofeachruleisaDF.Aggregationiscarriedout usingtheweightedarithmeticmeanoftheseconsequentDFsof all therules.AlinearcombinationisclosedforDFsandsothe resultofaggregationisalsoaDF.

6.Defuzzification in this case is only a single-step calculation (findingthepointthathasthehighestvalue oftheaggregated DF).Thisiswhyitissimpleandcomputationallyefficient.

7.Using our proposed approach, we design an adaptive fuzzy controller. It consists of tuning the DF parameters using gra- dientdescent optimization.The adaptivecontrollercanhandle the changing process dynamics withincreased computational efficiency.

We combine the advantagesof Mamdani andTS methods. Here, the antecedent and consequent parts of the rule base are fuzzy sets,so it isvery closeto directhuman linguisticinputs. Related work for designing an adaptive fuzzy controller for a nonlinear system with unknown dynamics was carried out by Ning Wang et al.[13,14]. However, there are two main differences with our approach:1) Productinference(operatorandimplication)is used for evaluating the fuzzy rules and designing controller in [14]; 2)AdaptivityisachievedusingRetractableMembershipFunctions (RMFs)in[13],whicharesymmetricmembershipfunctions.Inour approach, we have used a more general operator system which canutilizevariousavailablefuzzyoperators(e.g.min/max,product, Einstein, Hamacher,Dombi, drastic). Fuzzy arithmetic is used in- steadofimplicationi.e.weusedaregression-likeapproach.Inour study,thesymmetricandasymmetricDFsareused.Theasymmet- ricDFprovides moreflexibility inadaptive controllerdesign.The methoddescribedin[13]andourapproachovercomethecurseof dimensionalityissue,butin slightlydifferentways.The efficiency ofthis newapproach is shown by designing an adaptivecontrol systemforawatertanklevelandvehiclelateraldynamics.

The rest of the paper is structured as follows. In Section II, we briefly introduce the distending function, its properties and an overview of fuzzy arithmetic. In Section III, we explain the proposed design approach using fuzzy arithmetic. In Section IV, we describe the adaptive control design using an optimization method.InSection V,we outlinethebenchmarksystems,simula- tionsanddiscusstheresults.Lastly,inSectionVI, wepresentour mainconclusions.

2. Thedistendingfunction

TheDistendingFunction(DF)isacontinuousfunctionwhichis monotonically increasing inthe interval (−∞, 0) ^{and monoton-} ically decreasing in the interval (⁰, +∞) ^{and it takes values in} [0,1].The DF(

δ

_ε^(λ),ν(^x))^{isaparametric membershipfunction. The} parameters are the threshold (

ν

^), tolerance/error (

ε

^{) and sharp-}

ness (

λ

^{). The DF has a peak value of 1 at x}=0. If the input is intheinterval[−

,

^], thevalueoftheDFisgreaterthan

ν

^and

also

δ

^(λ)ε,ν(

ε

)=

ν

^{.When the input is in theinterval [}−

,

^], it is treatedasatruthvalue.The threshold(

ν

^{) dividesthe[0,1]inter-}

valintotruthandfalsenessregions.Andtheparameter

λ

^controls

the sharpnessof the DF. If

λ

→ ∞, then the DFapproaches the characteristicfunction.With anappropriate values of

ν

^,

ε

^and

λ

^,

alltheexisting membershipfunctions(Trapezoidal, Gaussian,Sig- moidal,etc) can beapproximated using theDF. Themembership functioncanbeshiftedbyaparametercandweshallusetheno- tation (

δ

_ε^(λ),ν(^x−c))^{. We can interpret it as x approaches c, i.e. x} isequal toc (soft equality). Herec isthe centerpoint ofthe DF (

δ

ε^(λ),ν(^c)=1)^{.NowwewillintroducetwotypesofDFnamely,sym-} metricandasymmetric.

2.1.Thesymmetricdistendingfunction

TheSymmetricDFissymmetricaroundx−candisdefinedas:

Definition1. ThesymmetricDF(showninFig.1)isgivenby

δ

ε^(λ),ν

(

^x−c

)

= 1

1+¹⁻_ν^ν

^x−_ε^c

^{λ, (2)}

where

ν

∈(0,1),

ε

>0,

λ

∈(¹,+∞)^andc∈R.

δ

ε^(λ),ν(^x−c)^willbe denotedby

δ

^s(x).

2.2.Theasymmetricdistendingfunction

TheasymmetrictypeoftheDFcanbedefinedinthefollowing way:

Definition2. TheasymmetricDF(showninFig.2)isgivenby

δ

A

(

^x

)

= 1

1+¹⁻_νR^νR

^x_ε^−c

R

^λR_1+e−¹_λ∗(x−c)+¹⁻_νL^νL

^x_ε^−c

L

^λL_1+eλ¹∗(x−c)

, (3)

where

ν

R,

ν

L ∈ (0, 1),

ε

R,

ε

L > 0,

λ

L,

λ

R∈(¹,+∞), c∈R and

λ

^∗∈(¹,+∞)^.

λ

^{∗isatechnicalparameteranditsvalueisverylarge}

comparedto

λ

Rand

λ

L.

ν

L,

ε

Land

λ

Laretheparametersoftheleft handsidewhereas

ν

R,

ε

R and

λ

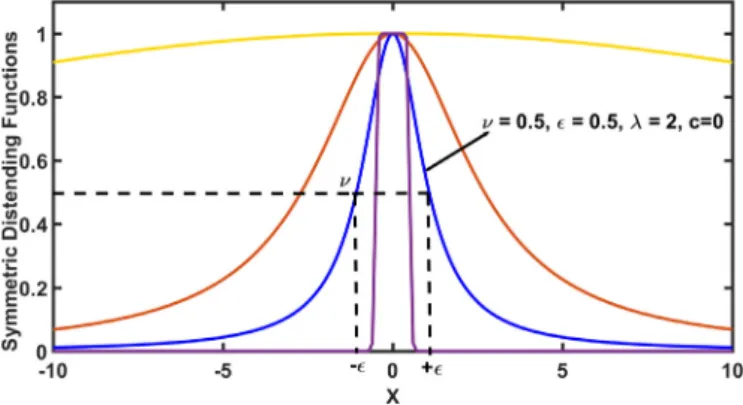
R arethe parametersofthe right

Fig. 1. Various shapes of symmetric Distending Functions depending on parameter values.

Fig. 2. The asymmetric Distending Function ( νL= 0 . 5 , εL= 0 . 5 , λL= 5 , νR= 0 . 8 , εR= 0 . 7 , λR= 5 , λ= 5 , c = 0 ).

handsideoftheasymmetric DF.Iftheinput liesbetween

ε

R and 0,thenthegradeofmembershipisgreaterthan

ν

R andthesame istruefor

ε

Land

ν

L.Here,cisthecentrepointi.e.

δ

A(^c)=1.

Theasymmetric DFprovides moreflexibility incontroldesign.

Here, theright andleft handsides ofthe asymmetric DFcan be controlledindependently.Next,wewillgiveaformulatocalculate the coordinateof the Center ofGravity (COG) ofthe asymmetric DF.ThecoordinateoftheCOGisusedfordefuzzification.First,we calculatethearea undertheDF.We willconsideronlyone (right hand)side oftheDF.Usingthisarea,we deriveanexpressionfor thecoordinateoftheCOGfortherighthandside.Thenwegivean expressionoftheCOGforbothsidesoftheasymmetricDF.

2.3. Areaunderthedistendingfunction

TheintegraloftheDFcanbewrittenintheform I=

_+∞

0

1

1+¹⁻_ν^ν

_ε^x

^{λdx. (4)}

Theresultis I=

ε ν

1−

ν

_λ¹ π

λ

sin^π_λ. (5)

2.4. Centerofgravity(COG)defuzzification

Let the function

δ

_ε^(λ)_,ν,+(^x) ^{(”+” means the right hand side) be} definedasfollows:

δ

⁽_ε^λ),ν,+

(

^x

)

=

0, ifx<0

1

1+¹⁻_ν^ν

|

^xε

|

^{λ, ifx≥0, (6)}

where

ν

∈(0,1),

ε

>0 and

λ

∈R,

λ

>1.Letx^∗denote thehori- zontalcoordinateoftheCOG,asshowninFig.3.Itiswellknown that

x^∗= _+∞

−∞x

δ

ε^(λ),ν,+

(

^x

)

^dx _+∞

−∞

δ

_ε^(λ),ν,+

(

^x

)

^{dx. (7)}

Thenthecoordinatex^∗oftheCOGofthearea underthecurvefor

δ

_ε^(λ)_,ν,+(^x)^is x^∗=1

2

ε ν

1−

ν

¹_{λ 1}

cos^π_λ. (8)

Usingthis,thecoordinatex^∗ofCOGforbothsidesofasymmet- ricDFis

x^∗= ^2LS₁− ²_RS₂

L+ R , (9)

Fig. 3. The COG of the DF (RHS).

where

L=

ε

^L

ν

L

1−

ν

^L

_λ¹

L π

λL

sin_λ^π

L

; R=

ε

^R

ν

R

1−

ν

^R

_λ¹

R π

λR

sin_λ^π

R

S1= sin_λ^π

L 2π λL cos_λ^π

L

; S2= sin_λ^π

R 2π

λR cos_λ^π

R

.

Remark1. Somespecialcases:

1. If

ν

L=

ν

R=

ν

^and

λ

L=

λ

R=

λ

,then x^∗=

ε

L²

_ν

1−ν

1λ−

ε

²R

_ν

1−ν

1λ

ε

L+

ε

R

1 cos^π_λ. 2. If

ν

=0.5,then

x^∗=1

2

( ε

^L−

ε

^R

)

_cos¹_π

λ andifc=0,then x^∗−c= 1

2

( ε

L−

ε

R

)

_cos¹_π

λ. (10)

3. ForsymmetricDFs,

ε

R=

ε

L,so

x^∗=c, (11)

whichgivestheexpressionforthecoordinateoftheCOGofthe symmetricDFs.

Now,wewillevaluatethederivativesofDF.Thesewillbeused intheoptimizationprocess.

2.5. Derivativesofthedistendingfunction

Let

δ (

^x

)

⁼

δ

ε^(λ),ν

(

^x

)

^{= 1}

1+¹⁻_ν^ν

_ε^x

^{λ. (12)}

ThenthefirstderivativeofEq.(12)is:

∂ ∂

^x

δ (

^x

)

⁼⁻

λ

x

δ (

^x

) (

¹⁻

δ (

^x

) )

^.

ThepartialderivativesoftheDFwithrespectto

ε

^is

∂ε ∂ δ (

^x

)

=−

λ

ε δ (

^x

)(

¹−

δ (

^x

))

.

ItisworthmentioningthatthederivativesofDFaresimilartothe derivativesofthesigmoidfunctionandthesederivativescanread- ilybecalculatedjustusingtheDF.

2.6. Fuzzyarithmeticoperationsondistendingfunctions

It was suggested by Zadeh [25] that fuzzy quantities can be combinedarithmeticallyusingthelawsoffuzzytheory.Thisdirec- tion was then explored independently by manyresearchers [26–

28]. Laterit wasestablished that fuzzytheory isan extension of thealgebraofmany-valuedlogicandintervalanalysis[29,30].Thus interest in fuzzyinterval domain hasincreased[31]. Fuzzyarith- metic can be viewed asthe arithmetic of

α

^{cuts. It handles the}

fuzzyquantitieswhichareobtainedbymappingarealnumberto realinterval[0,1]. Wecreatea

α

^cuts(

α

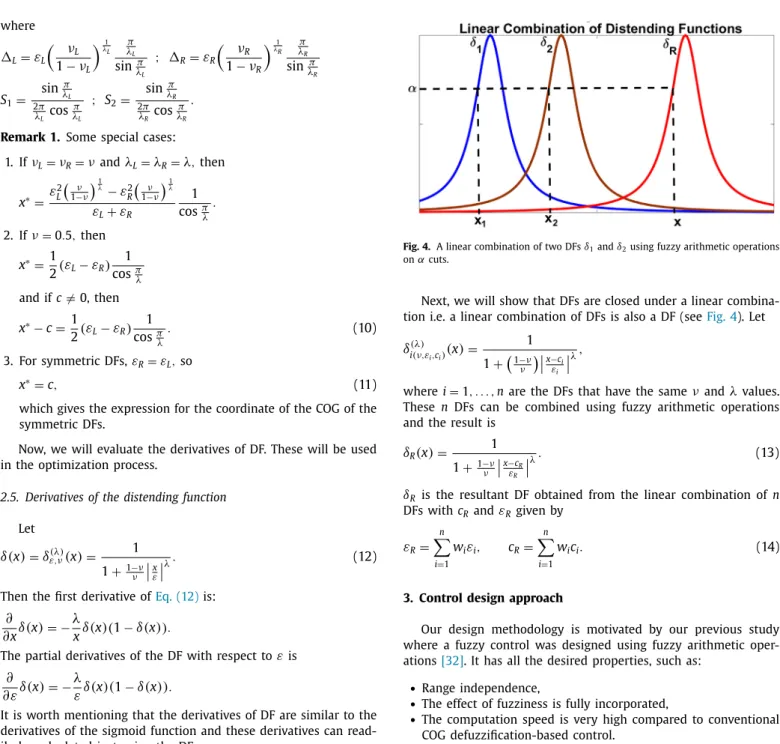
∈[0,1])foreach fuzzy quantity andthen performtherequiredoperationusingtheprin- ciplesofintervalarithmetic.Here,insteadofintervals,wewilluse the left andright handsidesof DFs,which are definedon these intervals.Thisispossibleinthecasewheretwosidesofthegiven functionsaremonotonouslyincreasingordecreasingfunctions.The detailsandadvantagesofusingfuzzyarithmeticoperationsincon- troldesignaregivenin[32].

Fig. 4. A linear combination of two DFs δ1and δ2using fuzzy arithmetic operations on αcuts.

Next,wewillshowthatDFsareclosedunderalinearcombina- tioni.e.alinearcombinationofDFsisalsoaDF(seeFig.4).Let

δ

i^(λ)(ν,εi,ci)

(

^x

)

^{= 1} 1+

_1−ν

ν ^x−εi^ci

^λ,

wherei=1,...,naretheDFsthathavethesame

ν

^and

λ

^values.

These n DFs can be combined using fuzzy arithmetic operations andtheresultis

δ

^R

(

^x

)

= 1 1+¹⁻_ν^ν

^x−_ε^cR

R

^{λ. (13)}

δ

R isthe resultant DFobtainedfromthe linearcombinationof n DFswithcRand

ε

R givenby

ε

R= n

i=1

w_i

ε

i, c_R= n

i=1

w_ic_i. (14)

3. Controldesignapproach

Our design methodology is motivated by our previous study wherea fuzzycontrol wasdesignedusingfuzzyarithmetic oper- ations[32].Ithasallthedesiredproperties,suchas:

• Rangeindependence,

• Theeffectoffuzzinessisfullyincorporated,

• The computationspeedisvery highcomparedtoconventional COGdefuzzification-basedcontrol.

Usingexpertknowledgeorprocessdata,themulti-inputmulti- outputsystem(MIMO)isdescribedby:

Ifx1isAⁱ₁and.... . .andxnisAⁱ_n

theny1isBⁱ₁;. . .;ymisBⁱ_m, (15)

where x₁,x₂,...,xn are the input linguistic variables which take thevaluesfromtheinputfuzzysubsetsA₁,A₂,...,An.Thevariables y₁,y₂,...,y_maretheoutputlinguisticvariableswhichtaketheval- uesfromtheoutputfuzzysubsetsB₁,B₂,...,Bm.i=1,...,listhe numberoffuzzyrules.Iftheoutput variablesare independentof eachother,theneachruleoftherulebasegivenbyEq.(15)canbe writtenasmmultiinputsingleoutput(MISO)rules

Ifx₁isAⁱ₁and ... andxnisAⁱ_nthenyisBⁱ. (16) We will try to find the fuzzy inference mechanism to map the input-outputspaceandgenerateacrispoutputforthecontrolsig- nal. In our approach, we handle the antecedent andconsequent partsoftheruleseparately.

3.0.1. Theantecedentpart

Theantecedentpartoftheithfuzzyruleis

L

( δ

1

(

^x1

)

ⁱ,

δ

2

(

^x2

)

ⁱ,. . .,

δ

n

(

^xn

)

ⁱ

)

=wˆi

(

^x

)

, (17) wherewˆ_i(^x)^{isthe rule}applicability function.L isthe fuzzylog- icalexpression anditmay includeand(x₁ ∈A₁ andx₂ ∈A₂), or (x₁ ∈A₁ orx₂ ∈A₂) andnot (x₁∈A₁) operators. Here, we use a verygeneralparametricoperator[33]

D_γ

(

^x

)

= 1

1+

γ1

n i=1

1+

γ

_1−δ(xi)

δ(^xi) α

−1

¹_α^{. (18)}

Most of the conjunctive or disjunctive operators used (e.g min/max,product,Einstein,Hamacher,Dombi,drastic)arecovered byEq.(18).

Foraspecificinputvaluesx^∗,Eq.(17)canbeevaluatedandthis resultsinasinglenumericvaluewˆ_i(^x∗)

L

( δ

ⁱ1(x^∗₁),

δ

ⁱ2(x^∗₂),...,

δ

nⁱ(x^∗n)

)

=wˆi

(

^x∗

)

, (19) wherewˆ_i(^x∗) ^{iscalledthestrength oftheith rule.We normalize} thesestrengths (to comparethe rules)to getthe firingstrengths w_i(x^∗).Thefiringstrengthgivestheprobabilityoftherule.Thefir- ingstrengthoftheithruleis

w_i

(

^x∗

)

= wˆ_i

(

^x∗

)

l

i=1wˆ_i

(

^x∗

)

^{, (20)}

where l

i=1

w_i

(

^x∗

)

=1. (21)

3.0.2. Theconsequentpart

Thispartofthe ruleisafuzzysetrepresentedby asingleDF.

The firing strength of each rule (calculated from the antecedent part)ismultiplied bythe consequent part.Alsothefuzzyoutput ofeachrule isa DF.Bycombiningall therules, wecan generate an aggregated output. If w₁(^x∗),w₂(^x∗),...,w_l(^x∗) ^{are the firing} strengthsand

δ

1o(^x),

δ

2o(^x),...,

δ

lo(^x) ^{are thel} consequents,then theaggregatedoutputofthelfuzzyruleisgivenby:

δ

^a

(

^x

)

⁼ l

i=1

w_i

(

^x∗

) δ

io

(

^x

)

^{. (22)}

Ofcourse,

δ

^{a(x)isalsoaDF.WecalculatetheparametersoftheDF}

usingEq.(14). The aggregatedoutput DF

δ

^{a(x) has the following}

form

δ

^a

(

^x

)

^{= 1} 1+¹⁻_ν^ν

^x−c_ε^a

a

^{λ, (23)}

where ca=

l

i=1

w_i

(

^x∗

)

^ci,

ε

^a= l

i=1

w_i

(

^x∗

) ε

i, (24)

wherec_iand

ε

iaretheparametersoftheithconsequent.Thecrisp controloutputwillbetheCOGoftheaggregatedDF

δ

^a(x).

ThewholeprocedureissummarizedinAlgorithm1.

Ourcontroldesignapproachhasthefollowinguniquefeatures:

• Ageneralparametricoperatorisusedforcalculatingthefiring strengthofrules.Thissingleoperatorcanbe employedtocal- culate theZadeh, product, Einstein,drastic andDombit-norm andt-conormswithappropriatevaluesoftheparameters.

• TheinputsarefuzzifiedusingDFs.TheseDFs canapproximate most types of bell-shaped membership functions. Also, the input member functions might have different shapes (Gaus- sian, Trapezoidal, Sigmoidal) at the same time for different categories.

Algorithm1:Algorithmforsynthesisoffuzzycontrollerusing DF.

Step1:DefinetheDFsfortheinputandoutputlinguistic variables.

Step2:FuzzifythecrispinputsusingEq.(2)orEq.(3).

Step3:Constructtherulebasefromtheexpertknowledge usingEq.(16).

Step4:CalculatethestrengthofeachruleusingEq.(18)by choosingtheappropriatefuzzyconjunctive/disjunctive operators.

Step5:CalculatethelfiringstrengthsusingEq.(20).

Step6:Calculatetheparameters(c_a,

ε

a)oftheaggregated outputDFbyusingEq.(24).

Step7:GeneratetheaggregatedoutputDFusingEq.(23).

Step8:Getthecrispoutputcontrolsignalubycalculatingthe COGoftheaggregatedoutputDFusingEq.(9)orEq.(11).

• TheaggregatefunctionsisalsoaDF.Thisisduetothefactthat alinearcombinationofDFsisaalsoaDF.

• Thedesignprocedureissimplifiedbecauseitdoesnotinclude implication. The aggregation is carried out using fuzzy arith- meticoperations.

• Defuzzificationisasingle-stepcalculation.

Hence,theproposedapproachiscomputationallyefficient.

4. Adaptivefuzzycontroldesign

If the process parameters vary with time, then the adap- tive controller changes the control signal in accordance withthe change in process dynamics. Therefore, the adaptive controller works even when the values of the parameters are outside the desiredrange. Here, we shall presenta hybrid scheme foradap- tive control.Wecallit ahybridbecauseitutilizes theknowledge baseandanoptimizationmethod.Thehybridschemeselects one fuzzyrulefromtheknowledgebaseandittunestheparametersof theantecedentpart.Thisrulewillbe selectedbasedonthefiring strength.The optimizationtechniqueisused totunetheparame- tersoftheantecedentpart.

Herewehavethreetunableparameters,namely

ν

^,

λ

^and

ε

^.We

shallfixthevaluesof

ν

^and

λ

^{andwe willtunethe}

ε

^parameter.

Theknowledgebaseofafuzzycontrollerconsistsof”Ifthen” rules thathavethefollowingform:

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎣

Ifx1 isA11 and,...,xn isA1nthenyisB1

.. .

Ifx1isAi1and,...,xnis Ainthenyis Bi

.. .

Ifx1 isAl1and,...,xnisAln thenyisBl

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎦

, (25)

wherei=1,2,...,l isthenumberofrules.A_i1,A_i2,...,A_inarethe inputlinguistictermsandB_iaretheoutputlinguisticterms.Allthe input andoutputs are associatedwithcorrespondingDFs.Here, y isthefuzzyoutput.Nowletwˆ₁,wˆ₂,...,wˆ_l bethestrengthsofthe lfuzzyrulesandc1,c2,...,c_l betheCOGvaluesoflcorresponding DFs.ThecrispvalueY(25)is

Y =c1wˆ1+c2wˆ2+· · · +c_lwˆ_l ˆ

w1+wˆ2+· · · +wˆ_l . (26) Letthesquarederrorfunctionhastheform

E=1 2

Y_{re f}−Y ², (27) whereY_Ref istheknownreferencecontrolsignalandYisthecon- trol signal (crisp output) generated by the fuzzy controller. Now

theadaptivecontrolproblemreducestothefollowingoptimization task

Minimise

ε>0

(

^E

)

^{. (28)}

Usingthegradientdescentmethod,

ε

^t+1=

ε

^t−

η

^s

∂

∂ε ⁽

^E

⁾

^{. (29)}

FromEq.(27),wehave

ε

t+1=

ε

^t+2

η

^sE

∂

∂ε

c1wˆ1+c2wˆ2+· · · +clwˆl

ˆ

w1+wˆ2+· · · +wˆl

, (30)

where

η

^{sisthestepsizeofthe}optimization.Toreduce thecom- plexity andcomputational cost, wewill selectone rule andtune theantecedentpartatthesametime.Therulewillbeselectedon thebasisofrulestrength(wˆ₁,wˆ₂,...,wˆ_l).Nowwewillexplainthis selectionandthetuningprocedure.

Letthe ith rulehas thehighestfiringstrength. The remaining (l−1)strengthswillbeconstant.Eq.(30)canbewrittenas

ε

^t+1=

ε

^t+2

η

^sE

∂

∂ε

i

ciwˆi+k1

ˆ w_i+k2

, (31)

where

k1=c1wˆ1+· · · +c_i−1wˆ_i−1+c_i+1wˆ_i+1+· · · +c_lwˆ_l k2=wˆ1+· · · +wˆ_i−1+wˆ_i+1+· · · +wˆ_l.

FromEq.(31),weget

∂ε ∂

i

ciwˆi+k1

ˆ wi+k2

=

(

^wˆi+k2

)(

^ciwˆ_i

)

+

(

^ciwˆi+k1

)

^wˆi

(

^wˆi+k2

)

^{2 , (32)}

where ˆ w_i=

∂

∂ε

i

(

^wˆi

)

. ByusingEq.(18),

wˆ_i=

∂

∂ε

i

⎛

⎜ ⎝

¹

1+

n i=1

_1−δi(xi)

δi(xi) α

_α¹

⎞

⎟ ⎠

^{. (33)}

Here

δ

1(^x1),...,

δ

ⁿ(^xn) ^{are the n antecedent DFs in the ith rule.}

Toreduce thecomputationcost,the

ε

^{parameterofonlyone an-}

tecedent DF will be tuned at a time. The DF to be tuned is se- lectedbycomparingthegradeofmembershipofthesenDFs.The DF with the highest grade is selected for tuning. The remaining (n−1)antecedentDFsintheithrulewillbetreatedasconstants.

Let

ε

ibetheparameteroftheithantecedentDFhavingthehighest gradevalue.ThenEq.(33)canbewrittenas

ˆ w_i=

∂

∂ε

i

⎛

⎜ ⎝

¹

1+

_1−δ

i(xi) δi(xi)

α+k3

¹_α

⎞

⎟ ⎠

^{, (34)}

where k3=

i−1

k=1

1−

δ

k

(

^xk

) δ

k

(

^xk

)

α +

n

k=i+1

1−

δ

k

(

^xk

) δ

k

(

^xk

)

α .

FortheDombiconjunctiveoperator,

α

=1.Sincek₃isindependent of

ε

i,

ˆ w_i=

∂

∂ε

i

δ

i

(

^xi

)

=−

λ

ε

ⁱ

δ

ⁱ

(

^xi

) (

¹⁻

δ

ⁱ

(

^xi

) )

^{. (35)}

Eq.(31)canbewrittenas

ε

^t+1=

ε

^t−2

λη

^sE

δ

i

(

^xi

) (

¹⁻

δ

i

(

^xi

) ) (

^2ciwˆ_i+c_ik2+k1

)

ε

i

(

^wi+k2

)

^{2 , (36)}

whichistheupdatefor

ε

^{oftheith antecedentDFoftheithrule.}

Theprocedurefordesigningtheadaptivefuzzycontrollerissum- marizedinAlgorithm2.

Algorithm 2: Algorithm for the synthesis of the adaptive fuzzycontrollerusingDF.

Step1:Defineatolerance

τ

^{asanacceptableupperboundon}

errorE.

Step2:CalculatetheerrorE betweenthefuzzycontrolY and referencecontrolY_{Re f}.

Step3:IfE≥

τ

^{,thenperformthefollowingsteps(steps4to9)}

elseexit.

Step4:Calculatetherulestrengthswˆ₁,...,wˆ_l ofl fuzzyrules.

Step5:Selecttherulewiththehighestrulestrength.

Step6:CalculatethegradeofmembershipofnantecedentDF withinintheselectedruleusingEq.(2)orEq.(3).

Step7:SelecttheantecedentDFwiththehighestgradeof membership.

Step8:Updatetheparameter

ε

^{oftheselectedantecedentDF}

usingEq.36.

Step9:GotoStep2.

5. Simulation,resultsanddiscussion

The effectiveness of the proposed technique is demonstrated usingthesimulationcasestudiesoftwopracticalsystems.

5.1. Watertanklevelcontrol

5.1.1. Watertankmodel

Consider awater tank system, asshowninFig. 5.Watercon- tinuouslyflowsinandoutofthetank.Thereisalsoavalveatthe inletpipetocontrol theinflowtothetank.The rateofchangeof thewatervolumeVinsidethetankis

dV

dt =q_in−qo, (37)

whereq_inandqoaretheinflowandoutflowrates.IfAt isthearea ofthetankbaseandlistheheightoftheliquidinthetank,then At

dl

dt=q_in−Ao

2gl, (38)

Fig. 5. Water Tank level system.

Fig. 6. Antecedent and Consequent DFs for the Water Tank level controller (Symmetric).

whereA_oisthecrosssectionalarea oftheoutletandgistheac- celeration dueto gravity. A control signal u is sent to the valve locatedon the inlet pipe and the height ofwater columninside thetankiscontrolledbythechangeintheratioofinletandoutlet flowrates.Thelevellofthewaterinthetankismeasuredusinga levelsensor.

5.1.2. Controlscenario(changingthewaterlevel)

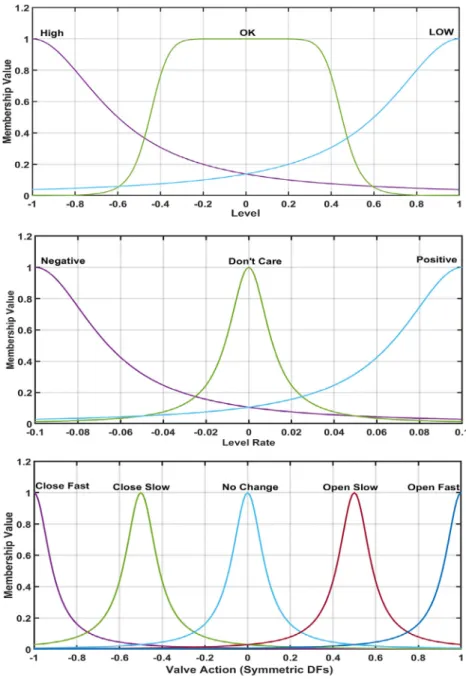
Afuzzycontrollerisdesignedusingourapproachtocontrolthe waterlevelofthetankatthespecifiedheight(reference)byopen- ing/closing the inlet valve. The difference in the measured level l and the reference height (called the Level Error) is fed to the fuzzy controller as an input. To control the level efficiently, the rateofchangeofthelevelinthetank isalsofedtothecontroller asa second input. The controller then generates the control sig- nalforopening andclosingthe valve.The controller rulebase is shownin theTable1.The multipleinputsarefuzzifiedusing the DF(Eq.(2)orEq.(3)). DFsare alsodefinedfortheoutputcontrol i.e.the valve opening/closing signal. The DFs for the antecedent

Table 1

The rule base for the Water Tank level fuzzy controller.

Rate of level

Level error Positive Negative Don’t care

High - - Close fast

Low - - Open fast

OK Close slow Open slow No change

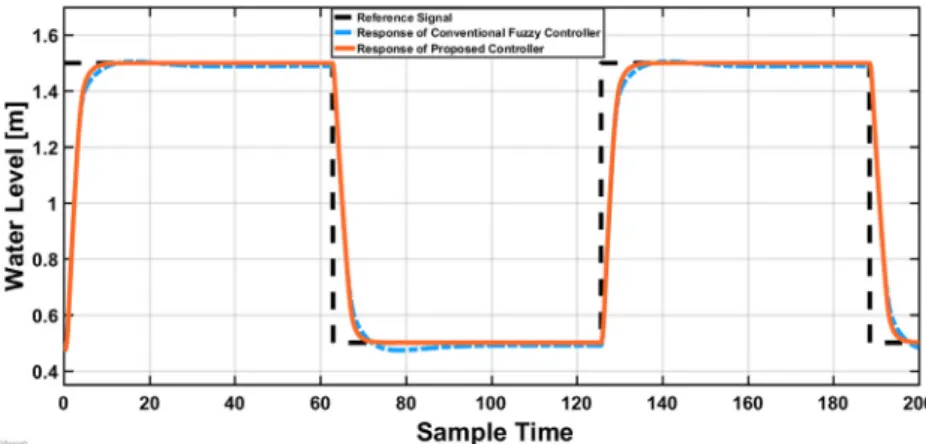
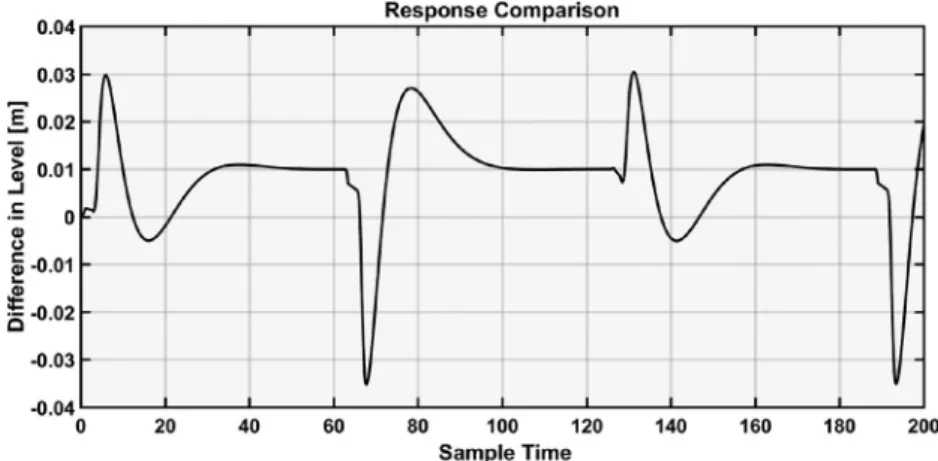
and consequent parts are shown in Fig. 6. The control action is generated usingAlgorithm 1. Here, Fig.8 showsthe control sur- face of the fuzzy controller. A reference signal for changing the levelofwaterinthetank between5mand15misfedtothesys- tem.Figs.9and10showtheresponsecomparisonoftheproposed andtheconventionalMamdanicontrollers.The conventionalcon- troller is based onGaussian membership functions, product con- junctionandimplicationoperators,maxaggregationandCOG de- fuzzification.Fig.11showstheperformanceoftheproposedfuzzy controllers usingsymmetricandasymmetricDFs.The consequent DFsfortheasymmetricDF-basedcontrollerareshowninFig.7.

Fig. 7. Consequent DFs for the Water Tank level controller (Asymmetric).

Fig. 8. The control surface for the Water Tank level controllers.

Fig. 9. The response comparison of our proposed controller with a conventional fuzzy controller.

5.2. Temperaturecontrolofthecontinuouslystirredtankreactor (CSTR)

5.2.1. CSTRdynamicalmodel

CSTRisachemicalreactor(showninFig.12) whichconvertsa hazardouschemicalAintoan acceptableproductB,whichisthen

disposedofin thenaturalenvironment. The reactorconsistsofa tank, a cooling jacket anda continuousstirring mechanism. The volume of thechemical inside the tank is usually kept constant.

The tank temperature(T_R) and concentration C_A ofthe chemical A in the outlet stream are the important variables. The reaction isexothermicandirreversible.Thetankiscontinuouslystirredfor

Fig. 10. The difference in response between the proposed controller and the conventional controller (proposed - conventional).

Fig. 11. The response comparison of the symmetric and asymmetric DF-based fuzzy controllers.

Fig. 12. Continuously Stirred Tank Reactor.

propermixingtogetuniformtemperatureandconcentration pro- files.Bychangingthejackettemperature(T_J),thetanktemperature T_R andconcentration C_A can becontrolled. IfT_R reachesthehigh thresholdlimitthentemperaturerunawaycanoccurinthereactor andresultinanunsafeoperation.ThedynamicalmodelofCSTRis derivedusingmolebalanceandenergybalanceequations.Itleads tothefollowingstateequations:

˙

x1=TF−x1+x2

Hrk₀e^−ERT

ρ

^{Cp +UA}

⁽

^TJ−x1

⁾

^;

˙ x2= q

V

(

^CAF−x2

)

−x2k0e^−ERT, (39) Here,x₁andx₂arethestatesoftheprocessandrepresentsT_Rand CA respectively.TJ isthecontrolvariable.Therelevantparameters ofthismodelaregiveninTable2.AnopensourceMatlabpackage wasusedforthesimulationsofCSTR[34].

Table 2

CSTR model parameters.

S.No Paramter Description

1 T J Temperature of cooling jacket ( K ) 2 q Volumetric Flowrate ( m ³/ sec ) 3 V Volume of liquid in CSTR ( m ³) 4 ρ Density of A → B Mixture ( kg / m ³) 6 C p Heat capacity of A-B Mixture ( J/kg −K) 7 H r Heat of reaction for A- > B ( J / mol ) 8 k 0 Pre-exponential factor (1/ sec )

9 U A Overall heat transfer coefficient ( U = W/m ²−K) 10 C AF Feed Concentration ( mol / m ³)

11 T F Feed Temperature (K)

12 C A Concentration of A in CSTR ( mol / m ³) 13 T R Temperature in CSTR ( K )

14 R T Residence Time ( Sec )

5.2.2. Controlscenario(trackingthereactortemperatureT_R)

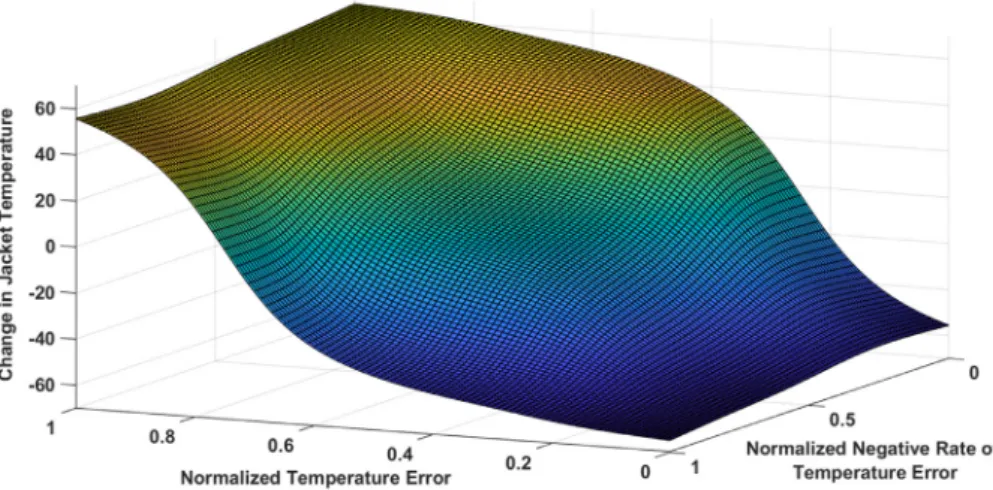
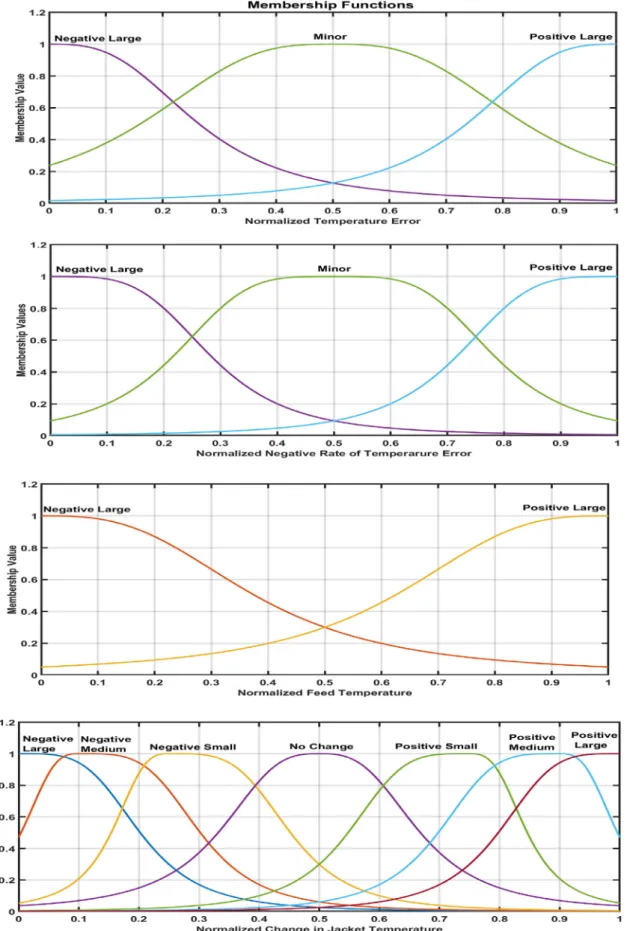
A fuzzy controller based on DFs is designed to trackT_R at a setpointof365kandC_A ratiointheoutletstreambelow0.3.The thresholdforthereactortemperatureis400K.T_R mustremainbe- low thisthreshold to avoidtemperature runaway. The controller generatesthechangeinT_JtoachievethedesiredT_R.Therulebase consistsof seven rules, asshown inTable 3. Inputsare fuzzified using the DF (Eq. (3)) and rules are evaluated using Dombi op- erators (see Eq. (18)). The reference signal governing the reactor temperatureissubtracted fromthe actualreactor temperatureT_R of theCSTR to generate an errorsignal E. The errorin thereac- tortemperature E,rateof changeofthe errorsignal dEandfeed temperature T_F form the input to the fuzzy controller. The an- tecedents and consequent DFs are shownin Fig. 16. The control

Table 3

Rule base of CSTR fuzzy controller. PL- Positive Large, NL- Negative Large, PM- Positive Medium, NM- Negative Medium, PS- Positive Small, NS- Negative Small, M- Minor, NC- No Change.

Rule no. Temperature error Negative rate of temperature error Feed temperature Change in jacket temperature

1 PL - - PL

2 NL - - NL

3 M - - NC

4 M PL - NM

5 M NL - PM

6 PL - PL NS

7 PL - NL PS

Fig. 13. Comparison of tracking responses generated using the PID (P = 4, I = .8, D = 0.5, N = 100) and DF-based controller for different feed temperatures. Both controllers track the reactor temperature when T F = 350 Kand they are within the safe operating temperature limits (Top). Only the DF-based controller tracks and keeps the reactor temperature below the high threshold when T F = 370 K(Bottom).

surface(fortwoinputs;EandTF)ofthefuzzycontrollerisshown inFig.15.Areferencesignaltellsthecontrollertoachievethede- sired T_R by changingT_J.Theresponse ofthetuned PIDcontroller (P =4,I= .8,D=0.5, N= 100)hasalsobeenplottedforcom- parisonpurposes.Fig.13showsthereactortemperatureduringthe simulationscenario.ThetopfigureshowstheresponseofthePID andDF-basedcontrollerswhenthefeedtemperatureis350K.The bottom figureshowstheresponses whenthefeedtemperatureis increasedto 370K.The parameters ofthe PIDandDF-based con- troller were kept the same.It isevident fromthe responses that the PID response exceeds thehigh temperaturethreshold (400K) when the feed temperature is increased. However the DF-based controllerkeepsthereactortemperaturewithinthethresholdlim- its, but with a slightly slow response. The concentration C_A has beenplottedinFig.14(theT_F =350K case).

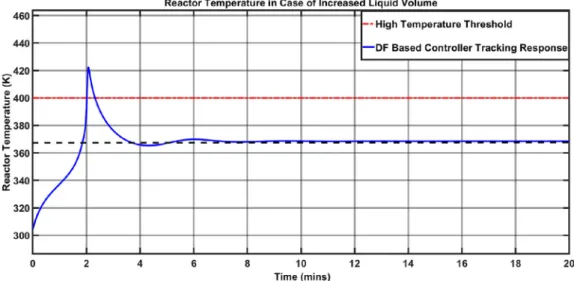
5.3.Adaptivecontrol

The effectiveness of the proposed adaptive fuzzy controller is examined in a reactor temperature tracking situation where the processdynamicschange.ThevolumeVofliquidinthereactoris animportantparameteranditmustremainconstant.Thisisusu- allyensured by a separate levelcontrol systemwhich keeps the liquidinthereactorata constantlevelandhencethevolumere- mainsunchanged. Howeverit mayhappen that thereactorliquid volumeincreasesordecreasesduetoafaultintheliquidlevelcon- trollerorsuddenincrease/decreaseinthechemicalAinventory.In suchcases,thereactortemperaturewillnotfollowthedesiredset pointanditmayleadtorunawaysituation.Now,considerthecase inwhichthereactorliquidvolumeincreaseby10percent.Without adaptivecontrol,thereactortemperatureisshowninFig.17.Itis