Asymptotic Properties of Multiplicative Arithmetic Functions of One and Several Variables DSc dissertation

(1)

Asymptotic Properties of Multiplicative Arithmetic Functions of One and Several

Variables DSc dissertation

L´ aszl´ o T´ oth

University of P´ ecs

2018

(2)

(3)

Chapter 1 Introduction

1.1 Multiplicative functions

Various asymptotic properties of multiplicative arithmetic functions, i.e., nonzero functionsf :NÑCsatisfying fpmnq “fpmqfpnq, provided thatpm, nq “1, are well known in the literature. It is one of the main objectives of elementary and analytic number theory to deduce asymptotic formulas with sharp error terms for sumsř

nďxfpnq, where fpnqis a special multiplicative function or it is belonging to a certain class of such functions.

For example, the Dirichlet divisor problem consists in finding the infimum of exponents θ such that the formula

ÿ

nďx

τpnq “xlogx` p2γ´1qx`Opx^θ`εq, (1.1) holds for every εą0. It is known that 1{4ďθ ď131{416 .

“0.314903. More exactly, the best error term in (1.1) up to date isOpx^131{416plogxq^26947{8320q, due to Huxley [46].¹

More generally, for positive integers a₁ ď ¨ ¨ ¨ ď a_k consider the generalized divisor functionτpa₁, . . . , a_k;nq:“ř

d^a₁¹¨¨¨d^ak_k “n1 and let ∆pa₁, . . . , a_k;xq stand for the remainder term in the related asymptotic formula, i.e.,

ÿ

nďx

τpa₁, . . . , a_k;nq “ Hpa₁, . . . , a_k;xq `∆pa₁, . . . , a_k;xq,

whereHpa1, . . . , ak;xqis the main term. See, e.g., the book by Kr¨atzel [56, Ch. 6]. In the case a₁ “ ¨ ¨ ¨ “a_k “1 we have the Piltz divisor functionτ_kpnq, and let ∆_kpxq denote, as usual, the corresponding error term (Piltz divisor problem).

1In a recent preprint of 13 September 2017, Bourgain and Watt [12] proved the better result θ ď 517{1648 .

“0.313713. The same error term is valid for the Gauss circle problem.

(6)

The squarefree divisor problem goes back to the work of Mertens (1874). Letτ^p2qpnq “ 2^ωpnq denote the number of squarefree divisors of n. One has

ÿ

nďx

τ^p2qpnq “ 6 π²x

ˆ

logx`2γ´1´2ζ¹p2q ζp2q

˙

`OpRpxqq, (1.2)

with Rpxq !x^1{2δpxq, where

δpxq:“expp´cplogxq^3{5plog logxq^´1{5q, (1.3) c being a positive constant. See Suryanarayana and Siva Rama Prasad [90]. If the Riemann hypothesis (RH) is true, then Rpxq !x^4{11`ε, due to Baker [6].

Another example, we quote here is the asymptotic formula ÿ

nďx

φpnq “ 3

π²x²`O`

xplogxq^2{3plog logxq^4{3˘

, (1.4)

concerning Euler’s functionφpnq, with the best error term known to date, due to Walfisz [120, Satz 1, p. 144]. The formula

ÿ

nďx

1

φpnq “Aplogx`γ´Bq `O`

x^´1plogxq^2{3˘

, (1.5)

where

A“ ζp2qζp3q

ζp6q “ 315ζp3q

2π⁴ , B “ÿ

p

logp

p²´p`1, (1.6)

with the weaker error termOpx^´1logxq goes back to the work of Landau. See the book by De Koninck and Iv´ıc [26, Th. 1.1]. The error term in (1.5) was obtained by Sita Rama Chandra Rao [81].

Now consider the class W of multiplicative functions f : N Ñ r0,1s. According to a celebrated result of Wirsing [123], iff is in the classW, then the mean value

Mpfq:“ lim

xÑ8

1 x

ÿ

nďx

fpnq exists and

Mpfq “ ź

p

ˆ 1´ 1

p

˙ 8

ÿ

ν“0

fpp^νq p^ν ,

with the convention that the product is zero provided that the seriesř

p 1´fppq

p diverges.

Other type of results are concerning the maximal order of certain multiplicative functions. For example, the following useful theorem on the maximal order of a class of prime-independent multiplicative functions was proved by Suryanarayana and Sita Rama

(7)

Chandra Rao [89]: Let f be a positive function satisfying fpnq “ Opn^βq for some fixed β ą0. Let F be the multiplicative function with Fpp^νq “fpνq for every prime power p^ν (ν ě1). Then

lim sup

nÑ8

logFpnqlog logn

logn “sup

mě1

logfpmq

m .

This applies to the function Fpnq “ τpnqand gives lim sup

nÑ8

logτpnqlog logn

logn “log 2, (1.7)

which is a well known result. The same formula is true for τpnq replaced by τ^p2qpnq. If Fpnq “τ^peqpnq, the number of exponential divisors of n, then we obtain

lim sup

nÑ8

logτ^peqpnqlog logn

logn “ log 2 2 , proved earlier by Erd˝os. See [87, Th. 6.2].

Ramanujan [77] derived pointwise convergent series representations of arithmetic functions with respect to the sums c_qpnq, now called Ramanujan sums. For example, letσpnq denote the sum of divisors of n. For every fixed n PN,

σpnq

n “ζp2q

8

ÿ

q“1

c_qpnq

q² (1.8)

“ π² 6

ˆ

1` p´1qⁿ

2² `2 cosp2πn{3q

3² ` 2 cospπn{2q 4² ` ¨ ¨ ¨

˙ ,

which shows how the values of σpnq{n fluctuate harmonically about their mean value π²{6.

Delange [30] proved the following general theorem concerning such expansions, called Ramanujan (or Ramanujan-Fourier) expansions of arithmetic functions. Let f : N ÑC be an arithmetic function. Assume that

8

ÿ

n“1

2^ωpnq|pµ˚fqpnq|

n ă 8. (1.9)

Then for every nP Nwe have the absolutely convergent Ramanujan expansion fpnq “

8

ÿ

q“1

a_qc_qpnq, where the coefficientsa_q are given by

a_q “

8

ÿ

m“1

pµ˚fqpmqq

mq pqPNq.

(8)

Delange also pointed out how this result can be formulated for multiplicative functions f. By Wintner’s theorem condition (1.9) ensures that the mean value Mpfq exists and a₁ “Mpfq.

A nonzero function f : N^k Ñ C is said to be multiplicative if fpm₁n₁, . . . , m_kn_kq “ fpm₁, . . . , m_kqfpn₁, . . . , n_kq, provided that pm₁¨ ¨ ¨m_k, n₁¨ ¨ ¨n_kq “ 1. Therefore, if f is multiplicative, then it is determined by the values fpp^ν¹, . . . , p^ν^kq, where p is prime and ν₁, . . . , ν_k PNY t0u. More exactly, fp1, . . . ,1q “ 1 and for anyn₁, . . . , n_kP N,

fpn₁, . . . , n_kq “ ź

p

fpp^ν^p^pn¹^q, . . . , p^ν^p^pn^k^qq.

If the case k “ 1 this reduces to the usual multiplicativity. Some simple examples of multiplicative functions of k variables are pn₁, . . . , n_kq and rn₁, . . . , n_ks. Among other examples of such functions we mention spn₁, . . . , n_kq and cpn₁, . . . , n_kq, representing the total number of subgroups and the number of cyclic subgroups, respectively, of the group pZn1 ˆ ¨ ¨ ¨ ˆZnk,`q. Let %_r denote the characteristic function of the set of ordered r- tuples pn₁, . . . , n_rq P N^r such that n₁, . . . , n_r are pairwise relatively prime. Then %_r is a multiplicative function ofr variables and it satisfies

ÿ

d1|n1,...,dr|nr

%_rpd₁, . . . , d_rq “τpn₁¨ ¨ ¨n_rq pn₁, . . . , n_r PNq. (1.10) A detailed study of multiplicative functions of several variables was carried out by Vai- dyanathaswamy [119] more than eighty-five years ago. However, the paper [119] includes algebraic and arithmetic properties, essentially. Even to the present day, there are only a few asymptotic results in the literature for multiplicative functions of several variables.

My paper [108] is a survey on this topic.

The mean value of a function f :N^kÑCis Mpfq:“ lim

x1,...,xkÑ8

1 x₁¨ ¨ ¨x_k

ÿ

n1ďx1,...,nkďxk

fpn₁, . . . , n_kq,

provided that this limit exists. As a generalization of Wintner’s theorem (valid in the one variable case), Ushiroya [116, Th. 1] proved the next result: If f is a function of k variables, not necessary multiplicative, such that

8

ÿ

n1,...,nk“1

|pµ_k˚fqpn₁, . . . , n_kq|

n1¨ ¨ ¨nk

ă 8, then the mean valueMpfq exists and

Mpfq “

8

ÿ

n1,...,n_k“1

pµ_k˚fqpn₁, . . . , n_kq n₁¨ ¨ ¨n_k ,

(9)

where˚ denotes the Dirichlet convolution defined by pf ˚gqpn1, . . . , nkq “

ÿ

d1|n1,...,dk|nk

fpd1, . . . , dkqgpn1{d1, . . . , nk{dkq,

and µ_kpn₁, . . . , n_kq “µpn₁q ¨ ¨ ¨µpn_kq is the M¨obius function of k variables (the inverse of the constant 1 function under ˚).

For multiplicative functions the above result was formulated by us [108, Prop. 19] as follows (see Ushiroya [116, Th. 4] for the same result in a slightly different form and for its proof): Letf :N^k ÑCbe a multiplicative function. Assume that

ÿ

p

8

ÿ

ν1,...,νk“0 ν1`¨¨¨`νkě1

|pµ_k˚fqpp^ν¹, . . . , p^ν^kq|

p^ν¹^`¨¨¨`ν^k ă 8.

Then the mean value Mpfq exists and Mpfq “ ź

p

ˆ 1´1

p

˙k 8

ÿ

ν1,...,νk“0

fpp^ν¹, . . . , p^ν^kq p^ν¹^`¨¨¨`ν^k .

We are not aware of more general mean value results concerning the several variables case. Asymptotic formulas for sums of typeř

n1,...,n_kďxfpn₁, . . . , n_kq, with certain special functionsf, were derived by Balazard, Naimi, P´etermann [8] and de la Bret`eche [28] using analytic methods. For example, in paper [8] the authors use an effective Perron inversion formula ink variables to prove (by a very complicated process) that

ÿ

n1,...,nkďx

µpn₁q ¨ ¨ ¨µpn_kq

rn₁, . . . , n_ks “P_kplogxq `Opδpxqq,

wherePkptqis a polynomial in t and δpxq is defined by (1.3). They also prove that Pkptq is identically zero, whenk is odd (in the case k“1 this is equivalent to the prime number theorem).

1.2 Summary of the main results

This thesis is based on my research work in the past 16 years. I collected the results which I consider the most relevant, related to those presented in Section 1.1. They were published in my papers [96, 97, 98, 100, 101, 103, 104, 105, 107, 109, 110, 111, 112, 113]

and [38] (joint work with Mario Hampejs), [42] (with Titus Hilberdink), [71] (with Werner Georg Nowak), [93] (with Marius T˘arn˘auceanu), [114] (with Eduard Wirsing), [115] (with Wenguang Zhai). I also present the significant preceding results and those obtained ulterior in the literature. Group theoretical, combinatorial and computational aspects are pointed out, as well.

(10)

Chapter 2 is concerning multiplicative functions of one variable. In Section 2.1 we present asymptotic formulas valid for wide classes of multiplicative functions. Theorem 2.1.1 applies to certain multiplicative functions f such that fpnq depends only on the

`-full kernel of n, where ` ě 2 is a fixed integer. It can be used to deduce asymptotic formulas for the r-th powers (r P N) of the following special functions: the exponential divisor function τ^peqpnq (Theorem 2.1.3); the function apnq, representing the number of non-isomorphic abelian groups of order n (Corollary 2.1.4); the exponential analogue of the Euler function (Theorem 2.4.1). Our result for ř

nďxapnq² improves the error term given by Zhang, L¨u and Zhai [124]. We also notice a result (Remark 2.1.7), which applies to multiplicative functions f such that fppq “k for every prime p, where k P N is fixed, and the valuesfpp^νq “are not too large” for prime powersp^ν with ν ě2.

Section 2.2 includes asymptotic formulas for alternating sums ř

nďxp´1q^n´1fpnq^´1, where fpnq are certain multiplicative functions. In particular, we consider the cases of fpnq “ φpnq(Corollary 2.2.2)fpnq “ σpnq(Corollary 2.2.3),fpnq “τpnq(Theorem 2.2.4) and fpnq “ σ^˚˚pnq, denoting the sum of bi-unitary divisors of n (Theorem 2.2.7). Our results improve the error terms obtained by Bordell`es and Cloitre [11].

Our method of Section 2.2 requires estimates of the coefficients of the reciprocals of some formal power series. If the coefficients of the original power series are positive and log-convex, then a result of Kaluza [52] can be used. We prove a new explicit Kendall-type inequality (Proposition 2.2.5) for reciprocals of power series, which can be applied in some other cases.

In Section 2.3 we present easily applicable results concerning the maximal order of certain multiplicative functions, such as σpnq, σ^peqpnq and P^peqpnq, the latter being the exponential analog of the gcd-sum function.

Section 2.4 is devoted to the study of functions defined by exponential divisors. In particular, Theorems 2.4.2 and 2.4.3 are results for the exponential M¨obius functionµ^peqpnq, while Theorem 2.4.4 is concerning the functiont^peqpnq, defined as the number of exponentially squarefree exponential divisors ofn.

In Section 2.5 we discuss properties of the gcd-sum function (Pillai’s function) and its analogs associated with exponential divisors and regular integers (mod n), respectively.

Section 2.6 is concerning certain weighted averages of the Ramanujan sums, involving logarithms, binomial coefficients and the Gamma function, as weights. I also present (see Section 4.6) a simpler proof of a related identity due to Alkan [1].

It is the aim of Section 2.7 to giveshort direct proofsfor the number of solutions of the quadratic congruencex²₁` ¨ ¨ ¨ `x²_k”n(mod r), obtained by Cohen [21], and to point out some new related asymptotic formulas. Theorems 2.7.1, 2.7.2 and 2.7.3 can be considered as analogs of Dirichlet’s formula (1.1), the squarefree divisor problem (1.2) and the Gauss circle problem, respectively.

One of the most important problems of combinatorial group theory is to determine the number of subgroups of a finite group. This is completely settled in the literature for finite abelian groups, by reducing the problem to p-groups. Instead of p-groups, we

(11)

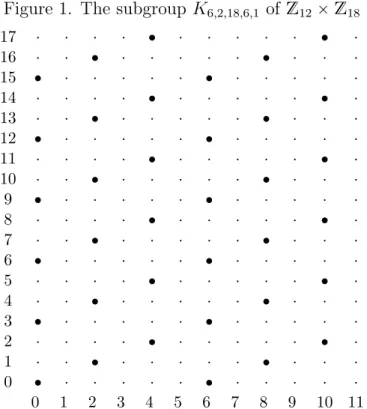
consider in Section 2.8 the group pZn1 ˆ ¨ ¨ ¨ ˆZnk,`q, where n₁, . . . , n_k P N and the functionsspn₁, . . . , n_kqand cpn₁, . . . , n_kq, denoting the total number of its subgroups and the number of its cyclic subgroups, respectively. These are multiplicative functions of k variables. The functions spn, . . . , nq and cpn, . . . , nq are multiplicative in n, as functions of a single variable.

Theorem 2.8.1 gives a compact formula for cpn₁, . . . , n_kq. We investigate the cases k“2 andk “3 and give complete representations of the subgroups ofZmˆZn(Theorem 2.8.2) and Zm ˆZnˆZr (Theorem 2.8.5). As applications, we deduce simple formulas for the number of subgroups and establish asymptotic formulas for related multiplicative functions of one variable.

In Chapter 2 we use theconvolution methodto establish asymptotic formulas for sums ř

nďxfpnq. This requires to write the function f as f “ g ˚h, the Dirichlet convolution of the functions g and h. If gpnq is “small enough” and there is a “good” formula for ř

nďxhpnq, then we can deduce an asymptotic formula with a sharp error term for ř

nďxfpnq.

Most of the error terms of our formulas are unconditional, but for some of them we assume the Riemann hypothesis (RH). Many of the error terms we obtain are related to the Dirichlet divisor problem (1.1), the squarefree divisor problem (1.2) or other similar remarkable problems.

In Chapter 3 we investigate multiplicative functions of several variables. We deduce asymptotic formulas with sharp error terms for the characteristic function of the set of r-tuples of positive integers with k-wise relatively prime components (Section 3.1), for fpn₁¨ ¨ ¨n_rq andfprn₁, . . . , n_ksqwith certain functionsf (Sections 3.2 and 3.3). For k ě3 the error term concerningr-tuples of positive integers withk-wise relatively prime components improves the result by Hu [43]. Our results of Section 3.2 generalize and refine the result ř

m,n,qďxrm, n, qs^r „c_rx^3pr`1q, valid for rP N, with a certain constant c_r, obtained by Fern´andez and Fern´andez [34]. The asymptotic formulas included in Section 3.3 refine and generalize a result of Lelechenko [59] deduced for the sum ř

m,nďxτp1,2;mnq, by using the complex integration method.

In order to establish the asymptotic formulas for multiplicative functionsFpn₁, . . . , n_kq, we elaborated some details of theconvolution method in the several variables case, which seems to be the most natural approach. In order to obtain and to apply a convolutional identity it is necessary a careful study of the corresponding multiple Dirichlet series and Euler products given by

8

ÿ

n1,...,nr“1

Fpn₁, . . . , n_rq n^s₁¹¨ ¨ ¨n^s_r^r “

ź

p 8

ÿ

ν1,...,νr“0

Fpp^ν¹, . . . , p^ν^rq p^ν¹^s¹^`¨¨¨`ν^r^s^r ,

but we use only elementary arguments (do not utilize analytic continuation and contour integration). The difficulty consists in estimating some intermediate multiple sums of the

(12)

type

ÿ

n1ďx,...,ntďx nt`1ąx,...,n_kąx

ψpn₁, . . . , n_kq, whereψ is a certain multiplicative function of k variables.

In Section 3.4, based on our paper [71], we investigate the multiplicative function spm, nq, representing the total number of subgroups of the group pZm ˆ Zn,`q. We obtain asymptotic formulas for the sum ř

m,nďxspm, nq(Theorem 3.4.2) and for the corresponding sum restricted topm, nq ą1, i.e., concerning the groupsZmˆZnhaving rank two (Theorem 3.4.5). The method we use to prove Theorem 3.4.2 is thehyperbola method adopted to this function of two variables. In paper [71] we proved Theorem 3.4.5 by analytic arguments, namely by using Perron’s formula in one variable. However, I present here the sketch of an elementary proof by using the Busche-Ramanujan identity for the divisor function (see Section 3.5).

We derive in Section 3.5 two new generalizations of the Busche-Ramanujan identities.

Namely, we consider the values of a specially multiplicative function for products of several arbitrary integers (Theorem 3.5.1). Then we deduce formulas for the convolution of several arbitrary completely multiplicative functions (Theorem 3.5.2). The proofs use arguments concerning formal Dirichlet series of arithmetic functions of several variables and properties of symmetric polynomials of several variables.

Finally, in Section 3.6 we obtain results on the Ramanujan-Fourier expansions of arithmetic functions of several variables. Our results generalize those of Delange [30] and Ushiroya [118].

1.3 Notations

Throughout the dissertation we use standard notations. Some of them are fixed below.

Further notations will be explained by their first appearance.

‚ N, Z, R, C denote the set positive integers, integers, real and complex numbers, respectively;

‚ Zn“Z{nZ is the set of residue classes modulo n (nP N);

‚ the prime power factorization of nP Nis n“ś

pp^ν^p^pnq, the product being over the primesp, where all but a finite number of the exponents ν_ppnq are zero;

‚ pn₁, . . . n_kqand gcdpn₁, . . . n_kqdenote the greatest common divisor ofn₁, . . . , n_kPN;

‚ rn₁, . . . , n_ksand lcmpn₁, . . . , n_kqdenote the least common multiple ofn₁, . . . , n_kPN;

‚ id is the function idpnq “n (n PN);

‚τpnqis the number of divisors ofn,σpnqis the sum of divisors ofn,σ_spnqis the sum of s-th powers of the divisors of n;

‚ φpnq is Euler’s totient function, φ_spnq “ n^sś

p|np1´1{p^sq is the Jordan function of orders;

(13)

‚ µpnq is the M¨obius function, ψpnq is the Dedekind function given by ψpnq “ nś

p|np1`1{pq,κpnq “ś

p|npis the squarefree kernel of n;

‚ ωpnq denotes the number of distinct prime factors of n, Ωpnq “ ř

pν_ppnq is the number of prime power divisors of n;

‚ τ^p2qpnq “ 2^ωpnq is the number of squarefree divisors of n;

‚τ_kpnqis the Piltz divisor function, representing the number of ways n can be written as a product of k factors;

‚ τ^peqpnq “ś

p^ν||nτpνq is the number of exponential divisors of n;

‚ σ^peqpnq “ś

p^ν||n

ř

d|νp^d denotes the sum of exponential divisors of n;

‚ apnq represents the number of non-isomorphic abelian groups of order n;

‚ Ppnq “řn

k“1pk, nq is the gcd-sum function (Pillai’s function);

‚ Ppnqalso denotes the number of unrestricted partitions of n;

‚ c_qpnq “ ř

1ďkďq,pk,qq“1expp2πikn{qq are the Ramanujan sums;

‚ ˚ is the Dirichlet convolution of arithmetic functions;

‚ ζ is the Riemann zeta function;

‚ γ .

“0.577215 is Euler’s constant;

‚ G“ř8 n“0

p´1qⁿ p2n`1q²

“. 0.915956 is the Catalan constant;

‚ ř

p and ś

p are sums and products over the primes;

‚ the O (!), o, Ω and „ notations are used in the usual way, for the first one the implied constant may depend on certain parameters;

(14)

Chapter 2 Results for multiplicative functions of one variable

2.1 Average orders

Let τpnq denote the number of divisors of n. Ramanujan [76] stated without proof that the estimate

ÿ

nďx

τpnq² “xpAplogxq³`Bplogxq²`Clogx`Dq `Opx^3{5`εq (2.1) holds for any realε ą0, withA “π^´2 and certain constants B, C, D. By using analytic methods, Wilson [122] proved Ramanujan’s claim and generalized it by showing that for any integer rě2 one has

ÿ

nďx

τpnq^r “xP₂^r_´1plogxq `Opx²

r´1 2r`2`ε

q,

whereP₂^r_´1ptq is a polynomial of degree 2^r´1 in t with leading coefficient Cr “ 1

p2^r´1q!

ź

p

ˆ 1´ 1

p

˙2^r 8

ÿ

ν“0

pν`1q^r p^ν .

Note that in the case r “ 2, Wilson’s error term is better than the one stated by Ramanujan.

Now consider τ^peqpnq, denoting the number of exponential divisors of n. See Section 2.4. The function τ^peq is multiplicative and τ^peqpp^νq “ τpνq for every prime power p^ν (ν ě1). Wu [121] showed, improving an earlier result of Subbarao [87], that

ÿ

nďx

τ^peqpnq “A1x`B1x^1{2`Opx^2{9logxq, (2.2)

(15)

where

A₁ :“ ź

p

˜ 1`

8

ÿ

ν“2

τpνq ´τpν´1q p^ν

¸ ,

B₁ :“ź

p

˜ 1`

8

ÿ

ν“5

τpνq ´τpν´1q ´τpν´2q `τpν´3q p^ν{2

¸ .

The error term in (2.2) is strongly related to the error term ∆p1,2;xq on the divisor functionτp1,2;nq “ ř

ab²“n1. It can be sharpened intoOpx1057{4785`εq. See [121, Remark, p. 135].

An asymptotic formula for the function fpnq “ τ^peqpnq^r with any integer r ě 1 follows from the following general result concerning certain multiplicative functionsf such that fpnq depends only on the `-full kernel of n, where ` ě 2 is a fixed integer. Let

∆_k,`pxq :“ ∆pp1, `, `, . . . , ` looomooon

k´1

q;xq denote the error term of the corresponding generalized divisor problem.

Theorem 2.1.1(T´oth [98], [103, Th. 2]). Letf :NÑCbe a multiplicative arithmetic function. Assume that

i) fppq “ fpp²q “ ¨ ¨ ¨ “fpp^`´1q “ 1, fpp^`q “k for every prime p, where `, k ě2 are fixed integers,

ii) fpp^νq ! 2^ν{p``1q (νÑ 8) uniformly for the primesp.

Then 8

ÿ

n“1

fpnq

n^s “ζpsqζ^k´1p`sqVpsq,

absolutely convergent for<psq ą1, where the Dirichlet seriesVpsqis absolutely convergent for <psq ą1{p``1q.

Furthermore, suppose that ∆_k,` !x^α^k,`plogxq^β^k,`, with 1{p``1q ăα_k,`ă1{`. Then ÿ

nďx

fpnq “ Cr_fx`x^1{`P_f,k´2plogxq `R_fpxq, (2.3) where P_f,k´2 is a polynomial of degree k´2,

Cr_f :“ź

p

˜ 1`

8

ÿ

ν“`

fpp^νq ´fpp^ν´1q p^ν

¸ ,

and R_fpxq !x^α^k,`plogxq^β^k,` (is the same).

Remark 2.1.2. For every k, ` ě 2, ∆_k,`pxq ! x^u^k,`^`ε, where u_k,` :“ _3`p2k´1q`^2k´1 P p_``1¹ ,¹_`q.

See [56, Th. 6.10]. Therefore,R_fpxq !x^u^k,`^`ε is valid, as well.

(16)

Applying Theorem 2.1.1 and Remark 2.1.2 to the functionfpnq “ τ^peqpnq^r with` “2, k“2^r, we deduce the following result.

Theorem 2.1.3 (T´oth [98, Eq. (4)]). Let r ě 1 be a fixed integer. The asymptotic formula

ÿ

nďx

τ^peqpnq^r “A_rx`x^1{2Q₂^r_´2plogxq `Opx^u^r^`εq holds for every εą0, where

A_r :“ ź

p

˜ 1`

8

ÿ

a“2

τpaq^r´τpa´1q^r p^a

¸ , Q₂^r_´2 is a polynomial of degree 2^r´2 and u_r :“ ²₂^r`1r`2^´1`1.

Theorem 2.1.1 applies to other special functions, as well. For example, consider the functionapnq, representing the number of non-isomorphic abelian groups of order n. The function apnq is multiplicative and for every prime power p^ν (ν ě 1), app^νq “ Ppνq is the number of unrestricted partitions ofν. Thus, for every prime p, appq “1,app²q “2, app³q “3, app⁴q “ 5, app⁵q “ 7, etc. An asymptotic formula for the sum ř

nďxapnq was obtained for the first time by Erd˝os and Szekeres [32]. The corresponding error term was investigated by several authors. See, e.g., [49, Ch. 14], [56, Ch. 7] for historical surveys.

It is known that

ÿ

nďx

apnq “ A₁x`A₂x^1{2`A₃x^1{3`Rpxq, whereAj :“ś8

k“1,k‰jζpk{jq(j “1,2,3), and the best result for the error term isRpxq ! x^1{4`ε for every εą0, proved by O. Robert and P. Sargos [78].

The asymptotic behavior of the sum ř

nďx1{apnqwas investigated by Nowak [70]. An asymptotic formula for the quadratic moment of the function a, i.e., for ř

nďxapnq² was given by Zhang, L¨u and Zhai [124].

Let ∆_rpxq:“∆pp1,2,2, . . . ,2 loooomoooon

2^r´1

q;xq. For the r-th moment of the functionapnqwe have the next result.

Corollary 2.1.4 (T´oth [103, Th. 1]). Let r ě 2 be a fixed integer. Assume that

∆_rpxq !x^α^rplogxq^β^r, with 1{3ăα_ră1{2. Then ÿ

nďx

apnq^r “C_rx`x^1{2S₂^r_´2plogxq `R_rpxq, where

C_r :“ź

p

˜ 1`

8

ÿ

ν“2

Ppνq^r´Ppν´1q^r p^ν

¸ ,

S₂^r_´2 is a polynomial of degree2^r´2andR_rpxq !x^α^rplogxq^β^r (is the same). The estimate R_rpxq !x^u^r holds true, where u_r is given in Theorem 2.1.3.

(17)

Remark 2.1.5. According to a result of Kr¨atzel [57],

∆₂pxq “ ∆pp1,2,2,2q;xq ! x^45{127plogxq⁵, where 45{127 .

“0.354330P p1{3,1{2q, hence the same is the remainder term forř

nďxapnq². This improves R₂pxq ! x^96{245`ε with 96{245 .

“ 0.391836, obtained in [124] by reducing the error term to the Piltz divisor problem concerning ∆₃pxq.

Remark 2.1.6. Referring to our paper [98], Lelechenko [60, Th. 4] pointed out that the error termR_fpxq !x^u^k,`^`ε given in Remark 2.1.2 can be improved by using another result included in the book by Kr¨atzel [56, Th. 6.8]. Namely, one can take u_k,` “ _``1´θ¹

k´1, where θ_t is an exponent such that ∆_tpxq ! x^θ^t^`ε in the Piltz divisor problem. Since θ_tpxq ď ^t´1_t`2 holds true for t ě 4, see Titchmarsh [94, Th. 12.3], it follows that u_k,` ď

k`1

`pk`1q`3 P p1{p``1q,1{`q for k ě 5. In particular, in the case r ě 3 the error terms of Theorem 2.1.3 and Corollary 2.1.4 can be improved by taking u_r“ ₂r`1²^r^`1`5.

Remark 2.1.7. An elementary proof of the asymptotic formula ÿ

nďx

τpnq² „Axplogxq³ pxÑ 8q,

appears in several places. See, for example, Nathanson [69, Th. 7.8]. Although this and related questions were investigated by several authors, we are not aware even of elementary proofs for the asymptotic formula

ÿ

nďx

τpnq^r „C_rxplogxq²^r^´1 pxÑ 8q,

valid for any integerr ě2. In the joint work with Luca [62] we gave a minimal elementary proof of the following more general result:

Let k P N and let f : N Ñ C be a multiplicative function satisfying the following properties:

(i)fppq “k for every primep,

(ii) fpp^νq “ ν^Op1q for every prime p and every integer ν ě 2, where the constant implied by the O symbol is uniform in p.

Then

ÿ

nďx

fpnq

n “ 1

k!C_fplogxq^k`D_fplogxq^k´1`Opplogxq^k´2q and

ÿ

nďx

fpnq “ 1

pk´1q!C_fxplogxq^k´1`Opxplogxq^k´2q, where

C_f “ ź

p

ˆ 1´1

p

˙k 8

ÿ

ν“0

fpp^νq p^ν

(18)

and D_f is another constant depending on f. In the case fpnq “ τpnq^r with r P N, this applies by selectingk “2^r. Also see Martin [63, Prop. A.3] for a similar result proved by using analytic arguments.

2.2 Alternating sums concerning multiplicative func- tions

In what follows we consider certain alternating sums ÿ

nďx

p´1q^n´1 1

fpnq, (2.4)

where fpnq is a nonvanishing multiplicative function. The exposition of this section is based on our paper [112].

Bordell`es and Cloitre [11] established asymptotic formulas with error terms for sums (2.4), wheref belongs to a class of multiplicative arithmetic functions, including Euler’s function φpnq, the sum-of-divisors function σpnq and the Dedekind function ψpnq. It seems that there are no other results in the literature for alternating sums of type (2.4).

Using a different approach, also based on the convolution method, we show that for many classical multiplicative arithmetic functions f, estimates with sharp error terms for the alternating sum (2.4) can be deduced by using known results for

ÿ

nďx

1 fpnq.

Iffpnqis multiplicative, then the function p´1q^n´1_fpnq¹ is also multiplicative. Further- more,

8

ÿ

n“1

p´1q^n´1 1 fpnqn^s “

˜ 8

ÿ

n“1

1 fpnqn^s

¸¨

˝2

˜ 8

ÿ

ν“0

1 fp2^νq2^νs

¸´1

´1

˛

‚,

but to obtain sharp error terms we need some auxiliary results.

Assume that f is a nonzero complex-valued multiplicative function. Consider the formal power series

S_fpxq:“

8

ÿ

ν“0

a_νx^ν,

wherea_ν “fp2^νq(ν ě0), a₀ “fp1q “1. Note thatS_fpxqis the Bell series of the function f for the prime p“2. Let

S_fpxq:“

8

ÿ

ν“0

b_νx^ν

(19)

be its formal reciprocal power series. Here the coefficientsb_ν are given by b₀ “1 and

ν

ÿ

j“0

a_jb_ν´j “0 pν ě1q. (2.5)

If both series S_fpxq and S_fpxq converge for an x P C, then S_fpxqS_fpxq “ 1. In particular, if r_f and r_f are the radii of convergence of S_fpxq, respectively S_fpxq, then S_fpxqS_fpxq “1 for every xPC such that |x| ăminpr_f, r_fq.

Theorem 2.2.1(T´oth [112, Prop. 7]). Letf be a nonvanishing multiplicative function.

Assume that

(i) there exist constants D_f and E_f such that ÿ

nďx

1

fpnq “D_fplogx`E_fq `O`

x^´1R_1{fpxq˘

, (2.6)

where 1!R_1{fpxq “ opxq as xÑ 8, and R_1{fpxq is nondecreasing;

(ii) the radius of convergence of the series S_1{fpxq isr_1{f ą1;

(iii) the coefficientsb_ν of the reciprocal power seriesS_1{fpxqsatisfyb_ν !M^ν asν Ñ 8, where 0ăM ă1 is a real number.

Then

ÿ

nďx

p´1q^n´1 1

fpnq “D_f

˜ˆ 2

S_1{fp1q ´1

˙

plogx`E_fq `2plog 2q

S_1{f¹ p1q S_1{fp1q²

¸

`O`

T_1{fpxq˘ , (2.7) where

T_1{fpxq “

$

’&

’%

x^´1R_1{fpxq, if 0ăM ă ¹₂; x^´1R1{fpxqlogx, if M “ ¹₂; x^log^M{^{log 2}maxplogx, R1{fpxqq, if ¹₂ ăM ă1.

(2.8)

By taking fpnq “ φpnq and M “ 1{2 we deduce the following result, which is the

“alternating version” of formula (1.5).

Corollary 2.2.2 (T´oth [112, Th. 17]).

ÿ

nďx

p´1q^n´1 1

φpnq “ ´A 3

ˆ

logx`γ´B´8 3log 2

˙

`O`

x^´1plogxq^5{3˘

, (2.9)

where γ is Euler’s constant, A and B being the constant defined by (1.6).

The result (2.9) improves the error term Opx^´1plogxq³q obtained by Bordell`es and Cloitre [11, Cor. 4, (i)].

(20)

The following asymptotic formula is due to Sita Ramaiah and Suryanarayana [83, Cor.

4.1]:

ÿ

nďx

1

σpnq “Eplogx`γ`Fq `O`

x^´1plogxq^2{3plog logxq^4{3˘

, (2.10)

whereγ is Euler’s constant, E “ź

p

αppq, F “ÿ

p

pp´1q²βppqlogp pαppq , αppq “

ˆ 1´ 1

p

˙ 8

ÿ

ν“0

1

σpp^νq “1´pp´1q² p

8

ÿ

j“1

1

pp^j ´1qpp^j`1 ´1q, βppq “

8

ÿ

j“1

j

pp^j ´1qpp^j`1´1q.

Iffpnq “ σpnq(and M “1{2 again), then Theorem 2.2.1 gives Corollary 2.2.3 (T´oth [112, Th. 23]).

ÿ

nďx

p´1q^n´1 1

σpnq “E ˆˆ 2

K ´1

˙

plogx`γ`Fq `2plog 2qK¹ K²

˙

(2.11)

`O`

x^´1plogxq^5{3plog logxq^4{3˘ , where

K “

8

ÿ

j“0

1

2^j`1´1, K¹ “

8

ÿ

j“1

j 2^j`1 ´1.

The result (2.11) improves the error term Opx^´1plogxq⁴q obtained by Bordell`es and Cloitre [11, Cor. 4, (v)]. HereK .

“1.606695 is the Erd˝os-Borwein constant, known to be irrational.

Our next formula is the analog of a result of Ramanujan [76, Eq. (7)] for the sum ř

nďx 1

τpnq. See Wilson [122, Sect. 3] for its proof.

Theorem 2.2.4 (T´oth [112, Th. 27]).

ÿ

nďx

p´1q^n´1 1 τpnq “x

N

ÿ

t“1

B_t

plogxq^t´1{2 `O

ˆ x plogxq^N^`1{2

˙

, (2.12)

valid for every real x ě 2 and every fixed integer N ě 1, where B_t (1 ď t ď N) are computable constants. In particular,

B1 “ 1

?π ˆ 1

log 2 ´1

˙ ź

p

ˆ

ap²´p log ˆ p

p´1

˙˙

.

(21)

To obtain the error terms of (2.11) and (2.12) we need to use the following result of Kaluza [52] on reciprocal power series: Letř₈

ν“0a_νx^ν be a power series such that a_ν ą0 (ν ě0) and the sequence pa_νqνě0 is log-convex, that is a²_ν ďa_ν´1a_ν`1 (ν ě1). Then for the coefficientsb_ν of the (formal) reciprocal power series ř8

ν“0b_νx^ν one has b₀ “1{a₀ ą0 and

´1

a²₀a_ν ďb_ν ď0 for all ν ě1.

Another result on estimates of the coefficients of reciprocal power series is Kendall’s renewal theorem. See Berenhaut, Allen, and Fraser [10, Th. 1.1]. An explicit form of Kendall’s theorem was proved in [10, Th. 1.2]. However, it cannot be used for our purposes. We prove the following new explicit Kendall-type inequality, which can be applied to some functions we deal with.

Proposition 2.2.5 (T´oth [112, Prop. 12]). Assume that ř8

ν“0a_νx^ν is a power series such that a₀ “1 and |a_ν| ďAq^ν (ν ě1) for some absolute constants A, q ą0. Then for the coefficients b_ν of the reciprocal power series one has

|b_ν| ďAq^νpA`1q^ν´1 pν ě1q.

Corollary 2.2.6(T´oth [112, Cor. 13]). Let f be a positive multiplicative function such that

(i) asymptotic formula (2.6) is valid with 1!R_1{fpxq “opxq as xÑ 8;

(ii) 1{fp2^νq ď Aq^ν (ν ě 1), where A, q ą 0 are fixed real constants satisfying M :“

qpA`1q ă 1.

Then the asymptotic formula (2.7) holds for ř

nďxp´1q^n´1_f_pnq¹ , with error term (2.8).

Let σ^˚˚pnq denote the sum of bi-unitary divisors of n. Recall that a divisor d of n is a unitary divisor if pd, n{dq “ 1. A divisor d of n is called a bi-unitary divisor if the greatest common unitary divisor ofdand n{dis 1. The functionσ^˚˚ is multiplicative and for every prime power p^ν (ν ě1),

σ^˚˚pp^νq “

#

σpp^νq, if ν is odd;

σpp^νq ´p^ν{2, if ν is even.

Sitaramaiah and Subbarao [82, Th. 3.2] established an asymptotic formula for the sum ř

nďx1{σ^˚˚pnq. By using Corollary 2.2.6 we show Theorem 2.2.7 (T´oth [112, Th. 50]).

ÿ

nďx

p´1q^n´1 1

σ^˚˚pnq “A^˚˚₁ logx`B₁^˚˚`Opx^cplogxq^14{3plog logxq^4{3q, where A^˚˚₁ , B₁^˚˚ are explicit constants and c“ plog 9{10q{plog 2q .

“ ´0.152003.

(22)

Our paper [112] also includes asymptotic formulas for the sums ř

nďxp´1q^n´1{fpnq, wherefpnq is replaced byψpnq(Dedekind function), Ppnq (gcd-sum function) and other special multiplicative functions. Furthermore, we derived formulas forř

nďxp´1q^n´1fpnq.

For example [112, Th. 15] states that ÿ

nďx

p´1q^n´1φpnq “ 1

π²x²`O`

xplogxq^2{3plog logxq^4{3˘ , which may be compared to (1.4).

2.3 Maximal orders

In this section we present easily applicable theorems for determining L“Lpfq:“lim sup

nÑ8

fpnq log logn,

wheref are certain nonnegative real-valued multiplicative functions. Let denote

%ppq “%pf, pq:“sup

νě0

fpp^νq, for the primesp, and consider the product

R“Rpfq:“ź

p

ˆ 1´ 1

p

˙

%ppq.

We formulate the conditions for lower and upper estimates forLseparately. Note that

%ppq ě fpp⁰q “1 for all p.

Theorem 2.3.1 (T´oth and Wirsing [114, Th. 1]). Let f be a nonnegative real-valued multiplicative function. Assume that %ppq ă 8 for all primes p and that the product R converges unconditionally (i.e. irrespectively of order), improper limits being allowed.

Then

Lďe^γR. (2.13)

The next result uses a different assumption.

Theorem 2.3.2 (T´oth and Wirsing [114, Th. 2]). Let f be any nonnegative real- valued multiplicative function. Suppose that %ppq ă 8 for all p and that the product R converges, improper limits being allowed, and that

%ppq ď1`o

ˆlogp p

˙ . Then (2.13) holds.

(23)

To establish e^γR also as the lower limit more information is required. Namely, the suprema %ppqmust be sufficiently well approximated by not too large powers of p.

Theorem 2.3.3 (T´oth and Wirsing [114, Th. 3]). Let f be a nonnegative real-valued multiplicative function. Suppose that

(i) %ppq ă 8 for all primes p,

(ii) for each prime p there is an exponent e_p “p^op1q PN such that ź

p

fpp^e^pq%ppq^´1 ą0, and

(iii) the product R converges, improper limits being allowed.

Then

Lěe^γR.

Corollary 2.3.4(T´oth and Wirsing [114, Cor. 1]). Letf be a nonnegative real-valued multiplicative arithmetic function such that for each prime p,

(i) %ppq ď p1´1{pq^´1, and

(ii) there is an exponent e_p “p^op1q PN satisfying fpp^e^pq ě 1`1{p.

Then

L“e^γR, that is the maximal order of fpnq is e^γRlog logn.

Corollary 2.3.4 applies, for example, to the functions fpnq “σpnqand fpnq “1{φpnq and we recover the well known results of Gronwall (1913) and Landau (1909). Further- more, let fpnq “σ^peqpnq, the sum of exponential divisors of n. See Section 2.4. Then we obtain that

lim sup

nÑ8

σ^peqpnq

nlog logn “ 6 π²e^γ,

which is a result of Fabrykowski and Subbarao [33]. Another application is Theorem 2.5.5.

Further applications were given by Apostol [3, Prop. 4], Apostol [4, Prop. 7], Apostol and Petrescu [5, Prop. 7] and by myself [99, Th. 7, 8].

2.4 Arithmetic functions associated with exponential divisors

Let d “ ś

pp^ν^p^pdq be a divisor of the integer n “ ś

pp^ν^p^pnq. Then d is called an exponential divisorof n, if ν_ppdq |ν_ppnq for every primep. Notation: d|en. This concept was introduced by Subbarao [87]. According to the definition, 1 |e 1, but 1 is not an

(24)

exponential divisor of n ą1. The smallest exponential divisor of n ą1 is its squarefree kernelκpnq “ś

p|np.

Let τ^peqpnq and σ^peqpnq denote the number and the sum of exponential divisors of n, respectively. The function τ^peq is called the exponential divisor function, already quoted in Section 2.1. The integer n “ ś

pp^ν^p^pnq is called exponentially squarefree if all the exponents ν_ppnq ě 1 are squarefree. By convention, 1 is also exponentially squarefree.

Letq^peqdenote the characteristic function of exponentially squarefree integers. Properties of these and related functions were investigated by several authors. See Cao and Zhai [16], Lelechenko [60, 61], P´etermann and Wu [75], Smati and Wu [85], Subbarao [87], Wu [121].

Two integers m, n ą 1 have common exponential divisors if and only if they have the same prime factors and in this case, i.e., for m “ śr

i“1p^a_iⁱ, n “ śr

i“1p^b_iⁱ, a_i, b_i ě 1 (1ďiďr), the greatest common exponential divisor of m and n is

pm, nq_peq :“

r

ź

i“1

p^pa_i ⁱ^,bⁱ^q.

Herep1,1q_peq “1 by convention and p1, nq_peq does not exist for ną1.

2.4.1 Exponential Euler function

The integers m, n ą 1 are called exponentially coprime, if they have the same prime factors and pa_i, b_iq “ 1 for every 1 ď i ď r, with the notation of above. In this case pm, nq_peq “ κpmq “ κpnq. 1 and 1 are considered to be exponentially coprime. 1 and ną1 are not exponentially coprime.

Forn “śr

i“1p^a_iⁱ ą1 witha_i ě1 (1ďiďr), denote byφ^peqpnqthe number of integers śr

i“1p^c_iⁱ such that 1 ď ci ď ai and pci, aiq “ 1 for 1 ď i ď r, and let φ^peqp1q “ 1. Thus φ^peqpnqcounts the number of divisorsd ofn such that dand n are exponentially coprime.

The function φ^peqpnq is called the exponential Euler function, it is multiplicative and for every prime power p^ν (ν ě1), φ^peqpp^νq “ φpνq, whereφ is Euler’s function.

As another consequence of Theorem 2.1.1 and Remark 2.1.2, by selecting fpnq “ φ^peqpnq^r with ` “3, k “2^r, we have the following result.

Theorem 2.4.1 (T´oth [96, Th. 1], [98, Eq. (6)]). Let rě1 be an integer. Then ÿ

nďx

φ^peqpnq^r “B_rx`x^1{3T₂^r_´2plogxq `Opx^t^r^`εq, (2.14) for every εą0, where

B_r:“ ź

p

˜ 1`

8

ÿ

a“3

φpaq^r´φpa´1q^r p^a

¸ ,

T₂^r_´2 is a polynomial of degree 2^r´2 and t₁ “1{5, t_r:“ ²_3¨2^r`1r`1^´1 for r ě2.

(25)

In the case r “ 1, P´etermann [74, Th. 1] improved the error term in (2.14) into Opx^1{5logxq. Cao and Zhai [17] obtained new results on the four dimensional divisor problem of pa, b, c, cq type, where 1 ď a ď b ă c are fixed integers. As an application, they proved in [17, Th. 3] the following more precise asymptotic formula:

ÿ

nďx

φ^peqpnq “B₁x`B₂x^1{3`D₁x^1{5logx`D₂x^1{5` `Opx^18{95`εq, (2.15) where 18{95 .

“0.189473ă1{5. They also showed that the error term in (2.15) is Ωpx^1{8q. In the case r ě 3 the error term of (2.14) can be improved by takingt_r “ _3p2²^rr^`1`2q, as shown by Lelechenko [60]. See Remark 2.1.6.

2.4.2 Exponential M¨ obius function

The exponential convolution of the arithmetic functions f and g is defined by pf dgqpnq “ ÿ

b1c1“a1

. . . ÿ

brcr“ar

fpp^b₁¹¨ ¨ ¨p^b_r^rqgpp^c₁¹¨ ¨ ¨p^c_r^rq, wheren “p^a₁¹¨ ¨ ¨p^a_r^r.

The convolution d is commutative, associative and has the identity element µ². Fur- thermore, a function f has an inverse with respect to d if and only if fp1q ‰ 0 and fpp₁¨ ¨ ¨p_sq ‰ 0 for any distinct primes p₁, . . . , p_s. The inverse with respect to d of the constant 1 function is called theexponential M¨obius functionand is denoted byµ^peq. Hence for every ně1,

ÿ

d|en

µ^peqpdq “ µ²pnq.

Hereµ^peqp1q “ 1 and forn “p^a₁¹¨ ¨ ¨p^a_r^r ą1,

µ^peqpnq “µpa₁q ¨ ¨ ¨µpa_rq.

Observe that |µ^peqpnq| “1 or 0, according as n is exponentially squarefree or not. Wu [121, Th. 2] deduced, improving a result by Subbarao [87] that

ÿ

nďx

|µ^peqpnq| “ C1x`Opx^1{4δpxqq, whereδpxqis defined by (1.3) and

C₁ “ź

p

˜ 1`

8

ÿ

a“4

µ²paq ´µ²pa´1q p^a

¸ .

I showed that the corresponding error term can be improved on the assumption of the Riemann hypothesis (RH).

Asymptotic Properties of Multiplicative Arithmetic Functions of One and Several Variables DSc dissertation