17-2 Symmetry and Symmetry Operations

CHAPTER SEVENTEEN

MOLECULAR

SYMMETRY AND BONDING

17-1 Introduction

The chemical bond presents quite a problem to the writer of a physical chemistry text. The numerous rather empirical rules that exist and are useful do not have enough solid theoretical content to be transferred out of their organic or inorganic chemical context and treated as true theory. Yet the exact wave mechanical approach becomes hopelessly bogged in mathematical complexities if one departs from diatomic molecules of the lightest elements. What, then, should be done ?

It turns out that if we know the geometry of a molecule, it is much easier to set up the wave mechanical treatment; also, a number of qualitative results can be demonstrated without calculation. The emphasis of this chapter is therefore on that discipline of mathematics which allows a concise and penetrating descrip- tion of the essential elements of molecular geometry, that is, group theory. As a branch of mathematics, group theory requires serious and extensive study. There are numerous theorems and lemmas to be proved and many special cases to be examined in detail. We will take a very pragmatic approach here, however.

Theorems will be stated rather than rigorously proved; their validity will lie in the success of their practical as opposed to their abstract demonstration. By allowing ourselves this latitude, it will be possible to present the group-theoretical approach to the symmetry properties of molecules in a rather efficient, and, this writer hopes, a stimulating way.

We proceed therefore to describe symmetry operations and to develop the concept of a set of such operations as defining a symmetry group. Some of the basic attributes of groups necessarily are introduced. The result will be a compact description of those aspects of molecular geometry that determine the qualitative application of wave mechanics to a set of chemical bonds. The group-theoretical approach also provides a means for simplifying quantitative wave mechanical calculations. This is illustrated in the Commentary and Notes section with a dis- cussion on the crystal field treatment of transition metal complexes.

The wave mechanics of chemical bonding, treated qualitatively and from the symmetry point of view in this chapter, is taken up more quantitatively in Chapter 18.

717

F I G . 17-1. (α-c) Symmetry elements for the molecule N H⁸ . id) Other objects having the same symmetry.

17-2 Symmetry and Symmetry Operations

A. Symmetry Elements and Stereographic Projection Diagrams

The objects that we shall be dealing with, namely simple molecules, will generally have a considerable degree of symmetry. The ammonia molecule, for example, can be viewed as a triangular pyramid whose base is formed by the hydrogen atoms and whose apex is a nitrogen atom, as illustrated in Fig. 17-l(a). There is an axis of symmetry, labeled C³, in recognition of the fact that if the molecule were rotated 120° about this axis, the result would be an equivalent configuration. That is, if the rotation were performed while the observer's eyes were closed, on looking again he could not tell that anything had occurred. The rotation is a symmetry operation—it gives an equivalent configuration. Were each hydrogen atom labeled, however, one could then tell that the rotation had been made. Only a rotation of 0°, 360°, and so on, would lead to a totally unobservable change; such an operation is called the identity operation E, since it results in a configuration identical to the starting one.

The ammonia molecule has other symmetry elements. A plane passing through the nitrogen and H³ atoms and midway between Η^χ and H² is a plane of symmetry.

As illustrated in Fig. 17-1(b), if some molecular feature, such as H j , occurs at a perpendicular distance χ in front of the plane, then an equivalent feature is found by extending the perpendicular to a distance — χ to the other side of the plane, which in this case locates H². A plane of symmetry is designated by the symbol σ, and if it contains the principal axis of symmetry, C³ in this case, it is called a vertical plane and written σ^ν. There are evidently three equivalent such planes in the case of N H³ .

Three-dimensional perspective drawings are difficult to work with, and it has become conventional to use a projection down the principal axis of symmetry

17-2 SYMMETRY AND SYMMETRY OPERATIONS 719

of the object. The ammonia molecule then looks as in Fig. 17-1(c), where the triangle imposed on the nitrogen atom stands for a C³ rotation axis and the lines labeled σ^ν locate the vertical planes of symmetry. Even Fig. 17-1(c) is too specific;

quite a variety of objects would have C³ and three a^v's as the only symmetry elements, as illustrated in Fig. 17-1(d), and therefore belong to the same sym­

metry class as N H³. A yet more abstract representation is desirable.

The next step is then to devise a geometric representation or pattern from which all superfluous features have been removed. It is customary to show the projection of this abstract figure as viewed down the principal axis—this is called a stereo- graphic projection diagram. Figure 17-2(a) shows such a diagram for the symmetry elements C³ and 3 σ^ν. The triangle represents the C³ axis and the three full lines represent the three σ^ν planes. The symmetry pattern produced by these symmetry elements is generated by supposing the circle to lie in the plane of the paper and that there is initially a mathematical point lying above the plane, denoted by the plus sign. The full pattern of points is then generated by carrying out the symmetry operations. As shown in Fig. 17-2(b), the operation σ^ν generates point 2 from point 1; application of Q¹ (meaning one unit of rotation on the C³ axis) generates point 3 from point 1 and point 4 from point 2 and application of C^{3 2} similarly produces points 5 and 6. We now have obtained Fig. 17-2(a). Disregarding the labeling, no new points are produced by σ^ν' or .

A second example of a symmetric molecule is H²0 , or Η—Ο—H. There is a twofold axis of symmetry passing through the oxygen atom, and a 180° rotation about this axis gives an equivalent configuration. In addition to the C² axis, there are two σ^ν planes. Both contain the C² axis, and one is just the Η—Ο—Η plane, while the other is perpendicular to it, as illustrated in Fig. 17-3(a). The stereographic projection diagram for an object having just these symmetry ele­

ments is shown in Fig. 17-3(b), the lens denoting a twofold rotation axis. The four plus points are generated from a single initial point by application of σ^ν and then C² (or vice versa).

A square planar molecule, such as PtClJ", possesses a number of symmetry features. There is a fourfold rotation axis C⁴ passing through the platinum atom and perpendicular to the molecular plane—successive rotations of 90° give equiva­

lent configurations. As illustrated in Fig. 17-4(a), there are also two pairs of C²

F I G . 17-2. Stereographic projection showing the symmetry features o / N H⁸.

(a)

/ +

\

(b)

F I G . 17-3. Stereographic projection showing the symmetry features of H20 .

CI- :C1

Pt*

CI- CI

(a)

V

ν

(b) ^(c)

F I G . 17-4. (a) Symmetry elements o / P t C l i " and (b) corresponding stereographic projection.

(c) Stereographic projection if no a^h and no a^v9s are present.

17-2 SYMMETRY AND SYMMETRY OPERATIONS 721 axes, labeled C² and C²' . The fourfold axis, being the highest-order one, is called the principal axis. The two pairs of σ^ν planes contain the C⁴ axis and either the C² or the C²' ones; in addition, the molecular plane itself is a plane of symmetry.

This last is a plane perpendicular to the principal axis, and is denoted ah .

The stereographic projection diagram generated by the symmetry features C⁴, C², C²', 2 σ^ν , 2σ^ν' (or 2σ<ι), and ah is shown in Fig. 17-4(b). The set of plus points is generated by carrying out σ^ν on the initial one, followed by the successive C⁴ operations. The circles denote mathematical points lying below the plane of the paper and are produced by the ah operation. The set of points implies all of the symmetry features—none of the other operations generate any further points. Figure 17-4(b) also illustrates some additional conventions. The presence of ah is signified by drawing the projection as a full rather than a dashed circle.

The secondary axes C² and C²' are indicated by the lenses located radially around the circle; the fact that the lines to the lenses are full means that corresponding a^v' s are also present; were they not, the lines would be dashed. Thus Fig. 17-4(c) shows the presence of the symmetry elements C⁴, C², and C²' only (no ah and no a^v's). A few remaining conventions will be illustrated later as they come up.

B. Symmetry Operations

A given symmetry element may generate more than one symmetry operation, and these will now be spelled out.

E: The identity operation has already been described; it is that which leaves the figure in an identical configuration to the initial one.

Cⁿ : A rotation axis is one about which the molecule may be rotated to give equivalent positions, η denoting the number of positions. Thus C⁴ denotes a fourfold rotation axis; it generates the individual symmetry operations C⁴\ C^{4 2}, C^{4 3}, and C^{4 4}, the superscript denoting the number of rotational increments of 2π/η degrees each. Since C^{4 2} is the same as C² and C^{4 4} = E, this sequence would usually be written C⁴\ C², C^{4 3}, E.

If a molecule has more than one rotation axis, then the one of largest η is called the principal axis and the others the secondary axes.

a: The symbol a denotes a plane of symmetry, that is, a plane passing through the molecule such that matching features lie on opposite sides of, or are "reflected"

by, the plane. A plane perpendicular to the principal axis is denoted ah (for horizontal) and one which contains the principal axis is called σ^ν (for vertical).

Finally, if a molecule has secondary rotation axes, a vertical-type plane of sym­

metry which bisects the angle between two such axes is called σα (for dihedral).

/: An inversion center is denoted by i. If present, matching features lie equi­

distant from a point or inversion center. Alternatively, if a feature has the coordi­

nates (x, y, z), then an equivalent feature is present at (—x, — y, — z). Thus PtClJ" has an inversion center but H²0 and N H³ do not.

Sⁿ : This symbol stands for an improper rotation axis. An improper rotation may be thought of as taking place in two steps. First, a proper rotation and then, a reflection through a plane perpendicular to the rotation axis, usually a ah plane.

The subscript η again denotes the order of the axis. By way of illustration, consider

5 1 1

3 6 6 (a) (b) (c)

F I G . 1 7 - 5 . Illustration of the symmetry operation S^1.

the triangular antiprism shown in Fig. 17-5(a). We are looking along the prism axis and see the staggered triangular ends. Rotation by 60° gives Fig. 17-5(b) and reflection in a plane perpendicular to the axis gives Fig. 17-5(c). The result is equivalent to the starting figure if the labeling is ignored, and hence is a sym­

metry operation. The figure therefore has the symmetry element S⁶, the operation being SQ¹. The complete set of operations would be S⁶\ C³\ /, C^{3 2}, 5^{6 5}, Ε (note that S^{6 2} = C³\ that is, gives the identical change, and similarly, S^{e 4} = C^{3 2}; also 5^{6 3} = /). As an exercise, the reader should examine the series 5s¹, S^B2,... for similar alternative statements—it is now necessary to go to S\° before the series repeats.

C. Naming of Symmetry Groups

Any object or molecule has some certain set of symmetry features and this set accordingly characterizes its symmetry. Each distinctive such set is called a point group. As is seen in the next section, the set of symmetry operations has the property of a mathematical group*and the term "point" refers to the fact that no translational motions are being considered. In the case of a crystal lattice, the addition of translations generates what are then called space groups.

Some easily recognizable, either very simple or highly symmetric, cases are summarized later, but the following is the general procedure for classifying a point group. The names or point group symbols used are those introduced by Schoenflies.

One first looks for rotation axes. If there is only one, then the naming is as follows:

Cⁿ N o other symmetry features are present.

C^nh There is also a ah plane.

C^nV There is no ah plane but there is a σ^ν plane. (There must then be η such planes.)

If the molecule or object possesses more than one rotation axis, the one of higher order becomes the principal axis, of order n. We will only consider cases where the secondary axes are perpendicular to the principal one. The naming is now as follows:

Dⁿ N o other symmetry features are present.

D^nh A ah is present.

D^nu There is no ah but there is a σα (necessarily η ad's).

17-2 SYMMETRY AND SYMMETRY OPERATIONS 7 2 3 If there is an S²ⁿ axis collinear with the principal Cⁿ axis and no other symmetry features, the group is then S²ⁿ . If there is only a plane of symmetry, the group is C^s, and if there is only an inversion center, it is C^t. If no symmetry elements at all are present, the group is named C^x.

D . Special Groups

There are some further groups whose symmetry properties can usually be recognized on sight. An A—Β type of molecule has a σ^ν and can be thought of as having a rotation axis of infinite order; this combination of symmetry elements is called Cov ; an A—A type of molecule has a ah and a twofold secondary axis, and the corresponding group name is .

Easily recognizable but more complicated to describe in terms of symmetry are tetrahedral and octahedral molecules, for which the corresponding point group names are 7d and Oh . The tetrahedral case is best constructed by using a cubic framework, as illustn: id in Fig. 17-6. The symmetry elements and opera­

tions are as follows.

1. The identity operation E.

2. Three C² axes coinciding with the x, y, and ζ axes of the figure. The operations characteristic of equivalent symmetry elements are often just totaled, and could be reported as 3 C² in this case.

3. Three S⁴ axes collinear with the preceding C² ones. These generate the operations 3 5^{4 x} and 3S^{4 3}. There is a total of 6 S⁴ operations, excluding the S^{4 2} ones already accounted for (being identical to C²).

4. Four C³ axes, each coinciding with a body diagonal of the cube. Counting C3¹ and C^{3 2} for each, the total is 8 C³.

5. There is a plane of symmetry containing each pair of apexes of the tetrahedron

F I G . 17-6. Some symmetry elements of a tetrahedron.

F I G . 17-7. Symmetry elements of an octahedron.

and bisecting the opposite edge, and examination of the figure shows six equivalent such planes. The symmetry operations are then 6σ, usually reported as 6σ<\.

The 7d group then has a total of 24 distinct symmetry operations.

Examination of the regular octahedron shown in Fig. 17-7 yields the following symmetry aspects.

1. The identity operation E.

2. Three C² axes collinear with the x, y, and ζ coordinates of the figure, or 3C² operations.

3. Three C⁴ axes collinear with the preceding C² axes, each generating Q¹ and C^{4 3} new operations, for a total of 6 C⁴.

4. Three S⁴ axes collinear with the preceding and generating S4 ¹ and 5^{4 3} new operations, or a total of 6.S⁴.

5. Six C²' axes each bisecting opposite edges. The total is then 6C²'.

6. Four C³ axes each passing through the center of opposite triangular faces, and giving 8 C³ operations in all.

7. Four S^e axes collinear with the C³ ones (note Fig. 17-5!). Each generates the operations .V, 5^{6 2} ( = C,¹), 5^{e 3} ( = /), 5^{e 4} ( = C^{3 2}), 5^{6 5}, or two new ones, for a total of 8 5^e.

8. An inversion center i.

9. Three planes of symmetry each of which passes through four of the six apexes, or 3ah.

10. Six planes of symmetry each of which passes through two apexes and bisects two opposite edges, or 6σ& .

The total number of symmetry operations for the octahedron is 48.

£. Some Illustrations of Point Groups

The stereographic projection diagrams for a number of point groups are shown in Fig. 17-8. The only additional convention to be noted is that an open geometric figure in the center of the diagram indicates a corresponding improper axis of rotation.

17-2 SYMMETRY AND SYMMETRY OPERATIONS 7 2 5

Θ

s' +

/ / /

\

\

\ X ^ _

c

\

\

\ / /

2v

\ L--^

c

1

c

/ " ^ 1° X

/ 1 \

/ " " ' + Τ Ο Χ

vXv

*>,

^^Τ5Χ

ν · }

V*/'! \ ° /

/ ^ ®

2h

u

X ^ ® i® •

ζ

® \

>4h D^5h

F I G . 1 7 - 8 . Stereographic projection diagrams for various point groups. {From H. Eyring, J.

Walter, and G. E. Kimball, "Quantum Chemistry," Copyright 1960, Wiley, New York. Used with permission of John Wiley & Sons, Inc.)

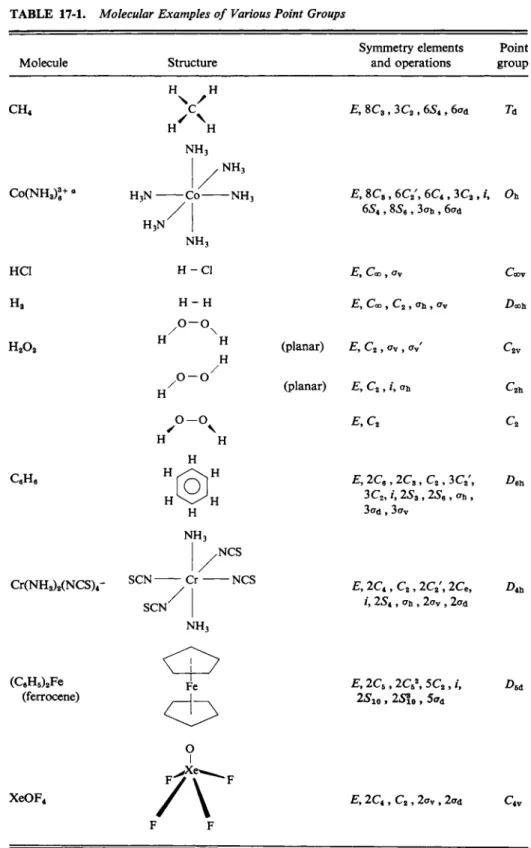
Some molecular examples are collected in Table 17-1 [for additional ones see Adamson (1969)]. The Schoenflies designation for each can be obtained by following the procedure described in Section 17-2C. A useful point to remember is that it is not necessary to identify all the symmetry elements present in order to determine the point group designation. Thus in the case of N H³ it is sufficient to determine that there is a C³ axis and no secondary axes and that there is a σ^ν but no ah, to establish the group as C^{3 v} . The D^2h designation for H²C = C H² follows on observing that there are two mutually perpendicular C² axes and a ah plane

—the presence of σ^ν planes is automatically assured. Dibenzene chromium is Z>^6h since the principal axis is C^e, there is at least one secondary axis, and a ah plane.

The remaining symmetry features are implicit.

The entries for H²O^a illustrate another point. The molecule has C^{2 v} symmetry if it is in the cis configuration with all atoms coplanar. Keeping this plane as a reference, one may then twist the molecule about the Ο—Ο axis, thus rotating one Ο—Η bond forward above the plane and the other backward below the plane.

A 90° rotation makes the molecule planar and trans; it now has C^{2 h} symmetry.

The actual configuration in the crystal is in between these positions, and for any

TABLE 17-1. Molecular Examples of Various Point Groups

Molecule Structure

Symmetry elements Point and operations group

C H⁴

C o ( N H3)3 e + e H3N -

HC1 H²

H²0²

C^eH^e

C r ( N H³)²( N C S )⁴

( Q H⁵)²F e (ferrocene)

X e O F⁴

HiN

Η Η

Χ

Η Η Ν Η3

/Ν Η³

- C o Ν Η³

Ν Η³ Η - C 1 Η - Η

Η Η

Η

Η Ο - Ο

Η Η • V

Η

(ρ)

Η Ν Η³

^ N C S SCN Cr NCS

S C N ^ N H³

Γ F e

Ο

7\

E, 8 C3, 3 C2, 6iS4 , 6σ<ι 7a

E, 8 C⁸, 6C²', 6 C⁴ , 3 C², 1 , 65*⁴ , 8»S^e, 3ah , 6σ<ι

Ε, Coo, <j\

E, Coo , C² , σΐι, σ^ν

(planar) £ , C², σ^ν , σ^ν'

(planar) £ , C2, i, ah

E, C²

2Γ, 2 C g , 2 C 3 , C², 3 C², 3 C², 1 , 25*3, 215*6, ah , 3σ<ι, 3 σ^ν

-C, 2 C⁴, C², 2 C²' , 2Ce,

1,

£ , 2 C⁵, 2 C^{6 8}, 5 C , , / , 2 5 Ί⁰ > 2 5 | ο , 5<r^d

2 C4, C2, 2σν , 2(T<i

Oh

Coov Dooh

C2 v

c2

β A s is customary with such complex ions, only the central metal ion and the atoms directly bonded to it are considered.

17-3 A SET OF SYMMETRY OPERATIONS AS CONSTITUTING A GROUP 727

such intermediate angle the symmetry is reduced to C². Thus the symmetry group of a molecule varies with molecular motions; one ordinarily takes the most probable positions of the atoms in the lowest vibrational energy state. In the case of C o ( N H³) 6⁺ the hydrogens are ignored in giving the symmetry as Oh ; were they included, then, depending on their assumed configuration, some much lower symmetry would be reported.

The symmetry properties of a molecule are thus not absolutely invariant or unique. We will be using symmetry to draw conclusions about chemical bonding and it is well to realize that assumptions as to what is important are inherent in most statements of molecular symmetry.

17-3 A Set of Symmetry Operations as Constituting a Group

A. The Multiplication Table for a Set of Symmetry Operations

The term "multiplication" has the meaning in group theory of sequential performance of designated operations. Thus AB means first operation B, then operation A. With this definition in mind one can construct a "multiplication table" for the set of symmetry elements possessed by any particular object, each symmetry operation being entered separately.

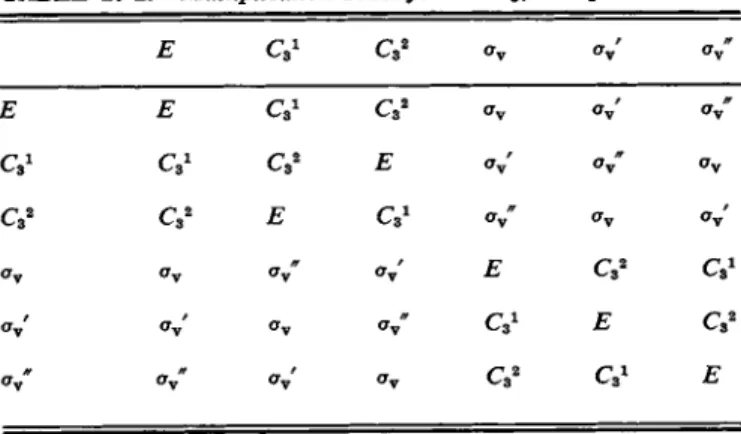
Table 17-2 shows the multiplication table for the point group C^{3 V} . The procedure for developing this table is as follows. It is simplest to make use of the stereographic projection diagram (Fig. 17-2 or Fig. 17-8), but with each plus identified by a number. As illustrated in Fig. 17-9, the effect of each separate symmetry opera­

tion is first diagrammed. Each possible symmetry operation is then performed again. Thus C^zx followed by Q¹ gives the identical result as C^{3 2}; Q¹ followed by σ^ν gives the identical result as σ^ν', and so on. In this way a table of all possible products is worked out. The convention we will follow is that in a multiplication table such as Table 17-2 the operation in the left-hand column is that performed first, followed by the one indicated by the top row.

There are several important features to notice in the table. First, each product

T A B L E 1 7 - 2 . Multiplication Table for the C^{8 V} Group

Ε CQ1 C32 oy oy' σν"

Ε Ε CQ1 Oy Oy Oy"

C3¹ C3¹ C^{3 2} Ε Oy' Oy" Oy

C3² C3² Ε Oy" Oy Oy Oy Oy Oy" Oy Ε

Oy Oy Oy Oy" Ε

Oy" Oy" Oy' Oy Ε

c

gives a result identical to the result of some single symmetry operation of the set.

Second, each symmetry operation occurs just once in each row and in each column.

Each operation has a reciprocal, that is, for each A there exists a Β such that AB = Ε (and we then say that A = B*¹). The associative law of multiplication holds, that is, A(BC) = (AB)(C). For example,

C^{3 1}( C^{3 2}a^v) = C³W = cr^v and (CJCf) σ^ν = Εσ^γ = σ^ν . (17-1) These features characterize a mathematical group, by definition; they hold for the multiplication tables of all of the point groups discussed here.

The multiplication of symmetry operations differs from ordinary multiplication in not being commutative, that is, the order of operation makes a difference.

Thus AB is not in general the same as BA. For example, C^{3 1}CT^v = σ^ν', while a^vC^{3 1} = σ^ν". Finally, notice that the identity operation Ε occurs either along the diagonal of the multiplication table or is symmetrically disposed to it. This behavior will be a general one of symmetry point groups.

β. Some Properties of Groups

Some general definitions and theorems for groups are now useful; we omit proofs for the latter, although in many cases the exercise is not difficult [see Cotton (1963)]. The order h of a symmetry group is the number of distinct sym­

metry operations, or captions to the rows and columns of the multiplication table;

the order of the C^{3 V} group is six, for example. A group may have subgroups; thus FIG. 17-9. Demonstration that a^vC^ = σ^ν' in the Csv group.

17-4 REPRESENTATIONS OF GROUPS 729 the set E, C³\ C^{3 2} obeys the rules for a group. It can be shown that the order g of any subgroup must be an integral divisor of the group order h.

An important item is that the symmetry operations of a group will generally subdivide into classes. Before defining the term class we must first consider an operation known as a similarity transformation.

If A and X are two elements of a group and X'¹ is the reciprocal of X, that is, X~^XX = £ , then the product X~^XAX will in general give some other element Β of the group. For example, in the C^{3 V} group if X is C³\ then X~^x is C^{3 2}; then C^{3 2} " = σ^ν'. Thus if A is σ^ν, its similarity transformation by Cjj¹

iS

We next take as X each element of the group in turn and apply the operation Χ~^τΑΧ; if this is done for the C^{3 V} group, with A = σ^ν, the result is always σ^ν, σ^ν', or σ^ν" . The same result obtains if A is σ^ν' or σ^ν". The last three elements are then said to be conjugate with each other and constitute a class of the group. If the procedure is repeated with A = C3¹ or C^{3 2}, the result of the similarity trans­

formation (with X equal to any element of the group) is always C³* or C^{3 2}, and these two symmetry operations constitute a second class. The identity operation always is a class by itself.

An important theorem is that the order of any class of a group must be an integral divisor of the order h of the group. We will henceforth group symmetry operations by classes—those for C^{3 V} are E, 2 C³, and 3 σ^ν . Note that this has been done in Table 17-1.

17-4 Representations of Groups

Just as the set of symmetry elements is an abstraction of the symmetry properties of an object, there is a very useful abstraction of a group multiplication table known as a representation. A representation of a group is a set of numbers (or, as seen in the next section, of matrices) which if assigned to the various symmetry operations, will obey or be consistent with the group multiplication table. It turns out that all of the symmetry operations of a given class must be given the same number if the set of assignments is to work as a representation.

Two representations for the C^{3 V} group are

(1) E=l,

< ν = ^

= 1 ,

(2) Ε = 1, Q¹ = C^{3 2} = 1, σ^ν = σ^ν' = σ^ν" = - 1 .

If these simple designations are substituted into Table 17-2, then a self-consistent multiplication table is obtained. Considering representation 2, a^vC^{3 2} = σ^ν' and (—1)(1) = (—1). It will be customary to show a representation in the more compact form given in Table 17-3, where Γ is the general symbol for a representa­

tion.

As a second example, the multiplication table for the group C^{2 V} is given by Table 17-4. In this case each symmetry operation constitutes a separate class (as may be verified as an exercise). A set of simple representations for this group turns out to be as shown in Table 17-5. The designations A¹, A², and so on will be discussed later.

T A B L E 17-3. Two Representations of C^{8 V} Ε 2 C^S 3 σν

1 1 1

A 1 1 - 1

T A B L E 17-4. Multiplication Table for the C^{a v} Group

Ε c² σ^ν σ^ν'

Ε Ε c² σ^ν σ^ν'

c² c² Ε σ^ν' σ^ν

σ^ν σ^ν c²

σ^ν' σ^ν c²

T A B L E 17-5. Representations for C⁵

c² σν σν'

Λ = Λ , 1 1 1 1

1 1 - 1 - 1

Λ = *ι ^{1 - 1 1 - 1}

1 - 1 - 1 1

The concept of a representation as developed so far seems rather trivial. It provides, however, the key to using the symmetry properties of a molecule in wave mechanical treatments. To develop this application, we proceed to examine how representations may be generated.

A. Geometric Transformations; Matrix Notation

An important method of generating a representation will be to carry out the symmetry operations of a group on some elementary object such as a point or a vector. Suppose a point is located at ( χ^χ, y^x, z^x) and we apply the symmetry operations of the C^{2 V} group to it. These consist of E, a C² axis collinear with the ζ axis, a σ ^ν in the xz plane, and a σ^ν' in the yz plane. As illustrated in Fig. 17-10(a), application of this last changes the point to (—x^x, y¹, Zj), or

x² = —x^x + 0y¹ + Οζχ, y² = 0χ^χ + y^x + 0z¹,

<^{1 7}-^{2 )} z2 = OXi + Ovj + z¹.

As shown in Fig. 17-10(b), the operation C² gives

x² = —*i + Qyx + Ozi, y² = Οχχ — y^x + 0 ζ^χ, z² = Οχχ + 0y¹ + z^x.

In these cases the new coordinates are just 1, 0, or —1 times the old ones, with no mixing—that is, x² does not depend on y^x or z^x, and so on. This will not in general be true. For example, were the C^v group involved, the operation C3¹

17-4 REPRESENTATIONS OF GROUPS 731

(*2» ^ 2 . Ζχ)

<jy (yz)

(a)

to.

(*l..Vb*l)

60°

c

(b)

120°

(xuyuzo

c³'

(c)

F I G . 17-10. The C^{2 v} point group, (a) The a^v(yz) operation on a general point and (b) the C² operation, (c) The C V operation of the C^{8 V} group as applied to a general point.

would be as shown in Fig. 17-10(c), leading to

x² = ^{X l} cos(f TT) — y^x sin(f π) + 0 z^x,

y2 = χλ sin(f TT) + yx cos(f ΤΓ) + 0 zx,

z² = Q^Xl + Ojx + Z j .

(17-4)

Here the χ and y coordinates mix with each other but not with the ζ coordinate.

A set of transformation equations such as Eqs. (17-2), (17-3), or (17-4) may be expressed in matrix notation. Equation (17-2) becomes

(17-5) - 1 0 0' _{0 1 0} ~x{

'*2

yi =

y2

0 0 1 _{_zi _}

-

2_

That is, multiplication of the matrix

yields the new set

~Xi " - 1 0 0"

y-i by 0 1 0

.^Zl. 0 0 1

Similarly, Eqs. (17-3) and (17-4) become - 1 0 0

0 - 1 0 0 0 1

yi

~*2 y2 .

2_

(17-6)

and

COS(|TT) sin(fTr)

0 0 1

x²

y i

=

_Z1_ ^-Z2_

(17-7)

The preceding statements follow from the rules for matrix multiplication. If we have the product srf@i = when a capital script letter denotes a matrix, or, for example,

0 n «12

#21 022

_ «31 032

*11 *12 *13 *14

*21 *22 *23 *24

C21 C22 C23 C24

CZ1 C32 ^33 C34

then the rule is

cn = Σ ^aik^bki. (17-8)

k

That is, the entry in row / and column / of the product matrix is the sum of the products of row i of matrix e^with column / of matrix ^ , with the restriction that the column number of a must match the row number of b. The idea of rows

" i n t o " columns may by illustrated more explicitly:

Cll = Σ 01 A l = 01 A l + 012*21 »

k

C2 1 = Σ ^fl2 A l = 021*11 + 022*21 j

k

^34 = Σ 03**fc4 = 031*14 + 032*24 >

A;

and so on. A requirement implicit in Eq. (17-8) is that in order to multiply two matrices, the number of columns of the left-hand one must equal the number of rows of the right-hand one.

Application of the multiplication rule to Eq. (17-7) yields

* 2 = = [cos(f TT)] X^X + [ - s i n( f TT)] y^x + 0z^x , y 2 = C21 = [sin(§7r)] xx + [cos(f TT)] yx + 0zx ,

z2 = 4ji = o * i + Qyi + 1*1 >

or Eq. (17-4) again.

17-4 REPRESENTATIONS OF GROUPS 733

To return to the C^{2 V} case, the matrices which transform the point (x^x, y^x, z^x) into a point (x², y², z²) are, for the various symmetry operations,

1 0 0" " - 1 0 0

0 1 0 0 - 1 0

0 0 1_ 0 0 1

σ^γ(χζ) o^w{yz) (or σ^ν' ) 1 0 0

0 - 1 0 0 0 1

- 1 0 0 0 1 0 0 0 1

(17-9)

These matrices will turn out to be representations of the C^{2 V} group. Referring to Table 17-4, C²o^v = σ^ν' and multiplication of the matrix for the σ^ν transformation by that for the C² one will yield the matrix for the σ^ν' transformation.

A further point is that the matrices of Eq. (17-9) can all be blocked into smaller matrices, outside of which the only entries are zeros. A check on the application of Eq. (17-8) will confirm that the products of such matrices are just the separate products of the blocked-out areas. In this case these are just matrices of dimension one. Where such blocking reduces a set of matrices to ones of lower dimension, then, necessarily, each of these last must be a representation of the group if the original matrices were. As a confirmation, representations A^x, B^l9 and B² of Table 17-5 correspond to the three blocked-out sets of Eq. (17-9).

The set of matrices for the transformations of a point in the C^{3 V} group are

Ε Ί 0 0"

0 1 0 0 0 1_

σν(χζ) 1 0 0"

0 - 1 0 0 0 1_

cos(§7r) — s i n( § 7 r ) s i n( | 7 r ) c o s( § 7 r )

0 0

—sin(iTr)

— COS($77) + s i n ( £ 7 r ) 0

0 0 1

COS(fTr)

sin(fTr)

0 0 1

(17-10)

- s i n ( ^ ) COS(£TT) 0

COS(&TT)

sin(iTr)

0 0 1

Remember that in C^{3 v} , σ^ν' is a plane rotated 120° from σ^ν(χζ) and σ^ν" is one rotated 240° from σ^ν(χζ). This set of matrices is a representation of the C^{3 V} group, that is, the matrices obey the group multiplication table. They may be blocked off into a 2 χ 2, or two-dimensional, set and a 1 X 1, or one-dimensional, set of matrices; each set is then also a representation of the group. The l x l matrices constitute the representation Γ^χ given in Table 17-3.

E: 2, C3¹: ( - 0 . 5 ) + ( - 0 . 5 ) = - 1 , C^{3 2} σ^ν(χζ): (1) + ( - 1 ) = 0, σ^ν'

σ^ν': ( - 0 . 5 ) + (0.5) = 0.

( - 0 . 5 ) + ( - 0 . 5 ) = - 1 ,

( - 0 . 5 ) + (0.5) = 0, (17-11)

An important point is that while the matrices for the symmetry operations within a given class may differ in detail, their traces are the same. Also, the matrix corre­

sponding to the identity operation must consist of just ones along the diagonal, so its trace must be equal to the dimension of the matrix.

It is customary to describe a representation of a group by giving just the traces of the matrices involved. Thus for C^{3 V}, the result is as shown in Table 17-6. The symbols A¹, A², and so on used to label the representations will be described later. In the case of a representation which is higher than one-dimensional, such as that for E, it is important to remember that matrices are involved. While the traces serve to characterize them, it is the actual matrices that must be multiplied in verifying that they obey the group multiplication table.

T A B L E 17-6. Representations for C^x

Ε 2 C³ 3 σ^ν

Ax 1 1 1

A² 1 1 - 1

Ε 2 - 1 0

β. The Trace of a Matrix

We have shown that while a set of simple numbers may constitute a representa­

tion of a group, one may also have a set of matrices. This last is the more general situation. In fact, an infinite number of matrix representations may be generated for a given symmetry group merely by taking more and more complicated func­

tions through the symmetry transformations. In the C^{2 V} group, for example, the molecule H²0 (or any A²B molecule) could be taken through the transformations by locating the oxygen atom at the origin and assigning x, y, and ζ coordinates to each hydrogen. The original six coordinates would then transform into six others upon application of a symmetry operation, thus producing a 6 χ 6 matrix.

The set of these would again be a representation of the C^{2 V} group. Such transforma­

tion matrices are always square ones, that is, they have the same number of rows as of columns.

It is unnecessarily cumbersome to write down complete matrices for a repre­

sentation since it turns out that the sum of the diagonal elements sufficiently characterizes a matrix for our purposes. This sum is called the trace χ of a matrix.

In the case of a 1 x 1 matrix χ is just the matrix itself, of course. For the set of 2 x 2 matrices of Eqs. (17-10) the traces are

17-4 REPRESENTATIONS OF GROUPS 735 C. Reducible and Irreducible Representations

The concept of a similarity transformation discussed in Section 17-3B may also be applied to square matrices. The reciprocal of a matrix 1, denoted by J^{- 1}, is defined by = δ, where δ is the identity matrix, that is, a matrix having ones on its diagonal and zeros elsewhere. The similarity transformation on a matrix si is then written

» = (17-12) A theorem which we will not prove is that the resultant matrix 88 must have the

same trace as does si (but may otherwise be different). A related consequence is that if the set of matrices si^x,si²,... constitute a representation of a group, so also will the set 9i^x, ,... .

The importance of the similarity transformation is that it is usually possible to find one which reduces some set si^x, s/²,... to a new set which has blocked-out sections and therefore decomposes into simpler matrices which are also representa­

tions. A representation which can be so simplified is termed reducible. There will remain, however, certain sets of matrices which cannot be simplified further by any possible similarity transformations. Such a set is then an irreducible representa­

tion, hereafter abbreviated IR, of the group. It is the irreducible representations of a group which are of fundamental importance. The set of traces which a representation has for the various symmetry operations is called the character of the representation. Also, the tabular listing of the characters of the IR's of a group is called a character table.

There are several important theorems concerning the irreducible representations of a group which we will state without derivation.

1. The sum of the squares of the dimensions / of the irreducible representations of a group is equal to the order h of the group. Thus

Z V = A- (17-13) For example, the representations A^l9 A², and Ε given by Table 17-6 for the C^{3 V}

group constitute the complete set of irreducible representations (and the display is just the character table for that group). The group is of order 6 (the total number of symmetry operations) and the dimension of each representation is given by the trace for the Ε symmetry operation. We see that l² + l² + 2² = 6, as required by Eq. (17-13). A corollary is evidently that the sum of the squares of the traces of the irreducible representations for the Ε operation also be equal to h, or

£ Xi\E) = h. (17-14) 2. The number of irreducible representations of a group is equal to the number

of classes in the group. The C^{3 V} group has three classes and just three irreducible representations.

3. The sum of the squares of the traces of any IR is equal to h. In applying this rule, we sum the squares of the traces over all the symmetry operations R:

£ x²(R) = h. (17-15)

R

Again referring to the C^{3 V} group, we have

A^x: l² + (2)(1²) + 3(1²) = 6, A²: l 2 + ( 2) ( l 2 ) + 3( - l )² = 6,

E: 2² + ( 2 ) ( - l )² + (3)(0) = 6.

4. It will be recalled that if a representation is reducible, there will be some similarity transformation that will convert it into a set of matrices having blocked- out areas. The ultimate case is one in which each set of blocked-out areas consti­

tutes an irreducible representation. In general, not all of the possible irreducible representations will appear, or a given one may show up in two or more sets of blocked-out areas. There is a very useful rule which determines the number of times, a^t, the ith IR occurs in a given reducible representation:

n R

The statement is that one sums over all symmetry operations the product of the trace of the IR and that of the reducible one in question. Using the C^{3 V} group as an example, Eqs. (17-10) provide an obviously reducible representation (the matrices being already, blocked out). The traces for the whole matrices are

Ε 2 C3 3<7V

3 0 1 Application of Eq. (17-16) gives

^ = *[(3)(1) + 2(0)(1) + 3(1)(1)] = 1, a A, = *[(3)(1) + 2(0)(1) + 3(1)(-1)] = 0,

aE = M(3)(2) + 2(0)(-l) + 3(1)(0)] = 1,

which confirms that the set of matrices (17-10) consists of the irreducible represen­

tations A¹ + E.

17-5 Atomic Orbitals as Bases for Representations

It was demonstrated in the preceding section that a general point (x^±, y^x, z^x) generates a representation of a symmetry group when carried through the various symmetry operations. The same is true of wave functions of an atom when all symmetry operations are about the nucleus. Since symmetry properties involve the angular rather than the radial aspect of an object, it is only necessary to consider the former portion of a wave function; we will further restrict ourselves to the hydrogen-like set of functions derived in Chapter 16.

An s function is angularly symmetric, and hence is unchanged by any symmetry operation. From Eq. (16-84), the A^v function is proportional to cos 0, which is just the projection of a vector on the ζ axis; Α^Ώ is proportional to sin θ cos φ [Eq. (16-85)] or to the χ projection of a vector, and A^p is proportional to the y projection [Eq. (16-86)]. If, for example, these vectors are put through the operations of the C^{2 V} group, we obtain

17-6 CHARACTER TABLES 737 or the transformation matrix

~ - l 0 0"

0 - 1 0 . 0 0 1 The operation σ^ν(χζ) leads to the matrix

"1 0 0"

0 - 1 0 . 0 0 1 The identity operation Ε leads, of course, to

Ί 0 0"

0 1 0 . 0 0 1 The set of matrices for the transformations

PaT

Pv

is thus blocked out into three one-dimensional matrices, and a check with Table 17-5 identifies the matrix for ρ*, to be the same as B^x, that for p^y as B², and that for p^z as A^x. We therefore say that p^x transforms as does the B^x irreducible represen­

tation, or forms a basis for it, p^y transforms as does B², and so on.

Similarly, each d wave function will transform as one or another irreducible representation of a group, or is said to form a basis for it. Thus d^X2 has the angular

nature of the product of the χ and ζ projections of a vector. Since the ζ projection is unchanged by any of the operations of the C^{2 V} group, d^xz transforms as does p*. , and thus is a basis for the B^x irreducible representation.

17-6 Character Tables

It is customary to assemble the basic information concerning each symmetry point group in what is called a character table. Several such tables are given in Table 17-7. Their organization is as follows. The first column designates each irreducible representation, the naming scheme being outlined shortly. The next group of columns lists the traces of each representation for each class of symmetry operation. The next to last column lists the types of vectors which form a basis for each representation. Thus for the C^{2 V} group, the row designated A^x shows that the ζ projection of a vector is appropriate, which means that the p^z wave function will form a basis for this representation. The last column lists products of vectors which are appropriate. The designation yz after the B² representation then means that d^yz orbitals will form a basis for the B² representation, and so on.

There are occasional entries R^x, R^y, or R^z in the next to last column. These refer to a circular vector whose plane is perpendicular to the named axis. Although such vectors will not be of direct interest to us, they also form a basis for a represen­

tation.