Nanopórusos rendszerek vizsgálata molekuláris szimulációkkal

Nanopórusos rendszerek vizsgálata molekuláris szimulációkkal

Doktori (PhD) értekezés

Készítette:

Rutkai Gábor

okleveles informatikus vegyész

Témavezető:

dr. Kristóf Tamás

Pannon Egyetem Kémiai Intézet

Fizikai Kémia Intézeti Tanszék

2010

Nanopórusos rendszerek vizsgálata molekuláris szimulációkkal

Értekezés doktori (PhD) fokozat elnyerése érdekében Írta:

Rutkai Gábor

Készült a Pannon Egyetem Kémiai és Környezettudományi Doktori Iskolája keretében

Témavezető: dr. Kristóf Tamás

Elfogadásra javaslom (igen / nem)

……….

(aláírás) A jelölt a doktori szigorlaton ...%-ot ért el,

Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: …... …... igen /nem

……….

(aláírás) Bíráló neve: …... …... igen /nem

……….

(aláírás) Bíráló neve: …... …... igen /nem

……….

(aláírás) A jelölt az értekezés nyilvános vitáján …...%-ot ért el.

Veszprém, ……….

a Bíráló Bizottság elnöke A doktori (PhD) oklevél minősítése…...

………

Az EDHT elnöke

Kivonat

Doktori munkám során egyensúlyi vagy stacionárius összetett rendszerek molekuláris szimulációs vizsgálatát végeztem saját fejlesztésű molekuláris szimulációs programcsomag segítségével. Elsősorban molekuláris fluidumok határfelületeken való megkötődését tanulmányoztam.

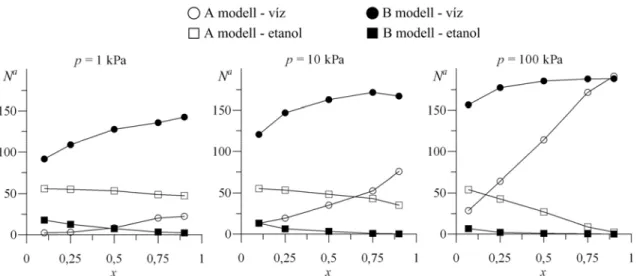
Az egyensúlyi számítások első részében metanol/víz és etanol/víz elegyek adszorpciós egyensúlyának meghatározását végeztem el NaA-4 zeoliton, elsősorban az általam kifejlesztett, adszorbensre vonatkozó potenciálmodell tesztelésének céljából. A számításokban egyensúlyi adszorbeált mennyiségeket és a komponensek izosztér adszorpciós hőjét határoztam meg nyomás, illetve elegyösszetétel függvényében. A vizsgált egyensúlyi rendszerek következő csoportját a réteges szerkezetű kaolinit agyagásványnak a dimetil-szulfoxid, formamid, karbamid valamint a kálium-acetát interkalációjával létrehozható stabil komplexei képezték. A számítások során az interkalációs komplexekre jellemző rétegtávolságok és betöltöttségek mellett az interkalált molekulák egyedi orientációját, valamint a molekulák összességének elhelyezkedését leíró eloszlásokat is meghatároztam.

Munkám további részében egy olyan eljárást dolgoztam ki, amellyel dinamikus Monte Carlo szimulációban a többkomponensű rendszerek komponenseinek relatív dinamikája helyesen leírható, majd az eljárást biológiai ioncsatorna stacionárius membrán- transzportjának molekuláris szintű szimulációjában teszteltem.

Abstract

A molecular simulation study was performed in, equilibrium and steady state, complex molecular systems by a Monte Carlo molecular simulation program package developed by ourselves. The properties of molecular fluids were determined primarily in confined systems.

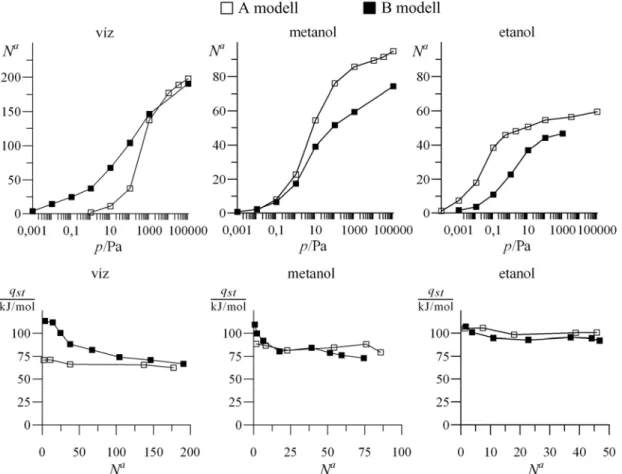
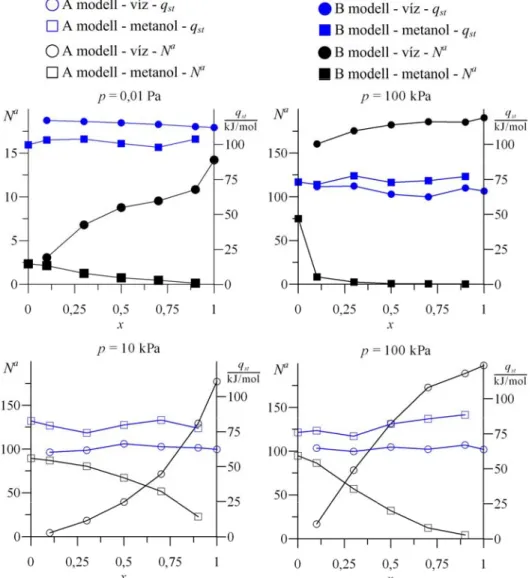
First, equilibrium adsorption properties of water/alcohol mixtures in zeolite NaA-4 have been determined to investigate the behaviour of our novel potential model for the zeolite.

The pressure and the mole fraction dependence of the adsorption properties such as equilibrium amount of adsorption and isosteric heat of adsorption were calculated.

As a further application, the intercalation of dimethyl sulphoxide, formamide, urea and potassium-acetate into kaolinite was examined with simulations. The key characteristics of the stable intercalation complexes, i.e. basal spacing and loading of kaolinite, were calculated and the arrangements of the intercalated molecules were described by density profiles and orientation distributions.

A new method was also proposed that allows the dynamic Monte Carlo to realize the correct time proportionality in many-component systems. The method was applied to simulate the steady state transport of a biological ion channel.

Abstrakte

Eine molekulare Simulationsuntersuchung von komplex molekularen Gleichgewichts- und Stationärsystemen wurde durch ein molekulares Monte-Carlo- Programm erforscht, die von mir selbst entwickelt wurde. Die Eigenschaften der molekularen Fluiden wurden in erster Linie in räumlich begrenzten Systemen festgestellt.

Zuerst wurde die Bestimmung des Adsorptionsgleichgewichts von Wasser/Alkohol- Gemischen an Zeolith NaA-4 durchgeführt, um in erster Reihe unseres neuen Potentialmodells für den Zeolith zu testen. In den Rechnungen wurden die Gleichgewichtsmenge und die isostere Adsorptionswärme der Komponenten in Abhängigkeit von dem Druck und dem Molbruch festgestellt. Im Weiteren wurde die Interkalation von Dimethylsulfoxid, Formamid, Harnstoff und Kaliumacetat in Kaolinit untersucht. Neben den auf die Schichtsabstände und Gleichgewichtsmenge der Interkalationskomplexe wurden auch die Orientierungsverteilungen und Dichteprofile der interkalierten Moleküle festgestellt.

Eine neue Methode wurde auch ausgearbeitet, mit der die relative Dynamik der Komponenten von mehrkomponenten Systemen in dynamischer Monte-Carlo-Simulation richtig beschrieben werden kann. Die Methode wurde in der Simulation des stationären Membrantransport vom biologischen Ionkanal getestet.

TARTALOMJEGYZÉK

BEVEZETÉS ... 9

1. MOLEKULÁRIS SZIMULÁCIÓK ... 10

1.1. Mérhető mennyiség meghatározása ...10

1.2. Kölcsönhatások modellezése és számítása ...10

1.2.1. Effektív párpotenciálok...10

1.2.2. Rövid- és hosszútávú kölcsönhatások...13

1.3. A Monte Carlo szimulációkban használt szokásos alapsokaságok ...19

1.3.1. A kémiai potenciál meghatározásának standard módszere...24

1.4. Speciális részecsketranszfer-technikák...25

1.4.1. Forgatással irányított beillesztés...26

1.4.2. Identitáscsere-eljárás...28

1.4.3. Energia szerint irányított identitáscsere-eljárás ...29

1.5. Megkötődés vizsgálata molekuláris szimulációkkal ...30

1.6. A DCV-GCMD technika ...32

1.7. A dinamikus Monte Carlo módszer ...34

1.7.1. Ellenőrzés és kalibráció elegyekre...37

1.7.2. Saját szerkezeti függvény ...37

2. A SZIMULÁCIÓS PROGRAM FUNKCIÓI... 39

3. ADSZORPCIÓ ZEOLITON ... 41

3.1. Alkalmazott potenciálmodellek ...42

3.2. Elvégzett számítások...45

3.3. Számított mennyiségek ...47

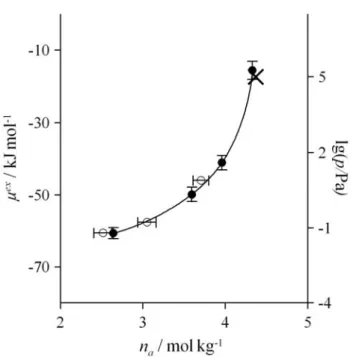
3.4. Eredmények...48

3.4.1. Tiszta anyagok ...48

3.4.2. Elegyek ...49

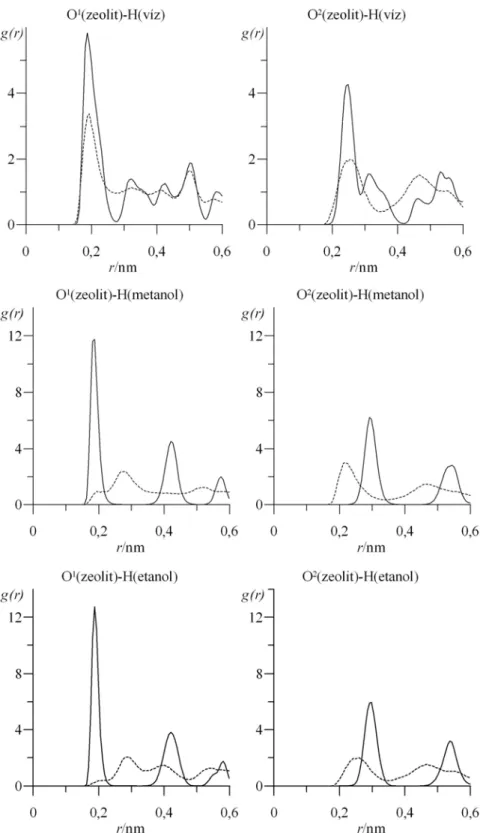
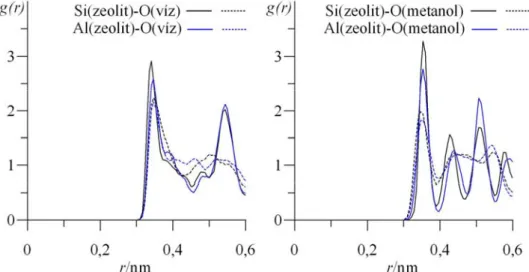
3.4.3. Szerkezeti vizsgálatok...52

3.4.4. Adszorpció vizsgálata NVT szimulációkkal ...56

4. INTERKALÁCIÓ KAOLINITBAN... 58

4.1. Alkalmazott potenciálmodellek ...59

4.2. Elvégzett számítások...61

4.3. Eredmények...62

4.3.1. µVT szimulációk ...62

4.3.2. µpT szimulációk...63

4.3.3. NpT szimulációk ...67

4.3.4. Szerkezeti vizsgálatok...75

4.3.5. A kaolinit rácshibáinak hatása ...84

5. DINAMIKUS MONTE CARLO TÖBBKOMPONENSŰ RENDSZEREKBEN... 86

5.1. A véletlenszerű bejáráson alapuló módszer ...86

5.1.1 Tesztrendszerek és elvégzett számítások...88

5.1.2. Eredmények ...93

5.2. Membrántranszport szimulációja dinamikus Monte Carlo módszerrel ...97

5.2.1. Az ioncsatornák ...97

5.2.2. Alkalmazott potenciálmodellek és elvégzett számítások...98

5.2.3. Eredmények ...100

ÖSSZEFOGLALÁS... 104

SUMMARY ... 109

FÜGGELÉK... 115

FELHASZNÁLT IRODALOM ... 117

BEVEZETÉS

A számítógépes modellezés rohamos fejlődése mára lehetővé tette egészen bonyolult rendszerek, összetett jelenségek hatékony molekuláris szintű szimulációs vizsgálatát. A molekuláris szimulációk célja, hogy egy részecskeszinten modellezett rendszer kívánt makroszkopikus jellemzőit meghatározzuk. A szimulációk egyaránt használhatók gáznemű és kondenzált fázisok viszonyainak atomi szintű modellezésére. A kondenzált fázisok vizsgálata legtöbbször egyet jelent az azokban előálló, ideális kristályokhoz viszonyított rendezetlenség tanulmányozásával, miközben a molekulák egymáshoz való közelsége szükségszerűen meghatároz egyfajta rendezettséget. Az az elméleti határeset, mikor az anyag mikroszkopikus alkotórészei a tökéletes rendnek megfelelően helyezkednek el, energetikai és geometriai megfontolások alapján meghatározható. A valós rendszerek azonban ettől a szerkezettől nagymértékben eltérhetnek. Az olyan rendszerek vizsgálatára, ahol a szerkezeti rendezetlenség már néhány molekulányi távolságban is megfigyelhető, kiválóan alkalmazhatók a számítógépes szimulációk. Molekuláris szimulációkkal gyorsan és - megfelelő intermolekuláris kölcsönhatási modellek birtokában - kellő pontossággal leírhatjuk fluidumok viselkedését olyan állapotokban is, ahol a termodinamikai illetve egyéb tulajdonságok nehezen hozzáférhetőek, vagy egyáltalán nem határozhatók meg kísérleti módszerek segítségével.

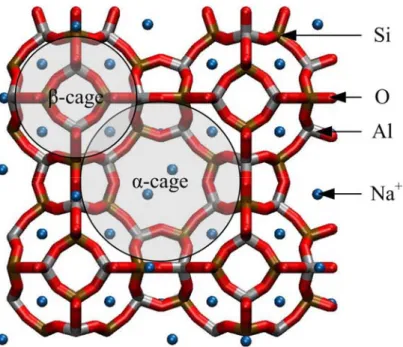
A molekuláris szimulációkról szóló bevezető után a disszertációban fejezetekre bontva ismertetem a különböző összetett molekuláris rendszerek szimulációjára vonatkozó eredményeimet. A szimulációk során nagyrészt különböző nanopórusos alumínium- szilikátok (NaA-4 zeolit és kaolinit agyagásvány) egyensúlyi adszorpciós tulajdonságainak meghatározását végeztem, továbbá biológiai ioncsatorna stacionárius membrántranszportjának dinamikus tulajdonságait vizsgáltam. Annak ellenére, hogy az értekezésben bemutatott számítások túlnyomó többségéhez egy általam fejlesztett szimulációs programcsomagot használtam, a disszertációban mégis elsősorban a kapott eredmények bemutatására koncentrálok, és a program fejlesztésének illetve funkcióinak leírására csak röviden térek ki.

1. MOLEKULÁRIS SZIMULÁCIÓK

1.1. Mérhető mennyiség meghatározása

A molekuláris szimulációk lényege, hogy - statisztikus mechanikai alapelvek alkalmazásával - a rendelkezésre álló mikroszkopikus információkból további mikroszkopikus információkat illetve makroszkopikus adatokat nyerjünk. Rendezetlen szerkezetű rendszerek viselkedésének számítógépes vizsgálatára alapvetően két szimulációs technika létezik: a sztochasztikus Monte Carlo (MC) [1] és a determinisztikus molekuláris dinamika módszere (MD). A molekuláris dinamika a rendszert alkotó részecskék mozgásegyenleteinek megoldásával időben követi a rendszer változásait. A Monte Carlo módszer egy kívánt tulajdonság meghatározásához véletlenszerűen járja be az adott sokaságnak megfelelő állapotokat, és így mintavételez az állapottérből. A mintavételezés a gyakorlatban azt jeleni, hogy a rendszert alkotó részecskék bizonyos szabályszerűségek alapján megvalósuló elrendeződéséből (amelyet a továbbiakban nevezzünk a rendszer egy konfigurációjának) meghatározzuk egy kiszámítandó tulajdonság aktuális értékét. Valamely tulajdonság a rendszert alkotó részecskéknek a rendszer konfigurációjától függő kölcsönhatásainak segítségével határozható meg. Egy adott termodinamikai állapotban megvalósítható konfigurációk, elrendeződések folyamatos generálásával és mintavételével számítható egy keresett tulajdonság átlagos értéke.

1.2. Kölcsönhatások modellezése és számítása 1.2.1. Effektív párpotenciálok

A molekuláris szimulációk abból indulnak ki, hogy modellezzük a rendszert alkotó részecskék kölcsönhatásait. A kölcsönhatások határozzák meg a szimulációban kialakult struktúrát, vagyis a részecskék elrendeződését, és ezáltal a számítandó mennyiség pontos értékét (ha az konfigurációs tulajdonság). A számítási idő jelentős részét a kölcsönhatások számítása teszi ki, ezért a szimulációs eljárások egyik kulcsfontosságú gyakorlati kérdése a

kölcsönhatások számítási idejének csökkentése. A kondenzált rendszerekre jellemzően két részecske kölcsönhatását befolyásolja a többi jelenléte. Ez ugyan első megközelítésben többtest-potenciálok alkalmazását követelné meg, azonban helyettük gyakran ún. effektív párpotenciálokat használunk, alkalmazva azt a közelítést, hogy a fázisban érvényes kölcsönhatásokat fel lehet bontani páronkénti járulékok összegére. A párpotenciál- függvények használatával jelentős számítási erőforrások takaríthatóak meg. A párpotenciál- függvények írják le két tetszőleges részecske kölcsönhatási energiáját a távolság függvényében. A számítások kezdetekor tehát alapvetően ismerni kell a vizsgálandó anyagra jellemző effektív párpotenciálokat.

A párpotenciálok egyik leggyakrabban használt formája a Lennard-Jones (LJ) párpotenciál:

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

−⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

= ⎛

6 12

4

ij

ij r

u_LJ ε rσ σ ^, (1)

ahol u jelöli a rendszer kölcsönhatási energiájának a két gömb alakú, i és j részecskére eső részét, r_ij jelenti ezen részecskék távolságát, σ és ε pedig a párpotenciál méret- és energiaparamétere. Ahhoz, hogy megkapjuk a rendszer U potenciális energiáját, összegeznünk kell minden egyes részecskének a többivel való kölcsönhatását, vagyis u-t minden lehetséges (i,j)-párra.

Pontosabb, vagy összetettebb számításokban, ahol a modellezett anyagok nemritkán többatomos molekulák, a molekulák minden egyes atomjához más-más LJ-kölcsönhatás tartozhat, és a részecskék kölcsönhatási modelljei további, pl. Coulomb-tagokat is tartalmazhatnak [1]. Molekuláris fluidumok esetén gyakran több kölcsönhatási centrummal - vagy idegen szóhasználattal „site”-tal - rendelkező (Lennard-Jones+Coulomb) típusú modelleket szoktak használni. Kölcsönhatási centrumnak tekinthető minden olyan egység (pl: atom vagy atomcsoport), amelyhez az alkalmazott potenciálmodell kölcsönhatási paramétert rendel. Ekkor a rendszer potenciális energiájának páronkénti járuléka i-edik és j- edik részecske között, ahol a és b a kölcsönhatási centrumok futó indexe:

∑∑

∑∑

⎠

⎞

⎜⎜

⎝ + ⎛

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

−⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

= ⎛

+

a b iajb

jb ia

a b ia jb

ab jb

ia ab

ab r

q q r

u r

, 0 6

, 12

, 4

4 1

πε σ

ε σ

Coulomb

LJ . (2)

Itt r_ia,jb jelöli az i-edik és j-edik részecske a-adik és b-edik kölcsönhatási centrumainak távolságát, ε₀ a vákuum permittivitása, és q_ia az i részecske a kölcsönhatási centrumának parciális töltése. Az ε_ab és σ_ab energia- és távolságparaméterek kiszámítására több

„keverési szabály” ismert. Ezek közül leggyakrabban a Lorentz–Berthelot-szabályt [1]

használják:

2

jb ia ab

σ

σ =σ ⁺ , (3)

illetve

jb ia

ab ε ε

ε = ⋅ , (4)

ahol ε_ia és σ_ia az i részecske a kölcsönhatási centrumának energia- ill. méretparamétere. A kölcsönhatási centrumokat általában atomi tömegközéppontokhoz rendelik. A rendszer teljes potenciális energiájának kiszámításához összegeznünk kell az összes molekula minden egyes kölcsönhatási centrumának a többi molekula minden egyes kölcsönhatási centrumával vett párenergiáját.

Az irodalomban a talán leggyakrabban alkalmazott LJ-potenciál mellett egyéb, pl.

pont-dipólus vagy pont-kvadrupólus kölcsönhatásokat leíró potenciálok is gyakran használatosak [1]. Az LJ-potenciál helyett sokszor az ún. Buckingham-féle modellt [2]

használják, ahol az LJ-potenciál taszító tagját exponenciális alakú összefüggéssel helyettesítik.

Ha a rendszert alkotó molekulákat több kölcsönhatási centrumból felépülő modellek reprezentálják, akkor a molekula belső struktúrájának lehetséges megváltozásaiból, tehát az atomok vagy atomcsoportok molekulán belüli átrendeződéséből eredő energiajárulékokat is figyelembe kell venni a potenciális energia számításánál. A különböző atomi szintű modellekben a molekulán belüli kölcsönhatási centrumok helyzete által meghatározott kötéstávolságok, kötésszögek valamint torziós szögek meghatározott módon változhatnak a szimuláció során, megváltoztatva ezáltal a molekulapárok aktuális kölcsönhatási energiáját is [1, 2].

A potenciálmodellek finomításának további lehetősége a molekulák polarizálhatóságának figyelembevétele [3]. E jelenség modellezésére az irodalomban elterjedten használják azt a módszert, amely a molekulákon a többi molekula által keltett lokális térerősség hatására

indukálódott pont-dipólusok számításán alapul [4]. A módszer lényege, hogy a rendszer potenciális energiájának a molekulák polarizációjából származó járuléka meghatározható a molekulákon indukált dipólusmomentumok és a molekulák polarizációs centrumában keltett lokális elektromos térerősségek ismeretében. Mivel egy tetszőleges molekula polarizációs centrumában a többi molekula által keltett lokális elektromos térerősséget a többi molekula ponttöltései és az ezeken a molekulákon indukálódott pont-dipólusok együttesen határozzák meg, ezért az adott molekulán indukálódott dipólusmomentum kiszámításához ismerni kell az összes többi molekulán indukálódott dipólusmomentum értékét is. A molekulák polarizációjából származó energia tehát nem határozható meg egy lépésben a párkölcsönhatások összegzésével. Ennek az energiajáruléknak az értékét a szimulációkban iterációs megoldások segítségével számítják.

1.2.2. Rövid- és hosszútávú kölcsönhatások

Általában egy molekuláris szimulációs eljárás felépítésének első lépése egy V szimulációs térfogat kijelölése, melyben N darab részecske foglal helyet. A szimulációs doboz leggyakrabban egy L élhosszúságú kocka. A jelenlegi számítástechnikai kapacitások mellett a szimulációkban alkalmazható részecskeszám és dobozméret erősen korlátozott, ezért a felületi effektusok nagyban befolyásolhatnák a számított tulajdonságokat (például még néhányszor 10000 részecskét tartalmazó szimulációs dobozban is a részecskéknek hozzávetőleg egytizede a rendszer felületén van, míg 1 mol részecske esetén ez az arány kb.

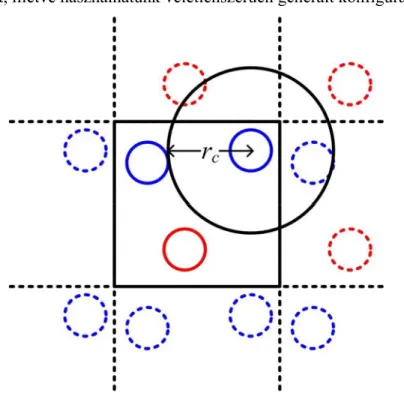
10^-5 %). Ennek elkerülése érdekében ún. periodikus határfeltételeket (1. ábra) alkalmazunk [1]. A rendszert ilyenkor úgy kezeljük, mintha az aktuális szimulációs dobozunk a tér minden irányából önmaga képmásaival lenne körülvéve. A szimuláció során a képmás dobozokban lévő részecskék az eredeti dobozban lévő részecskékkel megegyező mozgást végeznek. Ennek megfelelően, ha az egyik részecske kilép a központi doboz egyik oldalán, akkor az azonnal meg fog jelenni a doboz átellenes oldalán. Ez a megközelítés ugyan némi transzlációs periodicitást visz a rendszerbe, de nagyobb részecskeszám mellett ez a hatás már elhanyagolható. Ha a rendszerünk kristályos, akkor a központi doboz felépíthető akár egyetlen elemi cellából, amelyet a kristály szimmetriájának megfelelően önmaga képmásaival veszünk körül. Folyadékoknál a központi dobozt alkotó részecskék kiindulási

konfigurációját megadhatjuk például a részecskék valamilyen szabályos rácsszerű elrendeződéseként, illetve használhatunk véletlenszerűen generált konfigurációt is.

1. ábra A periodikus határfeltételek alkalmazása.

A kölcsönhatások számítása általában a szimulációs algoritmusok leghosszabb részét képzi. A számítási idő csökkentésének érdekében a kölcsönhatások számítását fel szokás bontani rövid és hosszú távú részre. A rövid távú kölcsönhatásokat a „minimum image”-nek nevezett konvenció alapján számítjuk ki [1]. A konvenció lényege, hogy egy adott részecskének a többivel való kölcsönhatása számításakor a részecskét a térben végtelen rendszer egy cellája középpontjának tekintjük, és az így definiált cellában található részecskékkel való párkölcsönhatásokat számítjuk. A rövid távú kölcsönhatások számításánál gyakran csak azokat a részecskéket vesszük figyelembe, amelyek a középpontinak választott részecskétől bizonyos távolságon belül helyezkednek el (1. ábra).

Ezt a távolságot szokás levágási hossznak („cut-off”) nevezni, és általában r_c-vel jelöljük (r_c nagysága nem haladja meg a cella legrövidebb élhosszának felét). Egyszerű LJ- párpotenciál esetén a rövid távú kölcsönhatást a (1) kifejezéssel számítjuk. A többi részecske hatását ún. hosszú távú korrekcióval vesszük figyelembe, amelynek számítási

módja az aktuális párpotenciál függvényében változik [1, 5]. A hosszú távú korrekció LJ- párpotenciálra az alábbi képlettel adható meg [1]:

6 3 12 9

2 ( ) (8/9) (8/3)

2 ^{− −}

∞

⋅

−

⋅

=

=

∫

r

r N r

N dr

r u r N U

c

ρσ π ρσ

π ρ

π _LJ

LRC

LJ . (5)

A képletben ρ jelöli a rendszer részecskeszám-sűrűségét, amely a szimulációs doboz részecskeszámának és térfogatának hányadosa.

A Coulomb-kölcsönhatások hosszútávú kölcsönhatásának számítását legtöbbször a reakciótér-korrekció módszerével (RF) [1, 6, 7], illetve az ún. Ewald-összegzésnek [8]

megfelelően szokás elvégezni. Megválasztásuk annak figyelembevételével történik, hogy rendszerünkben neutrális vagy eredő töltéssel rendelkező részecskék vannak-e, és a rendszert külső elektromos térben vagy nélküle vizsgáljuk-e. A reakciótér-korrekció során a rendszernek egy adott részecskétől rc-nél nagyobb távolságra eső részét εRF permittivitású dielektromos kontinuumnak tekintjük. A Coulomb-kölcsönhatást a módszerrel a következőképpen számíthatjuk:

∑∑

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟⎟⎠

⎜⎜ ⎞

⎝ +⎛ + + −

=

a b c

jb ia jb

ia jb ia

r r r

q u q

3 , ,

0 2 1

1 1 4

1

RF RF RF

Coulomb ε

ε

πε ^{. (6)}

A kölcsönhatási energia kiszámításához szükség van εRF értékének ismeretére. Gyakran az εRF = ∞, azaz a vezető határfeltételnek megfelelő közelítést alkalmazzuk (tehát a levágási hosszon kívül eső környezetet tökéletes elektromos vezetőnek tekintjük), és így a számításokban az (ε_RF −1)/(2ε_RF +1)faktort 1/2-del helyettesíthetjük.

A kölcsönhatások számításához használt módszerek szempontjából nem mellékes a szimulációs dobozt felépítő olyan részecskék mérete, melyek több kölcsönhatási centrumból épülnek fel. Ugyanis a rövid és hosszú távú kölcsönhatások számításakor valamilyen elv alapján meg kell határozni, hogy a minimum image eljárás részeként középpontinak választott részecskéhez képest a többi részecske a levágási hosszon belül vagy kívül esik. Egyszerűbb esetben, amikor kisméretű több kölcsönhatási centrummal rendelkező molekulák alkotják a vizsgált rendszert, célszerű okokból két molekula tömegközéppontjának térbeli távolsága dönti el, hogy egymáshoz képest a két molekula a levágási hosszon belül helyezkedik-e el vagy sem. Makromolekulák illetve kristályos anyagok szimulációjakor ennek az elvnek a használhatósága már erősen korlátozott.

Amikor például két nagyméretű molekula tömegközéppontjának távolsága nagyobb, mint a levágási hossz, de kölcsönhatási centrumaiknak jelentős része levágási hosszon belül helyezkedik el egymáshoz képest, kézenfekvő megoldást nyújthat egy olyan módszer használata, amely a kölcsönhatások számításakor lehetővé teszi a molekulák kölcsönhatási centrumok szerinti szétválasztását. Ennek értelmében szükség van arra, hogy az adott molekula egy részét a rövid távú kölcsönhatásoknál vegyük figyelembe, másik részét pedig a hosszú távú kölcsönhatásoknál, oly módon, hogy két kölcsönható molekula levágási hosszra vonatkozó vizsgálatát kölcsönhatási centrumonként végezzük. Ilyen makromolekulás rendszerekre használható a reakciótér-korrekció módszerének erre az elvre átdolgozott változata, az ún. „site-site” reakciótér-korrekció módszere [9, 10]. A módszer használatához át kell dolgozni a szimulációs eljárásnak a levágási hosszt kezelő funkcióját, lehetővé téve a kölcsönhatási centrumok távolságainak molekulánként egyedileg történő összehasonlítását rc-vel, és módosítani kell a részecskék Coulomb-kölcsönhatására vonatkozó (6)-es képletet a következő korrigáló tényező levonásával:

∑ ∑

r q q

2

3 . (7)

A hosszú hatótávolságú Coulomb-kölcsönhatás számításához használt Ewald- összegzés [8] megvalósításakor a rendszerünket egy végtelen sugarú gömb középpontjába helyezzük el, és a gömböt a rendszernek a három térirányban periodikusan ismétlődő másolataival töltjük fel. A rendszer teljes Coulomb-energiájába a központi cella töltéseinek kölcsönhatása mellett a központi cella töltéseinek a másolatok töltéseivel vett kölcsönhatásait is beleszámítjuk. A rendszer teljes Coulomb-energiája a következő képlettel adható meg:

⎟⎟

⎠

⎞

⎜⎜

⎝

=

∑ ∑ ∑ ∑

=

= +

=

−

= iajb

jb j ia

n

b i n

a N

i j N

i r

q U q

, ) (

1 ) (

1 1 1

0 1

4 1 πε

Coulomb , (8)

ahol n(i) az i-edik molekula kölcsönhatási centrumainak a száma. A kifejezés a számítás szempontjából egy kedvezőbb alakra hozható, felbontva az 1/r_ia,jb kifejezést. erfc és erf függvények bevezetése mellett

⎟×

⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

∑ ∑ ∑ ∑ ∑

=

=

= +

=

−

= r_iajb n L

jb j ia

n

b i n

a N

i j N

i

q U q

0 , ) (

1 ) (

1 1 1

0 1

4 1

n

Coulomb πε

( ) ( )

[

]

× erfcα_{E ia,jb} erf α_{E ia,jb} , (9)

ahol az n vektor adja az L élhosszúságú doboz három térirányban vett másolatait, )

, , (L_x L_y L_z

L= L , és αE a módszer konvergenciaparamétere, továbbá r_ia,jb = r_ia,jb . Az erfc és erf függvények a következő alakban írhatók fel:

( )

( )

erf

r E

∫

=

α

α π

0

2 2

/

1 exp

2 , (10)

(

)

(

)

erfcα_E =1− α_E . (11)

A (9)-es összefüggés az erf függvény további átalakításaival a következő három tag összegeként adható meg, ha az eredeti vákuum-határfeltétel helyett vezető határfeltételt alkalmazunk, azaz a rendszert körülvevő környezetet tökéletes elektromos szigetelő helyett tökéletes elektromos vezetőnek tekintjük:

( )

⎟+

⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅ +

⋅

=

∑ ∑ ∑ ∑ ∑

=

=

= +

=

−

= r n L

L n r

jb ia

jb ia E jb

j ia n

b i n

a N

i j N

i

erfc q U q

, , 0

) (

1 ) (

1 1 1

0 1

4

1 α

πε n

Ewald Coulomb

( )

⎪⎭

⎪⎬

⎫

⎪⎩

⎪⎨

⎧ ⋅ + ⋅

+

∑

∑∑ ∑∑

= =

= =

∞

≠

2

1 ) (

1 2

1 ) (

1

0 2

2 2

0

) sin(

) 4 cos(

/ exp 4

1

2 ^N

i i n

a

ia ia

N

i i n

a

ia

ia q

k q k

V k r k r

k

α πε

π

( )

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝ + ⎛

−

∑∑ ∑ ∑ ∑

=

−

= = +

= = iab

b ia N E

i i n

a i n

a b

ib ia N

i i n

a ia E

r r q erf

q q

, , 1

1 ) (

1 ) (

1 1

) (

1 2 2

/ 1

4 0

1 α

π α

πε ^{. (12)}

A képletben r_ia vektor jelöli az i-edik molekula a-adik kölcsönhatási centrumainak helykoordinátáit, k = k, ahol k=2πn/L a reciproktér-vektor, n∈Z³(Z az egész számok halmaza). A második tag szükségszerűen tartalmazza a töltések önmagukkal vett kölcsönhatását. A harmadik tag ezt a többletkölcsönhatást korrigálja, levonva ezzel a töltések önmagukkal illetve egymással számított Coulomb-kölcsönhatását. Az irodalomban a hagyományos Ewald-eljárás mellett annak különböző változatai is gyakran használatosak.

Ilyenek pl. az ún. „particle-mesh” módszerek (P³M [11] és PME [12, 13]), melyek leírására itt nem térek ki.

A Coulomb-energia számítására léteznek más módszerek is, ezek közül a Wolf- eljárás [14] nagyban hasonlít az Ewald-eljárásra, azonban lényegesen kevesebb számítást igényel. Az eljárás lényege, hogy a hosszú hatótávolságú Coulomb-potenciál egy aránylag

határolt gömbtérfogaton belül történő töltéskiegyenlítés segítségével. A töltéssemlegesítés érdekében - amely matematikai értelemben valójában egy eltolás - módosítani kell a (12)- es kifejezés harmadik tagjának alakját. A módszer szerint a (12)-es kifejezés második tagja ekkor elhanyagolható, továbbá az első tag esetén - az Ewald-összegzés elterjedt gyakorlati alkalmazásaihoz hasonlóan - csak a központi dobozban összegzünk (nL elhagyható a képletből). A Wolf-eljárással a rendszer teljes Coulomb-energiáját a következő összefüggéssel számíthatjuk:

( ) ( )

⎜ −

⎜

⎝

⎛

⎟⎟

⎠

⎞

⎪⎭

⎪⎬

⎫

⎪⎩

⎪⎨

− ⎧

≈

<

= →

= +

=

−

=

∑ ∑ ∑

∑

c jb ia c

jb ia

r jb r

ia

jb ia w jb

ia r jb r

ia

jb ia w jb

j ia n

b i n

a N

i j N

i r

r erfc q q r

r erfc q U q

,

, ,

, ,

) , (

1 ) (

1 1 1

0 1

4 lim

1 α α

πε

Wolf Coulomb

( )

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ ⎟⎟⎠

⎜⎜ ⎞

⎝

⎛ +

−

∑∑

= = N

i i n

a ia c

c w

w q

r r erfc

1 ) (

1 2 2

/ 1

0 2

4

1 α

π α πε

( ) ( )

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛ +

−

∑ ∑ ∑

=

−

= = + c

c w b

ia b ia N w

i i n

a i n

a b

ib

ia r

r erfc r

r q erf

q 2

4 1

, , 1

1 ) (

1 ) (

0 1

α α

πε ^{. (13)}

(A képlet első tagjának második része hivatott biztosítani a központi tartomány - az r_c sugarú gömb - töltéssemlegesítését a rendszerben.)

Az irodalomban mára több munka jelent meg annak igazolására, hogy bizonyos feltételek teljesülése mellett a Wolf-eljárás az Ewald-összegzéssel azonos eredményt ad több kölcsönhatási centrummal rendelkező, neutrális molekulákból álló fluidumok és ionos rendszerek esetén is [15-¹⁶17]. A megfelelő egyezés érdekében a vizsgálatok szerint garantálni kell a Wolf-eljárásnál, hogy a levágási hossz ötször-tízszer nagyobb legyen, mint két szomszédos molekula legközelebbi ellentétes töltésű kölcsönhatási centrumai között mérhető legnagyobb távolság [15]. Megmutatták, hogy a legtöbb vizsgált rendszerben Wolf-összegzéssel a legjobb eredmények akkor érhetők el, ha a levágási hosszt a szimuláció minimális cellahossza felének (r_c = L_min/2), a konvergenciaparamétert pedig αw= 2/rc értékűnek választjuk [15].

1.3. A Monte Carlo szimulációkban használt szokásos alapsokaságok

A Monte Carlo módszer alapelgondolása a statisztikus mechanikai várható érték számítására a következő [1]: legyen A = A(ξ) a rendszer valamilyen mérhető fizikai mennyisége, és ξ jelölje a rendszer mikroállapotát. Ekkor az A mennyiség várható értékét folytonos mikroállapot-eloszlás esetén az

ξ ξ Γ

ξ d

N A

A ( ) ( )

! 1

∫

= (14)

kifejezés határozza meg, ahol Γ(ξ) az adott sokaság valószínűségi sűrűségfüggvénye a mikroállapotok felett (N!-sal a részecskék megkülönböztethetetlensége miatt kell osztani).

Az A mennyiség átlagát a szimuláció során tehát úgy kaphatjuk meg, hogy minden létrejött konfigurációhoz kiszámítjuk A értékét, majd az átlag képzésénél súlyozzuk ezt a konfiguráció valószínűségével. A meghatározandó mennyiség átlagának kiszámításához használt Γ(ξ) valószínűségi sűrűségfüggvény alakja annak függvényében változik, hogy a rendszert milyen termodinamikai sokaságon kívánjuk modellezni. Az MC szimulációk során legtöbbször használt sokaság a kanonikus vagy NVT sokaság [1, 5]. Itt állandó N részecskeszám mellett állandó a V térfogat és a T hőmérséklet. Ekkor, ha a meghatározni kívánt A mennyiség csak a részecskék helykoordinátáitól függő, ún. konfigurációs tulajdonság, akkor a Γ(ξ)=Γ(r^N) függvény a következő alakban írható fel [1, 5]:

( )

NVT B N N

N

NVT Z

T k U

V exp(− (r )/( ))

=

Γ r . (15)

Az egyenletben ZNVT a kanonikus sokaság konfigurációs állapotösszege, r^N = (r1, r2, ….. , rN) az adott N darab részecske térbeli pozícióit jelöli, kB pedig a Boltzmann állandó. A konfigurációs állapotösszeg a kanonikus sokaságra [1, 5]:

N B

N N

NVT V U k T d

Z ⁼ N¹_! ^⋅

∫

A (14), (15) és (16)-os kifejezésekből egyszerűsítések után kapjuk az A mennyiség várható értékét kanonikus sokaságon:

N B

N

N B

N N

d T k U

d T k U

A A

r r

r r

r

)) /(

) ( exp(

)) /(

) ( exp(

) (

∫

∫

−

= − (17)

Az integrálást szummázással helyettesítve az átlagértéket numerikus eljárással becsüljük:

∑

∑

=

=

−

−

= _k

i

B N k

i

B N N

i

T k U

T k U

A A

1 1

)) /(

) ( exp(

)) /(

) ( exp(

) (

r r r

, (18)

ahol az i index a konfigurációs tér i-edik vizsgált pontjára utal, k pedig a mintapontok száma. A számításhoz az egész konfigurációs térből kell egyenletes eloszlásban mintát venni, és ezeket az exp(-U/(k_BT)) Boltzman-faktorral súlyozva figyelembe venni. Ennek a feladatnak a megoldása még ma is túlmutat a számítástechnikai lehetőségek határain. A probléma a Metropolis és munkatársai által javasolt módszerrel [18, 19] azonban áthidalható. A megoldás alapja, az hogy Γ(r^N) értéke exponenciálisan csökken a növekvő U(r^N)-nel, tehát a szummákhoz csak a „néhány” legkisebb energiájú állapot ad érdemi hozzájárulást. Ezért ha a mintát nem-egyenletes eloszlás szerint vesszük, és a konfigurációs térnek a szummákhoz nagyobb hozzájárulást adó tagjai jóval gyakrabban kerülnek a mintába, mint a kis járulékot adó tagok, akkor a számítási idő jelentősen csökkenthető. Az átlagolásban természetesen a konfigurációk kiválasztásán alapuló súlyozást kompenzálni kell:

∑

∑

=

=

−

−

= _k

i N

i

B N k

i N

i

B N N

i

W

T k U

W

T k A U

A

1 1

) (

)) /(

) ( exp(

) (

)) /(

) ( )exp(

(

r r

r r r

, (19)

ahol W_i(r^N) a mintavétel során alkalmazott súlyozás. Legyen a W_i(r^N) súlyozó tényező arányos a Boltzman-eloszlással, azaz

NVT B

N

i U k T Z

W ∝exp(− (r )/( ))/ , (20)

ekkor a (19)-es összefüggés jelentősen leegyszerűsödik:

k A A

k

i

N

∑

= =¹

) (r

. (21)

Tehát ahelyett, hogy egyenletes valószínűséggel vennénk mintát a konfigurációs térben, majd a Boltzmann-eloszlás szerinti súlyozással átlagolnánk azokat, a Boltzmann-eloszlás szerinti valószínűséggel választjuk ki a konfigurációkat és az átlagolásnál egyforma súllyal vesszük őket figyelembe.

A mikroállapotoknak a hozzájuk tartozó W_i eloszlások szerinti generálását a Metropolis- féle Monte Carlo módszer a következő módon valósítja meg [18, 19]. A mintához tartozó ξ1

,ξ2, …, ξi,… mikorállapotokat egy Markov-lánc tagjaiként értelmezzük. Markov-láncról akkor beszélhetünk, ha a rendszernek nincs „memóriája”, vagyis a rendszer pillanatnyi állapotának ismerete elegendő a következő állapot meghatározásához. A lánc egy tetszőleges i állapotához először П_ij valószínűséggel sorsoljunk egy j állapotot, majd j-t P_ij valószínűséggel fogadjuk el a lánc következő tagjának. Ekkor az i állapot után a j állapot Ψij = PijПij valószínűséggel fog következni. Megköveteljük, hogy

=1

∑

Πij és i

j

ij = ∀

∑

továbbá

W Ψ = W , azaz W W_i i

j ij

jΨ = ∀

∑

Matematikai értelemben véve a (23)-as kifejezés azt jelenti, hogy a Ψ mátrix sajátvektora a W határeloszlás, és a Ψ mátrix sajátértéke egységnyi. Az ismert W határeloszláshoz olyan Ψ átmeneti mátrixot kell találni, amely a fenti feltételeket kielégíti, és elemei függetlenek az állapotösszegtől. Ezt például a következő konstrukció elégíti ki:

ji j ij

i W

WΨ = Ψ . (24)

A fenti egyenletet a mikroszkopikus reverzibilitás elvének nevezik, amelynek lényege röviden az, hogy a szimulációban az i állapotból a j-be jutás valószínűsége ugyanakkora, mint a j állapotból az i-be jutás valószínűsége.

Ha a П mátrix szimmetrikus (П_ij = П_ji) , akkor a fenti egyenletet átalakítva kapjuk, hogy:

i j ji ij ji ji

ij ij ji ij

W W P P P

P = =

=Π Π Ψ

Ψ . (25)

Metropolis és munkatársai a következő megoldást adták a fenti problémára [18, 19]:

(

)

min W W o n

P_on = _{n o} ∀ mikroállapot-párra, (26)

ahol n mindig az új és o pedig a megelőző mikroállapotot jelöli. Tehát az új konfiguráció elfogadására vonatkozó valószínűséget kanonikus sokaságon úgy kapjuk, hogy a (20)-as kifejezést a (26)-os összefüggésbe helyettesítjük:

[ ]

{

}

{

[ (

) ] }

min U U k T U k T

P_ij^NVT = − _j− _{i B} = ∆ − _B . (27)

Ez azt jelenti, hogy az új konfigurációt elfogadjuk, ha az előzőhöz képest a rendszer potenciális energiája csökkent, és exp(–∆U/(kBT)) valószínűséggel fogadjuk el, ha nőtt. Az utóbbi esetben a gyakorlatban úgy járunk el, hogy az exp(–∆U/(kBT)) faktort egy 0 és 1 közé eső egyenletes eloszlású véletlenszámmal hasonlítjuk össze, és az új állapotot akkor fogadjuk el, ha e két érték közül a véletlenszám a kisebb.

A П_ij elemek meghatározása és az új konfiguráció kijelölése az ún. „szimulációs lépés”

(MCS) végrehajtásával történik [18, 19]. Hagyományos NVT MC szimulációban a П mátrix az i állapot adott kis környezetében lévő j állapotokra egyenletes eloszlásnak megfelelően konstans, azon kívül nulla. Ez a gyakorlatban azt jelenti, hogy egyetlen szimulációs lépésben egy adott részecske elmozdításának nagyságát egy r_max szimulációs paraméter határozza meg, ahol r_max annak a kockának az oldalhossza, amelyen belül az aktuálisan kiválasztott részecskét egyenletes eloszlás szerint véletlenszerűen elmozgatjuk. Több kölcsönhatási centrummal rendelkező részecskék esetén még egy véletlen térszöggel való elforgatás is része az eljárásnak (flexibilis molekulamodellek esetén pedig további, belső mozgásokat megvalósító lépések is szükségesek). E lépések általában a molekula tömegközéppontjának pozícióját nem befolyásolják, bár a gyakorlatban a részecskék forgatását gyakran a transzlációs lépéssel együtt hajtják végre. Rotációs mozgatás során a szimulációs doboz valamely élével párhuzamos tengely körül egy adott [-αmax, αmax] intervallumon belül egyenletes eloszlásnak megfelelően sorsolt véletlen szöggel történik az elforgatás. Mivel a részecskék elmozdítását és elforgatását egyenletes valószínűséggel hajtjuk végre, és a részecskéket egyenletes valószínűséggel választjuk ki, az i állapot adott kis környezetében lévő j állapotot ugyanolyan valószínűséggel sorsoljuk ki, mint a j állapot adott kis környezetében lévő i állapotot. Ekkor Пij = Пji azaz a П mátrix valóban szimmetrikus (ld. a (25)-ös egyenlet feltétele). A gyakorlatban tehát az elfogadási kritériumban (27) nem jelenik meg, hogy az új állapotot milyen valószínűséggel sorsoljuk ki.

A mikroszkopikus reverzibilitás elvének egyik fontos következménye az, hogy bármelyik mikroállapotból bármelyik mikroállapotba el lehet jutni véges sok mozdítással.

Ezért a számítás kiindulási konfigurációja elvben nem befolyásolja a végeredményt. A központi dobozt alkotó részecskék kiindulási konfigurációját megadhatjuk például a részecskék valamilyen szabályos rácsszerű elrendeződéseként, illetve használhatunk

véletlenszerűen generált konfigurációt is. A szimuláció elején a rendszer energiája gyakorlatilag minden lépésben csökken (ez az „egyensúlyba hozó” szakasz), majd elegendő számú mozgatás után adott érték körül fluktuálni kezd. Ez jelenti azt, hogy a rendszer egyensúlyi állapotba jutott, vagyis ezután kezdhető meg a végső eredmény szempontjából reprezentatív mintavételezés.

Hasonló gondolatmenettel kapható meg a gyakran használt NpT (izoterm-izobár) sokaság elfogadási kritériuma a rávonatkozó ΓNpT és ZNpT ismeretében [1, 5]. Itt az algoritmus része - a részecskeelmozdítás mellett - egy olyan eljárás, amely bizonyos határokon belül véletlenszerűen változtatja a rendszer térfogatát, hogy a rendszerben egy adott p nyomás valósuljon meg. A térfogatváltoztatás célszerűen úgy történik, hogy a részecskék abszolút koordinátáit relatív koordinátákkal helyettesítjük, normálva őket a kocka alakú doboz élhosszával (tehát a rendszer térfogatának változtatása során a részecskék abszolút koordinátái is változnak). Az NpT sokaság esetében az elfogadási kritérium a következő összefüggéssel adható meg [1, 5]:

( )

[ ]

{

}

P^NpT =min1,exp∆ − ( + )/( _B )+ ln . (28)

Belátható, hogy a részecskeelmozgatási lépésnél ez a valószínűség a kanonikus MC szimuláció lépéseinek elfogadási kritériumára egyszerűsödik (ld. (27)).

A harmadik izoterm sokaság, a nagykanonikus (µVT) [1, 5] sokaság esetében állandó térfogatú rendszerben a részecskeszám változik olyan módon, hogy állandó µ kémiai potenciál mellett történjen a szimuláció. A részecskeszám megváltozása részecskék eltávolítása és beillesztése által valósul meg. A szimulációban bizonyos időközönként véletlenszerűen kiválasztott részecskét kísérlünk meg a rendszerből eltávolítani.

Hasonlóképpen, időközönként megpróbálunk egy-egy további részecskét a rendszerbe beilleszteni úgy, hogy véletlenszerűen generálunk a beillesztésre szánt részecskének térbeli pozíciót a szimulációs dobozban. Az eltávolítási/beillesztési lépésekhez szabályos elfogadási kritérium tartozik. A µVT sokaság esetében az elfogadási kritérium a következő összefüggéssel adható meg [1, 5]:

( )

[ ]

{

}

min U k T N V N

P^µVT = ∆− _B + ϑ − . (29)

A fenti képletben ϑ =exp(µ^~/k_BT), ahol µ^~ az állandó hőmérsékleten vett konfigurációs kémiai potenciál, amelyet a teljes kémiai potenciál alábbi felbontása definiál:

µo

µ µ µ

µ= ^ex+ ^id = ^~+ , (30)

ahol µ^id =k_BTlnN −k_BTlnZ_m és µ^~ =µ^ex +k_BTlnN −k_BTlnV . A Zm molekuláris állapotösszeg [1] a de Broglie-hullámhosszt tartalmazó transzlációs állapotösszeg mellett egyéb, a molekulák forgásából és belső mozgásaiból származó ideális járulékokat is tartalmazhat. A szimulációhoz tehát alapvetően az ún. excess kémiai potenciál (µ^ex) ismerete szükséges, amely az állapotösszeg kölcsönhatási járulékából adódik.

A gyakorlatban a részecskék számát egy lépésben szokás megváltoztatni. Ekkor a részecskék beillesztésére vonatkozó elfogadási kritérium a

⎭⎬

⎫

⎩⎨

⎧ ⎥⎦⎤

⎢⎣⎡

+ +

−

+ =

ln 1 ) /(

exp , 1

1 min N

T V k U

P_N^µVT ∆ _B ϑ (31)

összefüggéssel, a részecskék eltávolítására vonatkozó kritérium pedig a

⎭⎬

⎫

⎩⎨

⎧ ⎥⎦⎤

⎢⎣⎡− +

− =

V T N

k U

P_N^VT _B

∆ ϑ

µ₁ min 1,exp /( ) ln (32)

összefüggéssel adható meg [1, 5].

Nagykanonikus sokaságon végzett részecskeelmozdítási szimulációs lépés esetén a (29)-es összefüggés szintén a kanonikus MC szimuláció lépéseinek elfogadási kritériumára egyszerűsödik (ld. (27)).

1.3.1. A kémiai potenciál meghatározásának standard módszere

A Widom-féle tesztrészecske-beillesztési módszerrel elvileg az excess kémiai potenciál értéke molekuláris szimulációkban meghatározható [20]. A módszer lényege, hogy egy N részecskés szimulációban időről-időre beillesztünk egy virtuális (N+1)-edik részecskét, majd kiszámítjuk annak a többi részecskével való kölcsönhatásából származó

+1

UN energiáját. Ebből µ^ex értéke NVT sokaságon a következő összefüggéssel határozható meg:

(

)

exp

ln U_{N 1} k_BT

ex

− +

−

µ = ^{. (33)}

A módszer alkalmazhatóságát limitálja, hogy kis hőmérsékletű és/vagy sűrű kondenzált fázisokban, illetve olyan rendszerekben, melyeket nagyméretű és/vagy több kölcsönhatási centrumból felépülő molekulák alkotnak, a sikeres részecskebeillesztések száma elenyészően kicsi (számos esetben gyakorlatilag zérus). A virtuális részecske ugyanis más molekulákkal részlegesen vagy teljesen átlapolódik, U_N+1 extrém nagy pozitív (vagy végtelen) értéket vesz fel, és a kémiai potenciálhoz gyűjtött járulék közelítőleg vagy pontosan zérus lesz.

1.4. Speciális részecsketranszfer-technikák

A leggyakrabban használt speciális részecsketranszfer-technikák alkalmazása mögött rejlő alapvető cél az, hogy standard MC algoritmus hatékonyságát javítsuk. Ez sok esetben azért szükséges, mert az elfogadott szimulációs lépések száma nem elegendően sok, ahhoz, hogy a szimuláció során statisztikailag értékelhető végeredményt kapjunk egy meghatározandó mennyiségre (vagyis a szimuláció során rendszerünk nem jár be elegendően sok különböző - az adott termodinamikai állapotban megvalósítható - konfigurációt). A speciális részecsketranszfer-technikák alapgondolata az, hogy a mintavételezés javítható azáltal, hogy a szimulációs lépéseket nem véletlenszerűen, hanem irányítottan - bizonyos konfigurációk kiválasztását preferálva - hajtjuk végre. A

„véletlenszerűség megzavarását” ekkor az elfogadási kritériumban ellensúlyozni kell a mikroszkopikus reverzibilitás (24) elvének tejlesüléséhez. Ez legegyszerűbben kanonikus sokaságon szemléltethető: tegyük fel, hogy a rendszer az i-edik konfigurációban van és a j- edik konfigurációt olyan valószínűség szerint kívánjuk kiválasztani, amely a potenciális energia függvénye, azaz П_ij = f(U_ij). Ez esetben megmutatható, hogy akkor teljesül a mikroszkopikus reverzibilitás elve, ha a kanonikus sokaság elfogadási kritériumát (27) az alábbi alakra hozzuk [5]:

( ) ( ) [ ]

⎪⎭

⎪⎬

⎫

⎪⎩

⎪⎨

⎧ −

=min 1, exp(U U )/(k T) U

f U

P f _{j i B}

ij NVT ji

ij , (34)

ahol Пji = f(Uji). Hasonlóan kell eljárni egyéb tetszőleges f valószínűség és a kanonikus sokaságtól különböző sokaságok esetén is [5].

A következő alfejezetekben az általam fejlesztett programba épített olyan, nagykanonikus (µVT) sokaságon alkalmazható technikák kerülnek bemutatásra, amelyekkel a részecskeeltávolítás és -beillesztés hatékonysága nagymértékben javítható. Manapság elterjedten vizsgálnak olyan kondenzált fázisokat, melyeket nagyméretű és/vagy több kölcsönhatási centrumból felépülő molekulák alkotnak. Ha egy ilyen rendszer számítógépes szimulációját nagykanonikus sokaságon valósítjuk meg, akkor a részecskék mérete és a rendszer sűrűsége miatt gyakran a sikeres beillesztések száma rendkívül kevés lesz. Egy viszonylag sűrű rendszerben ilyenkor (ahol a szimulációs doboz nagyjából már

„telített”) nehezen találhatók olyan pozíciók, ahol a beillesztendő további részecske nem lapolódik át egy, már bent lévő másik részecskével.

1.4.1. Forgatással irányított beillesztés

Az eltávolítási és beillesztési lépések elfogadási arányának javítására használható az ún. forgatással irányított beillesztés („rotational bias”) technika [21], melynek lényege, hogy beillesztéskor az adott molekula több, véletlenszerűen megadott térbeli orientációját próbáljuk ki, és ezek közül az adott molekula tényleges térbeli elhelyezkedésének az energetikailag kedvezőbbeket nagyobb valószínűséggel választjuk ki. A technika merev részecskemodellekre az alábbi módon alkalmazható:

A beillesztési lépéskor először a beillesztendő molekula középpontjának sorsolunk egy dobozon belüli pozíciót. Ezután ebben a pozícióban az adott molekulára m számú különböző, véletlenszerűen generált térbeli orientációban kiszámítjuk az

)) /(

exp(−U_N^l₊₁ k_BT kifejezés értékét (U^l_N+1 jelöli az N+1-edik, beillesztendő molekulának a többi dobozban levő molekulával vett kölcsönhatási energiáját a l-edik térbeli orientációban). Az eltérő orientációjú térbeli elhelyezkedéseket úgy kaphatjuk, hogy az adott molekulát adott szöggel elforgatjuk saját tömegközéppontja körül. Először az így kapott m darab különböző orientációkhoz tartozó energiaértékekből a beillesztendő molekula véglegesnek szánt térbeli elhelyezkedését választjuk ki az

∑

+ −

− ^m

l

B l N B

l

N k T U k T

U

1

1

1/( ))/ exp( /( ))

exp( valószínűséggel. A véletlenszerűség ezen

„megzavarását” később az elfogadási kritériumban figyelembe vesszük. Az új (j) és korábbi