Közbülső tárolók méretezése szakaszos folyamatrendszerekben stochasztikus környezetben

KÖZBÜLS İ TÁROLÓK MÉRETEZÉSE SZAKASZOS FOLYAMATRENDSZEREKBEN

SZTOCHASZTIKUS KÖRNYEZETBEN

Doktori (PhD) értekezés

Készítette: MIHÁLYKÓNÉ DR. ORBÁN ÉVA

a Veszprémi Egyetem

Informatikai Tudományok Doktori Iskolája keretében a doktori iskola vezet ı je: Dr. Friedler Ferenc egyetemi tanár

Konzulens: Dr. Lakatos Béla

egyetemi docens, a m ő szaki tudományok kandidátusa

Matematikai és Számítástechnikai Tanszék Veszprémi Egyetem

2003

KÖZBÜLS İ TÁROLÓK MÉRETEZÉSE

SZAKASZOS FOLYAMATRENDSZEREKBEN

SZTOCHASZTIKUS KÖRNYEZETBEN

Értekezés doktori (PhD) fokozat elnyerése érdekében a Veszprémi Egyetem Informatikai Tudományok

Doktori Iskolájához tartozóan Írta:

MIHÁLYKÓNÉ DR. ORBÁN ÉVA

A jelölt a doktori szigorlaton …... % -ot ért el.

Veszprém, …...

a Szigorlati Bizottság elnöke Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: …... …... igen /nem

……….

(aláírás) Bíráló neve: …... …... igen /nem

……….

(aláírás) ***Bíráló neve: …... …...igen /nem

……….

(aláírás) A jelölt az értekezés nyilvános vitáján…...% - ot ért el.

Veszprém,

……….

a Bíráló Bizottság elnöke A doktori (PhD) oklevél minõsítése …...

………

Az EDT elnöke

TARTALOMJEGYZÉK

TARTALMI KIVONAT V

ABSTRACT VI

ZUSAMMENFASSUNG VII

BEVEZETÉS 1

1. Irodalmi áttekintés 4

2. Szakaszos és folyamatos alrendszerek összekapcsolódásának modellezése 13 2.1. A vizsgált modell. Alapvetı jelölések, definíciók és feltételezések 13 2.2. A megbízhatóságokatmegadó függvények analitikus vizsgálata 19

2.3. Állandó nagyságú betöltések esete 29

2.4. Véges idıhorizonton történı méretezési problémák vizsgálata 39 2.5. Monte-Carlo szimuláció és szimulációs eredmények 48

2.6. Numerikus eljárások és eredmények 55

3. Szakaszos-szakaszos alrendszerek összekapcsolódásának modellezése 68 3.1. A vizsgált modell. Alapvetı jelölések, definíciók és feltételezések 68 3.2. Az anyagmennyiség-változást leíró függvény vizsgálata 75 3.3. Algoritmus és numerikus eredmények a méretezési probléma

megoldására 83

3.4. Az állandó betöltési és letöltési intenzitások esete 93 4. Az összekötı csıhálózat méretezési problémája 102 4.1. A vizsgált modell és a használt jelölések 102 4.2. A véges idıintervallumon vizsgált probléma pontos megoldása

speciális esetekben állandó nagyságú betöltések esetén 104 4.3. Közelítı formulák a valószínőségek meghatározására állandó

nagyságú betöltések esetén 112

4.4. Aszimptotikus eredmények 119

4.5. Általános eloszlású betöltések esete 122

ÖSSZEFOGLALÁS 133

IRODALOMJEGYZÉK 136

AZ ÉRTEKEZÉS ÚJ TUDOMÁNYOS EREDMÉNYEI 140

Tartalmi kivonat

Közbüls ı tárolók méretezése szakaszos folyamatrendszerekben sztochasztikus környezetben

A disszertáció témája számítógéppel támogatott modellezés és tervezés, amelyben a modellek vizsgálata, matematikai elemzése után megoldási algoritmusok konstruálása révén a szerzı tervezési feladatok megoldására keresett választ.

A disszertáció két közbülsı tartály modellt és egy csıhálózati modellt elemez sztochasztikus mőködési feltételek közepette. Mindkét közbülsı tartály modellben kettıs feladattal foglalkozik a szerzı: egyrészt a folyamatos mőködéshez szükséges kezdı anyagmennyiség a hibátlan mőködés adott megbízhatósági szintjéhez történı meghatározása problémájával, másrészt a tartály méretének a hibátlan mőködés adott megbízhatósági szintjéhez történı meghatározásával.

Az elsı modellben szakaszos és folytonos alrendszerek összekapcsolódását te- kinti a szerzı olyan feltételek esetén, amikor a beérkezı anyagmennyiség tartályba táp- lálásának idıpontjait Poisson folyamat írja le, a beérkezett anyagmennyiség nagysága pedig véletlen nagyságú vagy állandó, s a tartályból távozó anyagmennyiség intenzitása állandó. A két problémára vonatkozó véges és végtelen idıintervallumon való megbízhatóságot megadó függvények definiálása, analitikus vizsgálata, az általuk kielé- gített integrál- és differenciálegyenletek analitikus és numerikus megoldása után a szer- zı megadta a kezdımennyiség meghatározási, valamint a tartály méretezési probléma megoldását.

A második modellben szakaszos betöltı és szakaszos letöltı alrendszerek összekapcsolódását vizsgálta a szerzı. A betöltı és letöltı egységek periodikus mőködését feltételezve véletlen meghibásodások mellett véges idıintervallumon vizsgálta a szerzı a két problémát oly módon, hogy a betöltési és letöltési intenzitásokat általánosnak feltételezte. A közbülsı tartályban levı anyagmennyiség változását leíró függvény minimumának és maximumának eloszlását Monte-Carlo szimuláció segítségével adta meg. A szélsıértékek hosszú idıintervallumon történı meghatározásá- ra a modell esetében a szerzı új algoritmust dolgozott ki. Állandó intenzitású betöltések és letöltések esetén speciális esetben a szélsıértékek eloszlását analitikusan megadta és módszert adott az optimális késleltetési idık meghatározására.

A csıhálózat méretezésének problémáját a szerzı Poisson folyamattal megadott betöltési vagy letöltési folyamat esetén állandó, illetve véletlen nagyságú mőködési idı mellett vizsgálta. Állandó nagyságú betöltések esetén a párhuzamosan mőködı egységek maximális számának eloszlását speciális esetekben analitikusan megadta, más esetekben approximációs formulát dolgozott ki rájuk, amelyek segítségével megadta a csıhálózat méretezési problémájának adott megbízhatósági szint melletti megoldását. A Véletlen nagyságú ideig tartó betöltések esetén fellépı megbízhatóságokat összehasonlította az állandó ideig tartó betöltések során kialakuló megbízhatóságokkal, és ezen elemzések alapján heurisztikus módszert adott a csıhálózat méretezési problémájának megoldására.

Az eredmények alkalmazhatók anyag-, energia-, valamint információátviteli rendszerek közbülsı tárolóinak (pufferjainak) tervezésében, illetve az anyag, energia, valamint az információ átvitelét lebonyolító hálózat méretezési problémáinak megoldásában. Kiemelt szerepük lehet környezetvédelmi beruházások tervezésénél, amikor a nem megfelelı méretezésbıl fakadó meghibásodások jóvátehetetlen környezeti károkat okozhatnak.

Abstract

Sizing intermediate storages in batch processes under stochastic operation conditions

The object of the dissertation is modelling and model-based design of the operation of finite capacity intermediate storages and pipeline networks in processing systems under stochastic operational conditions. Two models for describing the intermediate storages, and a model for the operation of pipeline networks are developed. In the case of storage models, the problem of determining the initial amount of the material to be processed, as well as a method of sizing the capacity of the finite storage necessary to operate the system without failures at a given reliability level are investigated. In the case of pipeline networks, the problem of sizing the pipeline capacity for a number of processing units working parallel under uncertain conditions are considered.

The first storage model is presented for designing the intermediate storages aiming to buffer the operational differences between the batch and continuous subsystems in processing systems. The occurrence times of the inputs are assumed to be described by a Poisson process, while the amounts of the material transferred by the batch units allowed changing according to general probability distributions. Analytical solutions to the integral equations for infinite horizons are derived in the cases of constant and exponentially distributed inputs. For the batch sizes described by general distribution functions, solutions to the integral equations numerical solutions are obtained on the bases of stochastic simulation.

In the case of batch/batch subsystems, an algorithm and simulation program is described for sizing intermediate storages taking into account stochastic equipment failures under general operation conditions. The method is based on the observation that any process of this system can be built up from a random sequence of failure cycles of finite number. In special case analytical formulae are derived for the distributions and for the expectations of differences of maximal and minimal values of the intermediate storage hold up as a function of delay times and of their differences. By means of simulation and statistical evaluation of the results of the simulation runs the storage is sized at a given significance level.

Finally, a method is presented for rational sizing of the capacity of pipelines aiming to transfer material or energy in batches under stochastic operation conditions.

The occurrence times of the transfers are assumed to be described by Poisson processes, while the amounts of the material and energy transferred may be constant or may vary randomly. Approximations of the reliability are derived for constant batches, developed in terms of scan statistics, based on which a method is developed for sizing the pipeline capacities for constant batches. In the case of transferring random batches described by general distribution functions, solutions are obtained by means of the combination of approximation and stochastic simulation.

Zusammenfassung

Bemessung intermediärer Speicher in etappenmäßigen Systemen von Prozessen in einer stochastischen Umgebung

Die Dissertation befasst sich mit Modellierung und auf Modellbasis beruhende Planung von Prozess-Systemen im Falle von stochastischen Betriebsbedingungen von intermediären Speichern und Rohrnetzen mit endlicher Kapazität. Zur Beschreibung der intermediären Speicher bzw. der Rohrnetzen wurden zwei Modelle bzw. ein Modell ausgearbeitet. Im Falle von Intermediären Speichern wurden die folgende Aufgaben konzipiert: Bestimmung die zur irgendwelchen Verlässigkeitsniveau fehlerlosen Betrieb notwendige Quantität von Anfangsmaterial, ferner die Bestimmung der notwendigen Kapazität von endlichen Speichern. Im Falle von Rohrnetzen wurde die Bemessung von das unter zufälligen Betriebsbedingungen parallel funktionierende etappenmäßige Systemen gegebenes Verlässigkeitsniveau fehlerlos bedienende Rohrnetz untersucht.

Das erste intermediäre Speichermodell dient zur Passung von etappenmäßigen und kontinuierlichen Subsystemen der Prozess-Systeme und zur Ausgleichung der aus verschiedengestaltigen Betriebsbedingungen sich ergebene Differenzen. Die Einfüllungsereignissen können - laut der Annahme - mit Poisson-Verteilung beschrieben werden, während die einzelnen eingefüllten Materialsquantitäten sich nach irgendeiner allgemeinen Verteilung verändern. Für die Intergralgleichung mit unendlichem Zeithorizont wurden für konstanten und für nach Exponentialverteilung sich verändernde Materialsquantitäten analytische Lösungen gegeben. Die für allgemeine Verteilungen von Materialsquantitäten bekommene Integralgleichung wurde durch stochastische Simulation gelöst.

Während der Untersuchung der etappenmäßigen/halbkontinuierlichen Systeme wurde für Bemessung der unter stochastischen Bedingungen funktionierenden intermediären Speicher ein Algorithmus und ein Simulationsprogram formuliert. Die Methode beruht auf eine Beobachtung: Beliebige Prozesse solcher Systeme lassen sich als endliche Sequenzen beliebiger Fehlercyklen aufbauen. In der Dissertation wurden analytische Formeln – abhängig von den Verspätungszeiten – über die Verteilung und Erwartungswert der Differenz der Maxima und Minima der in den Speicher befindlichen Materialsquantität bekannt gemacht. Ferner wurde durch Computersimulation und statistische Bewertung des Ergebnisses eine Methode für die Planung im gegebenen Verlässigkeitsniveau intermediärer Speicher gegeben.

Letztens, wenn die Transportereignisse in zufälligen Zeitpunkten nach Annahme laut der Poisson-Verteilung vorgehen, formuliert die Dissertation eine Methode für die rationelle Planung von Kapazität der Rohrnetze, die die Materialen und Energiequellen etappenmäßig transportieren. Die Werte der in einzelnen Etappen zu transportierende Quantitäten können sowohl konstante, als auch zufällig verändernde Quantitäten sein.

Für konstante Quantitäten – unter Benutzung der Scanstatistik – wurden analytische Näherungsformeln angegeben, auf deren Grund für Bemessung von Rohrnetzen zwei Heuristiken formuliert wurden. Wenn die transportierten Qualitäten sich laut allgemeiner Verteilung verändern, wird die Lösung mit Hilfe eines, auf stochastischer Simulation beruhenden Algorithmus gegeben.

Bevezetés

A különbözı mőszaki rendszerek megvalósításánál gyakran alkalmazott eljárás közbülsı tárolók használata.

Könnyen elképzelhetı ez egy vegyipari gyárnál, ahol egy tartályban győjtik a megtermelt anyagot, és ebbıl a tartályból veszik ki a felhasználás esetén. A győjtés oka lehet az eltérı ütemő termelés és felhasználás, de például okot adhat erre az is, hogy véletlen meghibásodások esetén is legyen raktáron felhasználható anyag.

Ez utóbbi gondolat már sugallja azt, hogy tulajdonképpen a raktározás elméleténél a raktár is egy közbülsı tárolónak számít. A raktározás elméletében általában az anyag elfogyása nem okoz jóvátehetetlen hibát, sıt esetenként a raktár mérete sem korlátozó tényezı, viszont mindennek ára van. Pénzbe kerül a raktározás, de az is, ha nem tudják kielégíteni az igényeket. Így a költségek optimalizálására törekednek a probléma megoldásakor. Ez azt jelenti, hogy a modell vizsgálatakor egy célfüggvényt adnak meg, amelynek optimalizálása a cél.

De gondolhatunk közbülsı tárolóként az orvosi várókra, ahol a vizsgálatra várakozó egyének érkezése és a vizsgálatok idıtartamának különbözısége folytán sokszor még akkor is hosszú idıt tölt a beérkezı személy, ha elızıleg megbeszélt idıpontra érkezik. Hát még akkor, ha ilyenrıl szó sincs. Természetesen ilyenkor már sorbanállás-kiszolgálással állunk szemben, s mint ilyenre példát számtalant említhetünk:

gyakori hétköznapi eseteink a posta, az áruház, esetenként a nagyvárosi tömegközlekedésben a busz, illetve a metró. Ezekben az esetekben a termelt anyagot az érkezı emberek helyettesítik, a közbülsı tároló az a hely, ahol várunk, míg a felhasználást az igény kiszolgálása jelenti. Hasonló esettel állunk szemben, amikor egy telekommunikációs központba futnak be az igények, azok felhasználását pedig a továbbításuk jelenti. Amennyiben a közbülsı tárolóban eltöltött idı csak a kényelem szempontjából fontos, másként kezelhetjük a problémát, mintha a túlságosan felgyülemlett igény hibát okoz a rendszerben. Ha a felhasználható anyagmennyiség kifogyása csupán a kiszolgáló egység számára némi várakozási (pihenési) idı beiktatását jelenti, akkor egészen más a probléma, mintha az a feldolgozó mővelet leállítását és késıbbi újraindítását igényli esetleg igen nagy költségek árán. Amennyiben a felgyülemlett nagy anyagmennyiség, illetve az anyag elfogyása nem jelent meghibásodást, akkor általában olyan kérdéseket teszünk fel, hogy mennyi a közbülsı tárolóban eltöltött idı, kell-e várni a kiszolgálásra. De ha az elfogyás-túltöltıdés hibát okoz, akkor már inkább azt kérdezzük, hogy milyen feltételek esetén nem fog hiba történni.

A meghibásodások elkerülése, mint cél, gyakran elıfordul tervezési feladatokban. Nézzük azt az esetet, amikor egy biztosítótársaság pénztára mőködik közbülsı tárolóként. A beérkezı anyagot a beérkezı pénz helyettesíti, a letöltött anyag pedig a kárigényekre kifizetett összeg. Amennyiben a pénztárból kifogy az anyagmennyiség, az azt jelenti, hogy a biztosítótársaság tönkremegy, amely valóban mindenáron elkerülendı esemény a biztosítótársaság mőködése szempontjából. A tervezési feladatot a megfelelı kezdeti tıke meghatározása jelenti. Így a közbülsı tartály probléma a gazdasági (pénzügyi) életben is elıfordul.

Kimondottan győjtıszerep jut egy tartálynak szennyvíztisztításnál, illetve egyéb környezetvédelmi problémák megoldásánál. Itt az anyag a tartályban eltöltött idı alatt ülepedik, tisztul, a tartályban bizonyos biológiai folyamatok mennek végbe.

Elkerülendı jelenség például a tartály túltöltıdése, de a tartályban levı anyag mennyiségének egy adott szint alá csökkenése is, mivel ekkor kipusztulhatnak a

biológiai folyamatot biztosító mikroorganizmusok, ezért ezek a jelenségek hibajelenségként is interpretálhatók.

Felmerül még az a probléma is, hogy ha a beérkezı anyagmennyiség egy csatornán érkezik, akkor a csatorna áteresztı-képességének nem megfelelı volta is okozhat hibát.

Gondolhatunk a forgalomszervezés problematikájára, amikor gépkocsik érkeznek egy úthálózatra, amelynek áteresztı képessége véges. Ha a beérkezı autók túl sokan vannak az úthálózat áteresztı képességéhez képest, akkor nagy dugók alakulhatnak ki. Más esetben, például információ továbbítása esetén az elveszett információ esetleg pótolhatatlan veszteség, és ezért úgy kell méretezni az összekötı csıhálózatot, hogy az ilyen hibákat elkerüljük. Számítógépek mőködése esetén a feldolgozásra váró feladatok (például e-mailek egy szerveren) túl nagy száma szintén a rendszer megbénulásához vezet. Fontos kérdés tehát az, hogy hogyan méretezzük a csıhálózatot (kábelrendszert), hogy ezt elkerüljük.

Csoportosíthatjuk a problémákat aszerint is, hogy a betöltést, illetve letöltést végzı alrendszerek mőködése determinisztikus vagy sztochasztikus. Ha az egységek mőködése determinisztikus, akkor a meghibásodások megfelelı mőködtetés esetén vagy biztosan elkerülhetık, vagy bármilyen mőködtetés esetén bekövetkeznek. Annak megtervezése, hogy milyen mőködtetés esetén kerülhetık el a meghibásodások, ütemezési probléma megoldását jelenti. Más a helyzet, ha az egységek mőködése sztochasztikus jellegő. Ebben az esetben kérdésként fogalmazható meg, hogy a meghibásodás milyen valószínőséggel következik be.

Az eddigiek alapján látható, hogy a közbülsı tárolók alkalmazása nagyon sokrétő. A feladat megfogalmazása attól függ, hogy a mőködés szempontjából milyen aspektusok fontosak. A mőködést alapvetıen befolyásolják a tartályhoz csatlakozó betöltı és letöltı alrendszerek mőködésére tett feltételezések. A betöltést, illetve letöltést végzı egységek mőködése szempontjából megkülönböztetünk szakaszos mőködéső, illetve folyamatos mőködéső alrendszereket. A szakaszos egységek bizonyos idıintervallumokban mőködnek, más idıintervallumokban pedig nem végeznek semmiféle tevékenységet, ami a közbülsı tartályban levı anyagmennyiséget befolyásolná. A betöltés, illetve letöltés lehet pillanatszerő, illetve adott ideig tartó. A folyamatos mőködéső egységek bármely idıpillanatban betöltenek valamennyi anyagot a tartályba, illetve letöltenek anyagot onnan. Amennyiben a betöltés, illetve a letöltés intenzitása idıben nem változik, akkor állandó betöltési, illetve letöltési intenzitással rendelkezı modellel állunk szemben.

Az irodalom alapján nyilvánvaló, de a dolgozatom alapján is látható, hogy a különbözı modellek esetén a megoldáshoz alkalmazott technikák igen különböznek egymástól. A modell némi módosítása esetén a megoldásra addig alkalmazott technika már nem mőködik, és nem is módosítható úgy, hogy alkalmazható legyen az új problémára. A modelleket megérteni könnyő, de a problémák megoldása sokszor nem várt módon nehéz, mint ezt Chen és Salamam is megfogalmazták (Chen & Salamam, 1995].

Dolgozatomban elıször szakaszos betöltéső és folyamatos letöltéső alrendszerek, majd szakaszos betöltéső és szakaszos letöltéső alrendszerek illesztésével, végül az összekötı csıhálózat méretezési problematikájával foglalkoztam abban az esetben, ha a túltöltés vagy az anyag elfogyása meghibásodást okoz, és az egységek mőködését véletlen hatások befolyásolják.

A szakaszos betöltés és a folyamatos letöltés esetén a biztosításelméletben alkalmazott technikához hasonlóan a rendszer megbízhatóságát megadó függvényekre

integrálegyenleteket írtam fel, amiket elemeztem és speciális esetekben analitikusan, más esetben numerikusan megoldottam. Ezen megoldások alapján a méretezési és kezdımennyiség meghatározási problémára megoldást adtam. A szakaszos-szakaszos alrendszerek esetén a méretezési problémát csak szimulációval tudtam megoldani, de kidolgoztam egy olyan eljárást, amely nem csupán állandó betöltési és letöltési intenzitások, hanem idıben változó betöltési és letöltési intenzitások esetén is hatékonyan mőködik. A csıhálózat méretezési problémájánál állandó betöltési idıt feltételezve a klasszikus tükrözési elv segítségével tudtam speciális esetekben a pontos megbízhatóságot megadni, más esetben approximációt alkalmaztam. A véletlen nagyságú betöltési idık esetén a szimuláció segítségével kapott meghibásodási valószínőségeket összehasonlítottam a konstans betöltési esethez tartozó hiba bekövetkezési valószínőségével, s a méretezési feladat megoldását az állandó betöltések esetére vezettem vissza.

Dolgozatom elsı részében irodalmi áttekintést adtam, a második fejezet tartalmazza a szakaszos-folyamatos alrendszer illesztésével nyert rendszer elemzését és méretezését, a harmadik fejezet mutatja be a szakaszos-szakaszos alrendszerek illesztésével nyert rendszerrel kapcsolatos eredményeinket, míg a negyedik fejezet tárgyalja az összekötı csırendszer méretezési problémáinak megoldását. A dolgozat összefoglalással, irodalomjegyzékkel és a tézisek ismertetésével zárul.

1. Fejezet Irodalmi áttekintés

Dolgozatom témája számítógéppel támogatott modellezés és tervezés, amelyben a modellek vizsgálata, matematikai elemzése után megoldási algoritmusok konstruálása révén tervezési feladatok megoldására keresünk választ.

Dolgozatomban a következı problémakört vizsgálom: adottak egyes termelési egységek, amelyek valamilyen terméket, anyagot gyártanak. Mőködési jellemzıiket ismertnek feltételezzük. A legyártott anyagot a késıbbiekben más egységek felhasználják. Addig is, amíg az anyagot felhasználják, a gyártó egységek azt egy tartályba töltik. A felhasználó egységek ebbıl a tartályból veszik ki az anyagot olyan ütemben, ahogyan azt felhasználják. A termelési rendszer megtervezése érdekében arra a kérdésre keresünk választ, hogy mekkora legyen a tartály mérete, hogy adott ideig (esetleg akármennyi ideig) elegendıen nagy legyen a tartály az anyag tárolására, illetve mekkora legyen a tartályban a kezdeti idıpontban levı kezdımennyiség, hogy a felhasználók (letöltı egységek) számára adott ideig (esetleg soha) ne fogyjon el az anyag. További kérdés az, hogy mekkorára tervezzük az összekötı csıhálózatot, hogy rajta keresztül zavartalanul bonyolódhasson a betöltés és a letöltés folyamata.

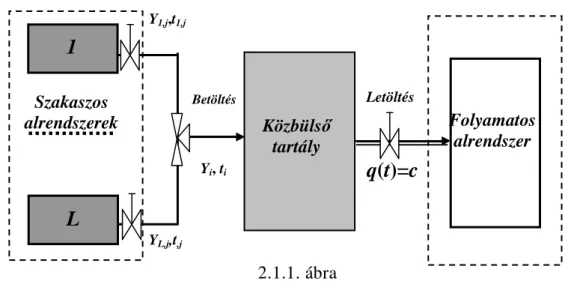
Rendszerünk sematikus rajza a 1.1. ábrán látható.

1.1. ábra

A közbülsı tartályra, illetve a folyamatos mőködéshez szükséges kezdı anyagmennyiség meghatározására vonatkozó tervezési feladat determinisztikus mőködési feltételek esetén matematikai szempontból az alábbi módon fogalmazható meg. Amennyiben ismerjük a betöltési és letöltési egységek mőködését idıben, akkor a tartályban levı anyagmennyiség változása a betöltı egységek által betöltött anyagmennyiség és letöltött anyagmennyiség különbségeként megadható. A tartályban levı kezdeti anyagmennyiséget ehhez hozzáadva megkapjuk a tartályban levı anyagmennyiséget az idı függvényében. A tartály mérete elegendıen nagy, ha a méret az anyagmennyiség-változást leíró függvény maximális értéke a kezdı anyagmennyiséggel megnövelve. A szükséges kezdı anyagmennyiség pedig az anyagmennyiség változását leíró függvény minimumának a mínusz egyszerese.

Sztochasztikus mőködési feltételek esetén azonban az anyagmennyiség-változást leíró függvények sem determinisztikusak, így az említett szélsıértékek eloszlását kell

Betöltı egységek

Letöltı egységek Közbülsı tartály

meghatároznunk a megfelelı méretek meghatározásához, vagyis a hibátlan mőködés adott megbízhatósági szint mellett való biztosításához.

A közbülsı tartályok problémaköre a bevezetésben vázoltak szerint több kontextusban is vizsgálható. Amennyiben sorbanállás-kiszolgálási rendszerként értelmezzük, akkor ennek az elméletnek rengeteg irodalma van. Alapmőként említeném L. Kleinrock Queueing systems címő könyvét, amelyben ismerteti a sorbanállási rendszerek alapmodelljeit és alapvetı problémáit. A modellek jellemzıi az igények beérkezése közt eltelt idı eloszlása, a kiszolgáláshoz szükséges idık jellemzıi, valamint a kiszolgálók száma. A rendszereket általában egy jelhármassal jellemzik, amelyben az elsı jel a beérkezı igények eloszlását, a második jel a kiszolgálási idık eloszlását, a harmadik jel a kiszolgálók számát jelenti. Az M jel az exponenciális eloszlásra, a G jel az eloszlás általános jellegére utal. Általában azt feltételezik, hogy amennyiben érkezik egy igény, és nem talál üres kiszolgálót, akkor vár, de vannak olyan modellek is, amelyben azt feltételezik, hogy az érkezı túl sok várakozó láttán távozik a rendszerbıl.

Ezeket elriasztott igényeknek nevezik. A probléma a várakozási idık eloszlásának vizsgálata, illetve a másodjára említett modelleknél azon esemény esélyének a meghatározása, hogy egy adott igénybıl elriasztott igény válik. Természetesen a sorbanállási rendszereknél nem gond az, ha az igények kifogynak, illetve egy igény várakozási ideje eloszlásának vizsgálatakor nem foglalkoznak azzal a kérdéssel, hogy korábban vajon nem volt-e már túl sok igény egyszerre a rendszerben. Az M/M/m típusú rendszerek problémáira a válaszok könnyen megkaphatók, az M/G/m és a G/M/m típusú rendszerek elméletéhez jól ismert a Pollaczek-Hincsin formula a rendszerben tartózkodó igények várható értékére, illetve az eloszlásfüggvény momentumgeneráló függvényére, amibıl a rendszerbeli igények momentumai megkaphatók, de ismert a várakozási idık eloszlásának Laplace transzformáltjára vonatkozó egyenlet, a kiszolgálóegységek foglaltsági intervallumai hosszának várható értéke, momentumai, sıt eloszlása is (Kleinrock, 1975). Azonban igen nehéz terepen találjuk magunkat, ha a G/G/1, de még inkább, ha a G/G/m (m>1) típusú rendszereket vizsgáljuk (Lindley, 1952). Ebben az esetben az n. igény várakozási idejének eloszlására a rendszer stacionárius állapotának fennállása esetén egy Wiener-Hopf típusú integrálegyenletet tudtak felírni, amelyet Lindley-féle integrálegyenletnek nevez a szakirodalom. Ennek az egyenletnek a megoldása igen nehéz feladat. Módszerként a spektrálfelbontás módszerét alkalmazzák, amely bizonyos speciális esetben megadja a várakozási idık eloszlásfüggvényét (Smit, 1953). A spektrálmódszer hátránya, hogy a rendszer általános viselkedési szabályait nem lehet a segítségével megállapítani, hanem minden új sort külön kell megvizsgálni.

A sorbanállási rendszerek elmélete még ma is erısen kutatott terület még az M/G/m típusú sorok esetén is. Nagyon sokféle feltételezés lehet a beérkezı, illetve a kiszolgálási idık eloszlására, a köztük levı korrelációra. Cidon és társai (1991) egy olyan G/M/1 típusú sort vizsgáltak, amelyben a beérkezési idık közti idıtartamok és a kiszolgálási idık közt összefüggés áll fenn, és a Lindley-féle integrálegyenlet transzformációs algoritmussal történı megoldása során a visszatranszformálást is sikerült elvégezniük. Perry és Posner (2000) olyan M/G/1 típusú sort vizsgáltak, amelyekben az elızıleg említett összefüggés mellett még azt is feltételezik, hogy a kiszolgálás a kiszolgáló egység meghibásodása miatt késlelkedhet. Általános G/G/1 típusú sornál, amelyben a kiszolgálási idı összefüggésben van a beérkezések közt eltelt idıvel, a várakozási idı Laplace transzformáltjára írtak fel egyenletet Boxma és Perry (2001). Napjainkban foglalkoznak olyan modellekkel is, amikor valamelyik jellemzıt (a kiszolgálási idık közt eltelt idıt, vagy az érkezési idıközt) olyan eloszlással jellemzik, amelyek farokrésze az exponenciális eloszlás farokrészénél vastagabb (Mandjes, 2000;

Duffield, 1998). Ilyen eloszlásokra példa a Weibull, a lognormális, illetve a Pareto

eloszlás. A tapasztalat szerint például továbbított file-ok (e-mailek) mérete, s ezért a továbbítási (kiszolgálási) idık exponenciális eloszlás helyett inkább vastagabb farokrésszel rendelkezı eloszlásúak, így ezen vizsgálatok az informatika szempontjából is gyakorlati jelentıséggel bírnak. A modellek tehát nagyon sokfélék, azonban a sorbanállási modellek esetén nem vizsgálják azt a kérdést, hogy a modellekben valaha történt-e már túltöltıdés, illetve azt, hogy elfogyott-e a feldolgozandó anyag, hanem csak azt, hogy mennyi az esélye, hogy az adott pillanatban üres periódus van-e, illetve jelentkezik-e túltöltıdés.

A sorbanállási modellek alkalmazása valódi fizikai értelemben vett tartályok esetén a tartályban levı pillanatnyi folyadékszint leírására különbözı modellek esetén gyakran megtörténik, de ilyenkor a pillanatnyi állapottal foglalkoznak, továbbá a stacionárius állapotot tekintik. Ez történik például Mitra (1998) dolgozatában, ahol exponenciális eloszlású betöltési és letöltési idık, továbbá exponenciális eloszlású pihenési idık esetén vizsgálja a szerzı a mőködésben levı egységek számának eloszlását, valamint a folyadékszint stacionárius állapotát jellemzı eloszlásfüggvényt. A mőködésben levı egységek száma egy speciális Markov folyamattal írható le, amelynek átmenetmátrixa megadható. A Markov lánc stacionárius állapotát jellemzı valószínőségekre egy differenciálegyenlet-rendszert ír fel a szerzı, amelynek megoldására módszert is javasol. Ezután a Markov lánc stacionárius állapotának felhasználásával a tartályban levı anyagmennyiség eloszlásfüggvényére differenciálegyenlet-rendszert adott meg a szerzı.

Ren és Kobayashi (1995) exponenciális eloszlású betöltések és letöltések esetén a folyadékszint stacionárius eloszlását Laplace transzformált használatával adták meg.

Általános Markov típusú bemenetek és kimenetek esetét vizsgálják munkáikban Anick és Stern (Anick et al., 1982; Stern & Elwalid, 1991). Sericola (1998) szintén Markov folyamattal leírt betöltések és letöltések esetén nézi a pillanatnyi folyadékszint eloszlását azon eseménnyel együttesen, hogy az utolsó betöltéssel a Markov folyamat állapota egy rögzített állapot lett, s az együttes eloszlásfüggvényre egy parciális differenciálegyenletet írt fel, amelynek explicit megoldását is meg tudta adni. Ezekben a publikációban is az eredmények a rendszer stacionárius állapotára vonatkoznak, így a meghibásodást elkerülendı méretezési problémák megoldására nem alkalmasak.

Közbülsı tartályok méretezési problémáival direkt módon Ross (1973) kezdett el foglalkozni, feltéve a kérdést, hogy mekkora tartály elegendı bizonyos vegyipari mőveletek során képzıdött anyagok elhelyezéséhez és ezáltal a folyamatok elvégzéséhez. A kérdés felvetését azzal indokolta, hogy kémiai technológiák tervezésekor arra is figyelemmel kell lenni, hogy mekkora a megtermelt és a felhasználásra váró anyagmennyiség tárolási igénye. Ha ez túl nagy, akkor feleslegesen megnıhetnek a termelési költségek. Takamatsu és társai (1979) azt a célt tőzték maguk elé, hogy megállapítsák, hogy a betöltı és letöltı alrendszer periodikus mőködése esetén hogyan válasszák meg az egységek mőködési idıintervallumát ahhoz, hogy minél kisebb mérető közbülsı tartály elegendı legyen a mőködtetéshez. Tehát a termelés ütemezésének problémáját egy tartályméretezési problémával kapcsolták össze. İk egy olyan modellt tekintettek, amiben több szakaszos mőködéső és egy folyamatos mőködéső egységet tételeztek fel, és analitikus formulát adtak a minimálisan szükséges tartályméretre az egységek mőködésbe lépésének függvényében. Ez a munka indította el a közbülsı tartályban levı anyagmennyiség változásának, mint az idı függvényének a vizsgálatát. Késıbb általánosították módszerüket arra az esetre is,

amikor nem egyfajta, hanem többfajta terméket is termelnek. Modelljeikben a termelés determinisztikus folyamat (Takamatsu et al., 1982).

Általánosabban, periodikus mőködés esetén, rögzített periódusidıkkel dolgozva, determinisztikus betöltés és letöltés mellett, amennyiben a periódusidıknek létezik olyan többszöröse, hogy addig a betöltött anyagmennyiség megegyezik a letöltött anyagmennyiséggel, az anyagmennyiség-változás periodikus függvénye lesz az idınek.

Ebben a modellben egy betöltı egység, egy letöltı egység és állandó letöltési és betöltési intenzitás mellett Karimi és Reklaitis (1983) analitikus formulát adtak mind a folyamatos mőködéshez szükséges kezdı anyagmennyiségre, mind a szükséges tartályméretre. Mindezt úgy érték el, hogy a konstans és lineáris függvényekbıl összetevıdı anyagmennyiség-változást leíró periodikus függvényt Fourier sorba fejtették, és ennek a soralaknak határozták meg a szélsıértékeit. Vizsgálták továbbá az egységek késleltetési idıinek (mőködésbe lépése idıinek) hatását a szükséges tartályméretre és a szükséges kezdı anyagmennyiségre. Igazolták, hogy a szükséges tartályméret nem, de a szükséges kezdı anyagmennyiség függ a késleltetési idıktıl. Így a késleltetési idık helyes megválasztásával a kezdetben szükséges anyagmennyiség minimálissá tehetı. Munkájukat tovább általánosították azáltal, hogy több betöltı és letöltı egység esetén vizsgálták a szükséges tartályméretet determinisztikus, periodikus letöltés és betöltés, valamint állandó betöltési és letöltési intenzitások mellett (Karimi &

Reklaitis, 1985). Ekkor már nem tudtak analitikus képletet adni az anyagmennyiség- változást leíró függvény szélsıértékeire, így a minimumok és maximumok értékének meghatározására a gradiens módszert javasolták.

A gyakorlati életben gyakran tapasztalható, hogy az egyes egységek mőködését véletlen hatások is befolyásolják. Példaként említhetı, hogy a betöltések vagy letöltések idınként teljesen kimaradnak valamely véletlen hiba folytán. Lee és Reklaitis 1989-ben olyan modellt publikáltak, amelyben egy betöltı és egy letöltı egység esetén az egyik egységnél meghibásodásokat tételeztek fel (Lee & Reklaitis, 1989b). A meghibásodások esetén a meghibásodási periódusban nem történik betöltés a betöltı, illetve letöltés a letöltı egységnél, a másik egység viszont ebben az esetben is meghibásodás nélkül mőködik. Megtartották továbbá azt a feltételezést, hogy van olyan szám, amely mindkét periódusidınek többszöröse, amely idıtartam alatt figyelembe véve a meghibásodást is, a betöltött anyagmennyiség és a letöltött anyagmennyiség megegyezik. Ezen idıpontokban az anyagmennyiség-változás nulla lesz, s az anyagmennyiség változást leíró függvény periodicitása ebben az esetben is kihasználható, amennyiben a meghibásodás mindig ugyanazon a helyen történik. Ez az eset azonban inkább a karbantartás esetének feleltethetı meg, míg ha hiba történik, akkor a kimaradó betöltések és letöltések helye általában nem mindig ugyanoda esik, hanem a hely egy valószínőségi változóval adható meg.

A véletlen jellegő zavaró hatások kezelésére a tervezések során gyakorta azt az elvet alkalmazzák, hogy a véletlen hatások kiátlagolása után a várható érték szerint terveznek. Amennyiben a tartályban levı anyagmennyiség adott pillanatbeli várható értékéhez tervezzük a tartályméretet, akkor a korábbi idıpontokban a tartályban levı anyagmennyiség nagyságát figyelmen kívül hagynánk. Ennél finomabb módszer, hogy a tartályban levı anyagmennyiség változás legnagyobb értékének várható értékét és szórását határozzák meg, s a Csebisev egyenlıtlenséggel becslést adunk arra a méretre, amely már adott megbízhatósággal elegendı. Azonban tudjuk, hogy a Csebisev egyenlıtlenség által adott becslés arra a valószínőségre, hogy a valószínőségi változó értéke és a várható érték közti eltérés adott határt meghalad, pontatlan, s így ez alapján a rendszert erısen túlméreteznénk. Így az adott megbízhatósággal való méretezés esetén

sokkal pontosabb értéket kapunk, ha a valószínőségi változó eloszlását is vizsgáljuk, ami viszont nehéz feladat.

Lee és Reklaitis (1989a) publikáltak egy olyan modellt is, amelyben a meghibásodás során be nem töltött anyagmennyiség normális eloszlást követ, s a normális eloszlású valószínőségi változó értékeire adott korlátok segítségével adtak becslést a szükséges tartályméretre, és megállapították, hogy a determinisztikus esetben szükségeshez képest a szükséges tartályméret igen megnı, példájukban megnégyszerezıdik.

Odi és Karimi (1990) általános sztochasztikus modellt állítottak fel a közbülsı tartály problémára. Ebben a modellben azt feltételezték, hogy mind a betöltött/letöltött anyagmennyiség, mind a betöltési/letöltési idık, s így a betöltési intenzitások is sztochasztikusak. A probléma matematikai szempontból egy sztochasztikus folyamat szuprémuma és infimuma eloszlásának a megadása, amely nem könnyő feladat.

Klasszikus aszimptotikus eredmény ebben a témakörben az iterált logaritmus tétele független azonos eloszlású valószínőségi változók átlagára (Rényi, 1981). Odi és Karimi ebben a modellben olyan becslést adtak a szükséges tartályméretre, amely a szimulációból adódó eredményeket általában 10-20%-kal haladta meg. Modelljüket alkalmazták véletlen meghibásodások esetére oly módon, hogy a meghibásodási periódusokat beolvasztották a véletlen hosszúságú mőködési periódusokba, és ez esetben is azt tapasztalták, hogy a becslésük segítségével méretezett tartály mérete általában 10-20%-kal nagyobb csak a valóban szükségesnél, amelynek méretét Monte- Carlo szimulációval adták meg (Odi & Karimi, 1991). A túlméretezés abból származik, hogy az anyagmennyiség változást leíró függvény szélsıértékeinek eloszlását nem tudták meghatározni, csupán korlátokat tudtak rá adni, valamint véges intervallumokon való méretezéshez is aszimptotikus tételeket alkalmaztak. Munkájukban hangsúlyozzák, hogy a probléma elméletileg szimulációval kezelhetı, de a szimulációval történı megoldás hátránya a nagy idıigény. Ennek ellenére ezt az utat is választják (Djavdan, 1992), olyannyira, hogy tartályméretezési problémák számítógépes szimulációs megoldására szakértıi rendszert is kidolgoztak (Trepstra et al., 1994).

Közbülsı tartályokkal kapcsolatos sztochasztikus modellekkel olyan felfogásban is foglalkoznak, hogy a tartályban, raktárban levı anyagmennyiségnek sztochasztikus feltételeket kell kielégíteni és a feladat egy célfüggvény (általában a költségek várható értékének) optimalizálása. A 90-es évek közepén jelentek meg nagy számban publikációk ezen a területen. A véletlen mennyiségeket osztályozták, megkülönböztetve a paraméterek bizonytalanságából fakadó, illetve a külsı feltételektıl függı véletlen mennyiségeket (Rotstein et al., 1996). Az elıbbiek esetén a feladatok a determinisztikus esettel hozhatók kapcsolatba, míg a második típusú véletlent tartalmazó modellek matematikai szempontból sztochasztikus programozási feladatra vezetnek. A problémák itt is nagyon összetettek, megoldásuk nagyon sok gépidıt igényel. A modellek filozófiailag különböznek az általunk vizsgált problémától. Ugyanis azt feltételezik, hogy amennyiben a feltételeket nem sikerül kielégíteni, akkor a rendszer nem romlik el végzetesen, csupán büntetést kell fizetni, s ez a büntetés a célfüggvényen belül jelenik meg. Tehát a feltételeket igazából akkor érdemes kielégíteni, ha a kielégítésük (az esetleg feleslegesen raktározott mennyiség raktározási költsége) nem kerül többe a büntetésnél. Természetesen lehet a büntetés olyan nagy, hogy annak elkerülése igen fontos feladat. Mi azonban azt gondoljuk, hogy léteznek olyan dolgok is, amelyeknek értéke nem fejezhetı ki pénzben, azaz nincs ára, és így ezek a modellek ilyen esetekben nem megfelelıek. Gondoljunk például olyan esetekre, amikor a túltöltıdés, vagy az

anyagelfogyás miatt jóvátehetetlen környezeti károk alakulnak ki! Gazdasági szempontok alapján azonban ezek a modellek jól használhatók, és fıleg többféle anyagot termelı rendszerek esetén nagy a létjogosultságuk. Ilyen megközelítéső modelleket mutat be Pistikopoulos (1995), Ierapetritou és Pistikopoulos (1995), valamint Ierapetritou (Ierapetritou et al., 1996). A modellek megoldásában közös, hogy a problémát több, a korlátoknak megfelelı determinisztikus problémára bontják, ezeken belül külön-külön megkeresik a megengedett megoldásokat, majd ezek között megkeresik a célfüggvény szempontjából az optimálisat. A modelleknek nagyon sok változata lehetséges. A megoldások megkeresésekor a számolások leegyszerősítésére és lerövidítésére érdemes megkeresni a modell adta speciális lehetıségeket. Kimondottan közbülsı tartály-problémára alkalmaztak modellt Kim és társai (1996). Ezt fejlesztették tovább Ha és társai (2000), olyan módon általánosítva a modellt, hogy már több tartályt feltételeztek és a tartályok között is mozgatták az anyagot, valamint a tartályokban eltöltött idıt is szerepeltették a célfüggvényben, és így már a raktározási modell irányába mozdultak el felfogásukkal .

A raktározási modellek alkalmazása logisztikai feladatok esetén is igen gyakori.

Katonai felhasználásokkor is érthetı, ha nagy figyelmet fordítanak arra, hogy a raktárból ne fogyjon el az anyag. A logisztikában gyakran alkalmaznak determinisztikus modelleket, és tekintenek olyan problémákat is, amikor a raktárkészlet egy része valamilyen elıre nem látható ok miatt egyik pillanatról a másikra elveszik. Ilyen modellt mutatott be Barankin és Denny (1965). Ugyancsak ilyen problémát elemezett David és Greenshtein (1996) olyan feltételezéssel, amikor a véletlen veszteségek bekövetkezése között eltelt idı exponenciális eloszlású, s a raktár állapota egydimenziós Brown folyamattal jól modellezhetı. A modellben egy költségfüggvényt határoztak meg és ennek várható értékére írtak fel explicit formulát.

A közbülsı tartályba való anyagbeáramlás ideje, ami természetesen a betöltési intenzitásokkal van kapcsolatban, a gyakorlatban általában nem nulla, de bizonyos esetekben a mőködésbe lépési idıközökhöz képest kicsi. Ezért felmerül az a modellezési lehetıség, hogy a betöltési idıket zérusnak tekintjük és így próbálunk eredményeket elérni. Ez a megközelítés más területeken alkalmazott modelleknél is elıfordul. Például az anyag elfogyása egyfajta tönkremenésként is megélhetı, s ezért a játékelmélet tönkremenés-elméleti problémái is logikailag kapcsolatba hozhatók modellünkkel. Diszkrét eloszlású, fix idıben történt nyeremény-veszteség kifizetések esetén a tönkremenési problémára Feller (1978) könyvében találunk modellt. A modell megoldására differenciaegyenlet-rendszert írtak fel, s ezt egy nagyon egyszerő, speciális esetben sikerült is megoldani, azaz a tönkremenés valószínőségét a kezdıtıke és az egy fordulóban való nyerési és vesztési valószínőség arányában megadni. Jobban használhatók esetünkben azonban a nem diszkrét modellek, s azt vettük észre, hogy az általunk a második fejezetben tárgyalt modell, amely szakaszos és folyamatos mőködéső alrendszerek összekapcsolásával foglalkozik, éppen a biztosításelméletben használt alapmodellel analóg. A biztosításelméletben azonban általában a betöltés helyett a letöltés (a kifizetések nagysága) sztochasztikus, és csak a kezdı tıkenagyság függvényében vizsgálják annak a valószínőségét, hogy a pénztárban levı pénzmennyiség valamely idıpontban elfogy, azaz a biztosítótársaság tönkremegy.

Amennyiben a folyamatot nem véges idıintervallumon vizsgálják, akkor a végtelen idıintervallumon tekintett probléma megoldása során a hibátlan mőködés valószínőségére egy Volterra típusú integrálegyenletet tudtak felírni (Karlin & Taylor, 1975). Bár a bizosításelméleti alapmodell megoldása általános esetben nem ismert, bebizonyították hogy a megoldás alulról becsülhetı egy exponenciális típusú

függvénnyel, amelynek együtthatója (az un. Lundberg kitevı) becslésére különbözı módszereket dolgoztak ki (Csörgı & Steinebach, 1991).

Volterra típusú egyenletek más jellegő modellezési feladatoknál is elıbukkannak.

Érdekességként említeném csupán, hogy szemcsediszperziós rendszerek, például ırlési folyamatok modellezése során is a modellek Volterra típusú integrálegyenletre vezetnek (Austin, 1971/1972), (Lakatos et al., 1996). A Volterra típusú integrál-egyenleteknek széleskörő irodalma van, az irodalomban megtalálhatók a rájuk vonatkozó egzisztencia és unicitás tételek, valamint a megoldásukra kidolgozott numerikus módszerek.

Alapmőként említem Linz (1985) könyvét, valamint Gripenberg és társai (1990) könyvét, amelyek többfajta magfüggvénnyel nagyon részletesen tárgyalják a Volterra egyenletek témakörét.

A differenciálegyenletek és integrálegyenletek használata a véges idıintervallumon történı méretezési problémákra a legújabb kutatásoknak is része olyan aspektusban, hogy a méretezési problémát szintátmetszési problémaként fogják fel. Ha a kezdı anyagmennyiséget, illetve a szükséges tartályméretet keressük, amely elegendı a rendszer folyamatos mőködéséhez rögzített T ideig sztochasztikus mőködési feltételek esetén, akkor azt nézzük, hogy az adott idıintervallumon a sztochasztikus folyamat realizációja átlép-e egy bizonyos alsó vagy felsı korlátot, és ha igen, akkor mikor. Az elsı átlépés idıpontjának eloszlását vizsgálva tehát a méretezési probléma megoldását is vizsgáljuk. Az elsı szintátlépés idejének várható értékét a kezdımennyiség függvényében vizsgálva inhomogén differenciálegyenletet állított fel Kulkarni és Tzetova (2002), s ennek exponenciális típusú megoldását meg is találták. Az elsı átlépés idıpontjának sőrőségfüggvényére állít fel integrálegyenletet és ennek differenciálhatósági tulajdonságairól bizonyít állításokat Lehmann (2002) Markov folyamattal leírt bemenetek esetén. A véges idıintervallumra a biztosítási matematikában használt modell esetén is megvan a megfelelı integrálegyenletet (Thorin, 1982), és megoldására Thorin az egyenlet Laplace-transzformációját javasolta, azonban a visszatranszformálások már csak egyes esetekben mennek.

Kulkarni (2000) a közelmúltban vizsgált olyan modellt, amelyben a közbülsı tartályban levı anyagmennyiség-változást egy sztochasztikus folyamat vezérli, s azt vizsgálta, hogy az anyagmennyiség-változás adott korlátok között marad-e, ha a folyamat már beállt egy stacionárius állapotba. A problémának telekommunikációs alkalmazásai is vannak. A vezérlı folyamatról különbözı feltételezéssel éltek: folytonos idejő Markov folyamat, Markov folyamat fehér zajjal, illetve Orstein-Uhlenbeck folyamat. Abban az esetben, amikor a vezérlı folyamat egy Markov folyamat, az anyagmennyiség-változás (feltételes) eloszlásfüggvényére írtak fel parciális differenciálegyenletet. Amennyiben a vezérlı folyamat egy Markov folyamat fehér zajjal terhelve, akkor az anyagmennyiség-változásra speciális esetben egy sztochasztikus differenciálegyenletet írtak fel, az anyagmennyiség-változás feltételes eloszlásfüggvényére felírt parciális differenciálegyenletet pedig speciális esetekben meg is tudták oldani. Amennyiben pedig a vezérlı folyamat egy Orstein-Uhlenbeck folyamat, akkor a sőrőségfüggvényre felírt másodrendő parciális differenciálegyenlet explicit megoldását is sikerült megadni.

Fredholm típusú integrálegyenletet vezetett le Chen és Salamam (1995) Markov típusú diffúziós beáramlási folyamatot és állandó letöltési intenzitásokat feltételezve. Az általa alkalmazott megoldási módszer nagyon kecsegtetınek tőnt a számunkra is. İk ugyanis az integrálegyenletet egy lineáris operátorként fogták fel, és ezek alapján a megoldást az operátor Neumann sorba fejtésével igyekeztek megtalálni. A megoldásnak egy közelítı

függvényét úgy kapták meg, hogy az operátor Neumann sorának elsı néhány tagjából képezett összeget alkalmazták szukcesszív módon egy kezdıfüggvényre. A Neumann sor konvergenciája attól függ, hogy az operátor normája kisebb-e egynél. Bár a publikációban elméletileg nem tudták bebizonyítani, hogy az operátor normája egynél kisebb, a Neumann sor mégis konvergensnek mutatkozott, és a segítségével kapott approximáció a tapasztalat szerint igen gyorsan a pontos megoldás közelébe került.

Azonban számunkra ez az út nem volt járható, mert az általunk felírt egyenlet jobb oldalán természetesen adódó operátor normája nem kisebb egynél, s így Neumann sora biztosan nem konvergens.

A biztosításelméleti problémák approximációs módszerrel történı megoldásairól is születtek publikációk. A biztosításelméleti alapmodell olyan módosítása esetén mutatott be módszert Vazquez-Abad (2000), amikor a meglevı haszon egy nem nulla hányadát visszaforgatják a társaság alaptıkéjébe. Ez esetben természetesen a közbülsı tartályban levı anyagmennyiség-változás (pénzmennyiség-változás) már függ a közbülsı tartályban levı anyagmennyiségtıl (pénzmennyiségtıl). Módszerének alkalmazása után szimulációból kapott eredményekre illesztett kétváltozós függvényeket, amelyek a kezdeti tıke és a folyamat paramétere függvényében mutatják be a tönkremenési valószínőségeket. Megemlítjük, hogy a nyereség visszaforgatásának esetével a biztosításelméleti publikációkban máshol is találkozhatunk (Wang & Wu, 2001) de ennek a termelési rendszerekre vonatkozó modelleknél nincs megfelelı értelmezése.

Különösen távközlési problémáknál jellemzı, de természetesen a fizikai anyagátvitel szempontjából sem elhanyagolható az összekötı kábelrendszer (csıhálózat) méretezési problémája. Ahhoz, hogy ne alakuljon ki torlódás és ebbıl kifolyólag meghibásodás, az szükséges, hogy egyetlen idıpillanatban se mőködjön egyidejőleg több betöltési egység, mint amennyit a hálózat áteresztı képessége engedélyez. Abban a speciális esetben, amikor a betöltési idık állandó nagyságúak, ez a megkötés azt jelenti, hogy bármely betöltési idı hosszúságú intervallumon legfeljebb adott számú, a hálózat áteresztı képességét meg nem haladó számú betöltés (input) érkezik. A feladat megfogalmazása nagyon egyszerő, viszont megoldása most is bonyolult. Matematikai szempontból a vizsgálandó probléma egy sztochasztikus folyamat növekménye szuprémuma eloszlása megadására vezet, amely igen nehéz feladat. Azokat az adat-elhelyezkedési problémákat, amelyben azt vizsgálják, hogy mennyi az adott hosszúságú intervallumra esı véletlen mennyiségek (valószínőségi változók) maximális száma, scan statisztikáknak nevezik. Poisson eloszlás esetén elıször Wallenstein és Naus (1974), majd Huntington és Naus (1975) adtak egzakt formulát a keresett valószínőségekre egész T értékek esetén. Képleteik azonban nehezen használhatók, mert nagyszámú, nagymérető mátrix determinánsának kiszámolását követelik meg. Ezért aztán elıtérbe kerültek a becslések (Janson, 1984) és a valószínőségekre adott approximációs módszerek (Alm, 1999). A méretezés nagyságrendjére elızetes felvilágosítást az irodalomban fellelhetı aszimptotikus tételekbıl kapunk (Révész, 1984, Auer at al., 1991). A probléma matematikai nehézségét az is mutatja, hogy a Révész-publikáció anyaga részét képezte Révész Pál akadémiai székfoglalójának.

Természetesen a scan statisztikákat nemcsak egydimenziós Poisson folyamatok esetén, hanem többdimenziós Poisson folyamatok esetén is vizsgálják (Alm, 1998), aminek különösen nagy jelentısége lehet anyagszerkezeti vizsgálatokban az anyaghibák sőrősödésébıl származó hibajelenségek elıfordulási valószínőségének megadásában.

Vizsgálatok folynak olyan esetekben, amikor az egymást követı betöltések közti idı nem exponenciális, hanem más típusú valószínőségi változó (Glatz & Naus, 1991). Ez

utóbbi eredmények modellünknek olyan általánosítását teszik lehetıvé, miszerint a beérkezı inputok általános eloszlás szerint követik egymást, bár a telekommunikációban jól magyarázható és általánosan elfogadott az exponenciális idıköz, legfeljebb a homogenitás nem mindig teljesül. Érdekes továbbá az az eset, amikor a betöltött anyagmennyiség általános eloszlás szerint töltıdik be, de erre vonatkozólag ez idáig nem találtunk eredményeket a szakirodalomban.

Összefoglalva elmondhatjuk, hogy közbülsı tartályok méretezési problémáival fıként szakaszos betöltı és szakaszos letöltı alrendszerek esetén foglalkoztak, s egy mőködési periódus esetén a betöltési és letöltési intenzitást állandónak tekintették.

Sztochasztikus mőködési feltételek esetén az anyagmennyiség változást leíró függvények szélsıértékeinek eloszlását explicit módon nem tudták megadni, adott megbízhatósági szinten történı tartályméretezési problémát valószínőségelméleti becslések alapján, túlméretezésekkel sikerült megoldani. Nem vizsgáltak olyan modellt, amikor sztochasztikus mőködési feltételek esetén történı szakaszos betöltési és folyamatos letöltéső alrendszereket közbülsı tartály kapcsolja össze. Nincsenek tudományos eredmények idıben változó intenzitással mőködı alrendszerek esetén sem.

Nem vizsgálták továbbá az összekötı csıhálózat méretezési problémáját sztochasztikus mőködési feltételek esetén.

Célkit ő zések

Munkám során célul tőztem ki olyan sztochasztikus mőködéső rendszerek vizsgálatát, amelyben közbülsı tárolók szakaszos és folyamatos alrendszereket kapcsolnak össze. A szakaszos alrendszerek véletlen idıpillanatokban lépnek mőködésbe, és véletlen, vagy állandó nagyságú anyagmennyiséget töltenek a tartályba.

Célul tőztem ki továbbá olyan szakaszos betöltéső és szakaszos letöltéső alrendszerekbıl álló rendszer vizsgálatát, amelyekben a betöltési, illetve letöltési intenzitások idıben változnak, és az alrendszerek mőködését véletlen hibák befolyásolják. További feladatnak tekintettem az összekötı csıhálózat méretezési problémáinak elemzését véletlen idıpillanatokban történı, állandó ideig, illetve véletlen hosszúságú idıintervallumon végbemenı betöltések és letöltések esetén. Végsı célom tervezési feladatok modellezés révén történı megoldása volt. A modellek felállítása, az egyenletek matematikai elemzése, analitikus és numerikus megoldása, szimulációval történı vizsgálata révén olyan tervezési feladatok megoldására kerestem eljárásokat, mint a közbülsı tárolók tartályméretezési, illetve a tartályokhoz kapcsolódó csıhálózat méretezési problémái, valamint a folyamatos mőködés biztosításához szükséges kezdı anyagmennyiség meghatározásának problémái.

2. Fejezet

Szakaszos és folyamatos alrendszerek összekapcsolódásának modellezése

2.1. A vizsgált modell.

Alapvet ı jelölések, definíciók és feltételezések

Ebben a fejezetben olyan rendszereket vizsgálunk, amikor a betöltés szakaszos, de a letöltés folyamatos mővelet. Természetesen annak a vizsgálata, amikor a betöltés történik idıben folyamatosan, a letöltés pedig szakaszosan, analóg módon tárgyalható.

Modellünk a következı: legyen L darab betöltı egység, amelyek mőködése nem periodikus, hanem véletlen idıpillantokban lépnek mőködésbe. Minden betöltı egységrıl feltételezzük az alábbiakat: a k-adik egység mőködésbe lép a t_k,1,

2 ,

tk ,…,t_k,i (k=1,…,L) idıpillanatokban. Legyen t_k,0 =0 k=1,…,L. Feltételezzük, hogy az egymást követı mőködésbe lépési idık közt eltelt idık, vagyis a

,...

1 ,...,

1 1

,

, −t ₋ k = L i=

t_{ki ki} valószínőségi változók egymástól függetlenek és azonos eloszlásúak; eloszlásuk λ_k>0 paraméterő exponenciális eloszlás. Ekkor a k- adik mőködési egység által T ideig betáplált inputok száma Poisson eloszlást követ

kT

λ paraméterrel. Az egyes betöltések során betöltött anyagmennyiségek szintén lehetnek véletlen nagyságúak. Jelen fejezetben tárgyaljuk azt az esetet is, amikor ezek a mennyiségeket egy-egy valószínőségi változóval adhatjuk meg, valamint azt is, amikor a betöltött anyagmennyiségek mindig ugyanakkorák. Jelölje Y_k,j k=1,…,L j=1,… a k-adik egység által az j-edik betöltés alkalmával betöltött anyagmennyiséget. Legyenek az Y_k,j valószínőségi változók minden k=1,…,L és j=1,… érték esetén független, azonos eloszlású valószínőségi változók G eloszlásfüggvénnyel, µ várható értékkel és σ szórással, amennyiben a betöltött anyagmennyiségek véletlen nagyságúak, illetve legyen Yk_,j =1 k=1,…,L és j=1,…

esetén, ha mennyiségük állandó. Az alábbi feltételezésekkel kívánunk még élni: az egyes betöltések során a közbülsı tartályba töltött anyagmennyiség független a betöltés idejétıl is, továbbá a betöltés pillanatszerő, azaz a betöltési idı kezdetekor a betöltendı anyagmennyiség egyszerre megjelenik a közbülsı tartályban. Ez a feltételezés akkor tehetı, ha a betöltés fizikai megvalósítása során a tényleges betöltési idık sokkal kisebbek, mint az egyes inputok között eltelt idık várható értéke, azaz λ_k^.

Most fésüljük össze az egyes egységek által szolgáltatott input-folyamatokat, azaz tekintsünk el attól, hogy az inputot melyik egység szolgáltatta, csupán azt nézzük, hogy melyik idıpillanatban mennyi anyagmennyiség ömlik a közbülsı tartályba. Ha feltételezzük, hogy az egyes betáplálási egységek mőködése egymástól független, akkor az összes betáplálás által megadott folyamat szintén Poisson folyamattal írható le (Karlin & Taylor, 1975). Ennek az összefésült input (betöltési) folyamatnak a paramétere az egyes paraméterek összege, azaz

∑

=

= ^L

k k 1

λ

λ ^{. Ha az}

összefésült folyamatban gondolkodunk, akkor mind a betáplálás idejénél, mind a

betöltött anyagmennyiség megadásánál elhagyhatjuk a kettıs indexet, és csupán azt jelöljük, hogy hányadik anyagmennyiség-betöltéssel állunk szemben. Jelölje az i- edik input során betöltött anyagmennyiséget Y i=1,… . Feltételezésünk szerint az _i Y _i i=1,… valószínőségi változók függetlenek a betöltés idıpontjától. Az összes anyagmennyiség, ami a közbülsı tartályba kerül, az

∑

=

= ⁽⁾

1

) (

t N

i

Yi

t

f függvénnyel

adható meg, ahol N(t) egy λ>0 paraméterő Poisson folyamat, az Y i=1,… _i valószínőségi változók pedig mind egymástól, mind a Poisson folyamattól független valószínőségi változók, amik csupán nemnegatív értéket vehetnek fel. Jelölje eloszlásfüggvényüket G( y), várható értéküket µ, szórásukat pedig σ ^{. Mivel} Y_i ≥⁰ i=1,... , ezért µ ≥0.

A közbülsı tartályból távozó anyagmennyiségrıl az alábbi feltételezésekkel élünk. Tegyük fel, hogy az M letöltı egység mindegyike idıben állandó intenzitással vonja ki az anyagmennyiséget a közbülsı tartályból. Ha c_j jelöli a j-edik letöltési egység intenzitását, akkor a t ideig a j-edik egység által letöltött anyagmennyiség

t

c_j⋅ . A t ideig a tartályból távozó anyagmennyiség g t c t

M

j

∑

=

=

1

)

( , az intenzitás állandó, nevezetesen

∑

=

= ^M

j

cj

c

1

. Természetesen c≥0, sıt általában c>0 teljesül.

A leírtakat az alábbi 2.1.1. ábra szemlélteti:

2.1.1. ábra

A közbülsı tartály szerepe az, hogy tárol bizonyos mennyiségő anyagot, ami által egyrészt biztosítja a folyamatos letöltést azokban az idıintervallumokban is, amikor éppen nincs betöltés, továbbá tárolja a betöltött anyagmennyiséget abban az esetben, amikor a folyamatos letöltéshez nincs rá éppen szükség. A rendszer mőködéséhez két feltételt kell biztosítani: kell lennie anyagnak a közbülsı tartályban, amikor szükség van rá, illetve a közbülsı tartályban levı anyag- mennyiségnek egy meghatározott korlát alatt kell maradnia.

Az elsınek említett feltétel magyarázata az, hogy ha nincs anyag a közbülsı tartályban, akkor leállhat a rendszer mőködése, ami rendkívül költséges lehet bizonyos gépek mőködtetésénél. De ezen felül bizonyos esetekben környezetvédelmi

Szakaszos

alrendszerek Folyamatos

alrendszer Közbülsı

tartály

Betöltés Letöltés

1

L

q(t)=c

Y_1,j,t_1,j

Y_L,j,t_,j Y_i, t_i