transmission with partial immunity in humans Threshold and stability results in a periodic model for malaria Applied Mathematics and Computation

ContentslistsavailableatScienceDirect

Applied Mathematics and Computation

journalhomepage:www.elsevier.com/locate/amc

Threshold and stability results in a periodic model for malaria transmission with partial immunity in humans

Mahmoud A. Ibrahim

^a,b,∗

, Attila Dénes

^a

aBolyai Institute, University of Szeged, Aradi vértanúk tere 1., Szeged H-6720, Hungary

bDepartment of Mathematics, Faculty of Science, Mansoura University, Mansoura 35516, Egypt

a rt i c l e i nf o

Article history:

Received 18 April 2020 Revised 22 September 2020 Accepted 27 September 2020 Available online 9 October 2020 MSC:

34D23 92D30 Keywords:

Periodic epidemic model Malaria transmission Partial immunity Basic reproduction number Global stability

Uniform persistence

a b s t ra c t

Wedevelopaperiodiccompartmentalpopulationmodelforthespreadofmalaria,divid- ingthe human populationintotwo classes:non-immune and semi-immune. Theeffect ofseasonalchangesinweatheronthemalariatransmissionisconsidered byapplyinga non-autonomousmodelwheremosquitobirth,deathandbitingratesaretime-dependent.

Weshowthattheglobaldynamicsofthesystemisdeterminedbythebasicreproduction number,whichwedefineasthespectralradiusofalinearintegraloperator.Forvaluesof thebasicreproductionnumberlessthanunity,thedisease-freeperiodicsolutionisglob- allyasymptoticallystable,whileifR0>1,thenthediseaseremainsendemicinthepopu- lation.Weshowsimulationsinaccordancewiththeanalyticresults.Finally,weshowthat thetime-averagereproductionrategivesanunderestimationformalariatransmissionrisk.

© 2020 The Authors. Published by Elsevier Inc.

ThisisanopenaccessarticleundertheCCBY-NC-NDlicense (http://creativecommons.org/licenses/by-nc-nd/4.0/)

1. Introduction

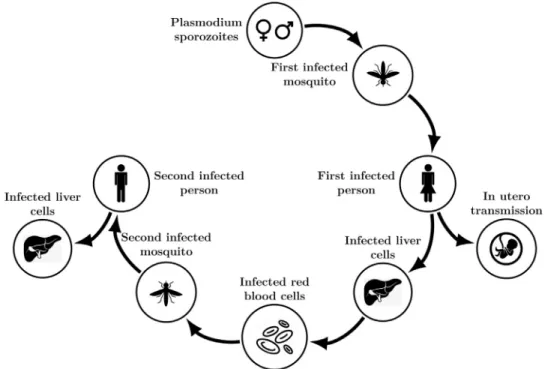
Malaria is an acute febrile illness caused by Plasmodium microorganisms spread to humans by female Anopheles mosquitoes. Out ofthe five Plasmodium species,most ofthe lethal malaria cases can be attributed to P. falciparum.The latest malaria report of WHOfrom December 2019 estimated around 230million malariacases andmore than 400,000 deathsinbothoftheprecedingtwoyears[1].

Fig.1showsthemalariatransmissioncycle.

Inapersonwithoutimmunity,symptomsusuallyappeartentofifteendaysafterinfection.Thesymptomsofthedisease, includingfever,headache,andchillsareoftenmild,makingmalariadifficulttorecognizeatearlystages.P.falciparummalaria can develop to a serious, oftenlethal illness ifnot treatedwithin one day. Children suffering fromsevere malaria often showsevereanemia,respiratorydistressorcerebralmalaria[1,2],whilemulti-organfailureisfrequentininfectedadults.In regionswherethediseaseisendemic,severalyearsofexposuremaycontributetoapartialimmunity,makingasymptomatic infections are possible.Partial immunity doesnot provide a complete protection, though it reduces the risk of a severe disease duetomalariainfection.Hence,mostmalaria-relateddeath casesinAfricaaffectyoungchildren,whileinregions

∗Corresponding author at: Bolyai Institute, University of Szeged, Aradi vértanúk tere 1., Szeged H-6720, Hungary.

E-mail address: mibrahim@math.u-szeged.hu (M.A. Ibrahim).

https://doi.org/10.1016/j.amc.2020.125711

0 096-30 03/© 2020 The Authors. Published by Elsevier Inc. This is an open access article under the CC BY-NC-ND license ( http://creativecommons.org/licenses/by-nc-nd/4.0/ )

Fig. 1. Malaria transmission cycle.

withlowertransmissionandimmunity,everyagegrouphasanequalthreat.Itisimportanttonotethatheterozygotesfor thesicklegene(AS)alsohaveapartialprotectionagainstmalaria[3].

Several sophisticated mathematicalmodels of malariatransmission have beenpreviously established, the first one by RonaldRoss[4],laterextendedbyMacdonald[5].Ducrotetal.[6]presentedadeterministicmodelformalariatransmission inwhichthepopulationofhumansisdividedintotwo hosttypes:non-immuneswhoareespeciallyvulnerabletomalaria andsemi-immuneswhoarelessvulnerablebecauseofanearliermalariainfectionprovidingpartialimmunity.Furtherworks also(seee.g.[7,8])studythetransmissionofmalariawiththehumanpopulationdividedintotwotypesofhosts.

Periodicityofweatherandclimatechangeareveryimportantfactorsinthelifecycleoftheparasitesandthemosquitoes transmittingthem.Hence,itisofcrucialimportancetounderstandhowchangesinweatheraffectthespreadofmalaria[9]. Mordecaietal.[10]formulatedanonlinearthermal-responsemodeltoexplaintheroleoftemperaturechangesinthespread ofmalaria.Otherworks[7,11–19]havediscussedtheimpactsofweatheronmosquitopopulationsandmalariatransmission.

Inthecaseofadiseaselikemalaria,whichdependsontheabundanceofmosquitoes,which,inturn,ishighlydependent ontheperiodicallychangingweather,itisespeciallyimportanttoincludethisseasonalityinourmodels.

Forperiodicepidemiccompartmentalmodels,BacäerandGuernaoui[20]providedadefinitionofthebasicreproduction number asthe spectral radius ofan integral operator actingon the space ofcontinuous periodic functions. Later, Wang andZhao [21]characterized thebasicreproductionnumberforsuch modelsandproved that itserves asathresholdpa- rameterregardingthe localstabilitypropertiesofthedisease-freeperiodic solution.Rebeloetal.[22] studiedpersistence inepidemiologicalmodels inaseasonalenvironment. BacaërandAitDads [23]gavea morebiologicalexplanation ofthe reproduction numberforcompartmentalepidemicmodels withperiodicparameters. Severalpapers [7,9,24–28]studythe spreadofmalariatransmissionwithperiodicallychangingmosquitobirth,deathandbitingrates.

Inourpresentwork,motivatedby[6,7]wesetupandstudyacompartmentalpopulationmodelformalariatransmission in a periodically changing environment: we extend the model givenin [6] by including periodicity ofthe environment.

Unlike[7],weconsiderperiodicvitaldynamicsofmosquitoesbysettingthemosquitobirthratesandmosquitodeathrates aswellasthebitingratestobeperiodicwithoneyearasperiod,followingtheannualchangeofweather.Wenote,however, thatthemodelgivenin[7]includedacompartmentforimmaturemosquitoes,whichwedonotconsider.Thetotalhuman population is divided into two major categories: non-immune and semi-immune. We determine the basic reproduction numberR0tocharacterizethedynamicsofourmodel,andweshowtheglobalstabilityofthedisease-freeperiodicsolution ortheendemicityofmalariaaswellastheexistenceofapositive

ω

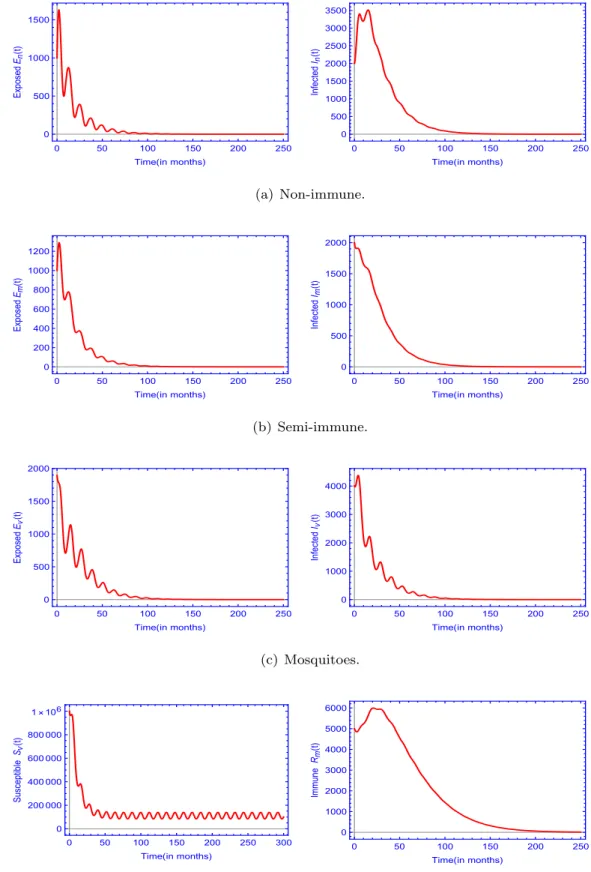
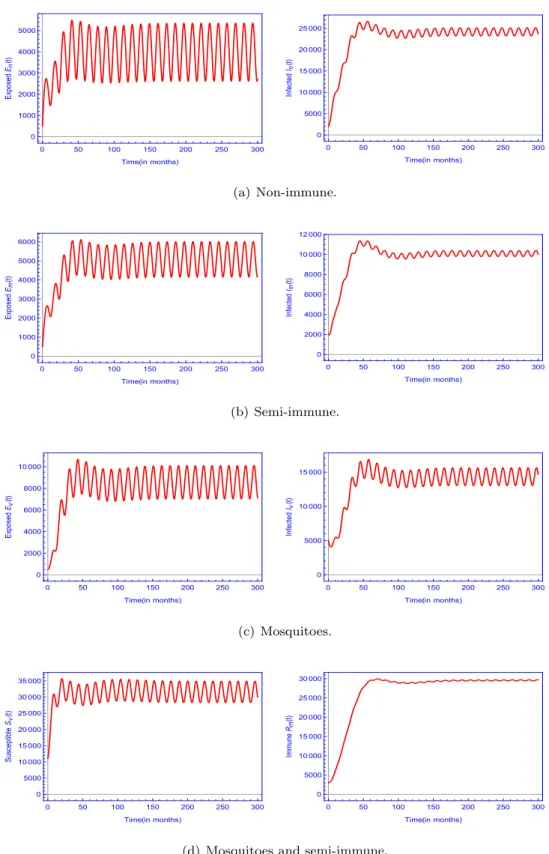
^{-periodicsolution,dependingonthebasic}reproduction number.Weshownumericalsimulationstoillustrateandsupporttheanalyticalresults.

2. Mathematicalmodel

In ourmodel,humanpopulation isdividedinto twotypesbased ontheir immunitylevel:the non-immune, i.e.those who have not developedanyimmunity against malaria,andthe semi-immune, that isthose who havesome partial im-

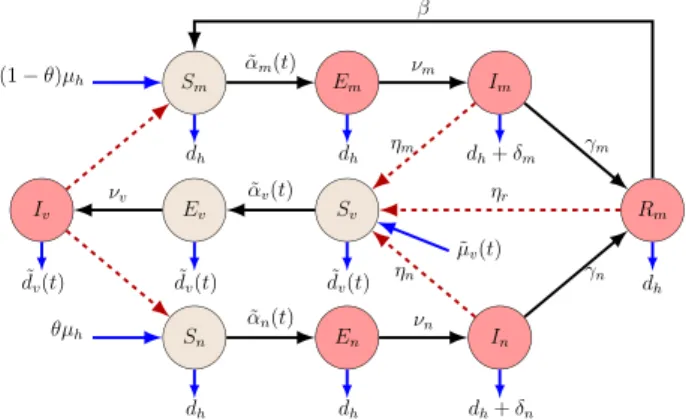
Fig. 2. Flow diagram of model (1) . Red nodes are infectious and brown nodes are non-infectious. Black solid arrows show the progression of infection, while red dashed arrows show direction of transmission between humans and mosquitoes. Blue solid arrows show birth and death. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

munity duetotheir geneticsorbycontractingthediseaseearlierintheirlife.Semi-immunehuman,non-immunehuman andmosquitocompartmentsaredenotedbythelowerindicesm,nandv.Susceptiblehumans(SmandSn)canbeinfected by malaria.Following theinfectiousmosquitobite,susceptiblesproceedtothe exposedcompartment (Em,En). Individuals in these compartmentshave no symptoms yet.After the incubation time, exposed individuals proceed to the infectious class (Im,In). Forsemi-immune, thereis an additional immune compartment (Rm). Humans in theclass Rm are partially immune tothedisease,buttheirbloodstreamstillhasalowlevelofparasitesandtheyarestillabletoinfectsusceptible mosquitoes[29].Wehavethreecompartmentsforthemosquitoes:susceptibles(Sv),exposed(Ev)andinfected(Iv).

We denotethetotal populationofhumans byN_h(t) andtotalpopulationofmosquitoes by Nv(t). Thetransmissiondy- namicsisillustratedinFig.2.Withtheabovenotations,ourmodelequationscanbewrittenas

S_n

(

^t

)

⁼

θμ

h−

α

˜ⁿ

(

^t

)

^Iv

(

^t

)

N_h

(

^t

)

^Sn

(

^t

)

^−dhSn

(

^t

)

^, E_n

(

^t

)

=

α

˜ⁿ

(

^t

)

^Iv

(

^t

)

N_h

(

^t

)

^Sn

(

^t

)

−

ν

^nEn

(

^t

)

−d_hEn

(

^t

)

, I_n

(

^t

)

⁼

ν

^nEn

(

^t

)

⁻

γ

^nIn

(

^t

)

⁻

(

^dh+

δ

ⁿ

)

^In

(

^t

)

^, S_m

(

^t

)

=

(

¹−

θ ) μ

h−

α

˜m

(

^t

)

^Iv

(

^t

)

Nh

(

^t

)

^Sm

(

^t

)

−dhSm

(

^t

)

+

β

^Rm

(

^t

)

, E_m

(

^t

)

⁼

α

^˜m

(

^t

)

^Iv

(

^t

)

N_h

(

^t

)

^Sm

(

^t

)

⁻

ν

^mEm

(

^t

)

^−dhEm

(

^t

)

^, I_m

(

^t

)

=

ν

mEm

(

^t

)

−

γ

mIm

(

^t

)

−

(

^dh+

δ

m

)

^Im

(

^t

)

, R_m

(

^t

)

=

γ

^nIn

(

^t

)

+

γ

^mIm

(

^t

)

−

β

^Rm

(

^t

)

−dhRm

(

^t

)

,

S_v

(

^t

)

=

μ

˜v

(

^t

)

−

α

˜v

(

^t

) η

^nIn

(

^t

)

+

η

^mIm

(

^t

)

+

η

^rRm

(

^t

)

N_h

(

^t

)

^Sv

(

^t

)

−d˜_v

(

^t

)

^Sv

(

^t

)

, E_v

(

^t

)

=

α

˜v

(

^t

) η

nIn

(

^t

)

+

η

mIm

(

^t

)

+

η

rRm

(

^t

)

Nh

(

^t

)

^Sv

(

^t

)

−

ν

vE_v

(

^t

)

−d˜_v

(

^t

)

^Ev

(

^t

)

,

I_v

(

^t

)

=

ν

vE_v

(

^t

)

−d˜_v

(

^t

)

^Iv

(

^t

)

, (1)

where

μ

˜v(^t),

α

˜ⁿ(^t),

α

˜^m(^t),

α

˜v(^t)^andd˜v(^t)^{arethemosquitobirthrate,therateof}transmissionfromaninfectedmosquito to anon-immunesusceptiblehuman,transmissionratefroman infectiousmosquitotosusceptiblesemi-immunehumans, thetransmissionratefrominfectedhumanstosusceptiblemosquitoesandmosquitodeathrate,respectively.Inourmodel we assumed

μ

˜v(^t),

α

˜ⁿ(^t),

α

˜^m(^t),

α

˜v(^t)^andd˜v(^t)^{to be}continuous, positive

ω

^{-periodic functions.The} explanationof the modelparametersissummarizedinTable1.

Wefirstengageinthestudyoftheexistenceanduniquenessofsolutionsof(1).Introducethenotation

(

^Sn

(

⁰

)

,En

(

⁰

)

,In

(

⁰

)

,Sm

(

⁰

)

,Em

(

⁰

)

,Im

(

⁰

)

,Rm

(

⁰

)

,S_v

(

⁰

)

,E_v

(

⁰

)

,I_v

(

⁰

) )

=

(

^S0n,E_n⁰,I_n⁰,S_m⁰,E_m⁰,I_m⁰,R⁰_m,S⁰_v,E_v⁰,I_v⁰

)

∈R¹⁰₊, whereR+:=[0,∞)^.

First,weshowthat(1)hasadisease-freeperiodicsolution.Forthehumansubsystemofsystem(1)withapositiveinitial condition(^S0n,E_n⁰,I_n⁰,S⁰_m,E⁰_m,I_m⁰,R⁰_m,S⁰_v,E⁰_v,I⁰_v)∈R¹⁰₊,wehavethelineardifferentialequation

dN_h

(

^t

)

dt =

μ

h−d_hN_h

(

^t

)

⁻

δ

^nIn

(

^t

)

⁻

δ

^mIm

(

^t

)

^{. (2)}

Table 1

Summary of parameters and notations of model (1) . Parameters Description

μh Humans birth rate d h Humans death rate

θ Probability of recruitment for humans

δn, δm Disease mortality rate for non-immune and semi-immune humans β Rate of losing immunity for humans

ηn, ηm, ηr Relative transmissibility of infectious humans to mosquitoes γn, γm Transfer rate of humans from I nand I mto R m

νn, νm Non-immune and semi-immune human incubation rate ν^v Mosquitoes incubation rate

αn, αm Baseline value of mosquito-to-human transmission rate αv Baseline value of human-to-mosquio transmission rate μv, d v Baseline value of mosquito birth and death rates

If thedisease isnot presentin thepopulation, (2)hasa unique, globallyasymptotically stableequilibriumN^∗_h=^μ_d^h

h,and

N_h(t)isbounded.

Toobtainthedisease-freeperiodicsolutionof(1),letusconsidertheequation dS_v

(

^t

)

dt =

μ

˜v

(

^t

)

^−d˜v

(

^t

)

^Sv

(

^t

)

^{, (3)}

withinitialconditionS_v(⁰)=S⁰_v∈R+.Eq.(3)clearlyhasasinglepositive

ω

^{-periodicsolution,givenby} S^∗_v

(

^t

)

=

_t

0

μ

˜v

(

^r

)

^{e0rd˜v(s)dsdr}+ _ω

0

μ

˜v

(

^r

)

^{e0rd˜v(s)dsdr} e^0ωd˜v(s)ds−1

e^{−0td˜v(s)ds}>0. (4)

ThissolutionisgloballyattractiveinR+ yieldingthat(1)hasasingledisease-freeperiodicsolution E0=

S^∗_n,0,0,S^∗_m,0,0,0,S^∗_v

(

^t

)

,0,0

, withS^∗_n=

θ

^μ_d^h

h andS_m^∗ =(¹−

θ

)^μ_d^h

h.

Tointroducethefollowingresult,weseth^L=sup_t∈[0,ω)h(^t)^andhM=inf_t∈[0,ω)h(^t)^{forapositive,continuous}

ω

^-periodic

functionh(t).

Lemma2.1. ThereisN_v^∗=_d^μM^Lv

v >0suchthateachsolutioninXof(1)eventuallyenters GN^∗:=

(

^{Sn,En,In,Sm,Em,Im,Rm,S}v,E_v,I_v

)

^∈R10+ : N_hN^∗_h, N_vN_v^∗ , andforeachN_v(^t)N_v^∗,G_Nispositivelyinvariantforsystem(1).Also,wehavethat

t→lim+∞

(

^Nv

(

^t

)

^−S∗v

(

^t

) )

^=0.

Proof. From(1),forthemosquitosubsystemwehave dN_v

(

^t

)

dt =

μ

˜v

(

^t

)

^−d˜v

(

^t

)

^Nv

(

^t

)

μ

^Lv−d_v^MN_v

(

^t

)

^{0, ifN}v

(

^t

)

^Nv^∗,

whichimpliesthatG_N,N_v(^t)N_v^∗,ispositivelyinvariantandeventually,eachforwardorbitentersG_N∗.Tofinishtheproof, letusassumey(^t)=N_v(^t)−S^∗_v(^t), t0.Hence,wehave

dy

(

^t

)

dt =−d˜_v

(

^t

)

^y

(

^t

)

, fromwhichwehave

t→lim+∞y

(

^t

)

=0.

Hence,theproofiscomplete.

ThenextlemmawillbeneededinprovingglobalstabilityofE₀ andthepersistenceofmalariainSection4.

Lemma2.2[30,Lemma2.1]. Let

μ

=_ω¹ln

ρ

(

Φ

A(·)(

ω

))^{.Thenthereexistsan}

ω

^{-periodicpositivefunctionv(t)suchthateμtv(t)}

isapositivesolutionofx=A(^t)^x.

3. Basicreproductionnumbersandlocalstability

In this section, following the technique introduced by Wang and Zhao [21], we will show the local stability of the disease-free periodic solution E₀ of (1). First, we identify the basic reproduction number R0 for system (1). Let X= (^En,In,Em,Im,Rm,E_v,I_v,Sn,Sm,S_v)^{T where En,In, Em, Im,Rm, Ev andIv are infected}compartments, andSn, Sm and Sv are uninfectedcompartmentswith

F

(

^t,X

(

^t

))

⁼

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

α˜n(^t)

Nh(t)I_v

(

^t

)

^Sn

(

^t

)

0 α˜m(^t)

Nh(t)I_v

(

^t

)

^Sm

(

^t

)

0 0

α

˜v

(

^t

)

^ηnIn(t)+ηm_N^I_h^m₍⁽_t^t₎^)+ηrRm(t)Sv

(

^t

)

0

0 0 0

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

,

V⁻

(

^t,X

(

^t

))

⁼

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

( ν

^n+dh

)

^En

(

^t

) ( γ

^n+dh+

δ

ⁿ

)

^In

(

^t

)

( ν

^m+dh

)

^Em

(

^t

) ( γ

^m+dh+

δ

^m

)

^Im

(

^t

)

( β

+dh

)

^Rm

(

^t

) ( ν

v+d˜_v

(

^t

))

^Ev

(

^t

)

d˜_v

(

^t

)

^Iv

(

^t

)

dhSn

(

^t

)

d_hSm

(

^t

)

d˜_v

(

^t

)

^Sv

(

^t

)

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

, V⁺

(

^t,X

(

^t

))

⁼

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎣

0

ν

nEn

(

^t

)

0

ν

^mEm

(

^t

) γ

^nIn

(

^t

)

⁺

γ

^mIm

(

^t

)

0

ν

vE_v

(

^t

) θμ

h

(

¹−

θ ) μ

h

μ

˜v

(

^t

)

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎦

.

(5)

Weneedtoverifythattheconditions(A1)–(A7)in[21,Section1]aresatisfied.Eq.(1)isequivalentto

X

(

^t

)

=F

(

^t,X

(

^t

))

−V

(

^t,X

(

^t

))

, (6)

where we introduce the notationV(^t,X(^t)) ^for V⁻(^t,X(^t))−V⁺(^t,X(^t))^{. It is} straightforward to check that conditions (A1)–(A5)hold.

ItisclearfromtheabovethatEq.(6)hasthedisease-freeperiodicsolution X^∗

(

^t

)

=

(

^{0,0,0,0,0,0,0,S∗}n,S^∗_m,S^∗_v

(

^t

) )

^.

Let us introduce f(^t,X(^t)) ^for F(^t,X(^t))−V(^t,X(^t)) ^{and the matrix function M}(^t)=

_∂f_i(t,X^∗(t))

∂Xj

8i,j10 where f_i(^t,X(^t)) ^{is theith coordinateof f}(^t,X(^t))^and Xi is the ithcomponent ofX. From (5),the matrix function M(t) can becalculatedas

M

(

^t

)

=

_−d

h 0 0

0 −dh 0

0 0 −d˜_v

(

^t

)

. (7)

Letusdenoteby

Φ

M(^t)^{themonodromymatrixof} _d^d_t^z=M(^t)^{zandwewillusethenotation}

ρ

(

Φ

M(^t))^{forthespectral} radiusof

Φ

M(

ω

)^.Hence,

ρ

(

Φ

M(^t))<1,whichimpliesthatX^∗(^t)^isalinearlyasymptoticallystablesolutioninthedisease- freesubspaceXs=

{

(⁰,0,0,0,0,0,Sn,Sm,S_v)∈R¹⁰₊

}

^{.Thisimpliesthatthecondition(A6)holdsaswell.}

Weintroducethe7×7matrixfunctionsF(t),V(t)givenasF(^t)=

_∂Fi(t,X^∗(t))

∂Xj

1i,j7,V(^t)=

_∂Vi(t,X^∗(t))

∂Xj

1i,j7withFi

andVidenotingthei-thcoordinateofthevectorfunctionsF andV,respectively.Thenfrom(5),wehave

F

(

^t

)

=

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

0 0 0 0 0 0

α

˜ⁿ

(

^t

)

^SN^∗n∗_h

0 0 0 0 0 0 0

0 0 0 0 0 0

α

˜^m

(

^t

)

^SN^∗m∗_h

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0

η

ⁿ

α

^˜v

(

^t

)

^S∗vN⁽_h^∗t) 0

η

^m

α

^˜v

(

^t

)

^S∗vN⁽_h^∗t)

η

^r

α

^˜v

(

^t

)

^S∗vN^(∗_h^t) 0 0

0 0 0 0 0 0 0

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

,

V

(

^t

)

=

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

ν

^n+dh 0 0 0 0 0 0

−

ν

^{n Ln 0 0 0 0 0}

0 0

ν

^m+dh 0 0 0 0

0 0 −

ν

^{m Lm 0 0 0}

0 −

γ

^{n 0 −}

γ

^m

β

^+dh 0 0

0 0 0 0 0

ν

v+d˜_v

(

^t

)

⁰

0 0 0 0 0 −

ν

v d˜_v

(

^t

)

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

,

(8)

whereL_n=

γ

n+d_h+

δ

nandL_m=

γ

m+d_h+

δ

m.F(t)isanon-negativematrix,and−V(^t)^iscooperative.

DenotebyY(t,s),t≥stheevolutionoperatorofequation dy

dt =−V

(

^t

)

y, (9)

meaningthat,foranys∈R,the7×7matrixfunctionY(t,s)fulfils dY

(

^t,s

)

dt =−V

(

^t

)

^Y

(

^t,s

)

, forallts, Y

(

s,s

)

=I,

withI beingthe7× 7 unit matrix.From this,

Φ

−V(^t), themonodromy matrixof(9)is equalto Y(t, 0),t ≥0. Wehave shownthatcondition(A7)holds.

Assumethat theinitialdistributionofinfectedisgivenby

φ

^(s),whichis

ω

^{-periodicins.F(s)}

φ

^{(s)givestherateofnew}

casesduetothoseinfectedwhowereintroducedattimes.Fort≥s,theformulaY(t,s)F(s)

φ

^{(s)providesthe}distributionof theinfectiousindividualswhowerenewly infectedattimesandwhoarestillinfectedattimet.Fromthisweobtainthat thedistributionofcumulativenewinfectionsatt,generatedbyallinfected

φ

^{(s)introducedatanytimes}≤tis

ψ (

^t

)

^:= t

−∞Y

(

t,s

)

^F

(

^s

) φ (

^s

)

^ds=

_∞

0

Y

(

t,t−a

)

^F

(

^t−a

) φ (

^t−a

)

da.

LetusintroducethenotationC_ωfortheorderedBanachspace

{

^h:R→R⁷:his

ω

^-periodic

}

,

withthemaximumnorm · ∞.ConsiderthepositiveconeC⁺_ω definedas C_ω⁺:=

{ φ

∈C_ω:

φ (

^t

)

0,

∀

^t∈R

}

.

ThenthelinearnextinfectionoperatorLfromC_ωtoC_ω,definedas

(

L

φ )(

^t

)

=

_∞

0

Y

(

^t,t−a

)

^F

(

^t−a

) φ (

^t−a

)

^da,

∀

^t∈R,

φ

∈C_ω, (10)

canbeusedtodefinethebasicreproductionnumberof(1)asthespectralradiusoftheoperatorL[21]. LetW(t,

λ

^{)denotethemonodromymatrixofthe}

ω

^{-periodiclinearequation}

dw

(

^t

)

dt =

−V

(

^t

)

+1

λ

^F

⁽

^t

⁾

w

(

^t

)

,

∀

^t∈R,

where

λ

∈(0,∞)isaparameter.F(t)beingnon-negativeand−V(^t)^beingcooperativeimplythat

ρ

^(W(

ω

^,

λ

^{))iscontinuous}

andnon-increasingin

λ

∈(0,∞)andlim_λ→∞

ρ

^(W(

ω

^,

λ

⁾⁾<1.

We evoke thefollowing theoremfrom[21] aswewill need itforthe numericalcalculation ofthebasic reproduction rate.

Theorem3.1[21,Theorem2.1].

(i) If

ρ

(^W(

ω

,

λ

))=1hasasolution

λ

0>0,then

λ

0 isaneigenvalueofL,andthusR0>0. (ii) IfR0>0,then

λ

=R0istheonlysolutionof

ρ

(^W(

ω

,

λ

))=1.

(iii)R0=0ifandonlyif

ρ

^(W(

ω

^,

λ

⁾⁾<1forall

λ

>0. Theorem3.2[21,Theorem2.2].

(i) R0=1isequivalentto

ρ

(

Φ

F−V(

ω

))=1. (ii) R0>1isequivalentto

ρ

(

Φ

F−V(

ω

))>1. (iii)R0<1isequivalentto

ρ

(

Φ

F−V(

ω

))<1.

Based on the results so far, we can formulate the following theorem concerning the local stability properties ofthe disease-freeperiodicsolutionE₀of(1).

Theorem 3.3. The disease-free periodic solution E₀ is locally asymptoticallystable if R0<1, whileit is unstable in thecase R0>1.

Proof. J(t)istheJacobianof(1)calculatedinE₀: J

(

^t

)

=

F

(

^t

)

−V

(

^t

)

⁰ J1

(

^t

)

^M

(

^t

)

, withM(t)definedin(7)andJ₁(t)isgivenby

⎡

⎣

^{0 0 0 0 0 0 −}

θ α

^˜n

(

^t

)

0 0 0 0

β

^{0 −}

(

¹⁻

θ ) α

^˜m

(

^t

)

0 −

η

ⁿ

α

^˜v

(

^t

)

^S∗vN⁽_h^t∗) 0 −

η

^m

α

^˜v

(

^t

)

^S∗vN⁽_h^∗t) −

η

^r

α

^˜v

(

^t

)

^S∗vN⁽_h^∗t) 0 0

⎤

⎦

.

By[31],E₀isalocallyasymptoticallystableperiodicsolutionif

ρ

(

Φ

M(

ω

))<1aswellas

ρ

(

Φ

F−V(

ω

))<1hold.Fromcon- dition (A6), we have

ρ

(

Φ

M(

ω

))<1. It then follows that the stabilityof E₀ is determined by

ρ

(

Φ

F−V(

ω

))^{.Hence, E}0 is locallyasymptotically stableif

ρ

(

Φ

F−V(

ω

))<1,andunstableif

ρ

(

Φ

F−V(

ω

))>1.ByusingTheorem 3.2,we completethe proof.

3.1. Derivationofthebasicreproductionnumberoftheautonomousmodel

TocalculatethebasicreproductionnumberR^A₀oftheautonomousmodelwhichweobtainfrom(1)bysettingthetime- varying parametersmosquitobirth(

μ

˜v(^t)≡

μ

v) anddeathrates(d˜_v(^t)≡d_v)andbitingrates(

α

˜ⁿ(^t)≡

α

ⁿ,

α

˜^m(^t)≡

α

^mand

α

˜v(^t)≡

α

v)toconstant,wefollowthegeneralapproachestablishedin[32].

Substitutingthevaluesinthedisease-freeequilibriumS^∗_v(^t)≡S^∗_v=^μ_dv^v inEq.(8),forallt≥0,weobtaintheJacobianF givenby

F=

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

0 0 0 0 0 0

α

ⁿN^S∗n_h^∗

0 0 0 0 0 0 0

0 0 0 0 0 0

α

^mSN^∗m_h^∗

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0

η

ⁿ

α

v^S

∗v

N^∗_h 0

η

^m

α

v^S

∗v

N^∗_h

η

^r

α

v^S

∗v

N_h^∗ 0 0

0 0 0 0 0 0 0

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

,

andtheJacobianVgivenby

V=

⎡

⎢ ⎢

⎢ ⎢

⎢ ⎢

⎣

ν

^n+dh 0 0 0 0 0 0

−

ν

n Ln 0 0 0 0 0

0 0

ν

^m+d_h 0 0 0 0

0 0 −

ν

^{m Lm 0 0 0}

0 −

γ

^{n 0 −}

γ

^m

β

^+dh 0 0

0 0 0 0 0

ν

v+d_v 0

0 0 0 0 0 −

ν

v d_v

⎤

⎥ ⎥

⎥ ⎥

⎥ ⎥

⎦

,

thereforethecharacteristicpolynomialofthenextgenerationmatrixFV⁻¹is

λ

⁵

λ

²−

α

v

ν

vS^∗_v d_v

(

^dh+

β )( ν

v+d_v

)

^N∗_h

R²0n+R²0m

=0,

where

R²_0n=

θα

ⁿ

ν

ⁿ

( η

ⁿ

(

^dh+

β )

+

γ

ⁿ

η

^r

)

Ln

(

^dh+

ν

ⁿ

)

^, R²0m=

(

¹−

θ ) α

m

ν

m

( η

m

(

^dh+

β )

+

γ

m

η

r

)

Lm

(

^dh+

ν

m

)

^.

Thecharacteristicpolynomialthereforeisthequadraticequation

λ

²⁻

ν

v

α

vS^∗_v d_v

(

^dh+

β )( ν

v+d_v

)

^Nh^∗

R²_0n+R²_0m

=0. (11)