The complexity of recognizing minimally tough graphs

(1)

The complexity of recognizing minimally tough graphs

Gyula Y Katona^∗

Department of Computer Science and Information Theory

Budapest University of Technology and Economics, Hungary

and

MTA-ELTE Numerical Analysis and Large Networks Research Group, Hungary

kiskat@cs.bme.hu

Istv´an Kov´acs^† Shapr3D Hungary

istvan.kovacs@shapr3d.com

Kitti Varga^‡

Alfr´ed R´enyi Institute of Mathematics Hungarian Academy of Sciences, Hungary

vkitti@cs.bme.hu

Abstract: Lettbe a real number. A graph is calledt-tough if the removal of any vertex set S that disconnects the graph leaves at most|S|/t components. The toughness of a graph is the largest t for which the graph is t-tough. A graph is minimallyt-tough if the toughness of the graph is tand the deletion of any edge from the graph decreases the toughness. The complexity class DP is the set of all languages that can be expressed as the intersection of a language in NP and a language in coNP. We prove that recognizing minimallyt-tough graphs is DP-complete for any positive rational numbert. We introduce a new notion called weighted toughness, which has a key role in our proof.

Keywords: minimally toughness, complexity, DP-completeness

1 Introduction

All graphs considered in this paper are finite, simple and undirected. Let ω(G) denote the number of components and α(G) denote the independence number of a graphG. For a graphGand a vertex set V⁰⊆V(G) letG[V⁰] denote the subgraph ofGinduced byV⁰.

Definition 1 Let t be a real number. A graphGis called t-tough if ω(G−S)≤ |S|

t

for any vertex setS⊆V(G)that disconnects the graph (i.e. for any S⊆V(G)withω(G−S)>1). The toughnessofG, denoted byτ(G), is the largesttfor which G ist-tough, takingτ(Kn) =∞for alln≥1.

We say that a cutset S⊆V(G)is atough setif ω(G−S) =|S|/τ(G).

∗Research supported by National Research, Development and Innovation Office NKFIH, K-116769, K-108947 and by the BME-Artificial Intelligence FIKP grant of EMMI (BME FIKP-MI/SC).

†Research supported by National Research, Development and Innovation Office NKFIH, K-111827.

‡Research supported by National Research, Development and Innovation Office NKFIH, K-108947.

(2)

Definition 2 A graphG is minimallyt-tough if τ(G) =t andτ(G−e)< tfor all e∈E(G).

Lett be an arbitrary positive rational number and consider the following problem.

t-Tough

Instance: a graphG.

Question: is it true thatτ(G)≥t?

Bauer et al. [1] proved that for any positive rational numbertthe problemt-Toughis coNP-complete.

However, in some graph classes the toughness can be computed in polynomial time, for instance, in the class of split graphs [7].

The focus of our investigation is on the critical version of the problemt-Tough. Lettbe an arbitrary positive rational number and consider the following problem.

Min-t-Tough Instance: a graphG.

Question: is it true thatGis minimallyt-tough?

Extremal problems usually seem not to belong to NP∪coNP; therefore, the complexity class called DP was introduced by Papadimitriou and Yannakakis [5].

Definition 3 A languageLis in the class DPif there exist two languagesL₁∈NP andL₂∈coNP such that L=L₁∩L₂.

A language is called DP-hardif all problems in DP can be reduced to it in polynomial time. A language is DP-completeif it is in DP and it is DP-hard.

In our proofs we use the following problem for reduction.

α-Critical

Instance: a graphGand a positive integerk.

Question: is it true thatα(G)< k, butα(G−e)≥kfor any edgee∈E(G)?

Theorem 4 ([6]) The problem α-Critical is DP-complete.

Definition 5 A graphG is called α-criticalif α(G−e)> α(G)for alle∈E(G).

Our main result is the following.

Theorem 6 The problem Min-t-Toughis DP-complete for any positive rational number t.

The paper is organized as follows. In Section 2 we prove some useful lemmas, including that the problemMin-t-Toughbelongs to DP for any positive rational numbert. In Section 3 we prove Theorem 6 for any positive rational number 1/2< t <1, then we prove the theorem for any positive rational number t≥1 in Section 4. Finally, in Section 5 we prove the theorem for any positive rational numbert≤1/2.

2 Preliminaries

In this section we cite some results.

Proposition 7 ([2]) For every positive rational numbert the problem Min-t-Toughbelongs to DP.

Lemma 8 (Problem 14of §8 in [3]) If we replace a vertex of an α-critical graph with a clique, and connect every neighbor of the original vertex with every vertex in the clique, then the resulting graph is stillα-critical.

Lemma 9 ([4]) Let Gbe an α-critical graph and w an arbitrary vertex of degree at least two. Splitw into two vertices y andz, each of degree at least 1, add a new vertex xand connect it to both y andz.

Then the resulting graphG⁰ isα-critical, andα(G⁰) =α(G) + 1.

(3)

For one of our proofs we also need the following observation, which is a straightforward consequence of Theorem 4 and Lemmas 8 and 9.

Proposition 10 For any positive integersl andm the following variant of the problemα-Critical is DP-complete.

Instance: anl-connected graphGand a positive integerkthat is divisible bym.

Question: is it true thatα(G)< k, butα(G−e)≥kfor any edgee∈E(G)?

3 Minimally t-tough graphs, where 1/2 < t < 1

Before proving Theorem 6 for any positive rational number 1/2< t <1, we need some preparation: first we construct some auxilary graphs.

Lett be a rational number such that 1/2< t <1. Leta, bbe relatively prime positive integers such thatt=a/b. Letkbe a positive integer, and letW ={w1, . . . , wak}andW⁰={w₁⁰, . . . , w⁰_(b−1)k}. Place a clique on the vertices ofW and a complete bipartite graph on (W;W⁰). Obviously, the toughness of this complete split graph is a/(b−1) > t. Deleting an edge may decrease the toughness, and now we delete edges incident toW⁰ until the toughness remains at leasttbut the deletion of any other such edge would result in a graph with toughness less thant. LetH_t,k^∗ denote the obtained split graph. Now delete all the edges induced byW, and letH_t,k^∗∗ denote the obtained bipartite graph.

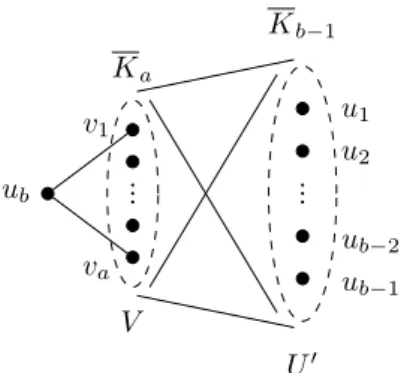
Claim 11 Let tbe a rational number such that1/2< t <1. Leta, bbe relatively prime positive integers such that t=a/band letH_t be the following graph. Let

V ={v₁, v₂, . . . , v_a}, U ={u₁, u₂, . . . , u_b}.

For any i ∈[a] and j ∈ [b−1] connect vi to uj, and connect ub to v1 and va. (See Figure 1.) Then τ(Ht) =t.

Ka

v₁

va

V ub

K_b−1

U⁰ u1

u2

u_b−2 u_b−1

Figure 1: The graphHt, when 1/2< t <1.

By repeatedly deleting some edges of H_t, eventually we obtain a minimally t-tough graph, let us denote it with H_t⁰ (i.e. if there exists an edge whose deletion does not decrease the toughness, then we delete it). Obviously, we could not delete the edges incident tou_b, so the vertexu_b still has degree 2. Let edenote the edge connectingv₁ andu_b and letH_t⁰⁰=H_t⁰−e.

Theorem 12 For any rational numbert with1/2< t <1 the problemMin-t-Toughis DP-complete.

(4)

Proof: Lettbe a rational number such that 1/2< t <1. By Proposition 7, the problemMin-t-Tough is in DP. To show that it is DP-hard, we reduceα-Criticalto it.

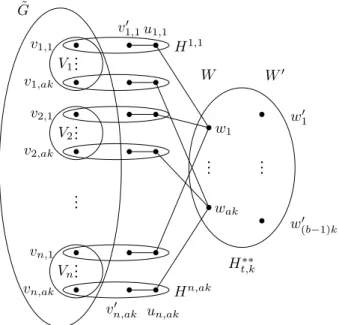
Let a, b be relatively prime positive integers such that t = a/b, let G be an arbitrary 2-connected graph on the verticesv1, . . . , vn and letGt,k be defined as follows. For alli∈[n] let

Vi={vi,j|i∈[n], j∈[ak]}

and place a clique on the vertices ofVi. For alli1, i2∈[n] ifvi₁vi₂ ∈E(G), then place a complete bipartite graph on (Vi₁;Vi₂). (This subgraph is denoted by ˜G in Figure 2.) For all i ∈[n], j ∈ [ak] “glue” the graphH_t⁰⁰ to the vertexvi,j by identifying vi,j with the vertexv1 ofH_t⁰⁰and letH^i,j denote the (i, j)-th copy ofH_t⁰⁰and letA^i,j denote its color class which containsvi,j, and letv_i,j⁰ andui,j denote the (i, j)-th copies of the verticesva andub, respectively. Let

V =

n

[

i=1

Vi

and

U ={ui,j |i∈[n], j∈[ak]}.

Add the vertex sets

W ={wj |j∈[ak]}

and

W⁰ ={w⁰₁, . . . , w_(b−1)k⁰ }

to the graph and place the bipartite graphH_t,k^∗∗ on (W;W⁰). For alli∈[n] andj ∈[ak] connect wj to ui,j. See Figure 2. Nowkis part of the input of the problemα-Critical, therefore the graphH_t,k^∗∗ must be constructed in polynomial time, which is possible since the tougness of split graphs can be computed in polynomial time [7]. On the other hand,tis not part of the input of the problemMin-t-Tough, therefore the graphH_t⁰⁰can be constructed in advance. Hence,G_t,k can be constructed fromGin polynomial time.

G˜

V1

V2

V_n v_1,1 v_1,ak v_2,1 v_2,ak

vn,1

vn,ak

H^1,1

H^n,ak v⁰_1,1

v_n,ak⁰ u_1,1

un,ak

w1

w_ak W

w⁰₁

w_(b−1)k⁰ W⁰

H_t,k^∗∗

Figure 2: The graphG_t,k, when 1/2< t <1.

To show that G is α-critical with α(G) = k if and only if Gt,k is minimallyt-tough, we need the following lemma.

(5)

Lemma 13 LetGbe a 2-connected graph with α(G)≤k. ThenG_t,k ist-tough.

Let us assume thatGisα-critical withα(G) =k. By Lemma 13,Gt,k ist-tough, i.e.τ(Gt,k)≥t.

LetI be an independent vertex set of sizeα(G) inGt,k[V]. Let J ={(i, j)∈[n]×[ak]|vi,j∈I}

and

S=



 [

(i,j)/∈J

A^i,j



∪W. ThenS is a cutset inGt,k with

|S|=a |V| −α(G)

+ak=a|V| and

ω(G_t,k−S) =α(G) +b |V| −α(G)

+ (b−1)k=b|V|=|S|

t , soτ(G_t,k)≤t.

Therefore,τ(G_t,k) =t.

Lete∈E(G_t,k) be an arbitrary edge. Ifehas an endpoint inU, then this endpoint has degree 2, so τ(Gt,k−e)≤1/2< t. Ifehas an endpoint inW⁰, then by the properties ofH_t,k^∗ , it can be shown that τ(G_t,k−e)< t. If e is induced by Hⁱ⁰^,j⁰ for some i₀ ∈[n], j₀ ∈[ak], then by the properties ofH_t⁰, it can be shown that τ(G_t,k−e)< t. Ife connects two vertices ofV, then using the fact thatG_t,k[V] is α-critical by Lemma 8, it can be shown thatτ(Gt,k−e)< t.

Now let us assume that G is not α-critical with α(G) = k, i.e. either α(G) 6= k or even though α(G) =k, the graphGis notα-critical.

Case 1: α(G)> k.

LetI be an independent vertex set of sizeα(G) inGt,k[V] and let J ={(i, j)∈[n]×[ak]|vi,j∈I}

and

S=



 [

(i,j)/∈J

A^i,j



∪W. ThenS is a cutset inGt,k−ewith

|S|=a |V| −α(G)

+ak=a|V| −a α(G)−k and

ω(G_t,k−S) =α(G) +b |V| −α(G)

+ (b−1)k=b|V| −(b−1) α(G)−k

> b|V| −b α(G)−k

=|S|/t, soτ(G_t,k)< t, which means thatG_t,k is not minimallyt-tough.

Case 2: α(G)≤k.

Since Gis notα-critical withα(G) =k, there exists an edgee∈E(G) such thatα(G−e)≤k. By Lemma 13, the graph (G−e)t,kist-tough, but we can obtain (G−e)t,k fromGt,k by edge-deletion, which means thatGt,k is not minimallyt-tough.

(6)

4 Minimally t-tough graphs, where t ≥ 1

This section resembles the previous one in structure. However, it requires some additional ideas that make the proofs more complicated.

Let t ≥ 1 be a rational number. It is easy to see that either d2te = 2dte or d2te = 2dte −1. Let T =dte, andT⁰ =d2te − dteandM =

2dte/d2te

. Leta, bbe the smallest positive integers such that b≥3 andt=a/b.

Letkbe a positive integer that is divisible by a, and let

W ={wj,l,m |j∈[k], l∈[T⁰], m∈M} and

W⁰={w₁⁰, . . . , w⁰_{(M T}0/t−1)k}.

Place a clique on the vertices ofW and a complete bipartite graph on (W;W⁰). Obviously, the toughness of this complete split graph is

kM T⁰

(M T⁰/t−1)k = 1

1 t −_{M T}¹0

> t.

Deleting an edge may decrease the toughness, and now we delete edges incident toW⁰until the toughness remains at least t but the deletion of any other such edge would result in a graph with toughness less thant. LetH_t,k^∗ denote the obtained split graph. Now delete all the edges induced byW, and letH_t,k^∗∗

denote the obtained bipartite graph.

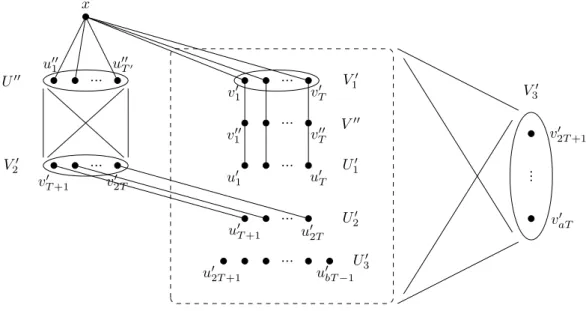
LetHtbe the following graph. Let

V₁⁰={v⁰₁, . . . , v⁰_T}, V₂⁰={v_T⁰₊₁, . . . , v_2T⁰ }, V₃⁰ ={v_2T⁰ ₊₁, . . . , v_aT⁰ }, V⁰⁰={v₁⁰⁰, . . . , v_T⁰⁰},

U₁⁰ ={u⁰₁, . . . , u⁰_T}, U₂⁰ ={u⁰_T+1, . . . , u⁰_2T}, U₃⁰ ={u⁰_2T+1, . . . , u⁰_bT₋₁}, U⁰⁰={u⁰⁰₁, . . . , u⁰⁰_T0},

and

U₁⁰⁰={u⁰⁰₁, . . . , u⁰⁰_T}.

Place a clique on the vertices of V₁⁰, V₂⁰, V₃⁰, and U⁰⁰. For all l ∈ [T] connect v⁰⁰_l to v⁰_l and tou⁰_l, and connectv⁰_T+ltou⁰_T_+l. Connect all the vertices ofV₃⁰ to all the vertices ofV₁⁰∪V⁰⁰∪U₁⁰∪U₂⁰, and connect all the vertices ofV₂⁰ to all the vertices ofU⁰⁰. Finally, add a new vertexxto the graph and connect it to all the vertices ofV₁⁰∪U⁰⁰. See Figure 3.

Lettbe a real number. Given a graphGand a positive weight functionwon its vertices, we say that the graphGis weightedt-tough with respect to the weight functionwif

ω(G−S)≤w(S) t

holds for any vertex setS⊆V(G) whose removal disconnects the graph; where w(S) =X

v∈S

w(v).

We define the weighted toughness of a noncomplete graph (with respect to the weight functionw) to be the largestt for which the graph is weightedt-tough, and we define the weighted toughness of complete graphs (with respect tow) to be infinity.

(7)

x

u⁰⁰₁ u⁰⁰_T0

U⁰⁰

v_T⁰₊₁ v⁰_2T V₂⁰

v₁⁰ v_T⁰ V₁⁰ v₁⁰⁰ v_T⁰⁰ V⁰⁰ u⁰₁ u⁰_T U₁⁰

u⁰_T₊₁ u⁰_2T U₂⁰ u⁰_2T+1 u⁰_bT₋₁U₃⁰

v_2T⁰ ₊₁

v_aT⁰ V₃⁰

Figure 3: The graphH_t, whent≥1.

Claim 14 For any rational number t ≥ 1 the graph Ht has weighted toughness t with respect to the weight function w that assigns weight 1 to all the vertices of Ht except for the vertex x, to which it assigns weightt.

Deleting an edge may decrease the weighted toughness, and now we delete edges not induced by U⁰⁰ until the weighted toughness with respect to the weight functionwremains at leasttbut the deletion of any other edge not induced byU⁰⁰ would result in a graph with weighted toughness less thant. LetH_t⁰ denote the obtained graph.

According to the following claim we could not delete the edges induced by V₁⁰ or incident to any of the vertices of{x} ∪V₂⁰∪U⁰⁰.

Claim 15 Let t ≥ 1 be a rational number. For any edge e ∈ E(H_t) induced by V₁⁰ or incident to any of the vertices of {x} ∪V₂⁰ ∪U⁰⁰ there exists a cutset S = S(e) ⊆ V(H_t) in H_t−e for which ω (H_t−e)−S

> w(S)/t.

Claim 16 Let t≥1 be a rational number andH_t⁰⁰=H_t⁰− {x}. Then the following hold.

(i) The graph H_t⁰⁰ is connected.

(ii) For any cutsetS of H_t⁰⁰,

ω(H_t⁰⁰−S)≤ |S|

t + 1.

(iii) IfV₁⁰⊆S holds for a cutsetS of H_t⁰⁰, then

ω(H_t⁰⁰−S)≤ |S|

t .

(iv) For any edge e∈E(H_t⁰⁰) not induced by U⁰⁰ there exists a vertex setS =S(e) whose removal from H_t⁰⁰−edisconnects the graph and

ω (H_t⁰⁰−e)−S

>|S|

t .

(8)

Theorem 17 For any rational numbert≥1 the problem Min-t-Tough is DP-complete.

Proof: Lett≥1 be a rational number. By Proposition 7, the problemMin-t-Toughis in DP. To show that it is DP-hard, we reduce the variant ofα-Criticalmentioned in Proposition 10 to it.

Let T =dte, and T⁰ =d2te − dte, and M =

2dte/d2te

. Let a, b be the smallest positive integers such that b ≥3 and t = a/b, let G be an arbitrary 3-connected graph on the vertices v1, . . . , vn with n ≥t+ 1, let k be a positive integer that is divisible by a and let Gt,k be defined as follows. For all i∈[n], j∈[k], m∈[M] let

Vi,j,m={vi,j,l,m|l∈[T]}.

For alli∈[n] let

Vi= [

j∈[k], m∈[M]

Vi,j,m

and place a clique on the vertices ofV_i. For alli₁, i₂∈[n] ifv_i₁v_i₂ ∈E(G), then place a complete bipartite graph on (V_i₁;V_i₂). (This subgraph is denoted by ˜Gin Figure 4.) For all i∈[n], j∈[k], m∈[M] “glue”

the graph H_t⁰⁰ to the vertex set V_i,j,m by identifying v_i,j,l,m with the vertexv_l⁰ ofH_t⁰⁰ for alll∈[T]. For alli∈[n], j∈[k], l∈[T⁰], m∈[M] letu⁰⁰_i,j,l,m denote the (i, j, m)-th copy ofu⁰⁰_l. For allj∈[k], m∈[M] add the vertex set

Wj,m={wj,l,m |l∈[T⁰]}

to the graph and for alli∈[n], j∈[k], l∈[T⁰], m∈[M] connectw_j,l,m to u⁰⁰_i,j,l,m. Let

W = [

j∈[k], m∈[M]

Wj,m.

Add the vertex set

W⁰={w₁⁰, . . . , w⁰_{(M T}0/t−1)k}

to the graph and place the bipartite graph H_t,k^∗∗ on (W;W⁰). See Figure 4. Similarly as in the previous case,Gt,k can be constructed fromGin polynomial time.

G˜

V_1,1,1

V_n,k,M

H^1,1,1

H^n,k,M U_1,1,1⁰⁰

U_n,k,M⁰⁰ u⁰⁰_1,1,1,1

u⁰⁰_n,k,T0,M

w1,1,1

wk,T⁰,M

W

w₁⁰

w⁰_{(M T}0/t−1)k

W⁰

H_t,k^∗∗

Figure 4: The graphGt,k, when t≥1.

Using a similar but more complicated argument as in the proof of Theorem 12, it can be shown that Gisα-critical withα(G) =kif and only if Gt,k is minimallyt-tough.

(9)

5 Minimally t-tough graphs with t ≤ 1/2

The case whent≤1/2 is special in some sense: graphs with toughness at most 1/2 can have cut-vertices.

Unlike in the previous cases, we reduceMin-1-Toughto this problem.

Proposition 18 Let t≤1/2 be a positive rational number. Leta, b be relatively prime positive integers such that t=a/band letHt be the following graph. Let

V ={v1, v2, . . . , va}, U ={u1, u2, . . . , ub−a}, W ={w1, w2, . . . , wa}.

Place a clique on the vertices ofV, connect every vertex of V to every vertex ofU, and connectv_i tow_i for alli∈[n]. Thenτ(H_t) =t.

By repeatedly deleting some edges of Ht, eventually we obtain a minimally t-tough graph; let us denote it with H_t⁰ (i.e. if there exists an edge whose deletion does not decrease the toughness, then we delete it). Obviously, we could not delete the edges between V and W, so the vertices ofW still have degree 1 inH_t⁰.

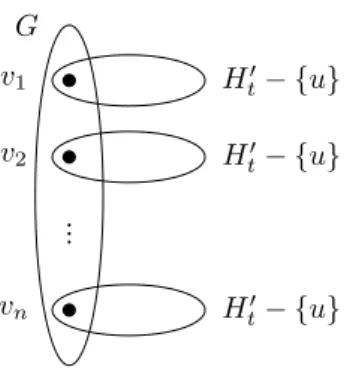
Definition 19 LetH be a graph with a vertexuof degree 1, and letv be the neighbor of u. LetGbe an arbitrary graph, and “glue”H − {u} separately to all vertices of Gby identifying each vertex of Gwith v. LetG⊕vH denote the obtained graph.

Theorem 20 For any positive rational numbert≤1/2 the problem Min-t-Toughis DP-complete.

Proof: Lett≤1/2 be a positive rational number. By Proposition 7, the problem Min-t-Toughis in DP. To show that it is DP-hard, we reduce a variant ofMin-1-Toughto it.

LetG be an arbitrary graph andn=|V(G)|. Consider the graphH_t⁰ and letu∈U be an arbitrary vertex ofH_t⁰ having degree 1, and letv be its neighbor.

It can be shown thatGt=G⊕vH_t⁰ (see Figure 5) is minimallyt-tough if and only ifGis minimally 1-tough orG'K₂ orG'K₃.

G v1

v2

v_n

H_t⁰− {u}

Figure 5: The graphGt=G⊕vH_t⁰, whent≤1/2.

References

[1] D. Bauer, S. L. Hakimi, E. Schmeichel, Recognizing tough graphs is NP-hard,Discrete Applied Mathematics(1990)28

[2] G. Y. Katona, I. Kov´acs, K. Varga, The complexity of recognizing minimally t-tough graphs, Proceedings of the 10th Japanese-Hungarian Symposium on Discrete Mathematics and Its Applica- tions(2017)

(10)

[3] L. Lov´asz, Combinatorial problems and exercises, AMS Chelsea Publishing, Providence, Rhode Island(2007)

[4] L. Lov´asz, M. D. Plummer, Matching Theory, Annals of Discrete Mathematics, Volume 29, North-Holland, Amsterdam(1986)

[5] C. H. Papadimitriou, M. Yannakakis, The Complexity of Facets (and Some Facets of Complex- ity), Journal of Computer and System Sciences(1984)28

[6] C. H. Papadimitriou, D. Wolfe, The Complexity of Facets Resolved, Journal of Computer and System Sciences(1988)37

[7] G. J. Woeginger, The toughness of split graphs, Discrete Mathematics(1998)190