In the current thesis, a new approach for the statistical analysis of Hidden Markov Models (HMM-s), in particular for the analysis of maximum probability estimation, is established. The main technical results provide conditions for the functions of the input-output process of a nonlinear stochastic system to be L-mixing. The channel is characterized by an infinite range of transition densities, indexed by the states of the Markov chain.
Araposthatis and Marcus in [1] found strong consistency of the maximum likelihood estimator for the final state and binary readout of HMMs. The strong consistency of the maximum likelihood estimator for the continuous reading space was first proved by Leroux in [41] using the subadditive ergodic theorem. To conclude Section 4.1, we compare our conditions with those of [40], which ensure the geometric ergodicity of the extended process.
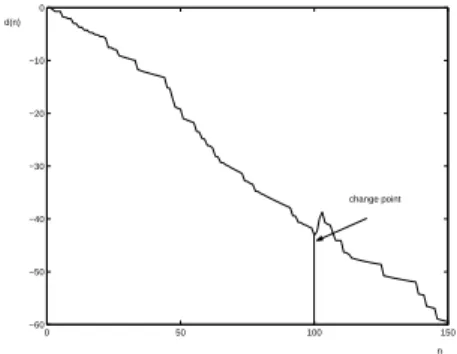
In Chapter 8, using the above representation of the error term, we investigate the effect of parameter uncertainty on the performance of an adaptive coding procedure.
Hidden Markov Models
The true value of the parameter (or the unknown quantities) is the one used to generate the process. For notational convenience, we write Q > 0 if all the elements of the transition probability matrix are strictly positive. In practice, the transition probability matrix Q∗ and the initial probability distribution p∗0 for the unobserved Markov chain (Xn) as well as the conditional probabilities b∗i(y) for the observation sequence (Yn) may be unknown.
We will take an arbitrary probability vector q as initial condition, and the solution of the Baum equation will be denoted by pn(q). An essential feature of the result is that q−qT V appears in the upper bound, see [2]. We will need the total variation norm when the state space is not nine, see Section 4.2.
2.7) A standard step to prove the consistency of the maximum likelihood estimator is to show that.
Entropy Ergodic Theorems
Let Pθ denote a distribution of the misspecified Hidden Markov model and let p(y1, ..., yn, θ) denote the induced n-dimensional density. The series almost certainly converges to the upper Lyapunov exponent of the series of auxiliary random matrices. They arrived at a similar ergodic theorem for the normalized conditional log probability, also using Kingman's ergodic theorem following Leroux's, see [34].
LeGland and Mevel proved the geometric ergodicity of the Markov chain and showed the existence of a unique invariant distribution under appropriate conditions. In particular, this property implies an ergodic theorem for general finite state HMMs similar to (2.9). They developed an ergodic theorem for HMMs with arbitrary, not necessarily stationary, initial density of states.
They proved an ergodic theorem similar to (2.9) for almost certain and L1 convergence of the normalized conditional log-likelihood of a sequence of observations.
L-mixing processes
However, a much simpler method is to find any Fn−τ+ measurable random variable that approximates Xn with reasonable accuracy, and then use the following lemma (see Lemma 2.1 in [23]). Two applications of this theorem are given below. In the first we take fn= 1 for alln. In the second, the process (Xn) is subject to exponential smoothing. Let (Xn(θ)) be a measurable, separable, M-bounded random field that is M-Hölder continuous in θ with exponent α for θ ∈ D.
A useful application of the above result is obtained by combining it with Theorem 2.3.5 to obtain the following unified version of Theorem 2.3.5, see Theorem 1.2 in [23]. The following lemma, see [7], shows the relationship between the Doeblin condition and the representation of the Markov chain. The Doeblin condition is valid with m = 1 if and only if there exists a representation such that Q(Tn ∈ Γc) ≥ δ, where Γc is the set of constant maps.
The Doeblin condition is valid with m≥1 if and only if there exists a representation such that.
Markov chains and L -mixing processes
Exponentially stable random mappings I
Since g(x, z) is bounded, the first term on the right-hand side can be trivially bounded from above. Using the Minkowski inequality, condition 3.3.5 and lemma 3.3.8 (the distribution of X∗ is stationary), we have that Zm and Zm+,m are M-bounded.
Exponentially stable random mappings II
We start with a lemma about the existence of a stationary distribution for the process (Xn, Zn). It was shown in the proof of Proposition 3.1.4 that the limit is well bounded. So the distribution of (X0, Z0∗) is the same as the distribution of (X1, Z1), the theorem is proved.
According to Lemma 3.4.6 under the conditions of Theorem 3.4.3 there is a stationary distribution of the process (Xn, Zn). Let this stationary distribution be denoted by μ and for an arbitrary initialization let the (Xn, Zn)beµn distribution. If we replace condition 3.4.1 with the following conditions, then Lemma 3.4.2 is still true: the Radon-Nikodym derivative of µ0 w.r.t.
Exponentially stable random mappings III
For the L-mixing property, we follow the same path as in the proof of Theorem 3.3.10. E3q1Zm+,m3q+E3q1 Zm)3q E3q1 Zn3q+E3q1 Zn,m+ 3q The second inequality is a consequence of condition 3.5.1, the third inequality is a consequence of Hölder's inequality, and the fourth inequality follows from the exponential stability of f.
On-line estimation
The BMP scheme
In this section we present the basic principles of the theory of recursive estimation developed by Benveniste, Metivier and Priouret, BMP henceforth (see Chapter 2, Part II. of [6]). To specify the class of functionsH for which the theory is developed, consider a Lyapunov functionV: U → R+ and dene for real-valued functions gonU and any p≥0th norms. All but one condition will be formulated in terms of the Markov chain {Un(θ): n ≥ 0} for a fixed θ ∈ D with an arbitrary, non-arbitrary initial value U0(θ) =u.
Conditions A1 and A2 imply geometric ergodicity of the Markov chains in the following sense: for any θ ∈ D, u ∈ U and any g ∈ C(p+ 1) there exists a Γθg such that. A key contribution of BMP theory is that the above geometric ergodicity is derived by verifying conditions on a much more convenient class of test functions, namely Li(p). In other words, the kernels Πnθ are assumed to be Lipschitz continuous, uniform in n, with respect to the parameter θ when applied to a small set of test functions Li(p).
For any compact subset Qof D there exists a constant K =K(Q) such that for any n≥0 and arbitrary initial values θ∈Q, u∈ U. Remark: In fact, it is sufficient to require the above condition forΠθHθ, thus H be discontinuous.
Application for exponentially stable nonlinear systems 40
Since we did not use the metric property in Theorem 3.6.4X, it can be any abstract measurable space. Moreover, we have used the Doeblin property only for the existence of a stationary distribution of the Markov chain (Xn). Thus from the denition of d and the exponential stability of the reflection f we have in the set A.
Thus we get that if assumption (A5) is satisfied for a function H, and we have a Lyapunov function that satisfies (A6), then convergence result Theorem 3.6.1 holds for the algorithm (3.48). This chapter demonstrates the relevance of the previous results for the estimation of Hidden Markov models. Instead, the true value of the corresponding unknown quantity is indicated by ∗ and the current value is indicated by letters without ∗.
A central question in estimation problems is to prove the ergodic theorem for (2.9), see Chapter 2, which is equivalent to the existence of the limit. Let the running value of the transition probability matrix Q and the running value of the conditional read densities all be positive, that is, the initialization of the process (Xn, Yn) is arbitrary, where the Radon-Nikodym derivative of the initial distribution π0 is relative to the stationary distribution π is bounded, i.e.
Therefore, the function g(y, p) is Lipschitz continuous and thus Theorem 3.4.3 implies that g(Yn, pn) is an L-mixture process. Furthermore, let us identify the initialization of the true process (Xn, Yn) by η and the initialization of the predictive lter by ξ. This case follows from Theorem 4.1.1, but the integrability condition (4.7) is simplified due to the discrete measure.
Let the transition probability matrix of the unobserved Markov chain be primitive and the conditional reading density be positive, i.e. Assume that the process (Xn) satisfies the Doeblin condition with m = 1 and let be the run value of the transition probability matrix. positive, i.e.
Extension to general state space
Estimation ofHMMs: continuous state space
This implies that the density of the invariant distribution of the pair (Xn, Yn) is. Let the initialization of the process (Xn, Yn) be random such that the Radon-Nikodym derivative of the initial distribution π0 w.r.t the stationary distribution π is bounded, i.e. Furthermore let us identify the initialization of the true process (Xn, Yn) by η and the initialization of the predictive lter by ξ.
In this case, θ is often the parameter of the model that parametrizes the transition matrix Q and the conditional readout probabilities bi(y). Furthermore, suppose that for an estimation of the parameter of the Hidden Markov Model we have θ ∈ D. Furthermore, let us identify the initialization of the true process (Xn, Yn) by η and the initialization of the process (pn, Wn) by ξ .
From Lemma 3.3.8, we have the M-boundedness Wn (the conditions of the lemma are satisfied, see (6.10) and (6.9)) with arbitrary initialization. Let the initialization of the process (Xn, Yn) be random, where the Radon-Nikodym derivative of the initial distribution π0 with respect to the stationary distribution π is bounded, i.e. Let the initialization of the process (Xn, Yn) be random, where the Radon -Nikodymov derivative of the initial distribution π0 with respect to the stationary distribution π is bounded, i.e. 6.23) We use the method of maximum likelihood (ML) to estimate an unknown parameter.
We will refer to this as the cost function associated with the ML estimate of the parameter. Indeed if the initial value of the predictive lter process is from a stationary distribution, then δn = 0. Consider the Taylor series expansion of LθN(θ, θ∗) around θ = θ∗ and evaluate the value of the function atθ = ˆθN.
Furthermore, we assume that for a Hidden Markov Model parameter estimate we have θ∈D. Let the initialization of the process (Xn, Yn) be random, where the Radon-Nikodym derivative of the initial distribution π0 w.r.t the stationary distribution π is bounded, so 7.2) If the dynamics changes slowly in time, then we have to adapt to the current system . We will refer to this as the cost function associated with the modified ML parameter estimate.
A key result in the theory of the stochastic complexity can be extended for the present case (see [26]).