J. Leroux and J.-F. Raskin (Eds.): Tenth International Symposium on Games, Automata, Logics, and Formal Verification (GandALF’19).
EPTCS 305, 2019, pp. 169–182, doi:10.4204/EPTCS.305.12
© Kitti Gelle & Szabolcs Iván This work is licensed under the Creative Commons Attribution License.
Kitti Gelle
University of Szeged, Hungary kgelle@inf.u-szeged.hu
Szabolcs Iván
University of Szeged, Hungary szabivan@inf.u-szeged.hu
We show that if a context-free grammar generates a language whose lexicographic ordering is well- ordered of type less thanω2, then its order type is effectively computable.
1 Introduction
If an alphabetΣis equipped by a linear order<, this order can be extended to the lexicographic ordering
<ℓ on Σ∗ as u<ℓv if and only if either u is a proper prefix of v or u=xay and v =xbz for some x,y,z∈Σ∗and lettersa<b. So any languageL⊆Σ∗can be viewed as a linear ordering (L, <ℓ). Since {a,b}∗contains the dense ordering(aa+bb)∗aband every countable linear ordering can be embedded into any countably infinite dense ordering, every countable linear ordering is isomorphic to one of the form(L, <ℓ) for some language L⊆ {a,b}∗. A linear ordering (or an order type) is called regular or context-free if it is isomorphic to the linear ordering (or, is the order type) of some language of the appropriate type. It is known [2] that an ordinal is regular if and only if it is less thanωω and is context- free if and only if it is less thanωωω. Also, the Hausdorff rank [13] of any scattered regular (context-free, resp.) ordering is less thanω (ωω, resp) [10, 8].
It is known [9] that the order type of a well-ordered language generated by a prefix grammar (i.e. in which each nonterminal generates a prefix-free language) is computable, thus the isomorphism problem of context-free ordinals is decidable if the ordinals in question are given as the lexicograpic ordering of prefixgrammars. Also, the isomorphism problem of regular orderings is decidable as well [15, 3]. At the other hand, it is undecidable for a context-free grammar whether it generates a dense language, hence the isomorphism problem of context-free orderings in general is undecidable [7].
Algorithms that work for the well-ordered case can in many cases be “tweaked” somehow to make them work for the scattered case as well: e.g. it is decidable whether(L, <ℓ) is well-ordered or scat- tered [6] and the two algorithms are quite similar.
In this paper we continue to explore the boundary of decidability of the isomorphism problem of context-free orderings. We show that if the order type o(L) of a context-free language Lis known to have the formω×k+nfor some integerskandn, thenkandncan be effectively computed. The main building block for proving this is a decision procedure for solvingo(L(X))=? ω for each nonterminalX, and a recursive algorithm that terminates for languages of order type less thanω2.
2 Notation
Alinear ordering is a pair (Q, <), where Q is some set and the< is a transitive, antisymmetric and connex (that is, for eachx,y∈Qexactly one ofx<y,y<xorx=yholds) binary relation onQ. The pair
*Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT is acknowledged. Szabolcs Iván was supported by the János Bolyai Scholarship of the Hungarian Academy of Sciences. Kitti Gelle was supported by the ÚNKP-19-3-SZTE-86 New National Excellence Program of the Ministry of Human Capacities.
(Q, <)is also written simplyQif the ordering is clear from the context. A (necessarily injective) function h:Q1→Q2, where(Q1, <1)and(Q2, <2)are some linear orderings, is called an(order) embeddingif for eachx,y∈Q1,x<1yimpliesh(x)<2h(y). Ifhis also surjective,his anisomorphism, in which case the two orderings areisomorphic. An isomorphism class is called anorder type. The order type of the linear orderingQis denoted byo(Q).
For example, the class of all linear orderings contain all the finite linear orderings and the orderings of the integers (Z), the positive integers (N) and the negative integers (N−) whose order type is denoted ζ,ω and−ωrespectively. Order types of the finite sets are denoted by their cardinality, and[n]denotes {1, . . . ,n}for eachn≥0, ordered in the standard way.
The ordered sum∑x∈QQx, whereQis some linear ordering and for eachx∈Q,Qxis a linear ordering, is defined as the ordering with domain{(x,q):x∈Q,q∈Qx}and ordering relation(x,q)<(y,p)if and only if eitherx<y, orx=yandq<pin the respectiveQx. If eachQxhas the same order typeo1andQ has order typeo2, then the above sum has order typeo1×o2. IfQ= [2], then the sum is usally written as Q1+Q2.
If(Q, <)is a linear ordering andQ′⊆Q, we also write(Q′, <)for the subordering of(Q, <), that is, to ease notation we also use<for the restriction of<toQ′.
A linear ordering (Q, <)is calleddense if it has at least two elements and for eachx,y∈Qwhere x<ythere exists az∈Qsuch thatx<z<y. A linear ordering isscatteredif no dense ordering can be embedded into it. It is well-known that every scattered sum of scattered linear orderings is scattered, and any finite union of scattered linear orderings is scattered. A linear ordering is called awell-orderingif it has no subordering of type−ω. Clearly, any well-ordering is scattered. Since isomorphism preserves well-orderedness or scatteredness, we can call an order type well-ordered or scattered as well, or say that an order type embeds into another. The well-ordered order types are calledordinals. For any setΩof ordinals,(Ω, <)is well-ordered by the relationo1<o2 ⇔ “o1can be embedded injectively intoo2but not vice versa”. The principle of well-founded induction can be formulated as follows. AssumePis a property of ordinals such that for any ordinalo, ifPholds for all ordinals smaller thano, thenPholds foro. ThenPholds for all the ordinals.
For standard notions and useful facts about linear orderings see e.g. [13] or [14].
Hausdorff classified the countable scattered linear orderings with respect to their rank. We will use the definition of the Hausdorff rank from [8], which slightly differs from the original one (in whichH0
contains only the empty ordering and the singletons, and the classesHα are not required to be closed under finite sum, see e.g. [13]). For each countable ordinalα, we define the classHαof countable linear orderings as follows. H0 consists of all finite linear orderings, and whenα >0 is a countable ordinal, thenHα is the least class of linear orderings closed under finite ordered sum and isomorphism which contains all linear orderings of the form∑i∈ZQi, where eachQi is inHβi for someβi<α.
By Hausdorff’s theorem, a countable linear orderQis scattered if and only if it belongs toHα for some countable ordinalα. Therank r(Q)of a countable scattered linear ordering is the least ordinal α withQ∈Hα.
As an example, ω,ζ,−ω and ω+ζ or any finite sum of the form ∑
i∈[n]
oi withoi∈ {ω,−ω,1}for eachi∈[n]each have rank 1 while(ω+ζ)×ωhas rank 2.
LetΣbe an alphabet (a finite nonempty set) and letΣ∗(Σ+, resp) stand for the set of all (all nonempty, resp) finite words overΣ, ε for the empty word, |u|for the length of the word u,u·vor simply uvfor the concatenation ofuandv. Alanguageis an arbitrary subsetLofΣ∗. We assume that each alphabet is equipped by some (total) linear order. Two (strict) partial orderings, the strict ordering<sand the prefix ordering<pare defined overΣ∗as follows:
• u<svif and only ifu=u1au2andv=u1bv2for some wordsu1,u2,v2∈Σ∗and lettersa<b,
• u<pvif and only ifv=uwfor some nonempty wordw∈Σ∗.
The union of these partial orderings is the lexicographical ordering<ℓ=<s∪<p. We call the language L well-ordered or scattered, if (L, <ℓ) has the appropriate property and we define the rank r(L) of a scattered languageLasr(L, <ℓ). The order typeo(L)of a languageLis the order type of(L, <ℓ). For example, ifa<b, theno
{akb:k≥0}
=−ω ando
{(bb)ka:k≥0}
=ω.
Whenρis a relation over words (like<ℓor<s), we writeKρLifuρvfor each wordu∈Kandv∈L.
An ω-word over Σ is an ω-sequence a1a2. . . of letters ai ∈Σ. The set of all ω-words over Σis denoted Σω. The orderings <ℓ and <p are extended to ω-words. An ω-word w is called regular if w=uvω =uvvvv. . .for some finite wordsu∈Σ∗and v∈Σ+. Whenwis a (finite orω-) word overΣ andL⊆Σ∗is a language, thenL<wstands for the language{u∈L:u<w}. Notions likeL≥w,L<sware also used as well, with the analogous semantics.
Acontext-free grammaris a tupleG= (N,Σ,P,S), whereNis the alphabet of thenonterminal sym- bols,Σis the alphabet ofterminal symbols(orletters) which is disjoint fromN,S∈Nis thestart symbol andPis a finite set ofproductionsof the formA→α, whereA∈N andα is asentential form, that is,
α =X1X2. . .Xk for somek≥0 and X1, . . . ,Xk ∈N∪Σ. The derivation relations ⇒, ⇒ℓ, ⇒∗ and ⇒∗ℓ
are defined as usual (where the subscriptℓstands for “leftmost”). Thelanguage generated bya gram- mar Gis defined as L(G) ={u∈Σ∗ |S⇒∗u}. Languages generated by some context-free grammar are called context-free languages. For any set ∆ of sentential forms, the language generated by∆ is L(∆) ={u∈Σ∗|α ⇒∗ufor someα ∈∆}. As a shorthand, we defineo(∆)aso(L(∆)). A languageLis prefix(or prefix-free) if there are no wordsu,v∈Lwithu<pv. A context-free grammarG= (N,Σ,P,S) is called aprefixgrammar ifL(A)is a prefix language for eachA∈N. WhenX,Y∈N∪Σare symbols of a grammarG, we writeY XifX⇒∗uY vfor some wordsuandv;X≈Y ifX Y andY X both hold; andY ≺X ifY X but notX Y. A production of the formX→X1. . .XnwithXi≺X for each i∈[n]is called anescaping production.
A regular language over Σis one which can be built up from the singleton languages {a}, a∈Σ and the empty language /0 with finitely many applications of taking (finite) union, concatenationKL= {uv:u∈K,v∈L} and iteration K∗={u1. . .un:n≥0,ui∈K}. For standard notions on regular and context-free languages the reader is referred to any standard textbook, such as [11].
Linear orderings which are isomorphic to the lexicographic ordering of some context-free (regular, resp.) language are calledcontext-free (regular, resp.) orderings.
3 If o(L) < ω
2, then o(L) is computable
In this section we consider a context-free grammar G= (N,Σ,P,S) which contains no left recursive nonterminals, and generates a(n infinite) scattered language such that for eachX ∈N,X is usable and L(X)is an infinite language of nonempty words, moreover, each nonterminal but possiblySis recursive and there is no left recursive nonterminal (that is,X⇒+uX vimpliesu6=ε). Any context-free grammar can effectively be transformed into such a form, see e.g. [9].
The section is broken into two parts: the first subsection contains some technical decidability lemmas, while the second one contains the main result that if we know thato(L)<ω2for a well-ordered context- free languageL(so that the Hausdorff-rank ofLis at most one), theno(L)is effectively computable. This computability is already known for so-called ordinal grammars which generate a well-ordered language such that for each nonterminalX,L(X)is a prefix language [9]. However, this is a serious restriction and
makes many proofs easier since ifKis a prefix language, theno(KL) =o(L)×o(K)for any languageL.
This does not hold for arbitrary languages since e.g.o(a∗) =ω,o(b) =1 ando(a∗b) =−ω,o(a∗a∗) =ω, o((ac)∗) =ω ando((ac)∗(b+ab)) =ω+ (−ω)so a more careful case analysis is required. The reader is advised to skip the first subsection at first read – the proofs of the second part extensively refer to the lemmas of the first part.
3.1 Some technical lemmas
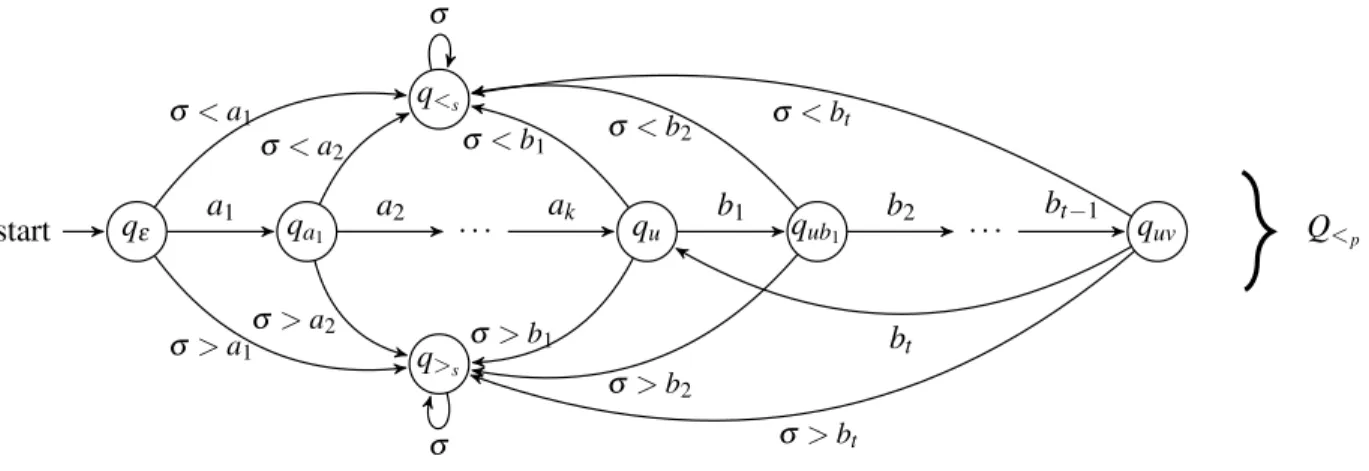
For anω-wordw, letPref(w)⊆Σ∗stand for the set of the finite prefixes ofw. For eachu=a1. . .ak∈Σ∗
andv=b1. . .bt ∈Σ+letMu,v denote the automaton (without specified final states) depicted in Figure 1.
qε
start qa1 · · · qu qub1 · · · quv
q<s
q>s
Q<p
a1 a2 ak b1 b2 bt−1
bt σ<a1
σ<a2 σ<b1 σ<b2 σ<bt
σ>a1
σ>a2 σ>b1
σ>b2
σ>bt
σ
σ
Figure 1: The automatonMu,v
Proposition 1. For any words u∈Σ∗ and v∈Σ+, the languages Pref(uvω),{w∈Σ∗:w<suvω}and {w∈Σ∗:uvω<sw}are regular.
Proof. Letu=a1. . .ak andv=b1. . .bt for the integersk≥0,t>0 and letters ai,bj and consider the automatonMu,vgiven in Figure 1. Then, by settingq<s (q>s, respectively) for the unique accepting state we recognize{w∈Σ∗:w<suvω}({w∈Σ∗:uvω <sw}, resp.), and by settingQ<pas the set of final states we recognizePref(uvω).
Lemma 1. For each sentential formαwith L(α)being infinite, we can generate a sequence w0,w1, . . .∈ L(α)and a regular word w∈Σω satisfying one of the following cases:
i) w1<sw2<s. . .and w= W
i≥0wi ii) w1>sw2>s. . .and w= V
i≥0wi
iii) w1<pw2<p. . .and w= W
i≥0wi
Proof. By the pumping lemma of context-free languages, asL(α)is infinite, one can generate a word u∈L(α)and a partitionu=u1u2u3u4u5such that|u2u4| ≥1 and for eachn≥0, the wordu1un2u3un4u5is inL(α).
Based on the relative order of the five subwords we consider the following cases:
1. There exists ann0such thatu3un40 <su2u3un40
Let us define the sequence aswn=u1un20+nu3un40+nu5. Let us fixnand letmdenotem=n0+n.
Here we get that wn<swn+1 if and only ifu3um4u5<su2u3um+14 u5, which is true since u3un40 <s u2u3un40impliesu3un40x<su2u3un40yfor anyx,y∈Σ∗, thus in particular forx=un4u5andy=un+14 u5
as well.
Hence the type of the sequence is of i) and the supremum isw= W
i≥0wi =u1uω2. (Observe that u26=εas that could not satisfyu3un40 <su2u3un40).
2. There exists ann0such thatu2u3un40 <su3un40
Again, u2 cannot be the empty word. Similarly to the first case, let us define the sequence as wn=u1un20+nu3un40+nu5and fixnand letmdenotem=n0+n.
Here we get thatwn+1<swnif and only ifu2u3um+14 u5<su3um4u5, which is true sinceu2u3un40 <s u3un40 impliesu2u3un40x<su3un40yfor anyx,y∈Σ∗, thus in particular forx=un+14 u5andy=un4u5
as well. So we get that the type of the sequence is ii) (with order type of−ω) and the infimum is w= V
i≥0wi=u1uω2.
3. For eachnit holds thatu3un4≤pu2u3un4andu46=ε In this caseu3uω4 =u2u3uω4.
Let us fixN=l
|u2|
|u4|
m
+1 and the sequence aswn=u1uN+n2 u3uN+n4 u5. Furthermore, letx∈Σ∗ be the unique word withu3uN4x=u2u3uN4. That is,xis the unique suffix ofuN4 of length|u2|. Hence, for anyn≥Nwe also haveu3un4x=u2u3un4for the samex(as we know thatu3un4≤pu2u3un4, their length differ by|u2|, and the latter word ends withuN4).
We have three subcases:
(a) It holds thatu3uN4u5<su2u3uN+14 u5
First observe that asu2u3uN+14 u5=u3uN4xu4u5, the assumption of the subcase yields u5<s
xu4u5. Then for eachm≥N we have u3um4u5<su3um4xu4u5=u2u3um4u4u5 =u2u3um+14 u5, implyingu1um2u3um4u5<su1um+12 u3um+14 u5. So the sequence is of type i) and its supremum is eitheru1uω2 (ifu2is nonempty) oru1u3uω4 (otherwise).
(b) It holds thatu2u3uN+14 u5<su3uN4u5
First sinceu2u3uN+14 u5 can be written asu3uN4xu4u5, the assumption of the subcase yields xu4u5 <su5. Then for each m≥N we have u3um4xu4u5 =u2u3um4u4u5 =u2u3um+14 u5 <s u3um4u5, so we get a sequence of words such thatu1um+12 u3um+14 u5<su1um2u3um4u5. Hence, the sequence is of type ii) with the infimum of eitheru1uω2 (if u2 is nonempty) or u1u3uω4 (otherwise).
(c) It holds thatu3uN4u5<pu2u3uN+14 u5
In this case for eachm≤Nwe haveu3um4u5<pu2u3um+14 u5, so we get an ascending prefix chain. Hence the order type of this sequence of iii) isω with the supremum of eitheru1uω2 (ifu2is nonempty) oru1u3uω4 (otherwise).
4. It holds thatu3<pu2u3andu4=ε Note thatu2cannot be empty in this case.
We have three subcases:
(a) It holds thatu3u5<su2u3u5
In this case for each n≤0 we have u1un2u3u5 <su1un+12 u3u5 iff u3u5 <su2u3u5 which is the assumption of this subcase. So we get that the sequence type is i) and the supremum is w=u1uω2.
(b) It holds thatu2u3u5<su3u5
Here, similarly to the previous case for each n≤0 we have u1un+12 u3u5 <su1un2u3u5 iff u2u3u5<su3u5, which is implied by the assumption. Hence we have an infinite descending chain with the sequence type of ii) and infimumw=u1uω2.
(c) It holds thatu3u5<pu2u3u5
In the last case sinceu3u5<pu2u3u5, for eachn≤0 we haveu1un2u3u5<pu1un+12 u3u5which is a prefix chain with sequence type of iii) and supremumw=u1uω2.
Observe that it is also decidable which (sub)case applies: first we check for the condition of Case 4 (which is clearly decidable). Then, if that condition does not hold, we check whetheru3uω4 =u2u3uω4 holds. As equality of regular words is decidable, this can be done, and if they are the same, then we again have three sub-conditions concerning finite words. Otherwise, ifu3uω4 6=u2u3uω4, then either u3uω4 <s u2u3uω4, that is,u3un40 <su2u3un40 for somen0, oru2u3uω4 <su3uω4, in which caseu2u3un40 <su3un40 for some n0. But since we know that one of these two cases has to hold, we only have to iterate through all the integersnand compareu3un4 withu2u3un4 and eventually there will be annfor which these two become comparable by<s. (A more efficient algorithm also exists, e.g. by analyzing the direct product automatonMu3,u4×Mu2u3,u4.)
We recall the following characterizations of those context-free grammars generating a scattered (or well-ordered) language from [1]:
Theorem 1 ([1]). Assume G = (N,Σ,P,S) is a context-free grammar such that each nonterminal is usable,ε-free and there are no left-recursive nonterminals. Then
• L(G)is scattered if and only if for each recursive nonterminal X there exists a word uX ∈Σ+such that whenever X⇒+uXα for some u∈Σ∗,α ∈(N∪Σ)∗, then u∈u+X.
• If L(G)is scattered and X≈X′ are recursive nonterminals, then there exists a word uX,X′<puX such that whenever X⇒+uX′αfor some u∈Σ∗,α ∈(N∪Σ)∗, then u∈u∗XuX,X′.
• L(G)is well-ordered if and only if it is scattered and for each recursive nonterminal X , L(X)<ℓuωX. Moreover, for each X,X′the words uX and uX,X′ are effectively computable and it is decidable whether L(X)is scattered, or well-ordered.
Proposition 2. If L(X)is well-ordered for the recursive nonterminal X , thenWL(X) =uωX.
Proof. By Theorem 1,L(X)<ℓuωX. SinceXis recursive and all the nonterminals are usable, there exists some derivation of the formX ⇒uX vfor some wordsu,v∈Σ∗and sou=umX for somem>0. SinceX is usable, there exists some wordw∈L(X)and so for eachn>0, the wordum·nX wvnis inL(X)and is still upperbounded byuωX. As the supremum of these words isuωX, we got the claimed result.
We call an infinite languageL⊆Σ∗aprefix chainif for eachu,v∈L, eitheru≤pvorv≤pu, that is, Lis totally ordered by the prefix relation, or equivalently,L⊆Pref(w)for someω-wordw. Clearly, any languageLis either a prefix chain or contains two wordsu,vwithu<sv. Note that ifLis a prefix chain, theno(L) =ω.
Lemma 2. It is decidable for each nonterminal X whether L(X)is a prefix chain.
Proof. By Lemma 1 we can effectively generate an infinite sequence w0,w1, . . ., either ascending or descending, belonging toL(X)along with its limit, which is of the formuvω for some u∈Σ∗,v∈Σ+. Now if the sequence is either a>s-chain or a<s-chain, thenL(X)cannot be a prefix chain.
Otherwise, the sequence itself is a prefix chain and its limit isuvω, hence the whole language L(X) is a prefix chain if and only ifL(X)⊆Pref(uvω)which can be effectively decided sincePref(uvω)is a regular language.
Lemma 3. If L is a context-free language with o(L) =ω, thenWL is a computable regular word.
Proof. Applying Lemma 1 we can generate a (necessarily increasing) sequencew0<w1< . . .of words belonging toLalong with their supremumuvω. Since the order type ofLis alsoω, its supremum has to coincide byuvω.
Lemma 4. Let X be a nonterminal such that L(X)is not a prefix chain andα be a sentential form with L(α)being infinite. Then o(Xα)is an infinite order type different fromω.
Proof. SinceL(X)is not a prefix chain and is infinite, there existsu,v∈L(X)withu<sv. ThenuL(α)<s
vyfor any memberyofL(α), hence each suchvyhas infinitely many lower bounds inL(Xα), thuso(Xα) cannot beω.
The last lemma of the subsection is a bit technical:
Lemma 5. If L1⊆Pref(uvω)is a context-free prefix chain with order typeω for some words u∈Σ∗and v∈Σ+and L2⊆Σ∗is a context-free language with order typeω, then it is decidable whether there exists some w1∈L1, u′∈Σ∗and a∈Σwith w1u′<puvω, w1u′a<suvω and u′a<pWL2.
Proof. Let us writeu=a1. . .akandv=b1. . .bt and consider the automatonMu,v of Figure 1. For each stateqofMu,v, letLu,v(q)stand for the (regular) language{w∈Σ∗:qε·w=q}.
LetQ1⊆Q<p be the set of those states qfor whichL1∩Lu,v(q)is nonempty. Since eachLu,v(q)is regular,Q1is computable, moreover,q∈Q1if and only ifqε·w=qfor somew∈L1.
Now by Lemma 3 we can compute the regular wordu2vω2 =WL2 and consider the direct product automatonM=Mu,v×Mu2,v2 where inMu2,v2 we use the primed versionq′of each stateq.
We claim that there exists wordsw1,u′ and a letterasatisfying the conditions of the lemma if and only if a state of the form(q<s,q′)is reachable from a state(p,q′ε)inMfor someq′∈Q′<p and p∈Q1.
Indeed: assume (p,q′ε)·w= (q<s,q′) for such states: let us choose p,q′ and w so that |w|is the shortest possible. Sincep∈Q1andq<s ∈/Q1,w=u′afor some wordu′∈Σ∗anda∈Σ. Then,q′ε·u′∈ Q′<p, since bothq′<s andq′>sare trap states inMu2,v2. Sincewis a shortest possible word andq<s,q>s are trap states inMu,v, we get that p·u′∈Q<p. Since p∈Q1, there is some wordw1∈L1withqε·w1=p.
Thus, this choice ofw1,u′andasatisfies the conditions of the lemma.
And similarly, givenw1∈L1,u∈Σ∗anda∈Σsatisfying the conditions we can define p=qε·w1, q′=q′ε·u′a.
3.2 The main decision procedures
In this part we flesh out the “top-level” results leading to the aforementioned computability result: that the order type of well-ordered context-free languages with Hausdorff-rank at most 1 is computable.
The main building block is the result that it is decidable for any context-free language Lwhether o(L) =ω holds.
Lemma 6. Ifα=X1X2is a sentential form and for each1≤i≤2we know whether o(Xi) =ωholds or not, then it is also effectively computable whether o(α)isω.
Proof. Clearly, ifo(X1)oro(X2)is some infinite order type different fromω, theno(α)is also such an order type and we can stop. Also, ifX1∈Σ, then o(α) =o(X2) and we are done. We can also decide whetherL(X1X2)is well-ordered and if not, it cannot beω and we can stop.
So we can assume thatX1∈Nand thusL(X1)is infinite and hence o(X1) =ω by assumption. Let L1,L2andLrespectively stand forL(X1),L(X2)andL(X1X2).
IfX2∈Σ, then we have several subcases:
1. If there exists a wordu∈L1and some lettera<X2withuabeing a prefix of infinitely many words inL1, thenuX2 is strictly larger than each of these wordsv, and sovX2<suX2as well, thuso(L) cannot beωbut some other infinite order type (asuX2∈Lis preceded by infinitely many members ofL).
2. Otherwise, letu∈L1. It suffices to show that there are only finitely many elements inLwhich are smaller thanuX2. AssumevX2∈Lis so thatvX2<puX2 thenv<pu as well, and asuhas only finitely many proper prefixes, we have that there can only be a finite number of such wordsv. Now ifvX2<suX2, then eitherv<ℓu(that’s again a finite number of possibilities, aso(L1) =ωimplies that any wordu∈L1has only a finite number of lower bounds inL1) oru<ℓv. Thus, in this case (asvX2<suX2rules out the possibility ofu<sv) it has to hold thatu<pvandv=uaxfor some a<X2. There are only finitely many possible choices for such lettersa<X2and by assumption (see the condition of the previous subcase), for each such letter,uacan be a prefix of only finitely many wordsv∈L1.
Thus,uX2 is larger than only a finite number of members ofLfor eachu∈L1, ando(L) =ω in this case.
We still have to show that it is decidable which of the two cases holds. Observe that ifuais a prefix of infinitely many words inL1 for some wordu∈L1 and letter a<X2, then no wordw∈L1can satisfy ua<swas then the order type ofL1could not beω. Thus,ua<pWL1in this case for some wordu∈L1
and lettera<X2. On the other hand, ifua<pWL1for some wordu∈L1and lettera<X2, then for any w∈L1withua<ℓwwe cannot haveua<swsince in that caseua<sW
L1would hold sincew<ℓWL1. Hence, wheneverua<ℓwfor some wordw∈L1, thenuais a prefix ofw. Since the order type ofL1is assumed to beω, anduais a prefix ofWL1, there has to be an infinite number of such wordsw.
Thus, if X2 ∈Σ, then o(L) is not ω if and only ifua<p W
L1 for some u∈L1 and a<X2. This condition is decidable: WL1is a computable regular wordu1vω1 by Lemma 3 and we only have to check whether the language L1a∩Pref(u1vω1) is nonempty for some letter a<X2 and the latter is a regular language by Proposition 1.
IfX2∈N, and thuso(X2) =ω, then we again have several cases:
3. If there exist wordsu,v∈L1withu<sv, then by Lemma 4 we geto(L)is some infinite order type different thanω.
4. Otherwise,L1is an infinite prefix chain, that is,L1⊆Pref(uvω)for some wordsu∈Σ∗,v∈Σ+. We have several subcases.
(a) Assume WL1 <ℓWL. Since both are ω-words, we have<s here. Thus there exists some w=w1w2∈L,w1∈L1,w2∈L2withWL1<sw. SinceL1is an infinite prefix chain, there exists somew′1∈L1,w′1<pW
L1and|w′1|>|w|, yieldingw′1<sw. Sow′1L2<sw, thusw∈L has an infinite number of lower bounds inLando(L)6=ωin this subcase.
(b) Assume there exists some w1∈L1 such thatw1·WL2<ℓWL1. Again, both beingω-words this has to be a<srelation. This means that there exists somew′1∈L1withw1·WL2<sw′1 and sow1·L2<sw′1yfor any memberyofL2, thus again,o(L)6=ω in this case.
(c) Assume none of the previous conditions hold: WL≤ℓW
L1(henceWL1L2=WL1=uvω as well) and for eachw1∈L1we haveWL1≤ℓw1·WL2.
We claim that in this case o(L) =ω if and only if for each w1 ∈L1 and w<p uvω with w1<pwthere exist only finitely many wordsw2∈L2such thatw1w2<sw.
For one direction, assume the latter condition holds. It suffices to show that for eachw<puvω there exist only finitely many many wordsw1∈L1,w2∈L2with w1w2<ℓw, since (as the supremum of these words isWL1L2=uvω) this yields that each prefix ofo(L)is finite, thus o(L) =ω. So letw1w2<ℓw. Sincew1∈L1 andL2⊆Pref(uvω), and w<puvω, we either havew1<pworw≤pw1. The latter would contradict tow1w2<ℓw, hence we havew1<pw.
Thus, there are only finitely many options for choosing such a wordw1∈L1. Clearly, for each fixedw1∈L1 there are only finitely many options for choosing wordsw2 withw1w2<pw and by the condition there are only finitely many wordsw2∈L2 withw1w2<sw, hence in total, there are only finitely many words inL1L2precedingw, showingo(L) =ω.
For the other direction, assume the latter condition doesnot hold. Then there exists some w1∈L1,w<puvω withw1<pwsuch thatw1w2<swfor infinitely many wordsw2∈L2. In this case we can writew2=w′2axandw=w1w′2byuniquely for some lettersa<band words w′2,x,y. Since there are only finitely many options for the fixed wordswandw1to choosew′2, banda, for some paira<bof letters and wordw′2withw1w′2b≤pwthere are infinitely many wordsw2∈L2such thatw′2a≤pw2. LetL′2⊆L2denote the (infinite) set of these words and letw′1∈L1be some word inL1with|w′1| ≥ |w1w′2b|. SinceL1is an infinite prefix chain, such a wordw′1 exists andw1w′2b≤pw′1, thusw1L′2<sw′1, and sow1L′2<sw′1yfor an arbitrary memberyofL2, and sow′1yis preceded by infinitely many words inL, yieldingo(L)6=ω.
We still have to show that the condition of Subcase (c) is decidable. We claim that the condition doesnothold if and only if there exists somew1∈L1and wordsu′∈Σ∗,a∈Σwithw1u′<puvω, w1u′a<suvω and u′a<pWL2. Indeed, ifw1,u′,aare such objects, then there is a unique letter b∈Σwithw1u′b<puvω. Now we can choosew=w1u′bas the conditionu′a<pW
L2implies the existence of infinitely many wordsw2∈Lwithu′a≤pw2. The other direction is already treated in the proof of Subcase (c).
The condition in this form is decidable due to Lemma 5.
As we covered all the possible scenarios, and in each case we got decidability, we proved the lemma.
Corollary 1. Assumeα=X1. . .Xnis some sentential form where for each Xiwe know whether o(Xi) =ω holds. Then we can decide whether o(α) =ω holds.
Proof. We can assume thatα∈/Σ∗(otherwiseo(α) =1 and we can stop). Using the standard construc- tion of introducing fresh nonterminalsY1, . . .Yn−1 and productionsY1→X1Y2,Y2→X2Y3,. . . ,Yn−1→ Xn−1Xnwe can successively decide forYn−1,Yn−2, . . . ,Y1whethero(Yi) =ω; if for any of them we have thato(Yi)is some other infinite order type, then so iso(Y1) =o(α), otherwiseo(α) =ω.
Theorem 2. It is decidable for each recursive nonterminal X whether o(X) =ω holds.
Proof. By our assumptions ofG, L(X) is infinite. In the first step, we decide whether L(X) is well- ordered. If not, theno(X)is clearly notω and we can stop.