Az oktatáshoz szükséges függvénytani fogalmak beépítése a kísérleti fizika mechanika tananyagába

AZ OKTATÁSHOZ SZÜKSÉGES FÜGGVÉNYTANI FOGALMAK BEÉPÍTÉSE A KÍSÉRLETI FIZIKA MECHANIKA TANANYAGÁBA

MÁRKUS JENŐ

A fizika a természetben előforduló jelenségek meghatározott cso- p o r t j á n a k megismerésével foglalkozik. A természeti jelenségekről ta- pasztalat ú t j á n szerzünk tudomást. A jelenségeket kísérlettel többször megismételve, méréssel állapítjuk meg a természeti törvényeket. A fi- zikai jelenségek törvényeit, illetve a fizikai fogalmakat legcélszerűb- ben m a t e m a t i k a i egyenletekkel, illetve függvényekkel f e j e z h e t j ü k ki.

Ezáltal válik a matmatika a fizikai megismerés fontos segédtudomá- nyává.

Felsőoktatásunkban a fizika tanítását a kezdeti időszakban igen megnehezíti az a jelenlegi helyzet, hogy hallgatóinknak nincs olyan bő matematikai ismerete, mely elegendő volna a fizikának megfelelő szinten való tanításához. A középiskolában szerzett ismereteik erre elégtelenek, felsőoktatási tanulmányaik folyamán csak később jutnak el erre a szintre. Ez tette szükségessé annak a kérdésnek felvetését, hogy a középiskolai matematika oktatás anyagát át kell formálni. A je- lenlegi helyzet azonban a felsőoktatásban még több évig fennálló prob- léma: hogyan és milyen mértékben bővítsük a fizika tanításához szük- séges matematikai ismereteket. Ebben a dolgozatban csak a függvény- tani ismeretek bővítésével szeretnék foglalkozni.

A felvetett kérdés tartalmilag kettős:

I. Milyen mértékben?

II. Hogyan?

Az első kérdésre röviden lehet válaszolni: csak olyan mértékben, amennyire az a fizika tanításához szükséges.

Ez a megállapítás egyaránt vonatkozik a fogalmi ismeretekre és a számolási eljárásokra. Nem lehet azonban csak a számolási eljárások ismeretével megelégedni, mert ezáltal a fizikai fogalmak kialakítása is hiányokat szenved.

Hogyan bővítsük ki megfelelő m é r t é k b e n a matematikai hiányokat?

Figyelembe kell v e n n ü n k elsősorban azt, hogy az általunk n y ú j t a n d ó ezen ismeretekkel a hallgatók másik szaktárgyuk keretében is foglal-

kőzni fognak n e m sokkal későbbi időpontban. Fogalmak, jelölések és tételigazolások t e k i n t e t é b e n lehetőleg alkalmazkodnunk kell a szak- tárgy kívánalmaihoz. "Útmutatónak ezért a megfelelő szakkönyvet (tan- könyvet) kell t e k i n t e n ü n k . Ettől csak annyiban és olyan m é r t é k b e n t é r j ü n k el, a m e n n y i b e n az a fizika hagyományos és megszokott kívá- nalmai szerint szükséges. A hogyan kérdéshez tartozik az is, miképen kapcsoljuk hozzá a matematikai ismeretek bővítését a fizika oktatásá-

hoz. E tekintetben k é t szokás alakult ki:

1. A fizika oktatás megkezdése előtt n y ú j t j u k mindazokat a m a t e - matikai ismereteket, melyek a fizika tanításához szükségesek.

2. Szervesen beleillesztjük a fizika oktatásba, s az egyes m a t e - matikai kérdésekkel akkor foglalkozunk csak, mikor a fizika oktatás folyamán annak szükségessége jelentkezik.

Az első módszer mellett érvként lehet felhozni, hogy a fizika oktatást nem kell ismételten megszakítani a matematikai ismeretek bővítése céljából. Hátránya, hogy a rövid idő alatt k a p o t t sok ú j fogalom és is- m e r e t a kezdeti f o k o n nehezen s a j á t í t h a t ó el, s nem látszik annak szükségessége sem. Ezért rendszerint ismételnünk kell a m a t e m a t i k a i fogalmakat akkor is, mikor a fizika oktatásában használni a k a r j u k .

A másik módszer ugyan ismételten is megszakítja a szakoktatás menetét, mégis több előnye mutatkozik:

a j A fogalmak megismerése huzamosabb idő alatt megy végbe és részekre bomlik. í g y meginduláskor némikép csökkenti az ellentétet a közép- és felsőfokú oktatás között is.

b) Olyan fizika anyagba kell beépíteni, mely alapjaiban ismert a középiskolai fizikai tanulmányokból.

c) Látszik a m a t e m a t i k a i fogalmak megismerésének szükségessége a fizikai fogalmak elmélyítése céljából.

d) Látszik, hogy a fizika fejlődése hogyan teszi szükségessé a m a - tematikai fogalmak fejlesztését.

e) A fizikai f o g a l m a k elősegítik a m a t e m a t i k a i fogalmak m e g é r t é - sét.

F e l v e t h e t j ü k azt a kérdést is: a matematikai fogalmak bővítésé- nél példaként f e l h a s z n á l h a t j u k - e a meglevő fizikai ismereteket? Pl.

a f ü g g v é n y fogalmánál a már középiskolából ismert fizikai ismereteket.

Itt legyen szabad hivatkoznom R. Pohl n é m e t fizikusra, aki a felső- oktatás számára írt könyvét szerkezetileg ú g y alakította ki, hogy f e l - tételezett fizikai előismereteket. Az ismeretek ilyen irányú felhaszná- lása azért is előnyösnek látszik, m e r t a fizika területén világít rá m i n d - járt a matematikai fogalmakra.

Kétségtelen, hogy az említett f ü g g v é n y t a n i fogalmak alábbi t á r - gyalásmódja ellen a matematikai logika szempontjából lehet kifogá- sokat felhozni. S z á m u n k r a azonban a matematikai tételek felhasználása a lényeges, s éppen ezért a tételek igazolásába nem m e r ü l h e t ü n k bele olyan mélységig, m i n t azt a szaktárgy teszi. Legyen szabad hivatkozni:

„Joos—Kaluza: H ö h e r e M a t h e m a t i k " c. könyvére, melyet a szerzők azon célzattal állítottak össze, — m i n t az a k ö n y v előszavából megálla- pítható, — hogy fizikusok, kémikusok és mérnökök számára a m a t e m a -

tikai fogalmakat a gyakorlat követelményeinek megfelelően ismer- tessék.

Nézzük most m á r részleteiben, melyek azok a m a t e m a t i k a i fogal- mak, melyek a mechanika kísérleti úton való oktatásához szükségesek, és a fizika anyag mely részeinél válik szükségessé ezen fogalmak is- mertetése?

Ezek a fogalmak:

1. A f ü g g v é n y folytonossága a mozgás pályavonalával kapcsolat- ban.

2. A differenciálhányados fogalma a sebesség és gyorsulás f o - galmához.

3. H a t v á n y f ü g g v é n y differenciálhányadosa az egyenletesen vál- tozó mozgás mozgástani öszefüggéseinél.

4. Szorzatfüggvény differenciálhányadosa a felületi sebesség t é - teléhez.

5. Függvény függvényének differenciálhányadosa.

6. sin x és cos x trigonometrikus függvények d i f f e r e n c i á l h á n y a - dosa. A két utóbbi pont a rezgő mozgás sebesség és gyorsulás összefüggésének meghatározásához.

7. A f ü g g v é n y szélsőértékének fogalma és annak meghatározása pontmozgástani és ütközési feladatokhoz.

8. A határozatlan integrál fogalma és számítása a mozgások erő- tani tárgyalásához.

9. A határozott integrál fogalma és számítása a munkavégzés meghatározásához.

Az alábbiakban inkább a f ü g g v é n y t a n sorrendjében, mint a fizi- ka tárgyalásának s o r r e n d j é b e n foglalkozunk a felmerülő kérdések- kel. Ezért az egyes matematikai részek ismertetése mindig oda i k t a t a n - dó be, ahol az a fizikában szükségessé válik. Ez a beépítés a m a t e - matikai fogalmak kialakításában nem okoz zavart.

A f ü g g v é n y és a f ü g g v é n y folytonosság fogalmának meghatáro- zása a pályagörbével kapcsolatban látszik a legcélszerűbbnek. A moz- gás pályavonalát, mint az idő f ü g g v é n y é t adjuk meg:

s = s (t) vagy x = x (t); y = y (t); z = z (t) alakban.

A f ü g g v é n y fogalmának meghatározása középiskolából ismeretes:

„Minden olyan esetben, amikor egy számösszesség számaihoz hozzá- r e n d e l ü n k bizonyos számértéket (egyet, vagy többet), f ü g g v é n y k a p - csolatot létesítünk." (Matematika gimn. IV. o. számára XIII. kiadás, 38. old.). A mozgástanban a ,,t" számhalmaz számaihoz r e n d e l j ü k hozzá a „s" halmaz számait. A hozzárendelés az: s = s (t) egyenlettel, a pályavonal egyenletével történik. Célszerűnek látszik megemlíteni a többváltozós függvények fogalmát is. Ilyen a fizikában gyakran f o r d u l elő. Példaként fizikai egyenlet-összefüggéseket hozhatunk fel.

Pl. az ohm-törvény, ahol az áramerősség (I) a feszültség (U) és az ellen- állás (R) függvénye.

A folytonosság fogalma a középiskolából csak a pályavonal alap- ján szemléletesen ismeretes. Ezt a meghatározást m á r szükségesebb pontosan definiálni, m á r csak azért is, mivel közelebb kerülünk a d i f - ferenciálhányados fogalmához. A f ü g g v é n y folytonosság fogalmát a fő- iskolai t a n k ö n y v h a t á r é r t é k fogalommal á d j a meg: „Az f (x) f ü g g v é n y t folytonosnak nevezzük az xq pontban, ha az xq pontbeli h a t á r é r t é k e egyenlő az xq ponthoz tartozó helyettesítési értékkel, azaz:

h a : x,ⁿ x⁰ akkor: f (xⁿ) f (x⁰)"

(Szerényi T.: Analízis I. 64. old.)

A folytonosság fogalmához szükséges a f ü g g v é n y határértékének fogalma. Erre az idézett tankönyv 61. oldalán ezt a meghatározást t a l á l j u k : „Az f (x) f ü g g v é n y n e k az x0 helyen van határértéke és az A, ha valahányszor xn "^xq (xn+xo) mindannyiszor f ( x ^ - ^ A .

és így jelöljük:

lim f(xn) — A.

xn > xo

A f ü g g v é n y h a t á r é r t é k é n e k fogalmát tehát visszavezethetjük a so- rozat h a t á r é r t é k é n e k fogalmára.

Sorozatról és sorokról a gimn. III. osztályában m á r volt szó. A h a - t á r é r t é k e t n é h á n y egyszerűbb példával m u t a t h a t j u k meg.

Eltérés van fizika és m a t e m a t i k a között abban, hogy a fizika a mennyiségek változásával foglalkozik, míg a m a t e m a t i k a mennyisé- gekkel. Ezért célszerűbb a fenti meghatározásokat m i n d j á r t ilyen ala- pon megfogalmazni. A változások jelölésére a fizika a „A" jelölést használja (At; As; Av). így nem számsorozatok (független változó és függvény értékek sorozatának) határértékével kell definiálnunk, h a n e m intervallumok sorozatának határértékével. Ennek alapján a f ü g g v é n y - folytonosságát így a d h a t j u k meg: Legyen az f(x) f ü g g v é n y helyettesí- tési értéke egy xq h e l y e n f(xo). Képezzük az xq környezetében a válto- zónak x -f Axⁿ i n t e r v a l l u m sorozatát, (ahol Axⁿ lehet pozitív, negatív, vagy változó előjelű.) Az f(x) f ü g g v é n y t az x$ helyen akkor m o n d j u k folytonosnak, ha m i n d e n olyan Axⁿ sorozatra, m e l y r e :

[ A x n l ^ O az [f (xo + A xa) — ( f x0) ] - > 0 s ezt a következőkép jelöljük:

lim f (x0 + Jxu) — f (x0) —• 0

A differenciálhányados fogalmának bevezetése a változó mozgásokkal kapcsolatban válik szükségessé. A változó mozgás fogalma szerint a tömegpont egyenlő idők alatt nem egyenlő u t a k a t tesz meg. Nem le- het m e g t a r t a n i a sebességnek az egyenletes mozgásnál kapott fogal- m á t : sebességen az ú t és a megtételéhez szükséges idő hányadosát é r t -

dsN\

jük. Szükséges a pillanatnyi sebesség fogalma |v — ~ • Ugyanígy szükséges a pillanatnyi gyorsulás fogalma |^a — ~ J az egyenlőtlenül változó mozgásnál. Ezért a változó mozgásokkal kapcsolatban be kell vezetni a differenciálhányados fogalmát. A m á r idézett főiskolai tan- k ö n y v 120. és 121. oldalán e r r e a következőt t a l á l j u k : „A f(x) függ- v é n y az xq pontban differenciálható és differenciálhányadosa ,,A", ha valahányszor: h,,-*0 mindannyiszor:

f(x0 + hn) —f(x0) .

*• A.

h„

. . .a differenciálhányados geometriai jelentése: az xo pontbeli diffe- renciálhányados az x⁰ pontbeli érintő iránytangense." Ehhez a foga- lomhoz a tankönyv úgy jut el, hogy a hⁿ~*0 számsorozat segítségével az f(xo) és f(xo + hⁿ) végpontú függvény intervallumokat képezi, s vizsgálja az intervallumok végpontjain átmenő szelőket. Megállapítja a szelők iránytangenseiből alkotott sorozat határértékét, ha a hn~~

Itt csupán a jelöléseknek a fizika szempontjából célszerűbb és megszokottabb átírása szükséges. A folytonosságnál hasz- nált jelölést m e g t a r t v a : az x^-hoz a d j u k meg a Ax intervallumok szor- zatát, melyre a: Ax-^0 fennáll. Az x0 és x o + A x intervallumok vég- p o n t j a i n át húzott szelők sorozatának iránytangensére a következőket k a p j u k :

f(x„ + z i x ) - f ( x0) tg an =

JX

A szelők sorozatának határértéke a görbe x0 pontjához tartozó érintő, az iránytangensek sorozatának határértéke az érintő i r á n y t a n - gense.

, í(xQ + Jx)-f(x0) d f ( x ) hm tg«n = hm — = tga = 1 — f (x)

Jx—>0 JX—+Q ZÍX d x Formailag így ugyanazon értelmezéshez jutunk, m i n t a tankönyv:

geometriailag az xq ponthoz tartozó differenciálhányados n e m más, mint a görbe xq ponthoz tartozó érintő iránytényezője. Matematikailag ezt az iránytangenst úgy határozzuk meg, hogy kiválasztunk egy olyan tetszőleges szelő sorozatot, mely a kérdéses érintőhöz konvergál. A sze- lősorozat iránytangenséből alkotott sorozat határértéke, azaz az érintő iránytangense a differenciálhányados. Annak taglalásával n e m érde- mes foglalkoznunk, hogy h a a szelősorozat az érintőhöz konvergál, a szelősorozat iránytangenséből alkotott sorozatnak az érintő i r á n y t a n - genséhez kell konvergálnia. Ennek igazolását h a g y j u k a matematikai t a n u l m á n y o k r a .

Az y = f(x) jelölést használva, célszerűnek látszik a „differencia

h á n y a d o s " f o g a l m á n a k és elnevezésének bevezetése. Az Xo ponthoz m e g a d o t t Ax i n t e r v a l l u m o k segítségével az y = í(xq) és

y + Ay = í(xq + Ax) f ü g g v é n y é r t é k e k sorozatát k a p j u k , melyből Ay = f(xo + Ax) — f(xo) f ü g g v é n y intervallumok képezhetők. A Ax intervallumot a f ü g g e t l e n változó n ö v e k m é n y é n e k , a Ay intervallumot f ü g g v é n y n ö v e k m é n y n e k nevezzük. így

f(x0 + z?x)-f(x ( >) _ j y

z / X J X

a differenciahányados, a f ü g g v é n y növekmény és a f ü g g e t l e n változó n ö v e k m é n y é n e k a hányadosa.

lim f(*o> = l i m ^ Z ^ d y

z/x A* dx

a differenciálhányados h a t á r é r t é k e a differenciálhányados. Hasonló jelöléseket t a l á l u n k az idézett főiskolai t a n k ö n y v 124. oldalán is a d i f - ferenciálhányados fizikai értelmével kapcsolatban.

Az állandó f ü g g v é n y , h a t v á n y f ü g g v é n y , összeg és különbség f ü g g v é n y differenciálási m ű v e l e t é n e k levezetése n e m szükségképeni követelmény, s l e g f e l j e b b azért célszerű, hogy n é h á n y egyszerűbb f e l a d a t o n a differenciálást, m i n t műveletet, feladat-megoldó órán gyakorolni t u d j u k . A differenciálási műveletek m a t e m a t i k a i levezeté- sével a dolgozat k e r e t é b e n n e m foglalkozom. Ezek megtalálhatók b á r - m e l y ilyen t á r g y ú szakkönyvben, a m á r idézett főiskolai t a n k ö n y v b e n is. Mindezeket f e l a d a t megoldó órák k e r e t é b e n is b e i k t a t h a t j u k . El-

£

méleti órán m é g is szükségesnek látszik az: s = — t2 összefüggésből 2

a : v = a . t összefüggés megállapítása. Ugyanígy az: s = vot + t2- b ő i 2

v = vo + at meghatározása. Minthogy ezen összefüggések a fizika ke- r e t é b e tartoznak, foglalkozunk lealább az elsővel.

s = - t « 2

s + z/s = ~ (t + J t )2

2

j s = - . [ ( t + z / t )2- t2]

Js = -[(2t'Jt ) + z /2t ]

— = — (2t + /ít)

Jt 2

v = — = a • t ds dt

dv ds d²s

Az a = — - pillanatnyi gyorsulásnál, mivel v = —; a = — beszél-

dt dt dt²

h e t ü n k röviden a második és a magasabb rendű differenciálhányado- sokról is.

A fenti differenciálási szabályok megállapítása á t m e n e t e t ad a f ü g g v é n y függvényének differenciálhányadosához. E r r e u g y a n csak

2 n

a rezgőmozgással kapcsolatos: s = A s i n — t trigonometrikus f ü g g v é n y - nél van szükség. Gyakorlás szempontjából mégis itt célszerűbb vele fog- lalkozni. Kiindulásul az: y = (ax²-j-bx)² alakú függvények szolgálhatnak.

Ezek differenciálhányadosát a hatványozás elvégzése u t á n is meg t u d - juk határozni. Nem határozható meg így az y = f a x2 + bx alakú függ- vények differenciálhányadosa.

Mint matematikából ismeretes, a f ü g g v é n y függvényének d i f f e r e n - ciálhányadosára az alábbi öszefüggés érvényes:

dy df(u) du dx du dx

Az eredmény összehasonlítása az: y = (ax² + bx)² f ü g g v é n y n é l el is végezhető. A rezgőmozgással kapcsolatban szükséges az

y = sinx és y = cos x

függvények differenciálhányadosának meghatározása. Ezt, — az idézett t a n k ö n y v 143. és 58—59. oldalán t a l á l h a t j u k meg. E szerint h a :

dy

y == sinx —— = cosx dx

y = cosx — = — sinx dy dx

A rugalmas ütközéssel, vagy m á r előbb a tömegpont mozgásával kapcsolatban előfordulhatnak olyan feladatok, melyeknél szélsőérték számításra van szükség. Ha ilyen feladatokat is meg a k a r u n k oldani, matematikai részére is a feladatmegoldó órán t é r h e t ü n k ki. Legcél- szerűbben a fizikai feladathoz kapcsolva. Pl. „A" pontból m tömeg- pontú golyó úgy jusson el egyenletes mozgással ,,B" pontba, hogy köz- ben rugalmasan ütközzön a H — H falon. Milyen AOB úton kell a go- lyónak mozognia, hogy ez az útvonal a lehető legkisebb legyen? (1.

ábra)

Legyen: y = AO + O B a megtett út.

Legyenek: A j és Bi a vetületi pontok, OC az O pont beesési merőlegese.

A j B i = d A At = iri|

BBt = m-) a f e l a d a t s z e r i n t állandó t á v o l s á g o k .

ö s s z e f ü g g é s b ő l :

f ü g g v é n y é r t é k e i k ö z ö t t a l e g k i s e b b e t k e r e s s ü k . A f e l a d a t o t , — h a m a - t e m a t i k a i l a g n e m is t e l j e s e n , — s z á m u n k r a k i e l é g í t ő e n így o l d h a t j u k meg.

Az y = a x2 + b x + c f ü g g v é n y k é p e , h a a > 0 o l y a n p a r a b o l a , m e l y n é l a s z á r a k f e l f e l é h a l a d n a k (2. ábra). A f ü g g v é n y é r t é k e k f e l v e s z n e k egy l e g k i s e b b é r t é k e t . Ez a l e g k i s e b b f ü g g v é n y é r t é k a f ü g g v é n y m i n i m u m a . Az y = a x² + b x + c f ü g g v é n y k é p e , h a a < 0 o l y a n parabola, m e l y n é l a s z á r a k lefelé h a l a d n a k . (3. ábra). í g y a f ü g g v é n y é r t é k e k f e l v e s z n e k egy l e g n a g y o b b é r t é k e t . Ez a f ü g g v é n y m a x i m u m a . M a x i m u m és m i n i - m u m a f ü g g v é n y szélső értékei. (A f o g a l m a k a g i m n á z i u m a n y a g á b ó l ismertek.) A s z é l s ő é r t é k ű h e l y e k e n m e g h ú z o t t g ö r b e é r i n t ő k az x t e n - gellyel p á r h u z a m o s a k , i r á n y s z ö g ü k : 0° illetve 180°, így:

M i v e l az é r i n t ő i r á n y t a n g e n s e az illető p o n t b a n a d i f f e r e n c i á l h á - n y a d o s , a s z é l s ő é r t é k ű h e l y e k r e f e n n á l l , h o g y o t t

dx V i s s z a t é r v e az e r e d e t i f e l a d a t r a :

A számlálókkal a gyökök alá beosztva:

Vagyis a minimális ú t feltétele, hogy a golyó ugyanolyan szöggel v e - rődjön vissza, mint amilyennel beesett. Ezzel a rugalmas golyó rugal- mas falba való ütközésének törvényét igazoltuk.

A centrális mozgásoknál a felületi sebesség tételének igazolásához szükséges a szorzat f ü g g v é n y differenciálhányadosának szabálya. A f e - lületi sebesség tétele — mint ismeretes — azt m o n d j a ki, hogy a v e - zérsugár által az időegység alatt súrolt terület állandó. A tétel igazo- lását főiskolai t a n k ö n y v ü n k (Párkányi L.: Mechanika I. 132—134. old.) szerint kissé nehézkesnek találom. Áttekinthetőbb igazolást ad erre. A.

Recknagel: Physik, Mechanik kötete. Ez utóbbi gondolatmenetét kö- vetem.

A centrális mozgás feltétele, hogy a gyorsulás vektor a vezérsu- gárra essen. Az iránytényezőkre tehát f e n n á l l :

tg a^a = tg a^r ahol: tg a^a = — ^{e s} tg «r — —

y

ax x

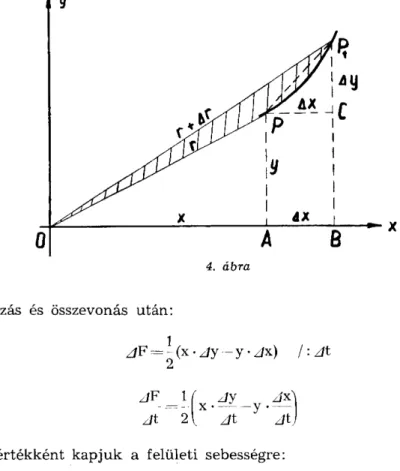
A centrális mozgást végző tömegpont „At" idő alatt elmozdul a P(x, y) pontból a Pi(x + Ax, y + Ay) pontba. (4. ábra). A vezérsugár ezen idő alatt a besatírozott ^ F = OPPi háromszög területét súrolja. Ha

„At" megfelelően kicsi, a „ P P i " ív helyett az összekötő h ú r vehető.

Ezen feltétellel:

4. ábra

Beszorzás és összevonás u t á n :

H a t á r é r t é k k é n t k a p j u k a f e l ü l e t i s e b e s s é g r e : dF W dy dx^i 1

A f e l ü l e t i s e b e s s é g t é t e l e s z e r i n t e n n e k á l l a n d ó n a k k e l l l e n n i . Ezt d2F

ú g y i g a z o l j u k , h o g y a k k o r = 0 kell l e g y e n . (Állandó f ü g g v é n y dt²

d i f f e r e n c i á l h á n y a d o s a zéró). A f e l ü l e t i s e b e s s é g f ü g g v é n y j o b b olda- l á n álló z á r ó j e l b e n o l y a n k ü l ö n b s é g f ü g g v é n y szerepel, a h o l m i n d k é t t a g k é t t é n y e z ő b ő l áll, s a t é n y e z ő k m i n d e g y i k e ,,t" f ü g g v é n y e . E z é r t s z ü k s é g e s k i t é r n i a s z o r z a t f ü g g v é n y d i f f e r e n c i á l h á n y a d o s á r a . E r r e n é z - v e m e g á l l a p í t h a t ó :

h a y = g(x) . h(x)

a k k o r ^dy _ Ü « W .h ( x ) + í r t x ). d h «

d x dx dx

Visszatérve a felületi sebesség tételére:

d2F 1 fdx dvv dy dvx

— -vy + x ^ • vx — y • —

dt² 2 [ót dt dt dt

= - ( vx- vy+ x - ay- vy. vx- y • ax)

a

d²F 1

= (x • av — y • ax) = 0 dt2 2 y

mert a centrális mozgás feltétele szerint:

tg oc^a = tg a^r ax x x • 3y—y • ax = 0

A mozgások dinamikai tárgyalásához szükséges a határozatlan integrál fogalma. A mozgások dinamikai tárgyalásánál az erő nagyságából in- dulunk ki.

Ebből a P = m . a

öszefüggés a l a p j á n a gyorsulás meghatározható. A gyorsulásból kell a sebességfüggvényt, m a j d a sebességfüggvényből a pályaegyenletet meghatározni. Az eljárás tehát f o r d í t o t t j a annak, amit a mozgások kinematikai tárgyalásánál használtunk.

A határozatlan integrált legegyszerűbb úgy értelmezni, mint a differenciálás fordított műveletét: a differenciálhányadosból keres- sük az eredeti függvényt. Jelöljük:

f(x)dx = F(x) h a : í í 5^cl ⁼ f(^x) dx

A h a t v á n y differenciálásánál megismert eljárást ezért fordítva használjuk: a hatványkitevőt eggyel növeljük, s az ú j kitevővel osztjuk a hatványmennyiséget.

xn + l

xndx — \-C n + 1

Szükséges megemlíteni, hogy az eljárásnál olyan függvénysereget kapunk, melyek egymástól tetszőleges állandóban eltérhetnek (ezek az integrálandó f ü g g v é n y primitív függvényei), mivel az állandó diffe- renciálhányadosa zéró. Mivel az állandó értéke tetszőlegesen választ- ható meg, a mozgástani képletek meghatározásánál a kezdeti feltételek szabják meg az állandó értékét.

A határozatlan integrál értelmezéséből tehát k a p j u k : v = j a dt

s = | v dt

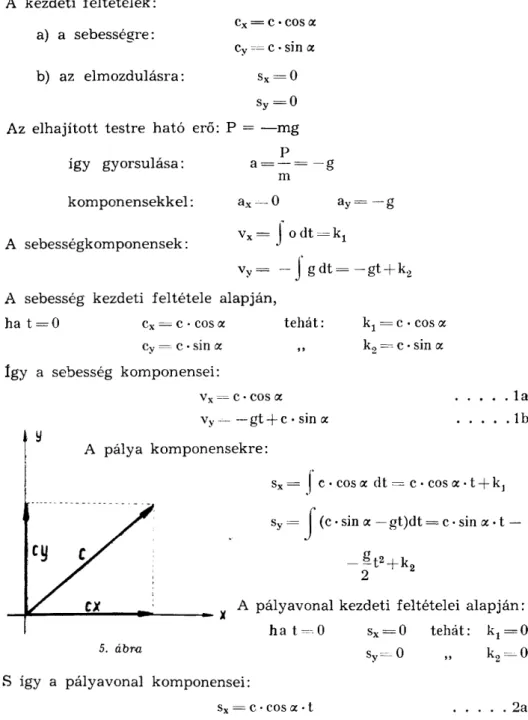
Példaként csak egyetlen mozgást nézzünk: a hajításokat. (5. ábra).

A vízszintessel „«" szöget bezáró „c" kezdősebességgel h a j í t j u k el az ,,m" tömegű testet a koordinátarendszer kezdőpontjából.

A kezdeti feltételek:

a) a sebességre:

b) az elmozdulásra:

c^x = c • cos a cy — c • sin a

sx = 0 sy= 0 Az elhajított testre h a t ó erő: P = — m g

így gyorsulása:

k o m p o n e n s e k k e l : A sebességkomponensek:

a = - = - g m

ax = 0 ^{ay —} ~ g vx = j o dt = k1

vy — - - j g d t = - g t + k² A sebesség kezdeti feltétele alapján,

ha t = 0 c^x = c • cos a cv = c • sin a

tehát: k± = c • cos a k„, = c - s i n a így a sebesség komponensei:

Vy = c • cos a

v^y — ^gt + c • sin a . . . . A pálya komponensekre:

sx = c • cos a dt = c • cos a • t + kj l a l b

sy = J^ (c • sin a —gt)dt == c • sin a • t —

A pályavonal kezdeti feltételei a l a p j á n : sx = 0 tehát: kx = 0 ha t = 0

5. ábra

S így a pályavonal komponensei:

sv=0

Sv = c • cos a • t

k0 = 0

2a

160

sv = c • sin a t 12

2 2b

Visszakapjuk a f e r d e h a j í t á s r a ugyanazon összefüggéseket, melyeket a mozgás kinematikai tárgyalásánál megismertünk.

A f e r d e h a j í t á s így megismert összefüggései speciális hajításokra is átvihetők:

a) Függőlegesen fel h a j í t á s : x = 90° (cosa = 0 ; sina = l) Cv = 0

kezdeti feltételek:

A mozgásegyenletek:

cy = 0 s^x = 0 ₅>v 0

0

VY = C - g . t Sv= C - t ~ ^ t2

2

b) Függőlegesen le h a j í t á s : « = 90° (cosa = 0 ; s i n a = — 1) Cv = 0 cv = — c

A kezdeti feltételek:

A mozgásegyenletek:

s_xx = 0 0 V x - 0

Sv = 0

V j = - c - g - t

Sv = — Ct - ^ t2

2

Mivel az „Y"

tengelyirányításával ellentétes

A tömegpont más mozgásának egyenletei hasonlóan határozhatók meg.

A P = P(s) alakú erő m u n k á j á n a k kiszámításánál válik szükségessé a határozott integrál fogalmának bevezetése.

6. ábra

— S

I l y e n t a n k ö n y v i a n y a g u n k s z e r i n t a r u g a l m a s erő (P = k .x) e l l e n é - b e n v é g z e t t m u n k a .

A h a t á r o z o t t i n t e g r á l f o g a l m á v a l n e m f o g l a l k o z h a t u n k o l y a n r é s z - letességgel, m i n t a z t a m a t e m a t i k a t a n k ö n y v teszi. ( S z e r é n y i T.: A n a l í - zis II.) M é g s e m n é l k ü l ö z h e t j ü k a z é r t e l m e z é s t t e l j e s egészében. M e g k e l l e l é g e d n ü n k e g y o l y a n é r t e l m e z é s s e l , m i n t a m i l y e t pl. Obádovics J . G y . : M a t e m a t i k a c. összefoglaló k ö n y v e ad. A h a t á r o z o t t i n t e g r á l f o g a l - m á n a k k i a l a k í t á s a a g i m n á z i u m b a n r é g e b b e n s z i n t é n i l y e n m ó d o n t ö r t é n t .

A h a t á r o z o t t i n t e g r á l é r t e l m e z é s e u t á n a P = P(s) e r ő á l t a l v é g z e t t m u n k á t m á r k ö n n y e n m e g h a t á r o z h a t j u k . A m u n k a k i s z á m í t á s á t t a n - k ö n y v ü n k ( P á r k á n y i L.: Fizika I.) a 162. o l d a l o n g e o m e t r i a i l a g é r t e l - mezi. Á l l a n d ó és s z a k a s z o n k é n t á l l a n d ó erő á l t a l v é g z e t t m u n k á t s í k - i d o m o k t e r ü l e t é n e k ö s s z e g e k é n t k a p j u k . (L.: 6. és 7. á b r á k . Az á b r á k a t a n k ö n y v 110. és l l l / b . ábrái.) E n n e k a l a p j á n a P = P(s) e r ő n e k az

„ s = Sj3 — s^a" ú t s z a k a s z o n v é g z e t t m u n k á j á t is ú g y é r t e l m e z z ü k , m i n t a z t a t e r ü l e t e t , a m e l y e t az „s = s ^ — s^a" útszakasz, a , , P ( s^a) " és „P(sb)"

o r d i n á t á k , v a l a m i n t a ,,P(s)" f ü g g v é n y g ö r b é n e k az e l ő b b i o r d i n á t á k k ö z é eső része h a t á r o l . Ez a t e r ü l e t a m á r i s m e r t m ó d o n h a t á r o z o t t i n t e g r á l l a l s z á m í t h a t ó k i :

F e l h a s z n á l á s a a r u g a l m a s erő e l l e n é b e n v é g z e t t m u n k a : (8. ábra).

L e g y e n a l e g n a g y o b b kitérés, a f é l a m p l i t ú d ó : ,,A", a m e l y h e z t a r t o z ó e r ő : „PA = k . A " A z e g y e n s ú l y i h e l y z e t t ő l a l e g n a g y o b b k i t é r é s i g v é g - z e t t m u n k a :

L = I' P • ds

s. 'a

ami a t a n k ö n y v szerint is (a 110 és 111/b. ábrákkal megegyezően) gra- fikusan a derékszögű háromszög területe (L.: 9. ábra).

A f e l a d a t k é n t kitűzött célt ezzel elértük. Láttuk a m a t e m a t i k a i fogalmak hogyan építhetők b e a megfelelő helyeken a fizika anyag ismertetésébe. Ha ezek a fogalmak nem is olyan szabatosak, mint aho- gyan azokat a m a t e m a t i k a i kollokviumokban meg f o g j á k ismerni, de azoknak nem m o n d a n a k ellent, és a fizikai fogalomalkatás számára kielé- gítőek. Kétségtelen, hogy ez a matematikai kiegészítés a fizika tanítására

szánt időt csökkenti. De nélkülük a fizikai fogalmak kialakítása és megértése n e m érhető el. Szükségesnek látszik ezért ezen ú j fogalmak beépítése az ú j megírandó tankönyvbe is. Ez a beépítés akkor sem nélkülözhető, h a a differenciál- és integrál-számításnak a gimnázium m a t e m a t i k a anyagába való beiktatása megvalósul. Ekkor is számítha- tunk olyan hallgatókra, akik nem ilyen tagozatú középiskolából jön- nek hozzánk.

F E L H A S Z N Á L T IRODALOM P á r k á n y i L.: Fizika I.

Szerényi T.: Analízis I.—II.

Obadovics J. Gy.: M a t e m a t i k a A. Recknagel: P h y s i k (Mechanik).

G i m n á z i u m o k III.—IV. o. M a t e m a t i k a tankönyve.