Complexity in the interdefinability of timelike, lightlike and spacelike relatedness of Minkowski spacetime
✩Hajnal Andrékaa, Judit X. Madarásza, István Németia, Gergely Székelya,b,∗
a AlfrédRényiInstituteofMathematics,H-1053Budapest,Reáltanodautca13-15,Budapest,Hungary
bUniversityofPublicService,H-1083Budapest,2Ludovikatér,Budapest,Hungary
a r t i cl e i n f o a b s t r a c t
Articlehistory:
Received10January2022
Receivedinrevisedform27January 2022
Accepted27January2022 Availableonline2February2022 MSC:
03B30 83A05 03B10 03C40 03G99 Keywords:
First-orderlogic Relativitytheory Definableconcepts Minkowskispacetime Quantifiercomplexity Definabilitytheory
Interdefinability of timelike, lightlike and spacelike relatedness of Minkowski spacetime is investigated in detail in the paper, with the aim of finding the simplest definitions. Based on ideas scattered in the literature, definitions are given between any two of these binary relations that use 4 variables, i.e., they useonly2auxiliaryvariables.Allthesedefinitions workoverarbitraryEuclidean fieldsinplaceofthefieldof reals,if thedimensionnofspacetimeisgreaterthan two. If n = 2,thedefinitions work over arbitraryordered fields excepttheones basedonlightlikerelatedness(wherenodefinitioncanworkbysymmetry).Noneof theserelationscanbedefinedfromanotheroneusingonlyoneauxiliaryvariable.
Thesedefinitionsuseonlyoneuniversalandoneexistentialquantifiersinaspecific order. Insome of the cases, weshow that the order of these quantifiers can be reversed forthepriceofusingtwiceasmany quantifiers.Exceptintwocases, we provideexistential/universaldefinitionsusing3auxiliaryvariablesorshowthatno existential/universaldefinitionexists.Therearenoexistential/universaldefinitions between any two of these relations using only 2 auxiliary variables. It remains open whether there is an existential (universal) definition of timelike (lightlike) relatednessfromspacelikerelatednessifn>2.Finally,severalotheropenproblems relatedtothequantifiercomplexityofthesimplestpossibledefinitionsaregiven.
©2022TheAuthor(s).PublishedbyElsevierB.V.Thisisanopenaccessarticle undertheCCBY-NC-NDlicense (http://creativecommons.org/licenses/by-nc-nd/4.0/).
1. Introduction
Thereis anextensiveliteratureontheaxiomatization ofMinkowskispacetime intermsof variousbasic concepts.Robb[14],revisedas[15],givesanaxiomatizationofMinkowskispacetimeusingonlyonebinary
“after” relation as primitive notion. Goldblatt [4, Appendix B] shows that “between” and “orthogonali-
✩ This researchis supported by the Hungarian National Research, Development andInnovation Office (NKFIH), grants no.
FK-134732andTKP2021-NVA-16.
* Correspondingauthorat:AlfrédRényiInstituteofMathematics,H-1053Budapest,Reáltanodautca13-15,Budapest,Hungary.
E-mailaddresses:andreka.hajnal@renyi.hu(H. Andréka),madarasz.judit@renyi.hu(J.X. Madarász),nemeti.istvan@renyi.hu (I. Németi),szekely.gergely@renyi.hu(G. Székely).
https://doi.org/10.1016/j.apal.2022.103100
0168-0072/©2022TheAuthor(s). PublishedbyElsevierB.V.ThisisanopenaccessarticleundertheCCBY-NC-NDlicense (http://creativecommons.org/licenses/by-nc-nd/4.0/).
ty”, theprimitives used therein, canbe definedin termsof Robb’s “after”relation. Latzer [8] showsthat Minkowski spacetime can be axiomatized using the relation of lightlike relatedness alone. Both in terms of thebinaryasymmetriclightlikeafter relationandintermsofthebinarysymmetriclightlikerelatedness relation,Mundy [12] axiomatizesMinkowskispacetimesignificantlysimplifyingRobb’saxiomsystem.Pam- buccian [13] explicitly definescollinearityand equidistancefrom lightlikerelatednessinmetric-affineFano spaces in order to present Alexandrov–Zeeman type theorems as definability results. Fora contemporary axiomatization ofMinkowskispacetime pursuedinthestyleofTarski,see[3].
The three most fundamentalsymmetric binary relationsinMinkowski spacetime aretimelike, lightlike and spacelikerelatedness. Scatteredintheextensiveliteraturementioned above,there canbe found some definitions andsomeclaimsabout certaininterdefinabilityamong these relations. Forexample,Malament [10, p. 294] claims thatthe three basic relationsare first-order definable interms of oneanother, buthe givesnoproofor referenceexceptforonespecificformulainfootnote3.Interdefinabilityresultsconcerning Minkowski spacetimeare usedingeneralrelativity,see e.g.,[7], [5, especiallyp. 180] and[11]. Theresults inthepresentpaperareused inthefollow-uppaper[1].
Hereinwecarefullyinvestigatetheinterdefinabilityoftimelike,lightlikeandspacelikerelatednessrelations aiming to find the simplest definitions. For each pair of these relations, we present definitions that are simplest intermsofnumberofvariables.Wealsoinvestigatehowdefinability dependsonthedimensionof spacetime andontheunderlyingorderedfield.Forexample,lightlikerelatednessisdefinablefrom timelike relatednesseven ifthedimensionn ofspacetimeis2(i.e.,notjusttime butspace isalsoonedimensional) but n has to be at least 3to be able to define timelike relatedness from lightlike relatedness. Inmost of the cases,weassumethateithern= 2 and theunderlyingfieldisanarbitrary orderedfieldor n>2 and the underlyingfieldisaEuclidean field(i.e., anorderedfieldinwhicheverypositive numberhasasquare root).
In Section 3, we show thatthe relations of timelike, lightlike and spacelikerelatedness can be defined from any of them using four variables, i.e., using only two auxiliary variables, see Theorems 1, 2 and 3. Then we show that the number of variables used in these definitions are minimal, i.e., none of these relations canbe defined from another oneusing onlyoneauxiliary variable, see Theorem4. InSection4, using awell-visualizableconstruction,weshowthatspacelikerelatednesscanbe definedexistentiallyfrom timelikerelatedness usingfour auxiliaryvariables,see Theorem 5, butno suchdefinitionsexistusing only two auxiliaryvariablescf. Theorem7.Inpreparationtotheproof ofTheorem7,wedevelop apicturesque graph-embedding-based methodto understandrelations definablebyexistentialformulas. Thenusing this method,wegiveanexistentialformuladefiningspacelikerelatednessfromtimelikerelatednessthatusesonly three auxiliaryvariables, see Theorem 8. Over arbitraryordered fields, weshow thatlightlike relatedness cannot be defined existentiallyneither from timelikenor from spacelikerelatedness, see Theorem 9. Over arbitraryorderedfields,weshowthatneithertimelikenorspacelikerelatednesscanbedefinedexistentially oruniversallyfromlightlikerelatedness,seeTheorem10.FinallyinSection5,wegiveseveralopenproblems related tothequantifiercomplexity ofthesimplest possibledefinitions.
2. Somenotationsanddefinitions
Here,wecollectthemostfundamentalnotationsusedinthispaper.Weworkoverarbitraryorderedfields.
So herein,weassumethat(Q,+,·,≤) isanorderedfield.1 LetQn denotetheset ofn-dimensionalvectors overQ.WealsousethevectorspacestructureonQn.Followingtheconventioncommoninrelativitytheory, we startcountingaxesfrom0,drawthe0thcoordinateaxis verticallyand consideritasthetime-axis.
1 That(Q,+,·,≤) isanorderedfieldmeansthat(Q,+,·) isafieldwhichistotallyorderedby≤,andwehavethefollowingtwo propertiesforallx,y,z∈Q:(1)x+z≤y+zifx≤y,and(2)0≤xyif0≤xand0≤y.
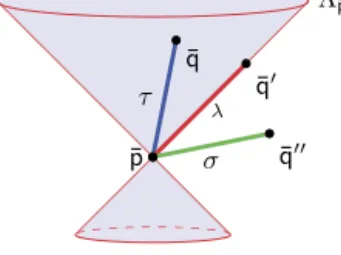
Fig. 1.Illustration for relations ¯pτ¯q, ¯pλ¯q, and ¯pσ¯q , as well as for light cone Λ¯p.
Inourformulas,weusethefollowingsymbolsfor logicalconnectives: both“∧”and “,”interchangeably for conjunction, “∨”for disjunction, “¬”for negation, “∃” forexistential quantifier,and “∀” foruniversal quantifier.
Let¯p= (p0,p1,. . . ,pn−1)∈Qnand¯q= (q0,q1,. . . ,qn−1)∈Qn.Wearegoingtoworkwiththefollowing relationsillustratedbyFig.1:
¯
pτ ¯q ⇐⇒def (p0−q0)2>(p1−q1)2+. . .+ (pn−1−qn−1)2
¯
pλ¯q ⇐⇒def (p0−q0)2= (p1−q1)2+. . .+ (pn−1−qn−1)2,p0=q0 p¯σ¯q ⇐⇒def (p0−q0)2<(p1−q1)2+. . .+ (pn−1−qn−1)2.
Wesaythat¯pand¯qare,timelike,lightlike,2spacelikerelatedintherespectivecases.Alineiscalledtimelike (lightlike,spacelike)iffallofitsdistinctpointsaretimelike(lightlike,spacelike)related.Bythat¯pisinthe timelikefutureof ¯q,wesimplymeanthat¯pτ¯qandp0>q0.Analogously,¯pisinthetimelikepast of ¯qiff
¯
pτq¯andp0<q0.
Wedenotethecomplementoftheserelationsbyτ,¯ ¯λ,¯σ.Byρ=,wearegoingtoabbreviatetheintersection of binary relations ρand =. Inour formulas, we use the samesymbols τ, λ and σ ininfix notation also to denotethe correspondingrelation symbols.We abbreviatenegatedatomicformulas ¬(x=y) to x=y,
¬(xτ y) tox¯τ y,etc.to makethemeasiertoread.Incaseϕ(x,y) isaformulahavingallitsfreevariables amongxandy,wewill writeϕ(¯x,¯y) todenotethatthebinaryrelationdefinedbyϕholdsfor¯x,¯y∈Qn.
Bybinary relationRon theuniverseof modelMisdefinablein Mbyusing kmanyauxiliaryvariables we mean thefollowing: there is aformula ϕ(x,y) inthe languageof Mand variables z1, z2, . . . ,zk such thatx,y,z1,. . . ,zk areallthevariablesthatoccurinϕandϕdefinesrelationRinM,inthesensethatthe expansionofMwithRvalidatestheformula∀x∀y[R(x,y)↔ϕ(x,y)].
BythelightconeΛ¯pthroughpoint¯p,weunderstandthesetofpointswhicharelightlikerelatedorequal top,¯ i.e.,
Λ¯p def=
¯
q∈Qn : ¯qλ¯por ¯p= ¯q .
By the causal cone C¯p through point ¯p, we understand the set of points which are equal, timelike or lightlike(aka.causally)relatedtop,¯ i.e.,
C¯p def=
¯q∈Qn : ¯qσ¯¯p ,
and¯pisinthecausalfuture(past)of q¯iff¯pσ¯¯qandp0≥q0 (p0≤q0).
2 Usually,itisallowedforlightlikerelatedpointstobeequal,seee.g.,[10].Hereweforbidequalitybyassumingp0=q0.From thepointofviewofdefinability,thisisanegligibledifferencesincethetwoversionsareclearlydefinablefromeachother.Weprefer tousethestrictonebecausethatisminimalamongthedefinablenonemptybinaryconcepts.
Remark 1 (n ≥ 2).The following is known and also straightforward to check. For all natural numbers n≥2,thefollowingsareallautomorphismsofmodel(Qn,τ ,λ,σ):anyuniformscaling,reversingtime,3any translation, anyspatialrotation,4 anyLorentzboost5 inanyspatial direction.
Anorderedfield(Q,+,·,≤) iscalledaEuclideanfieldifitseverypositiveelementhasasquareroot,i.e., iffthefollowing holdsinit
for allx∈Q, if 0≤x, there is ay∈Qsuch thatx=y2. (Eucl.) Infiguresandtables,wearegoingtorefertothispropertyas(Eucl.).Insomeproofs,wewillrefertoplane {(t,x,0,. . . ,0):t,x∈Q}astx-plane.
Proposition1(n≥2;(Eucl.) orn=2).Ifn= 2or(Q,+,·,≤)isaEuclideanfield,thentheautomorphism groupof (Qn,τ ,λ,σ)actstransitivelyon thetimelike,lightlikeandspacelikerelatedpairsof points,i.e.,for allρ∈ {τ ,λ,σ}andforall¯p,¯q,¯p,¯q∈Qn forwhichboth ¯pρ¯qand¯pρq¯ holds,thereisanautomorphism α of(Qn,τ ,λ,σ)forwhichα(¯p)= ¯p andα(¯q)= ¯q.
Proof. Because the inverses and the compositions of automorphisms are automorphisms, it is enough to show thatfor everytwo distinct points¯p,¯q∈Qn there is anautomorphism αof (Qn,τ ,λ,σ) such thatα maps ¯pto (0,0,. . . ,0) andα(¯q)= (1,0,. . . ,0) orα(¯q)= (1,1,0,. . . ,0) orα(¯q)= (0,1,0,. . . ,0).
Since translations are automorphisms of (Qn,τ ,λ,σ), cf. Remark 1, there is an automorphism which maps ¯p to (0,0,. . . ,0). So because the composition of two automorphisms is also an automorphism, we can assume that ¯p = (0,0,. . . ,0) without loosing generality. Similarly, because reversing time is also an automorphism,cf.Remark1, wecanalsoassumethatq0≥0.
Assume now that (Q,+,·,≤) is a Euclidean field. Then there is a spatial rotation R which does not change¯p= (0,0,. . . ,0) andmaps¯qto (t,x,0,. . . ,0) forsomenon-negative t,x∈Q. ThisrotationR isan automorphism, cf. Remark1. Hence wecan assumethat¯p= (0,0,. . . ,0) and ¯q= (t,x,0,. . . ,0) forsome t≥0,x≥0 forwhich(t,x)= (0,0).
Ift>x≥0,then¯pτ¯q.Letusconsider thefollowingmap:
Bτ: (r0,r1,r2, . . . ,rn−1)→ 1
√t2−x2
tr0−xr1
√t2−x2, tr1−xr0
√t2−x2,r2, . . . ,rn−1
.
This mapBτ isanautomorphism becauseitisthecompositionofaLorentzboostcorresponding tospeed v =x/t and auniformscaling bythe factor1/√
t2−x2. It isstraightforwardto verifythatBτ maps¯p to (0,0,. . . ,0) and ¯qto (1,0,. . . ,0).If t = x> 0,then ¯p λ¯q and there is auniform scaling thatmaps ¯p to (0,0,. . . ,0) and¯qto(1,1,0,. . . ,0).If0<t<x,then¯pσ¯qandlet
Bσ: (r0,r1,r2, . . . ,rn−1)→ 1
√x2−t2
xr0−tr1
√x2−t2,xr1−tr0
√x2−t2,r2, . . . ,rn−1
.
3 Thatis,thetransformation(p0,p1. . . ,pn−1)→(−p0,p1. . . ,pn−1).
4 Thatis,anydistance-preservinglineartransformationofdeterminant1thatfixesthetime-axis,i.e.,mapsvector(1,0,. . .0) to itself.
5 ALorentzboostinthei-thspatialcoordinatedirectionisatransformationoftheform
Bi: (p0,p1, . . . ,pn−1)→
p0−vpi
√1−v2,p1, . . . ,pi−1,pi−vp0
√1−v2,pi+1, . . . ,pn−1
forsomevelocityv∈Qforwhich−1<v<1 and√
1−v2∈Q.
∅
τ λ σ =
¯
τ= σ∪=
Fig. 2.The figure illustrates the Boolean algebra generated by relationsτ,λ,σ, and =.
Analogously,this Bσ isanautomorphism andmaps ¯pto(0,0,. . . ,0) and¯qto (0,1,0,. . . ,0).Ift= 0<x, thenp¯σ¯qandthereisauniformscalingwhichmaps¯pand¯qto(0,0,. . . ,0) and(0,1,0,. . . ,0),respectively.
Thiscompletes theproof inthecasewhen(Q,+,·,≤) isaEuclideanfield.
TherewereonlytwostepswhereweusedtheEuclideanproperty:theonewhereweusedtheexistenceof anappropriaterotationRtorotatepointsp¯and¯qtothetx-plane,andtheonewhereweusedtheexistence ofmapsBτ andBσ.Sincewhenn= 2,therotationstepisnotneededandBτ andBσ simplifyintorational functionsinboth coordinates,wealsohavethestatementoverarbitraryorderedfields ifn= 2.
Because any relationdefinable inamodelhastobe closed undertheautomorphisms ofthe model,the followingisacorollaryofProposition1.
Corollary1(n≥2;(Eucl.) orn=2).Letρandδbe anytwodifferent relationsfromtheset{τ ,λ,σ}.For any relationR definablein(Qn,ρ),ifn= 2 or(Q,+,·,≤)isaEuclidean field, wehave that
δ⊆R ⇐⇒ (p, q)∈R for somep, q∈Qn such that p δ q ⇐⇒ R∩δ=∅.
Because theunionofrelations τ,σ,λand = isthe universalrelation Qn×Qn, Corollary1implies the following.
Corollary 2(n ≥2;(Eucl.) or n =2). Letρ be any of relations τ, λ and σ. If n = 2or (Q,+,·,≤) is a Euclidean field, then any nonempty binary relation which is definable in (Qn,ρ) is the union of some of relationsτ,σ,λ and=.
Inother words,Corollary 2saysthat,assumingn= 2 or(Q,+,·,≤) isaEuclidean field,ifrelationsτ, σ andλ aredefinable inany ofstructures (Qn,τ),(Qn,λ) and (Qn,σ),then theyand = areatoms inthe corresponding Booleanalgebraofdefinable binaryconcepts. Wewillsee thattheyarealldefinable except in(Q2,λ),seeRemark2andTheorems1,2and3inSection3.Soexceptincase(Q2,λ),wehavethatthe Booleanalgebraof definablebinaryconceptsisthe16element oneillustratedbyFig.2.Incaseof(Q2,λ), thealgebraof definablebinaryconceptsisthe8element onegenerated byrelationsλand =.
Fig. 3.FormulaΨτ→σ(x,y),definingspacelikerelatednessσfromtimelikerelatednessτ,intuitivelysaysthatxandyaredistinct pointsandinsidethelightconeofeverypointz(differentfromxandy)thereisapointuwhichisinsideneitherthelightcone ofxnorthatofy.
3. Interdefinabilityusing minimalnumberofvariables
Inthissection,wearegoingto showthattimelike,spacelikeandlightlikerelatednessaredefinable from oneanotherusing2auxiliaryvariables,butnotdefinableusingonlyoneauxiliaryvariable.Todoso,letus introducefirstformulaΨτ→σ definingspacelikerelatednessσfromtimelikerelatednessτ:
Ψτ→σ(x, y)def=x=y ,∀z
z=x∨z=y∨ ∃u(u τ z , uτ x , u¯ τ y)¯ .
FormulaΨτ→σ(x,y) intuitivelysaysthatx=y andinsidethelightconeofeverypointz (differentfrom x andy)there is apointuwhich isinsideneither thelightcone ofxnorthatof y,see Fig.3. Using this definition,wecaneasilydefine λfromτ bythefollowingformula:
Ψτ→λ(x, y)def=¬Ψτ→σ(x, y), xτ y , x¯ =y.
Theorem 1(n≥2;(Eucl.) orn=2).Assume that n= 2 orthat (Q,+,·,≤)isaEuclidean field. Thenin model(Qn,τ),spacelikerelatedness σcan bedefined fromtimelikerelatedness τ using 2auxiliaryvariables by formula Ψτ→σ.Hencelightlike relatednessλ canbe definedfrom timelikerelatedness τ using 2auxiliary variables byformula Ψτ→λ.
Proof. Letus first show, forall¯x,¯y∈Qn, that¯x σ¯y holdsexactly ifΨτ→σ(¯x,¯y) holds. Todo so,assume that¯x¯σ¯y.ThenweshouldshowthatΨτ→σ(¯x,¯y) doesnothold.If¯x= ¯y,thenclearlyΨτ→σ(¯x,¯y) doesnot holdasitcontains¯x= ¯y.Soassumethat¯x= ¯y.Let¯zbethemidpointoflinesegment¯x¯y.Then,since¯x= ¯z and¯z= ¯y(as¯x= ¯y),weshouldshowthat¯uτ¯x or¯uτ¯yholdsforall¯uforwhich¯uτ¯zholds. Bysymmetry, withoutlossofgenerality,wecanassumethat¯yisinthecausalfutureof¯x.Therearetwopossibilities:if¯u is inthetimelikefutureof¯z,then ¯uisalso inthetimelikefutureof¯x and hence¯uτ ¯x holds; if¯uisinthe timelikepastof¯z,then ¯uisinthetimelikepastof¯yandhence¯uτ¯y holds,seeFig.4.
To show the other direction, assumethat¯x σ ¯y. Without loss ofgenerality, we can assumethat ¯x and
¯
y areinthesamehorizontalhyperplane H becausethereis anautomorphism of(Qn,τ ,σ) thatmaps any two spacelikerelated points to horizontallyrelated ones, cf. Proposition1. Weshould show thatfor all¯z which isdifferentfrom¯xand¯y,there isa¯utimelikerelatedto¯z,whichis timelikerelatedneitherto ¯xnor to ¯y.Thereare twocases,seeFig.5.
• Either¯zisnotinthehyperplaneH,andthenthereisa¯u∈H verticallyrelatedandhencealsotimelike relatedto¯z;since¯u∈H, this¯uisspacelikerelatedto both¯xand¯y;
Fig. 4.Illustration for the proof of Theorem1.
Fig. 5.Illustration for the proof of Theorem1.
• or¯zisinthehyperplaneH andthusspacelikerelatedtoboth¯xand¯y,andhencethereisacloseenough u¯whichistimelikerelatedto¯zbutstill spacelikerelatedto¯x and¯y.
Theproofofthesecond partisstraightforwardsinceforall¯xand¯yexactlyoneofrelations¯xτ ¯y,¯xλ¯y,
¯
xσ¯yand¯x= ¯yholds.
Timelikerelatednessandlightlikerelatednesscanbe definedfromspacelikerelatednessbythefollowing analogousformulas6 (seeFig.6):
Ψσ→τ(x, y)def=x=y ,∀z
z=x∨z=y∨ ∃u(u σ z , uσ x , u¯ σ y)¯ .
Ψσ→λ(x, y)def=¬Ψσ→τ(x, y), xσ y , x¯ =y.
Letus note herethat,even thoughthere isno symmetrybetweenrelations σandτ unless n= 2, thereis anicesymmetrybetween definingformulasΨσ→τ andΨτ→σ (as wellas Ψσ→λ and Ψτ→λ)as theycanbe achievedfrom eachotherbyinterchangingrelationsσandτ.
Theorem2(n≥2;(Eucl.) or n=2).Assumethat n= 2or that (Q,+,·,≤) isaEuclidean field. Thenin model(Qn,σ),timelike relatednessτ canbedefined fromspacelikerelatedness σusing2auxiliaryvariables byformula Ψσ→τ.Hencelightlikerelatedness λcanbedefinedfromspacelikerelatedness σusing2auxiliary variablesby formula Ψσ→λ.
Proof. Firstweshow, forall¯x,¯y∈Qn,that¯xτ ¯yholds exactlyifΨσ→τ(¯x,¯y) holds. Soletus assumethat
¯xτ ¯y.Without loss ofgenerality,we canassumethat¯x and¯y areinthesameverticalline becausethere is an automorphism of (Qn,σ,τ) that maps any two timelikerelated points to vertically related ones,cf.
Proposition1.Weshouldshow thatforall¯zwhichisdifferent from ¯xand ¯y,there is au¯spacelikerelated to ¯z, which is spacelikerelated neither to ¯x norto ¯y. To find such a¯u, letus consider the hyperplane H through¯zorthogonal to , seeFig.7. If¯z∈/ , let¯ube theintersectionpoint of and H;and if¯z∈, let
6 LetusnotethatthisformulaisbasicallytheonementionedbyMalament [10,footnote8] defininglightlikerelatednessfrom causalityrelationσ.¯
Fig. 6.FormulaΨσ→τ(x,y),definingtimelikerelatednessτfromspacelikerelatednessσ,intuitivelysaysthatxandyaredistinct andoutsidethelightconeofeverypointz(differentfromxandy)thereisapointuwhichisoutsideneitherthelightconeofx northatofy.
Fig. 7.Illustration for the proof of Theorem2.
Fig. 8.Illustration for the proof of Theorem2.
¯
u∈H be suchapointdistinctfrom¯zthatthedistancebetween¯uand¯zislessthanboththedistanceof¯z and ¯xandthedistanceof¯zand¯y.As desired,byitschoice,¯uisspacelikerelatedto¯zbutnotto¯xor ¯y.
To showtheotherdirection,assumethat¯x¯τ¯y. ThenweshouldshowthatΨσ→τ(¯x,¯y) doesnothold.If
¯
x= ¯y,thenclearlyΨσ→τ(¯x,¯y) doesnotholdasitcontains¯x= ¯y.Soassumethat¯x= ¯yandletuschoose¯z to be themidpoint ofline segment¯x¯y, seeFig.8.Then, since¯z= ¯xand¯z= ¯y (as¯x= ¯y),we shouldshow thatfor all¯u,if¯uσ¯¯xand ¯uσ¯¯y, thenu¯σ¯¯z. There aretwo casesto consider:either¯xλ¯y or¯xσ¯y (in this second case,wecanassumethat¯xand¯yarehorizontallyrelatedbytheusualautomorphismargument, cf.
Proposition1).Inbothcases,¯uσ¯¯zholdsforallthepointsforwhich¯uσ¯¯xand¯uσ¯¯ybecausetheintersection of causalconesthrough¯xand¯yarecontainedinthecausalcone through¯z.
As before, the proof of thesecond partis straightforwardsince forall ¯x and¯yexactly oneof relations
¯xτ¯y, ¯xλ¯y,¯xσ¯y and¯x= ¯yholds.
Fig. 9. Formula Ψλ→σ(x,y), definingspacelike relatedness σ fromlightlike relatednessλ, intuitivelysays thatxand y are not lightlikerelated,andthereisapointz=xonthelightconeofxsuchthatzisnotlightlikerelatedtoyandthereisnopointuon thelightconeofytowhichbothxandzarelightlikerelated.Sincetherearenonon-degeneratelightliketriangles,thisbasically meansthatthereisalightlikelinecontainingxbutnotysuchthatthereisnolightlikelinethroughywhichintersects.
Thefollowingformulasarebasedonideasused in[4,AppendixB]:
Ψλ→σ(x, y)def=x¯λy ,∃z
xλz , y¯λz ,¬∃u(uλx , uλy , uλz) . Ψλ→τ(x, y)def=¬Ψλ→σ(x, y), x¯λy , x=y.
Theorem3((Eucl.) andn≥3).Letn≥3andassume thatorderedfield(Q,+,·,≤)isEuclidean. Inmodel (Qn,λ), spacelike relatedness σ can be defined from lightlike relatedness λ using 2 auxiliary variables by formula Ψλ→σ. Hence timelike relatedness τ can be defined from lightlike relatedness λ using 2 auxiliary variablesby formula Ψλ→τ.
Proof. Firstweshow,forall¯x,¯y∈Qn,that¯xσ¯yholdsexactlyifΨλ→σ(¯x,¯y) holds.Thusletusassumethat
¯
xσ¯y.ThenweshouldshowthatΨλ→σ(¯x,¯y) alsoholds. Todoso,considerthelightconeΛ¯x through¯xand takea tangenthyperplane H to this light cone containing¯y,such H exists because¯x is spacelikerelated to¯yand (Q,+,·,≤) is aEuclidean field,see Fig.9.Let¯zbe any pointbut¯x fromline := Λ¯x∩H.Then
¯x¯λ¯yholdsbecause¯xand¯yareassumedto bespacelikerelated.Since¯z∈Λ¯x and¯z= ¯x,wehavethat¯xλ¯z.
Since itis atangenthyperplane of alightcone, alllightlike lines are parallel inH (sinceH is tangentto everylightcone throughany pointof H).Hence¯y¯λ¯zalso holdssince¯y∈/ (as ¯y∈/Λ¯x). Soit remainsto show thatthere isno ¯ufor which¯uλ¯x,¯uλ¯y and ¯uλ¯z. To showthis, let ¯ube lightlike relatedto both ¯x and¯z.Then¯u∈becausealllightliketrianglesaredegenerate7 and¯u¯x¯zisalightliketriangle.Therefore,¯u cannot be lightlikerelated to¯y becausealllightlike linesare parallel inH. Hence,there is no¯ufor which allof¯uλ¯x, ¯uλ¯yand¯uλ¯zhold.Consequently,Ψλ→σ(¯x,¯y) holdsandthis iswhatwewantedtoshow.
Letusnow assumethat¯x¯σ¯y.Then weshouldshow thatΨλ→σ(¯x,¯y) doesnothold,i.e., ¯xλ¯yor,forall
¯
zwhichis lightlike relatedto ¯x butnotlightlikerelated to ¯y, weshouldbe ableto find a¯usuchthat¯uis lightlikerelatedto¯x,¯yand¯z.Assumption¯xσ¯¯ymeansthat¯x= ¯y,¯xλ¯yor¯xτ¯y.Since¯xλ¯zand¯y¯λ¯zimply that¯x= ¯y,theonlynontrivialcasetobe checkedis¯xτ ¯y.
Soletusassumethat¯xτ¯yandtakeany¯zforwhich¯zλ¯xand¯z¯λ¯yhold.Thenletusconsiderthelightlike line containing¯xand ¯zand thenonparallel lightlikeline through¯y intheplane determined by¯x,¯y and¯z (this lightlike line through ¯y exists becausethe plane determined by ¯x, ¯y and¯zcontains atimelike line).
7 Thisissobecausetherearetreekinds ofplanes:timelikeplanes(thatcontainexactlytwolightlikedirections),Robbplanes (thatcontainonlyonelightlikedirections)andspacelikeplanes(thatcontainnolightlikedirectionatall)andnoneoftheseplanes cancontainalightliketriangleunlessitisdegenerate.
τ
σ λ
Ψτ
→σ
(n≥2;(Eucl.
)or n=2)
Ψσ
→τ
(n≥2;(Eucl.
)orn=2)
Ψσ→λ
(n≥2; (Eucl.) orn= 2) Ψλ→σ (n≥3; (Eucl.))
Ψ
λ→ τ (n
≥3;
(Eucl.
)) Ψ
τ→ λ
(n
≥2;
(Eucl.
)or n=
2)
Fig. 10.Hereweillustrateformulasdefiningtimelikeτ,spacelikeσ,lightlikerelatednessλfromeachotherusingonly2auxiliary variablesinthecorrespondingspace-timedimensionsn.
These two linesintersect becausetheyare coplanarnonparallellightlike lines. Let ¯ube theirintersection.
Byitschoice,this¯uislightlikerelatedto¯x,¯uand¯zas desired.
Againtheproof ofthesecondpartisstraightforwardsinceforall¯x and¯yexactlyoneofrelations¯xτ¯y,
¯
xλ¯y,¯xσ¯y, and¯x= ¯yholds.
InFig.10,wesummarizethevariousdefiningformulasofthissectionandtherequiredconditionsinthe corresponding theorems.
Remark2(n=2).Overanyorderedfield(Q,+,·,≤),ifn= 2,neitherspacelikerelatednessσnortimelike relatednessτ canbe definedfromlightlikerelatednessλbecausemapα: (t,x)→(x,t) isanautomorphism of model(Q2,λ) takingrelationσtoτ.
Remark3.Theassumption that(Q,+,·,≤) isEuclidean cannot beomitted from Theorem3.To seethis, let usconsider the set ofreal numberswhich canbe writtenas a+b√
2 forsome rationalnumbersa and b. It is knownand also easy to check that these numbersform an ordered subfield of real numbers. Map α:x+y√
2→x−y√
2 preservesthe additionand themultiplication inthisfield,and hencebijection αˆ: (p0,p1,. . . ,pn−1)→(α(p0),α(p1),. . . ,α(pn−1)) takeslinestolines,andpreserveslightlikerelatedness.Since
ˆ
α interchanges timelike vector
1,1−√
2/2,0. . . ,0
and spacelike vector
1,1 +√
2/2,0, . . . ,0
, neither timelike relatedness nor spacelike relatedness can be defined from lightlike relatedness over this ordered field.Thiscounterexamplecanbegeneralizedoveranyorderedfield(Q,+,·,≤) whichhasanautomorphism αof(Q,+,·) whichdoesnotpreservetheordering≤.Thisissobecauseinthosefields thereisanelement b > 0 such that α(b) <0. If b< 1, then (1,1−b,0,. . .0) is a timelikevector whose image is spacelike, otherwise(1,1−1/b,0,. . . ,0) is suchavector.
Remark4.Eventhoughthepicturesqueproofusedinthispaperdoesnotworkoverarbitraryorderedfields, sinceitusesProposition1(whichdoesnothold,forexample,inthefieldofrationalnumbers),Theorems1 and 2doholdover arbitraryordered fields.
Theorem 4 (n ≥ 2).Over any ordered field (Q,+,·,≤), none of the relations τ, λ and σ is definable in termsof oneof theothersusing only1auxiliary variable.
be builtupfrommembers ofRand theidentityrelation = byusing thefollowing operations:intersection
∩, union∪,complement ¯, relation composition; andconverse −1.Let ρbe any oftherelations τ, λand σ.Toshow thatnoneoftheotherrelationsisdefinablefrom ρ,wearegoingtoshow thatset
S =
∅, =, =, ρ, ρ,¯ ρ¯∩ =, ρ∪=, Qn×Qn
is closed under the above relation operations. S is clearly closed under complement by De Morgan’s law and itiseasyto check thatS is closedunderintersectionandunion,cf. Fig.2.HenceS is afieldof sets8 withatoms=,ρandρ¯=(whichisρ¯∩=).Sinceidentity (P∪Q);R≡(P;R)∪(Q;R) holdsforallbinary relations P, Qand R,it isenough to showthatthe various compositionsof atoms=, ρand ρ¯= are inS, whichholdsbecauseρ;ρandρ¯=; ¯ρ=aretheuniversalrelationQn×Qn,compositionsρ¯=;ρandρ; ¯ρ=are equaltotherelation=,and= isanidentity elementwithrespect totherelationcomposition.Sinceallthe relationsinS aresymmetric,theyareequaltotheirconverses.Therefore,allthebinaryrelationsfirst-order definablefrom ρusingonlyoneauxiliaryvariableareinS.Thiscompletes theproof ofthetheorem.
4. Quantifiercomplexity
Letus now investigatethe quantifiercomplexity of thepossible definitions.To doso, letus recallthat aformula iscalled universal iffit isof form ∀x1. . .∀xkψ for somequantifierfreeformula ψ andvariables x1,. . . ,xk.Aformulaisexistential inthecompletelyanalogouscasewhen∀ isreplacedby∃.Aformula is called universal-existential iff it isof form ∀y1. . .∀ym∃x1. . .∃xkψ forsome quantifierfree formulaψ and variablesx1,. . . ,xk,y1. . . ,ym.Thedefinitionofanexistential-universal formulacanbe obtainedfromthis by interchanging the universal and existential quantifiers. In the superscript, we indicate the number of quantifies, and we use * in case this number is not specified, e.g., by ∀1∃1-formulas we mean universal- existentialformulascontaining exactlyoneuniversaland oneexistentialquantifiers,andby∀∗∃∗-formulas wemeanalluniversal-existentialformulas.
Itisstraightforwardtoshow thatthedefiningformulasΨτ→σ,Ψσ→τ andΨλ→τ arelogicallyequivalent to ∀1∃1-formulas and Ψτ→λ, Ψσ→λ and Ψλ→σ are logically equivalent to ∃1∀1-formulas, see Table 1. So theseformulasare alsoquitesimpleintermsofquantifiers.
Itisanaturalquestionwhetheritispossibletofindevensimplerdefiningformulasintermsofquantifier complexity.Nowwearegoingtoinvestigatethisquestionlookingforexistentialanduniversaldefinitions.To makeourformulasmoreconcise,wearegoingtousethefollowingabbreviationforcertainbinaryrelations ρandδ:
x ρδ yz ⇐⇒def x ρ y , x δ z.
Wewillalsousethenaturalgeneralizationof thisabbreviationformorethantwobinaryrelations.
InTheorem5below,wearegoingtoshowthatthefollowing∃4-formulaEτ→σdefinesspacelikerelatedness σfrom timelikerelatednessτ in(Qn,τ):
8 ThatisasubalgebraofthepowersetBooleanalgebraofQn×Qn.
¯ ττ¯
τ τ τ τ
ττ¯
¯ ττ¯
¯ τ τ
¯ τ τ ττ¯
¯ ττ¯
¯
p ¯q
¯s
¯r
¯ z
¯ x
τ τ
τ τ τ τ
¯ τ τ
¯ ττ¯
¯ τ τ τ¯τ ττ¯
¯ τ¯τ
¯ p
¯ q
τ τ
¯ τ¯τ
¯ τ τ τ τ τ¯τ
¯ ττ¯
¯ p
¯ q
r s
x z
Fig. 11.Here,weillustratetheproofofthatEτ→σ(¯p,¯q) holdsexactlyif¯pσ¯qholds.(Forcoloredversionsofthefigure(s),thereader isreferredtothewebversionofthisarticle.)
Eτ→σ(p, q)def=∃r∃x∃s∃z(r τ τ pq , x ττ pq , s¯ τ¯τ pq , z¯ τ τ pq , r¯ τ τ¯ τ xsz),¯ and hence
Uτ→λ(p, q)def=¬Eτ→σ(p, q), p=q , p¯τ q givesauniversaldefinitionoflightlikerelatednessfromτ.
Theorem 5(n≥2;(Eucl.) orn=2).Assumethat n= 2 orthat (Q,+,·,≤)is aEuclideanfield, then:
1. Spacelike relatedness σ can be defined existentially from timelike relatedness τ by ∃4-formula Eτ→σ in (Qn,τ).
2. Lightlike relatedness λ can be defined universally from timelike relatedness τ by ∀4-formula Uτ→λ in (Qn,τ).
Proof. Firstwearegoingtoshowthat¯pσ¯qholdsexactlyifEτ→σ(¯p,¯q) holds.If¯pσ¯q,thenwecanassume, without loosing generality, that¯p andq¯are horizontallyrelated, cf. Proposition1.In this case,it is easy to verify thatthereare (even coplanar)points¯r,¯x,¯s,¯z∈Qn for whichrelations¯rτ τ ¯p¯q, ¯xττ¯¯p¯q,¯s¯ττ¯¯p¯q,
¯
z¯τ τ ¯p¯q,¯rτ¯sand¯rτ¯τ¯¯x¯zhold;and henceEτ→σ(¯p,¯q) also holds,see Fig.11,where theregionsarecolored andlabeledbasedonhowthepointsfromtherearerespectivelyrelatedto¯pand¯q.So,accordingtoFig.11,
¯rτ τ ¯p¯qholds iff¯risinabrownτ τ region,¯xττ¯p¯¯qholdsiff¯x isinablueττ¯region,¯s¯ττ¯p¯¯qholdsiff¯sisin aredτ¯τ¯region, and¯zτ τ¯ ¯p¯qholdsiff¯zinagreenτ τ¯ region.
Toprovetheotherdirection,letusassumethat¯pσ¯qdoesnotholdandprovethatEτ→σ(¯p,¯q) doesnot hold.Thenthere arethreecasestoconsider:either¯p= ¯qor¯pλ¯qor¯pτ ¯q.
If ¯pτ¯q,then, withoutloosinggenerality, wecanassumethat¯qisinthetimelikefutureofp¯and that¯p and¯qareverticallyrelatedbyProposition1.Inthiscase,wearegoingtoshowthattherearenoappropriate points¯r,¯x,¯s,¯z∈Qn.EventhoughFig.11istwo-dimensional,italsoillustratesthehigher-dimensionalcases well becauseof rotationalsymmetry withrespect to thetime-axis.So weare goingto useFig.11to refer theregionshaving appropriaterelationswithrespecttop¯and¯q.
futureof¯r; andhencerelation¯rτ¯¯x cannothold.
• If¯r is inthe middle brownτ τ region, then there is no¯s from a red ¯ττ¯region whichis τ-related to¯r.
This isso because,if¯sistimelikerelated to¯r,then itisalso timelikerelatedto ¯p(if¯s isinthefuture of¯r)or timelikerelatedto ¯q(if¯sisinthepastof¯r).Thus¯scannot be ¯τ-relatedto both ¯pand¯q;and henceitcannotbe fromared¯ττ¯region.
• If¯ris intheupperbrownτ τ region,then thereis no¯zfrom agreen τ τ¯ region,whichis τ-related¯ to¯r foracompletelyanalogous reasonas inthefirstcase.
Hencethereisnoappropriate¯rrequiredbyformulaEτ→σ.Therefore,Eτ→σ(¯p,¯q) cannotholdif¯pand¯qare timelikerelated.
If¯pλq,¯ thenbasically thesameargumentworksbutit issimplerbecausethereis nomiddlebrownτ τ region,cf. Fig.11. Here,insteadofthetransitivityofthetimelikepastandfuturerelations,weshoulduse thefactthatthetimelikepastofpointsfromthecausalpastofpointq¯isinthetimelikepastof¯q,andthe analogous fact thatwe get from this oneif we replace pastwith futureand ¯q with ¯p. If ¯p= ¯q, then the situationisevensimplerbecause,thentherearenogreenττ¯andblueτ τ¯ regionsatall.So,ifp¯σ¯qdoesnot hold,thenEτ→σ(¯p,¯q) doesnothold either.This completestheproof ofthis directionandhencetheproof ofItem (1).
Item (2) followsfrom Item (1) andthe factthatexactlyoneof relations¯pτ ¯q,¯pλ¯q,p¯σ¯q, and¯p= ¯q holdsforevery¯p,¯q∈Qn.
Since map α: (t,x) →(x,t) isan isomorphismbetween structures (Q2,τ ,σ) and (Q2,σ,τ), existential formula
Eσ→τ(p, q)def=∃r∃x∃s∃z(r σσ pq , x σσ pq , s¯ σ¯¯σ pq , zσσ pq , r¯ σσ¯¯ σ xsz) definestimelikerelatednessτ from spacelikerelatednessσin(Q2,σ),andhence,
Uσ→λ(p, q)def=¬Eσ→τ(p, q), p=q , pσ q¯
givesauniversaldefinitionoflightlikerelatednessfromσin(Q2,σ).Inotherwords,followingisanimmediate corollaryofTheorem 5.
Corollary3(n=2).Let(Q,+,·,≤)be anarbitrary orderedfield, then:
1. Timelikerelatedness τ can be defined existentially from spacelikerelatedness σby ∃4-formula Eσ→τ in (Q2,σ).
2. Lightlike relatedness λ can be defined universally from spacelike relatedness σ by ∀4-formula Uσ→λ in (Q2,σ).
Remark 5 (n ≥ 3).The assumption n = 2 cannot be omitted from Corollary 3, i.e., ∃4-formula Eσ→τ
does notdefine τ in(Qn,σ) if n≥3.Spacelike related points¯p and ¯qsatisfyingEσ→τ(p,q) can easily be foundsearchingtheminhorizontalslicesof (Qn,σ) looked fromabove,cf. Fig.12. ThatEσ→τ canalsobe