and Multiple Quantum Transitions, Double

C H A P T E R 9

Multiple Quantum Transitions,

Double Resonance and Spin Echo Experiments

T h e preceding chapters have been almost exclusively concerned with the theory of single quantum transitions induced by a linearly polarized rf field. This chapter will be concerned with introductory accounts of the multiple quantum transitions observed at increased amplitudes of a single rf field {1-8), the simultaneous application of two rf fields (9-22), and a single rf field applied in the form of a coherent pulse train (23-27).

It will be assumed throughout that the amplitudes of the applied rf fields are much smaller than the steady ζ field, so that only the appropriately sensed circularly polarized components need be retained in the hamiltonian operators. T h e discussion will be simplified further by ignoring the interactions coupling a representative spin system to its molecular surroundings. Although this limitation precludes a complete theoretical discussion, it is nevertheless possible to obtain useful results with the theory developed in earlier chapters.

1 . Multiple Quantum Transitions A. Introduction

An η-tuple or multiple quantum transition may be described as a transi- tion involving the exchange of η rf quanta between the rf field and the nuclear spin system. A multiple quantum transition is said to be absorptive or emissive, accordingly as the exchange of quanta increases or decreases the energy of the spin system. In an absorptive transition, the number of rf quanta transferred from the rf field to the spin system is equal to minus the change in the ζ component of angular momentum.

For example, if the ζ components of angular momenta of the initial

4 0 6

1. M U L T I P L E Q U A N T U M T R A N S I T I O N S 407 and final states are m and m'^y respectively, then, since m' < m, n = -(m' - m). In an emissive transition, m > m, so that η = - m).

Multiple quantum transitions were mentioned briefly in Section 3.C of Chapter 1 for the case of a single nucleus with / > \ , and in Chapter 3 it was shown that the transition probabilities corresponding to η = 0, 1, 2, 21 are given by the Majorana formula [equation (3.14), Chapter 3]. In Section 5.4 it was shown that multiple quantum transitions also occur in the more general AN system. T h e analysis of this system showed that the transition probabilities are independent of the spin-spin interactions, and are, in fact, still given by the Majorana formula.

Because of the importance of the Majorana formula in many problems, its physical significance will be restated.

Consider a single nucleus of spin / , or an irreducible component of an system, in a steady ζ field H⁰ . It will be assumed that γ > 0, that the angular momentum is quantized along the ζ axis, and that the system is initially in the eigenstate | / , tn). If the system is subjected to a circularly polarized rf field at t = 0, the Majorana formula gives the probability that the system is in the eigenstate | / , m'} at time t. For an alternative interpretation, and for later reference, suppose that at t = 0 the system is suddenly subjected to a constant field H ^ H ⁰. T h e Majorana formula, in the form [cf. Section 2.3, equations (3.45) and (3.48)]

PZL>-(<P) =

[^«Wl

= C + -

j y ( - l ) * [ t a n ( y > / 2 ) ] ^ ^ * j² i ft(I - m - k)\(m - m' + k)\(I + m! - k)\k\) ' K ' where φ is the angle between the positive ζ axis and H, gives the pro- bability that an angular momentum determination will yield the eigenvalue rri for the component of I along H. This interpretation of the Majorana formula will be used in the discussion of double resonance experiments.

T h e essential point concerning multiple quantum transitions between the energy levels of a nucleus with spin I > J , or an irreducible com- ponent of an AN system, is that, in either case, the levels are equally spaced. Although the rf field supplies monoenergetic quanta only at frequency ω> an w-tuple quantum transition can occur through the absorption of η equienergetic rf quanta via intermediate states connecting the initial and final states. T h e importance of the intermediate states in the calculation of the transition probability is explicitly indicated by the summation in the Majorana formula.

408 9. M U L T I P L E QUANTUM TRANSITIONS

The frequency of an absorptive w-tuple quantum transition is easily calculated. Let m and fiQm denote the ζ component of angular momentum and energy of the initial state, and m\ fiQm> the corresponding quantities for the final state. The energy given up by the rf field must be (approxi- mately) equal to the energy absorbed by the spin system. It follows that ηήω = fi(ß^m> — ßm) ; hence the (angular) frequency of an w-tuple quantum transition is

ω = i ( ßm* - f lm) . (1.2)

For a single nucleus with spin / , Qm> — Ωηι = (m — τη)γΗ0 = ηω0 , while Qm> — Ωηι = n(l — σ)ω0 , for an irreducible component of an AN

system. Equation (1.2) shows that, in either case, the resonance fre- quencies of all multiple quantum transitions (n = 1 , 2 , . . . , 21) are equal—specifically ω = ω0 , for a single nucleus, and ω = (1 — σ)ω0

for an irreducible component of an AN system.

Multiple quantum transitions can also occur in coupled nuclear spin systems with nonvanishing internal chemical shifts (2, 3). For the changes in the zero-order energies resulting from internal chemical shifts and spin-spin coupling constants are usually small compared to nuclear Larmor frequencies, so that normally only small deviations from the equal-spacing condition occur. For example, in the AB system (Table 6.1) the energy levels corresponding to m = 0 can be expected to be approximately halfway between the levels with m = 1 and m = — 1.

T h e only multiple quantum transition possible in an AB system is a double quantum transition (2). T h e frequency of the double quantum transition is, by (1.2) and Tables 6.1 and 6.2,

1(Ω_^λ - Ω^λ) = ±(ω^Α

+

) =

which shows that the frequency of the double quantum transition is midway between the frequencies of the single quantum transitions A1 , B1

and A2, B2. In general,

an identity that provides a simple relation between the frequencies of single and double quantum transitions. Similar rules are easily derived for

" = 3 , 4 , . . . .

One obvious application of multiple quantum transitions is the determination of frequency separations that cannot be obtained from single quantum transitions, provided, of course, that the multiple quantum transitions can be detected.

1 . M U L T I P L E Q U A N T U M T R A N S I T I O N S 409

T h e intensities of w-tuple transitions can be calculated by extending the time-dependent perturbation calculation developed in Section 5.3 to higher orders in the amplitude of the rf field. Before carrying out this program, a simple consequence of (1.2) will be noted. If it is assumed that the uncertainties of all energy levels are comparable, then, all other considerations aside, (1.2) shows that the width of an η-tuple quantum transition should be η times smaller than the width of a single quantum transition. This conclusion is confirmed by the general theory of multiple quantum transitions in coupled spin systems (4).

B. Theory of Multiple Quantum Transitions

Consider a coupled spin system in a stationary ζ field, and let | rri) denote an eigenstate of energy Q^m and ζ component of angular mo- mentum m. If the system is subjected to a circularly polarized (transverse) rf field at t = 0, the probability amplitude for the state | rri) at time t is given, to the second order in H1 , by (3.17) of Chapter 5. In the discussion of that equation, it was pointed out that the second-order term includes contributions from intermediate states. T h e second-order term is

( W A ) 2

Σ

r r m τη. \ 'r m m ' ' m ' * m

where W^m = — ( ß^m + τηω).

T h e study of the preceding expression is facilitated by replacing Ix

with J ( / + -f I~)y so that the product of the matrix elements in Ix becomes (m I Ix I m"){m" \Ix\m) = \[{m' \ Γ \ m")(m" \ Γ | m)

+ (w! 11 -

I

N o w (m'\ Ι± \m) = 0, unless rri — m ^ 1 , so that the first term within the square bracket vanishes, unless m' = m — 2. Terms of this form yield a contribution to the probability amplitude of an absorptive double quantum transition.

T h e second and third terms in the square bracket vanish, unless rri — m, so that terms of this form yield a second-order correction to the probability that the system is still in the initial state | tri) at time t. It will be assumed, as in Section 5.3, that the time interval t is short enough to ensure that P^mm{t) œ 1, so that higher-order corrections to P^mm(t)

410 9. MULTIPLE QUANTUM TRANSITIONS

can be neglected. It will also be assumed that / is long enough to permit a subsequent integration over a range of energies to obtain the transition probability per unit time (Section 3.B, Chapter 5).

T h e remaining term in the square bracket vanishes, unless rri = m + 2.

Terms of this form yield a contribution to the probability amplitude of an emissive double quantum transition.

T h e perturbation expansion may be carried out to higher orders, and an examination of these terms [Section 2, Appendix III] shows that the fourth-order terms also contribute to the probability amplitude of I m — 2) at time t. This contribution, and the contributions of all higher-order terms, will be neglected. Therefore, the second-order probability amplitude for | m — 2) at time t is

γΗλ

Γ

I /- I

M"T -

^\

W - W <> W — W W » — W

where m = m — 2, m" = m — 1, and the summation is to be taken over all states with m" = m — 1. T h e absolute square of this quantity gives the probability of the double quantum transition | rri) —> \ m — 2).

A simplification results upon noting that only the first term within the brackets gives an appreciable contribution to the transition probability when co ^ J( ß^M- 2 — ß^m) . Therefore,

γΗ

y I sin j(Q

_

-Q

- 2œ)T W?m 2 — &m —

P " 2 ( 0 - ( 72 ¹ ) ( 1

(m — 2 \ I" \ m")(m" \ I~ \ m)

Qm» — Ωπι + (m" — ηι)ω (1.3) T h e preceding argument can be extended to multiple quantum transitions with η > 2. With the same restrictions on the time interval t, the probability that the system is in the state | m — ri) at time t is

_ ( J F L ) "

C':^---/---")' ^{I K.}

\ 2 / \ f( Qm_n — Qm — no) ! T h e quantity Kⁿ is defined by

K = V ' j Π"^ο ( « - « + R

I

I «

" ^ I Π ^ Ί ( ΰ « - Γ - β » - « ) Ί' ( '

where the prime on the summation sign indicates multiple summations over all intermediate states connecting | m) and | m — ri). For η = 2, (1.4) reduces to (1.3).

1. M U L T I P L E Q U A N T U M T R A N S I T I O N S 411 Equation (1.4) shows that the transition probability of an η-tuple quantum transition is proportional to the 2wth power of the rf-field amplitude. Moveover, P^m^^m_ⁿ(t)> considered as a function of ω, has an absolute maximum at

ω = ±(Qm_n - Qm). (1.6) When the intensity of an η-tuple quantum transition is calculated,

the value of ω given by (1.6) is to be inserted in the denominator of (1.5).

It should also be noted that the absolute square of (m — η + r\ I~ \m — η + r + 1)> which appears in the numerator of (1.5), is the relative intensity of the single quantum transition \ m-n -\- r -\- 1 ) - > | w - « + r).

N o w the coefficients in the expressions that define the eigenvectors of Jf⁷ as linear combinations of basis vectors can be chosen to be real numbers, so that one can assume that

(m — n + r\r\m — n + r + l)= (Int)J^{l /}?^{n + r + 1}_^{> T O}_^{n +r} . (1.7) T h e intensity of an w-tuple quantum transition may be obtained by using (1.4) to determine the transition probability per unit time, defined by

Wm->m-n =

j

j

Once wm_>^m_ⁿ has been evaluated, the intensity of the transition may be determined by a procedure analogous to that used in Section 3.Ε of Chapter 5. T h e result is

,T n tx _ 2πΝ0γ2ηΗ?~xh\Qm^ - Qmf 1 Kn

I

V™)m->m-n 2*"kT dim S ' ^{K }} where dim S is the dimension of the spin space, and the usual approxima- tions have been introduced in the Boltzmann distribution.

Equation (1.8) shows that the integrated intensity of an w-tuple quantum transition is proportional to Η^~^χ. T h e increase of the signal intensity with H¹ may be used to distinguish multiple quantum transitions corresponding to different values of n. Indeed, (1.8) shows that the graph of l o g ( I n t )m^m_n vs. log H1 will have slope 2n — 1.

Equations (1.6) and (1.8) are strictly applicable only in the region where the rf-field amplitude is sufficiently small to avoid saturation of the multiple quantum transition. Unfortunately, it is often difficult to avoid some degree of saturation. In such instances it is then necessary to resort to the general theory of multiple quantum transitions for intensity

412 9. M U L T I P L E Q U A N T U M T R A N S I T I O N S

C. Elementary Applications

T h e preceding results will be illustrated for the AB, A²B , and the A B X systems.

1. The AB System. For the A B system, only a double quantum transition is possible: | m = + 1 ) - > | m' = —1). T h e intermediate states are | 0; r), where r = 1, 2, so that (1.5) reduces to

K =( - l | / - 1 0 ; l ) ( 0 ; l l / - | l ) ( - 1 | / - 1 0; 2)(0; 2 | / - [ 1)

2 [fl^{0 ;1} - Ω^χ - \{Ω_^λ - Ω,)] [Ω^0;2 -Ω,~ \(Ω_^Χ - Ω,)] ' T h e matrix elements and energy differences may be obtained from the work of Section 6.1:

( - 1 | / - | 0 ; 1 ) ( 0 ; 1 | / - | 1 ) = 1

/

( - 1 | / - | 0 ; 2 ) ( 0 ; 2 | / - | 1) = 1 + ^J (P + δ²)¹/² ' Ω^0Λ - Ω, - - Ω,) = 1 [ / + (ρ + Ω^ΟΆ - ß i - i( ß- x - β χ ) = i [ / - (Ρ + Βηνη.

From these results one finds | AT2 |2 = 6 4P/ 8ⁱ, so that

( l n t-)1 - A T l W *

where <ω> = ^ ( ω^Α + ω^Β). This shows that the intensity of the double quantum transition tends to zero as / —*• 0, or δ —»• oo.

and frequency calculations (4). In particular, the general theory shows that there is a shift in the resonance frequency proportional to Hx2. This shift is given by

d = Km I Jx 1 m' ) \2 - I K 1 4 1 " * — n)? ^ 9^

T h e resonance frequency is now given by

ω = -n{Qm_n~Qm + d). (1.10)

In the region where the transition is unsaturated, the frequency shift can be neglected. However, it should be included if accurate frequency differences are required.

1. M U L T I P L E Q U A N T U M T R A N S I T I O N S 413 T h e integrated intensities of the single quantum transitions may be calculated with (3.39) of Chapter 5. Neglecting corrections of the order of J and δ in the term ( ß^m_^x — ß^m)², one obtains

(i°t^

= ( i ^ W

= ^

j S '

j i +

(J² + 8²)¹/² V

L j (/* + δ

)

/

j'

Hence

( I n t ) , ^^a \ S² / r

(Int)i-,-i _ /

(/

+ δ

)

/

( I n t ) ^0 ;2 l

δ

) j

+ (/

+ δ 7

)»/

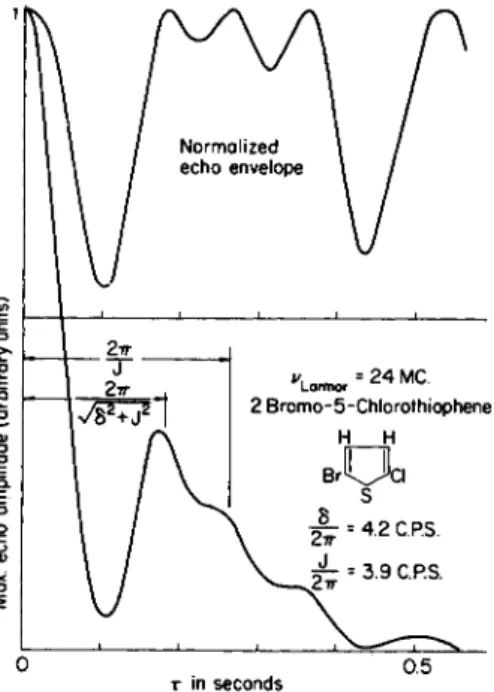
T h e single quantum transitions in the proton magnetic resonance spectrum of 2-bromo-5-chlorothiophene are shown in Fig. 9.1(a);

Fig. 9.1(b) shows the double quantum transition (2) at ^ ( ωΑ + ωΒ).

2. The A2B System. In the A2B system, multiple quantum transi- tions can occur only between states of the irreducible A¹B¹/² component.

T h e eigenvectors of the A¹B¹/² system are given in Table 6.4, and will be denoted | i f ) , | ± \ \ r\ where r = 1,2.

(a)

(b)

F I G . 9 . 1 . P r o t o n m a g n e t i c r e s o n a n c e spectra of p u r e 2 - b r o m o - 5 - c h l o r o t h i o p h e n e at 60 M c p s : (a) single q u a n t u m t r a n s i t i o n s ; (b) t h e d o u b l e q u a n t u m transition at ^ ( ωΑ -f ωΒ) .

414 9. M U L T I P L E Q U A N T U M T R A N S I T I O N S

There are four double quantum transitions:

D

: lf)-l-i;l),

D

: |f)-|-i ;2),

D

: li ;l)-H -f),

D

: | i ; 2 ) - > | - f ) .

T h e corresponding resonance frequencies are, by (1.2) and Table 6.4,

Di : i (3 <o

+ ω

+ f / + R

^) = ^ + A

),

D² : i(3o>^A + cob + f / - *i.-i) = i(A^x + B²), D³ : i(3œ^A + ω^Β - f / - Ä^{l t 0}) = i(A⁴ + B²),

#4 : 1( 3 ω^Α + ω^Β - f/ + Ä^{l e 0}) = i(A³ + A⁴),

where the A^ and denote the frequencies of the single quantum transitions given in Table 6.5.

T h e intensities of the double quantum transitions require the evalua- tion of the four K2s defined by (1.5) with η = 2. For example, K² for Ζλ is

u¹ : K²

&1/2,1 ~

^3/2 ^{2v ^-l /2 ;i} ^3/2)

(-j; 1 |/-|j;2)(i;2|/-|t)

^1/2 ;2 ^3/2 ^(^-1/2 ;i ^3/2)

+

T h e matrix elements appearing in the expressions for the K2s ^{a re} related to the intensities of the single quantum transitions of the A2B system by the following equations:

(i ; 1 I /- I f) = (Int (1. 2 I /- I f) = (Int B,)*/*, (-i ; 1 I 7- I i ; 1) = (Int A,)*/*, (--J ; 2 1 1~ \ \ ; 1) = (Int BjW,

{-i ; 1 I 7- 11 ; 2) = (Int M)1/2, ( - £ ; 2 | 7- | £ ; 2) = (Int A3)V\

( - 111 - I -i ; 1) = (Int B,)V*, ( - f I 7- I - 1 ; 2) = (Int Atfl*.

These relations yield the following expressions for the four K²'s:

D . K_ „ , [ ( I m A ^ I n t A ^ / * [(Int M)(Int B J ] ^ \ δ - f / - 27?^{1 >0} + δ - f/ + 2 Ä^{l i 0} + T f ^ Y D2: K2 = - 4 ; [(Int B2)(Int A J ] ^ + [(Int A2)(Int B J ] ^ )

1. M U L T I P L E Q U A N T U M T R A N S I T I O N S 415

A .

K^{9 =} 4 j [ ( I n t B³) ( I n t A²) ] V^{2 +} [(Int A⁴)(Int B^a)]V»

D⁴ : K² = 4

l δ + f / + 2R1,_¹ - Ä1 >0 δ + f / - 2Rlt_¹ - Λ1 β0 f [(IntB,)(Int M)}^{112 +} [(Int A⁴)(Int A3)]¹/² δ + f / + + R^lt0 δ + f / - 2 « ! . . ! + Ä^{l e0} T h e ratios of the absolute squares of these quantities may be taken as measures of the ratios of the integrated intensities of the double quantum transitions.

Figure 9.2(a) shows the single quantum transitions observed in the

FI G. 9.2. P r o t o n m a g n e t i c r e s o n a n c e s p e c t r a of 1,2, 3 - t r i c h l o r o b e n z e n e at 60 M c p s : (a) single q u a n t u m t r a n s i t i o n s of g r o u p s A a n d B ; (b) d o u b l e q u a n t u m t r a n s i t i o n s ; (c) t h e t r i p l e q u a n t u m transition at ^ ( 2 ωΑ + ωΒ) . T h e e x t r a n e o u s lines are a t t r i b u t e d to s p i n n i n g s i d e b a n d s .

proton magnetic resonance spectrum of 1 , 2 , 3-trichlorobenzene in carbon disulfide. An analysis of this spectrum yields¹1 δ \/2π = 12.89 cps, I J \\2TT = 8.08 cps. With these values one finds that

Int Dx : Int D2 : Int D3 : Int Z)4 = 2 : 13 : : 751.

T h e double quantum transitions are shown in Fig. 9.2(b). Transition Z)⁴ , which is calculated to be 58 times as intense as D² , is unobserved.

T h e reason is that Z)4 , which saturates at a lower power level than D2, is saturated in Fig. 9.2(b). This is illustrated in Fig. 9.3, which shows an

1 T h e value of δ/2π given h e r e differs f r o m t h a t cited in S e c t i o n 6.2 b y 1.08 c p s . T h e c o n c e n t r a t i o n of t h e 1, 2, 3 - t r i c h l o r o b e n z e n e s a m p l e u s e d to o b t a i n t h e s p e c t r u m of Fig. 9.2(a) differed from t h a t of t h e s a m p l e u s e d to o b t a i n t h e s p e c t r u m of Fig. 6.9, so t h a t t h e difference is a t t r i b u t e d to a solvent shift.

416 9. M U L T I P L E Q U A N T U M T R A N S I T I O N S

expanded trace of the single quantum transitions A³ , A⁴ , B^x , and the double quantum transitions D4 and D2 , at successively larger amplitudes of the rf field.

F I G . 9 . 3 . P r o t o n m a g n e t i c r e s o n a n c e spectra of 1, 2 , 3- t r i c h l o r o b e n z e n e at 60 M c p s : (a) t h e single q u a n t u m t r a n s i - tions A3 , A4 , Bx ; (b) t h e d o u b l e q u a n - t u m transitions Z>4 a n d D2 . T h e spectra s h o w n in p a r t s (c) a n d (d) w e r e o b t a i n e d at successively h i g h e r rf a m p l i t u d e s , a n d s h o w t h a t Z)⁴ saturates at a lower p o w e r level t h a n D2 .

T h e only other multiple quantum transition possible in an

A

B

/

system is a triple quantum transition: | f ) - > | — §). T h e frequency of this transition is

ϋ ί( 2 ωΑ + ωΒ — J) + |-(2ωΑ + ωΒ + / ) } = ^(2ωΑ + ωΒ),

which is just the mean resonance frequency of the A²B system. This is a special case of the following general result. T h e irreducible

A

B

C

* ··

component of an

A

B

C

A

B

C

G' ·

1. M U L T I P L E Q U A N T U M T R A N S I T I O N S 417 Hence the frequency of the 2(1A + IB + ---J-tuple quantum transition

| / Α + / Β + " · ) - * Ι - ' Α - / Β - · · · ) is

' G ' G

If all IG have their maximum values, that is, IG = \n^G , the resonance frequency is N~~x Σ nGœ^G = <ω>.

T h e triple quantum transition in the proton magnetic resonance spectrum of 1,2, 3-trichlorobenzene is shown in Fig. 9.2(c).

3. The A B X System. As a final application, consider the double quantum transitions appearing in the AB region of an A B X system. In Section 7.2 it is shown that the AB region consists of two pseudo AB quartets, so that double quantum transitions should occur at the centers of these quartets. This result can often be used to pick out the pseudo AB quartets in spectra where overlapping occurs.

Figure 9.4(a) shows the single quantum transitions of the proton magnetic resonance spectra of 2-fluoro-4,6-dichlorophenol. Although the decomposition into a pair of pseudo AB quartets is discernible, the decomposition becomes patently apparent with the assistance of the double quantum transitions [Fig. 9.4(b)]. T h e frequency separation of the double quantum transitions is ( 2 7 r )_ 1| ( /A X + 7BX)I — 8.2 cps, in agreement with the result obtained in Section 7.3. If approximate values

F I G. 9.4. P r o t o n m a g n e t i c r e s o n a n c e spectra of 2-fluoro-4,6-dichlorophenol at 60 M c p s : (a) single q u a n t u m transitions in t h e A B r e g i o n ; (b) d o u b l e q u a n t u m transitions at t h e m e a n frequencies of t h e p s e u d o A B q u a r t e t s .

418 9. M U L T I P L E Q U A N T U M T R A N S I T I O N S

of {2ττ)~¹\ /^{α χ} I , (277-)^_1| /^{B X} | are estimated (e.g., by first-order perturba- tion theory), the sign of /^{A X} relative to /^{B X} can be determined. This idea was used to determine the relative signs of the coupling constants in

1, 2-dibromopropionic acid (6).

Multiple quantum transitions have not, as yet, been extensively used in the analysis of high-resolution spectra. It seems likely, however, that the technique will enjoy greater popularity in the future. Recently, double quantum transitions have been used in conjunction with double resonance experiments to assign transitions in complex spectra (7).

2. Double Resonance Experiments A. Introduction

In a nuclear double resonance experiment, the spin system is subjected to a stationary ζ field H0 , and two linearly polarized rf fields directed along the ζ axis:

H ( 0 = (2HX cos w±t + 2H2 cos a>2ty 0, H0). (2.1) T h e rf field with maximum amplitude 2H¹ is called the stimulating field;

it is "weak" in the sense that it may be treated by first-order time- dependent perturbation theory. T h e stimulating field is used to observe the resonances of a particular group of nuclei; the second rf field, called the perturbing field, simultaneously irradiates a second group of nuclei.

T h e perturbing field is said to be weak or strong, accordingly, as I ylî² I < ξ I / 1 or I γΗ² | ^ > | / 1 , where γ is the gyromagnetic ratio of the nuclei subjected to H²(£), and / is the coupling constant describing the spin-spin interactions between the irradiated groups.

Double resonance experiments can be extremely useful in the study of high-resolution spectra. Experimental spectra can often be simplified through the selective decoupling (72, 13) of a particular group of s p i n -J nuclei, or by decoupling a quadrupolar nucleus that would otherwise broaden the resonance lines of interest. T w o elementary examples of these "decoupling" experiments are shown in Figs. 9.5 and 9.6.

Figure 9.5(a) shows the single resonance proton spectrum of trimethyl- phosphite [ P ( O C H³)³] at 60 Mcps. Figure 9.5(b) shows the collapse of the methyl-group doublet to a single line when a strong perturbing field is applied at the phosphorous resonance frequency. Figure 9.6(a) shows the single resonance proton spectrum of formamide ( H2N C H O ) at 60 Mcps. Figure 9.6(b) shows the sharpened proton resonances of formamide when a strong perturbing field is applied at the nitrogen

2. DOUBLE RESONANCE EXPERIMENTS 419

P ( 0 C H3) ,

(a) (b)

F I G . 9.5. P r o t o n m a g n e t i c r e s o n a n c e spectra of t r i m e t h y l p h o s p h i t e : (a) single r e s o n a n c e s p e c t r u m at 60 M c p s ; (b) d o u b l e r e s o n a n c e s p e c t r u m at 60 M c p s w i t h t h e p h o s p h o r u s n u c l e u s s i m u l t a n e o u s l y i r r a d i a t e d at 24.28 M c p s ( N M R Specialties).

NH2CH0

F I G. 9.6. P r o t o n m a g n e t i c r e s o n a n c e spectra of f o r m a m i d e : (a) single r e s o n a n c e s p e c t r u m at 60 M c p s ; (b) d o u b l e r e s o n a n c e s p e c t r u m at 60 M c p s w i t h t h e n i t r o g e n n u c l e u s s i m u l t a n e o u s l y i r r a d i a t e d at 4.33 M c p s ( N M R Specialties).

420 9. M U L T I P L E Q U A N T U M T R A N S I T I O N S

resonance frequency. T h e quantum mechanical reason for the collapse of spin-spin multiplets in double irradiation experiments will be given in Section 2.C.

Double resonance experiments can also be used to determine relative signs of spin-spin coupling constants (14, 15). It can be shown, through use of a generalized spin inversion operator (16), that a double resonance spectrum is independent of the absolute signs of the coupling constants.

A useful application is the determination of "hidden chemical shifts"

(i.e., the chemical shifts of nuclei whose resonances are obscured by other resonance lines), provided that the "hidden" nuclei are coupled to other nuclei whose resonances are unobscured (17).

Finally, the so-called "tickling experiments" (22), where the stimulating and perturbing fields are both weak, provide a method for determining the relative signs of coupling constants, and information that can be used to sketch energy-level diagrams.

An extensive review of double resonance experiments, their generaliza- tions, triple resonance, quadruple resonance, etc. (28-31), and their application to the study of high-resolution spectra, will not be attempted here.2 T h e discussion will be limited to the elementary physical theory of double resonance for two-group systems conforming to the X approxi- mation (18-20), and will be simplified by ignoring relaxation effects and deviations from a Boltzmann distribution that occur for sufficiently large amplitudes of the perturbing field (9b).

B. The Hamiltonian Operator

T h e magnetic field (2.1) may be written

H ( 0 = H⁺( i ) + H_(0 + H⁰. (2.2)

where

H±(t) = (Ηλ cos ωλί + H2 cos w2t, ±HX sin w±t ± H2 sin ω²ί, 0). (2.3) T h e effective transverse field for a group of magnetically equivalent nuclei is H⁺(t) or H_(£), accordingly as the common gyromagnetic ratio of the nuclei is negative or positive. In the special case of a system composed

2 T h e r e a d e r interested in a n extensive discussion of t h e subject s h o u l d c o n s u l t t h e references to this c h a p t e r ; references (19) a n d (20) are especially r e c o m m e n d e d . T h e discussion in this section is based on t h e w o r k of A n d e r s o n a n d F r e e m a n (19).

2. DOUBLE RESONANCE EXPERIMENTS 421 entirely of magnetically equivalent groups with positive gyromagnetic ratios, the time-dependent double resonance hamiltonian is

•#X0 = - X

Χ X

Χ X yG^JGx — {Hi Sin <V + # 2 ^{S IN Ω}2*) X yG^Gy · (2.4)

G G '

It will be assumed that y^G denotes 1 — a^G times the common gyro- magnetic ratio of the unshielded nuclei in group G, so that œ^G = | y^G \H⁰ .

If the weak-coupling approximation is valid for some of the groups, which will usually be the case if the groups possess different gyromagnetic ratios, one may use the notation introduced in Section 7.2 to indicate qualitatively large differences of the Larmor frequencies. More important, however, is the fact that the χ and y terms may be omitted from the bilinear interactions coupling groups that conform to the weak- coupling approximation.

T h e stationary terms of (2.4) collectively describe the stationary hamiltonian for a coupled spin system. T h e stationary hamiltonian admits Iz and all I^G2 as constants of the motion. However, aside from the possible existence of symmetry constants of the motion, only the I^G2 are conserved with respect to the time-dependent hamiltonian (2.4).

T h e conservation of all I^G2 is an important simplification, as it allows the discussion to be restricted to a particular irreducible component defined by a fixed set of total spin quantum numbers. All results established for a generic irreducible component may be adapted to the complete system by introducing the appropriate spin multiplicities and applying the superposition principle.

T h e state vector of a spin system described by the hamiltonian (2.4) satisfies

i ^ ( t ) = MT(t)W(t). (2.5)

T h e time-dependent terms in (2.4) represent the interaction of the nuclei with two circularly polarized rf fields, rotating in the negative sense about the ζ axis with frequencies ω1 and ω2 . This suggests a transformation of the form

W(t) = **^ω*'.Φ(ί), (2.6)

which is equivalent to describing the problem from a coordinate system rotating in the negative sense about the ζ axis with frequency ω. T h e

422 9. M U L T I P L E Q U A N T U M T R A N S I T I O N S

transformation (2.6) will remove the time dependence of the stimulating field or the perturbing field, accordingly as ω = ω1 or ω = ω2 . Taking α, — Q)^{2 9} equations (2.4) through (2.6) yield

i-L-t<P(t) = JFr(t)<P(t), (2.7)

where

K{t) = - S

Σ

+ Χ X

Σ

' G G < G ' G

+ HL X yG(^G* C S ω01 2 * — ^G» Sn ωi1 2 * ) L ( 2' 8) G '

ω1 2 = 1 —ω 2Ω · (2.9)

Equation (2.8) shows that a similarity transformation of Jf(t) with

E-IŒ2TIZ n ot o nj y ^{r e m o vs} t h^{e e} time dependence of the perturbing field but also preserves the form of the stationary hamiltonian. However, these remarks do not apply if the system contains groups characterized by gyromagnetic ratios with different algebraic signs. For simplicity, consider two groups A and X, with y^A > 0, y^x < 0. T h e time-dependent hamiltonian is

^ ( 0 = —{<»AIAZ + ω^χ/^{Χ ζ + / A X}IA * Ιχ

+ {H^x cos œ^xt + H² cos ω²ΐ)(γ^ΑΙ^Αχ + γ^χΙ^Χχ)

+ (H^x sin wjt + H² sin ω²ί)(γ^χΙ^Χυ — y^AI^Ay)}. (2.10) A similarity transformation with e~Xui<liIz will preserve the form of the

stationary terms but will not remove the time dependence of the perturbing field, since Ji?(t) includes the interactions of A and X with both circularly polarized components of (2H2 cos co2t)e^x . However, the time dependence of the perturbing field can be removed by a similarity transformation with

exp[—ιω2ΐ(Ι^Αζ — I^Xz)] = exp(—ΐω²ΐΙ^{Α ζ}) exp(iœ²tI^Xz). (2.11) In fact,

e x p [ — ι ω2ί ( /Α Α - Ixz)W(t)exp[iœ2t(I^Az - I^Xz)]

= — {<*>A!AZ + ω^χ/^{Χ 2} + / A X [ (IA " Ix — ^IAZIXZ) cos 2<x)²t

— ( IA X Ix)2 sin 2œ2t + 7^{A a}/xJ + H^yJ^ + γχΙ^Χχ) cos w¹²t + (γχΐχυ — YA^AY) sin w12t] + Η²[γ^ΑΙ^Αχ + γ^χΙ^Χχ]}.

2. DOUBLE RESONANCE EXPERIMENTS 423 This equation shows that a similarity transformation of (2.10) with (2.11) removes the time dependence of the perturbing field, but introduces an explicit time dependence into the χ and y components of the bilinear interaction IA · Ix . T h e reason is that the bilinear interaction is rotation- ally invariant, but (2.11) is not a rotation operator. A n operator representing a rotation φ about a direction η is of the form ei(pn'^ly where I is the total angular momentum in units of ft. Although it is in principle impossible to remove the difficulty, the situation is not hopeless. For, by assumption, yA and yx are of opposite sign, so that yA Φ yx . Hence, to a normally excellent approximation, JAXl^A · Ix may be replaced by ]^ΑχΙ^ΑζΙχ^ζ, which is invariant under a similarity transformation with (2.11). Because of this result, there is no essential loss of generality in restricting the subsequent discussion to systems for which all yG > 0.

T h e external parameters in a nuclear double resonance experiment are Hx , H2 , ωλ , ω2 , and H0 . In a given experiment it is customary to fix H1 and H2 at predetermined values, and to vary one of the remaining three parameters. A n experiment in which ωλ and ω2 are fixed, while H0

is varied, is called a "field sweep" experiment. Experiments in which ω1 or ω2 is varied are called "frequency sweep" experiments. T h e calculation of theoretical double resonance spectra will be carried out for the frequency sweep experiment in which ω2 and H0 are fixed, while ω1 is varied through the A resonances of the Α^{η Α}Χ^{η χ} system. A procedure for obtaining theoretical spectra in the field sweep experiment will be described in Section 2 . D .

C. The Irreducible Α^{/ Α}Χ^{/ χ} System

In the special case of two groups, (2.8) reduces to

^M) = — {(ωΑ — OJ2)I^AZ + (ωΒ — ω2)Ι^ΒΖ + / IA · IB + Η2(γ^ΑΙ^ΑΧ + γΒΙ^ΒΧ) + ΗΙ[ΎΑ(ΙΑΧ cos œ12t — IAY sin œ12t)

+ ΎΒ(Ι*Χ cos œ12t — IBY sin œ12t)]}. (2.12)

If the gyromagnetic ratios for groups A and Β are not equal, Β is to be replaced by X, and I^A · I^B by I^AzI^Xz.

Since the double resonance spectrum does not depend upon the sign of / , it will be arbitrarily assumed that / > 0. It will also be assumed that

I ωΑ — ωχ I > / , γΑΗ² ,

w¹ ^ ω^Α , w² ^ ω^χ .

(2.13)

424

9. MULTIPLE QUANTUM TRANSITIONS

Under these conditions, (2.12) simplifies to

<K(t) = ~{(ΩΑ —

ω

)/

ζ + (ωχ —

+ ΎΑΗ\(ΙΑΧ COS œ12t - ΙΑΝ sin œ12t)}. (2.14) T h e term γΑΗ2ΙΑχ is omitted from (2.14) since, by (2.13), γΑΗ2/\ωΑΧ\ <^1 ;

the time-dependent terms containing IXx and IXy are omitted, since I ω12 I is off resonance for X transitions in the rotating frame:

I

—

I = I

I ^ I

I-

Equation (2.14) may be studied by the procedure used in Section 5.3.

In particular, the time dependence of ^r{t) can be removed by trans- forming the state vector with elüil*tlAz. T h e details of the analysis will not be repeated here. It need only be recalled that the time-dependent terms in (2.14) induce transitions between the energy levels of

J?^r =

—{(ω

— ω

)/

+ (ω

— ω

)/

+ //

/χ

+

N o w ΙΧζ does not commute with (2.15), but

IKJAA = 0 , (2.16) so that the selection rules for A transitions are

AI^A = AI^X = 0,

Δτη^Α = - 1 , (2.17)

Am^x = 0^y ± 1 , ± 2 , . . . , ± 2 /x.

T h e intensities associated with these transitions are proportional to the absolute squares of the matrix elements of IA~, all matrix elements being evaluated with respect to the eigenvectors of (2.15).

An initial basis for the eigenvalue problem defined by (2.15) is provided by the ( 2 /A + l ) ( 2 /x + 1) product kets {| IA , τη^Α}\ I^x , m^xy}. T h e commutation relation (2.16) implies that the hamiltonian matrix is the direct sum of 2 /^A + 1 ( 2 /^x + l)-dimensional submatrices, each sub- matrix being characterized by a fixed value of mA . T h e operator ^r(m^A) defining a generic submatrix may be obtained from (2.15) by replacing I^Az with m^A :

· % ) = ~ { (^ΩΑ - OJ²)m^A + [(ω^χ - ω²) + Jm^A]I^Xz + γ^ΧΗ²Ι^Χχ}. (2.18) T h e mathematical significance of this device is worth emphasizing.

T h e operator I^Az is more precisely written as the Kronecker product

2. DOUBLE RESONANCE E X P E R I M E N T S 425 IAZ ® 1χ > where lx is the ( 2 /x + l)-dimensional identity operator for the spin space of X. In the subspace defined by a fixed value of m^A , the submatrix of the complete matrix for I^Az (x) l^x is simply m^A times an identity matrix of dimension ( 2 /^x + 1 ) . Therefore, the first term within the curly bracket of (2.18) actually denotes (α>^Α — ω²)τη^Α times a ( 2 /x + l)-dimensional identity operator; hence this term is just an additive constant tacked on to the diagonal elements. T h e remaining terms in (2.18) show that when the system is in an eigenstate characterized by the eigenvalue m^A , group X experiences an effective field (Fig. 9.7)

H^r(X, m^A) = YxR(m^A)[e^x> sin Θ(τη^Α) + e^Ä- cos θ(τη^Α)], (2.19) where

R(m^A) = {[ω^χ -ω² + Jm^Af + γ^Η²ψ\

ΥχΗ2

tan θ(ηι^Α) —

ωχ — ω2 + JmA

(2.20) (2.21) T h e preceding remarks suggest a similarity transformation of ^r(tnA) with txp[ie(mA)I^Xy\:

exp\t0(m^A)I^Xv]Ji?^r(m^A) exp[-i6(m^A)I^Xy] = —{(ω^Α - ω²)ηι^Α + %^A) W » (2.22) by equations (3.10) of Chapter 2. Operating on | I^x , m^xy with (2.22), one obtains

exp[fÖ(ifi^A)/^{X l},]^^r(ifi^A) exp[-ie(m^A)I^Xy]\I^x , w^x> = Ω(ηι^Α , m^x) | 7^X , m^x>, (2.23) where

i2(w^A , mx) = — {(ωΑ — ω2)τηΑ + mxR(mA)}. (2.24)

ΛΧ 2

F I G . 9.7. Effective field (in e q u i v a l e n t f r e q u e n c y units) e x p e r i e n c e d b y g r o u p X in t h e r o t a t i n g frame w h e n t h e ζ c o m p o n e n t of a n g u l a r m o m e n t u m for g r o u p A is mA .