Discrete Applied Mathematics

(1)

Contents lists available atScienceDirect

Discrete Applied Mathematics

journal homepage:www.elsevier.com/locate/dam

The Turán number of the square of a path

Chuanqi Xiao

^a

, Gyula O.H. Katona

^b^,^∗

, Jimeng Xiao

^c^,^b

, Oscar Zamora

^a^,^d

aCentral European University, Budapest, Hungary

bMTA Rényi Institute, Budapest, Hungary

cNorthwestern Polytechnical University, Xi’an, China

dUniversidad de Costa Rica, San José, Costa Rica

a r t i c l e i n f o

Article history:

Received 2 March 2021

Received in revised form 3 October 2021 Accepted 5 October 2021

Available online 21 October 2021 Keywords:

Turán number Extremal graphs Square of a path

a b s t r a c t

The Turán number of a graphH, ex(n,H), is the maximum number of edges in a graph onnvertices which does not haveHas a subgraph. LetP_kbe the path withkvertices, the squareP_k²ofP_kis obtained by joining the pairs of vertices with distance one or two inPk. The powerful theorem of Erdős, Stone and Simonovits determines the asymptotic behavior of ex(n,^Pk²). In the present paper, we determine the exact value of ex(n,^P5²) and ex(n,P₆²) and pose a conjecture for the exact value of ex(n,P_k²).

1. Introduction

In this paper, all graphs considered are undirected, finite and contain neither loops nor multiple edges. LetGbe such a graph, the vertex set ofGis denoted by V(G), the edge set ofGbyE(G), and the number of edges inGbye(G). We denote the degree of a vertex

v

^by^d(

v

), the minimum degree in graphGby

δ

(G), the neighborhood of

v

^by^N(

v

^{) and the} chromatic number of graphGby

χ

(G). Denote bymHthe graph of the vertex-disjoint union ofmcopies of the graphH.

Two disjoint vertex setsUand W are completely joined inGifu

w ∈

E(G) for allu

∈

U,

w ∈

W. Given graphsG₁and G₂, whereG₁andG₂with disjoint vertex setsV(G₁) andV(G₂) and edge setsE(G₁) andE(G₂). The unionG

=

G₁

∪

G₂ is the graph withV(G)

=

V(G₁)

∪

V(G₂) andE(G)

=

E(G₁)

∪

E(G₂). Denote byG₁⨂

G₂the graph obtained fromG₁

∪

G₂by adding all edges betweenV(G₁) andV(G₂).

The Turán number of a graphH, ex(n

,

H), is the maximum number of edges in a graph onnvertices which does not haveHas a subgraph. The Erdős–Stone–Simonovits Theorem [4,5] asymptotically determines ex(n

,

H) for all non-bipartite graphsH:

ex(n

,

^H)

=

(1

−

¹

χ

^(H)

−

1)

(n 2 )

+

o(n²)

There are currently very few known exact results known. For example, Füredi and Gunderson [7] described all the graphs having ex(n

,

^C2k+₁) edges (k

≥

2) containing noC_2k+₁. Erdős, Füredi, Gould and Gunderson [2] determined the exact value of ex(n

,

^Fk) (k

≥

1,n

≥

50k²) fork-fan (a graph on 2k

+

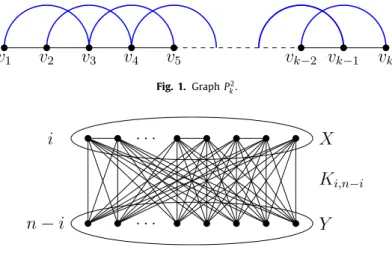
1 vertices consisting ofktriangles which intersect in exact one common vertex is called ak-fan and denoted byF_k).

The following graphs will be studied in the present paper. LetP_kbe the path withkvertices, the squareP_k² ofP_kis obtained by joining the pairs of vertices with distance one or two inP_k, seeFig. 1. Our goal in this paper is to study

∗ Corresponding author.

E-mail addresses: chuanqixm@gmail.com(C. Xiao),katona.gyula.oh@renyi.hu(G.O.H. Katona).

https://doi.org/10.1016/j.dam.2021.10.003

org/licenses/by-nc-nd/4.0/).

(2)

Fig. 1. GraphP_k².

Fig. 2. GraphE_nⁱ.

ex(n

,

^P_k²) and the extremal graphs for P_k². Since

χ

^(P_k²⁾

=

3, k

≥

3, by Erdős–Stone–Simonovits Theorem, we have ex(n

,

^P_k²⁾

=

ⁿ²

4

+

o(n²). Yet, it still remains interesting to determine the exact value of ex(n

,

^P_k²^).

The very first result of extremal graph theory gave the value of ex(n

,

^P₃²^).

Theorem 1(Mantel [10]).The maximum number of edges in an n-vertex triangle-free graph is

⌊

ⁿ₄²

⌋

, that isex(n

,

^P₃²⁾

= ⌊

ⁿ₄²

⌋

. Furthermore, the only triangle-free graph with

⌊

ⁿ₄²

⌋

edges is the complete bipartite graph K⌊ⁿ

2⌋,⌈ⁿ 2⌉. The casek

=

4 was solved by Dirac in a more general context.

Theorem 2(Dirac [1]).The maximum number of edges in an n-vertex P₄²-free graph is

⌊

ⁿ²

4

⌋

, that isex(n

,

^P₄²⁾

= ⌊

ⁿ²

4

⌋

,(n

≥

4).

Furthermore, when n

≥

5, the only extremal graph is the complete bipartite graph K⌊ⁿ 2⌋,⌈ⁿ

2⌉.

Fork

=

5, our results are given in the next two theorems, where we separate the result for the Turán number and the extremal graphs forP₅².

Theorem 3. The maximum number of edges in an n-vertex P₅²-free graph is

⌊

ⁿ²⁺ⁿ

4

⌋

, that isex(n

,

^P₅²⁾

= ⌊

ⁿ²⁺ⁿ

4

⌋

,(n

≥

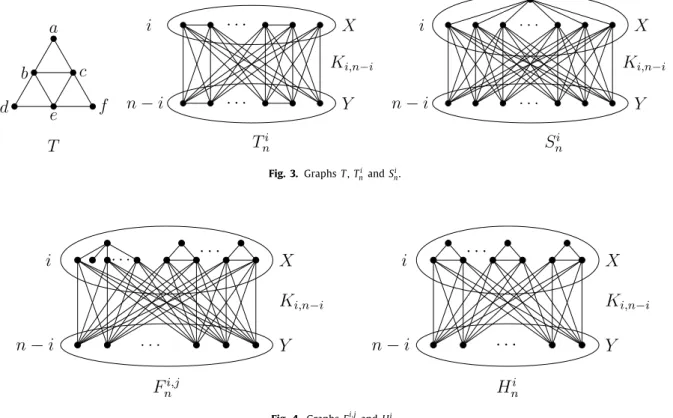
5).

Definition 1. LetEⁱ_ndenote a graph obtained from a complete bipartite graphK_i_,_n−_i plus a maximum matching in the class which hasivertices, seeFig. 2.

Theorem 4. Let n be a natural number, when n

=

5, the extremal graphs for P₅² are E₅², E₅³and G₀, where G₀is obtained from a K₄plus a pendent edge. When n

≥

6, if n

≡

1

,

2 (mod 4), the extremal graphs for P₅²are E^⌈

n 2⌉ n and E^⌊

n 2⌋

n , otherwise, the extremal graph for P₅²is E^⌈

n 2⌉ n .

Definition 2. LetT denote the flattened tetrahedron, seeT inFig. 3.

Although the determination of ex(n

,

^T) is not within the main lines of our paper, we need the exact value of ex(n

,

^T⁾ in order to determine ex(n

,

^P₆²^).

Theorem 5. The maximum number of edges in an n-vertex T -free graph (n

̸=

5) is,

ex(n

,

^T⁾

=

⎧

⎪⎪

⎨

⎪⎪

⎩

⌊n² 4

⌋

+

⌊_n 2

⌋

,

ⁿ

̸≡

2 (mod 4)

,

n²

4

+

ⁿ

2

−

1

,

ⁿ

≡

2 (mod 4)

.

Definition 3. LetT_nⁱ denote a graph obtained from a complete bipartite graphK_i_,_n−_i plus a maximum matching in the classXwhich hasivertices and a maximum matching in the classY which hasn

−

ivertices, seeT_nⁱinFig. 3. LetS_nⁱ denote a graph obtained fromK_i_,_n−i plus ani-vertex star in the classX, seeSⁱ_ninFig. 3.

2

(3)

Fig. 3. GraphsT,T_nⁱandS_nⁱ.

Fig. 4. GraphsFnⁱ^,^jandH_nⁱ..

Theorem 6. Let n(n

̸=

5

,

⁶⁾be a natural number, when n

≡

0 (mod 4), the extremal graph for T is T

n n2, when n

≡

1 (mod 4), the extremal graphs for T are T^⌈

n 2⌉ n and S^⌈

n 2⌉ n , when n

≡

2 (mod 4), the extremal graphs for T are T

n n2, T

n 2+₁ n and S

n n2, when n

≡

3 (mod 4), the extremal graphs for T are T^⌈

n 2⌉ n and S^⌈

n 2⌉ n .

These two results are known for sufficiently largen^′s[9], here we are able to determine the value for smalln^′s.

UsingTheorems 5and6, we are able to prove the next two results forP₆². Theorem 7. The maximum number of edges in an n-vertex P₆²-free graph(n

̸=

5)is:

ex(n

,

^P6²)

=

⎧

⎪⎪

⎨

⎪⎪

⎩

⌊n² 4

⌋

+

⌊n

−

1 2

⌋

,

ⁿ

≡

1

,

²

,

^{3 (mod 6)}

,

⌊n² 4

⌋

+

⌈_n 2

⌉

,

^otherwise

.

Definition 4. Suppose 3

̸ |

n, and 1

≤

j

≤

i. LetF_nⁱ^,^jbe the graph obtained by adding vertex disjoint triangles (possibly 0) and one star withjvertices in the classXof sizeiofK_i_,_n−_i, seeFig. 4(of course 3

|

(i

−

j) is supposed). On the other hand if 3

|

ithen add ₃ⁱ vertex disjoint triangles in the classXof sizei. The so obtained graph is denoted byH_nⁱ, seeFig. 4.

Theorem 8. Let n

≥

6be a natural number. The extremal graphs for P₆²are the following ones.

When n

≡

1 (mod 6)then F^⌈

n 2⌉,^j n and H^⌊

n 2⌋ n , when n

≡

2 (mod 6)then F

n 2,^j n and F

n 2+₁,^j

n ,

when n

≡

3 (mod 6)then F^⌈

n 2⌉,j n and H^⌈

n 2⌉+₁

n ,

when n

≡

0

,

⁴

,

^{5 (mod 6)}^{then H}nⁿ², H

n 2+₁ n and H^⌈

n 2⌉

n , respectively.(j can have all the values satisfying the conditions j

≤

i and3

|

(i

−

j)).

(4)

On the basis of these results let us pose a conjecture for the general case.

Conjecture 1.

ex(n

,

^Pk²)

≤

max {i(⌊_2k

3

⌋

−

2)

2

+

i(n

−

i) }

.

If⌊_2k

3

⌋

−

1divides i then the following graph gives equality here. Take a complete bipartite graph with parts of size i and n

−

i, add vertex disjoint complete graphs on⌊_2k

3

⌋

−

1vertices to the part with i elements.

Observe thatTheorems 1,2,3and7justify our conjecture for the cases whenk

=

3

,

⁴

,

⁵

,

6. We will give some hints in Section3how we arrived to this conjecture. A weaker form of this conjecture is the following one.

Conjecture 2.

ex(n

,

^Pk²)

=

ⁿ

2

4

+

(⌊_k

3

⌋

−

1) n 2

+

O_k(1) where O_k(1)depends only on k.

2. Proofs of the main results

2.1. The Turán number and the extremal graphs for P₅²

Proof ofTheorem 3. The fact that ex(n

,

^P₅²⁾

≥

⌊n²+_n 4

⌋

follows from the constructionE

⌈

ⁿ₂

⌉

n .

We prove the inequality ex(n

,

^P5²)

≤

⌊n²

+

n 4

⌋

(n

≥

5) (1)

by induction onn.

We check the base cases first. Since our induction step will go fromn

−

4 ton, we have to find a base case in each residue class mod 4.

LetGbe ann-vertexP₅²-free graph. Whenn

≤

3,K_nis the graph with the most number of edges and does not contain P₅²,e(K_n)

≤

⌊n²+_n 4

⌋

. This settles the casesn

=

1

,

²

,

3. However, whenn

=

4,e(K₄)

=

6

> ⌊

⁴²⁺⁴

4

⌋

, the statement is not true.

Then we show that the statement is true forn

=

8. IfP₄²⊈G,e(G)

≤ ⌊

⁸²

4

⌋

. IfP₄²

⊆

GandK₄⊈G, each vertex

v ∈

V(G

−

P₄²) can be adjacent to at most 2 vertices of the copy ofP₄², sincee(G

−

P₄²)

≤

5, we havee(G)

≤

5

+

8

+

5

≤

18

= ⌊

⁸²⁺⁸

4

⌋

. If K₄

⊆

G, then each vertex

v ∈

V(G

−

K₄) can be adjacent to at most one vertex of theK₄, sincee(G

−

P₄²)

≤

6, we have e(G)

≤

16.

Suppose(1)holds for allk

≤

n

−

1, the proof is divided into 3 parts, Case 1. IfP₄²⊈G, then byTheorem 2,e(G)

≤ ⌊

ⁿ²

4

⌋

.

Case 2. IfP₄²

⊆

GandK₄⊈G, then each vertex

v ∈

V(G

−

P₄²) can be adjacent to at most 2 vertices of the copy ofP₄², otherwise,P₅²

⊆

G. SinceG

−

P₄²is an (n

−

4)-vertexP₅²-free graph, we have

e(G)

≤

5

+

2(n

−

4)

+

e(G

−

P₄²)

≤

2n

−

3

+

ex(n

−

4

,

^P5²)

.

By the induction hypothesis, ex(n

−

4

,

^P₅²⁾

≤

⌊(n−4)²+n−4 4

⌋ then

e(G)

≤

2n

−

3

+

ex(n

−

4

,

^P₅²⁾

≤

2n

−

3

+

⌊(n

−

4)²

+

n

−

4 4

⌋

=

⌊n²

+

n 4

⌋

(n

≥

5)

.

⁽²⁾

Case 3. IfK4

⊆

G, then each vertex

v ∈

V(G

−

K4) can be adjacent to at most one vertex of theK4, otherwise,P₅²

⊆

G.

SinceG

−

K₄is an (n

−

4)-vertexP₅²-free graph, we have e(G)

≤

6

+

(n

−

4)

+

e(G

−

K₄)

≤

n

+

2

+

ex(n

−

4

,

^P₅²⁾

.

By the induction hypothesis, ex(n

−

4

,

^P₅²⁾

≤

⌊(n−₄₎²+_n−₄ 4

⌋ , thus

e(G)

≤

n

+

2

+

⌊(n

−

4)²

+

n

−

4 4

⌋

=

5

+

⌊n²

−

3n 4

⌋

≤

⌊n²

+

n 4

⌋

(n

≥

5)

.

□ (3)

4

(5)

Proof ofTheorem 4. We determine the extremal graphs forP₅² by induction onn. LetGbe ann-vertexP₅²-free graph satisfying(1)with equality. It is easy to check, whenn

=

5, the extremal graphs forP₅²areG₀,E²₅andE₅³. Whenn

=

6

,

⁷

,

^8, the extremal graphs forP₅²areE₆³andE₆⁴,E₇⁴,E₈⁴, respectively.

SupposeTheorem 4is true fork

≤

n

−

1, whenn

≥

9, the proof is divided into 3 parts.

Case 1. IfP₄²⊈G, the equality in(1)cannot hold, then we cannot find any extremal graph forP₅²in this case.

Case 2. IfP₄²

⊆

GandK₄⊈G, the equality holds in inequality(2)if and only if each vertex

v ∈

V(G

−

P₄²) is adjacent to 2 vertices of theP₄²andG

−

P₄²is an extremal graph onn

−

4 vertices forP₅². Leta

,

^b

,

^c^and^dbe four vertices of a copy ofP₄²,d_P2

4(b)

=

d_P2

4(c)

=

3. By the induction hypothesis,G

−

P₄²is obtained from a complete bipartite graphK_i_,_n−₄−_i plus a maximum matching inX^′, whereX^′is the class ofG

−

P₄²with sizei. It is easy to check that every vertex

v ∈

V(G

−

P₄²) can be adjacent to eitheraanddorbandc.

Since

|

V(G

−

P₄²)

| ≥

5, we have

|

V(X^′)

| ≥

2. The endpoints of an edge inG

−

P₄²cannot be both adjacent tobandc, otherwise, they form aK₄. Also, the endpoints of an edge inG

−

P₄²which have one end vertex as a matched vertex in X^′and one end vertex inY^′can be both adjacent to none of

{

a

,

^b

,

^c

}

andd, otherwise, these would create aP₅². If there exists a matched vertex

v ∈

X^′which is adjacent tobandc, then all vertices

w ∈

N(

v

) should be adjacent toaandd, these form aP₅². Hence, it is only possible that all matched vertices inX^′are adjacent to bothaandd, all vertices inY^′ are adjacent tobandc. When there exists an unmatched vertex

v

0

∈

X^′, sinceN(

v

0)

=

Y^′, if

v

0 is adjacent tobandc, we haveP₅²

⊆

G. ThusGis obtained from a complete bipartite graphK_i+₂,n−_i−₂plus a maximum matching inX, where X

=

X^′

∪ {

b

,

^c

}

andY

=

Y^′

∪

a

∪

d. Therefore, ifG

−

P₄²isE^⌈

n−4 2 ⌉

n−₄ thenGisE^⌈

n 2⌉ n , ifE^⌊

n−4 2 ⌋

n−₄ thenGisE^⌊

n 2⌋ n .

Case 3. IfK₄

⊆

G, the inequality in(3)can be equality only whenn

=

5 and the vertex

v ∈

V(G

−

K₄) is adjacent to one vertex of theK₄, that isG₀. □

2.2. The Turán number and the extremal graphs for T

To proveTheorem 5, we need the following lemmas.

Lemma 9. Let G be an n-vertex T -free nonempty graph such that for each edge

{

x

,

^y

} ∈

E(G), d(x)

+

d(y)

≥

n

+

2holds, then we have K₄

⊆

G.

Proof. From the condition we know that each edge belongs to at least two triangles. Letabcandbcdbe two triangles, ifa is adjacent todthena

,

^b

,

^c^and^d^{induce a}^K4, if not, since edge

{

b

,

^d

}

is contained in at least two triangles, there exists at least one vertexesuch thatbdeis a triangle. Similarly, edge

{

c

,

^d

}

is also contained in at least two triangles, then, either there exists a vertexf which is adjacent tocandd, this implies that verticesa

,

^b

,

^c

,

^d

,

^e^and^f ^{induce a}^T^{, or}^cis adjacent toe, this implies that verticesb

,

^c

,

^d^and^e^{induce a}^K4. □

Lemma 10. Let G be an n-vertex(n

≥

7)T -free graph and K₄

⊆

G, then e(G)

≤

2n

−

2

+

ex(n

−

4

,

^T^{). For n}

≥

8, the equality might hold only if each vertex

v ∈

V(G

−

K₄)is adjacent to 2 vertices of the K₄.

Proof. If there exists vertex

v ∈

V(G

−

K₄), such that

v

is adjacent to at least 3 vertices of the K₄, it is simple to check that every other vertexu

∈

V(G

−

K₄) can be adjacent to at most one vertex of the K₄, otherwiseT

⊆

G, then e(G)

≤

6

+

4

+

(n

−

5)

+

e(G

−

K₄)

≤

n

+

5

+

ex(n

−

4

,

^T). If not, each vertex inG

−

K₄is adjacent to at most 2 vertices of theK₄, thene(G)

≤

6

+

2(n

−

4)

+

e(G

−

K₄)

≤

2n

−

2

+

ex(n

−

4

,

^T^{). When}ⁿ

≥

8,e(G)

≤

2n

−

2

+

ex(n

−

4

,

^T^{), the} equality holds only if each vertex

v ∈

V(G

−

K₄) is adjacent to 2 vertices of theK₄. □

Proof ofTheorem 5. Let

f_T(n)

=

⎧

⎪⎪

⎨

⎪⎪

⎩

⌊n² 4

⌋

+

⌊_n 2

⌋

,

ⁿ

̸≡

2 (mod 4)

,

n²

4

+

ⁿ

2

−

1

,

ⁿ

≡

2 (mod 4)

.

The fact that ex(n

,

^T⁾

≥

f_T(n) follows from the constructionT

⌈

ⁿ₂

⌉

n . Next, we show the inequality

ex(n

,

^T⁾

≤

f_T(n) (4)

by induction onn.

LetGbe ann-vertexT-free graph. first, we show the induction steps, in the end we will show the base cases which are needed to complete the induction.

Suppose (4) holds for alll

≤

n

−

1, in the following cases, we will assume thatk

≥

2, the proof is divided into 4 cases.

Case 1. Whenn

=

4k, we divide the proof of ex(4k

,

^T⁾

≤

f_T(4k)

=

4k²

+

2kinto 2 subcases. LetGbe a 4k-vertexT-free graph.

(6)

(i) If

δ

^(G)

≤

2k

+

1, after removing a vertex of minimum degree and by the induction hypothesis ex(4k

−

1

,

^T⁾

=

4k²

−

1, we get

e(G)

≤

ex(4k

−

1

,

^T⁾

+

2k

+

1

≤

4k²

−

1

+

2k

+

1

=

fT(4k)

.

⁽⁵⁾

(ii) If

δ

^(G)

≥

2k

+

2, then for each edge

{

u

, v } ∈

E(G), d(u)

+

d(

v

⁾

≥

4k

+

4. ByLemmas 9and10 and the induction hypothesis ex(4k

−

4

,

^T⁾

=

4(k

−

1)²

+

2(k

−

1), we get

e(G)

≤

2n

−

2

+

ex(4k

−

4

,

^T⁾

=

8k

−

2

+

4(k

−

1)²

+

2(k

−

1)

=

f_T(4k)

.

⁽⁶⁾ Therefore, ex(4k

,

^T⁾

≤

f_T(4k).

Case 2. Whenn

=

4k

+

1, we divide the proof of ex(4k

+

1

,

^T⁾

≤

f_T(4k

+

1)

=

4k²

+

4kinto 3 subcases. LetGbe a (4k

+

1)-vertexT-free graph.

(i) If

δ

^(G)

≤

2k, after removing a vertex of minimum degree and by the induction hypothesis ex(4k

,

^T⁾

=

4k²

+

2k, we have

e(G)

≤

ex(4k

,

^T⁾

+

2k

≤

f_T(4k

+

1)

.

⁽⁷⁾

Now, we assume that in the following two cases

δ

^(G)

≥

2k

+

1. Then for any pair of vertices

{

u

, v } ∈

E(G),d(u)

+

d(

v

⁾

≥

4k

+

2 holds.

(ii) Suppose that there exists an edge

{

u

, v } ∈

E(G), such thatd(u)

+

d(

v

⁾

=

4k

+

2. This implies thatuand

v

have at least one common neighbor. Deleting

{

u

, v }

we can use the induction hypothesis ex(4k

−

1

,

^T⁾

=

4k²

−

1. Then

e(G)

≤

4k

+

1

+

ex(4k

−

1

,

^T⁾

=

f_T(4k

+

1)

.

⁽⁸⁾

(iii) For each edge

{

u

, v } ∈

E(G), d(u)

+

d(

v

⁾

≥

4k

+

3 holds. By Lemmas 9 and 10 and the induction hypothesis ex(4k

−

3

,

^T⁾

=

4(k

−

1)²

+

4(k

−

1) we get

e(G)

≤

2n

−

2

+

ex(4k

−

3

,

^T⁾

=

8k

+

4(k

−

1)²

+

4(k

−

1)

=

f_T(4k

+

1)

.

⁽⁹⁾ Therefore, ex(4k

+

1

,

^T⁾

≤

f_T(4k

+

1).

Case 3. Whenn

=

4k

+

2

,

^T⁾

≤

f_T(4k

+

2)

=

4k²

+

6k

+

1 into 2 subcases. LetGbe a (4k

+

(i) If

δ

^(G)

≤

2k

+

1

,

^T⁾

=

4k²

+

4k, we get

e(G)

≤

ex(4k

+

1

,

^T⁾

+

2k

+

1

≤

4k²

+

6k

+

1

=

f_T(4k

+

2)

.

⁽¹⁰⁾

(ii) If

δ

^(G)

≥

2k

+

{

u

, v } ∈

E(G), d(u)

+

d(

v

⁾

≥

4k

+

4. ByLemmas 9and10 and the induction hypothesis ex(4k

−

2

,

^T⁾

=

4(k

−

1)²

+

6(k

−

1)

+

1, we get

e(G)

≤

2n

−

2

+

ex(4k

−

2

,

^T⁾

=

8k

+

2

+

4(k

−

1)²

+

6(k

−

1)

+

1

=

f_T(4k

+

2)

.

⁽¹¹⁾ Therefore, ex(4k

+

2

,

^T⁾

≤

f_T(4k

+

2).

Case 4. Whenn

=

4k

+

3

,

^T⁾

≤

f_T(4k

+

3)

=

4k²

+

8k

+

3 into 2 subcases. LetGbe a (4k

+

(i) If

δ

^(G)

≤

2k

+

2

,

^T⁾

=

4k²

+

6k

+

1, we get

e(G)

≤

ex(4k

+

2

,

^T⁾

+

2k

+

2

≤

4k²

+

8k

+

3

=

f_T(4k

+

3)

.

⁽¹²⁾

(ii). If

δ

^(G)

≥

2k

+

{

u

, v } ∈

E(G),d(u)

+

d(

v

⁾

≥

4k

+

6. By Lemmas 9and 10and the induction hypothesis ex(4k

−

1

,

^T⁾

=

4(k

−

1)²

+

8(k

−

1)

+

3, we get

e(G)

≤

2n

−

2

+

ex(4k

−

1

,

^T⁾

=

8k

+

4

+

4(k

−

1)²

+

8(k

−

1)

+

3

=

f_T(4k

+

3)

.

⁽¹³⁾ Therefore, ex(4k

+

3

,

^T⁾

≤

f_T(4k

+

3).

Now we show the base cases which are needed to complete the induction steps. Since our induction steps will go from n

−

1 ton,n

−

2 tonandn

−

4 ton, we will require to show the statement is true for cases whenn

=

3

,

⁴

,

^{6 and 9.}

Whenn

≤

4,K_nis the graph with the most number of edges, ande(K_n)

=

f_T(n).

Whenn

=

5,e(K₅)

=

10

>

^fT(5), the statement is not true, but we will see that the statement is true forn

=

9.

Whenn

=

6, let

v

be a vertex with minimum degree. If

δ

^(G)

=

1, sincee(G

− v

⁾

≤

10, we gete(G)

≤

11. If

δ

^(G)

=

2 ande(G)

=

12, then the only possibility is that G

− v

^is^K5, but thenT

⊆

G, and we havee(G)

≤

11. Suppose now

δ

^(G)

≥

3. IfK₄

⊆

Gand there exists a vertexu

∈

V(G

−

K₄) which is adjacent to at least 3 vertices of the copy ofK₄, then

w ∈

V(G

−

K₄

−

u) can be adjacent to at most one vertex of theK₄, otherwise,T

⊆

G. This contradicts

δ

^(G)

≥

3. Then in this case it is only possible that

{

u

, w } ∈

E(G) and bothuand

w

are adjacent to 2 vertices of theK₄which implies that e(G)

≤

11. IfK4⊈G, then by Turán’s Theorem, we havee(G)

≤

12 and the Turán graphT(6

,

3) is the uniqueK4-free graph which has 12 edges, however,T

⊆

T(6

,

^{3), then}^e(G)

≤

11

=

f_T(6). Summarizing:e(G)

≤

11

≤

f_T(6).

6

(7)

Fig. 5.

Fig. 6.

Whenn

=

9, suppose first that there exists a pair of vertices

{

u

, v } ∈

E(G), such thatd(u)

+

d(

v

⁾

≤

10. Deleting

{

u

, v }

and using ex(7

,

^T⁾

=

15, we gete(G)

≤

9

+

15

=

24

=

f_T(9). If for each pair of vertices

{

u

, v } ∈

E(G),d(u)

+

d(

v

⁾

≥

11 holds, byLemma 9, we obtainK₄

⊆

G. LetG^′denote the graphG

−

K₄. Ife(G^′)

≤

8, since the number of edges betweenK₄ andG^′is at most 10, we havee(G)

≤

6

+

10

+

8

=

24. Ife(G^′)

≥

9, thenK₄

⊆

G^′and the vertex

w ∈

G^′

−

K₄is adjacent to at least 3 vertices of the copy ofK₄inG^′. This implies that each vertex fromG

−

G^′can be adjacent to at most 1 vertex ofG^′

− w

, then the number of edges betweenG

−

G^′andG^′is at most 8, we can conclude that,e(G)

≤

6

+

8

+

10

=

24, e(G)

≤

24

=

f_T(9).

It is easy to see that the casen

=

7 can be proved usingn

=

3 andn

=

6 (Case 4). Similarly, the casen

=

8 follows byn

=

7 andn

=

4 (Case 1). Hence the casesn

=

6

,

⁷

,

⁸

,

9 are settled forming a good bases for the induction. □

Now, we determine the extremal graphs forT.

Proof ofTheorem 6. Similarly to the proof ofTheorem 5, first, we show the induction steps, in the end we will show the base cases which are needed to complete the induction.

Suppose that the extremal graphs forTare as shown inTheorem 5forl

≤

n

−

1. In the following cases, we will assume thatk

≥

2.

LetGbe ann-vertexT-free graph withe(G)

=

f_T(n). The proof is divided into 4 cases following the steps of the proof ofTheorem 5.

Case 1. Whenn

=

4k,f_T(n)

=

4k²

+

2k.

(i) If

δ

^(G)

≤

2k

+

1, the equality in(5)holds only when there exists a

v ∈

V(G), such thatd(

v

⁾

= δ

^(G)

=

2k

+

1 and G

− v

is an extremal graph forT on 4k

−

1 vertices. By the induction hypothesis,G

− v

can be eitherT_4k^2k₋₁orS_4k^2k₋₁. Let X^′andY^′be the classes inG

− v

with size 2kand 2k

−

1, respectively.

WhenG

− v

^is^T4k^2k−1, it can be easily checked that

v

cannot be adjacent to the two endpoints of an edge which have two matched vertices located in different classes, otherwise,T

⊆

G, seeFig. 5. Let

w

be the unmatched vertex inY^′. Sinced(

v

⁾

=

2k

+

1,N(

v

) must contain the unmatched vertex

w ∈

Y^′, then the only way to avoidT

⊆

Gis choosing N(

v

⁾

= w ∪

X^′. Consequently,G

=

T_4k^2kholds.

WhenG

− v

^is^S_4k^2k−₁, letx₁denote the center of the star inX^′. If

v

is adjacent to the two endpoints of the edge

{

x_i

,

^yj

}

(x_i

∈

X^′

,

^yi

∈

Y^′

,

²

≤

i

≤

2k

,

¹

≤

j

≤

2k

−

1), thenT

⊆

G(seeFig. 6). We obtained a contradiction. Butd(

v

⁾

=

2k

+

1 implies that this is always the case.

(ii) If

δ

^(G)

≥

2k

+

2, this implies thate(G)

≥

2k(2k

+

2)

=

4k²

+

4k, which contradicts the fact that ex(4k

,

^T⁾

=

4k²

+

2k.

That is,Gcan only beT

n 2 n .

Case 2. Whenn

=

4k

+

1,f_T(n)

=

4k²

+

4k.

(i) If

δ

^(G)

≤

2k, the equality in(7)holds only if there exists

v ∈

V(G), such thatd(

v

⁾

= δ

^(G)

=

2kandG

− v

^{is an} extremal graph forT on 4kvertices. By the induction hypothesis,G

− v

^is^T_4k^2k. All neighbors of

v

should be located in the same class, otherwise,T

⊆

G, we get thatGisT_4k^2k₊⁺₁¹, that isT^⌈

n 2⌉ n .

(8)

Fig. 7.

If

δ

^(G)

≥

2k

+

1, then for any pair of vertices

{

u

, v } ∈

V(G),d(u)

+

d(

v

⁾

≥

4k

+

2. Here we distinguish two subcases.

(ii)Suppose that there exists an edge

{

u

, v } ∈

E(G) such thatd(u)

+

d(

v

⁾

=

4k

+

2. The equality in(8)holds only if whend(u)

=

d(

v

⁾

=

2k

+

1 andG

−

u

− v

−

1 vertices. By the induction hypothesis, G

−

u

− v

can be eitherT_4k^2k₋₁orS_4k^2k₋₁. LetX^′andY^′be the classes inG

−

u

− v

with size 2kand 2k

−

1, respectively.

WhenG

−

u

− v

^is^T_4k^2k−₁, as in the previous case, neitherunor

v

can be adjacent to the two endpoints of an edge which have two matched vertices located in different classes, seeFig. 5. If N(u)

− v ̸=

X^′, thenu is adjacent to the unmatched vertex

w

ⁱⁿ^Y^′and the other 2k

−

1 neighbors ofuare all located inX^′, say,N(u)

− v − w = {

x₁

, . . . ,

^x2k−₁

}

and

{

x_2k−₁

,

^x2k

} ∈

E(X^′), otherwise,T

⊆

G. Since

|

X^′

| ≥

4, in this case,

v

cannot be adjacent tox_i (1

≤

i

≤

2k

−

2), otherwise,T

⊆

G, seeFig. 7. Now

v

should choose 2kneighbors among the rest 2k

+

1 vertices inV(G

−

u

− v −

⋃2k−₂

i=₁ x_i), which implies that

v

is adjacent to the two endpoints of an edge which have two matched vertices located in different classes as endpoints, thenT

⊆

G. Hence,N(u)

− v =

X^′, similarly,N(

v

⁾

−

u

=

X^′. Thus,GisT_4k^2k₊⁺₁¹

=

T_4k^2k₊₁, that isT^⌈

n 2⌉ n . Let us now consider the case whenG

−

u

− v

^is^S_4k^2k−₁. Letx₁denote the center of the star inX^′. Ifuis adjacent to the two endpoints of the edge

{

x_i

,

^yj

}

(2

≤

i

≤

2k

,

¹

≤

j

≤

2k

−

1), thenT

⊆

G. Thus, there are only two possibilities for T ⊈G:N(u)

− v =

X^′orN(u)

− v =

Y^′

∪

x₁. The same holds for

v

and it is easy to check that ifN(u)

− v =

N(

v

⁾

−

u, thenT

⊆

G. From the above, the only possibility forT ⊈Gis that whenN(u)

− v =

X^′andN(

v

⁾

−

u

=

Y^′

∪

x₁or in the another way around, which implies thatGisS_4k^2k₊⁺₁¹, that isS^⌈

n 2⌉ n .

(iii) Suppose that for each edge

{

u

, v } ∈

E(G),d(u)

+

d(

v

⁾

≥

4k

+

3 holds. Letd(

v

⁾

= δ

(G), then eitherd(

v

⁾

=

2k

+

1 ord(

v

⁾

≥

2k

+

2, but in both cases, each neighbor of

v

has degree at least 2k

+

2. Then all 4k

+

1 vertices have degree at least 2k

+

1, but 2k

+

1 of them, which are the neighbors of

v

, have degree at least one larger. This implies that e(G)

≥

^(4k⁺^1)(2k⁺¹⁾⁺^2k⁺¹

2

=

4k²

+

4k

+

1, which contradicts the fact that ex(4k

+

1

,

^T⁾

=

4k²

+

4k.

That is,Gcan be eitherT^⌈

n 2⌉ n orS^⌈

n 2⌉ n .

Case 3. Whenn

=

4k

+

2 we havef_T(n)

=

4k²

+

6k

+

1.

(i)If

δ

^(G)

≤

2k

+

1, the equality holds in(10)only if there exists

v ∈

V(G), such thatd(

v

⁾

= δ

^(G)

=

2k

+

1 andG

− v

+

− v

can be eitherT_4k^2k₊⁺₁¹orS_4k^2k₊⁺₁¹.

Suppose first thatG

− v

^is^T_4k^2k+⁺₁¹. LetX^′anyY^′be the classes inG

− v

with size 2k

+

1 and 2k,

w

be the unmatched vertex inX^′. The vertex

v

cannot be adjacent to the two endpoints of an edge which have two matched vertices located in different classes. Sinced(

v

⁾

=

2k

+

1, there are two possibilities to avoidT:N(

v

⁾

=

X^′orN(

v

⁾

=

Y^′

∪ w

, which implies thatGis eitherT_4k^2k₊⁺₂¹orT_4k^2k₊⁺₂², that isT

n 2 n orT

n 2+₁

n .

WhenG

− v

^is^S4k^2k+⁺1¹. LetX^′be the class inG

− v

which contains a star andY^′be the other class of theG

− v

. Also, letx₁ denote the center of the star inX^′. Since,d(

v

⁾

=

2k

+

1 and

v

cannot be adjacent to the two endpoints of an edge which is not incident withx₁, we get eitherN(

v

⁾

=

Y^′

∪

x₁orN(

v

⁾

=

X^′. IfN(

v

⁾

=

X^′,GisS_4k^2k₊⁺₂¹, that isS

n 2

n. IfN(

v

⁾

=

Y^′

∪

x₁,G isS_4k^2k⁺₊₂², that isS

n 2+₁

n . It is easy to see thatS

n 2+₁

n is isomorphic toS

n n2.

(ii)If

δ

^(G)

≥

2k

+

2, thene(G)

≥

(k

+

1)(4k

+

2)

=

4k²

+

6k

+

2

,

^T⁾

=

4k²

+

6k

+

1.

Therefore,Gcan beT

n 2 n,T

n 2+₁

n orS

n 2 n.

Case 4. Whenn

=

4k

+

3 we havef_T(n)

=

4k²

+

8k

+

3.

(i)If

δ

^(G)

≤

2k

+

2, the equality holds in(12)only if there exists

v ∈

V(G), such thatd(

v

⁾

= δ

^(G)

=

2k

+

2 andG

− v

+

− v

^{can be}^T_4k^2k+⁺₂¹,T_4k^2k₊⁺₂²orS_4k^2k⁺₊₂¹.

WhenG

− v

^is^T4k^2k+⁺₂¹orT_4k^2k₊⁺₂², similarly to Case 1 (i),Gcan only beT_4k^2k₊⁺₃², that isT

⌈

ⁿ₂

⌉

n .

WhenG

− v

^is^S^2k_4k+⁺₂¹, similarly to Case 2 (ii),Gcan only beS_4k^2k₊⁺²₃, that isS

⌈

ⁿ₂

⌉

n .

(ii) If

δ

^(G)

≥

2k

+

3, then e(G)

≥

^(2k⁺^3)(4k⁺³⁾

2

>

^4k²

+

9k

+

4

>

^4k²

+

8k

+

3

,

^T⁾

=

4k²

+

8k

+

3.

Therefore, in this case,Gis eitherT

⌈

ⁿ₂

⌉

n orS

⌈

ⁿ₂

⌉

n .

Now we check the base cases which are needed to complete the induction.

8