Dipoláris fluidumok dielektromos, mágneses és transzporttulajdonságainak vizsgálata

Dipoláris fluidumok dielektromos, mágneses és transzporttulajdonságainak vizsgálata

Doktori (PhD) értekezés

Készítette:

Nagy Sándor

okleveles fizikus

Készült a Pannon Egyetem

Kémiai és Környezettudományi Doktori Iskolájának keretében Témavezető: Dr. Szalai István

Pannon Egyetem Fizika és Mechatronika Intézet 2012

Értekezés doktori (PhD) fokozat elnyerése érdekében Írta:

Nagy Sándor

Készült a Pannon EgyetemKémiai és Környezettudományi Doktori Iskolájának keretében

Témavezető: Dr. Szalai István

Elfogadásra javaslom (igen / nem)

(aláírás)

A jelölt a doktori szigorlaton ...%-ot ért el,

Az értekezést bírálóként elfogadásra javaslom:

Bíráló neve: …... …... igen /nem

……….

(aláírás) Bíráló neve: …... …... igen /nem

……….

(aláírás)

A jelölt az értekezés nyilvános vitáján …...%-ot ért el.

Veszprém, 2012. ……….

a Bíráló Bizottság elnöke A doktori (PhD) oklevél minősítése:…...

………

Az EDHT elnöke

Kivonat

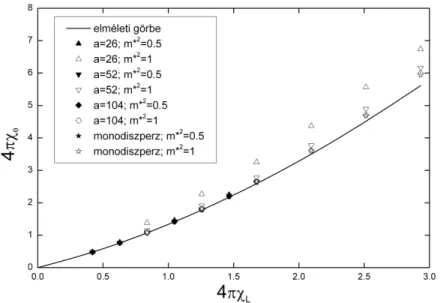
Egy új perturbációelméleti összefüggést adtunk meg monodiszperz dipoláris fluidumok mágnesezettségére nagy dipólusmomentumok és kis sűrűségek esetén. Az eredményeket Stockmayer-rendszeren végzett Monte Carlo szimulációs módszerrel ellenőriztük.

A gamma-eloszlással jellemzett polidiszperz dipoláris fluidumokra Monte Carlo szimulációkkal igazoltuk az MSA-elmélet mágnesezettségre vonatkozó előrejelzéseit a nagy sűrűségek és a kis dipólusmomentumok tartományában.

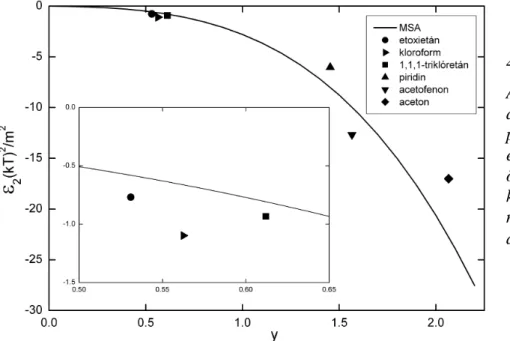
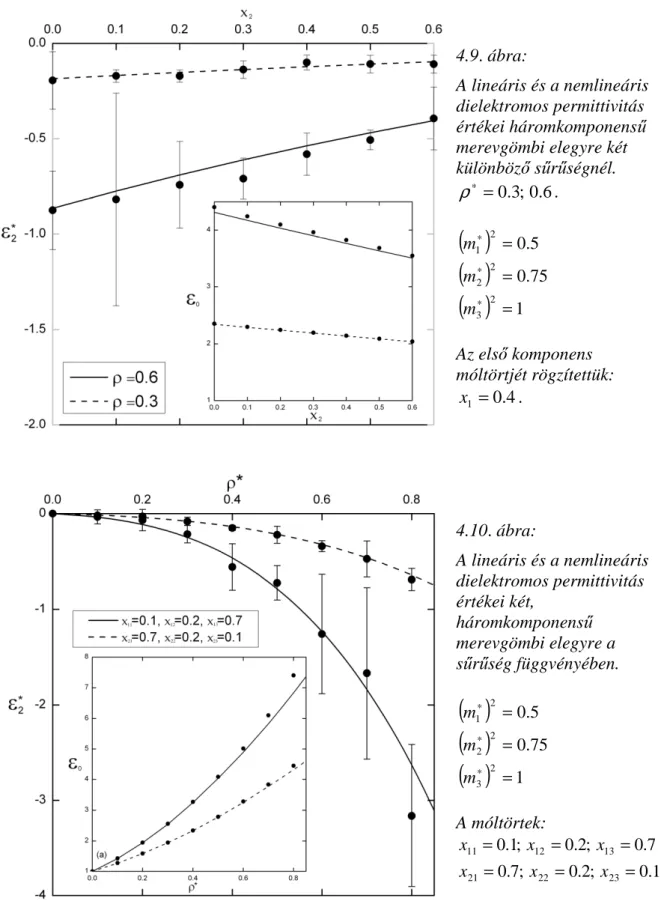
Ugyancsak az MSA-módszer keretein belül elméleti összefüggést adtunk meg a dipoláris Yukawa-fluidumok nemlineáris dielektromos permittivitására. Szimulációs összefüggést határoztunk meg a nemlineáris dielektromos állandó számolásához.

Eredményeinket valódi anyagok mérési eredményeinek felhasználásával igazoltuk. Mind az elméletet, mind a Monte Carlo szimulációkat kiterjesztettük két- és többkomponensű fluidumok nemlineáris dielektromos állandójának meghatározására.

Molekuladinamikai szimulációkat végeztünk Stockmayer-fluidumok viszkozitásának és öndiffúziós állandójának meghatározására. Korrelációs egyenleteket dolgoztunk ki ezen transzportegyütthatók számolására a hasonló paraméterekkel jellemzett, de dipólusmomentummal nem rendelkező Lennard–Jones rendszerre megadott értékekből.

Valódi anyagok viszkozitásának mérési eredményeivel igazoltuk eredményeink helyességét.

Stockmayer-rendszereken végzett nemegyensúlyi molekuladinamikai szimulációkkal megvizsgáltuk, hogyan növekszik a ferrofluidumok viszkozitása külső mágneses tér hatására.

A new perturbation theoretical formula has been introduced for the magnetization of monodisperse dipolar fluids for high dipole moments and low densities. The results were checked by Monte Carlo (MC) simulations for the Stockmayer fluid.

The Mean Spherical Approximation (MSA) theory for the magnetization of polydisperse dipolar fluids characterized by a gamma distribution has been confirmed by MC simulations for small dipole moments and high densities.

New theoretical and simulation formulas have been given for the nonlinear dielectric permittivity of dipolar Yukawa fluids within the MSA approach. The theoretical calculations and MC simulations have been extended to multicomponent compounds.

Molecular dynamics simulations have been performed to determine the share viscosity and self-diffusion coefficient of Stockmayer fluids. New correlation equations have been developed to calculate the difference from Lennard-Jones transport coefficients.

Nonequilibrium molecular dynamics simulations have been executed for Stocmayer- systems to demonstrate the effect of the magnetic field on the share viscosity in ferrofluids.

Zusammenfassung

Eine neue Formel wurde mit Perturbationstheorie für den Magnetismus von monodispersen dipolaren Fluiden angegeben, im Fall von großen Dipolmomenten und geringer Dichte. Die Ergebnisse wurden mit Monte-Carlo-Simulation an Stockmayer-Fluiden kontrolliert.

Die MSA-Theorie des Magnetismus von mit Gammaverteilung charakterisierten polydispersen dipolaren Fluiden wurde mit der Monte-Carlo-Simulation im Fall von kleinen Dipolmomenten und hoher Dichte bestätigt.

Eine neue theoretische und Simulationsformel wurde mit der MSA-Methode für die nichtlineare dielektrische Konstante von dipolaren Yukawa-Fluiden angegeben. Sowohl die Theorie als auch die Monte-Carlo-Simulation wurden auf die Bestimmung der nichtlinearen dielektrischen Kostante von Zwei- und Mehrkomponentenfluiden erweitert.

Molekulardynamik-Simulationen wurden durchgeführt, um die Viskosität und den Selbstdiffusionskoeffizienten von Stockmayer-Fluiden zu bestimmen. Es wurden neue Korrelationsformeln entwickelt, um die Differenz von Lennard-Jones-Transportkoeffizienten zu kalkulieren.

Nichtgleichgewichts-Molekulardynamik-Simulationen wurden in Stockmayer- Systemen durchgeführt, um die Wirkung des magnetischen Feldes auf die Viskosität in Ferrofluiden zu zeigen.

Nova formulo estis enkondukita pri la magnetismo de monodispersaj dipolusaj fluidoj de perturbacioteorio ĉe granda dipolusomomentumoj kaj malgrandaj densecoj. La rezultos estis atestita de Monte Carlo simuladoj estis praktikita de Ŝtokmajer sistemo.

La MSA teorio de magnetismo de la polidispersaj dipolusaj fluidoj estis karakterizita de gama distribuo estis konfirmita de Monte Carlo simuladoj ĉe malgrandaj dipolusomomentoj kaj grandaj densecoj.

Nova teoria kaj simulada formuloj estis donita pri la nelineara dielektra permitivo de la dipolusaj Jukava fluidoj en la MSA metodo. La teoria kaj Monte Carlo simulada rezultoj estis etendita al multkomponantaj miksaĵoj ankaŭ.

Molekulodinamikaj simuladoj estis rulita pri la viscozeco kaj siadifuza koeficiento de Ŝtokmajer fluidoj. Nova korelacia formuloj estis disvolvita kalkuli la diferenco de Lenard- Ĝons transportaj koeficientoj.

Neekvilibra molekulodinamikaj simuladoj estis ekzekutita en Ŝtokmajer sistemoj demonstri la efekto de la magneta spaco al tonda viscozeco en ferofluidoj.

Tartalomjegyzék

Kivonat ... 3

Abstract ... 4

Zusammenfassung ... 5

Resumo ... 6

Tartalomjegyzék ... 7

Bevezetés ... 8

A jelölések és rövidítések jegyzéke ... 10

1. Irodalmi áttekintés ... 12

1.1 Szimulációs technikák, a Monte Carlo és a molekuladinamikai módszer ... 12

1.2 A modellpotenciálok áttekintése ... 17

2. Monodiszperz dipoláris fluidumok mágnesezettségének perturbációelméleti vizsgálata .... 20

2.1. Irodalmi előzmények ... 20

2.2. Saját eredmények: mágnesezési tulajdonságok perturbációelméleti származtatása ... 26

2.3. A mágnesezettség meghatározása Monte Carlo szimulációs módszerrel ... 32

3. Polidiszperz dipoláris fluidumok mágnesezettségének MSA-elméleti vizsgálata ... 36

3.1. Irodalmi előzmények ... 36

3.2. Az MC szimulációk és az eredmények ... 40

4. Nemlineáris dielektromos effektus dipoláris fluidumokban ... 45

4.1. Irodalmi előzmények ... 45

4.2. Saját eredmények: MSA-elméleti háttér ... 48

4.3. A Monte Carlo szimulációs eredmények ... 51

4.4. Saját eredmények: az elmélet és az MC szimulációk kiterjesztése elegyekre ... 56

5. Stockmayer-fluidum viszkozitása és öndiffúziós állandója ... 62

5.1. Irodalmi előzmények ... 62

5.2. Saját eredmények: a transzportegyütthatók korrelációs egyenleteinek megadása 69 5.3. A molekuladinamikai szimulációk és az eredmények... 73

6. Magnetoreológiai folyadékok viszkozitása ... 78

6.1. Irodalmi előzmények ... 78

6.2. A nemegyensúlyi molekuladinamikai szimulációk és az eredmények ... 82

Összefoglalás ... 85

Irodalomjegyzék ... 87

Saját publikációk ... 91

Mindennapi tapasztalataink szerint az anyagok szilárd, folyékony vagy gáz halmazállapotúak. Ugyanazon anyag egymással egyensúlyt tartó gőz és folyadék fázisának fizikai tulajdonságai a hőmérséklet növelésével egyre jobban hasonlítanak egymásra; a kritikus hőmérsékleten a különbségek eltűnnek, és a kritikus hőmérséklet felett az anyag szuperkritikus állapotban van. A gőz és folyadék halmazállapotot és a szuperkritikus állapotot hívjuk fluidum állapotnak.

Az ún. dipoláris anyagok vizsgálatának az elektroreológia és magnetoreológia fejlődése adott újabb lökést az utóbbi évtizedekben. Az előbbi az elektromos, az utóbbi a mágneses tér hatására, a dipólusmomentummal rendelkező anyagok fizikai jellemzőinek változásával foglalkozó tudományág. Ezek a folyadék halmazállapotú anyagok, nano- vagy mikrométeres nagyságú részecskéket tartalmaznak. Mikroszkópikusan ezen folyadékok leírhatók olyan potenciálmodellel, ahol az eredeti diszperziós tagon kívül megjelenik a dipoláris, vagy más néven dipólus-dipólus kölcsönhatás is.

Dolgozatunk a dipoláris fluidumok mágnesezettségével, mágneses szuszceptibilitásával, lineáris és nemlineáris dielektromos állandójával, és transzporttulajdonságaival, ezen belül viszkozitásával és öndiffúziójával foglalkozik.

Az makroszkópikus rendszerek vizsgálatának ma alapvetően három módja létezik:

elméleti, szimulációs és kísérleti. A számítógépek és a szimulációs technikák fejlődésével a szimulációk az anyagi tulajdonságok teljesen új megközelítését tették lehetővé. Molekuláris szinten olyan pontosan lehet szimulálni a különböző anyagokat, hogy elegendő az elméleti megfontolásokat szimulációs eredményekkel igazolni. A modell kísérleti alátámasztása végül sosem maradhat el.

Mi is ezt az utat követtük. Elméleti megfontolások alapján új összefüggéseket származtattunk, amelyek jóságát minden esetben szimulációkkal vizsgáltuk és ahol lehetett a modellt irodalomból vett kísérleti adatokkal alátámasztottuk.

A dolgozat felépítése a következő. A bevezetés után a használt jelöléseket és rövidítéseket soroljuk fel. Az első (1) fejezet irodalmi áttekintést tartalmaz, amiben általános témaköröket fejtünk ki: az alkalmazott szimulációs technikák, és a használt modellpotenciálok.

Az ezután következő öt fejezet alkotja a dolgozat törzsét.

A második (2) fejezetben a monodiszperz dipoláris fluidumok mágnesezési tulajdonságával és mágneses szuszceptibilitásával foglalkozunk dipoláris merevgömbi modell keretében. A rendszer szabadenergiájából indultunk ki, aminek a térerősség szerinti deriváltja adja a mágnesezettséget. A szabadenergiát referenciarendszer és perturbációs tagok szabadenergiáinak összegéből kapjuk, a perturbációs együtthatókat pedig az irodalomban jól ismert, és elméletileg gyakran tárgyalt párkorrelációs függvények és az ún. Mayer- függvények segítségével számoljuk.

A harmadik (3) fejezetben az MSA-elmélet polidiszperz merevtörzsű rendszerek mágnesezettségére vonatkozó összefüggését szimulációkkal ellenőriztük. A ferrofluidumokban a részecskék méret szerinti eloszlását általában az ún. gamma-eloszlással közelítik, így tettük ezt mi is.

A negyedik (4) rész a lineáris és nemlineáris dielektromos állandó MSA-elméletével foglalkozik egykomponensű dipoláris merevtörzsű Yukawa- és többkomponensű dipoláris merevgömbi potenciállal jellemzett fluidumokban. Összefüggést adtunk meg a nemlineáris dielektromos állandóra az MSA-elmélet keretein belül és a szimulációkból történő számolására is.

A ötödik (5) fejezet a Stockmayer-fluidumok viszkozitását és öndiffúziós állandóját vizsgálja. Széles hőmérséklettartományon, négy különböző sűrűségen és négy különböző dipólusmomentumnál végeztünk molekuladinamikai szimulációkat. Mivel az irodalomban nagyon pontos sokparaméteres elméletek léteznek mindkét transzportegyüttható elméleti meghatározására, ezért az azonos paraméterekkel jellemzett Lennard–Jones és Stockmayer- rendszerek viszkozitásának és öndiffúziójának különbségére adtunk összefüggést.

A Stockmayer-fluidum külső tér hatására bekövetkező viszkozitás-növekedését vizsgáltuk az utolsó, hatodik (6) fejezetben. Ehhez nemegyensúlyi molekuladinamikai szimulációkat végeztünk, és módosított periodikus határfeltételeket kellett használnunk.

A dolgozatot összefoglalás, irodalomjegyzék, köszönetnyilvánítás és a függelékek zárják.

Megjegyezzük, hogy bár a dolgozatban az elméleti és szimulációs eredmények közel azonos súllyal szerepelnek, a doktori cselekmény alapját a számítógépes szimulációk elkészítése és azok alkalmazása jelentette.

Jelölések:

V térfogat

T hőmérséklet

N részecskeszám

t idő

I tehetetlenségi nyomaték

p nyomás

ρ sűrűség

F szabadenergia

g radiális párkorrelációs függvény

h teljes korrelációs függvény

c direkt korrelációs függvény

k Boltzmann-állandó

β 1/kT reciprok hőmérséklet

* redukált mennyiség

E, E elektromos térerősség

P, P elektromos polarizáció

H, H mágneses térerősség

M, M mágnesezettség

m dipólusmomentum

y dipóluserősség

v sebesség

a gyorsulás

r pozíció

f erő

τ forgatónyomaték

ω szögsebesség

u kerületi sebesség

g segédnyomaték

e egységvektor

S rendparaméter

s szórás

γ nyírósebesség

P nyomástenzor

r c levágási távolság

rij részecskék távolsága

ωi részecske iránya

σ párpotenciálok távolságparamétere

ε párpotenciálok energiaparamétere, vagy dielektromos állandó

ε0 lineáris dielektromos állandó

ε2 nemlineáris dielektromos állandó

χ mágneses szuszceptibilitás

χ0 lineáris mágneses szuszceptibilitás

χ2 nemlineáris mágneses szuszceptibilitás

x móltört

D öndiffúziós állandó

η viszkozitás vagy kitöltési tényező

q merevgömbi fluidum inverz kompresszibilitási függvénye

ξ MSA-paraméter

Γ gamma-fügvény

, x0

a gamma-eloszlás paraméterei

( )

^′ differenciálás vagy polidiszperz mennyiség

Rövidítések:

MC Monte Carlo

MD molekuladinamika

MSA mean spherical approximation

HS merev gömb, hard sphere

DHS dipoláris merev gömb

LJ Lennard–Jones

STM Stockmayer

DY dipoláris Yukawa

RF reakciótér, reaction field

NDE nemlineáris dielektromos effektus

DW Debye–Weiss

DD dipól-dipól

L Langevin

hcp hexagonális rács, hexagonal close packed

ccp egyszerű köbös rács, cubic close packed

sat szaturációs

1.1. Szimulációs technikák, a Monte Carlo és a molekuladinamikai módszer

A számítógépes szimulációknak alapvetően két, egymástól merőben különböző technikája ismert. A Monte Carlo módszer a konfigurációs tér egy lehetséges állapotát annak előző állapotából egy véletlenszám segítségével állítja elő és az új állapot megvalósulását egy energetikai kritériumhoz köti. Ezzel szemben a molekuladinamikai módszer teljesen determinisztikus, a newtoni mozgásegyenletek megoldásával lépünk a konfigurációs tér előző állapotából az újba.

Néhány, mindkét módszer esetén használatos szimulációs technika leírása után kitérünk röviden a két módszer ismertetésére.

Kanonikus (NVT) sokaságon szimuláltunk, azaz a szimulációs cella térfogatát (V) és hőmérsékletét (T), illetve a cellában elhelyezkedő részecskék számát (N) állandónak tekintettük. Mivel a számítási sebesség a részecskeszám négyzetével arányos, ezért általában 512 részecskét alkalmaztunk, ami a mai számítógépek számítási teljesítménye mellett sem kevés. A határfelületi hibák elkerülésére periodikus határfeltételt használtunk: a szimulációs teret a V térfogatú cella végtelen ismétlődésével mindhárom irányban végtelenítettük, és minden részecskéhez minden „szellemcellában” egy „szellemrészecske” tartozott. Tehát ha egy részecske egyik irányba elhagyta az eredeti cellát, akkor „szellemképe” a szemben lévő irányból belépett. Így már végtelen számú alkotóelemünk volt, amit véges számú koordinátával le tudtunk írni.

A számítási idő csökkentésére be szoktak vezetni egy ún. levágási távolságot

( )

r , c

aminél kisebb távolságban elhelyezkedő részecskék párenergiáit közvetlenül veszik figyelembe. Az ennél egymástól távolabb eső részecskék párenergiáit hosszútávú korrekcióval számoltuk (lásd.: 1.2. fejezet). A levágási távolságot minden esetben a maximálisra, a szimulációs cella élhosszának felére választottuk. Ennél nagyobb azért nem lehet, mert ekkor a levágási távolságon belülre némely részecskének egynél több képe is bekerülhet, ami egyfajta szisztematikus hibát visz a számolásba. Ha rendelkezésre áll nagyobb számítási kapacitás, akkor célszerű a részecskék számát növelni, az előbb említett maximális levágási távolság betartásával.

A Monte Carlo módszernél nagy szerep jut a véletlennek. Azon túl, hogy a konfigurációs tér kezdeti állapotában a részecskék irányát véletlenszámokkal tetszőlegesre

állítottuk be, a szimuláció alatt azok lehetséges transzlációs és rotációs elmozdulásait is a véletlen irányította a következő összefüggések szerint:

( )

( )

( )

( )

( )

max

1

max 1

max 1

max 1

max 1

cos 1 2 cos cos

1 2

1 2

1 2

1 2

ϑ υ

ϑ ϑ

ϕ υ

ϕ ϕ

υ υ υ

ϑ ϕ

d d

dr z

z

dr y

y

dr x

x

i i

i i

z i i

y i i

x i i

− +

=

− +

=

− +

=

− +

=

− +

=

+ + + +

+ (1.1)

ahol υx^,υy^,υz^,υ_ϕ^,υ_ϑ egy a program által létrehozott véletlenszám a

( )

^0,1 intervallumon, z

y

x, , és ϕ^,ϑ pedig a szokásos Descartes- és gömbi polárkoordináták. (Megjegyezzük, hogy a részecskéket kezdetben, az egyszerűség jegyében, a 128 és 256 elemű esetekben hexagonális (hcp, hexagonal close packed), 512 elemű esetben pedig egyszerű köbös rács (ccp, cubic close packed) pontjaira helyeztük el.)

Az (1.1) egyenletekkel létrehozott új állapotot elfogadjuk, ha annak összenergiája kisebb mint az előző állapoté, vagy ha az energiaváltozás pozitív, akkor az elfogadás valószínűsége a változás növekedésével exponenciálisan csökken: e^(−β∆U), ahol β =1kT ^{, k} a Boltzmann-állandó, T a hőmérséklet. (1.1 ábra)

A transzlációs és a rotációs elmozdításokat külön kezeltük, tehát egy lépésben egy részecskét vagy csak eltoltunk vagy csak elforgattunk. Ahhoz, hogy a szimuláció megfelelően gyorsan és megfelelően sűrűn mintavételezve járja be a konfigurációs teret, célszerű meghatározni egy átlagos elfogadási arányt, amit transzlációra az általánosan elfogadott 50%-ban határoztunk

1.1. ábra:

Az új állapot elfogadásának valószínűsége az energiaváltozás függvényében a Monte Carlo szimulációban.

1.1. Szimulációs technikák, a Monte Carlo és a molekuladinamikai módszer

csökkentettük. Rotáció esetében az elfogadási valószínűség nagyon függ a sűrűségtől. Azt mondhatjuk, hogy a maximális elforgatás szögét 15º-20º alatt kell tartani.

Az (1.1) egyenletek alapján elmondhatjuk, hogy véletlenszerűen veszünk mintát a konfigurációs térből, és így a fizikai mennyiségeket sokaságátlagok, nem pedig időátlagok alapján kapjuk meg. Ezért ez a módszer nem alkalmas transzportfolyamatok és nemegyensúlyi folyamatok vizsgálatára.

Másképpen megfogalmazva: a Monte Carlo szimuláció elég sok idő alatt bejárja a konfigurációs tér időben egymást követő pontjait, csak nem egymás után, hanem az (1.1) ábrán látható elfogadási valószínűségek szerint. Az így létrehozott mintavételezés biztosítja, hogy a trajektória az energetikailag jelentős járulékot adó konfigurációs pontokon haladjon végig. Egy X fizikai mennyiség várható értéke a Boltzmann-eloszlás szerint:

( ) ( )

∑

∑

=

−

=

−

= _I

i u I

i

u i

i i

e e X X

1 1

β β

,

(1.2)

ahol I a mintapontok száma. A konfigurációs térből történő véletlenszerű mintavételezést és az adott fizikai mennyiség e^−βU Boltzmann-faktorral történő súlyozását helyettesítjük a Boltzmann-faktorral vezérelt mintavételezéssel (Boltzmann-mintavételezés) és a fizikai mennyiség számtani átlagként történő számításával. Tehát az X mennyiség várható értékét a szimuláció során a következőképpen kaphatjuk meg:

I X X

I

i

∑

i

≈ =¹ .

(1.3)

Látható, hogy a kezdeti állapotból indulva a következő állapotok sorozatát egy Markov-lánc tagjaiként foghatjuk fel. A fent vázolt eljárást elsőként Metropolis és munkatársai [Me1953]

alkalmazták.

A molekuladinamikai módszernél a véletlennek kisebb szerep jut, csupán a kezdeti konfiguráció beállításánál játszik szerepet. A továbbiakban a részecskék mozgását a newtoni mozgásegyenletek irányítják. Ezen egyenletekben fontos tényező az ún. időállandó (vagy időlépés), ami két egymást követő molekuladinamikai ciklus között eltelt időt jelent. A fizikai mennyiségeket így időátlagokból kapjuk meg.

A mozgásegyenletek megoldására több módszer is ismeretes. Mi itt az eredetileg Verlet [Ve1967] nevéhez fűződő algoritmus egy – Hockney és Potter által [Ho1970, Po1972]

– módosított változatát mutatjuk be, az ún. „leap-frog” (bakugrás) algoritmust.

Egy molekuladinamikai ciklus alatt minden részecske pozícióját, helyzetét, sebességét és gyorsulását megváltoztatjuk. Az algoritmus működését az (1.2) ábra mutatja. Látható, hogy a sebességet a t-(1/2)dt időpillanatban ismerjük, ahol dt az időállandó. Ez az eltérés az eredeti Verlet algoritmussal szemben, mert abban a sebesség hasonlóan a pozícióhoz és a gyorsuláshoz, a t-dt időpillanatban ismeretes, de ez a számolás során pontatlansághoz vezet.

A leap-frog algoritmus a következő három lépésből áll.

(1) Egy molekula adott pozíciójából ki tudjuk számolni a rá ható erőket, abból pedig, tömegének ismeretében a gyorsulását.

(2) A sebesség előző, és a gyorsulás aktuális értékéből megkapjuk az aktuális sebességet:

( )

^{t dt}

dt t dt

t v a

v +



 



 −

=



 



 +

2 1 2

1 . (1.4)

(3) A pozíció előző és a sebesség aktuális értékéből pedig megkapjuk az új pozíciót:

(

^{t dt}

) ( )

^{t t dtdt}



 



 + +

=

+ 2

v 1 r

r . (1.5)

A később tárgyalt termosztáláshoz szükséges a sebesség ^v

( )

^t értékének ismerete, amit a

( )









 



 



 − +



 



 +

= t dt t dt

t 2

1 2

1 2

1 v v

v (1.6)

sebességátlagolásból kaphatunk meg.

A részecskék forgását hasonló egyenletek írják le. Erők helyett forgatónyomatékról (τ), térbeli koordináták helyett a molekula dipólusmomentumának irányához rendelt egységvektorról (e), sebesség helyett szögsebességről (ω) és kerületi sebességről (u) kell beszélnünk.

1.2. ábra: Az ún. leap-frog algoritmus működése.

1.1. Szimulációs technikák, a Monte Carlo és a molekuladinamikai módszer

(2) A kerületi sebesség megváltozása, a kerületi gyorsulás megkapható, ha bevezetjük az I tehetetlenségi nyomatékot és a λ mennyiséget:

g e u= +λ

& I . (1.8)

A második tag egy kényszer, ami biztosítja, hogy a forgás során e vektor hossza egységnyi maradjon. λ mennyiséget felfoghatjuk egy Langrange-multiplikátornak és a következő összefüggésből számolhatjuk:

( )

^{t dt u t dte}

( )

^t



 



 −

−

= 2

2 1

λ ^{. (1.9)}

(3) A kerületi sebességet hasonlóan kapjuk mint a transzlációs sebességet:

( )

^{t dt}

dt t dt

t u u

u +&



 



 −

=



 



 +

2 1 2

1 . (1.10)

(4) A dipólusmomentum iránya pedig:

(

^{t dt}

) ( )

^{t t dtdt}



 



 + +

=

+ 2

u 1 e

e . (1.11)

Hasonlóan az (1.6) egyenlethez, a kerületi sebesség ^u

( )

^{t értéke:}

( )





 



 



 



 − +



 



 +

= t dt t dt

t 2

1 2

1 2

1 u u

u . (1.12)

A hőmérsékletet a szimuláció során az ekvipartíció tétele alapján állítottuk be. Tehát a három transzlációs és a két rotációs szabadsági fokra egyenként 1 2kT átlagos mozgási energia jutott. Az irodalomban többféle termosztát ismeretes. A legegyszerűbb a sebesség átskálázása [Wo1971]. Ekkor minden részecske sebességét megszorozzák a

(

T^/Tc

)

¹²

faktorral, ahol T az aktuális hőmérséklet, T pedig az előre beállított, elérni kívánt _c hőmérséklet. Egyfajta sebesség átskálázásos módszer az általunk használt Berendsen- termosztát is [Be1984]. Itt a következő faktorral kell megszorozni a sebességeket:

2 1

1

1 

















 −

+

=

c T

v T

T t

χ dt ^{, (1.13)}

ahol t_T egy előre beállított időállandó (nem összekeverendő dt időállandóval). t_T kisebbre vagy nagyobbra állításával tudjuk szabályozni a skálázás erősségét. Ha t_T =dt^{, akkor} visszakapjuk az egyszerű sebességskálázást. Minél nagyobb t_T értéke, annál finomabb a hőmérséklet hangolása.

1.2. A modellpotenciálok áttekintése

Ebben az alfejezetben a dolgozatban alkalmazott párpotenciálokat tekintjük át. Azzal az általánosan elfogadott feltevéssel élünk, hogy a potenciális energia minden esetben páronként additív, tehát eltekintünk a többtest-kölcsönhatásoktól:

( ) ∑ ( )

<

=

j i

j i ij N

N U

U ^{r ,}ω ^{r ,}ω ^,ω ^{, (1.14)}

ahol ω_i^,ω_j a részecskék irányát, N a részecskeszámot jelöli. Látható, hogy ebben az esetben a potenciális energia ^N

(

^N−1

)

^/2 darab párenergia összegzésével adódik, tehát a szimuláció sebessége, az időegység alatt elvégzett MC vagy MD ciklusok száma N-el négyzetesen csökken. Ez a tény a részecskeszám növelésének legnagyobb korlátja. Itt kell megemlítenünk, hogy a párenergiák számolásakor minden részecskepárnak az egymáshoz legközelebb eső szellemképeit vettük figyelembe. Ez az ún. minimum-image konvenció.

A legegyszerűbb, éppen ezért széles körben elterjedt párpotenciál a merevgömbi potenciál (HS, hard-sphere):

( )

^{0 ,}





<

∞

= ≥

σ σ r r r

U_HS (1.15)

ahol σ a részecskék átmérőjét jelöli; ennél közelebb a molekulák nem kerülhetnek egymáshoz (1.3.c ábra).

A vonzó taggal is rendelkező párpotenciálok közül talán a legelterjedtebb a Lennard–

Jones potenciál (LJ, 1.3.b ábra):

( )

_^









 



 



−



 



= 

6 12

4 r r

r

U_LJ ε_LJ σ σ ^{, (1.16)}

1.3. a,b,c ábra: A merev törzsű Yukawa-, a Lennard–Jones-, és a merevgömbi potenciál.

1.2. A modellpotenciálok áttekintése

Az ilyen hatványfüggvényekkel leírható, vonzó és taszító tagot is tartalmazó kölcsönhatásokat általánosan Mie-féle potenciáloknak hívjuk.

A dolgozatban használunk még ún. keménymagú Yukawa-kölcsönhatást, ami egy vonzó részből és egy merevgömbi taszító részből áll (1.3.a ábra):

( ) ( ( ) )







<

∞

− ≥

− −

=

σ σ σ

σ κ ε

r r r

r r

U_Y ^Y

exp

,

(1.17)

ahol σ^,κ ^és εY ugyancsak a kölcsönhatás paraméterei.

A dipoláris kölcsönhatásnál minden részecskéhez hozzárendelünk egy pontszerű dipólust, így a közöttük lévő potenciál nagysága nem csak a távolság, hanem az irányok függvénye is:

( )

3

(

12 1 2

)

12 2 2

1

12,ω ,ω ^Dω ,ω ,ω

r

U_D r =−m , (1.18)

(

ω12^,ω1^,ω2

) (

=³m^ˆ1⋅r^ˆ12

)(

m^ˆ 2⋅r^ˆ12

) (

− m^ˆ1⋅m^ˆ 2

)

^,

D ^(1.19)

ahol az 1. illetve a 2. részecske az r₁ és r₂ helyen található; m nagyságú dipólusmomentummal és ^mˆ1

( )

ω1 ^{illetve m}ˆ 2

( )

ω2 egységvektorokkal jellemzett irányultságuk van; r₁₂ =r₁−r₂ a második részecske középpontjából az első középpontjáig húzott vektor;

12 12 = r

r .

Mindhárom felsorolt párpotenciált kiegészíthetjük a dipoláris kölcsönhatással, így rendre a dipoláris merevgömbi (DHS), Stockmayer- (STM) és dipoláris Yukawa- potenciálokat (DY) kapjuk.

Ahogy már említettük, a párpotenciálokat a számítási idő csökkentése miatt, egy levágási távolságon kívül hosszútávú korrekcióval veszik figyelembe. A merevgömbi potenciálnál nyilvánvalóan nincs szükség ilyen korrekcióra. Lennard–Jones rendszerre az energia és a nyomás hosszútávú korrekciója [Al1987]:

( )

⁹

( )

³

, 8 9 ^{∗ ∗−} 8 3 ^{∗ ∗−}

∗ _LJ = _c − _c

lrc N r N r

U π ρ π ρ ^{, (1.20)}

( )

^{2 9}

( )

^{2 3}

, 32 9 ^{∗ ∗−} 16 3 ^{∗ ∗−}

∗ _LJ = _c − _c

lrc r r

p πρ πρ ^{, (1.21)}

ahol ρ^∗ =ρσ³ és rc^∗ =rc σ . A merev törzsű Yukawa-rendszer hosszútávú korrekciói:

(

¹

)

^exp

( (

¹

) )

2 ²

, =− ^{∗ ∗} + ⋅ − ^∗ −

∗

c c

Y

lrc N r r

U π ρ κ κ κ ^{, (1.22)}

(

^{3 1}

)

^exp

^{( (}

¹

^{) )}

2 ^{2 2 2}

, =− ^{∗ ∗} + ^∗ + ⋅ − ^∗ −

∗

c c

c Y

lrc N r r r

p π ρ κ κ κ ^{. (1.23)}

A dipólus-dipólus kölcsönhatás hosszútávú korrekcióját két módszerrel szokták kiszámolni.

Az egyik az ún. Ewald-összegzés [Ew1921], a másik a reakciótér módszer [Al1987]. Mi minden esetben az utóbbit használtuk, ezért ezt ismertetjük.

A reakciótér módszer esetén egy adott dipólusra ható térerősség két forrásból ered. Az egyik a rövidtávú hatás, ami egy bizonyos levágási távolságon belül eső részecskékből a dipólus-dipólus kölcsönhatás szerint hat a molekulára, a másik pedig az ugyanezen távolságnál távolabb lévő molekulákból ered. Ez utóbbi hatást úgy vesszük figyelembe, mintha a levágási távolságon kívül egy homogén ε_s dielektromos állandójú, végtelen közeg helyezkedne el. A gömb (vagy üreg) középpontjában a gömbben lévő dipólusok által a dielektrikum határfelületén indukálódott polarizációs töltések reakcióteret hoznak létre:

( ) ∑

+ ∈

= −

G j

j c

s s

i r m

E 1₃

1 2

1 2

ε

ε , (1.24)

ahol most r_c a gömb sugara, j pedig a gömbben lévő részecskéken fut végig. Mivel általában εs nem ismert ezért az ε_s =∞ vezető határfeltétel közelítéssel élnek, így (1.24) egyenlet leegyszerűsödik. A reakciótér energiajáruléka az i. dipólusra :

( )

i i i

URF_, =−12m ⋅E . (1.25)

A reakciótérből erő ugyan nem hat a molekulákra, de forgatónyomaték igen:

i i i

RF, =m ×E

τ ^{. (1.26)}

Ha egy dipólusra külső, homogén erőtér hat, akkor ez minden egyes részecskére

i külső i

UE_, =−E ⋅m (1.27)

energiajárulékot ad.

1.2. A modellpotenciálok áttekintése

vizsgálata

2.1. Irodalmi előzmények

A mágnesezettség legegyszerűbb, ún. Langevin-modellje [La1905] elhanyagolja a dipólusok kölcsönhatását, csak a külső mágneses térrel való kölcsönhatást veszi figyelembe azzal a kiegészítéssel, hogy a részecskék energia szerinti eloszlására érvényes a Boltzmann- eloszlás. Az M mágnesezettséget megkaphatjuk ha összegezzük a térfogategységbe eső dipólusmomentumokat:

=

∑

i

V mi

M 1

. (2.1)

Külső mágneses tér alkalmazása nélkül a fluidum izotrop, a (2.1) egyenlet szerint a mágnesezettség zérus. Ha külső teret alkalmazunk, a mágnesezettséghez a térfogategységben lévő permanens mágneses dipólusok térerősség irányába eső komponenseit kell összegeznünk:

H

M=ρm cosΘ H ^{, (2.2)}

ahol ρ a számsűrűséget, m a dipólusmomentumot, Θ az m és a H vektorok által bezárt szöget, pedig a sokaságátlagot jelöli. (Mivel M és H iránya azonos, ezért a továbbiakban az M és H skalár jelölést alkalmazzuk; M = M , és H = H .) A Boltzmann-eloszlás szerint, annak a valószínűsége, hogy a dipólus tengelye a H mágneses térerősséggel Θ szöget bezáró irány ^dω környezetébe essen:

( ) ∫

^Θ

= Θ

ω ω ω

ω mH kT d

d kT d mH

P

) / ) cos exp((

) / ) cos exp((

, (2.3)

mivel egy dipólus potenciális energiája külső térben Θ

−

= mHcos

U . (2.4)

Az (1.3) egyenlet szerint:

∫

∫

Θ Θ

= Θ

Θ ω

ω d kT mH

d kT mH

m m

) / ) cos exp((

) / ) cos exp((

cos

cos . (2.5)

Az integrálások elvégzése után cosΘ átlagértéke:

(

^{mH kT}

) (

^{− kT mH}

)

= Θ coth

cos . (2.6)

A (2.6) egyenlet jobb oldalán a jól ismert Langevin-függvény szerepel:

( )

^x

( )

^{x x}

L =coth −1 ^{. (2.7)}

Így a mágnesezettség a Langevin-modell szerint, az ún. Langevin-mágnesezettség:



 



= 







 −



 



= 

kT mL mH mH

kT kT

m mH

M_L ρ ^coth ρ ^.

(2.8)

Ez a közelítés visszaadja a mágneses telítődést, hiszen nagy argumentumok esetén a Langevin-függvény alulról egyhez konvergál. Ebből a H=0 térerősséghez tartozó mágneses szuszceptibilitás (vagy lineáris mágneses szuszceptibilitás):

( )

kT m H

kT mH m L

H M

H H

2

0 0

0 3

1 ρ ρ

χ =

∂

= ∂

∂

= ∂

= =

(2.9) Ezt a mennyiséget az irodalom Langevin-szuszceptibilitásnak [Pa1996] nevezi:

kT m

L

2

3 1 ρ

χ = . (2.10)

A kifinomultabb Weiss-modell [We1907] figyelembe veszi, hogy a fluidumban lévő helyi térerősség

( )

He nem egyenlő a külső térrel, hanem az alábbi formula alapján számolható:

( )

^H

M H

H_e

3 4π +

= , (2.11)

amit Lorentz-féle belső térnek is neveznek. Ezt figyelembe véve a mágnesezettségre a (2.8) egyenlethez alakilag hasonló, implicit egyenletet kapunk:



 



= 

kT mL mH

M ρ ^{e . (2.12)}

Egyszerű számolás elvégzése után a lineáris mágneses szuszceptibilitásra azt kapjuk, hogy:

( )

L L

χ π χ χ

3 4

0 =1− . (2.13)

Ez az összefüggés χL =^3/4π szuszceptibilitásnál divergenciát mutat, ami a ferromágneses- paramágneses fázisátalakulást jelzi, de eddig ezt ferrofluidumokban nem detektálták.

Buyevich és Ivanov [Bu1992, Iv1992] perturbációelméleti módszert dolgozott ki a mágneses tulajdonságok számítására. Elméletükben a perturbációs potenciál a dipólus-dipólus kölcsönhatás. Referenciarendszerként a mágnesesen nem-kölcsönható merevgömbi fluidumot, az ún. merevgömbi Langevin-gázt választották. A mágnesezettség könnyen szeparálható a

2.1. Irodalmi előzmények



 





∂ + ∂

= H

M M

M _L ^L

3 1 4π

. (2.14)

Ha a térerősség értéke nagy, akkor a mágnesezettség értéke a telítési értéknél nagyobb, ami nyilvánvalóan helytelen, azonban a szuszceptibilitásra az eddigieknél pontosabb összefüggéseket kaptak:



 



 +

=χL π χL

χ 3

1 4

0 . (2.15)

Pshenichnikov és munkatársai [Ps2000] a Weiss-modellt fejlesztették tovább. A mágnesezettséget a (2.12) egyenlet adja meg. A helyi térerősség kifejezése is azonos alakú, mint a (2.11) egyenlet:

( )

^H

M H

H_{e L}

3 4π +

= , (2.16)

azonban fontos különbség, hogy itt a Langevin-mágnesezettség jelenik meg. A szuszceptibilitásra a (2.15) kifejezést kapjuk.

Ivanov és Kuznetsova [Iv2001, Iv2006] a dipoláris merevgömbi rendszer párkorrelációs függvényének analízisével új, kibővített formáját adták meg a mágneses mennyiségeknek. Az effektív térerősségbe egy új tagot javasoltak, a Langevin- mágnesezettség deriváltját:

48 . 1 4 3

4 



 





∂ + ∂ +

= H

M M H

H_e π _L π ^L _(2.17)

Így a szuszceptibilitás a Langevin-szuszceptibilitásnak, és így a sűrűségnek is az eddigi másodfokú helyett harmadfokú függvénye lett:

( )











 + +

= ^{2 2}

0 144

4 3

1 4 _{L L}

L π χ π χ

χ

χ ^{, (2.18)}

a mágnesezettség pedig:

( )













∂ + ∂

+

= H

M M kT M m

kT m kT

mL mH

M _{L L} ^L

144 4 3

4π π ²

ρ ^{. (2.19)}

Huke és Lücke [Hu2000] a dipoláris merevgömbi rendszer külső térben vett állapotösszegét (Z) a Born–Mayer-sorfejtés segítségével írta fel. Az állapotösszegből szabadenergiát (F), abból pedig mágnesezettséget kaphatunk:

kT Z

F =−ln , (2.20)



 





∂

− ∂

= H

F

M V1

. (2.21)

Ennek megfelelően a mágnesezettség kifejezése a jól ismert Langevin-függvénnyel indul:

( ) ( )

²

2

, 1

8 η ^m 2 ^{L O}η

kT L mH kT L mH kT

L mH M

M

n

n n sat

+ +



 



′



 

 + 



 



= 

∑

^∞

=

∗ , (2.22)

ahol M_sat = ρm,

6 ρ π

η= ^∗ a kitöltési tényező. A harmadik tagban lévő kifejezések függvény tripleteket jelölnek, amiknek egy-egy tagja is bonyolult függvénye a térerősségnek. Az ebből származtatható szuszceptibilitás hátránya, hogy χ_L csak az első és a második hatványkitevővel szerepel benne:



 



 + + + +

= ^{∗ ∗} ...

3675 16 75

4 3

1 4 ^{4 8}

0 χL π χL π m χL π m χL

χ ^{. (2.23)}

Szalai és munkatársai [Sza2000, Sza2003] a Ruelle-féle [Ru1969] perturbációelmélet alkalmazása során – Kalikmanovhoz [Ka1999] hasonlóan – ugyancsak a dipoláris merevgömbi rendszer szabadenergiájából indultak ki, ami kis külső tér alkalmazása esetén másodrendig felírva a következő alakot ölti:

2 2 1

0 2 4

1

4 b b

F

F 



 



− 



 



−

= ρπ

π β ρ

β ^{, (2.24)}

ahol F a referenciarendszer, a dipoláris merevgömbi rendszer szabadenergiája külső tér ₀ alkalmazása nélkül, b pedig az i. térfüggő perturbációs tag, amit a megfelelő rendű _i párkorrelációs függvények segítségével kaphatunk meg:

∫ ( )

= _{1 1 1}

1 ^{d d}ω ^f ω

b r , (2.25)

( ) ( [

12 1 2

) ] ( )

2 0

2 1 2 1 2 1

2 ^{d d d}ω ^dω ^f ω ^g ,ω ,ω 1^f ω

b ⁼

∫

^{r r r − ,} (2.26)

ahol ^f

( )

^{ωi =exp}

(

^αcosϑi

)

^{−1≅αcosϑi +}

( )

^{α2 2 cos2ϑi} (2.27) a külső térrel való kölcsönhatásnak megfelelő Mayer-függvény a második tagig sorba fejtve, és ϑ_i a részecske dipólusmomentumának a külső térrel bezárt szöge, α =mH kT ^{. A DHS} rendszer párkorrelációs függvénye zárt alakban nem ismert, ezért azt egy másodrendű perturbációs összeggel közelítjük [Ba1976]:

( ) ( ) ( )

²

( ) ( )

^{2 2}

( )

0 ^r ,ω ,ω ^{g r} β^{m g r} ,ω ,ω β^{m g r} ,ω ,ω

g = + + , (2.28)

2.1. Irodalmi előzmények

( ) (

3 1 2 12

)

12 12

1 ^Dω ,ω ,ω

r r

g = g^d , (2.29)

( ) ( ) ( ) ( ) ( )

(

1 2

) ( ) ( )

12 12 12 12 12 2 6 1

12 12 12

2 1 2 2

3 , 1

, 6 ,

, 1 2 ,

1

r g r a

r g r a r D

r D g

g

d d D d

ω ∆

ω ρ

ω ω ω ρ ω

ω ω

∆ +

−

= (2.30)

a megfelelő perturbációs tagok, valamint ∆

(

ω₁,ω₂

)

=mˆ1⋅mˆ 2^{. Az} aD és a_∆ függvények az alábbi formulákba írhatók:

( ) ( )

3

( ) ( )

13 23

23 13

3 2 1 3

12

cos cos cos 3

1 g r g r

r r d

r

a_D =

∫

^r + γ γ γ _{d d} ^{, (2.31)}

( ) ( )

3

( ) ( )

13 23 23

13 3 2 3 12

1 cos

3 g r g r

r r d r

a∆ =

∫

γ − _{d d}

r , (2.32)

Ahol γ₁,γ₂,γ₃ a három részecske által kijelölt háromszög belső szögeit jelölik. Ezeket a mennyiségeket különböző rendszerekre Høye és munkatársai [Ho1974, Ho1975] illetve Goldmann [Go1990] számolták ki. Kis sűrűségű határesetben – a számolások részletezése nélkül – a következő egzakt kifejezések adódnak:

( )











 ≥









 <











 



 

 + 



 



−

×

=

2 3 ,

8

2 ,

12 6 1

12 3

12

12 12

3 12

12 3

d ha r r

d

d ha r d

r d

r

r d a_D

π π

,

(2.33)

( )













≥

 <











 +



 



− 



 





×

∆ =

2 ,

0

2 ,

32 24

12 2 1

12 12 12

3 12

12 3

d ha r

d ha r d

r d

r

r d a

π

.

(2.34)

A (2.33) és (2.34), illetve a (2.29) és (2.30) egyenleteket beírva a (2.28) egyenletbe, azt pedig felhasználva a (2.25), (2.26) és (2.24) egyenletekben, a szerzők a szabadenergiára a következő összefüggést kapták:

( )

^{2 2 2 2 3}

( )

^{2 2 2}

3 2 2 2 2 2

0 486

17 243

8 54

4 6

1 ρα π ρ β α π ρ β α π ρ β α

β

β^F = ^F − ^V − ^{V m} + ^{V m} − ^{V m} , (2.35)

amiből a mágneses szuszceptibilitásra kis sűrűségű határesetben Ivanov és Kuznetsova (2.18) egyenleteit kapták meg. (A számolást itt nem részletezzük, mert annak elemei megjelennek majd a következőkben.)

Tani, Henderson, Barker és Hecht [Ta1983] nagy sűrűségen is érvényes összefüggést adtak meg a mágneses lineáris szuszceptibilitásra:











  +



 



− +

= ² _∆ ²

2

0 3

4 3

1 4 _{L L dd L}

L π χ π χ I χ

χ

χ ^{, (2.36)}

ahol I_dd∆ egy sűrűségtől függő mennyiség, amelynek értéke kis sűrűségű határesetben:

9

17π² . Ezt az értéket beírva a (2.36) egyenletbe, ugyancsak megkapjuk Ivanov és Kuznetsova (2.18) egyenleteit.

Tani és munkatársai [Ta1983] a számolásokat H=0 külső térben végezték el, tehát a (2.36) egyenletet nem mágnesezettségi összefüggésből származtatták. Célunk egy – a fent leírt perturbációelméleti alapokon nyugvó, nagy sűrűségen is érvényes – mágnesezettségi összefüggés megadása, amely a H →0 határesetben visszaadja a (2.18) egyenletet.

2.1. Irodalmi előzmények

2.2. Saját eredmények: mágnesezési tulajdonságok perturbációelméleti származtatása Az ω szerinti integrálok tanulmányozása során észrevettük, hogy azok a (2.27) egyenlettel megadott f

( )

ωi függvény sorfejtése nélkül is kiszámíthatóak analitikusan. Ez a módszer azonban a nagy terek tartományában divergenciát eredményez. Ennek kiküszöbölésére a Mayer-függvények egy speciális „normálását” vezettük be. Ennek megfelelően a klaszter-sorfejtést az

( ) ( ) (

^{exp cos}

)

¹

sinh

~

~fi = f i = α ϑi −

α

ω α ^(2.37)

függvények segítségével végeztük el. Ezek a függvények akkor definiálhatók a Ruelle-féle perturbációelméletben, ha a dipoláris merevgömbi referenciarendszer helyett egy speciális ún.

DHS+Langevin-modellen alapuló referenciarendszert vezetünk be. Ekkor a DHS részecskék külső térben vett energiája:

( )

^{N U}

(

^{N N}

) ( )

^{U N}

U r = 0 r ,ω + 1 ω , (2.38)

ahol U a merevgömbi és a dipoláris kölcsönhatásból származó energia, ₀ U₁ pedig a külső tér

energiajáruléka

( ( ) (

N

) )

N N

N ≡ r1^,r2^...r ^;ω ≡ ω1^,ω2^...ω

r . Az állapotösszeg így két tényezőre

szeparálható:

[ ( )

^N

]

^{N N}

[ (

^{N N}

) ] [ ( )

^N

]

N

Nd U d d U U

d

Z =

∫

^r ω exp−β ^r =

∫

^r ω exp−β 0 ^r ,ω exp−β 1 ω (2.39)

( )

[ ] ( )





 



−

−

=

∫ ∑

= N

i

i i N

N N

Nd U U

d

1 1

0 , exp

exp β ω β ω

ω ^r

r (2.40)

( )

[ ] ∏ [ ^{( )} ]

∫

=

−

−

= ^N

i

i i N

N N

Nd U U

d

1

1

0 , exp

exp β ω β ω

ω ^r

r .

(2.41)

A depolarizáció elkerülése végett a helykoordináták szerinti integrálok végtelen prolát ellipszoid alakú mintára értendők. Mivel U1i

( )

ωi =−mH^cosϑi, ezért:

( )

[ ] ∏ [ ]

∫

=

−

= ^N

i

i N

N N

Nd U

d Z

1

0 , exp cos

exp β ω α ϑ

ω ^r

r . (2.42)

Jelöljük a DHS fluidum állapotösszegét Z -val, az ideális Langevin-gáz állapotösszegét ₀ Z_L- el, ami:

( )

( )

^N

ZL = ^sinhα α . (2.43)

A (2.42) egyenlet mindkét oldalát elosztva Z₀ ⋅Z_L-el azt kapjuk, hogy:

( )

[ ]

( ) [ ]

∏

∫

=

= − ^N

i

i N

N N

N

L Z

d U Z d

Z Z

0 1 0 0

cos sinh exp

,

exp α ϑ

α ω α

ω β ^r

r . (2.44)