K
OVÁCSB
ÉLA,
M ATEMATIKA II.
2
II. T
ÖBBVÁLTOZÓS FÜGGVÉNYEKINTEGRÁLÁSA1. K
ettős INTEGRÁLLegyen f(x,y) a T tartományon nemnegatív kétváltozós függvény. Jelölje V azt a hengerszerű testet, amelyet alulról a z
= 0 sík, felülről a z = f(x, y) felület, oldalról a T határára emelt, a z tengellyel párhuzamos alkotójú hengerfelület zár közre (3.118. ábra). Ennek a hengerszerű testnek a térfogatát akarjuk meghatározni.
3.118. ábra
Kettős integrál téglalap tartomány felett
Próbáljuk megoldani a fenti feladatot amikor a T tartomány egy téglalap. Legyen az , , ,
egyenesek által határolt téglalap tartományon értelmezett z = f(x, y)
kétváltozós függvény sehol sem negatív, azaz minden esetén. Ebben az esetben a V azt a testet jelenti, amelyet alulról a z = 0 sík, felülről a z = f(x, y) felület, oldalról pedig az T határára emelt, a z tengellyel
párhuzamos , , , síkok határolnak, azaz:
Tehát a célunk a V térrész térfogatának meghatározása. Érdemes lesz bevezetni a
téglalap tartományra jelölést.
Az első lépés az lesz, hogy a T téglalapot felosztjuk kis téglalapokra úgy, hogy az intervallumot n egyenlő részre a intervallumot pedig m egyenlő részre osztjuk. Ebben az esetben a kis téglalapok hosszai
lesznek. Legyenek , , . Így a következő un. osztópontokat kapjuk:
illetve az ezeknek megfelelő zárt kis részintervallumok:
.
A téglalap tartományra bevezetett jelölés mintájára a kis téglalapokból néhányat felsorolunk:
...,
Ha mindet meg akarjuk adni, akkor indexes jelölést kell bevezetni a következőképpen:
ahol és
Tehát és egy ilyen kis téglalap területe
Ekkor a kis téglalapok oldalai párhuzamosak lesznek az x és az y koordinátatengelyekkel és ezek uniója egyenlő a T- vel.
Válasszunk ki minden egyes kis téglalapon belül egy tetszőlegesen választott
ún. kiszemelt helyet:
, ahol és
Közelítsük a z = f(x, y) kétváltozós függvény kis téglalap feletti térfogatot a következő módon:
.
Ez nem más mint az alapterületű magasságú hasáb térfogata. Számítsuk ki ezt térfogatot minden
egyes kis téglalap esetén majd adjuk őket össze:
ezt az összeget integrál közelítő összegnek vagy röviden csak közelítő összegnek nevezzük.
A közelítő összeg tehát a V térrész térfogatának egy közelítő meghatározása:
.
Azt várjuk, hogy ha a függvény elegendően sima (például ha folytonos), akkor minél finomabb a felosztás (n és m minél nagyobbak), annál pontosabban közelíti a közelítő összeg a V térrész térfogatát. Az integrál fogalmához (illetve a V térrész térfogatának pontos értékéhez) úgy juthatunk el, hogy a felosztást minden határon túl finomítjuk, azaz praktikusan n és m tartanak a végtelenhez. Ekkor az
közelítő összeg határértékét vizsgáljuk meg abban az esetben, amikor n és m tartanak a végtelenhez, jelben
és Tételezzük fel, hogy a V térrész térfogata létezik, ez tehát egy valós, jelen esetben pozitív, szám.
Adjunk meg egy tetszőlegesen kicsi pozitív valós számot. Ha minden számhoz létezik olyan N természetes szám (küszöbszámnak is szokás nevezni), hogy esetén
teljesül, bármilyen kiszemelt helyekkel számított közelítő összeg esetén, akkor azt mondhatjuk, hogy közelítő összeg határértéke létezik és esetén és ez egyenlő a valós számmal, ami nem más mint a V térrész térfogata.
Ezt szimbolikusan is jelölhetjük:
Másképpen is szokás ezt jelölni:
ha és .
Ezt a határértéket, ha létezik, akkor a z = f(x, y) kétváltozós függvény téglalap tartományon vett kettős integráljának nevezzük abban az esetben is, amikor nem kötjük ki az f(x, y) függvényről, hogy nem negatív. Lényegében a z = f(x, y) kétváltozós függvényről csak annyit kötünk ki, hogy a téglalap tartományon korlátos legyen (természetesen mindenhol értelmezve van). Ez azt jelenti, hogy létezik olyan pozitív szám amelyre teljesül az
feltétel minden esetén.
Definíció A téglalap tartományon értelmezett korlátos z = f(x, y) kétváltozós függvény kettős integrálján a
határértéket értjük, feltéve, hogy létezik.
Megjegyzés Ha és , vagyis a felosztást minden határon túl finomítjuk, akkor a kis téglalapok és oldalhosszai pedig zérushoz tartanak: Ez a korábbi és összefüggésekből következik. Így a kettős integrál definícióját másképpen is (az előzővel egyenértékű módon) is megadhatjuk.
Definíció A téglalap tartományon értelmezett korlátos z = f(x, y) kétváltozós függvény kettős integrálján a
határértéket értjük, feltéve, hogy létezik.
Sőt még egyszerúbbé tehetjük a fenti definíciót, ha bevezetjük a téglalap átmérőjének fogalmát, ami a legnagyobb mérete a téglalapnak, -vel fogjuk jelölni. Ez pontosan a téglalap átlójának hosszát jelenti.
Definíció A téglalap tartományon értelmezett korlátos z = f(x, y) kétváltozós függvény kettős integrálján a
határértéket értjük, feltéve, hogy létezik, ahol a kis téglalap átmérője.
Megjegyzés A későbbiek során szükségunk lesz tetszőleges korlátos részhalmaz átmérőjének fogalmára. Egy tetszőleges korlátos részhalmaz esetén definiálható a halmaz átmérője, ami röviden a halmaz legnagyobb méretét jelenti, feltéve ha létezik ilyen. Van amikor nem létezik ilyen. Tekintsünk egy egységnyi sugarú nyílt körlapot:
Ez az sík egy nyílt halmaza, ugyanis csak kör belső pontjai tartoznak a halmazhoz a körvonal nem. Vegyük a
számhalmaz maximális értékét minden pontok esetén, ez a maximum lenne az halmaz átmérője, ha létezne. Tudjuk, hogy nem minden valós számokból álló halmaznak létezik maximális eleme, illetve maximuma. Tekintsük például a nyílt intervallumot ennek nincs legnagyobb eleme (legkisebb sincs), hiszen az 1 nem a maximum, mert ez nem eleme a nyílt intervallumnak. Van azonban sok felső korlátja, sőt ezek között van legkisebb, ezt legkisebb felső korlátnak idegen szóval szuprenumnak nevezzük.
A lényeg az, bár ezt itt nem igazoljuk, hogy egy felülről korlátos, nem üres számhalmaznak mindig létezik legkisebb felső korlátja. Tehát a maximum szerepét a szuprenum veszi át, mert a szuprenum mindig létezik, szemben a maximummal amelyik esetleg nem. Az is igaz, hogy egy alulról korlátos, nem üres számhalmaznak mindig létezik legnagyobb alsó korlátja (infinuma).
Tehát a fenti számhalmaznak nem létezik maximális
értéke (ez azért van mert a körtartomány nyílt). De létezik a felső korlátjai között legkisebb (idegen szóval szuprénum), és ez az érték éppen kettővel egyenlő. Tehát:
Jordan-féle terület
Mielőtt általánosítanánk a kettős integrál fogalmát tetszőleges A tartományra, foglalkozzunk egy kicsit egy tetszőleges korlátos síkbeli halmaz területének definíciójával.
Nyilvánvaló, hogy egy téglalap területe , jelöljük ezt
vel: Egy halmaz korlátos, ha létezik olyan
téglalap tartomány amely lefedi t:
Külső terület
Definíció Legyen adott egy korlátos halmaz, amely nem üres . Fedjük le t véges számú téglalappal: Majd adjuk össze a lefedő téglalapok területeinek összegét, ekkor egy pozitív valós számot kapunk: Ha ezután az összes lehetséges lefedést tekintjük, akkor a lefedő téglalapok területeinek összege egy valós számokból álló halmazt eredményez:
Ekkor e számhalmaz legnagyobb alsó korlátját (infinumát) az halmaz külső területének nevezzük, jele:
Az utóbbi definícióban a legjobb ill. "leggazdaságosabb" lefedést szeretnénk megtalálni, feltéve hogy van ilyen. Nem mindig létezik ilyen. Tekintsünk például egy kört; ezt nem tudjuk véges számú téglalappal úgy lefedni, hogy a lefedő téglalapok területének összege pontosan megegyezzen a kör területével. Emiatt a kört lefedő téglalap rendszerekhez rendelt összegeknek nincs minimális értéke (ehhez az értékhez tartozó lefedő rendszer lenne a legjobb lefedő rendszer, de ilyen nincs), de az alsó korlátok között létezik legnagyobb (idegen szóval infinum), és ezt az értéket nevezzük a kör külső területének.
Megjegyzések:
1. Azért kell, hogy az halmaz korlátos legyen, hogy lefedhető legyen véges számú téglalappal.
2. A számhalmaz nem üres hiszen korlátos, tehát a korlátos halmaz
definíciója szerint van az t lefedő téglalap.
3. A számhalmaz alulról korlátos, hiszen csupa pozitív számból áll, így egy alsó korlátja például a nulla.
4. Egy korlátos (és nem üres) halmaznak létezik külső területe, mert az analízis egy alapvető tétele szerint egy nemüres, alulról korlátos valós számhalmaznak létezik infinuma.
Belső terület
Definíció Legyen adott egy korlátos halmaz, amely nem üres . Helyezzünk el ban véges számú olyan téglalapot, amelyek egymásba nem nyúlók (határuk lehet közös, de belső pontjuk nem):
, feltéve, hogy tartalmaz egyáltalán téglalapot. Majd adjuk össze a téglalapok területeinek összegét, ekkor egy pozitív valós számot kapunk: Ha ezután az összes lehetséges
összeget tekintjük, akkor a belső téglalapok területeinek összege egy valós számokból álló halmazt eredményez:
Ekkor e számhalmaz legkisebb felső korlátját (szuprénumát) az halmaz belső területének nevezzük, ha pedig nem tartalmaz egyetlen egy téglalapot sem, akkor a belső terület legyen nulla. A belső terület jele: . Megjegyzés:
Egy korlátos halmaz esetén, hasonlóan a külső területhez, a belső terület is mindig létezik. Valóban, ha nem tartalmaz egyetlen egy téglalapot sem tartalmaz, akkor a belső területet nulla, így ebben az esetben létezik az belső területe. Ha pedig
tartalmaz téglalapot, akkor a számhalmaz nem üres, és felülről korlátos
hiszen a külső terület egy felső korlátja a belső téglalapokhoz rendelt terület összegének. Így az analízis egy alapvető tétele szerint egy nemüres, felülről korlátos valós számhalmaznak létezik szuprénuma, tehát a belső terület is mindig létezik. Az is bizonyítható, hogy Azokat a halmazokat fogjuk mérhetőnek nevezni és területet rendelni hozzájuk, amelyek esetén a külső és a belső terület megeggyezik.
Definíció Egy korlátos halmazt akkor nevezünk mérhetőnek, ha , és ezt a közös értéket az halmaz területének nevezzük, amit val jelölünk:
Megjegyzés:
Megjegyezzük, hogy egy tartomány pontosan akkor mérhető, ha korlátos és a tartomány határa nulla területű.
PÉLDA
Példa
Tekintsünk egy három pontból álló halmazt a síkon: Memutatjuk, hogy ez
a halmaz mérhető és a területe nulla. A belső terület a definíció alapján nulla, hiszen nem helyezhető el benne téglalap: Vizsgáljuk meg az A halmaz külső területét.
Ez a három pont lefedhető akár egyetlen egy téglalappal is, de nem ez a lefedés a leggazdaságosabb. Sokkal érdemesebb három különböző kis téglalapot venni, és ezekkel külön-külön lefedni a három pontot. Sőt ezek a téglalapok lehetnek akár kis négyzetek is a oldalhosszúsággal. Ekkor a három négyzet területe: . Bármilyen kicsi négyzettől van kisebb olyan négyzet ami lefed egy pontot. Így ha a négyzetek oldalait minden határon túl csökkentjük, praktikusan határértéket vesszük, akkor a külső terület nulla lesz:
Más szóval a legnagyobb alsó korlát (infinum) zérus lesz. Tehát a külső és a belső terület megegyezik, vagyis A mérhető és a területe nulla:
Ezután szeretnénk a kettős integrált nemcsak téglalap tartomány esetén, hanem ettől általánosabb tartományra is definiálni. Legyen a tartomány, amin definiálni akarjuk az integrált, korlátos és mérhető.
Kettős integrál korlátos és mérhető tartományon
Az f kétváltozós függvény az A korlátos és mérhető tartományra vonatkozó kettős integrálján az
határértéket értjük (feltéve, hogy az létezik és véges). Itt az A tartomány egy olyan mérhető halmazokból álló felosztása, amelyek egymásba nem nyúlók (határuk lehet közös, de belső pontjuk nem) és uniójuk az
val egyenlő , a résztartomány területe, az átmérője,
pedig egy tetszőleges pontja.
A kettős integrál néhány tulajdonsága:
, c állandó;
;
Ha és , ekkor
;
Ha , ill. , akkor
, ill. .
Kettős integrál kiszámítása
A kettős integrál a 3.119., 3.120. és 3.121. ábrákon látható tartományok esetén az alábbi, ún kétszeres integrálokkal számítható ki:
A 3.119. ábrán látható téglalap tartomány esetén:
3.119. ábra
Tétel Legyen az kétváltozós függvény integrálható az , , , egyenesek
által határolt téglalap tartományon (3.119. ábra). Ekkor
; (7)
feltéve hogy a
integrál létezik minden esetén.
Természetesen az és az szerepe felcserélhető és adott feltételek mellett
.
A fenti feltételek teljesülnek például akkor, ha az kétváltozós függvény folytonos a téglalap tartományon.
Tétel Legyen az kétváltozós függvény folytonos a téglalap
tartományon (3.119. ábra). Ekkor
.
Hasonlóan az és az szerepének felcserélésével kimondhatjuk a következő tételt is.
Tétel Legyen az kétváltozós függvény folytonos a téglalap
tartományon (3.119. ábra). Ekkor
.
3.120. ábra
A 3.120. ábrán látható tartományt y-ra nézve normáltartománynak mondjuk, ha a és folytonosak az
intervallumban és teljesül minden esetén.
Tétel Legyen az kétváltozós függvény integrálható az , egyenesek és a és függvények által határolt normáltartományon (3.120. ábra). Ekkor
;
feltéve hogy a integrál létezik minden esetén.
3.121. ábra
A 3.121. ábrán látható tartományt x-re nézve normáltartománynak mondjuk, ha a és folytonosak az
intervallumban és teljesül minden esetén.
Tétel Bármely normáltartomány korlátos, zárt és mérhető.
Tétel Legyen az kétváltozós függvény integrálható az , egyenesek és a és függvények által határolt normáltartományon (3.121. ábra). Ekkor
. (8)
feltéve hogy a
integrál létezik minden esetén.
3.122. ábra
A 3.122. ábrán látható tartomány esetén, amikor a tartományt alulról az , felülről az görbe határolja,
; (9)
3.123. ábra
A 3.123. ábrán látható tartomány esetén, amikor a tartományt balról az , jobbról az görbe határolja,
. (10)
A kettős integrál kiszámításánál gyakran előnyös lehet a változók helyett új változókat bevezetni. Az (1) integrál kiszámításához alkalmazzuk az
(11)
helyettesítést. Ha ez a folytonosan differenciálható függvénypár kölcsönösen egyértelmű leképezést létesít a T (korlátos és zárt) tartomány és az (u, v) sík tartománya között, akkor
, (12)
ahol J az ún. Jacobi-determináns és
. (13)
Speciális eset, amikor az x és y változók helyett a poláris koordinátarendszer r, változóit vezetjük be az , (14)
formulákkal. Ekkor , és
. (15)
A (12) és (15) integrálok határainak megállapításához természetesen fel kell írni a tartományt határoló görbék egyenletét.
2. H
ÁRMASINTEGRÁLHármas integrál téglatest tartományon
Próbáljuk megoldani a következő feladatot. Legyen az , , , , , és a síkok által határolt (itt a,b,c,d,e és f valós számok, emelyekre teljesülnek az feltételek) téglatest tartományon értelmezett w = f(x, y, z) háromváltozós függvény sehol sem negatív, azaz minden esetén.
Legyen ennek a függvénynek a fizikai jelentése az anyag sűrűsége; köztudott, hogy a dimenziója . Bár a fizikában a sűrűséget -val szokták jelölni, mi nem használjuk ezt a jelölést. Abban az esetben ha az anyag sűrűsége állandó a teljes térfogaton (tehát a test minden pontjában azonos a sűrűség: ahol kostans), akkor könnyen ki tudjuk számítani a test tömegét, nevezetesen , ahol a téglatest térfogata. Érdemes
lesz bevezetni a téglatest tartományra a
jelölést.
Az első lépés az lesz, hogy a T téglatestet felosztjuk kis téglatestekre úgy, hogy az intervallumot n egyenlő részre, a intervallumot m egyenlő részre, a intervallumot pedig l egyenlő részre osztjuk. Ebben az esetben a kis téglatestek hosszai
lesznek. Legyenek , , , , Így a következő un. osztópontokat kapjuk
rendre az x, y, és a z tengely mentén:
illetve az ezeknek megfelelő zárt kis részintervallumok:
.
A téglatest tartományra bevezetett jelölés mintájára a kis téglatestekből néhányat felsorolunk:
, ...,
Ha mindet meg akarjuk adni, akkor indexes jelölést kell bevezetni a következőképpen:
ahol , és
Tehát és
egy ilyen kis téglatest térfogata Ekkor a kis téglatestek oldallapjai párhuzamosak lesznek az xy , yz és a xz koordináta síkokkal és ezek uniója egyenlő a V- vel.
Válasszunk ki minden egyes kis téglatesten belül egy
tetszőlegesen választott ún. kiszemelt helyet:
, ahol , és
Közelítsük a w = f(x, y, z) háromváltozós függvény (sűrűség függvény) pontbeli értékének a
segítségével a kis téglatest tömegét a következő módon:
.
Ez nem más mint az olyan térfogatú téglatest tömege amelynek minden pontjában állandó a sűrűsége. Az gondoljuk, hogy ha elég kicsi a térfogat, akkor ez a közelítés elég jó. Számítsuk ki ezt a
tömeget minden egyes kis téglatest esetén majd adjuk őket össze:
ezt az összeget integrál közelítő összegnek vagy röviden csak közelítő összegnek nevezzük.
A közelítő összeg tehát a V térrész tömegének egy közelítő meghatározása:
.
Azt várjuk, hogy ha a függvény elegendően sima (például ha folytonos), akkor minél finomabb a felosztás (n, m és l minél nagyobbak), annál pontosabban közelíti a közelítő összeg a V térrész tömegét. Az integrál fogalmához (illetve a V térrész tömegének pontos értékéhez) úgy juthatunk el, hogy a felosztást minden határon túl finomítjuk, azaz praktikusan n, m és l tartanak a végtelenhez. Ekkor az
közelítő összeg határértékét vizsgáljuk meg abban az esetben, amikor n,m és l tartanak a végtelenhez, jelben , és Tételezzük fel, hogy a V térrész tömege létezik, ez tehát egy valós, jelen esetben pozitív, szám. Adjunk meg egy tetszőlegesen kicsi pozitív valós számot. Ha minden számhoz létezik olyan N természetes szám (küszöbszámnak is szokás nevezni), hogy esetén
teljesül, bármilyen kiszemelt helyekkel számított közelítő összeg esetén, akkor azt mondhatjuk, hogy közelítő összeg határértéke létezik , és esetén, és ez egyenlő a valós számmal, ami nem más mint a V térrész tömege.
Ezt szimbolikusan is jelölhetjük:
Másképpen is szokás ezt jelölni:
ha , , .
Ezt a határértéket, ha létezik, akkor a z = f(x, y, z) háromváltozós függvény téglatest tartományon vett hármas integráljának nevezzük abban az esetben is, amikor nem kötjük ki az f(x, y,z) függvényről, hogy nem negatív.
Lényegében a w = f(x, y, z) háromváltozós függvényről csak annyit kötünk ki, hogy a V téglatest tartományon korlátos legyen (természetesen mindenhol értelmezve van). Ez azt jelenti, hogy létezik olyan pozitív szám amelyre teljesül az
feltétel minden esetén.
Definíció A téglatest tartományon értelmezett korlátos w =
f(x, y, z) háromváltozós függvény hármas integrálján a
határértéket értjük, feltéve, hogy létezik.
Megjegyzés:
Ha , és vagyis a felosztást minden határon túl finomítjuk, akkor a kis
téglalatestek , és oldalhosszai pedig zérushoz tartanak:
és Ez a korábbi , és összefüggésekből
következik. Így a hármas integrál definícióját másképpen is (az előzővel egyenértékű módon) is megadhatjuk.
Definíció A téglatest tartományon értelmezett korlátos w =
f(x, y, z) háromváltozós függvény hármas integrálján a
határértéket értjük, feltéve, hogy létezik.
Sőt még egyszerúbbé tehetjük a fenti definíciót, ha bevezetjük a téglatest
átmérőjének fogalmát, ami a legnagyobb mérete a téglatestnek, -vel fogjuk jelölni. Ez pontosan a téglatest
testátlójának hosszát jelenti.
Definíció A téglatest tartományon értelmezett korlátos w = f(x,
y, z) háromváltozós függvény hármas integrálján a
határértéket értjük, feltéve, hogy létezik. ahol a kis téglatest
átmérője.
Megjegyzés:
A későbbiek során szükségunk lesz tetszőleges korlátos részhalmaz átmérőjének fogalmára. Egy tetszőleges korlátos részhalmaz esetén definiálható a halmaz átmérője, ami röviden a halmaz legnagyobb méretét jelenti, feltéve ha létezik ilyen. Van amikor nem létezik ilyen. Tekintsünk egy egységnyi sugarú nyílt gömböt:
Ez az tér egy nyílt halmaza, ugyanis csak gömb belső pontjai tartoznak a halmazhoz a gömb felülete nem. Vegyük a
számhalmaz maximális értékét minden pontok esetén, ez a maximum lenne az halmaz átmérője, ha létezne. Tudjuk, hogy nem minden valós számokból álló halmaznak létezik maximális eleme, illetve maximuma.
Tekintsük például a nyílt intervallumot ennek nincs legnagyobb eleme (legkisebb sincs), hiszen az 1 nem a maximum, mert ez nem eleme a nyílt intervallumnak. Van azonban sok felső korlátja, sőt ezek között van legkisebb, ezt legkisebb felső korlátnak idegen szóval szuprenumnak nevezzük.
A lényeg az, bár ezt itt nem igazoljuk, hogy egy felülről korlátos, nem üres számhalmaznak mindig létezik legkisebb felső korlátja. Tehát a maximum szerepét a szuprenum veszi át, mert a szuprenum mindig létezik, szemben a maximummal amelyik esetleg nem. Az is igaz, hogy egy alulról korlátos, nem üres számhalmaznak mindig létezik legnagyobb alsó korlátja (infinuma).
Tehát a fenti szám halmaznak nem
létezik maximális értéke (ez azért van mert a gömbtartomány nyílt). De létezik a felső korlátjai között legkisebb (idegen szóval szuprénum), és ez az érték éppen kettővel egyenlő. Tehát:
Jordan-féle térfogat
Mielőtt általánosítanánk a hármas integrál fogalmát tetszőleges A térbeli tartományra, foglalkozzunk egy kicsit egy tetszőleges korlátos térbeli halmaz térfogatának definíciójával.
Nyilvánvaló, hogy egy téglatest térfogata
, jelöljük ezt vel: Egy halmaz korlátos ha
létezik olyan téglatest tartomány amely lefedi t:
Külső térfogat
Definíció Legyen adott egy korlátos halmaz, amely nem üres . Fedjük le t véges számú téglatesttel: Majd adjuk össze a lefedő téglatestek térfogatainak összegét, ekkor egy pozitív valós számot kapunk: Ha ezután az összes lehetséges lefedést tekintjük, akkor a lefedő téglatestek térfogatainak összege egy valós számokból álló halmazt eredményez:
Ekkor e számhalmaz legnagyobb alsó korlátját (infinumát) az halmaz külső térfogatának nevezzük, jele:
Megjegyzések:
1. A számhalmaz nem üres hiszen korlátos, tehát a korlátos halmaz definíciója szerint van az t lefedő téglatest.
2. A számhalmaz alulról korlátos, hiszen csupa pozitív számból áll, így egy alsó korlátja például a nulla.
3. Egy korlátos (és nem üres) halmaznak létezik külső térfogata, mert az analízis egy alapvető tétele szerint egy nemüres, alulról korlátos valós számhalmaznak létezik infinuma.
Belső térfogat
Definíció Legyen adott egy korlátos halmaz, amely nem üres . Helyezzünk el ban véges számú olyan téglatestet, amelyek egymásba nem nyúlók (határuk lehet közös, de belső pontjuk nem):
, feltéve, hogy tartalmaz egyáltalán téglatestet. Majd adjuk össze a téglatestek térfogatainak összegét, ekkor egy pozitív valós számot kapunk: Ha ezután az összes lehetséges esetet tekintjük, akkor a belső téglatestek térfogatainak összege egy valós számokból álló halmazt eredményez:
Ekkor e számhalmaz legkisebb felső korlátját (szuprénumát) az halmaz belső térfogatának nevezzük, ha pedig nem tartalmaz egyetlen egy téglatestet sem, akkor a belső térfogat legyen nulla. A belső térfogat jele: . Megjegyzés:
Egy korlátos halmaz esetén, hasonlóan a külső térfogathozz, a belső térfogat is mindig létezik. Valóban, ha nem tartalmaz egyetlen egy téglatestet sem tartalmaz, akkor a belső térfogat nulla, így ebben az esetben létezik az belső
térfogata. Ha pedig tartalmaz téglatestet, akkor a számhalmaz nem
üres, és felülről korlátos hiszen a külső térfogat egy felső korlátja a belső téglalapokhoz rendelt térfogat összegének. Így az analízis egy alapvető tétele szerint egy nemüres, felülről korlátos valós számhalmaznak létezik szuprénuma, tehát a belső térfogat is mindig létezik. Az is bizonyítható, hogy Azokat a halmazokat fogjuk mérhetőnek nevezni és térfogatot rendelni hoozájuk, amelyek esetén a külső és a belső térfogat megeggyezik.
Definíció Egy korlátos halmazt akkor nevezünk mérhetőnek, ha , és ezt a közös értéket az halmaz térfogatának nevezzük, amit val jelölünk:
Hármas integrál korlátos és mérhető térfogaton
Definíció Az f háromváltozós függvény A korlátos mérhető tartományra vonatkozó hármas integrálján az
határértéket értjük (feltéve, hogy az létezik és véges). Itt az A térbeli tartomány egy olyan mérhető halmazokból álló felosztása, amelyek egymásba nem nyúlók (határuk lehet közös, de belső pontjuk nem) és uniójuk
az val egyenlő , a résztartomány térfogata, az
átmérője, pedig egy tetszőleges pontja.
A továbbiakban a hármas integrál integrálási tartományát inkább V–vel fogjuk jelölni az A helyett.
A hármas integrál kiszámítása
A hármas integrál kiszámítása három határozott integrál egymás utáni kiszámításával történhet. Ha a (térbeli) V tartományt alulról a , felülről a felületek, oldalról például a 3.122. ábrán vázolt T síkbeli tartomány határgörbéjére emelt, a z tengellyel párhuzamos alkotójú hengerfelület határolja, akkor
.
Új változók bevezetése a hármas integrál kiszámításánál is lehetséges. Legyen x x(u, v, w), , z z(u, v, w).
Ekkor
ahol J az ún. Jacobi-determináns, és
.
Hengerkoordináták bevezetése esetén . Ekkor
.
Gömbi koordináták esetén
.
Itt r a (térbeli) P pont origótól való távolsága vagyis az OP szakasz hossza, az OP szakasznak az (x, y)-síkkal bezárt szöge (a magassági szög), pedig az OP szakasz (x, y) -síkon vett vetületének az x tengely pozitív felével bezárt szöge. Ekkor
.
3. M
INTAPÉLDÁKMegoldások: láthatók nem láthatók Számítsuk ki az alábbi függvények kettős integrálját a megadott tartományokon:
1. f(x, y) xy, , ;
.
Itt az integrálás határai állandók (téglalap tartomány esete), ezért az integrálás sorrendje felcserélhető:
.
2. f(x, y) x sin y, , ;
.
3. g(x, y) 1, , ;
.
4. , , ;
.
5. f(x, y) x, , ;
.
6. , , ;
.
7. , ;
Megoldás. Az integrációs tartomány az körlap (3.124. ábra).
3.124. ábra
Az integrál kiszámításához célszerű polárkoordinátákat bevezetni. A (14) szerint
, és J = r.
Az origó középpontú, egységsugarú körvonal polárkoordinátás egyenlete r = 1. Ezeket felhasználva, a (15) alapján
.
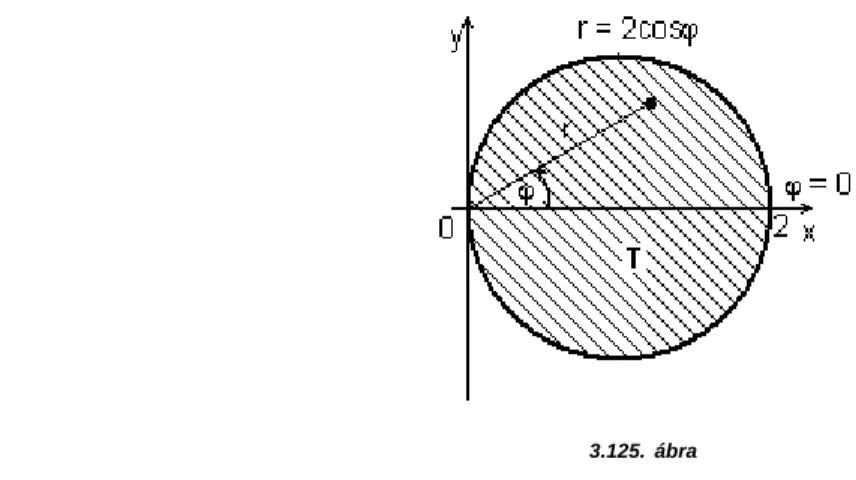
8. f(x, y) 1, ;
Megoldás. Az integrációs tartomány az azaz
körlap (3.125. ábra).
3.125. ábra
Itt is célszerű polárkoordinátákat bevezetni. A körvonal polárkoordinátás egyenlete
, azaz .
Az ábrán látható, hogy és . Tehát
.
9. Számítsuk ki az f(x, y) = xy függvény T tartományra vonatkozó kettős integrálját, ha T az , ,
és y = 2x görbék (vonalak) által határolt tartomány (3.126. ábra).
3.126. ábra
Megoldás. A T tartományt határoló , ill. görbék az görbesereg elemei u =
1, ill. u = 3 esetére. A másik két határoló vonal, az és y = 2x egyenes az
egyenessereg két eleme v = 1/2 és v = 2 esetére. Vezessünk be tehát új változókat az és y
= vx egyenletekkel. Innen x és y kifejezhető az u és v új változókkal. Így a (11) -nek megfelelő
egyenletek
, .
A Jacobi-determináns:
.
Ezzel a leképezéssel a T tartomány kölcsönösen és egyértelműen képezhető le az (u, v) koordinátarendszerben lévő , téglalapra. A kérdéses integrál a (12) szerint:
.
Megjegyezzük, hogy ez az integrál "hagyományos" módon is kiszámítható, csak ekkor a T tartományt alkalmas módon fel kell darabolni. Így az integrál a következőképpen számítható:
.
Cseréljük fel az integrálások sorrendjét a következő integrálokban:
10. ;
Megoldás. Az integrációs tartomány a 3.127. ábrán látható.
3.127. ábra
A példaként felírt integrálban először y szerint kell integrálni az "alsó görbétől a felső görbéig", azaz
a parabolától az egyenesig. Ez a sorrend jelen esetben csak úgy cserélhető fel, ha a tartományt két részre bontjuk az ábra szerinti módon. A csere folytán a résztartományon először a bal oldali parabolaívtől a jobb oldali parabolaívig kell integrálni (x szerint), a résztartományon pedig a bal oldali parabolaívtől az egyenesig. Az parabola bal oldali, ill. jobb oldali ívének
egyenlete ill. . Így az új integrál:
.
11. ;
Megoldás. A tartomány a 3.128. ábrán látható.
3.128. ábra
A tartomány bal oldali határa az görbe, jobb oldali határa az x = e egyenes. Az új integrál:
.
12. .
Megoldás. Ha , akkor a 3.129. ábrán látható tartományt bal oldalról az , jobb oldalról az görbe határolja.
3.129. ábra
Így az új integrál:
.
13. Számítsuk ki az kettős integrált, ha a T tartomány az körlap.
Megoldás. Számítsuk ki előbb az függvény integráját, ha a tartomány az első síknegyedben lévő negyed körlap. Polárkoordinátákat vezetve be,
.
A második síknegyedben . Itt az integrál
.
Ugyanezt az eredményt kapjuk a harmadik és a negyedik síknegyedben is. Az eredeti integrál értéke
tehát .
A szimmetriákból egyébként is következik, hogy mindegyik síknegyedben az integrál értéke ugyanaz.
Számítsuk ki az alábbi hármas integrálokat:
14. , ahol a V tartományt a z = x y, y = x, x = 1, z = 0 felületek zárják közre;
Megoldás. Először z szerint, majd y szerint, végül x szerint kell integrálni. A V tartományt alulról a z = 0 sík, felülről a z = xy felület, oldalról pedig az y = x és x = 1 síkok határolják. Ez utóbbi két sík párhuzamos a z tengellyel. A z = xy felület (nyeregfelület) a z = 0 síkot az x tengelyben és az y tengelyben metszi. A V tartomány z = 0 síkra való vetülete a 3.130. ábrán látható.
Tehát
.
15. , ahol , , ;
.
16. , ha ;
Megoldás. A V tartomány origó központú, a sugarú gömbtest. Célszerű gömbi koordinátákat bevezetni. A (23) szerint
, , , .
Ekkor és az integrál:
.
Az integrálás határai állandók, ezért tetszőleges sorrendben lehet integrálni. Tehát
.
17. , ahol V az és a z = 1 felületekkel
határolt tartomány.
Megoldás. A V tartomány olyan forgáskúptest, amelynek csúcsa az origó, forgástengelye a z tengely, fedőlapja a z = 1 magasságban lévő egységsugarú körlap (középpontja a z tengelyen van). Célszerű hengerkoordinátákat bevezetni
, , , .
Ekkor , a kúpfelület egyenlete , azaz z = r. Az integrál:
.
4. F
ELADATOKAlakítsa át az kettős integrált kétszeres integrállá úgy, hogy először y szerint történjen az integrálás, majd fordítva, ha a T tartomány az alábbi:
1. y = , y = 1 + x és y = 0 egyenesek által közrezárt háromszög(lap);
2. félkörlap;
3. és parabolaszelet;
4. görbe íve és az x tengely által közrezárt síkidom.
5. Cserélje fel az integrálás sorrendjét az alábbi integrálban:
.
Számítsa ki az alábbi függvények kettős integrálját a megadott tartományokon:
6. , T az y = x, y = x + a, y = a és y = 3a egyenesek által határolt paralelogramma;
7. f(x, y) = x, , .
8. f(x, y) = x + y, ha T az , x + y = 4, x + y = 12 görbékkel határolt tartomány.
9. , ahol T az parabola és az egyenes által közrezárt síkrész (p > 0);
10. , ha T a , téglalap;
11. , ha T az és y = 2 görbék által határolt síkidom;
12. , ahol a T tartományt az xy = 1, görbék határolják.
Polárkoordináták bevezetésével számítsa ki az alábbi függvények kettős integrálját:
13. , , félkörlap;
14. f(x, y) = x, körlap;
15. f(x, y) = , körgyűrű;
16. , , háromszög(lap);
17. , , téglalap.
Új változók bevezetésével számítsa ki az alábbi kettős integrálokat, ahol a T tartományt a megadott görbék határolják:
18. , x + y = a, x + y = b, , , (0 < a < b, );
19. , , , y = x, y = 2x , (x > 0, y > 0);
20. , , , , ;
Számítsa ki az alábbi hármas integrálokat:
21. ;
22. , ha a V tartományt a z = sík, a z = 0 sík és az parabolikus henger zárja közre;
23. , ahol V az x + y + z = a (a > 0) sík és a koordinátasíkok által határolt tartomány.
24. , ha V határai a z = xy, x + y = 1, z = 0 felületek.
Hengerkoordináták bevezetésével számítsa ki az alábbi hármas integrálokat:
25. ;
26. , ahol V az , félgömbtest.
Gömbi koordináták bevezetésével számítsa ki az alábbi hármas integrálokat:
27. ;
28. , ahol V az , félgömbtest;
29. , ahol V az , , , nyolcadgömbtest;
30. , ahol V az felülettel határolt tartomány.
Megoldások
1. A T tartomány a 3.131. ábrán látható.
A bal oldali, ill. jobb oldali határvonal egyenlete (x -re kifejezve) x = , ill. x = . Így
.
2. Az egyenletből a bal-, ill. jobb oldali határgörbe egyenlete , ill.
(3.132. ábra).
Ezeket felhasználva,
.
3. Az parabola és az y = 1 metszéspontjainak abszcisszái x = és x = 1. A bal-, ill. jobb oldali határgörbe egyenlete , ill. , így
.
4. Itt a bal oldali határgörbe egyenlete , a jobb oldalié (3.133. ábra).
.
5. A T tartomány az körlap jobb oldali fele. A jobb oldali körvonal egyenlete . Így
.
6. Az integrációs tartomány a 3.134. ábrán vázolt paralelogramma.
Célszerű előbb x szerint integrálni.
.
7. Az integrálás tartománya az , felső félkörlap.
.
A feladat egyszerűbben oldható meg polárkoordináták bevezetésével. Elvégezve az , helyettesítést és figyelembe véve, hogy J = r,
.
8. A tartomány a 3.135. ábrán látható.
Ez alapján
.
9. Tekintsük a 3.136. ábrát.
.
10. .
11. A tartomány a 3.137. ábrán látható
3.137. ábra
.
3.138. ábra
A 3.138. ábrát felhasználva,
.
13. A tartomány a 3.132. ábrán látható.
.
14. A tartomány egy a/2 sugarú körlap. A körvonal polárkoordinátás egyenlete (l. a 8. mintapéldát és a 3.125. ábrát). Kihasználva, hogy J = r,
.
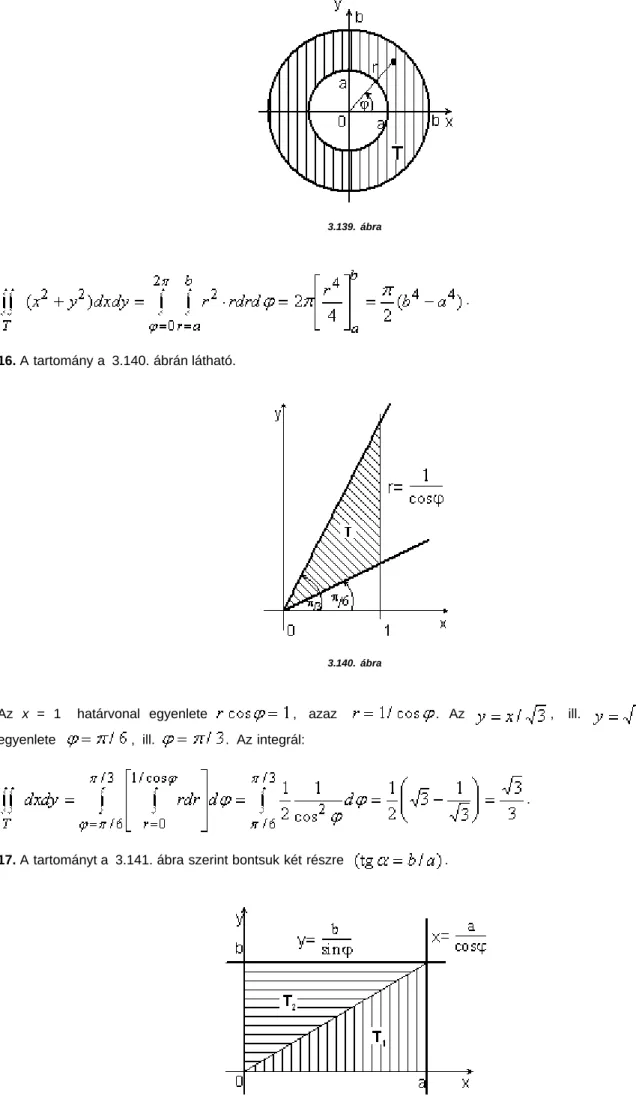
15. A tartomány a 3.139. ábrán látható.
3.139. ábra
.
16. A tartomány a 3.140. ábrán látható.
3.140. ábra
Az x = 1 határvonal egyenlete , azaz . Az , ill. egyenes
egyenlete , ill. . Az integrál:
.
17. A tartományt a 3.141. ábra szerint bontsuk két részre .
3.141. ábra
Így
.
18. Az x + y = u, y = vx egyenlőségekkel vezessünk be új változókat (3.142. ábra).
3.142. ábra
Innen
, ; ,
.
19. Az xy = u, y = vx egyenlőségekkel vezessünk be új változókat. Ekkor
, ; , és
.
20. Az , egyenlőségekkel új változót vezetve be,
, ; .
.
21.
.
22. A V térbeli tartományt a 3.143. ábrán vázoltuk.
3.143. ábra
Innen leolvashatók az integrálás határai.
.
23. A 3.144 ábra alapján
3.144. ábra
.
24. A 3.145 ábra alapján
3.145. ábra
.
25. A V (térbeli) tartomány a 3.146. ábrán látható.
3.146. ábra
Hengerkoordináták esetén , , és J = r.
.
26. Hengerkoordináták esetén , , z = z, és így az gömbfelület
egyenlete , a felső félgömbfelület egyenlete pedig .
.
27. Gömbi koordináták esetén
, , , .
A V tartományt egy origó középpontú, sugarú gömbfelület és egy z tengelyű körkúpfelület zárja közre a féltéren. A (z, x) -síkkal való metszete a 3.147. ábrán látható.
3.147. ábra
.
28. Gömbi koordináták esetén .
.
29. Gömbi koordináták esetén , .
.
30. A felület egyenlete kis átalakítással . Innen látszik, hogy M(0;0;1) középpontú, egységsugarú gömbfelületről van szó. Vezessünk be új változókat az
, ,
egyenlőségekkel . Itt , így
.
5. A
KettősÉSHÁRMASINTEGRÁL ALKALMAZÁSAIA (x, y) - síkon lévő T tartomány területe
. (1)
Legyen f a T tartományon nemnegatív függvény. Jelölje V azt a hengerszerű testet, amelyet alulról a z = 0 sík, felülről a z = f(x, y) felület, oldalról a T határára emelt, a z tengellyel párhuzamos alkotójú hengerfelület zár közre (3.148. ábra).
3.148. ábra
Ennek a hengerszerű testnek a térfogata
. (2)
A 3.148. ábrán látható F felületdarab felszíne:
. (3)
Ha a felület egyenlete vektorosan van megadva módon, akkor
. (4)
A sűrűségű T lemez tömege:
. (5)
Ha a lemez homogén, akkor .
Ugyanennek a lemeznek az x, ill. y tengelyre vonatkozó elsőrendű (statikai) nyomatéka:
, ill. (6)
súlypontjának koordinátái pedig:
, . (7)
Ugyanennek a lemeznek az x és y tengelyekre, ill. origóra vonatkozó másodrendű (tehetetlenségi, inercia) nyomatéka:
, , ill. . (8)
A 3.148 ábrán vázolt hengerszerű test térfogata:
. (9)
Ha a V térrész sűrűsége , akkor annak tömege:
. (10)
Ha a térrész homogén, akkor .
Ugyanennek a testnek az (y, z), (x, z), ill. (x, y) síkra vonatkozó elsőrendű (statikai) nyomatéka:
, , ill. , (11)
súlypontjának koordinátái pedig:
, , . (12)
Ugyanennek a testnek az x, y, z tengelyekre, ill. origóra vonatkozó másodrendű (tehetetlenségi, inercia) nyomatéka:
, ,
, ill. . (13)
6. M
INTAPÉLDÁKMegoldások: láthatók nem láthatók Számítsuk ki az alábbi görbékkel határolt tartományok (síkidomok) területét:
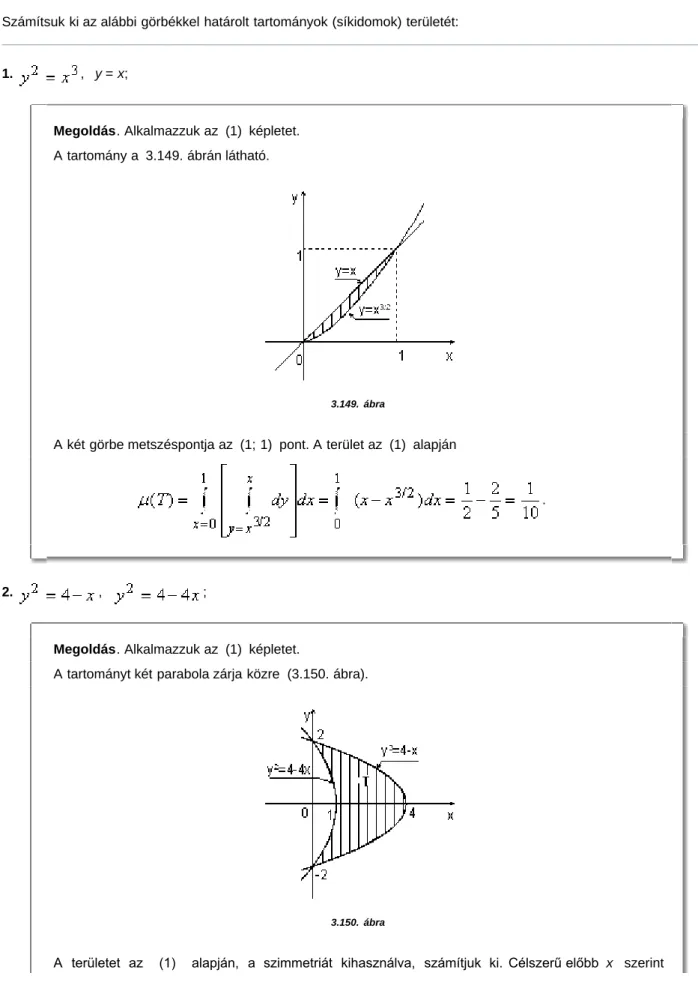
1. , y = x;
Megoldás. Alkalmazzuk az (1) képletet.
A tartomány a 3.149. ábrán látható.
3.149. ábra
A két görbe metszéspontja az (1; 1) pont. A terület az (1) alapján
.
2. , ;
Megoldás. Alkalmazzuk az (1) képletet.
A tartományt két parabola zárja közre (3.150. ábra).
3.150. ábra
A területet az (1) alapján, a szimmetriát kihasználva, számítjuk ki. Célszerű előbb x szerint
integrálni.
.
3. y = ln x, x = 1, y = ;
Megoldás. Alkalmazzuk az (1) képletet.
Az (1) képletet alkalmazva, célszerű először x szerint integrálni, amint az a 3.151. ábrán látható.
3.151. ábra
.
4. r = 2, , r és poláris koordináták;
Megoldás. Alkalmazzuk az (1) képletet.
A 3.152. ábrán látható, hogy a tartomány szimmetrikus a tengelyre.
Ezt a szimmetriát célszerű kihasználni. A két görbe (kör és kardioid) metszéspontjainak meghatározására megoldjuk a
egyenletet. A szóbajöhető gyökök: és . Az (1) kettős integrált polárkoordináták bevezetésével számítjuk ki. A r koordináta a körtől (2 -től) a kardioidig változik.
.
5. ;
Megoldás. Alkalmazzuk az (1) képletet.
Írjuk fel a görbe polárkoordinátás egyenletét:
.
Ez lemniszkáta (3.63. ábra). A szimmetria miatt elegendő a tartomány első síknegyedben lévő részét kiszámítani, majd ezt néggyel szorozni.
.
6. xy = 1, xy = 8, , ;
Megoldás. Alkalmazzuk az (1) képletet.
A tartomány a 3.152.a. ábrán látható.
Vezessünk be új változókat az xy = u,
egyenlőségekkel. Innen
, , .
.
7. ;
Megoldás. Alkalmazzuk az (1) képletet.
Vezessünk be polárkoordinátákat. A görbe (kör) egyenlete . Területe:
.
8. .
Megoldás. Alkalmazzuk az (1) képletet.
Ellipszis területéről van szó (3.153. ábra).
Vezessünk be új változókat (elliptikus koordinátákat) az ,
egyenlőségekkel. Ekkor , és az ellipszis új egyenlete:
.
Területe:
.
Számítsuk ki az alábbi felületekkel határolt testek (hengerszerű testek) térfogatát:
9. z = 1 + x + y, z = 0, x + y = 1, x = 0, y = 0;
Megoldás . Alkalmazzuk a (2) képletet.
3.154. ábra
A test a 3.154. ábrán vázolt tartomány fölött, a z = 0 sík és a z = f(x, y) = 1 + x + y sík között van. Térfogata a (2) szerint
.
10. , z = 0, , y = 1;
Megoldás . Alkalmazzuk a (2) képletet.
A test a 3.155. ábrán látható tartomány fölött, és a paraboloid alatt helyezkedik el.
3.155. ábra
Térfogata (a szimmetriát kihasználva):
.
11. x + y + z = 2a, z = 0, ;
Megoldás . Alkalmazzuk a (2) képletet.
A testet a z = 0, a z = f(x, y) = 2a síkok és az henger zárják közre.
Alaptartomány az körlap (3.156. ábra).
3.156. ábra
Célszerű polárkoordinátákat bevezetni. Ekkor
, , J = r ,
a felület egyenlete pedig . A térfogat:
= itt célszerű előbb szerint integrálni =
.
Itt kihasználtuk azt, hogy .
12. ;
Megoldás . Alkalmazzuk a (2) képletet.
A a sugarú gömb térfogatát kell kiszámítani. A szimmetriát kihasználva, a
felső félgömb felület alatti (és a z = 0 sík fölötti) test térfogatát számítjuk és azt szorozzuk 2 -vel.
Az alaptartomány az körlap (3.156. ábra). Polárkoordinátákat használva, a térfogat:
.
13. , z = 0, .
Megoldás . Alkalmazzuk a (2) képletet.
A forgásparaboloid és a z = 0 sík közötti térrész térfogatát kell kiszámítani,
alaptartomány az körlap (3.156. ábra). Polárkoordinátákat vezetve be, a térfogat:
.
Számítsuk ki az alábbi felületdarabok felszínét:
14. , ha , ;
Megoldás. Használjuk a (3) képletet. Mivel , ezért
, , .
A felszín:
.
Itt azt használtuk ki, hogy értéke a T tartomány területével egyenlő. Mivel a tartomány az , körlap, ennek területe .
15. z = xy, ha ;
Megoldás . Alkalmazzuk a (3) képletet.
Ha , akkor , és így a (3) képlet szerint, polárkoordinátákat vezetve be,
.
16. , , , h állandó;
Megoldás . Alkalmazzuk a (3) képletet.
A felület vektorosan van megadva, ezért a (4) képletet fogjuk használni.
, ,
.
A felszín:
.
Számítsuk ki az alábbi görbékkel határolt homogén síkidomok súlypontjának koordinátáit.
17. , x + y = 2;
Megoldás Először kiszámítjuk a síkidom (lemez) (3.157. ábra) tömegét.
Mivel a lemez homogén, ezért . Az (5) képlet szerint a tömeg (jelen esetben terület):
A statikai nyomatékokat a (6) képletekkel számítjuk:
,
A súlypont koordináti a (7) képletekkel:.
, .
18. , x = 0, y = 0, , ;
Megoldás Itt egy negyedkörlap (lemez) súlypontját kell meghatározni (3.158. ábra).
A szimmetria miatt . A lemez tömege, azaz területe .
A görbe egyenlete (felső félkörív!), . A (6) képlet szerint
.
A súlypont koordinátái a (7) szerint .
19. , , y = 0, .
Megoldás A síkidom a 3.159. ábrán látható lemez, amelyet felülről egy ciklois ív határol.
A szimmetria miatt a súlypont abszcisszája . A lemez tömege, azaz a síkidom területe az (5) szerint :
.
Itt alkalmaztuk az helyettesítést.
Az x tengelyre vonatkozó statikai nyomaték a (6) szerint
.
A súlypont koordinátái: .
20. Számítsuk ki az és y = 1 görbék által közrezárt síkidom (lemez) súlypontjának a koordinátáit, ha a) ; b) .
Megoldás. A síkidom a 3.155. ábrán látható. A szimmetria miatt a súlypont abszcisszája mindkét
esetben: .
a) A lemez tömege :
.
Az x tengelyre vonatkozó statikai nyomaték:
.
A súlypont ordinátája: .
b) A lemez tömege
.
Az x tengelyre vonatkozó statikai nyomaték:
.
A súlypont ordinátája: .
21. Számítsuk ki az , homogén félkörlemez koordinátatengelyekre és az origóra vonatkozó tehetetlenségi nyomatékát.
Megoldás. Alkalmazzuk a (8) képleteket, mellett. Célszerű poláris koordinátákat bevezetni.
,
,
.
Számítsuk ki hármas integrállal az alábbi felületekkel határolt testek térfogatát:
22. , z = 0, x = 0, x = 3, y = 0, y = 2;
Megoldás. Alkalmazzuk a (9) képletet.
A test a , téglalap "fölött" helyezkedik el.
.
23. , z = x + y + 2, y = 0, y = 1, x = 0, x = 2;
Megoldás. Alkalmazzuk a (9) képletet.
A testet (hasábot) alulról ill. felülről a ill. síkok határolják. Az (x, z) –sikon lévő oldallapja a 3.160. ábrán látható.
3.160. ábra
Alaptartomány a , téglalap. A térfogat:
.
24. z = xy + 10, z = 0, ;
Megoldás. Alkalmazzuk a (9) képletet.
A test a z = 0 sík és a z = xy + 10 nyeregfelület között helyezkedik el. Alaptartomány az körlap. Vezessünk be hengerkoordinátákat. Ekkor
, , z = z, J = r.
A felület egyenlete: . A térfogat:
.
25. , z = 0;
Megoldás. Alkalmazzuk a (9) képletet.
A testet a z = 0 sík és a paraboloid határolja. A (z, x) - síkkal való metszete a 3.161. ábrán látható.
3.161. ábra
Hengerkoordinátákat alkalmazva, a térfogat:
.
26. , z = 1;
Megoldás. Alkalmazzuk a (9) képletet.
A test a forgási paraboloid és a z = 1 sík közé esik. A (z, x)- síkkal való metszete a 3.162. ábrán látható.
3.162. ábra
A két felület metszetgörbéje az kör, amely a z = 1 síkon van. Hengerkoordinátákat alkalmazva, a térfogat:
.
27. ;
Megoldás. Alkalmazzuk a (9) képletet.
Az a sugarú gömb térfogatáról van szó. A "felső" félgömb térfogatát számítjuk, majd ezt szorozzuk 2 -vel.
a) Hengerkoordinátákat használva, a gömbfelület egyenlete: .
Alaptartomány az origó közepű, a sugarú körlap. A térfogat:
.
b) Gömbi koordinátákat használva,
, , , .
A térfogat:
.
28. .
Megoldás. Alkalmazzuk a (9) képletet.
Vezessünk be új változókat a következőképpen:
, , .
Ekkor , a felület (ellipszoid) egyenlete pedig r = 1. A térfogat:
.
29. Számítsuk ki a forgásparaboloid és z = 4 sík által közrezárt homogén test súlypontjának koordinátáit.
Megoldás. Mivel forgástestről van szó (forgástengely a z tengely), ezért a súlypont rajta van a z tengelyen. Így . A harmadik koordináta ( ) kiszámításához használjuk a (12) képletek közül a harmadikat. Hengerkoordinátákat használva, a test tömege a (10) szerint :
.
Az (x, y) - síkra vonatkozó statika nyomaték a (11) szerint:
.
A súlypont koordinátája: .
30. Számítsuk ki az , , , homogén nyolcadgömbtest koordinátatengelyekre és az origóra vonatkozó tehetetlenségi nyomatékát.
Megoldás. A koordinátatengelyekre vonatkozó nyomatékok egyenlők, tehát elegendő az egyiket kiszámítani. Számítsuk ki a z tengelyre vonatkozót. Gömbi koordinátákat használva, a (13) szerint
.
Az origóra vonatkozó nyomaték:
.
7. F
ELADATOKSzámítsa ki kettős integrállal az alábbi görbékkel határolt tartományok (síkidomok) területét:
1. , ;
2. xy = 4, y = x, x = 4;
3. y = sin x, y = cos x, ;
4. , ;
5. , , x = 4;
6. ;
7. , ( ), , ;
8. , , y = 0, ; x = ln 5;
9. ;
10. , ;
11. y = ax, y = bx, , , ).
Számítsa ki kettős integrállal az alábbi felületek által határolt testek térfogatát:
12. , , ;
13. , , , , , ;
14. , , , , ;
15. , , , , ;
16. , ;
17. , , ( );
18. ;
19. , ;
20. , ( ).
Számítsa ki az alábbi felületdarabok felszínét:
21. , ;
22. , ;
23. , ;
24. , , ;
25. , ;
26. .
Számítsa ki az alábbi görbékkel határolt homogén lemezek (síkidomok) súlypontjának koordinátáit:
27. , , ;
28. , , .
Számítsa ki az alábbi görbékkel határolt homogén lemezeknek (síkidomoknak) a koordináta tengelyekre vonatkozó tehetetlenségi nyomatékát:
29. , , ;
30. ;
31. , , x = 2y, 2x = y (x > 0, y > 0) .
Számítsa ki hármas integrállal az alábbi felületek által határolt testek térfogatát:
32. , , , , , ;
33. , , , ;
34. , ;
35. , , ;
36. z = xy, z = x + y, x + y = 1, x = 0, y = 0;
37. , ;
38. , ;
39. , , , .
Számítsa ki az alábbi felületekkel határolt homogén testek súlypontjának koordinátáit:
40. , , ;
41. x + y + z = a, , , ;
42. , , .
43. Számítsa ki a , , egységkocka tömegét, ha a P(x, y, z) pontban a sűrűség:
.
Számítsa ki az alábbi felületekkel határolt homogén testeknek a koordinátatengelyekre vonatkozó tehetetlenségi nyomatékát:
44. , , , , , ;
45. , , .
46. Számítsa ki az homogén gömbtest origóra vonatkozó tehetetlenségi nyomatékát.
Megoldások
1. A tartomány a 3.163. ábrán látható.
Területe
.
2. A 3.164. ábrát felhasználva,
3. A 3.165. ábra szerint
.
4. A tartományt egy parabola és egy egyenes határolja (3.166. ábra).
.
5. A 3.167. ábra alapján
.
6. A tartomány a 3.168. ábrán látható.
Vezessünk be (általánosított) polárkoordinátákat az ,
egyenlőségekkel. Ekkor . A terület:
.
A tartomány a 3.169. ábrán látható.
Polárkoordinátákat felhasználva,
.
8. A 3.170. ábra alapján, a szimmetriát kihasználva,
.
9. Polárkoordinátákra áttérve, a görbe egyenlete: . Ez egy lemniszkáta (3.171. ábra).
Területe:
.
10. A 3.172. ábrán látható kardioid és kör közötti síkidom területét kell kiszámítani:
.
11. Vezessünk be új változókat az y = ux és egyenlőségekkel. Innen , , .
A négy görbe által közrezárt síkidom (3.173. ábra) területe:
.
12. A z = 0 sík, a z = 10 sík és az parabolikus henger közötti test (3.174. ábra) térfogata:
.
13. Az alaptartomány a , téglalap.
.
14. Alaptartomány a 3.175. ábrán vázolt háromszög.
.
15. A test a és felületek között, a , négyzet alaptartomány alatt és fölött helyezkedik el. Az y = x síkkal való metszete a 3.176. ábrán látható.
3.176. ábra
Térfogata:
.
16. Alaptartomány a 3.177. ábrán látható (a függvény a vonalkázott tartományon van értelmezve).
A szimmetriát kihasználva, polárkoordinátákat vezetve be,
.
17. A 2a sugarú gömbtestnek az a sugarú henger belsejébe eső részének térfogatát kell kiszámítani.
Polárkoordinátákat bevezetve,
.
18. Két azonos sugarú henger (test) közös részének térfogatát kell kiszámítani. A 3.178. ábrán ennek a testnek a felső felét ábrázoltuk.
3.178. ábra
A szimmetriákat kihasználva,
.
19. Két paraboloid közötti test térfogatát kell kiszámítani. Az (x, z) - síkkal való metszete a 3.179. ábrán látható.
3.179. ábra
A szimmetriát kihasználva és polárkoordinátákat használva,
.
20. A gömbtestnek arról a részéről van szó, amely az henger belsejében van. A 3.180. ábrán ennek a testnek a felső részét ábrázoltuk.
3.180. ábra
Polárkoordinátákat bevezetve,
.
21. A paraboloid henger belsejébe eső részének felszínét kell kiszámítani.
, , .
A felszín:
.
22. A gömbfelületnek a hengeren belüli részéről van szó.
, , ;
.
23. A kúpfelületnek az hengeren belüli részét számítjuk. Az alaptartomány a 3.181. ábrán látható egységsugarú körlap.
3.181. ábra
, , ;
.
Itt kihasználtuk azt, hogy a tartomány területével egyenlő, amely jelen esetben .
24. A parabolikus hengernek (3.182.b ábra) a 3.182.a ábrán vázolt tartomány fölötti és alatti részének a felszínét számítjuk.
3.182.a. ábra 3.182.b. ábra
, , , ;
.
A kérdéses felületdarab a gömbfelületnek az henger belsejébe eső része (Viviani-levél). Felső része a 3.180. ábrán látható.
, , .
A szimmetriákat kihasználva,
.
26. A felület olyan gyűrűfelület (tórusz), amely az kör y tengely körüli forgásával keletkezik.
Alkalmazzuk a (4) képletet:
. A felszín:
.
27. A lemez (síkidom) a 3.183. ábrán látható.
Tömege (területe) az (5) képlettel :
.
A statikai nyomatékok:
,
.
A súlypont koordinátái: , .
28. A síkidom szimmetrikus az egyenesre, ezért a súlypont ezen az egyenesen van, így (3.184.
ábra).
,
.
A súlypont koordindátái: .
29. Használjuk a (8) képleteket.
A 3.185. ábra szerint
,
.
30. A görbe kardioid (a 3.172. ábrán a külső görbe).
Használjuk a (8) képleteket és vezessünk be poláris koordinátákat. A szimmetriát is kihasználva,
,
.
31. A lemez alakja a 3.186. ábrán látható.
Szimmetrikus az y = x egyenesre, ezért a két tehetetlenségi nyomaték egyenlő. Vezessünk be új változókat az xy = u, y = vx egyenletekkel. Ekkor , , (l. a 3.8. pont 9. mintapéldáját is).
A (8) képletet alkalmazva,
.
32. A V testet (térrészt) alulról a z = 0 sík, felülről a z = 2xy nyeregfelület, oldalról pedig az x = 0, x = 1, y = 0, y = 2 síkok határolják.
.
33. A test a 3.187. ábrán vonalkázott tartomány fölött, a két forgási paraboloid között helyezkedik el
.
34. A test közös (z) tengelyű forgásparaboloid és forgáskúp között helyezkedik el. A (x, z) - síkkal való metszete a 3.188. ábrán látható.
Alaptartomány az körlap. Hengerkoordinátákat bevezetve, a térfogat:
.
35. A gömbtest hengeren belüli részéről van szó. A 3.180. ábrán egy ilyen test felső fele látható. Hengerkoordinátákat használva,
.
A test a z = xy nyeregfelület és a z = x + y sík között, az , , háromszöglap fölött helyezkedik el.
Térfogata:
.
37. A két paraboloid közötti térrész térfogatát kell kiszámítani. A két paraboloid a
z = 2 magasságban, az körben metszi egymást. Hengerkoordinátákat használva,
.
38. A felső félgömbtestnek a paraboloid "belsejében" lévő térfogatát számítjuk. Az (x, z) - síkkal való metszete a 3.189. ábrán látható.
3.189. ábra
Először hengerkoordinátákat használva számítjuk a térfogatot.
.
Gömbi koordinátákat használva:
.
39. Vezessünk be új koordinátákat a következő módon:
, , .
Ekkor . A felület egyenlete pedig
. A térfogat:
.
40. A test a z = 0 sík és a paraboloid között, az henger belsejében van. Tömege (térfogata)
.
A statikai nyomatékok a (11) képletek szerint:
,
(a szimmetria miatt),
.
A súlypont koordinátái: , , .
41. Az első térnyolcadban lévő gúla (test) szimmetrikus a z = x = y egyenesre nézve, ezért súlypontjának koordinátái egyenlők. Tömege (térfogata): . A statikai nyomatékok:
.
A súlypont koordinátái: .
42. A felső félgömbtest súlypontja rajta van a z tengelyen, azaz . Tömege: . Az statikai nyomaték számításánál használjunk gömbi koordinátákat:
.
A súlypont harmadik koordinátája: . 43. Használjuk a 10. képletet:
.
44. Mindhárom tehetetlenségi nyomaték azonos. A (13) képletek szerint:
.
45. A felső félgömbtest nyomatékáról van szó. A (13) képletek szerint, gömbi koordinátákat használva:
.
Hasonlóan látható be, hogy
.
46. A (13) képlet szerint, gömbi koordinátákat használva:
.
Digitális Egyetem, Copyright © Kovács Béla, 2011