l6-l8, f 3 _ow

RAREFIED HYPERSONIC FLOW OVER A SPHERE E. S. Levinskyl and H. Yoshihara^

Convair Division of General Dynamics, San Diego, California

ABSTRACT

The flow over a sphere at large hypersonic Mach numbers and low Reynolds numbers has been computed by using the Navier- Stokes equations as simplified by Probstein and Kemp. A sim- ilarity solution, valid about the stagnation streamline, is used. Both the adiabatic and cold wall cases are treated.

Solutions, in particular the shock structure, the inviscid compression zone and the stagnation point boundary layer have been obtained at a Mach number of 10 and Reynolds numbers of 10^, 1θ3 and 10^ based on the sphere radius, free stream velocity, and adiabatic stagnation values of density and viscosity.

INTRODUCTION

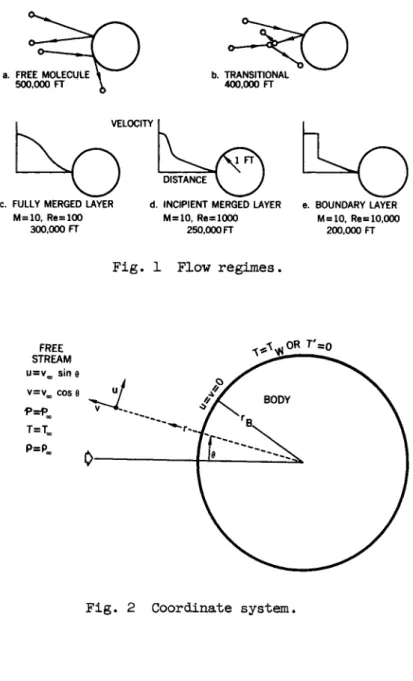
The flow about an object re-entering Earth's atmosphere assumes a myriad of patterns caused by the wide range of den- sity during the descent (Fig. l ) . At the higher altitudes the air is sufficiently rarefied so that collisions are highly im- probable of air molecules with other air molecules compared with collisions between the air molecules and the body, and molecule-molecule interactions may be neglected. For this "free molecular flow," the trajectories of the molecules and, there- fore, the complete flow pattern can be determined, provided that the particle-body surface interactions are known. Here the region of f3_ow influenced by the body extends indefinitely upstream.

Presented at ARS International Hypersonics Conference, Cambridge, Massachusetts, August l 6 - l 8 , I96I; this research was supported in part by Convair REA 9009 and 8005 and in part by Advanced Research Projects Agency Order no. 1ΐβ-6θ (Project Defender) through Contract AF 19(6θ4)-5554.

^ s i g n Specialist, Fluid Dynamics Research.

As the body enters regions of higher density, collisions be- tween air molecules become important. For example, air molecules reflected upstream by the body will now collide with other on- coming molecules instead of traveling unhindered. There will be a tendency now for the molecules to pile up in front of the body. With further increase in ambient density this pile-up will increase, and the upstream extent of this region will con- tract toward the body. The particle number density in the pile- up region will be much greater than in the undisturbed free stream.

Consider next the more familiar high density extreme of the continuum flow regime encountered by the body. Here one finds the well-known flow pattern of an infinite s imally thin bow shock, a thin viscous boundary layer adjacent to the body and an inviscid region inbetween (Fig. le). For sufficiently high free stream densities the flow details within the shock struc- ture need not be considered, and the shock may be bridged, to a good approximation, by the usual shock jump conditions. The remainder of the flow can then be computed in a piecemeal fashion, first by assuming that the flow is inviscid throughout, and then by modifying the flow near the body by a stagnation point bound- ary layer flow analysis (Ref. l ) .

As the free stream density is decreased (for a constant free stream Mach number), the thickness of both the shock wave and boundary layer will grow. In general, the shock wave will in- crease in thickness more rapidly than the boundary layer, and a flow configuration will be achieved in which the thickness of the shock wave may no longer by ignored (Fig. Id). The inviscid region separating the shock wave from the boundary layer is now reduced in thickness for this flow pattern which has been termed an "incipient merged layer" by Probstein (Ref. 2 ) .

A further decrease in free stream density causes this inviscid layer to be eliminated entirely, and the shock wave and boundary layer are then said to be fully merged (Fig. lc). The simplified piecemeal approach described is no longer permissible for the latter two cases, and the flow as a whole must be considered.

For the dilute gases considered, the Boltzmann equation for the one-particle distribution function is, to be sure, adequate to describe the entire spectrum of flows encountered by a re- entry body. This equation generally furnishes more information than is frequently required, and except in extremely simplified cases it is impossible to solve.

If the density of the fluid particles, however, is sufficiently high so that averages of the number density and;say;the random

8 2

k i n e t i c e n e r g y o f t h e m o l e c u l e s p e r u n i t v o l u m e a s s u m e s t e a d y v a l u e s , t h e n o n e may d e r i v e a f u l l y d e t e r m i n a t e s y s t e m o f c o n - t i n u u m e q u a t i o n s i n t e r m s o f m a c r o s c o p i c q u a n t i t i e s , s u c h a s t h e t e m p e r a t u r e , p r e s s u r e a n d f l u i d f l o w v e l o c i t i e s . H e r e t h e f l o w i s a s s u m e d t o b e m a c r o s c o p i c a l l y s t e a d y w i t h r e s p e c t t o c o o r d i n a t e s f i x e d w i t h t h e b o d y , a n d t h e a v e r a g e s a r e t a k e n o v e r a n e l e m e n t o f s p a c e a n d d u r a t i o n o f t i m e e a c h v e r y much l e s s t h a n t h e c o r r e s p o n d i n g m e a n i n g f u l m a c r o s c o p i c q u a n t i t i e s . The l a r g e r t h e g r a d i e n t s o f t h e m a c r o s c o p i c q u a n t i t i e s w i t h i n t h e f l o w , t h e g r e a t e r w i l l b e t h e c o m p l e x i t y o f t h e a p p l i c a b l e m a c r o s c o p i c e q u a t i o n s .

A t t e n t i o n w i l l b e f o c u s e d i n t h e p r e s e n t p a p e r on t h e t r a n - s i t i o n o f t h e f l o w f r o m t h e h i g h d e n s i t y e x t r e m e t o a c a s e i n w h i c h t h e s h o c k wave a n d b o u n d a r y l a y e r h a v e m e r g e d . ( F o r a r e v i e w o f p r e v i o u s work on t h i s s u b j e c t , s e e H a y e s a n d P r o b s t e i n i n R e f . 3 · ) 3 n p a r t i c u l a r , & s e r i e s o f s t e a d y f l o w s o v e r a s p h e r e a t a f i x e d h y p e r s o n i c Mach number a n d v a r y i n g f r e e s t r e a m d e n s i t i e s w i l l b e c o n s i d e r e d w h i c h w i l l i n c l u d e t h e i n c i p i e n t m e r g e d l a y e r a n d f u l l y m e r g e d l a y e r c a s e s . The v a l i d i t y o f t h e N a v i e r - S t o k e s e q u a t i o n s w i l l b e p o s t u l a t e d f o r t h i s f l o w s e q u e n c e . The u s e o f t h e s e e q u a t i o n s f o r t h e h i g h d e n s i t y p o r t i o n o f t h e s h o c k l a y e r i s p l a u s i b l e , b u t a t f i r s t g l a n c e t h e i r u s e m i g h t b e q u e s t i o n e d w i t h i n t h e s h o c k s t r u c t u r e , s i n c e h e r e t h e m a c r o - s c o p i c q u a n t i t i e s s u c h a s t h e t e m p e r a t u r e v a r y a p p r e c i a b l y o v e r a mean f r e e p a t h . H o w e v e r , t h e r e i s e v i d e n c e t h a t t h e N a v i e r - S t o k e s e q u a t i o n s g i v e e x c e l l e n t a g r e e m e n t w i t h e x p e r i m e n t s f o r t h e s t r u c t u r e o f n o r m a l s h o c k s ( R e f s . 3 and- 4 ) . T h i s c o r r e l a - t i o n i s a t l o w Mach n u m b e r s , b u t , n e v e r t h e l e s s , t h e g o o d a g r e e - m e n t h e r e l e n d s s u p p o r t f o r t h e u s e o f t h e " N a v i e r - S t o k e s "

e q u a t i o n s a s a f i r s t a p p r o x i m a t i o n f o r t h e h y p e r s o n i c c a s e . To s i m p l i f y t h e f u l l " N a v i e r - S t o k e s " e q u a t i o n s a p r o c e d u r e d e v e l o p e d b y P r o b s t e i n a n d Kemp ( R e f . 5 ) w i l l b e f o l l o w e d . T h i s p r o c e d u r e i s b a s e d upon t h e f a c t t h a t t h e s h o c k l a y e r i s v e r y t h i n c o m p a r e d w i t h t h e b o d y r a d i u s f o r t h e l a r g e h y p e r s o n i c Mach numbers c o n s i d e r e d h e r e . L o c a l f l o w s i m i l a r i t y i s t h e n e n f o r c e d^#w h i c h y i e l d s a s y s t e m o f o r d i n a r y d i f f e r e n t i a l e q u a - t i o n s w h i c h w i l l b e v a l i d i n t h e f l o w domain n e a r t h e a x i s o f s y m m e t r y u p s t r e a m o f t h e b o d y . The r e s u l t a n t s y s t e m o f e q u a - t i o n s w i l l t h u s n o t d e s c r i b e t h e e n t i r e f l o w b u t w i l l y i e l d i n - f o r m a t i o n on t h e s h o c k d e t a c h m e n t d i s t a n c e a n d t h e s h o c k s t r u c - t u r e , a s w e l l a s c o n d i t i o n s a t t h e s t a g n a t i o n p o i n t .

B o t h t h e i n s u l a t e d a n d " c o l d w a l l " c a s e s w i l l b e t r e a t e d . The c a s e f o r w h i c h t h e b o d y i s a p e r f e c t h e a t i n s u l a t o r i s s i m - p l i f i e d b y a s s u m i n g t h e h a r d s p h e r e m o d e l o f t h e g a s w i t h a P r a n d t l number o f t h r e e - f o u r t h s . The e n e r g y e q u a t i o n i s t h e n d e c o u p l e d f r o m t h e r e m a i n i n g e q u a t i o n s a n d may b e i n t e g r a t e d

to yield a particular solution, the so-called Becker's integral, which is valid from the free stream to the body.

A more practical case is one in which the body is a good conductor of heat passing, for example, sufficient heat to maintain the surface at a constant tolerable temperature. The

surface temperature will be taken equal to the static free stream temperature for this so called "cold wall" case. The solutions for this case should differ from the insulated case primarily within the temperature boundary layer adjacent to the body, and will effect the shock structure only when the boundary layer and shock are merged.

DISCUSSION

To simplify the problem and avoid real-gas effects and the question of the bulk viscosity, a monatomic gas with a "billiard ball" model for the interaction potential will be considered.

The coefficients of viscosity and heat conductivity will then be proportional to the square root of the absolute temperature.

In addition, a perfect gas with constant specific heats will be assumed. The value for the Prandtl number Pr = 3/4 was chosen, instead of the consistent value 2 / 3 , to simplify the energy equation.

Basic Equations

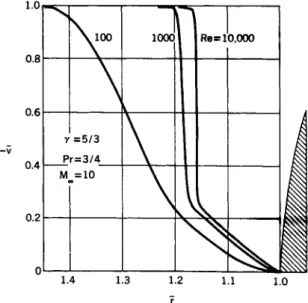
The validity of the "Navier-Stokes" approximation for the stress term and the heat fluxes will be assumed. Thus, in spherical coordinates (defined in Fig. 2 ) the basic equations become

(pv)^r +

ψ

r = 0 (1)

. J L (rv + 2v + + u cot θ)

Γ υ ( 2 )

8 4

θ

+ Η { c o t θ [ r ⁺ £ ] - § ( ν ⁺ u c o t β)} ( 2 )

Ρθ Γ u UV Ί

— + ρ Ι v u + - u^A + — Ι

r L r Γ θ J r

μ

Ä I

e )j

(3)

+ 2 % c o t θ ( u^a - u c o t θ )

{v

S h

) - vp

Ä ρ

& [ ( M ^ )

( f ^ ) + . u ^

J

+ μ [*ξ+ % u ^e . v )^{2 +} 4( v - u c o t θ )^{2 +} (r(H)^{r +} ^ f ]

2μ Γ 2 2 2 v2 + u² + u² c o t² θ + fcrvv + 2 r v u r θ

+ 2 r v^ru c o t θ + + kvu c o t θ + 2u^Qu c o t θ "j (1).)

and

ρ = C pT ( 5 )

where the symbols axe defined in the Nomenclature, and the sub- scripts denote partial differentiation. The boundary conditions are as follows:

l) Far from the body a uniform free stream is assumed with the conditions

u = ν s i n θ

V s -V cos θ

2 ) At the surface of the body the no slip condition is postulated

u = ν = 0

and in addition either the insulated or adiabatic wall condition

ι -

or the cold wall condition

Τ s Τ - Τ V oo

For the extremely low Reynolds number cases the no slip condi- tion for the adiabatic wall case may be somewhat questionable but should be a good approximation for the cold wall case

(Ref. 3 ) .

Simplification of Basic Equations

The boundary value problem as formulated here is, of course, difficult to solve. To simplify the equations the authors shall follow the procedure of Probstein and Kemp. This is based upon on order of magnitude evaluation of the various terms in the differential equations using the fact that for large hypersonic Mach numbers the shock layer is extremely thin and that distur- bances near the sonic line do not appreciably influence the flow on the axis. The resultant simplified equations become

86

(pu)^fi Ρ s

ΓΒ ^ΓΒ ^ΓΒ (6)

puv- 2 Ρ ⁺ p w ⁺_ θ . £ ϋ _

Γ ΓΒ ΓΒ

[f + i ) j fc>

(7)

j | + p v ur + ρ 2 - ( ue + ν ) = ( μ υΓ)Γ

a n d

pv ( - i H H 4 » i ) J ^t

(8)

(9)

where r_> i s t h e body r a d i u s .

D

T h e s e e q u a t i o n s , t o b e s u r e , a r e c o n s i s t e n t t o t h e l o w e s t o r d e r , b u t t h e e x p a n s i o n p r o c e d u r e i s n o t s y s t e m a t i c s i n c e i t does n o t p r o v i d e f o r h i g h e r o r d e r a p p r o x i m a t i o n s .

With t h e P r a n d t l number o f 3 A , t h e e n e r g y E q . 9 niay "be i n - t e g r a t e d t o o b t a i n t h e s o - c a l l e d B e c k e r ' s i n t e g r a l

2

C Τ + — = constant Ρ 2

and t h e f l o w i s s a i d t o b e i s o e n e r g e t i c .

This integral requires that Τ ' = 0 at ν = 0, so that it may be used only for the adiabatic wall condition. Thus, for this case the number of differential equations may be reduced by one,

For the solution of these equations the following set of similarity postulates is introduced near the axis of symmetry θ = 0

u = u (r) sin θ ο

ν = ν (r) cos θ ο

Ρ - Ρ0( Γ )

Τ = TQ(r) cos2 θ + T2(r) sin2 θ

h = hQ(r) cos θ + h2 2 2(r) sin θ

μ = μο(τ) cos θ

and

Ρ - Ρ „ + j " Ρ⁰( Ρ ) - p j cos2 θ + £p²(r) - ^{Ρ ο ο} "J sin2 θ

where the terms with subscripts 0 and 2 are functions of r only.

Introducing this into the basic Eqs. 5 to 9, and carrying out the nondimensionalization

ο ο *ο y2

V = U = P = —

ν ν y 2 y2

PA W^V » ^PA W^V «ο 8 8

Ρ = Τ = μ =

^AW AW ^AW

VB^PA W

MAW

Pr ^{^AWCp}

kAW

where the subscripts « and AW refer, respectively, to the free stream condition and to the stagnation point of the body with adiabatic wall conditions, one obtains

(ρν)' + 2ρ(ΰ + ν) = ο (11)

μ u (12)

Pp - p û (û + v ) = 0 (13)

2( P2 - ρ ) + Ρ ν Ü ' + ρ ΰ (ϋ + ν ) = (EgT

pv (15)

and

ρ = σ A ρ Τ (16)

where

C T _AW

For the adiabatic wall condition, Becker's integral becomes

- 2 (17)

and the constant A may "be evaluated in terms of the free stream Mach number M as

A = | + [(7 - IK

]'

The boundary conditions for the adiabatic wall case are:

1 ) In the free stream

ΰ = 1 ν = - 1 Ρ = P o = Ρ Τ = Τ

c. oo 00

2 ) On the body

û = ν = 0 ρ = Τ = 1 Τ' = 0

In addition, the requirement ν ' = 0 must be imposed at the body to ensure a finite density gradient. The fulfillment of the conditions Τ = in the free stream and T ' = 0 at the body is ensured by a suitable choice of the constants of integration in Becker's integral.

For the cold wall case, Becker's integral is no longer valid throughout the flow. The boundary conditions in the free stream remain the same; however, the boundary conditions at the body are now

û = ν = ^{0 Τ = Ϊ} Solution of the Problem

The method of integration of a two-point boundary value pro- blem with nonlinear differential equations is to convert the problem into an initial value problem and then to vary parame- trically those initial conditions not originally specified until the boundary conditions are fulfilled. An additional difficulty arises, however, because the solutions cannot be integrated all the way from the free stream to the body, or from the body to the free stream, because of instabilities in the integration procedure. The equations are therefore integrated from each end. The unassigned initial conditions in the free stream and at the body are then adjusted such that the two solutions match at a common point between the shock and the boundary layer where the integration procedure is still stable.

90

1. F r e e S t r e a m I n t e g r a t i o n

B e c a u s e o f t h e s i n g u l a r n a t u r e o f t h e f r e e s t r e a m , t h e s o l u t i o n i s i n t e g r a t e d f r o m t h i s e n d b y p e r t u r b i n g t h e f l o w a b o u t t h e f r e e s t r e a m c o n d i t i o n s , a n d i n i t i a t i n g t h e i n t e g r a t i o n w i t h t h e l i n e a r s o l u t i o n . By i n t r o d u c i n g t h e s e t o f p e r t u r b a t i o n q u a n t i - t i e s p , ? , ; , e t c . , w h e r e

Ρ = ~ ( 1+ p ) v s - l + v û = 1 + u

PAW

' ο ο ' 0 0

* = — — 5 + τ 5 = — (ι

+ α>

Air-DM.2 ^AW V V

a s e t o f l i n e a r i z e d f l o w e q u a t i o n s v a l i d n e a r t h e f r e e s t r e a m i s o b t a i n e d

v ' - p ' + 2 (v + Ù) = ο (18)

p'-ï'-iÛr (19)

00

ν - AT = - jjZi (v - A T ) ' ( 2 0 )

Ρ = OA — χ + Τ

U(r-i)M

2 + 'il] (21)

i; -

and

2(P² - P ) - u ' + ( u + v) = ^ — (23)

00

Here Re^ is the Reynolds number based on free stream conditions.

This set of equations is readily solved by making the assump- tions that the perturbation û « ν , and that the term u ' '/Re^

may be considered small in Eq. 23· Both of these assumptions may be varified a posteriori. The first enables Eqs. 18 to 21 to be separated from the remainder, and permits solutions for ν , ρ , T and Ρ to be found independently of the cross flow quanti- ties ϋ and p² . Thus

ν

and

where

(210

Here and Cg are arbitrary constants of integration, r^ is the radius at which the perturbations are evaluated, and

(25)

whereas

92

1 + ^L 8/3

( 7 - l ) M „² ( r - l ) M ² R e^e

(26)

For the adiabatic vail case, = 0, and the constant ^C2 ^{m < u}s t vanish. For the cold wall case, Becker¹s integral may still be satisfied in the free stream provided the cold wall effects are restricted to the temperature boundary layer adjacent to the body. Solutions in the free stream for the cold wall case will first be attempted with Ti * 0. However, if these solutions do not match the solutions obtained by integrating from the wall, then the value τ will be varied parametrically. The initial value Vj^ will be assumed fixed at one per cent of the free stream velocity.

Neglecting the term in u' Y R e ^ permits Eqs. 22 and 23 to be readily integrated giving

û = u^± + k²v^t + ^\tä±

and

l+kg _ 1+1^

p2 = " Τ " ^vi " 3 7 5 ^ k1ATi - u^± ( 2 7 )

where

Here is an arbitrary constant

^ = - ( 2 8 ) m - m - 2

and

Re (29)

- 2

A zero value for the constant was found to yield solu- tions which matched those obtained by integrating from the body for all cases considered. Since both kg and. k- are of order l/Re^ , the assumptions concerning the perturbations u and

Re appear justified.

The linear solutions Eqs. 2k and 27 are used to initiate the integration of the nonlinear system, Eqs. 11 to 17 from the free stream end. This procedure was convergent until the bound- ary layer was approached.

2. Integration From the Body

The expansion of the solution about the stagnation point of- fers no essential difficulties, and is similar to the classical incompressible solutions (Ref. 6 ) . The fundamental differences in the present integration result from the variable density and temperature and from the introduction of a variable transverse pressure term p^ , as given by Eq. 13· In addition, the inte- gration from the stagnation point may be carried out, in prin- ciple at least, as far as the free stream, since the nonlinear system is valid throughout the flow domain in front of the body. In practice, however, the solution becomes unstable be- fore the shock is reached, limiting the outward extent of the integration.

3. Review of Parametric Problem

Before discussing the numerical results, the parametric problem required to match the solutions from the free stream and from the body will be reviewed. For the cold wall case, the boundary conditions at the body are four in number, includ- ing the requirement thatv'= 0· Since the order of the nonlinear system is eight, four parameters, namely û , τ ' , Ρ² aui^ Ρ > must be adjusted at_the wall to match the free stream solution.

The parameter in the free stream solution must also be var- ied from the zero value if the temperature boundary layer is merged with the shock.

The adiabatic wall case is much simpler since only two 9*

parameters, û'and Ρ 2 , must be adjusted at the body. In addi- tion, equals 0 in the free stream solution.

Numerical Results

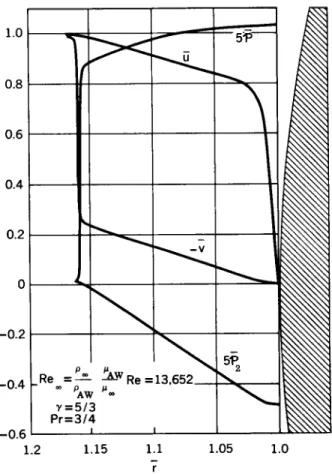
The system of Eqs. 11 through 17 has been programmed for so- lution on the IBM 7(A digital computer. All solutions were carried out for a monatomic gas withy = 5/3> for a free stream Mach number M^œ equals 10 (which should be representative of the hypersonic conditions encountered during re-entry); and for Reynolds numbers, based on adiabatic stagnation temperature and density, of 10,000, 1000 and 100 to illustrate the transi- tion from relatively dense to rarefied conditions. The results are summarized in Fig. 3 for adiabatic wall conditions, and in Fig. k for cold wall conditions. It is seen that for both con- ditions the shock is essentially a discontinuity at the largest Reynolds number. However, for Re = 1000, the shock thickness is of the order of 10$ of the detachment distance. For this case, the shock and the boundary layer remain distinct and are sepa- rated by an inviscid region. For a Reynolds number of 100, the shock thickness has increased to approximately 50$ of the detachment distance, and a distinct inviscid region is no longer present indicating a fully merged layer.

The growth in the upstream influence of the body at the low- er densities is shown by the substantial increase in the de- tachment distance at the lower Reynolds numbers. This increased detachment distance is due to both the thickened shock wave and the increased boundary layer thickness at the lower Reynolds numbers. The shock thickness varies as R^e > whereas the boundary layer height varies with p^E" 2 . Cooling the wall reduces the upstream influence of the body by reducing the boundary layer thickness.

The variation in the quantities û , γ > Ρ and. ^ρ2 f^{r o m} ^ ^β free stream to the body is shown in Figs. 5 to 7 for the adia- batic wall case. Figures 8 to 10 show velocity and temperature profiles for the cold wall cases. The shock temperature pro- files for the adiabatic and cold wall cases are identical at the higher Reynolds numbers, but differ for the fully merged case because the influence of the cold body extends to the free stream.

The heat transfer to the stagnation point of the sphere has been computed for the cold wall cases and is presented in Fig.

1 1 . The Stanton number is readily shown to be given as

η

c^HV R T = g . £121 (30)

where the free stream Reynolds number Re is related to Re by Re =(=-)Re. . A comparison of these results with free molec- ular flow theory

and boundary layer theory (Ref. l) S l * ^ - 3-92

is included in Fig. 1 1 .

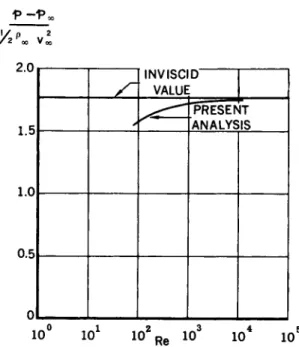
The variation in the stagnation point pressure coefficient with Re is shown in Fig. 1 2 . Within the accuracy of the plot, the variation of the adiabatic and cold wall cases was identical.

The decrease in stagnation pressure with decreasing Re is con- trary to the experimental trend found by Sherman (Ref. 7 ) with adiabatic wall conditions, and may result from the neglect of slip effects which could become significant with adiabatic wall conditions (Ref. 8 . However, slip effects should be negligible for the cold wall case.

FINAL REMARKS

Solutions have been obtained for the hypersonic flow of a monatomic gas past a sphere under highly rarefied conditions and give the shock structure and stagnation point boundary lay- er profiles for the incipient merged and fully merged cases.

For the incipient merged layer case, the shock wave and bound- ary layer are distinct, and are separated by an inviscid zone.

The flow is isoenergetic in the shock wave for this case, even for a highly cooled wall. With a fully merged layer, the cool- ing effect of the wall is felt in the shock resulting in noniso- energetic conditions near the free stream.

On the basis of the result shown, further extensions appear warranted. These include the consideration of diatomic gases with the complicating real-gas effects and the addition of bulk viscosity, as well as the extension to lower Reynolds number

(e.g., Re = 10) with a more exact slip boundary condition still using the Navier Stokes equations.

ACKNOWLEDGMENT

The authors are indebted to F. Cochran of the General I)y- namics/Convair Digital Computing Laboratory for his highly

00

96

Re = Reynolds number

T = temperature

μΑν/

u = velocity component in θ direction ν - velocity component in r direction γ = ratio of specific heats

θ = angle from axis

competent programming in handling of the numerical equations, NOMENCLATURE

( ) ' = prime, differentiation with respect to r ( ) - bar, nondimension quantity

(~) = tilde, perturbation quantity

A - constant dependent on free stream Mach number

C1 '^C2^{, C}3 ^{= c o n s}~^{t a r r ts} °f integration, Eqs. 2k and 27 CR = Stanton number

C^p = specific heat at constant pressure h - enthalpy

k^k^k. = constants defined by Eqs. 26, 28 and 29, respec- tively

k = thermal conductivity M - Mach number

m = constant defined by Eq. 25 ρ = pressure

Pr = Prandtl number

r - radius

r^ß = body (sphere), radius

rB ^Voo ^PAW

= viscosity

ρ - density

σ = function of y Subscripts

= similarity values

AW = adiabatic wall stagnation point values i = initial perturbation values

= undisturbed free stream values REFERENCES

1 Lees, L., "Laminar Heat Transfer Over HLunt Nosed Bodies at Hypersonic Flight Speeds, " Jet Propulsion,vol. 26, no. k, April 1956.

2 Probstein, R.F., "Shock Wave and Flow Field Development in Hypersonic Re-£ntry," ARS J., vol. 31, no. 2, pp. 185-194, Feb. 1961.

3 Hayes, W.D. and Probstein, R.F., "Hypersonic Flow Theory,"

Academic Press Inc., New York, 1959·

k Sherman, F.S., "A Low Density Wind-Tunnel Study of Shock- Wave Structure and Relaxation Phenomena in Gases," NACA TN 3^98, July 1955.

5 Probstein, R. and Kemp, N., "Viscous Aerodynamic Charac- teristics in Hypersonic Rarefied Gas Flow," Avco Research Rep.

no. 1*8, June 1959.

6 Schlichtung, H., "Boundary Layer Theory," Pergamon Press, New York, 1955, pp. 73-75-

7 Sherman, F.S., "New Experiments on Impact-Pressure Inter- pretation in Supersonic and Subsonic Rarefied Airstreams,"

NACA TN 2995y Sept. 1953-

8 Lin, T.C. and Schaaf, S.A., "Effect of Slip on Flow Near a Stagnation Point and in a Boundary Layer," NACA TN 2568, Dec. 1951.

98

c. FULLY MERGED LAYER d. INCIPIENT MERGED LAYER e. BOUNDARY LAYER M=10, Re=100 M=10, Re=1000 M = 10, Re =10,000

300,000 FT 250,000 FT 200,000 FT

Fig. 1 Flow regimes.

Fig. 2 Coordinate system.

Fig. 3 Effect of Reynolds number on shock thickness and veloc- ity profiles, adiabatic wall.

1 0 0

Fig. 5 Adiabatic stagnation line flow characteristics; Re = 10,000, = 10.

1 0 2

1.5

1.0

0.5

Ol

INVISCID VALUE

PRESEI^

AN A LYS JT AS

10° ίο¹ i o^{2 R e} io³ io⁴ io⁶

Fig. 12 Stagnation point pressure coefficient; M =10.

106