Szegedi Tudományegyetem Cím: 6720 Szeged, Dugonics tér 13.
www.u-szeged.hu www.szechenyi2020.hu
MÉRNÖKKÉPZÉS
MATEMATIKAI ALAPJAI
Dr. Fabulya Zoltán
2019.
Szegedi Tudományegyetem Cím: 6720 Szeged, Dugonics tér 13.
www.u-szeged.hu www.szechenyi2020.hu
Jelen tananyag a Szegedi Tudományegyetemen készült az Európai Unió támogatásával.
Projekt azonosító: EFOP-3.4.3-16-2016-00014.
Szerző:
Dr. Fabulya Zoltán PhD Szegedi Tudományegyetem Mérnöki Kar
ISBN: 978-963-306-641-6
© Dr. Fabulya Zoltán PhD 2019
TARTALOMJEGYZÉK
BEVEZETÉS ... 3
1. MŰVELETEK SZÁMOKKAL ... 8
1.1. Műveleti sorrend, zárójel ... 9
1.2. Alapműveletek negatív számokkal ...10
1.3. Alapműveletek közönséges törtekkel ...11
1.3.1. Törtek egyszerűsítése, bővítése ...13
1.3.2. Törtek értelmezése ...13
1.3.3. Tört szorzása, osztása...14
1.3.4. Törtek összeadása kivonása ...15
1.4. Hatványozás és gyökvonás ...16
1.5. Ellenőrző kérdések, feladatok ...20
2. ALGEBRAI ÁTALAKÍTÁSOK ...21
2.1. Műveletek tulajdonságai ...22
2.2. Nevezetes azonosságok ...24
2.3. Kifejezések egyszerűbb alakra hozása...25
2.3.1. Szorzattá alakítás ...25
2.3.2. Négyzetgyökös kifejezések átalakítása ...27
2.4. Műveletek algebrai törtekkel ...28
2.5. Ellenőrző kérdések, feladatok ...30
3. FÜGGVÉNYEK ...31
3.1. Függvények ábrázolása koordinátarendszerben ...32
3.2. Műveletek függvényekkel ...33
3.2.1. Összetett függvény...34
3.2.2. Inverz függvény ...36
3.3. Függvények tulajdonságai...37
3.3.1. Zérushely ...37
3.3.2. Tengelymetszet ...37
3.3.3. Paritás ...38
3.3.4. Periodikusság ...39
3.3.5. Korlátosság ...40
3.3.6. Monotonitás ...41
3.3.7. Szélsőérték ...42
3.3.8. Görbület ...43
3.3.9. Inflexiós pont ...45
3.3.10. Folytonosság...45
3.4. Fontosabb elemi függvények ...46
3.4.1. Konstans és identikus függvény ...48
3.4.2. Páros és páratlan kitevős hatvány függvény ...49
3.4.3. Reciprok és lineáris törtfüggvény ...50
3.4.4. Exponenciális függvény ...51
3.4.5. Logaritmus függvény ...52
3.4.6. Szinusz és koszinusz függvény ...53
3.4.7. Tangens és kotangens függvény ...54
3.5. Ellenőrző kérdések, feladatok ...55
4. EGYENLETEK ÉS EGYENLŐTLENSÉGEK ...56
4.1. Algebrai megoldás ...56
4.1.1. Másodrendű egyenletek, egyenlőtlenségek ...57
4.1.2. Gyököt tartalmazó egyenletek, egyenlőtlenségek ...58
4.1.3. Exponenciális egyenletek, egyenlőtlenségek ...59
4.1.4. Logaritmusos egyenletek, egyenlőtlenségek ...59
4.2. Grafikus megoldás...60
4.3. Ellenőrző kérdések, feladatok ...61
5. TRIGONOMETRIA ...63
5.1. Nevezetes szögek szögfüggvény értékei...65
5.2. Trigonometrikus azonosságok ...66
5.3. Ellenőrző kérdések, feladatok ...67
6. MEGOLDÁSOK ...68
BEVEZETÉS
Az elmúlt két esztendőben a Matematika 1. kurzust nem teljesítők aránya a műszaki szakterületen 55% körül alakult. Ebből is látható, hogy a hallgatók számára nehezen vagy egyáltalán nem teljesíthető tantárgy/kurzus a matematika. Mindemellett a műszaki képzés területén a matematikai ismeretek hiányossága több természettudományos tárgy megértéséhez, megtanulásához nélkülözhetetlen.
A középiskolai matematikai alapok hiányossága, nem eléggé készség szintjén történt elsajátítása okozza, hogy a hallgatók jelentős hányada nem tudja elsajátítani a szakja elvégzéséhez szükséges matematikai ismereteket. Oktatási tapasztalataink alapján azt is látjuk, hogy melyek azok a témakörök, amelyeket a középiskolában a hallgatók egy része nem kellő mértékben sajátított el, de az adott szakon (jelen esetben a műszaki szakterületen) szükségesek a matematika kurzusok és az erre épülő tárgyak sikeres teljesítéséhez.
Ez a jegyzet egy felzárkóztató kurzus anyagát tartalmazza, de a fejezetek elején olyan útmutatás szerepel egy-egy feladattal, melyből a hallgatók megismerik, hogy mely egyetemi, aktuális tanulmányukhoz kapcsolódik a tárgyalt téma. Így a hallgató a jegyzet segítségével nem csak korábbi hiányosságait tudja pótolni, de egyetemi felkészülését is segíti. Elsődleges szempont volt, hogy példákon keresztül kapjon részletes magyarázó ismeretet az olvasó. Emiatt minden feladat lépésenkénti megoldása is megtalálható a jegyzetben.
A diákoknál sokszor tapasztaltam, hogy kevéssé hajlandóak belegondolni a matematikában megjelenő törvényszerű összefüggések okaiba. Elegendőnek éreznek pusztán megtanulni egy-egy új ismeretet még olyan esetben is, amikor egy kis gondolkodás után, azaz tanulás nélkül is az új ismeret birtokába juthatnának korábbi ismereteik logikus következményeként. Ezért a jegyzetben fontosnak tartottam bemutatni a bizonyításokat is. Így a diákok nem csak megtanulandó, száraz tényekkel találkoznak a jegyzetben, hanem azok okait is átlátva, új szemlélettel fordulhatnak matematikai tanulmányaik felé. Arra buzdítanám a jegyzet használóit, hogy mindig kritikusan fogadják az új ismereteket, tegyék fel magukban a miért kérdést. Ezzel a szemlélettel egy izgalmas, szórakoztató logikai játékként tekinthetünk a matematikára, melyben sok kihívással találkozhatunk, és sok sikerélményben lehet részünk.
Bízom abban, hogy a jegyzet segítségével az olvasó nagy segítséget kap matematika tanulmányai terén, s olyan szemlélethez jut, mely más irányú ismeretszerzését is megalapozza.
A tanulási eredmény alapú szemléletnek megfelelően e jegyzet segítségével az olvasók azokat az ismereteiket frissíthetik fel, melyeket a tartalomjegyzék tükröz, és amelyek alapján képesek a felsőfokú matematika tanulmányaik megkezdésére. Az ismereteket a korábbi tanulmányok során kellett volna elsajátítani és készség szintjén alkalmazni, ennek megfelelően a jegyzet tartalma számonkérésre nem kerül a felsőfokú képzés során. A tartalmak gyakorlásával az itt bemutatott tananyagot a hallgató alkalmazni tudja, felelőssége, hogy önállóan, autonóm módon bepótolja hiányosságait. A jegyzet elősegíti azoknak az attitűdöknek a kialakulását, amelyek szükségesek a továbbfejlődés igényének kibontakozásához. Mivel a tanulási eredmény alapú szemléletet figyelembe véve készült ez a tananyag, ezért a könyvben foglaltak elsajátítását követően a hallgatók tudása, képességei, attitűdje, autonómiája és felelőssége is fejlődik. Ennek eredményeként a hallgató
a) tudása szempontjából elmondható, hogy ismeri a műszaki szakterület műveléséhez szükséges alapvető matematikai témaköröket:
1. MŰVELETEK SZÁMOKKAL 1.1. Műveleti sorrend, zárójel
1.2. Alapműveletek negatív számokkal 1.3. Alapműveletek közönséges törtekkel
1.3.1. Törtek egyszerűsítése, bővítése 1.3.2. Törtek értelmezése
1.3.3. Tört szorzása, osztása 1.3.4. Törtek összeadása kivonása 1.4. Hatványozás és gyökvonás
2. ALGEBRAI ÁTALAKÍTÁSOK 2.1. Műveletek tulajdonságai 2.2. Nevezetes azonosságok
2.3. Kifejezések egyszerűbb alakra hozása 2.3.1. Szorzattá alakítás
2.3.2. Négyzetgyökös kifejezések átalakítása 2.4. Műveletek algebrai törtekkel
3. FÜGGVÉNYEK
3.1. Függvények ábrázolása koordinátarendszerben 3.2. Műveletek függvényekkel
3.2.1. Összetett függvény 3.2.2. Inverz függvény 3.3. Függvények tulajdonságai
3.3.1. Zérushely 3.3.2. Tengelymetszet 3.3.3. Paritás
3.3.4. Periodikusság 3.3.5. Korlátosság 3.3.6. Monotonitás 3.3.7. Szélsőérték 3.3.8. Görbület 3.3.9. Inflexiós pont 3.3.10. Folytonosság
3.4. Fontosabb elemi függvények
3.4.1. Konstans és identikus függvény
3.4.2. Páros és páratlan kitevős hatvány függvény 3.4.3. Reciprok és lineáris törtfüggvény
3.4.4. Exponenciális függvény 3.4.5. Logaritmus függvény
3.4.6. Szinusz és koszinusz függvény 3.4.7. Tangens és kotangens függvény 4. EGYENLETEK ÉS EGYENLŐTLENSÉGEK
4.1. Algebrai megoldás
4.1.1. Másodrendű egyenletek, egyenlőtlenségek 4.1.2. Gyököt tartalmazó egyenletek, egyenlőtlenségek 4.1.3. Exponenciális egyenletek, egyenlőtlenségek 4.1.4. Logaritmusos egyenletek, egyenlőtlenségek 4.2. Grafikus megoldás
5. TRIGONOMETRIA
5.1. Nevezetes szögek szögfüggvény értékei 5.2. Trigonometrikus azonosságok
b) képességei is fejlődnek, így képes alkalmazni a műszaki szakterület műveléséhez szükséges alapvető matematikai elveket, szabályokat, összefüggéseket az alábbi témakörökben:
1. MŰVELETEK SZÁMOKKAL 1.1. Műveleti sorrend, zárójel
1.2. Alapműveletek negatív számokkal 1.3. Alapműveletek közönséges törtekkel
1.3.1. Törtek egyszerűsítése, bővítése 1.3.2. Törtek értelmezése
1.3.3. Tört szorzása, osztása 1.3.4. Törtek összeadása kivonása 1.4. Hatványozás és gyökvonás
2. ALGEBRAI ÁTALAKÍTÁSOK 2.1. Műveletek tulajdonságai 2.2. Nevezetes azonosságok
2.3. Kifejezések egyszerűbb alakra hozása 2.3.1. Szorzattá alakítás
2.3.2. Négyzetgyökös kifejezések átalakítása 2.4. Műveletek algebrai törtekkel
3. FÜGGVÉNYEK
3.1. Függvények ábrázolása koordinátarendszerben 3.2. Műveletek függvényekkel
3.2.1. Összetett függvény 3.2.2. Inverz függvény 3.3. Függvények tulajdonságai
3.3.1. Zérushely 3.3.2. Tengelymetszet 3.3.3. Paritás
3.3.4. Periodikusság 3.3.5. Korlátosság 3.3.6. Monotonitás 3.3.7. Szélsőérték 3.3.8. Görbület 3.3.9. Inflexiós pont
3.3.10. Folytonosság
3.4. Fontosabb elemi függvények
3.4.1. Konstans és identikus függvény
3.4.2. Páros és páratlan kitevős hatvány függvény 3.4.3. Reciprok és lineáris törtfüggvény
3.4.4. Exponenciális függvény 3.4.5. Logaritmus függvény
3.4.6. Szinusz és koszinusz függvény 3.4.7. Tangens és kotangens függvény 4. EGYENLETEK ÉS EGYENLŐTLENSÉGEK
4.1. Algebrai megoldás
4.1.1. Másodrendű egyenletek, egyenlőtlenségek 4.1.2. Gyököt tartalmazó egyenletek, egyenlőtlenségek 4.1.3. Exponenciális egyenletek, egyenlőtlenségek 4.1.4. Logaritmusos egyenletek, egyenlőtlenségek 4.2. Grafikus megoldás
5. TRIGONOMETRIA
5.1. Nevezetes szögek szögfüggvény értékei 5.2. Trigonometrikus azonosságok
c) attitűdje pozitívan módosul, törekszik hiányos ismereteinek pótlására,
d) autonómiája és felelőssége is fejlődik az ismeretek önálló elsajátításával és a gyakorló feladatok autonóm megoldásával.
Jelen tananyag a Szegedi Tudományegyetemen készült az Európai Unió támogatásával. Projekt azonosító: EFOP-3.4.3-16-2016-00014.
1. MŰVELETEK SZÁMOKKAL
Ez a fejezet az egyetemi tananyag: mindegyik témaköréhez kapcsolódik, de kiemelkedően a vektorok és a lineáris algebra részekhez, ahol jellemzően sok számítási művelet végrehajtása szükséges.
Ebben a fejezetben a négy alapműveletet (összeadás, kivonás, szorzás és osztás), valamint a hatványozást tartalmazó kifejezések kiértékelésével foglalkozunk. De kezdjük egy példával! Számítsuk ki a következő kifejezés értékét:
Értelmeznünk kell a kifejezésben megjelenő számokat, előjeleket, műveleteket, valamint ismernünk kell a kiértékelés sorrendjét. A megoldás:
Első évfolyamos hallgatók középiskolai tudását felmérő tesztjénél tapasztaltam, hogy majdnem mindenki hibásan értelmezi a fenti kifejezést, s így negatív szám négyzetét számolja ki. Nézzük meg egy másik megközelítéssel is ezt a problémát: számoljuk ki esetén a következő kifejezés értékét:
Ekkor már jobban látható a helyes megoldás, hogy a szám négyzete előtt szerepel a negatív előjel. A megoldás emiatt:
A végrehajtás sorrendjét a műveletek prioritása határozza meg. A negatív előjel is értelmezhető műveletként, mégpedig mínusz eggyel szorzásnak. Az alapműveletek és a hatványozás esetén a prioritás a következő:
1. hatványozás, 2. szorzás, osztás 3. összeadás, kivonás
Ez alapján a hatványozást hamarabb kell elvégezni, mint a szorzást. Az első példában a negatív előjelet mínusz eggyel szorzással jelölve nézzük meg ismét a végrehajtás menetét lépésenként:
1.1. Műveleti sorrend, zárójel
A matematikában mindig nagyon fontos, hogy csak egyetlen módon legyen értelmezhető mindenki számára egy leírt kifejezés. Az előző példa legutóbbi megoldásánál az összeadás végrehajtása előtt két szorzást kellett még elvégezni, de ezek végrehajtásának sorrendje nem befolyásolta a végeredményt. Viszont két osztás esetén már problémák adódhatnak:
( ) vagy
( )
Természetesen az egyik (a második) értelmezés hibás. Zárójelekkel lehetőségünk van a végrehajtás sorrendjét jelölni. Erre akkor van szükség, ha a műveleti jelek prioritásától eltérő sorrendű végrehajtás szükséges, vagy a „többféle”, azaz a könnyen hibás értelmezhetőség miatt. Zárójelek nélkül az azonos prioritású műveletek esetén balról- jobbra kiértékelést kell alkalmazni:
( )
Az osztás műveletét ritkán jelöljük a kettőspont (: vagy ÷) jellel. Az Excel táblázatkezelő programban és általában a programozási nyelvekben a per (/) az osztás műveleti jele, míg kézírás során törtként jelenik meg az osztás:
⁄
Viszont a törtként alkalmazott írásmód során újabb fontos szempontként jelenik meg, hogy a számláló (a törtvonal felett), a nevező (a törtvonal alatt) vagy a törtvonal szintjén helyezünk el a kifejezésben további jeleket. Ez sok esetben nem értelmezhető, hibás írásmódot okozhat, de a kiértékelés sorrendjét is megváltoztathatja:
A fenti példákban azt látjuk, hogy az egyenlőségjel helyzete mutatott rá az emeletes tört kiértékelésének sorrendjére. Egy tört után csak a törtvonal szintjén helyezhetünk el újabb műveleti jelet, vagy egyenlőségjelet, különben nem értelmezhető a kifejezés.
Emeletes törteknél hosszabb törtvonallal is szokás jelezni a főtörtet. A fenti példákban az egyenlőségjel szintjén lehetne a hosszabb főtört. Így a felső példában a főtört számlálójában szerepel egy tört, míg az alsó példa esetén a főtört nevezőjében láthatunk törtet.
Nézzünk egy összetett kifejezésre példát:
( ) ( )
( )
1.2. Alapműveletek negatív számokkal
A számokat, nagyságukat szemléltetni a számegyenesen elhelyezkedésükkel lehet.
A számegyenes jellemzően egy vízszintes egyenes, melynek minden pontja egy-egy valós számot jelöl úgy, hogy kijelöljük rajta a 0 helyzetét, melytől jobbra a pozitív, balra pedig a negatív számok találhatók a 0-tól a szám abszolútértékének megfelelő távolságra egy alkalmas lépték szerint (például 1 cm-re a 0-tól balra a -1, míg jobbra a +1). Vagyis a szám nagysága (abszolútértéke) a számnak a 0-tól mért távolsága a számegyenesen. Így könnyen ábrázolható az összeadás és kivonás eredménye (1. ábra). A kiszámításakor kiindulunk a helyzetéből a számegyenesen, majd a hozzáadása miatt jobbra lépünk 3- at. Tehát pozitív szám hozzáadásakor jobbra lépéssel kapunk eredményt, míg pozitív szám kivonásakor balra lépéssel.
1. ábra Összeadás és kivonás ábrázolása a számegyenesen
Negatív szám hozzáadásakor illetve kivonásakor fordított irányú lépés alkalmazandó:
( ) ( )
Azt is vegyük észre, hogy egy előjel és egy műveleti jel közvetlen találkozását zárójelezéssel kell elkerülni. Nézzünk pár további példát összeadásra és kivonásra:
( )
( )
Szorzás és osztás során azonos előjelű résztvevők esetén pozitív eredményt kapunk, míg különböző előjelűeknél negatívat:
( ) ( ) ( ) ( ) Nézzünk erre is pár példát:
( ) ( ) 1.3. Alapműveletek közönséges törtekkel
Eddig csak olyan egész számokkal vizsgáltuk a műveleteket, melyek eredménye is egész szám volt. Összeadás, kivonás és szorzás esetén ez minden esetben így alakul, de két egész szám osztásakor általában az eredmény nem lesz egész szám. Racionális számoknak nevezzük azokat a számokat, melyek két egész szám hányadosaként, vagyis osztásuk eredményeként kapható meg. Természetesen az osztás művelete nem csak egész számokon értelmezhető. Fontossága miatt nézzük meg az egyetlen nem értelmezhető esetet, a nullával osztást. Sokan tényként elfogadják, hogy a 0-val osztás nem értelmezhető, de nem gondolnak bele ennek miértjébe. Most ezt tegyük meg!
Az osztás művelete a szorzás ellentétének, inverzének is tekinthető abban az értelemben, hogy az osztandó szám ( ) osztása az osztóval ( ) azt a hányadosnak ( ) nevezett számot kell, hogy eredményezze, melyre a hányados és az osztó szorzataként az osztandó szám adódik:
Viszont nullával osztáskor ( ) a következőt kapjuk:
Ez azt jelenti, hogy 0-val osztáskor az osztandónak is 0-nak kell lennie ( ).
Tehát csak a értelmezhető 0-val osztáskor. Ráadásul vizsgáljuk még meg azt is, hogy ekkor mi az eredmény, a hányados (c=?):
Vagyis olyan eredményt kell kapnunk, melyet nullával szorozva nulla adódik. Ez viszont bármely számra teljesül. Annak a műveletnek nincs értelme, melynek eredménye
bármilyen szám lehet. Csak akkor értelmezhető egy művelet, ha az mindenki számára ugyanazt az eredményt jelenti. Ezért a nullával osztás nem értelmezhető.
Két egész szám osztása ábrázolható a számegyenesen. A 2. ábrán a művelet látható, ahol a 4 nagyságú számot osztottuk 6 részre. Az eredmény egy olyan szám, melynek a nagysága az így keletkezett részek egyikének a hossza. Ez az eredmény nem egész szám, melynek pontos tizedes tört alakja ̇. A 6 számjegy feletti pont azt jelenti, hogy a tizedes törtben a 6 számjegy a végtelenségig ismétlődne. Szokásos még pont nélküli írásmódot is alkalmazva egy kerekített értékkel jelezni az eredményt: ̇ .
2. ábra Osztás ábrázolása számegyenesen
Belátható, hogy két egész szám hányadosa, vagyis egy racionális szám, amennyiben nem egész szám, akkor tizedes tört alakjában vagy véges számú tizedes jegyet tartalmaz, vagy ha nem véges számú tizedest, akkor ez csak véges hosszúsági számjegysorozat ismétlődésével lehetséges. Tehát tizedes tört alakjában leírni egy racionális számot pontosan nagyon nehézkes lehet:
̇ ̇
A esetén 6 számjegyből álló sorozat végtelenszer ismétlődését jelöli az első és utolsó tag feletti pont. Ezt az írásmódot tudjuk leegyszerűsíteni, ha tizedes tört helyett megtartjuk a tört alakját a számnak. Így a 4-nek 7-tel osztásának eredményét közönséges tört alakban, azaz formában írjuk. Ekkor a törtvonalat értelmezhetjük továbbra is úgy, mint az osztás műveleti jelét, de a tört leírására használható jelnek is. A törtként írásmódja a számoknak a pontosságán túl azért is előnyösebb, mert könnyebb velük további műveleteket végezni. Példaként számoljuk ki pontos és 4 tizedesre kerekített értékével ( ) a következő kifejezés értékét:
( )
Ebből a példából is látható, hogy közönséges törtként pontos eredmény adódik akár számológép használata nélkül, míg tizedes tört alakban csak számológéppel célszerű dolgozni. Ráadásul az eredmény sem lesz pontos, ha csak a kerekített kiinduló értéket tudjuk begépelni kiinduló adatként. Emiatt szükséges a törtekkel és a rajtuk végzett műveletekkel tisztában lenni.
1.3.1. Törtek egyszerűsítése, bővítése
Nem változik meg egy tört értéke, ha a számlálóját és a nevezőjét is ugyanazzal a nullától különböző számmal szorozzuk vagy osztjuk. Ezeket a műveleteket a tört egyszerűsítésének, illetve bővítésének nevezzük. A 2. ábrán jól látható, hogy a 4-nek 6-tal osztása megegyezik 2-nek 3-mal osztásával:
A tört egyszerűsített alakja , míg a fordított irányú átalakítást a tört bővítésének nevezzük. Egy tört esetén mindig törekedjünk az egyszerűsítésre, hiszen így kisebb számokkal megadva a törtet a további műveletek a törttel könnyebben elvégezhetők.
Egy tört bővítése a következő formájú:
( ) A tört egyszerűsítése a fordított irányú átalakítás.
1.3.2. Törtek értelmezése
A tört eddigi értelmezésünk szerint a 2-nek 3-mal osztásaként adódik. Ezzel szemben célszerűbb úgy értelmeznünk a törteket, hogy a nevező (3) azt mutatja, hogy az 1- et hány részre osztjuk, míg a számláló (2) jelentése, hogy ekkora részekből hányat veszünk. Így a kétharmad ( ) esetén harmadokból kell kettő:
3. ábra Tört értelmezése
A 3. ábrán megfigyelhetjük a fenti egyenlőség teljesülését. Az előző összefüggésből az is kiolvasható, hogy a hárommal osztás tekinthető egyharmaddal szorzásnak. Mivel a három és az egyharmad egymás reciprokai, ezért egy számmal osztás egyenértékű a szám reciprokával szorzással.
Az eddigiek általánosításaként a következő adódik:
( ) 1.3.3. Tört szorzása, osztása
A törtek legutóbbi értelmezése alapján könnyen adódik a törttel szorzás művelet végrehajtása. Ezt elsőként egy példán nézzük meg:
Általánosítva:
( )
A tört osztásának megértését egy példa fogja segíteni, kétharmad osztása öttel.
Mint látni fogjuk, ez a feladat visszavezethető az egyharmad öttel osztására. De a számegyenesen ez úgy interpretálható, hogy egy egyharmad hosszúságú szakaszt ót egyenlő részre osztunk, Egy ilyen eredmény szakasz hossza egy-tizenötöd nagyságú: mivel az 1 egész mind a három harmadán elvégezve az öt részre osztást, 15 részre osztottuk az 1- et.
Általánosítva:
( )
Egy tőrt osztásának művelete megközelíthető a bővítés és egyszerűsítés segítségével is. Nézzük meg így az előző példát!
Két tört szorzását is először egy példával nézzük meg. Itt ismét felhasználjuk, hogy egy számmal osztás egyenértékű a szám reciprokával szorzással.
Általánosítva:
( )
Két tört osztását emeletes törtként értelmezhetjük, ahol a tört számlálója és nevezője is tört. Az átalakítás során bővítést és egyszerűsítést alkalmazunk:
Ebben a példában megfigyelhetjük, hogy egy tört reciproka úgy adódik, hogy felcseréljük a számlálóját a nevezőjével. Még egy észrevétel, hogy egy egész szám is tekinthető törtnek, melynek nevezője egy (1).
Általánosítva:
( ) Tehát törttel úgy osztunk, hogy a tört reciprokával szorzunk.
1.3.4. Törtek összeadása kivonása
A kivonás és összeadás csak úgy végezhető el, ha a törteket közös nevezőre hozzuk. Ezt a törtek bővítésével érhetjük el. Célszerű a két nevező legkisebb közös többszörösét tekinteni közös nevezőnek. Legrosszabb esetben ez a két nevező szorzata.
Nézzünk erre egy példát:
Könnyen ellenőrizhető, hogy bármely más közös nevezővel is helyes eredmény adódik, mely akkor még egyszerűsíthető is. Általánosítva a következő adódik:
( ) A kivonás teljesen hasonló módon végezhető el.
Összefoglalva az eddigieket, a törtekkel a következő műveleteket végezhetjük el:
( )
( )
( )
( )
1.4. Hatványozás és gyökvonás
A hatványozás eredménye képezhető szorzással abban az esetben, ha a kitevő egynél nagyobb egész szám:
A hatványozásban szereplő mennyiségeket alapnak (2) és kitevőnek (5) nevezzük.
A fenti példa a hatványozás értelmezését mutatja. A hatványozás egy olyan szorzatnak tekinthető, ahol a hatvány alapja jelenik meg a szorzat tényezőiként, míg a hatvány kitevője a tényezők darabszáma. Persze ez az értelmezés csak akkor lehetséges, ha a tényezők darabszáma (kitevő) legalább kettő és egész szám. Ki fogjuk terjeszteni ellentmondásmentes (konzisztens) módon ezt az értelmezést úgy, hogy a kitevő tetszőleges valós szám lehessen. De elsőként a műveleti sorrendet tisztázzuk több hatványozást tartalmazó kifejezésnél:
( ) ( )
Az eddigiekben láttuk a hatványozás és szorzás műveletek „rokonságát”. Mivel az osztás tekinthető a szorzás inverz műveletének is, így a hatványozás az osztáshoz is szorosan kötődik. Viszont a nullával osztás nem értelmezhető, emiatt a hatványozásnál is meg fog jelenni olyan eset, amikor az alap nem lehet nulla. Elsőként nézzünk meg olyan kifejezéseket, melyekben a hatványozással együtt jelenik meg a szorzás, illetve az osztás:
( ) ( )
Mint látható, azonos alapú hatványok szorzásakor a közös alapot a kitevők összegére hatványozással kapunk eredményt, míg osztáskor a kitevők különbsége jelenik meg. Ezek az összefüggések általánosíthatók, csak osztáskor ne feledjük, hogy nullával nem oszthatunk. Viszont eddig a kitevőről kikötöttük, hogy legalább kettő legyen és egész.
Ez viszont az osztás eredményében, már nem fog mindig így adódni:
Terjesszük ki a hatványozás értelmezését tetszőleges egész kitevőre! A fenti példa alapján ezt megtehetjük a törtek egyszerűsítése alapján:
Az utóbbi összefüggés általánosításaként a következő adódik:
( )
A hatványozás így már tetszőleges egész kitevő esetére értelmezhető, de még vizsgáljuk meg a kitevő 0 és 1 értékét:
( )
( )
Nézzük meg egy-egy példával a hatványozás végrehajtását szorzaton, hányadoson és hatványon:
( ) ( ) ( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
Összeg és különbség hatványozása egészen más szabályokat igényel. Súlyos hiba lenne egy összeg tagonkénti hatványozása:
( )
Tehát összeg (különbség) hatványozását szigorúan tilos a tagok hatványának összegeként képezni!
Amíg a kitevő egész szám, addig az alapnak csak a nulla értéke vezetett nem értelmezhető hatványhoz. Amikor a kitevőt törtek esetén is értelmezzük, akkor már az alap negatív értéke is problémát okozhat az értelmezhetőségben. A tört kitevő értelmezésében a hatványra vonatkozó hatványozási összefüggést használjuk fel, azaz hatványt úgy hatványozunk, hogy az alapot a kitevők szorzatára emelünk. Nézzük meg a következő példát:
( )
Így az kitevős hatvány értelmezését olvashatjuk ki, mely a négyzetre emelés inverz művelete. Ez abból állapítható meg, hogy értéke az a szám, melynek a négyzete 9. A fenti példában a 9 helyén tetszőleges nem negatív számot is írhattunk volna, s így bármely ilyen számból kiindulva visszakapjuk a számot. Azaz az kitevőre hatványozás és a négyzetre emelés műveletek egymás inverzei. Persze a négyzetre emelés inverzét gyökvonásnak (négyzetgyök-vonásnak) nevezzük:
√ ( )
Negatív szám gyöke azért nem értelmezhető, mert ekkor a gyökvonás eredményének négyzeteként ezt a negatív számot kellene kapnunk, de ilyen valós szám nincs. Ehhez hasonlóan adódik a harmadik-gyök törtkitevős alakja:
√ ( )
Ekkor negatív szám is lehet az alap. Páratlan gyök negatív számokon is elvégezhető:
√ ( )
√ ( )
Az eddigiek alapján könnyen kiterjeszthetjük a hatványozás értelmezését arra az esetre, amikor a kitevő tetszőleges racionális szám:
√ ( )
Ez az összefüggés a törtek értelmezéséből és a hatvány hatványozásából azonnal adódik:
( ) √
Az értelmezhetőség feltételében láthatjuk, hogy egy valós szám hatványozása racionális kitevő esetén negatív és nulla alap estén is problémás lehet a kitevő értékétől függően. Folytatva a hatványozás értelmezhetőségének kiterjesztését, irracionális kitevő esetén már azt is megköveteljük, hogy az alap pozitív legyen. Az irracionális számok a nem racionális valós számok.
Összefoglalva az eddigieket, a hatványozás értelmezhetőségéről a következőket mondhatjuk:
Negatív kitevő, mely osztásra vezet, nulla alapra nem értelmezhető.
Páros gyök, mint a racionális kitevő egyik esete, negatív alapra nem értelmezhető.
Irracionális kitevőjű hatvány csak pozitív alapra értelmezhető.
Nulla a nulladikon nem értelmezhető.
Hatványozási azonosságok szorzatra, hányadosra és hatványra vonatkozhatnak általánosan valamely valós kitevő esetén:
( ) ( ) ( )
√
Összeg és különbség hatványozására csak a kitevő pozitív egész értéke mellett alkalmazhatunk azonosságot, melyet binomiális tételnek nevezünk:
( ) ( ) ( ) ( ) ( )
1.5. Ellenőrző kérdések, feladatok
Határozza meg az alábbi kifejezések értékét!
1.5.1.
(megoldás)
1.5.2.
(megoldás)
1.5.3.
(megoldás)
1.5.4.
(megoldás)
1.5.5.
(megoldás)
1.5.6.
(megoldás)
1.5.7.
(megoldás)
1.5.8.
(megoldás)
1.5.9.
(megoldás)
1.5.10.
√ √ √
√ √ √ (megoldás)
1.5.11.
(megoldás)
1.5.12.
√ √ √ √ √ (megoldás)
2. ALGEBRAI ÁTALAKÍTÁSOK
Ez a fejezet az egyetemi tananyag: mindegyik témaköréhez kapcsolódik, de kiemelkedően
a komplex számok,
a határérték,
határozatlan integrál
részekhez, ahol az algebrai átalakítások nélkülözhetetlenek.
A különböző tudományterületek sokszor a matematika eszközeit használják fel a törvények, összefüggések leírására:
Ezekben a kifejezésekben változókkal jelölünk egy-egy mennyiséget. Feladataink során a kifejezések átalakítására is szükségünk lehet. Egy kifejezésnek más-más alakjára lehet szükségünk akkor, amikor ki szeretnénk számítani az értékét a bennük szereplő változók különböző értékei mellett, mint amikor a határozatlan integrálját kell képeznünk.
Nézzünk erre egy példát!
Számoljuk ki az alábbi kifejezés értékét √ esetén!
A kifejezést célszerű átalakítanunk:
( )( )
( )( )
( )
Így már könnyen kiszámolható az eredmény:
√
A kifejezés eredeti alakja alkalmas a határozatlan integrál elvégzéséhez. Fordított irányú átalakítás szükséges, ha a másik alakjával rendelkezünk Az átalakítás részleteit most nem tárgyaljuk.
A kifejezésekben szereplő műveleti jelektől függ, hogy milyen szabályokat alkalmazhatunk az átalakítás során. Ebben a fejezetben először áttekintjük a műveletek tulajdonságait, a legfontosabb nevezetes azonosságokat, majd a leggyakoribb átalakításnak, a kifejezések egyszerűbb alakra hozásának technikáit.
A kifejezések leírásakor néhány szabályt ismernünk kell:
A szorzás jelét általában nem írjuk le, kivéve két szám szorzásakor.
Zárójelezést alkalmazunk műveleti jel és előjel találkozásának elkerülésére.
Feleslegesen zárójelet ne alkalmazzunk, csak ha hangsúlyozni szeretnénk a végrehajtás sorrendjét, vagy el szeretnénk kerülni a hibás értelmezést kritikusnak tűnő esetekben.
Tört utáni vagy előtti jel (műveleti jel, egyenlőség jel) csak a törtvonal szintjén állhat.
2.1. Műveletek tulajdonságai
A kifejezések átalakítása során a bennük szereplő műveletekre vonatkozó tulajdonságokat alkalmazzuk. Ebben a részben a négy alapművelet tulajdonságait tekintjük át, de kiemelten csak az összeadásra és a szorzásra vonatkozókat. A kivonás tulajdonságai az összeadáséból adódnak, míg az osztás tulajdonságai a szorzáséból, hiszen a kivonás visszavezethető a kivonandó ellentettjével végzett összeadásra, míg az osztást elvégezhetjük az osztandó reciprokával szorzásra:
( ) ( ) Az összeadás és a szorzás is kommutatív:
Az összeadás és a szorzás is asszociatív:
( ) ( ) ( ) ( ) A szorzás disztributív az összeadásra:
( ) ( )
Tehát teljesül mindkét irányban a disztributivitás. Valójában az egyik irányú disztributivitásból már következik a másik irányú is a szorzás kommutativitása miatt.
Könnyen belátható, hogy az osztás csak az egyik irányban disztributív az összeadásra, mert az osztás nem kommutatív:
( ) ( )
Sokszor tapasztaltam, hogy az osztásra vonatkozó disztributív tulajdonságot abban az irányban is alkalmazzák, amikor az nem teljesül. Ezért nézzünk erre egy példát is:
}
Ha a kivonást visszavezetjük összeadásra az ellentett segítségével, akkor azonnal adódik, hogy a szorzás a kivonásra is disztributív:
( ) ( ( )) ( ) ( ) A fordított irányú disztributivitás is teljesül, ami a fentiekhez hasonló módon levezethető. Mivel a szorzás az összeadásra és a kivonásra is disztributív, ezt szokás összevontan leírni:
( )
( ) } ( )
Most nézzünk arra példákat, hogy ezeket a tulajdonságokat használva, hogyan tehetjük fejben is könnyen kiszámolhatóvá a kifejezések értékét:
( ) ( ) ( )
( ) ( )
A disztributivitás kétszeri alkalmazásával könnyen belátható a következő összefüggés:
( ) ( ) ( ) ( )
Mint látható, kéttagú összegek szorzataként az eredmény négytagú összeg lesz, mert az első tényező minden egyes tagja szorzandó a második tényező minden tagjával.
Ehhez hasonlóan például egy háromtagú és egy öttagú összeg szorzata 15 tagú lesz.
Különbségek szorzásakor is hasonlóan járhatunk el, de a szorzás jelének elhagyásával fogunk most dolgozni:
( )( ) Nézzünk egy példát:
( )( )
( ) ( ) ( ) ( ) ( )
Amikor több sort igényel az átalakítás, akkor a sortörésnél csak „=” vagy „+” jel állhat a sor végén, amit a következő sor elején is el kell helyezni. Más jelnél sortörés nem lehet. A sor elején azért szükséges a sorvégi jel megismétlése, mert ezzel jelezzük, hogy ez
folytatás, nem pedig egy új rész. Például kivonás jel azért ne legyen sortörésnél, mert ennek ismétlése összeadásként érthető. Egy összeg tagjait célszerű úgy rendezni, hogy a nagyobb kitevős tagok előzzék meg a kisebb kitevős tagokat. Amikor egy tag szám és változó szorzata, akkor a szám álljon elől. a szokásos írásmód helyett.
2.2. Nevezetes azonosságok
Kifejezések átalakítása során gyakran találkozhatunk speciális alakúakkal, melyeket illik felismerni, hogy alkalmazhassuk a rájuk vonatkozó átalakítási lehetőségeket.
Ezek a nevezetes azonosságok a következők:
( ) ( )( ) ( )
( )( ) ( )( )
Ezek az azonosságok könnyen igazolhatók a műveletek tulajdonságai alapján. Most csak az utolsó bizonyítását nézzük meg, de javaslom a többi esetén is a bizonyítás önálló elvégzését.
( )( ) ( )
( ) Nézzünk egy-egy példát a fenti azonosságokra:
( ) ( )
A háromtagú eredmény középső tagját kétszeres szorzatnak nevezzük. Súlyos hiba, ha ez kimarad, s így csak a tagok négyzete jelenne meg az eredményben. Teljes négyzetté alakításnak hívjuk a fordított irányú átalakítást.
( ) ( )
A fenti példában maradék tag nélkül lehetett elvégezni a teljes négyzetté alakítást, de ez ritkán adódik így. Elsőként a , vagyis a keresett összeg első tagja határozható meg.
A kétszeres szorzat alapján kapjuk meg a keresett második tagot. Vagyis a kétszeres szorzatot a második tag értéke estén kapjuk a első tag alapján. De így a második tag négyzetével eltérés (maradék tag) nélkül kaptunk eredményt. Nézzünk most olyan példát is, melynél lesz maradék tag:
( ) ( )
Mivel a második tag négyzetétől eltérés jelentkezett, így maradék tagra is szükségünk volt. Nézzünk nehezebb teljes négyzetté alakítást is:
( ) ( ) (( ) ) ( ) ( )
Nézzünk példákat a többi azonosságra is:
( ) ( )( )
( ) ( )( ) ( )( ) ( )( ) ( )( ) 2.3. Kifejezések egyszerűbb alakra hozása
Az utóbbi két példa szorzattá alakítást oldott meg. Épp a fordított irányú átalakítás eredményezné a kifejezés egyszerűbb alakját, de osztás, azaz törtet tartalmazó kifejezések sokszor igénylik a szorzattá alakítást, hogy egyszerűbb közös nevezőt alakíthassunk ki, vagy, hogy egyszerűsíteni tudjuk a törtet.
( )
( )( )
Törtet egyszerűsíteni csak szorzattá alakítás után tudunk, mert csak olyan tényezővel egyszerűsíthetünk, mely a tört számlálójában és nevezőjében is előfordul.
( )
( )( )
Nagy hibának számít, ha a fenti példában a számlálót (1) elhagyjuk, és csak a nevezőt tekintjük eredménynek. Talán abból származik ez a hiba, hogy a nevezőben maradó 1 esetén ennek elhagyása megtehető:
( )( ) ( )
Ha a kifejezésben nincs osztás (tört), akkor többtagú összegek szorzását el kell végezni, majd összevonás után kapunk egyszerűbb alakot:
( ) ( )( ) ( )
2.3.1. Szorzattá alakítás
Nem csak a törtek esetén, de egyes feladat típusok megoldása során is alkalmazni kell a kifejezések szorzattá alakítását. Több technikát is alkalmazhatunk:
kiemelés,
nevezetes azonosságok,
gyöktényezős alak.
2.3.1.1 Kiemelés
A kiemeléssel szorzattá alakítás a műveleteknek abból a tulajdonságából adódik, hogy a szorzás disztributív az összeadásra (és a különbségre is). Emiatt, ha egy többtagú kifejezés minden tagjában szerepel ugyanaz a szorzótényező, akkor azt kiemelhetjük:
( ) Nézzünk erre egy példát:
( )
A fenti példában a középső lépést nem szokás leírni, azonnal írhatjuk a szorzat alakot. Sokszor olyankor is alkalmazzuk a kiemelést, amikor tört keletkezik:
( )
( )
Határérték számításnál az utóbbi típusú átalakítás gyakran szükséges. Ekkor úgy is gondolkodhatunk, hogy a kiemelt tényezővel minden tagot elosztunk, majd a kapott törtet egyszerűsítjük:
(
) ( ) (
) ( ) A feladattól függ, hogy a fenti változatok melyike segíti a megoldást.
2.3.1.2 Nevezetes azonosságok
A korábban már áttekintett nevezetes alkalmazások mindegyikét alkalmazhatjuk szorzattá alakításkor. Kellő gyakorlatra van szükségünk ahhoz, hogy megtaláljuk az alkalmas technikát, az alkalmazandó azonosságot. Rutin hiányában nem fogjuk meglátni, amikor teljes négyzettel van dolgunk. Sokszor több azonosságot is be kell vetnünk a szorzat kialakításához. Nézzünk előbb egyszerűbb, majd nehezebb példákat szorzat kialakítására:
( )( ) ( )( )( ) ( )( )
( )( ) ( )
( ) (( ) )(( ) ) ( )( ) Az utóbbi példában először a teljes négyzetté alakításkor maradék tagot kaptunk, majd két négyzet különbségére vonatkozó azonossággal alakítottunk szorzattá. Később látni fogjuk, hogy másodfokú kifejezések átalakítását szorzattá egyszerűbben is képezhetjük a gyöktényezős formával.
2.3.1.3 Gyöktényezős alak
Másodfokú kifejezések szorzattá alakítását sokszor nehéz elvégezni. Viszont ha ismerjük a kifejezés zérushelyeit (gyökeit), akkor ezekkel könnyen szorzattá tudunk alakítani. A másodfokú kifejezés zérushelyei (gyökei) azok az értékei a kifejezésben szereplő változónak, melyek behelyettesítésekor a kifejezés értéke nulla lesz. Ezeket a zérushelyeket megkaphatjuk az ismert másodfokú megoldóképlettel.
( ) √
Ekkor a szorzat:
( )( ) Példaként oldjuk meg így is a legutóbbi példát!
( ) √( )
√
( )( ) ( )( ) A következő példában a zérushelyeket javaslom önállóan meghatározni.
( ( )) ( ) ( ) ( ) ( )( ) 2.3.2. Négyzetgyökös kifejezések átalakítása
Amikor egész számok négyzetgyöke nem egész értékű, akkor irracionális szám, melynek tizedestört alakjában a tizedesjegyek ismétlődés nélkül végtelen számban követik egymást. Emiatt tizedestörtként nem tudjuk a pontos értékét leírni. Így a pontos értéket csak a gyökös forma megtartásával kapjuk. Ha ebben a gyökös alakban még számolási műveleteket is kell végeznünk vele, akkor ezt megkönnyíthetjük, ha:
kisebb értékre vonatkozik a gyökvonás,
a tört nevezőjében nincs gyök.
Nézzünk ilyen átalakításra pár példát!
√ √ √ √ √
√
√
√ √
√ √
√
√ √
√ √
Akkor tudunk kisebb egész számot szerepeltetni a gyök alatt, ha az eredeti olyan szorzattá alakítható, melynek egyik tényezője négyzetszám. A nevező gyöktelenítését a tört bővítésével oldhatjuk meg. Kéttagú nevező esetén a nevező konjugáltjával kell bővíteni a törtet. Két tag összegére ( ) és különbségére ( ) mondjuk, hogy egymás konjugáltjai.
√ √
√ ( √ ) ( √ )( √ )
√ √ √ √
√
√
√
√ √
√ (√ √ ) (√ √ )(√ √ )
√ √
√ √
√ √
√ √
√ √
√
√ √
√
√ √
√ √ √ √ √ √
2.4. Műveletek algebrai törtekkel
Azokat a törteket nevezzük algebrai törteknek, melyek nevezőjében változó szerepel. Összeadásuk során a nevezőik szorzattá alakításával kaphatjuk meg a legalkalmasabb közös nevezőt, mely azon tényezők szorzata, melyek legalább az egyik tört nevezőjében előfordultak. A több nevezőben is megjelenő tényezőt csak egyszer vegyük figyelembe. Nézzünk erre egy példát:
( )
( )( )
( )( ) ( )( )
( ) ( )( ) ( )
( )( )
( )( ) ( )
( )( )
( )
Amikor a közös nevező kialakítására nem fordítunk kellő figyelmet, és így olyan tényezőket szerepeltetünk, melyeknek van közös osztója, akkor bonyolultabb kifejezés adódik a számlálóban is. Ekkor az egyszerűbb alak elérése nagy nehézségekbe ütközik.
Kellő rutinnal elkerülhetjük az ilyen hibákat, s például észrevesszük két kifejezés esetén, ha egymásnak negatív konstans-szorosai.
( )
( )
Általánosítva az előző példában látottakat, ( ) és ( ) egymásnak ( )- szeresei. Nézzünk erre egy nehezebb példát is.
( )( ) ( ) ( )
( )( )
( ) ( ) ( )
( ) ( ) ( ) ( )
( )( )
( )( )
Az legegyszerűbb közös nevező kialakítását segítette, hogy az első tört ( ) tényezővel bővítésével ( ) helyett ( ) szerepelhetett a nevezőben, ( ) és ( ) egyenlők, míg a második törtben lehetett egyszerűsíteni. Sok gyakorlással ezeket a lehetőségeket meglátjuk, s így könnyebben megtaláljuk a kifejezések legegyszerűbb alakját.
Gyökvonást tartalmazó algebrai törteknél is szükségünk lehet konjugálttal bővítésre. Határérték meghatározásakor találkozhatunk sokszor ilyen átalakításokkal.
√
( )(√ ) (√ )(√ )
( )(√ )
√ ( )(√ )
( )(√ )
√
2.5. Ellenőrző kérdések, feladatok
Hozza egyszerűbb alakra az alábbi kifejezéseket!
2.5.1.
(megoldás)
2.5.2.
( ) ( ) ( ) (megoldás)
2.5.3.
( ) ( ) ( ) (megoldás)
2.5.4.
( ) ( ) ( ) (megoldás) 2.5.5.
( )
( ) (megoldás)
2.5.6.
( )
( )
(megoldás) 2.5.7.
√ √ √ (megoldás)
2.5.8.
√ √ √
(megoldás) 2.5.9.
(megoldás)
2.5.10.
(megoldás)
2.5.11.
( ) (
) (megoldás)
2.5.12.
( ) (
) (megoldás)
3. FÜGGVÉNYEK
Ez a fejezet az egyetemi tananyag témakörei közül szorosan kapcsolódik az alábbiakhoz:
elemi függvények,
határérték,
többváltozós függvények.
A matematikában fontos szerepet játszanak a függvények. Az egyváltozós valós függvények közül a fontosabb elemi függvényeket és tulajdonságaikat tekintjük át.
Függvénynek nevezünk egy hozzárendelést, mely egy halmaz minden eleméhez hozzárendeli egy halmaz egy-egy elemét. A halmazt a függvény értelmezési tartományának, míg az halmazt a függvény képhalmazának nevezzük. A képhalmaznak lehetnek olyan elemei is, melyek nem adódnak a hozzárendeléssel. A függvény értékkészletébe azok a képelemek tartoznak, melyeket valamely -beli elemhez rendeltünk.
Most csak olyan függvényeket tárgyalunk, melyeknél a hozzárendelést képlettel adott hozzárendelési szabállyal tudjuk megadni, és egy valós számhoz hozzárendelnek egy valós számot. Egy függvényt általánosan a következő formában adhatunk meg:
( ) Nézzünk erre egy példát:
)
A fenti példában a függvény jele, az értelmezési tartománya és a képhalmaza is a valós számok halmaza ( ), és minden elemhez ( ) annak négyzetét ( ) rendeli.
Alkalmazhatunk egy rövidebb írásmódot is függvény megadására:
( )
Ekkor a függvény hozzárendelési szabályát és értelmezési tartományát adtuk meg.
A legrövidebb megadási forma, amikor csak a hozzárendelési szabályt adjuk meg:
( )
Ekkor az értelmezési tartomány a valós számok legbővebb részhalmaza, melynek elemeivel elvégezhetők a hozzárendelési szabály műveletei.
Két függvényt akkor tekintünk egyenlőnek, amikor megegyezik az értelmezési tartományuk, és a hozzárendelési szabályuk is ugyanazt az értéket eredményezi. A következő két függvény megegyezik:
( ) { } ( ) { }
A fenti példában eltérő alakú a függvények hozzárendelési szabálya, de az értelmezési tartományuk minden eleméhez ugyanazt a számot rendelik:
( ) ( ) ( ) ( ) ( ) ( )
Ha az f függvény értelmezési tartományának egy eleme, akkor azt mondjuk, hogy az helyen a függvény értéke ( ).
Függvényeknél a következő jelöléseket alkalmazzuk:
Az függvény értelmezési tartománya
Az függvény értékkészlete
3.1. Függvények ábrázolása koordinátarendszerben
Korábban láttuk, hogy a valós számok ábrázolhatók egy számegyenes pontjaiként.
Egyváltozós valós függvények esetén, amikor egy valós számhoz ( ) egy valós számot ( ( )) rendelünk ( ), akkor ezt ábrázolhatjuk derékszögű koordinátarendszerben ( ) koordinátájú pontokkal, Egy pont azt mutatja meg, hogy az -tengely egy pontjához melyik pontját rendeljük az -tengelynek. A pontok összességeként megkapjuk a függvény grafikonját.
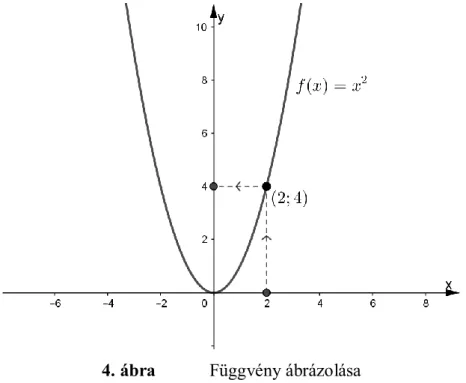
4. ábra Függvény ábrázolása
A 4. ábrán a függvény grafikonján kiemelten, teli karikaként megjelenített ( ) pont jelentése, hogy a függvény az értékhez az értéket rendeli. A
hozzárendelés pontjai általában a függvény grafikonjának egy folytonos szakaszát alkotják, és ekkor nem kell kiemelten megjeleníteni. Viszont a folytonos szakaszok végpontjait, ha vannak, akkor kiemelten ábrázoljuk. Üres karika szükséges, amikor az adott pont már éppen nem tartozik a grafikonhoz, különben teli karika. Ha a grafikon végén nincs kiemelt megjelenítésű pont, akkor ez folytatódást jelent, mely terjedelmi okokból hiányzik. Amikor a függvény grafikonja egy aszimptotának nevezett egyeneshez kerül egyre közelebb, akkor szaggatott egyenessel szerepeltetni kell, ha ez párhuzamos bármelyik tengellyel. Szebb az ábránk, ha akkor is megjelenítjük az aszimptotát, ha az nem párhuzamos a tengelyekkel, vagy esetleg nem is egyenes.
5. ábra Függvény aszimptotával és kiemelt pontokkal
Az ábrán az aszimptota miatt tudjuk, hogy ehhez tetszőlegesen közel kerül a függvény grafikonja (rásimul), de nem éri el Az üres karika jelzi, hogy ott nincs értelmezve a függvény, míg a teli karikánál befejeződik a grafikon.
3.2. Műveletek függvényekkel
Függvényekből újabb függvények képezhetők:
a négy alapművelettel,
összetett függvény képzéssel,
inverz függvény képzéssel.
Az összes elemi függvény így képezhető, csupán négy kiinduló függvényből:
Konstans függvény: ( )
Identikus függvény: ( )
Szinusz függvény: ( )
Exponenciális függvény: ( ) 3.2.1. Összetett függvény
Az összetett függvény képzéssel úgy kapunk újabb függvényt egy belső függvénynek és külső függvénynek nevezett két függvényből,, hogy a belső függvénnyel kapott értéken hajtjuk végre a külső függvényt. Az összetett függvény képzésének műveleti jele:
( ( ))
Ekkor az a külső, míg a belső függvény. Nézzünk erre egy példát!
( ) ( ) ( ( )) ( ( )) ( )
Legegyszerűbben úgy érthetjük meg az előző példát, ha az függvényre (külső) úgy tekintünk, amelyik a négyzetre emelés műveletet végzi el a változóján. De most ezt a műveletet a függvény (belső) értékén kell elvégezni, Persze a függvény értelmezése, hogy a változójának a kétszereséhez hozzáad egyet. Így már könnyen értelmezhetők ezekkel a függvényekkel további összetett függvények is:
( ( )) ( ) ( ( )) ( ( )) ( )
( ( )) ( ) ( )
Sok esetben arra is szükségünk lehet, hogy egy összetett függvény hozzárendelési szabálya alapján megállapítsuk, hogy mely függvényekből képezhető:
( ) ( ) ( ( )) ( ) ( ) Többszörösen összetett függvényt kettőnél több függvényből képezhetünk:
( ) ( ) ( )
( ( ( ))) ( ( )) ( ( )) ( ) 3.2.1.1 Függvény lineáris transzformációja
A fenti példában a ( ) függvény lineáris transzformáltját kaptuk az ( ) és ( ) lineáris függvényekkel. Bármely függvény lineáris transzformáltja hasonló módon
adódik. Egy összetett függvény esetén fel kell ismerni, ha az egy függvény lineáris transzformáltja:
( )
Ekkor az ( ) függvény lineáris transzformáltja a fenti függvény. A lineáris transzformációt a ( ) és ( ) függvények írják le. Ezek a többszörösen összetett függvény legkülső és legbelső függvényei:
( ) ( ( ( )))
Általánosságban egy függvény az függvénynek lineáris transzformáltja, ha ( ) ( )
Tehát a ( ) és a ( ) lineáris függvényekkel összetett függvényként kapjuk a függvény lineáris transzformáltját. Az függvény grafikonjából négy lépésben kapjuk meg lineáris transzformáltjának grafikonját:
1. ( ) ( ), az grafikonjának szorzó tényezővel nyújtása (| | ), zsugorítása (| | ), tükrözése ( ) az x tengely irányában:
2. ( ) ( ) ( ( )) ( ), az grafikonjának értékkel eltolása az x tengely irányában:
3. ( ) ( ), az grafikonjának szorzó tényezővel nyújtása (| | ), zsugorítása (| | ), tükrözése ( ) az y tengely irányában:
4. ( ) ( ) ( ), az grafikonjának értékkel eltolása az y tengely irányában:
Az egyes transzformációs lépések mindig az előző lépésben kapott függvényen értendők, míg az első lépéshez az függvény grafikonja szükséges. Az első két lépés x irányú változásokat jelent, melyek inverz módon alkalmazandók a grafikon x koordinátájának megváltozásában. A két utolsó transzformációs lépésben az y koordináták megváltozása a transzformációban megjelenő művelettel számolható ki.
Ezek a lineáris transzformációk a függvény grafikonjának jellegét alapvetően nem változtatják meg. Például egy egyenes lineáris transzformáltja egyenes lesz, parabolából is parabola marad.
3.2.2. Inverz függvény
Egy függvényből az inverz függvényt megkaphatjuk, ha a hozzárendelés irányát megfordítjuk. A fordított irányú hozzárendelés csak akkor tekinthető függvénynek, ha egyértelmű. Emiatt sok függvénynek nem létezik az inverze csak akkor, ha az értelmezési tartományát úgy korlátozzuk, hogy a hozzárendelési szabálya kölcsönösen egyértelmű legyen. Például az ( ) függvénynek nem létezik az inverze, ha az értelmezési tartománya a valós számok halmaza. Mivel ekkor például a és a elemek képe megegyezik ( ), így a fordított irányú hozzárendelés kétértelmű, tehát nem függvény. A negatív valós számokat kihagyva az értelmezési tartományból, már kölcsönösen egyértelmű lesz a hozzárendelés.
Az függvény inverzét jelöli, és a következők igazak rá:
( ( ))
Mindezek a fordított irányú hozzárendelésből adódnak. Az utolsó azt jelenti, hogy az inverz függvény az ( ) értékhez az értéket rendeli: ( )
Az inverz függvény hozzárendelési szabályát megkaphatjuk a függvény hozzárendelési szabályának átrendezésével. Így azt a képletet keressük, mellyel x adódik eredményként ( ) értékéből. Nézzünk erre egy példát:
( ) ( )
( ) ( ( ))
( )
Az és függvények grafikonjai egymás tükörképei az tükrözési tengely esetén. Ez szintén a fordított irányú megfeleltetés következménye, hiszen most az x tengely és y tengely szerepe felcserélődik. Ezt a cserét eredményezi az egyenesre tükrözés.
Az ábrán az előző példa függvényeinek grafikonjai láthatók, mint egymás tükörképei. Az egyenes szaggatott vonallal látható.
6. ábra Függvény és inverze 3.3. Függvények tulajdonságai
A függvényeket tulajdonságaikkal jellemezhetjük. Ezek a tulajdonságok legegyszerűbben a függvény grafikonjából állapíthatók meg. Ha viszont nem ismerjük a grafikont, akkor különböző matematikai módszerekkel adódnak a tulajdonságok, melyek alapján a grafikon elkészíthető.
3.3.1. Zérushely
Az érték az függvény zérushelye, ha ( ) teljesül. Tehát a zérushelyek az értelmezési tartománynak azok az értékei, melyekhez a függvény a 0 értéket rendeli. A függvény grafikonjának a zérushelyekhez tartozó pontjai ezért az x tengelyen találhatók. Tehát a grafikonról is megállapíthatók a zérushelyek, melyek az x tengelynek a grafikonnal közös pontjai, metszéspontjai.
3.3.2. Tengelymetszet
Tengelymetszetnek az ( ) értéket nevezzük, ha . A függvény grafikonja itt metszi az y tengelyt.
3.3.3. Paritás
A párosság és páratlanság a függvény grafikonjának szimmetriáját jelzik. Páros függvény grafikonja az y tengelyre szimmetrikus, míg páratlan függvény grafikonja középpontosan szimmetrikus az origóra. Ezeket a tulajdonságokat könnyen megtudhatjuk a függvény hozzárendelési szabályából. Az elnevezés onnan származik, hogy a hatvány függvények ( ( ) ) esetén a páros kitevőjűek a páros, míg a páratlan kitevőjűek a páratlan függvények.
• Az függvény páros, ha minden esetén és ( ) ( )
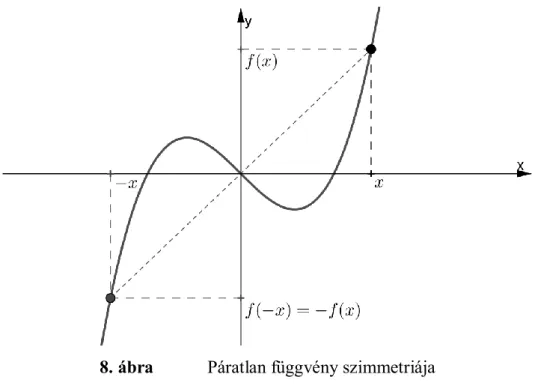
• Az függvény páratlan, ha minden esetén és ( ) ( ) A definíciók alapján egyszerűen belátható a függvények szimmetriája, ahogy ez a következő ábrákon látható.
7. ábra Páros függvény szimmetriája
8. ábra Páratlan függvény szimmetriája
A legtöbb függvény se nem páros, se nem páratlan. Ha egy függvény grafikonja tengelyesen szimmetrikus, de nem az y tengelyre, akkor nem páros. Ehhez hasonlón egy középpontosan szimmetrikus grafikonú függvény nem páratlan, ha nem az origó a szimmetria középpontja.
3.3.4. Periodikusság
Az elnevezés onnan származik, hogy periodikus függvény esetén a függvényértékek periodikusan ismétlődnek.
• Az függvény periodikus, ha van olyan valós szám, hogy minden esetén és ( ) ( ).
• A valós számot periódusnak nevezzük.
A függvény grafikonján is megfigyelhetjük a periodikusan ismétlődő szakaszokat, mint ahogy ez a következő ábrán látható.
9. ábra Periodikus függvény
Ha egy periódusú függvény, akkor a függvényértékek megegyeznek az [ ] és [ ] intervallumokon ( ).
3.3.5. Korlátosság
A függvény értékeinek, értékkészletének korlátok közötti elhelyezkedését mutatja a függvény korlátossága. Beszélhetünk a függvény alulról és felülről korlátosságáról.
Az ( ) függvény alulról korlátos, ha létezik olyan szám, hogy minden esetén ( ).
Az ( ) függvény felülről korlátos, ha létezik olyan szám, hogy minden esetén ( ).
Az ( ) függvény korlátos, ha alulról és felülről is korlátos.
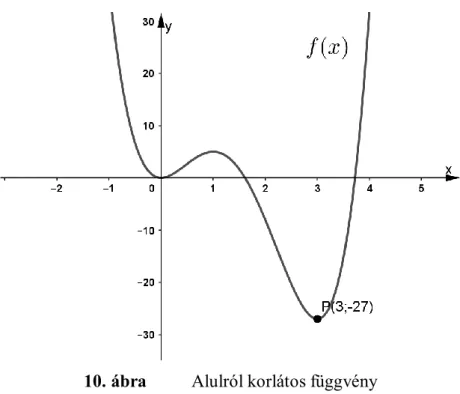
Egy függvény grafikonja alapján egyszerűen megállapítható a korlátossága. Ehhez példaként nézzük a következő ábrát.
10. ábra Alulról korlátos függvény
A függvény grafikonjának a pontjait az y tengelyre vetítve, megkapjuk az értékkészletét. Ebből látható, hogy -27 a legkisebb értéke a függvénynek, és bármilyen nagy értéke lehet. Így alulról korlátos, de felülről nem a függvény, tehát nem korlátos. Az y tengelyen a -27 alatti értékek is alsó korlátok, de a legnagyobb alsó korlát (infimum) a -27. Felülről korlátos függvénynél szuprémumnak nevezzük a legkisebb felső korlátot.
3.3.6. Monotonitás
A függvény értékek változását (növekedését, csökkenését) mindig az x értékek növelése esetén nézzük, különben csak nézőpont kérdése lenne, hogy növekvő vagy csökkenő a függvény. A függvények az értelmezési tartományuk egyes intervallumaiban eltérően viselkedhetnek, emiatt a monotonitás definíciók adott intervallumokhoz kötötten adottak.
• Az függvény monoton növekvő az ] [ intervallumon, ha minden esetén ( ) ( )
• Az függvény szigorúan monoton növekvő az ] [ intervallumon, ha minden esetén ( ) ( )
• Az függvény monoton csökkenő az ] [ intervallumon, ha minden esetén ( ) ( )
• Az függvény szigorúan monoton csökkenő az ] [ intervallumon, ha minden esetén ( ) ( )