c 2019 The Author(s)
https://doi.org/10.1007/s00012-019-0615-3 Algebra Universalis
Eighty-three sublattices and planarity
G´abor Cz´edli
Dedicated to professor George A. Gr¨atzer on his eighty-third birthday.
Abstract.Let Lbe a finite n-element lattice. We prove that ifL has at least 83·2n−8 sublattices, thenLis planar. Forn >8, this result is sharp since there is a non-planar lattice with exactly 83·2n−8−1 sublattices.
Mathematics Subject Classification.06B99.
Keywords. Finite lattice, Planar lattice, Sublattice, Number of sublat- tices, Subuniverse, Computer-assisted proof.
1. Our result and introduction
A finite lattice is said to beplanar if it has a Hasse diagram that is also a planar representation of a graph. Our goal is to prove that finite lattices with many sublattices are planar. Namely, we are going to prove the following theorem.
Theorem 1.1. Let Lbe a finite lattice, and let n:=|L| denote the number of its elements. IfL has at least 83·2n−8 sublattices, then it is a planar lattice.
Another variant of this result together with a comment on its sharpness will be stated in Theorem2.2.
Notes on the dedication
As a coincidence, the numbereighty-threeplays a key role in Theorem1.1, and I found this theorem recently, in the same year when professor George Gr¨atzer, the founder of Algebra Universalis, celebrates his eighty-third birthday. For more about him, the reader is referred to my biographic paper [2] and the interview [3] with him. Furthermore, the topic of the present paper is close to his current research interest on planar lattices; this interest has been witnessed, say, by Cz´edli and Gr¨atzer [6,7], Cz´edli, Gr¨atzer, and Lakser [8], Gr¨atzer [11,
Presented by R. Freese.
This research was supported by the Hungarian Research, Development and Innovation Office under Grant Number KH 126581.
0123456789().: V,-vol
12,13,14,15,16], Gr¨atzer and Knapp [17,18,19,20,21], Gr¨atzer and Lakser [22], Gr¨atzer, Lakser, and Schmidt [23], Gr¨atzer and Quackenbush [24], Gr¨atzer and Schmidt [25], and Gr¨atzer and Wares [26]. These facts motivate the dedication.
Remark 1.2. Although 41.5·2n−7, 20.75·2n−6, 10.375·2n−5, . . . and 166·2n−9, 332·2n−10, 664·2n−11, . . . are all equal to 83·2n−8, we want to avoid fractions as well as large coefficients of powers of 2. This explains the formulation of Theorem1.1.
Remark 1.3. For n ≥ 9, Theorem 1.1 is sharp, since we will present an n- element non-planar lattice with exactly 83·2n−8−1 sublattices. For n <9, Theorem1.1 can easily be made sharp as follows. Whenever n≤7, everyn- element lattice is planar, regardless the number of its sublattices. While the eight-element boolean lattice has exactly 73 sublattices, every eight-element lattice with at least 74 = 74·28−8 sublattices is planar.
Next, we mention some earlier results that motivate the present paper. As a counterpart of Theorem1.1, finite lattices with many congruences are also planar; see Cz´edli [5] for details. Finite lattices with “very many” congruences or sublattices have been described by Ahmed and Horv´ath [1], Cz´edli [4], Cz´edli and Horv´ath [9], and Mure¸san and Kulin [28].
Outline
The rest of the paper is devoted to the proof of Theorem 1.1. In Section 2, we recall the main result of Kelly and Rival [27]; this deep result will be the main tool used in the paper. Some easy lemmas and the proof of Remark1.3 are also presented, and we introduce a terminology that allows us to formulate Theorem1.1in an equivalent and more convenient form; see Theorem2.2. Also, this section describes our computer program that was used in the proofs of many lemmas in the paper. Section3gives some more details of this computer- assisted effort but the proofs of some lemmas stated there are available only from separate files or from the appendices of the extended version of the paper;
see Proof Technique 2.8 later for coordinates. Also, Section3combines many of our lemmas and corollaries to complete the proof of Theorem 2.2 and, thus, Theorem 1.1. Finally, Section 4 points out some difficulties explaining why we do not see a computer-free way to prove Theorem 2.2 (equivalently, Theorem1.1) and why a lot of human effort is needed in addition to the brutal force of computers.
2. Tools and difficulties
2.1. Relative number of subuniverses
Let F be a set of binary operation symbols. By a binary partial algebra A of type F we mean a structureA = (A;FA) such that A is a nonempty set, FA={fA:f ∈F}, and for eachf ∈F,fA is a map from a subset Dom(fA) ofA2 to A. That is, fA is a binarypartial operation onA. If Dom(fA) =A2 for allf ∈F, thenAis abinary algebra (without the adjective “partial”). In
particular, every lattice is a binary algebra; note that we write∨and∧instead of ∨A and ∧A when the meaning is clear from the context. A subuniverse of A is a subset X of A such that X is closed with respect to all partial operations, that is, whenever x, y ∈ X, f ∈ F and (x, y) ∈ Dom(fA), then fA(x, y)∈X. The set of subuniverses ofA will be denoted by Sub(A). For a latticeL= (L;{∨,∧}), we will writeLrather thanL. Note that the number of sublattices ofLis|Sub(L)|−1, since the set of sublattices ofLis Sub(L)\{∅}.
IfB= (B, FB) withB ⊆A is another binary partial algebra of type F such that Dom(fB)⊆B2∩Dom(fA) for every f ∈F andfB(x, y) =fA(x, y) for all (x, y)∈Dom(fB), thenBis said to be aweak partial subalgebra ofA.
It is straightforward to drop the adjective “binary” from the concepts defined above. Even if this adjective is dropped in Lemma 2.3, to be stated soon, we will use this lemma only for the binary case. All lattices, posets, and partial algebras in this paper are automatically assumed to be finite even if this is not repeated all the time.
This paper is about lattices withmanysublattices. Large lattices have a lot of subuniverses and sublattices since every singleton subset of a lattice is a sublattice. So it is reasonable to define the meaning of “many” with the help of the following notation.
Definition 2.1. Therelative number of subuniverses of ann-element finite bi- nary partial algebraA= (A, FA) is defined to be and denoted by
σ(A) :=|Sub(A)| ·28−n.
Furthermore, we say that a finite latticeLhasσ-many sublattices or, in other words, it hasσ-many subuniverses ifσ(L)>83.
This concept and notation will play a crucial role in the rest of the paper.
Since|Sub(L)|is larger than the number of sublattices by 1, we can reformulate Theorem1.1and a part of Remark1.3as follows.
Theorem 2.2. If Lis a finite lattice such thatσ(L)>83, thenLis planar. In other words, finite lattices with σ-many sublattices are planar. Furthermore, for every natural number n≥9, there exists ann-element lattice Lsuch that σ(L) = 83 andLis not planar.
The importance of the concepts introduced in this section so far is well explained by the following easy lemma.
Lemma 2.3. If B = (B, FB) is a weak partial subalgebra of a finite partial algebraA= (A, FA), thenσ(A)≤σ(B).
Proof. Letm:=|B| andn:=|A|. Thenk:=n−m=|A\B| ≥0. Define an equivalence relation∼on Sub(A) by lettingX ∼Y mean thatX∩B =Y∩B. Since X∩B ∈ Sub(B) for every X ∈ Sub(A), this equivalence has at most
|Sub(B)| blocks. Every block of ∼ is a subset of {U ∪X : X ⊆ A\B} for some U ∈Sub(B). Since A\B has 2k subsets, every block of∼consists of at most 2k elements of Sub(A). Therefore, |Sub(A)| ≤ |Sub(B)| ·2k. Dividing this inequality by 2n−8= 2m−8·2k, we obtain the validity of the lemma.
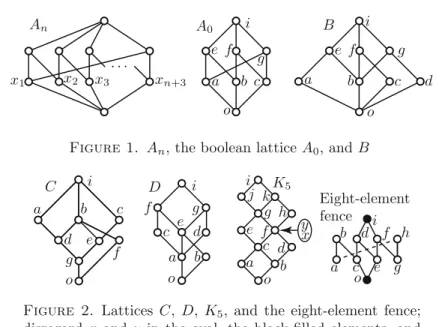
Figure 1. An, the boolean lattice A0, and B
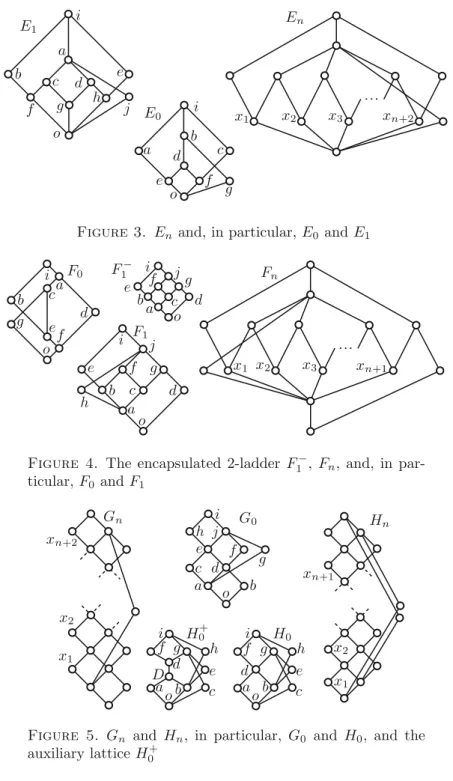
Figure 2. Lattices C, D, K5, and the eight-element fence;
disregard x and y in the oval, the black-filled elements, and the dashed line
Remark 2.4. Quite frequently, only the following particular and, in fact, trivial case of Lemma2.3will be used. Namely, assume that (B, F) is a finite partial algebra. For eachf ∈F, pick an extension f: Dom(f)→B of f. That is, Dom(f)⊇Dom(f) andf is the restriction off to Dom(f); possibly,f =f. Then, withF:={f :f ∈F}, we have thatσ(B, F)≥σ(B, F).
2.2. The Kelly–Rival list
For a poset P, its dual will be denoted by Pδ. With reference to Kelly and Rival [27] or, equivalently, to Figures1,2, 3, 4 and5, theKelly–Rival list of lattices is defined as follows.
LKR:={An, En, Enδ, Fn, Gn, Hn:n≥0} ∪ {B, Bδ, C, Cδ, D, Dδ}.
Note thatAn,Fn, Gn, andHn are selfdual lattices. The key tool we need is the following deep result.
Theorem 2.5 (Kelly and Rival [27]).A finite lattice is planar if and only if it does not contain any lattice inLKRas a subposet.
Note that being a subposet is a weaker assumption than being a sublat- tice.
2.3. A computer program
Since it would be a very tedious task to compute σ(X) manually even for the smallest latticeX ∈ LKR, we have developed a straightforward computer program for Windows 10 to do it. This program, calledsubsize, is downloadable from the author’s website. The input of the program is an unformatted text file describing a finite binary partial algebraA = (A;F); there are several word
Figure 3. En and, in particular,E0 andE1
Figure 4. The encapsulated 2-ladder F1−, Fn, and, in par- ticular,F0andF1
Figure 5. Gn and Hn, in particular, G0 and H0, and the auxiliary latticeH0+
processors that can produce such a file. In particular, the description of A includes a list of stringsx∗y=zof length five where∗is an operation symbol in F, (x, y)∈Dom(fA) and fA(x, y) =z; these strings are calledconstraints
in the input file. The output,σ(A), is displayed on the screen and saved into a text file. The algorithm is trivial: the program lists all the 2|A|subsets ofA and counts those that are closed with respect to all constraints.
Remark 2.6. The running time of our program depends exponentially on the input size|A|. Hence, a lot of theoretical considerations are necessary before resorting to the program and what is even worse, many cases have to be input into the program. Because of the exponential time, it is not clear (and it is not hopeful) whether the appropriate cases could be found by a much more involved (and so less reliable) computer program without a lot of human work.
So the program is simple, we believe it is reliable, and it is not to hard to write another program to test our input files. On the other hand, the exceptionally tedious work to find the appropriate cases and to create the input files needed several weeks.
However, it is quite easy to obtain the following statement with the help of our computer program.
Lemma 2.7 (on small Kelly–Rival lattices).
(i) For the smallest lattices inLKR, we have that σ(A0) = 74,σ(B) = 54, σ(C) = 68.5, σ(D) = 76,σ(E0) = 60.5, σ(F0) = 83, σ(G0) = 54.25, andσ(H0) = 49.75.
(ii) We also have thatσ(E1) = 31.125 andσ(F1) = 41.125.
Except forσ(A0) = 74, this lemma will not be used in the proof of Theo- rem2.2. However, a part of this lemma will be used in the proof of Remark1.3 below, and it is this lemma that tells us how the theorem was conjectured.
Even the proof of (part (i) of) this lemma requires more computation than a human is willing to carry out or check without a computer.
Proof of Remark1.3. For n = 9, the equality σ(F0) = 83 from Lemma 2.7 proves the validity of Remark 1.3 since F0 is not planar by Theorem 2.5.
Assume thatn >9, letCbe an (n−9)-element chain, and letLbe the ordinal sum ofF0 andC. That is,L is the disjoint union of its idealF0 and its filter C. By Theorem2.5,Lis not planar. Since a subset ofLis a subuniverse if and only if it is of the formX∪Y such thatX ∈Sub(F0) and Y ⊆C, it follows that
|Sub(L)|=|Sub(F0)| ·2n−9= (83·2|F0|−8)·2n−9= 83·2n−8,
wherebyLhas exactly 83·2n−8−1 sublattices, as required.
Proof Technique 2.8. For Lemma2.7and also for all other statements that re- fer to the program or mentionσ(. . .), the corresponding input files are avail- able from the author’s website http://www.math.u-szeged.hu/∼czedli/ The output files proving these statements are also available there and they are at- tached as appendices to the extended version of the paper; seehttp://arxiv.
org/abs/1901.00572 (and see the author’s website for the most current ver- sion). Note that the input files are not hard to obtain from the output files.
2.4. Lattice theoretical preparations
The proof of Theorem2.2 will be organized as follows. Due to Theorem2.5, it suffices to show that for each latticeX ∈ LKR, wheneverLis a lattice with σ-many subuniverses (that is,σ(L)>83), thenX cannot be a subposet ofL.
Although we present some uniform arguments for several infinite sub-families of LKR, separate arguments will be needed for most of the small lattices in LKR. The following lemma is crucial.
Lemma 2.9 (Antichain Lemma).If{a0, a1, a2}is a three-element antichain in a finite lattice withσ-many subuniverses, then
(i) There is ak∈ {0,1,2} such thata0∨a1∨a2=
{ai :i∈ {0,1,2}\{k}}.
(ii) If{i, j, k}={0,1,2} and none ofai∨aj andai∨ak equalsa0∨a1∨ak, thenai∨aj =ai∨ak.
Part (ii) of this lemma is trivial; we present it here to emphasize its implicit use in our considerations and in the input files of the program.
Proof. For the sake of contradiction, suppose that (i) fails for a lattice L with σ-many subuniverses. Then X := {a0∨a1, a0∨a2, a1∨a2} is a three- element antichain. It is well known that such an antichain generates a sub- lattice isomorphic toA0, the eight-element boolean lattice; see, for example, Gr¨atzer [10, Lemma 73]. Combining Lemmas 2.3 and 2.7, we obtain that σ(L)≤σ(A0) = 74, which contradicts the assumption thatσ(L)>83.
Lemma 2.10. IfL is a finite lattice withσ-many subuniverses, thenA0 is not a subposet ofL.
Proof. For the sake of contradiction, suppose thatA0 is a subposet ofL and σ(L)>83. Sincea, b, cplay symmetric roles, Lemma2.9(i) allows us to assume thatc≤a∨b∨c=a∨binL. Thenc≤a∨b≤eis a contradiction, as required.
The following lemma needs a bit longer proof and the use of the program.
This proof exemplifies many ideas that will be needed later. Note that K5, defined by Figure 2, is a sublattice of Gn and Hn for n ≥1, this is why it deserves our attention.
Lemma 2.11. IfL is a finite lattice withσ-many subuniverses, thenK5 is not a subposet ofL.
Proof. For the sake of contradiction, suppose that σ(L) > 83 but K5 is a subposet ofL. For the notation of the elements ofK5, see Figure2.
Lattice theoretical preparatory part. We modify K5 in L if necessary. The operations∨and ∧ will be understood inL. We can assume that e∨f =g, since otherwise we can replace g by e∨f. Of course, we have to show that this replacement results in an isomorphic subposet, but this is easy; analogous tasks will often be left to the reader. Namely,e∨f ≤hwould lead toe≤h, a contradiction, whilee∨f ≥hcombined withg≥e∨f would lead tog≥h, another contradiction. By duality, we also assume that e∧f = c. Next, we
can assumec∧d=band, dually,g∨h=k, because otherwise we can replace b and k by c∧dand g∨h, respectively. This is possible since, for example, a≤dimplies thata≤c∧dwhilec∧d≥band a≥b exclude thata≥c∧d.
In the next step, we assume similarly that a∧b = o and j∨k = i. Note that the equalities assumed so far and the comparability relations among the elements imply further equalities:e∧d=e∧(f∧d) = (e∧f)∧d=c∧d=b, a∧d=a∧c∧d=a∧b=oand, dually, e∨h=kandj∨h=i. The set
T :={e∨f =g, e∧f =c, g∨h=k, c∧d=b, a∧b=o, j∨k=i, e∧d=b, a∧d=o, e∨h=k, j∨h=i}
defines a partial algebraK5(0)on the setK5, which is a weak partial subalgebra ofL. Note (again) that the program calls the members ofT constraints.
Computational part.The program proves thatσ(K(0)5 ) = 97.375, which means that we are not ready yet. Here, there will be two cases. (In general, a whole hierarchy of cases have to be investigated.) The idea is that for incomparable elementsxandy, in notation,xy, such thatx∨y orx∧y is not defined in the partial algebra, the argument splits into two cases: eitherx∨y(orx∧y) is one of the elements already present, or it is a new element ofLthat we add to the partial algebra. In terms of the program, we add a new constraint with or without adding a new element. Also, when we add a constraint, then we also add its consequences similarly to the previous paragraph where, say,e∧d=b.
(Note that if an element had three covers or three lower covers, then we would use Lemma2.9to split a case into three subcases, but this technique will be used later, not in the present proof.) A case with name ∗will be denoted by (C∗).
(C1) We assume thatc∨d=f andg∧h=f. Thene∨d=e∨c∨d= e∨f =g and, dually, e∧h=c. Adding these four constraints to the earlier ones, we get a new partial algebraK(1)5 , which is a weak subalgebra ofL. The program yields thatσ(K(1)5 ) = 79.1875. Hence,σ(L)≤79.1875 by Remark2.4, contradicting the initial assumption thatσ(L)>83. This excludes (C1).
Based on the argument for (C1) above, to make our style more concise, let us agree to the following terminological issue, which will usually be used
implicitly in the rest of the paper.
Terminology 2.12. The cases we consider describe partial algebras, which are weak partial subalgebras of L; the σ-values of these partial algebras will be called theσ-values of the corresponding cases. If theσ-value of a case is not greater than 83, then the case in question is excluded.
(C2) We assume that c∨d =: x < y := g∧h. We remove f from the weak partial algebra and add xand y. We remove the constraints of T that containf but we add the new constraintsc∨d=x,g∧h=y,e∨y=g, and e∧x= c. The last two constraints we add follow from x≤ f ≤ y and the previous constraints containing f. Note that the oval in Figure2 reminds us that now{f}is replaced by{x, y}. Since theσ-value of the present situation is 80.5625, (C2) is excluded by Lemma2.3.
After excluding both cases, that is, all possible cases, the proof of the
lemma is complete.
Next, for later reference, we formulate a consequence, which trivially follows from Lemma2.11.
Corollary 2.13. If L is a lattice with σ-many subuniverses and n ≥ 1, then none ofGn andHn is a subposet ofL.
In order to formulate the following lemma about the encapsulated 2- ladder F1− given in Figure 4, we need the following definition. This concept will be motivated by Corollary2.16later.
Definition 2.14. LetLandK be finite lattices. A mappingϕ:K→Lwill be called a (2.1)-embedding if
ϕ is an order-embedding, ϕ(u) = ϕ(v)∨ϕ(w) holds for every triplet (u, v, w) ∈ K3 of distinct elements such that ucovers bothv andw, and dually.
⎫⎬
⎭ (2.1)
Note that if v and w are distinct elements covered by u in K, then u=v∨Kw, and the dual of this observation also holds. Hence, every lattice embedding is a (2.1)-embedding but, clearly, not conversely.
Lemma 2.15 (Encapsulated 2-ladder Lemma).If the encapsulated 2-ladderF1− is a subposet of a latticeL, then it has a (2.1)-embedding intoL.
Proof. We can assume thatF1− ⊆L. The notation of the elements ofF1− is given in Figure4. We are going to modify these elements in Lif necessary in order to obtain a (2.1)-embedding. The operations∨and∧will be understood inL. First, we letf:=b∨c. Sinceb≤g, we have thatf ≤g. Sincef≤f and f ≥g, we obtain thatf ≥g. That is,f is incomparable withg; in notation, f g. We obtain similarly thatf xfor all x∈F1− such thatx f. This allows us to replacef by f. To ease the notation, we will writef instead of f. So,F1− is still a subposet ofL but now f =b∨c. Next, we replace c by c:=f∧g≥c; then it is straightforward to see (or it follows by duality) that we still have a poset embedding. Sincef =b∨c ≤b∨c ≤f, we have that f =b∨c. Thus, after writing c instead ofc, the notation still gives a poset embedding ofF1−intoLwith the progress that nowb∨c=f andf∧g=c. We continue in the same way step by step, always defining a new poset embedding such that the already established equalities remain true; note that the order of adjusting the elements is not at all arbitrary. In the next step, we replaceb byb :=e∧f ≥bandg byg :=c∨d≤g to addb=e∧f and g=c∨dto the list of valid equalities. We continue with setting a=b∧c and j =f∨g similarly. Finally, redefiningiandoase∨j anda∧d, we complete the proof.
Armed with Lemma 2.15, we can give an easy proof of the following statement.
Corollary 2.16. If L is a lattice with σ-many subuniverses, then F1 is not a subposet ofL.
Proof. Suppose the contrary. ThenF1−, which is a sublattice of F1, is also a subposet of L. By Lemma 2.15, we can assume that F1− is a subposet of L such that the inclusion map is a (2.1)-embedding. Hence, we know that
e∧f =b, c∨d=g, b∧c=a, f∨g=j, (2.2) a∧d=o, e∨j=i, b∨c=f, f∧g=c, (2.3) b∨g=b∨c∨g=f∨g=j, b∧g=b∧f∧g=b∧c=a, (2.4) c∧e=c∧f∧e=c∧b=a, f∨d=f ∨c∨d=f∨g=j. (2.5) Theσ-value of the situation described by (2.2)–(2.5) is 81.75.
The eight-element fence is the poset formed by the eight empty-filled elements on the right of Figure 2. If we add the dashed line to its diagram, then we obtain the diagram of the eight-crown. So the diagram of the eight- crown consists of the eight empty-filled elementsa, b, . . . , h, seven solid edges and a dashed one. Note that the eight-crown is a subposet ofA1, see Figure1, but the eight-element fence is not.
Lemma 2.17. If L is a finite lattice with σ-many subuniverses, then neither the eight-element fence, nor the eight-crown is a subposet ofL.
Proof. To ease the terminology in this proof, by theeight-poset P8 we shall mean either the eight-element fence, or the eight-crown; see Figure2 for the notation of its elements. For the sake of contradiction, suppose thatσ(L)>83 butP8is a subposet ofL.
Lattice theoretical preparatory part.The set ofatoms and that ofcoatoms of P8 are{a, c, e, g} and{b, d, f, h}, respectively. We claim that the subposetP8
ofLcan be chosen so that
if x and y are distinct atoms of P8 and z ∈ P8 such that x≤zandy≤z, thenz=x∨Ly, and dually for coatoms.
(2.6) In particular, (2.6) implies that the equalities
a∨c=b, c∨e=d, e∨g=f, b∧d=c, d∧f =e, f∧h=g (2.7) hold; here and later in the proof, the lattice operations are understood inL.
In order to prove (2.6), we will modify the elements of P8 one by one until all equalities listed in (2.6) hold. By duality, it suffices to show that for each coatomz ofP8 covering two distinct atoms,xandy ofP8, if we replacez by z :=x∨y, then the subposet (P8\{z})∪ {z} of L is still isomorphic to P8
and, in addition to the progressx∨y =z, all the previously valid equalities from (2.6) remain true if we replacezbyz in them.
Ifzis a meetand in an equality from (2.6) that holds inL, then the meet isxor y, andx≤z ≤z or y≤z ≤z shows that the equality remains true after replacing z by z. As a coatom of P8, z can be neither a joinand, nor a meet in an equality from (2.6). Finally, the only stipulation of (2.6) withz being a join is the equality with joinandsxandy; this fails withzbut becomes true after replacingzbyz.
Next, we show that the mapP8 → (P8\{z})∪ {z}, defined by z → z andu→ufor u=z, is an order isomorphism. Let u∈P8\{z}. Sincez is a coatom ofP8,z ≤u. If we had z ≤u, then x≤u,y ≤u, andu∈P8 would give thatu=z, contradicting u∈P8\{z}. That is, neither u≤z, nor u≤z holds. Ifu≤z, then we concludeu≤zsincez < z. Conversely, ifu≤z, then u∈ {x, y}sincexandy are the only elements ofP8below z, wherebyu≤z. This shows that the map in question is an order isomorphism and completes the proof of (2.6). Thus, we have also proved (2.7).
Next, we define o := c∧e and i := d∨f in L. They are distinct new elements since{a, c, e, g}and{b, d, f, h}are antichains. We have that
d∨f =i, c∧e=o, b∧e=o, c∧f =o, d∨g=i, f∨c=i, (2.8) since the first two of these equalities are due to definitions and the rest are easy consequences; for example, b∧e=b∧d∧e=c∧e=o while the rest follow by duality or symmetry.
Computational part.For the elementsa, b, . . . , h, o, isubject to (2.7) and (2.8), theσ-value is 84.5; see Terminology2.12. In other words, we obtain with our usual technique (that is, using the program and Lemma2.3) thatσ(L)≤84.5.
Since this estimate is too week to derive a contradiction, we distinguish two cases.
(C1) We assume thatb∨d=i. Thenb∨e=i also holds sinceb∨e= b∨c∨e=b∨d=i. Adding these two equalities to (2.7) and (2.8), theσ-value is 79, which excludes this case by Remark2.4.
(C2) We assume thatx:=b∨d=i. We also have that b∨e=xsince b∨e=b∨c∨e=b∨d. Now we have eleven elements and, in addition to the two equalities just mentioned, (2.7), and (2.8). Since theσ-value is 77.25, this case is also excluded by Lemma2.3.
Both cases have been excluded, which proves Lemma2.17.
The lemma we have just proved trivially implies the following statement.
Corollary 2.18. If L is a lattice with σ-many subuniverses and n ≥ 1, then none ofAn,En+1, andFn+1 is a subposet ofL.
In the rest of the paper, due to Corollaries2.13and2.18and the Duality Principle, we need to exclude only finitely many members of the infinite list LKR as subposets of a finite lattice L with σ-many subuniverses. After the proofs of Lemmas2.11and2.17, our plan to exclude that a given memberX of LKR occurs as a subposet of a lattice L with σ(L) >83 is the following.
After assuming thatXis a subposet ofL, first we need some lattice theoretical preparation to ensure a feasible computational time. In the second phase, Lemma2.3(or, sometimes, even Remark2.4) allows us to reduce the estimate onσ(L) by assuming equations and introducing new elements in a systematic way until we obtain thatσ(L)≤83. In other words, we keep branching cases until all “leaves of our parsing tree” haveσ-values at most 83. Unfortunately, this plan requires quite a lot of work; see Table (3.2) later. In the rest of the paper, we present some of the details in order to give a better impression how
our plan works. The rest of the details are given by the output files of our program and some of them in the extended version of the paper; see Proof Technique 2.8 for their coordinates. Note that Lemma 2.3 or its particular case, Remark 2.4 will be used more than a hundred times in the proof of Theorem2.2; this will be clear from theσ-values occurring in Table (3.2). This lemma and Remark2.4 are so crucial in our plan that, to avoid a ponderous style, we will use them mostly in an implicit way.
3. The rest of the lemmas and some proofs
In order to complete the proof of Theorem2.2, we still need the following eight lemmas, in whichLdenotes a finite lattice.
Lemma 3.1. Ifσ(L)>83, thenB is not a subposet of L.
Lemma 3.2. Ifσ(L)>83, thenC is not a subposet of L.
Lemma 3.3. Ifσ(L)>83, thenD is not a subposet of L.
Lemma 3.4. Ifσ(L)>83, thenE0 is not a subposet of L.
Lemma 3.5. Ifσ(L)>83, thenE1 is not a subposet of L.
Lemma 3.6. Ifσ(L)>83, thenF0 is not a subposet of L.
Lemma 3.7. Ifσ(L)>83, thenG0 is not a subposet ofL.
Lemma 3.8. Ifσ(L)>83, thenH0 is not a subposet of L.
Proof of Lemma3.6. For the sake of contradiction, suppose that σ(L)> 83 butF0is a subposet ofL.
Lattice theoretical preparatory part.Unless otherwise stated, the lattice op- erations are understood inL; in notation,x∨y will mean x∨Ly and dually.
Note thatF0is a selfdual lattice and it has a unique dual automorphism i a b c d e f g o
o f g e d c a b i
.
Sincee∨F0g=c, we have thate∨g≤c. If c:=e∨g < c, then we replacec byc. Observe thate≤dandg≤bimply thatc≤dandc≤b. Sincec< c butb≤candd≤c, we also have thatb≤c andd≤c. So it follows that the subposet (F0\{c})∪ {c}ofLis isomorphic toF0. Hence, after replacingcby c if necessary, we can assume thate∨g=c. In the next step, after replacing ebye :=b∧c, we assume thatb∧c=e; we still have a subposet (isomorphic to)F0. Clearly, e∨g=c remains valid, becausec=e∨g≤e∨g≤c. With f := e∧d ≥ f, f ≥g would give that e ≥ g while f ≤ g would lead to f ≤g. Hence,fg. After replacingf byf if necessary, we can assume that e∧d=f. A dual argument allows us to assume thatc∨d=a. In the next step, we can clearly assume thata∨b =i andf ∧g=o. To summarize, we have assumed that the inclusion map is a (2.1)-embedding ofF0into L, that is,
b∧c=e, e∨g=c, c∨d=a, d∧e=f, a∨b=i, f∧g=o. (3.1)
Computational part.While splitting the possibilities into cases and subcases, we will benefit from the fact that bothF0 and (3.1) are selfdual. We keep s- plitting (sub)cases to more specific subcases only as long as theirσ-values are larger than 83; this tree-like splitting structure will have thirteen leaves, that is, thirteen subcases with smallσ-values that cover all possibilities. Every case below is eitherevaluated, that is, itsσ-value is computed by the program, or the case is split further. Of course, we have evaluated all cases to see which of them need further splitting, but we present theσ-values only of the non-split cases, because only the thirteen evaluated cases are needed in the proof. The (sub)cases are denoted by strings. When a case (Cx) is mentioned, all the “an- cestor cases”, that is, (Cy) for all meaningful prefixesyofx are automatically assumed.
(C1):b∨c=iis assumed; thenb∨g=b∨e∨g=b∨c=ialso holds.
(C1a): e∧g =o. Since this is the dual of the previous assumption, we are in a selfdual situation. Observe thatb∧g=b∧c∧g=e∧g=o.
(C1a.1):d∨e=a, thenb∨d=b∨e∨d=b∨a=i.
(C1a.1a):c∧d=f; thend∧g=d∧c∧g=f∧g=o. Again, we are in a selfdual situation.
(C1a.1a.1):a∧b=e; thenb∧d=b∧a∧d=e∧d=f.
(C1a.1a.1a):f∨g=c; thend∨g=d∨f∨g=d∨c=a. (Note that this case describes the situation whenF0is a sublattice ofL.) Since theσ-value of this case is 83,Lhas few subuniverses, whereby (C1a.1a.1a) is excluded.
(C1a.1a.1b):f∨g=:xsuch thatx=c. (The notation “=:” means that xis defined asf∨g andf∨g=xis a new constraint.) Clearly, x < c. Using the incomparabilities among the elements of F0, it is straightforward to see thatxis a new element. (In what follows in the paper, an element with a new notation will always be distinct from the rest of elements, but usually this fact will not be mentioned and its straightforward verification will be omitted.) Since c = e∨g ≤ e∨x ≤ c, we have that e∨x = c. Since the σ-value of this case is 74.25, (C1a.1a.1b) is excluded. Thus, the case (C1a.1a.1) is also is excluded. Since (C1a.1a) is seldfual, the dual of (C1a.1a.1) is also excluded;
this will be used in the next case.
(C1a.1a.2): a∧b =: x > e and f ∨g =: y < c. Since c∧b = e and e∨g =c, it follows easily that c∧x=e and e∨y =c Since the σ-value is now 68, (C1a.1a.2) is excluded. Thus, (C1a.1a) is also excluded.
(C1a.1b):c∧d=:x > f. Then e∧x=f sincee∧d=f. (C1a.1b.1):x∧g=o. Thend∧g=g∧c∧d=g∧x=o.
(C1a.1b.1a)a∧b=e. Now theσ-value is 78.25, excluding this case.
(C1a.1b.1b):a∧b=:y > e. This case is excluded again since itsσ-value is 78.5. Thus, (C1a.1b.1) is also excluded.
(C1a.1b.2): x∧g =: y > o. Here y is a new element since g > y > o, and we have that d∧g =d∧c∧g =x∧g = y. This case is excluded, be- cause itsσ-value is 79.375. Thus, (C1a.1b) and so (C1a.1) are also excluded.
Furthermore, since (C1a) is selfdual, we conclude that dual of (C1a.1) is also excluded; this fact will be used in the next case.
(C1a.2):d∨e=:v < aandc∧d=:u > f. Observe thatc∨v=aande∧ u=f, sincec∨d=aande∧d=f. Letx:=e∨u. In order to verify its novelty, observe thate≤x≤csincee < c andu≤c. But x=ewould implyu≤e, whenceu=e∧u=e∧c∧d=e∧d=f, a contradiction. Also,x=cwould lead tov=e∨d=e∨(u∨d) = (e∨u)∨d=x∨d=c∨d=a, a contradiction again.
Hence,e < x < c, which implies easily thatxis a new element. We have thatd∨
x=vsincee≤x≤v. Similarly,b∧x=esincee≤x≤c. Now theσ-value of the situation is 66, whereby this case is excluded. Thus, (C1a) is also excluded.
(C1b):e∧g=x > o; thenf∧x=osincef∧g=o.
(C1b.1):d∨e=a; thenb∨d=b∨e∨d=b∨a=i.
(C1b.1a):c∧d=f; thend∧g=d∧c∧g=f∧g=o.
(C1b.1a.1):a∧b=e. Now b∧d=b∧a∧d=e∧d=f andσ= 78.25 excludes this case.
(C1b.1a.2):a∧b=:y > e. Thenc∧y =esince c∧b =e, andσ = 72 excludes this case. Thus, (C1b.1a) is also excluded.
(C1b.1b): c∧d=: u > f; thene∧u=f sincee∧d= f, and σ = 80 excludes this case. Thus, (C1b.1) is also excluded.
(C1b.2):d∨e=:v < a; thenc∨v=asincec∨d=a.
(C1b.2a):c∧d=f. Thend∧g=d∧c∧g=f∧g=o andσ= 79.375 excludes this case.
(C1b.2b):c∧d=:u > f. Then e∧u=f sincee∧d=f, and σ= 75.5 excludes this case. Thus, (C1b.2), (C1b), and even (C1) are excluded. Further- more, since the underlying assumption, (3.1), is selfdual, the dual of (C1) is also excluded; this fact will be used below when (C2) is analyzed.
(C2)b∨c=:t < iande∧g=:s > o. Usinga∨b=iandf∧g=o, we obtain thata∨t =i and f ∧s =o. Also,b∨g =b∨e∨g =b∨c =t and b∧g =b∧c∧g=e∧g=s, and so σ= 82.5, excluding this case. All cases have been excluded, and the proof of Lemma3.6is complete.
Note that the proof above required to compute an estimate for σ(L) thirteen times. Let us call these thirteen values final σ-values. However, as mentioned previously, many more values were needed to find the proof. For example, theσ-value of (C1a.1a.1) is 90.5, and the inequality 90.5>83 is the reason to split the case (C1a.1a.1) into subcases.
Remark 3.9 (Notes on the proofs of Lemmas 3.1–3.8). First, observe that σ(F0) = 83 is the largestσ-value occurring in Lemma 2.7. Thus, Lemma 3.6 devoted toF0is the most crucial one in the paper. Since even the “human part”
of its computer-assisted proof is long and threatens with unnoticed human er- rors, we have elaborated two separate proofs of Lemma3.6. One of these proofs is optimized in some sense and it has already been given, and it is also available from the corresponding fileF0-output.txt. The other proof is less optimized and it is described only by its output file calledF0-alternative-output.txt.
One might think that, compared to Lemma3.6, the seven other lemmas of this section are easier simply because while Lemma3.6is devoted toF0and σ(F0) = 83, the other lemmas deal with latticesX ∈ LKR withσ(X)<83.
However, some of these lemmas need even more tedious proofs than Lem- ma 3.6. Because such amount of straightforward technicalities would not be too exciting for the reader and because of space considerations, these proofs are not given in the concise version of this paper; most of them are appendices in the extended version of the paper, and all of them are downloadable as out- put files of our computer program. Assuming that the reader shares our trust in our computer program or he writes another computer program, these files constitutecomplete proofs. In particular, these files include lots of comments that make them almost as detailed as the proof of Lemma3.6.
Remark 3.10 (On the lengths of the proofs of Lemmas 3.1–3.8). The table below gives the numbers of finalσ-values that our proofs, that is, the program output files, contain. We have already mentioned that the3.6-labeled column gives 13. The∗-labeled column refers to the second proof of Lemma3.6given in the downloadable fileF0-alternative-output.txt.
Lemma 3.1 3.2 3.3 3.4 3.5 3.6 ∗ 3.7 3.8 X∈ LKR B C D E0 E1 F0 F0 G0 H0
|{final σ-values}| 11 12 5 37 5 13 19 24 67 (3.2) In order to explain some large numbers in the third row of the table, note the following. IfX∈ LKRcontains no element with more than two covers or more than two lower covers, then the proof of the corresponding lemma is quite similar to that of Lemma 3.6; of course, we can exploit duality only if X itself is selfdual. Note that symmetries with respect to automorphisms can also be exploited. However, if there are elements with more than two lower covers or dually, like in case ofH0, then there can be cases that we split into three subcases according to Lemma2.9 as follows. Leta0, a1, and a2 be the three lower covers of an element b in X ∈ LKR; the case of upper covers is analogous. Let c := a0∨a1∨a2 in L. (Usually, b is meet-irreducible and we can let c := b.) Then the following three subcases are considered. First, a0∨a1=c. Second,a0∨a1:=x < cis a new element anda0∨a2=c. Third, a0∨a1 =:x < c, a0∨a2 =:y < c,x=y are new elements, and a1∨a2 =c.
It is not surprising now that this three-direction splitting leads to more final σ-values than the two-direction splittings in the proof of Lemma3.6. With an opposite effect, there is another factor related to the numbers of finalσ-values.
Namely,σ(X)<σ(F0) = 83 for allX ∈ LKR\{F0} that occur in the lemmas of this section, whereby we do not have to be so efficient for theseX as forF0; simply because our lemmas for theseX state less than an affirmative answer to Problem4.1(ii). To conclude Remark3.10, we mention that there are many ways to prove the eight lemmas with the help of our program, and not much effort has been devoted to reduce the numbers in the third row of Table (3.2);
such an effort would have required too much work. Some of these numbers might decrease in the future.
Finally, armed with our lemmas and corollaries, we are ready to present the concluding proof of the paper.
Proof of Theorem2.2. For the sake of contradiction, suppose thatLis a finite lattice such thatσ(L)>83. By Lemmas2.10and3.1–3.8and Corollaries2.13, 2.16, and 2.18, none of the lattices occurring as excluded subposets in these twelve statements is a subposet ofL. Usingσ(Lδ) =σ(L) and applying these twelve statements to Lδ, we obtain that none of the duals of the excluded lattices is a subposet ofL. Hence, no member ofLKRis a subposet ofL, and Theorem2.5implies thatLis planar, as required.
4. Concluding remarks
This section points out some difficulties explaining why we do not see a short- er way to prove Theorem 2.2 (equivalently, Theorem 1.1). Lemma 2.3 and Theorem2.5 raise the following problem; B, C, . . . , H0 still denote lattices in LKR.
Problem 4.1. LetX andLbe finite lattices such thatX is asubposet ofL.
(i) Isσ(L)≤σ(X) necessarily true in this case?
(ii) With the additional assumption that
X ∈ {B, C, D, E0, E1, F0, G0, H0}, isσ(L)≤σ(X) necessarily true?
If we could answer at least part (ii) of Problem4.1affirmatively, then the proof of Theorem 2.2would only require the lemmas of Section 2 and small input files for our computer program.
Remark 4.2. There are a lot of finite lattices X such that for every finite latticeL,σ(L)≤σ(X) ifX is a subposet ofL. For example,X =F0has this property.
Proof of Remark4.2. Every finite chain obviously has the property above, whence there are “a lot of” such lattices. The proof of Lemma 3.6 has, in effect, established the above property of X = F0. Also, we can derive this property of F0 from Theorem 2.2 as follows. For the sake of contradiction, suppose thatX =F0 is a subposet of L but σ(L)> σ(F0). We know from Lemma2.7that σ(F0) = 83. Soσ(L)>83, and we obtain from Theorem 2.2 thatLis planar. Hence, by Theorem2.5,F0 cannot be a subposet ofL, which
is a contradiction.
Remark 4.3. One may think of the following possibility: if X ∈ LKR is a subposet ofLwithσ(L)>83,c, e∈X, andc∨Xe=g, then eitherc∨Le=g inL, or x:=c∨Le < g∈L\X. If we could show that
ifX belongs to LKR, then the second alternative (withx) always yields a better (that is, smaller) estimate ofσ(L),
(4.1) thenX being asublatticewould give the worst estimate but even this estimate would be sufficient to imply Theorem2.2 by Lemma 2.7. We do not know if (4.1) is true; the following example, in whichX happens not to be in LKR, illustrates why (4.1) and Problem4.1are probably difficult.
Example 4.4 (Example to indicate difficulty). Let us denote by X the sub- poset{c, d, e, f, g, o, i} ofH0; see Figure5. Note that X is a lattice but not a sublattice ofH0. IfX is a subposet of a finite latticeL such that
c∨Le=g and g∧Lf =d, (4.2)
then σ for the weak partial subalgebra of L with base set {c, d, e, f, g, o, i}
and the equalities of (4.2) equals 192. So (4.2) is appropriate to show that σ(L) ≤ 192. However, if drop the first equality in (4.2) and replace it by c∨Le = x, where x < g, then the weak partial subalgebra with base set {c, d, e, f, g, o, i, x} and equalities c∨e = x and g∧f = d gives a worse estimate,σ(L)≤196.
Acknowledgements
Open access funding provided by University of Szeged (SZTE).
Open Access. This article is distributed under the terms of the Creative Common- s Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.
0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Publisher’s Note Springer Nature remains neutral with regard to jurisdiction- al claims in published maps and institutional affiliations.
References
[1] Ahmed, D., Horv´ath, E.K.: Yet two additional large numbers of subuniverses of finite lattices. Discussiones Mathematicae—General Algebra and Applications (in press)
[2] Cz´edli, G.: Celebrating professor George A. Gr¨atzer. Categor. Gen. Algebra.
Struct. Appl.11, 1–9 (2019)
[3] Cz´edli, G.: An interview with George A. Gr¨atzer. Categor. Gen. Algebra. Struct.
Appl.11, 11–17 (2019)
[4] Cz´edli, G.: A note on finite lattices with many congruences. Acta Univ. M. Belii Ser. Math.26, 19–25 (2018)
[5] Cz´edli, G.: Lattices with many congruences are planar. Algebra Univers.80, 16 (2019)
[6] Cz´edli, G., Gr¨atzer, G.: Planar Semimodular Lattices: Structure and Diagrams.
In: Gr¨atzer. G, Wehrung, F. (eds) Lattice Theory: Special Topics and Applica- tions. Vol. I. Birkh¨auser, Cham, pp. 91–130 (2014)
[7] Cz´edli, G., Gr¨atzer, G.: Notes on planar semimodular lattices. VII. Resections of planar semimodular lattices. Order30, 847–858 (2013)
[8] Cz´edli, G., Gr¨atzer, G., Lakser, H.: Congruence structure of planar semimodular lattices: The General Swing Lemma. Algebra Univers.79, 40 (2018)
[9] Cz´edli, G., Horv´ath, E.K.: A note on lattices with many congruences. Miskolc Mathematical Notes(in press)
[10] Gr¨atzer, G.: Lattice Theory: Foundation. Birkh¨auser, Basel (2011)
[11] Gr¨atzer, G.: Notes on planar semimodular lattices. VI. On the structure theorem of planar semimodular lattices. Algebra Univers.69, 301–304 (2013)
[12] Gr¨atzer, G.: Planar semimodular lattices: congruences. In: Gr¨atzer. G., Wehrung, F. (eds) Lattice Theory: Special Topics and Applications. Vol. I.
Birkh¨auser, Cham, pp. 131–165 (2014)
[13] Gr¨atzer, G.: On a result of G´abor Cz´edli concerning congruence lattices of planar semimodular lattices. Acta Sci. Math. (Szeged)81, 25–32 (2015)
[14] Gr¨atzer, G.: Congruences in slim, planar, semimodular lattices: the swing lemma.
Acta Sci. Math. (Szeged)81, 381–397 (2015)
[15] Gr¨atzer, G.: Congruences of fork extensions of slim, planar, semimodular lattices.
Algebra Univers.76, 139–154 (2016)
[16] Gr¨atzer, G.: Congruences and trajectories in planar semimodular lattices. Dis- cus. Math. Gen. Algebra Appl.38, 131–142 (2018)
[17] Gr¨atzer, G., Knapp, E.: Notes on planar semimodular lattices. I. Construct.
Acta Sci. Math. (Szeged)73, 445–462 (2007)
[18] Gr¨atzer, G., Knapp, E.: Notes on planar semimodular lattices. II. Congruences.
Acta Sci. Math. (Szeged)74, 37–47 (2008)
[19] Gr¨atzer, G., Knapp, E.: A note on planar semimodular lattices. Algebra Univers.
58, 497–499 (2008)
[20] Gr¨atzer, G., Knapp, E.: Notes on planar semimodular lattices. III. Rectangular lattices. Acta Sci. Math. (Szeged)75, 29–48 (2009)
[21] Gr¨atzer, G., Knapp, E.: Notes on planar semimodular lattices. IV. The size of a minimal congruence lattice representation with rectangular lattices. Acta Sci.
Math. (Szeged)76, 3–26 (2010)
[22] Gr¨atzer, G., Lakser, H.: Congruence lattices of planar lattices. Acta Math. Hun- gar.60, 251–268 (1992)
[23] Gr¨atzer, G., Lakser, H., Schmidt, E.T.: Congruence lattices of small planar lat- tices. Proc. Am. Math. Soc.123, 2619–2623 (1995)
[24] Gr¨atzer, G., Quackenbush, R.: The variety generated by planar modular lattices.
Algebra Univers.63, 187–201 (2010)
[25] Gr¨atzer, G., Schmidt, E.T.: An extension theorem for planar semimodular lat- tices. Period. Math. Hungar.69, 32–40 (2014)
[26] Gr¨atzer, G., Wares, T.: Notes on planar semimodular lattices. V. Cover- preserving embeddings of finite semimodular lattices into simple semimodular lattices. Acta Sci. Math. (Szeged)76, 27–33 (2010)
[27] Kelly, D., Rival, I.: Planar lattices. Can. J. Math.27, 636–665 (1975)
[28] Kulin, J., Mure¸san, C.: On the largest numbers of congruences of finite lattices.
Order(in press) G´abor Cz´edli Bolyai Institute University of Szeged Aradi v´ertan´uk tere 1 Szeged 6720
Hungary
e-mail: czedli@math.u-szeged.hu
URL: http://www.math.u-szeged.hu/czedli/
Received: 7 May 2019.
Accepted: 29 August 2019.