Gazdaságmatematikai és statisztikai ismeretek
/Gyakorlati jegyzet/
2
Gazdaságmatematikai és statisztikai ismeretek
/Gyakorlati jegyzet/
Szerző:
Kovács Sándor (9 - 15. fejezet)
Debreceni Egyetem Gazdaságtudományi és Vidékfejlesztési Kar
Vincze Szilvia (1 - 8. fejezet)
Debreceni Egyetem Gazdaságtudományi és Vidékfejlesztési Kar
Lektor:
Csatai Rózsa
Nyugat-Magyarországi Egyetem
Debreceni Egyetem, AGTC • Debrecen, 2013
© Kovács Sándor, 2013 Debreceni Egyetem
Gazdálkodástudományi és Vidékfejlesztési Kar
Pannon Egyetem Georgikon Kar
3
Kézirat lezárva: 2013. április 30.
ISBN 978-615-5183-44-7
DEBRECENI EGYETEM AGRÁR- ÉS GAZDÁLKODÁSTUDOMÁNYOK CENTRUMA
A kiadvány a TÁMOP-4.1.2.A/1-11/1-2011-0029 projekt keretében készült.
4
TARTALOMJEGYZÉK
Előszó ... 5
1. Halmazelmélet és számhalmazok ... 6
2. Relációk és függvények ... 15
3. Egyváltozós valós függvények ... 21
4. Sorozatok ... 33
5. Függvények határértéke és folytonossága ... 45
6. Differenciálszámítás és alkalmazásai ... 52
7. Mátrixok és determinánsok ... 64
8. Lineáris egyenletrendszerek ... 72
9. Vektorterek ... 78
10. A bázistranszformáció és alkalmazásai ... 85
11. Többváltozós függvények ... 91
12. Kombinatorika... 97
13. Valószínűségszámítás ... 103
14. Valószínűségi változók ... 112
15. Statisztikai alapfogalmak ... 124
16. Megoldások ... 136
17. Irodalomjegyzék ... 151
5
Előszó
A jegyzet a magyar felsőoktatás BSc képzésében résztvevő hallgatói számára készült a TÁMOP-4.1.2.A/1-11/1-2011-0029 sz. „A vidékfejlesztési és gazdasági agrármérnöki mesterképzési szakok és a feltétellel belépők felzárkóztatása, esettanulmányokon alapuló, gyakorlatorientált, modul rendszerű tananyagának fejlesztése, különös tekintettel az informatikai eszközök alkalmazására” című pályázat keretében. A gyakorlati jegyzet közvetlenül kapcsolódik a pályázat keretében készült elméleti jegyzethez. A példatár felépítésében követi az elméleti jegyzetet, és kiegészíti azt gyakorlati feladatok bemutatásával. A gyakorlati jegyzet elkészítésével igyekeztünk megkönnyíteni az elmélet értelmezését azok számára is, akiknek a matematika egy ijesztő világot jelent definícióival, tételeivel, azok bizonyításaival stb.
Célunk már az elméletei jegyzet összeállítása során is az volt, hogy a lehető legegyszerűbben, szemléletes módon jussunk el az alkalmazható matematikai módszerekhez. Fontosnak tartottuk azt, hogy a hallgatóinkat a lehető legegyszerűbb megfogalmazásokkal megismertessük azokkal a matematikai alapeszközökkel, amelyek a mezőgazdasági, közgazdasági, természettudományi, valamint informatikai tantárgyak elsajátításához nélkülözhetetlenek.
A gyakorlati jegyzet elkészítése során a fentiekben megfogalmazottakat tartottuk szem előtt. A példatár összefoglaló jellegű, ezekkel a feladatokkal az elméleti tananyagrészek figyelmes áttanulmányozása és a kapcsolódó mintafeladatok megoldása után érdemes foglakozni. Javasoljuk a jegyzetben szereplő összes feladat megoldását a tananyag biztos tudásához.
Debrecen, 2012. szeptember
a Szerzők
6
1. Halmazelmélet és számhalmazok
A halmazelmélet és számhalmazok kapcsán az elméleti fejezetben részletesen bemutattuk a főbb halmazműveleteket, valamint azok tulajdonságait. Definiáltuk a nevezetes számhalmazokat, megalapozva ezzel a matematika többi fejezetét. A matematikának a függvényektől kezdve a valószínűségszámítással bezárólag számos témakörében felbukkannak a halmazok, halmazműveletek, ezért elengedhetetlenül fontos ezek kellő ismerete. A függvény, illetve reláció fogalmának definiálása, valamint a művelet fogalma teljes mértékben a halmaz fogalmára épül. A Descartes- szorzat – ezen alapul a reláció és a koordinátarendszer, és így a függvények ábrázolása – is egy speciális halmaz., a vektortérhez hasonlóan. A halmazokra vonatkozó ismeretek nélkül a valószínűség fogalmának a bevezetése sem lenne kellően megalapozott, mivel az az eseményekre épül. Az események közötti műveletek pedig megfeleltethetők a halmazok közötti műveleteknek. A továbbiakban néhány egyszerű gyakorló példán keresztül mutatjuk be a halmazelmélet főbb műveleteit, majd komplex feladatokat tűzünk ki önálló megoldásra a példák alapján.
1.1. Példa. Döntsük el, hogy az alábbiak közül melyek határoznak meg matematikai értelemben vett halmazt:
H := { x | x valós szám és x2 = 4}
K := { a Debreceni Egyetem 50 m2-nél nagyobb helyiségei } L := { prímszámok }
M := { x | x páratlan természetes szám és x < 10}
N := { a világ legnagyobb kikötővárosai }
O := { x | x város és lakossága 2000. január 1-én több mint 500 000 fő}
Q := { tehetséges matematikusok}
Megoldás:
Egy halmaz akkor tekinthető adottnak, ha bármely dologról el tudjuk dönteni, hogy a halmazhoz tartozik-e vagy sem. Matematikai értelemben a példabeli H, K, L, M, O halmazt alkot, az N és a Q pedig nem határoznak meg halmazt.
1.2. Példa. Az alábbi halmazok közül adjon meg egyenlő halmazokat:
H := {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, K := {páratlan számok},
L := {n ≤ 20 | n természetes szám és páros}
Megoldás:
H = L, mivel elemenként egyenlők, a H K, mert nem azonos elemek alkotják.
7 1.3. Példa. Adjon két példát részhalmazra.
Megoldás:
(1) Az egész számok halmazának részhalmaza a páros számok halmaza.
(2) A háromszögek halmazának részhalmaza a szabályos háromszögek halmaza.
1.4. Példa. Adja meg a H = {1, 2, 3} halmaz összes lehetséges részhalmazainak halmazát, azaz a hatványhalmazt.
Megoldás:
P(H) = { , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}. Az üres halmaz bármely halmaznak része, így a H-nak is, és maga a H halmaz is részhalmaza (nem valódi) önmagának.
1.5. Példa. Adja meg a H = {1, 2, 3, 4, 5} és K = {3, 4, 5, 6, 7, 8} halmazok metszetét és unióját.
Megoldás:
H ∪ K ={1, 2, 3, 4, 5, 6, 7, 8}, mivel mindkét halmaz elemeit tartalmaznia kell az uniónak, és a közös elemeket csak egyszer soroljuk fel. H ∩ K ={3, 4, 5}, mivel ebbe a halmazba a közös, azaz mindkét halmazban megtalálható elemek tartoznak bele.
1.6. Példa. Tekintsük egy gazdaság állatállományából a következő halmazokat:
H = {magyartarka tehenek (200 db)},
K = {2.500 literes hozamon felüli magyartarka tehenek (120 db)}, L = {magyartarka-holstein fríz keresztezett tehenek (200 db)},
M = {2.500 literes hozamon felüli magyartarka-holstein fríz keresztezett tehenek (180 db)},
N = {2.500 literes hozamon felüli tehenek (300 db)}, Adja meg a H ∪ L; H ∩ K;
K ∪ M; H ∩ L; L ∩ N halmazokat.
Megoldás:
H ∪ L = {magyartarka, magyartarka-holstein fríz keresztezett tehenek (400 db)}, H ∪ K = H ={magyartarka tehenek (200 db)}, K ∪ M = N ={2 500 literen felüli
tehenek (300 db)},
H ∩ K = K ={magyar tarka tehenek, amelyek 2500 literen felüliek (120db)}, H ∩ L = ,
L ∩ N = M ={magyartarka-holstein fríz keresztezett tehenek, amelyek 2 500 literen felüliek (180 db)}.
8 1.7. Példa. Adjon példát diszjunkt halmazokra:
Megoldás:
(1) Legyen H = {páros számok} és K = {páratlan számok} halmaza. Ekkor a H és K diszjunkt halmazok.
(2) A tehenes példánkban a H és az L diszjunkt halmazok.
1.8. Példa. Az alaphalmazunk legyen a Szabolcs megyei almatermelő vállalkozók halmaza. A H halmaz tartalmazza azokat a vállalkozókat, akik Golden almát termelnek, a K halmaz azokat a vállalkozókat, akik Jonatán almát termelnek.
Halmazelméleti műveletekkel adja meg azon vállalkozók halmazát, akik (1) mindkettőt termelik
(2) legalább az egyiket termelik (3) nem termelnek jonatán almát
(4) nem termelnek sem Jonatán, sem Golden almát (5) legalább az egyik almát nem termelik
(6) pontosan az egyik fajta almát termelik Megoldás:
(1) H ∩ K (2) H ∪ K (3) Kc
(4) (H ∪ K)c = Hc ∩ Kc (5) (H ∩ K)c = Hc ∪ Kc (6) (H ∪ K) \ (H ∩ K)
1.9. Példa. Bizonyítsuk be, hogy (H ∪ K) ∩ L = (H ∩ L) ∪ (K ∩ L).
Megoldás:
Legyen (H ∪ K) ∩ L = A és (H ∩ L) ∪ (K ∩ L) = B.
Ha belátjuk, hogy A ⊆ B és B ⊆ A, akkor igaz, hogy A = B.
(1) Először lássuk be, hogy A ⊆ B.
Tegyük fel, hogy x ∈ (H ∪ K) ∩ L. Ez azt jelenti, hogy x ∈ (H ∪ K) és x ∈ L, vagyis x ∈ H vagy x ∈ K, és x ∈ L. Ha x ∈ H és x ∈ L, akkor x ∈ (H ∩ L).
Ha x ∈ K és x ∈ L, akkor x ∈ (K ∩ L). Így x ∈ (H ∩ L) vagy x ∈ (K ∩ L), azaz x ∈ (H ∩ L) ∪ (K ∩ L).
Ebből következik, hogy (H ∪ K) ∩ L ⊆ (H ∩ L) ∪ (K ∩ L).
9 (2) Most lássuk be, hogy B ⊆ A.
Legyen most x ∈ (H ∩ L) ∪ (K ∩ L). Ez azt jelenti, hogy x ∈ (H ∩ L), vagy
x ∈ (K ∩ L). Ha x ∈ (H ∩ L), akkor x ∈ H és x ∈ L. Ha x ∈ (K ∩ L), akkor x ∈ K és x ∈ L. Ennélfogva x ∈ H vagy x ∈ K, és x ∈ L. Így x ∈ (H ∪ K) és x ∈ L, azaz x ∈ (H ∪ K) ∩ L, így beláttuk, hogy (H ∩ L) ∪ (K ∩ L) ⊆ (H ∪ K) ∩ L.
Tehát a két halmaz egyenlő.
1.10. Példa. Legyen adott az U alaphalmaz és legyen H,K,L ⊆ U. Bizonyítsuk be, hogy az (1), (2) és (3) egyenlőségek fennállnak.
(1) H \ K = H \ (H ∩ K)
(2) H \ (K ∪ L) = (H \ K) ∩ (H \ L) (3) H \ (K ∩ L) = (H \ K) ∪ (H \ L) Megoldás:
(1) H \ (H ∩ K) = H ∩ (H ∩ K)c =H ∩ (Hc ∪ Kc) =
= (H ∩ Hc) ∪ (H ∩ Kc) = ∪ (H ∩ Kc) = H ∩ Kc = H \ K;
(2) (H \ K) ∩ (H \ L) = (H ∩ Kc) ∩ (H ∩ Lc) = (H ∩ Kc ∩ H) ∩ Lc = (H ∩ Kc) ∩ Lc = H ∩ (Kc ∩ Lc) = H ∩ (K ∪ L)c =H \ (K ∪ L);
(3) H \ (K ∩ L) = H ∩ (K ∩ L)c = H ∩ (Kc ∪ Lc) = (H ∩ Kc) ∪ (H ∩ Lc) = (H \ K) ∪ (H \ L).
Kitűzött feladatok
1. A következő definíciók közül melyek határoznak meg egyértelműen egy-egy halmazt?
a) A:
a c s o p o r t ta n u ló i
b) B:
M a g y a r o r s z á g v á r o s a i m a
c) C:
P ilin s z k y J á n o s v e r s e i
d) D:
a te m é s z e te s s z á m o k
e) F:
a z x2 5x 6 0 e g y e n le t v a ló s g y ö k e i
f) G:
a z x2 1 0e g y e n le t v a ló s g y ö k e i
g) H:
a p r ím s z á m o k
h) I:
a le g n a g y o b b p r ím s z á m
i) J:
n é h á n y p r ím s z á m
2. Alaphalmazunk legyen a H-B. megyei mezőgazdasági vállalkozók halmaza. Az A halmaz tartalmazza azokat a fenti halmazból, akiknek van traktoruk, a B halmaz tartalmazza
10
azokat a fenti halmazból, akiknek van kombájnuk. Írja fel halmazelméleti műveletekkel azon vállalkozók halmazát, akik
a) mindkettővel rendelkeznek,
b) legalább az egyikkel rendelkeznek, c) nincs traktoruk,
d) egyikkel sem rendelkeznek, e) csak traktorral nem rendelkeznek,
f) legalább egyikkel nem rendelkeznek, g) pontosan egyikkel rendelkeznek.
3. Adja meg a következő halmazok elemeit!
a) A:
a 1 0 0 n á l k is e b b n é g y z e ts z á m o k
b) B:
a 1 0 n é l k is e b b n é g y z e ts z á m o k
c) C a z x
x e g y e n le t p o z itív g y ö k e i
:
1 2
d)
az egyenlet pozitív gyökeinek aszáma
D 2
x 1 x :
e) E:
a z x2 2x 0 e g y e n lő tle n s é g e g é s z g y ö k e i
f) F:
a h á r o m je g y ű p á r a tla n s z á m o k h a lm a z a
g) G:
7 2 9 p o z itív o s z tó i
4. Válasszuk ki a következő halmazok közül az egyenlőket!
a) A:
a le g k is e b b p r ím s z á m
b) B:
e g y p r ím s z á m p o z itív o s z tó in a k s z á m a
c) C:
a z x3 2x2 0 e g y e n le t v a ló s g y ö k e i
d) D:
a z x3 2x2 0 e g y e n le t v a ló s g y ö k e in e k a s z á m a
e) E:
a 0 2, s z á m p á r
f) F:
a 1é s 3 k ö z é e s ő p á r o s s z á m o k
g) G:
a z x1 0 0 1e g y e n le t v a ló s g y ö k e i
h) H:
a z x 0 é s y 2 e g y e n le tű e g y e n e s e k m e ts z é s p o n tja in a k k o o r d in á tá i
i) I:
1n k ü lö n b ö z ő é r té k e i a h o l n te ts z ő le g e s p o z itív e g é s z s z á m, " "
11
5. Legyenek az A halmaz elemei 16 pozitív osztói, a B halmaz elemei 24 pozitív osztói, a
C halmaz elemei 12 pozitív osztói. Határozzuk meg az A B B, C C, A halmazokat.
Lesz-e a kapott halmazok között két egyenlő halmaz?
6. Adjon meg az A 10, 20, 30 halmazhoz olyan B C é s D, halmazt, hogy az alábbi összefüggések igazak legyenek! A B 10, 20, 30, 40, 50, A C 2 0 , A \ D . 7. Legyen A 2,1,0,1,2,3,4 és B
8 n á l n e m n a g y o b b p o z itív p á r o s s z á m o k
.Szemléltesse a halmazokat Venn-diagramon! Határozza meg az A B B, \ A
halmazokat!
8. Legyen A
tíz n é l k is e b b p o z itív e g é s z s z á m o k
, B 1,2,3,4,5,6,16,17,18,19,20 és C 1, 3,5,10,11,12,13,14,15, 20. Határozza meg az alábbi halmazok elemeit:
A B B, \ A C , A C \ B A C, \ !
9. Írja fel az 4, 5,6 halmaz összes részhalmazát!
10. Az M 1,2,3,4,5,6 halmaz A B é s C, részhalmazairól az alábbiakat tudjuk:
2 , 5, 6 , \ 2, 3, 4 , \ 1, 5
B A B C A C C B
A . Határozza
meg az A B é s C, halmazokat!
11. Tekintsük a következő halmazokat:
2 5 6 0, 0
x R x x x
A
x Z x 2 vel osztható egész szám
B
x R x 6k 1, k N
C
0
4 1 x x R x D
Állapítsa meg, hogy A B C, , és D halmazok közül melyik részhalmaza N -nek és melyik nem!
12. Adottak az
A n u llá r a v é g z ő d ő e g é s z s z á m o k ésB
5 te l o s ztha tó e g é s z s z á m o k
halmazok.Határozza meg a két halmaz különbségét!
13. Legyen az alaphalmaz H
x Z x 1 0
. Legyenek továbbá adottak a következő halmazok: A
x H n e g a tív s z á m o k
, B
x H p á r o s s z á m o k
,
C x H 4 g y e l o s ztha tó s z á m o k .
a) Határozza meg a B \C A, C A, B C halmazokat!
b) Határozza meg az a)-ban megadott halmazok számosságát!
c) Írjon fel a H -nak olyan részhalmazait, melyek egyenlő számosságúak!
12
d) Határozza meg a B C és B C halmazokat!
14. Adott a H x Z 0 x 25 alaphalmaz, valamint a következő halmazok:A
x H x p á r o s
,
B x H x e g y je g y ű s z á m ,C x H 8,9,10,11,12 .
Határozza meg az A B \C,A B
A C\
, C B
halmazok elemeit és számosságát!15. Az A
x Z x 3
és B
a 8 n á l n e m n a g y o b b n e m n e g a tív p á r o s s z á m o k
halmazokkal végezze el az alábbi műveleteket: A B A, B A, \B .
16. Legyen az alaphalmaz a H x Z 5 x 13 és az ezen értelmezett A B, és C
halmazok az alábbiak:
3, 2,0,3, 5,9
A
B x H x o s ztha tó 3 m a l
3
x H x
C
a) Készítsen Venn-diagramot a halmazokról!
b) Határozza meg az A C \B és B C halmazok elemeit és számosságát!
c) Műveleti jelek felhasználásával írja fel a H halmaznak olyan részhalmazait, melynek számossága 4.
17. Legyen adott az A
x R x2 2x 4 0
és B
x R x2 4x1 0
halmaz.Határozza meg az A B és A B halmazokat!
18. Határozza meg az A B halmazt, ha A x N 2x 4x 6 és
4 11 2 11
x N x x
B !
19. Az A és B halmazokról tudjuk, hogy A B 1,2,3,4,5,6 , A \B 2, 4, 6 ,
1,3
B
A . Határozza meg az A és B halmazt!
20. Hány elemű az alábbi két halmaz uniója illetve metszete?
A 7 te l o s z tha tó k é tje g y ű s z á m o k
B 3 m a l o s ztha tó k é tje g y ű s z á m o k
13
21. Egy mezőgazdasági üzemben bizonyos földterületre háromféle műtrágyát szórtak. Az első típusú műtrágyával 230, a második típusúval 170, a harmadik típusúval 190 hektárt szórtak meg. 100 hektárra első és második típusú, 70 hektárra második és harmadik típusú, 180 hektárra első és harmadik típusú műtrágya is került, 70 hektár területet mindhárom műtrágyával kezeltek. Hány hektár föld kapott műtrágyakezelést?
22. Egy osztályban három nyelvet tanulnak: angolt, németet és spanyolt. Mindenki tanul valamilyen nyelvet, de mindhárom nyelvet csak 1 tanuló tanulja. 12 olyan tanuló van, aki két nyelvet tanul. Angolul 15-en, németül 13-an, spanyolul 9-en tanulnak. Mennyi az osztály létszáma?
23. Egy repülőgépen 9 fiú, 4 lány, 5 magyar gyerek, 9 felnőtt férfi, 7 külföldi fiú, 14 magyar, 6 magyar férfi és 7 külföldi nő utazott. Hányan voltak a repülőgépen?
24. Egy munkahelyen 30-an dolgoznak. A dolgozók közül kilencnek van életbiztosítása, 16 dolgozónak pedig gépjármű-biztosítása, 8 dolgozónak nincs semmilyen biztosítása. Hány dolgozónak van mind a kétféle biztosítása? Hány dolgozónak van csak életbiztosítása?
25. Egy osztály létszáma 32 fő. Az osztályban angolul és oroszul tanulnak és mindenki tanul valamilyen nyelvet. Mindkét nyelvet kilencen tanulják. Bizonyítsa be, hogy angolul és oroszul nem tanulhatnak ugyanannyian!
26. Egy osztály létszáma 30. Az osztályban 3 nyelvet tanítanak: angolt, németet és franciát.
Azt tudjuk, hogy minden gyerek legalább egy nyelvet tanul. Angolul 20-an, németül 15- en, franciául pedig 7-en tanulnak. Pontosan két nyelvet összesen 6 diák tanul. Hányan tanulják mindhárom nyelvet?
27. Egy matematika versenyen két feladatot tűztek ki. Az első feladatot a tanulók 70%-a, a másodikat 60%-a oldotta meg. Minden tanuló megoldott legalább egy feladatot, és kilencen mindkét feladatot megoldották. Hányan indultak a versenyen?
28. Egy osztály 28 tanulója közül 8-an felvételizek matematikából, 6-an fizikából, és 4 tanuló mindkét tárgyból. Hányan nem felvételiztek egyik tárgyból sem?
29. Egy egyetem 500 hallgatója közül 300 tud oroszul, 200 angolul, 50 franciául, 20 tud oroszul és franciául, 30 tud angolul és franciául, 20 tud oroszul és angolul, 10 pedig mindhárom nyelven. Hányan tudnak legalább az egyik nyelven? Hányan vannak azok, akik egyik nyelvet sem beszélik?
30. Legyen A: 2, 1, 0,1, 2, 3, 4 és
B: a 8 n á l n e m n a g y o b b p o z itív p á r o s s z á m o k . Szemléltesse a halmazokat Venn- diagramon! Határozza meg az A B B, \ A halmazok elemit!
31. Legyenek az A B C, , halmaz elemi az alábbi gyümölcsnevek betűinek a karakterei.
A A L M A , B B A N Á N, C C I T R O M .
a) Határozza meg az A B C, , halmazok számosságát!
b) Határozza meg az A B \C halmaz elemeit!
14
c) Az elemek felsorolásával írja fel a B \ A halmaz összes részhalmazát!
32. Igazolja az X alaphalmaz A B C, , részhalmazaira az alábbi egyenlőségeket Venn- diagram segítségével.
a) A \A \ B B \B \ A
b) A \C \ B \C A \ B\C
c) A \C B \C A B\C d) A \C B \C A B\C
e) A B C A C B C f) A B A B
g) A B A B
h) A B A B A
i) A \B C A \B A \C
15
2. Relációk és függvények
Két halmaz elemei közötti kapcsolat matematikai leírása a relációval történik, melynek definiálásához szükség van a Descartes-szorzatra, ami két halmaz elmeiből vett rendezett elempárhalmaz. A Descartes-szorzat szemléltetése a derékszögű koordináta-rendszer segítségével történik, amely elvezet a függvények ábrázolásához.
A reláció voltaképpen a rendezett elempárhalmaz egy részhalmaza. Az egyértelmű relációk alkotják a függvényeket. Ebben a részben alakítjuk ki a függvény, illetve az inverz függvény fogalmát, valamint az összetett függvényeket. Sor kerül az értelmezési tartomány, értékkészlet megállapítására mind a relációkkal, mind a függvényekkel kapcsolatban. Az egyváltozós valós függvények osztályainak bemutatására, ábrázolására, jellemzésére csak a következő részben kerül sor.
2.1. Példa. Adjon példát relációkra úgy, hogy nem feltétlenül kell matematikai képletbe foglalható kapcsolatban gondolkodni.
Megoldás:
(1) A tér egyenesei és síkjai között a merőlegesség (2) A természetes számok halmazában az oszthatóság (3) Rokonsági kapcsolat (pl. szülő-gyerek)
(4) A sertésállomány nyilvántartása az egyed-fülszám alapján A (3) és (4) esetben nem foglalható matematikai képletbe a kapcsolat.
2.2. Példa. Tekintsük a H = {11, 13, 17} és K = {1, 2} halmazokat. Ezen halmazok Descartes-szorzata:
H×K = { (11,1), (11,2), (13,1), (13,2), (17,1), (17,2) }
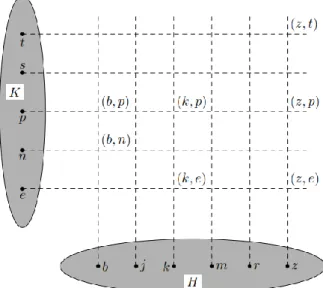
2.3. Példa. Legyenek adottak a következő halmazok: H = {b, j, k, m, r, z} és K ={e,n,p,s,t}. A tekintett reláció legyen
ϱ = {(b,n), (b,p), (k,e), (k,p), (z,e), (z,p), (z,t)}
Ábrázolja a relációt Descartes-féle derékszögű koordináta-rendszerben.
Megoldás:
A reláció Descartes-féle derékszögű koordinátarendszerben történő ábrázolásához tekintsük a 1. ábrát.
16
1. ábra: A ϱ reláció ábrázolása
Forrás: Bíró és Vincze (2000)
2.4. Példa. Határozzuk meg az alábbi ϱ reláció értelmezési tartományát, értékkészletét és inverzét!
H ={ 0, 1, 2 }, K ={ 0, 3, 5 },
ϱ ⊆ H × K és xϱy akkor és csakis akkor, ha x · y = 0.
Megoldás:
Mivel ϱ ={ (0,0), (0,3), (0,5), (1,0), (2,0) }
Dϱ = H, Rϱ = K, ϱ−1 = { (0,0), (3,0), (5,0), (0,1), (0,2) }.
Határozzuk meg az alábbi f reláció értelmezési tartományát, értékkészletét és inverzét!
A := { -5, 2, 3, 4, 5, 9 }, B := { -2, 1, 2, 3},
f ⊆ A × B és x f relációban áll y-nal akkor és csakis akkor, ha x + y = 7.
Megoldás:
Mivel f ={(4,3), (5,2), (9,-2)}
Dϱ ={ 4, 5, 9 }, Rϱ = {-2,2,3}, f−1 = {(3,4), (2,5), (-2,9)}.
2.5. Példa. Legyenek adottak a következő halmazok: H = { −2, −1, 0, 1, 2 } és K ={ −1, 0, 1, 2 } és L = { 0, 1, 2, 3, 4 } és az alábbi két reláció:
ϱ = { (h,k)H×K | |h| = k } ϱ’ = { (k,l)K×L | k + 3 = l } Adjuk meg a ϱ′ ◦ ϱ relációt!
17 Megoldás:
ϱ ={ (−2,2); (−1,1); (0,0); (1,1); (2,2) }, ϱ’ = { (−1,2); (0,3); (1,4) }.
Ekkor a definíció alapján: ϱ′ ◦ ϱ = { (−1,4); (0,3); (1,4) }.
2.6. Példa. Adottak az X = { −5, 2, 3, 4, 5, 9 } és az Y = { −2, 1, 2, 3 } halmazok és az f = { (x,y) X×Y | x + y = 7 } reláció. Állapítsuk meg, hogy az f reláció függvény-e!
Megoldás:
Mivel f = { (4,3); (5,2); (9,2) }, ami egyértelmű, azaz f függvény.
2.7. Példa. Döntsük el, hogy az alábbi relációk közül melyek függvények!
(1) P a prímszámok halmaza, f ⊆ P × P, és x f y pontosan akkor, ha x | y,
(2) A := { 0, 3, 5 }, B := { 1, 2, 5 }, f ⊆ A × B, és x f y pontosan akkor, ha x · y = 0, (3) f ⊆ N × N, és x f y pontosan akkor, ha 2x = y,
(4) f ⊆ Z × Z, és x f y pontosan akkor, ha x2 = y2, (5) f ⊆ N × N, és x f y pontosan akkor, ha x2 = y2, Megoldás:
Az (1)-beli f függvény, mert p,qP, p|q esetén p = q. A (2)-beli f nem függvény, mivel f = { (0,1);(0,2);(0,5) }. A (3)-beli f függvény, míg (4) nem függvény, mert pl. (1,-1)f és (1,1)f. Végül pedig az (5)-beli f függvény, mert negatív számokat nem tartalmaz N.
2.8. Példa. Tekintsük az X = { −2, -1, 0, 1, 2} és az Y = { 0, 1, 2 } halmazokat. Legyen adott a következő reláció f = {(x,y) X×Y | |x| = y}. Döntse el, hogy az f reláció függvény-e, ha igen, akkor invertálható-e.
Megoldás:
Az f = { (-2,2); (-1,1); (0,0); (1,1); (2,2) } reláció függvény, mivel egyértelmű. Az inverz reláció f-1 = { (2,-2); (1,-1); (0,0); (1,1); (2,2) } nem egyértelmű, így nem függvény, azaz f nem invertálható függvény.
2.9. Példa. Legyenek adottak a következő halmazok: X = { 1, 2, 3, 4, 5 } és az
Y = { 4, 5, 6, 7, 8 }. Tekintsük a g = {(x,y) X×Y | x + 1 = y} relációt. Döntse el, hogy a g reláció függvény-e, ha igen, akkor invertálható-e.
Megoldás.
A g = { (3,4);(4,5);(5,6) } reláció függvény, mivel egyértelmű. Az inverz reláció g-1 = { (4,3);(5,4);(6,5) } reláció is egyértelmű, így függvény, azaz g invertálható függvény.
2.10. Példa. Vizsgáljuk meg, hogy az f(x) = 2x-2 függvénynek van-e inverze, és ha van adjuk meg az inverz függvényt, és ábrázoljuk a függvényeket!
18 Megoldás:
Mivel az f függvény kölcsönösen egyértelmű, így van inverze. Az y = f(x)-ből fejezzük ki az x-e, majd hajtsunk végre változócserét, azaz:
y = f(x) y = 2x-2 y 1
2 1 2
2 y
x
.
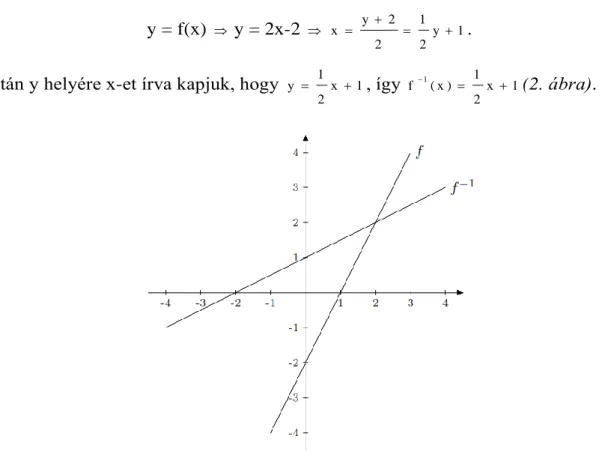
Ezután y helyére x-et írva kapjuk, hogy x 1 2 1
y , így x 1
2 1 ) x (
f1 (2. ábra).
2. ábra: A f függvény és inverzének grafikonja
Forrás: Bíró és Vincze (2000)
2.11. Példa. Döntsük el, hogy alábbi függvények közül melyek invertálhatók!
(1) f: R → R, f (x) = 5x − 3, (2) g: R → R, g (x) = 3x2, (3) h: R \ {0} → R, h (x) =
x 1
(4) k: R \ {−1} → R, k (x) =
x 1
x 1
Azokban az esetekben, amikor a függvény invertálható, határozzuk meg a függvény inverzét is!
Megoldás:
(1) Az f invertálható és inverze f−1: R → R, f−1 (x) = 1 2 x
(2) A g nem invertálható, mert például g(−1) = g(1) = 3, azaz (-1,3) g és (1,3) g .
(3) A h függvény invertálható és h−1 = h.
(4) A k függvény invertálható és k−1 = k.
19
2.12. Példa. Tudjuk, hogy a g(x) = x2 függvény nem kölcsönösen egyértelmű, így nincs inverze. Vegyük a g leszűkítését az R 0 = { x R | x ≥ 0 } halmazra, és legyen f függvény a következőképpen adott: f: R 0 → R, f(x) = x2. Vizsgáljuk meg, hogy f(x) invertálható-e, és adjuk meg az f függvény inverzét, majd ábrázoljuk f(x)-et az inverzével közös koordináta-rendszerben.
Megoldás.
Az f függvény már kölcsönösen egyértelmű, így biztosan van inverze:
y = x2 x = y változócsere után: y = x . f-1(x) = x (3. ábra).
3. ábra: Az f: [0,+ [ → R, f(x) = x2 függvény és inverzének grafikonja
Forrás: Bíró és Vincze (2000)
2.13. Példa. Határozzuk meg a g ◦ f függvényt az alábbi f és g függvények esetén:
(1) f: R → R, f(x) = x2 és g: [0,+ [ → R, g(x) = 2 x
(2) f: ]0,1[ → R, f(x) =
x 2
1 és g: [0,+[ → R, g(x) = 2
x 2
1
(3) f,g: R → R, f(x) = 1 - 2x2 és g: [0,+ [ → R, g(x) = 2
x 2
1
Megoldás:
(1) g ◦ f: R → R, (g ◦ f) (x) = g(f(x) = 2 x2 2x (2) g ◦ f: ]0,1[ → R, (g ◦ f) (x) = 2x2
(3) g ◦ f: R → R, (g ◦ f) (x) =
3 x 4 x 4
1
2
4
20 Kitűzött feladatok
1. Legyen A 1,3,5,7,9 és B 2, 4, 6, 8 . Ábrázolja derékszögű koordináta- rendszerben az A B halmazt!
2. Legyen A 1, 2 , B 1, 2,3 . Írja fel az alábbi halmazokat:
A B B A
A B \ B A
3. Határozza meg az alábbi relációk értelmezési tartományát, értékkészletét, majd ábrázolja őket derékszögű koordináta-rendszerben! Döntse el, hogy melyik reláció függvény!
Határozza meg, hogy melyik invertálható és írja fel az inverzét is!
a) A 5,2,3,4,5,9, B 2,1, 2, 3és
x y, A B x y 7
.b) A 0,1, 2, B 0, 3,5és x,y A B xy 0.
c) A 2,1,0,1,2,3, B 2, 1, 0,1 és
, 1
x y A B x y
.
d) A 1, 2,3,4,5, B 2, 4,6,8,10és
x, y A B x y
e) A 2, 1, 0,1, 2, B 0,1, 2 és
x y, A B x y
.4. Adottak a 1 és 2 relációk. Határozza meg a 1 2reláció elemeit!
a) A 1,2,3,4,5 , B 2, 4, 5 , C 2,4,8,16,32,64,128 .
x y AB x y
,
1 , 2
y,z BC y2 z
. b) A 2,1,0,1,2 , B 1,0,2 , C 0,1, 2,3, 4 .
x y A B x y
,
1 , 2 y,z BC y 3 z . c) A 2,3,4 , B 2, 4, 6,8,10 ,
0,1, 2,3
C .1
x,y A B x y
,
y z
C B z y
2
2 ,
.
21
3. Egyváltozós valós függvények
Az elemi függvénytípusok és grafikonjaik ismerete elengedhetetlen mind a gyakorlati élet szempontjából, mind a matematika további gyakorlati részeinek bemutatása végett. Ebben a fejezetben gyakoroljuk a függvények ábrázolását és jellemzését értelmezési tartomány, értékkészlet, monotonitás, korlátosság, szélsőérték, zérushely, inflexiós hely, konvexitás, paritás tekintetében. Külön feladattípus vonatkozik a zérushelyek keresésére, amelyre számos eljárás létezik (intervallum-felezés, Horner elrendezés). A gyakorlatban többnyire nem magukkal az elemi függvényekkel találkozunk, hanem azok valamilyen transzformáltjával (eltolás, tükrözés, nyújtás, stb…). A különböző függvénytípusok transzformálására külön gyakorlati példákat fogunk nyújtani. Az elemi függvények, illetve transzformáltjaik grafikonjai ismeretében kellő megalapozottsággal ismerkedhetünk meg a későbbiekben a függvények differenciálszámításával és a többváltozós függvényekkel.
3.1. Példa.
(1) Határozzuk meg az f(x) = x2 + 3x − 4 függvény zérushelyeit!
Megoldás:
Ez a függvény egyszerűen felírható a következő alakban:
f(x) = x2 + 3x − 4 = (x + 4)(x − 1), amelyből könnyen leolvasható, hogy az x1 = −4 és az x2 = 1 pontok a zérushelyek. Ezek a zérushelyek megkereshetők a másodfokú egyenlet megoldóképletével is, most azonban Horner elrendezéssel fogjuk megkeresni a megoldásokat. A megoldásokat -4 osztói között célszerű keresnünk (a nulla, -3, 3 nem osztói a -4-nek) (1. táblázat).
1. táblázat: Az f(x) = x2 + 3x – 4 függvény Horner-táblázata
x 1 3 -4
-4 1 -1 0
-2 1 1 -6 -1 1 2 -6
1 1 4 0
2 1 5 6
4 1 7 24
Forrás: Bíró és Vincze (2000)
Tehát f(-4) = 0 és f(1) = 0, azaz a -4 és az 1 helyen zérushelye van f(x)-nek.
(2) Határozzuk meg az f(x) = x3 − 3x + 2 függvény zérushelyeit!
Megoldás:
Egyszerű helyettesítéssel (2 osztóival) ellenőrizhető, hogy a p(x) = x3 − 3x + 2 függvénynek két zérushelye van, az x1 = 1 és az x2 = -2. Egy harmadfokú polinomnak az algebra alaptétele alapján 3 gyökének kell lennie. Mivel csak két gyököt kapunk, az egyik gyöknek kétszeres gyöknek kell lennie. A Horner táblázatból önmagában nem
22
derül ki ilyen esetekben, melyik a kétszeres gyök. Ezért polinom osztással fogjuk megkeresni a gyököket, de a Horner táblázatot is felhasználjuk és bemutatjuk (2. táblázat). Célszerű a megoldást a 2 osztóira keresni (a nulla azért maradt ki a táblázatból, mert nem osztója 2-nek).
2. táblázat: A p(x) = x3 − 3x + 2 függvény Horner-táblázata
x 1 0 -3 2
-2 1 -2 1 0
-1 1 -1 -2 4
1 1 1 -2 0
2 1 2 1 4
Forrás: Saját szerkesztés
Mivel p(-2) = 0 és p(1) = 0, ezért a -2 és 1 helyen p(x)-nek zérushelye van. A megoldást polinom osztással fogjuk keresni, de felhasználjuk a 2. táblázat eredményeit. A Horner táblázat szerint x = 1 helyen gyöke van a p(x)-nek ezért a gyöktényezős felbontásában szerepel az (x – 1) tényező. Első lépésben ezzel a polinommal osztunk:
(x3 – 3x + 2) : (x – 1) = x2 + x – 2 x3 – x2
x2 – 3x x2 – x
– 2x + 2 – 2x + 2 0
Ekkor már csak a g(x) = x2 + x – 2 polinom zérushelyeit kell megkeresni, amely történhet másodfokú egyenlet megoldó képletével is, amelyből megkapható a másik két gyök: 1 és -2. Osszuk tovább a g(x) polinomot a Horner táblázat alapján az
x – (-2) = x + 2 tényezővel:
(x2 + x – 2) : (x + 2) = x – 1 x2 + 2x
-x – 2 x + 2 0
Azaz a p(x) = x3 − 3x + 2 függvény felírható (x – 1 ) (x – 1) (x + 2) alakba, és az x = 1 kétszeresen gyök.
3.2. Példa. Döntsük el intervallumfelezéssel, hogy az f(x) = x3 − 3x2 − x + 3 függvénynek van-e zérushelye a [−4,4] intervallumban, és ha van, akkor adjuk meg egy zérushelyét.
Megoldás:
Mivel f(−4) = −105, f(4) = 15, azaz f(−4) < 0, f(4) > 0 így a függvénynek biztosan van legalább egy zérushelye a [−4,4] intervallumban. Vegyük az intervallum felezőpontját, ez a 0 pont, f(0) = 3, mivel f(0) > 0, így a [−4,0] intervallumban folytatjuk az eljárást. A [−4,0] intervallum felezőpontja a −2 pont, és f(−2) = −15,
23
azaz f(−2) < 0, így a [−2,0] intervallumban folytatjuk az eljárást, ennek felezőpontja az x = −1, amire f(−1) = 0, ami azt jelenti, hogy megtaláltuk az f függvény egy zérushelyét.
3.3. Példa. Határozza meg az alábbi függvények értelmezési tartományát!
(1) f(x) = ln(1 – x) (2) g(x) = x2 – 2 (3) h(x) =
1 x
1
(4) y = 1 x2
Megoldás:
(1) a logaritmus függvény változója pozitív valós szám (>0), vagyis 1-x > 0 x <1 és xR .
(2) x-re semmi kikötés nincs, xR .
(3) a nevezőben nem állhat 0, mivel 0-val való osztást nem értelmezünk x – 1 0, így x 1, xR .
(4) a négyzetgyök alatt csak 0, vagy annál nagyobb valós szám állhat 1– x20 , így 1 x2 . Ebből: -1 x 1, xR .
3.4. Példa. Ábrázolja és jellemezze monotonitása és szélsőértéke szempontjából a függvényeket:
(1) f(x) = x3 (2) g(x) = -x3 (3) h(x) =
2 x
2 x 2
2 x
, , ,
x 2 x
Megoldás:
(1) Az f(x) = x3 függvény az egész értelmezési tartományán szigorúan monoton növekedő (4. ábra), mivel x1 < x2 esetén f(x1) < f(x2) teljesül.
24
4. ábra: Az f(x) = x3 függvény grafikonja
Forrás: Bíró és Vincze (2000)
Az f(x) függvénynek nincs szélsőértéke az értelmezési tartományán.
(2) A g(x) = -x3 függvény az egész értelmezési tartományán szigorúan monoton csökkenő, mivel x1 < x2 esetén f(x1) > f(x2) teljesül. A függvény grafikonja az f(x) = x3 függvény grafikonjának az x tengelyre való tükrözésével kapható (5. ábra).
5. ábra: A g(x) = -x3 függvény grafikonja
Forrás: Bíró és Vincze (2000)
A g(x) függvénynek nincs szélsőértéke az értelmezési tartományán.